引用本文
李得恺, 张长胜, 杨雪松. 融合多策略改进的黏菌优化算法. 模式识别与人工智能, 2023,36(7): 647-660
LI Dekai, ZHANG Changsheng, YANG Xuesong. Improved Slime Mould Algorithm Fused with Multi-strategy. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(7): 647-660.  
Doi: 10.16451/j.cnki.issn1003-6059.202307006
Permissions
Copyright©2023, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
融合多策略改进的黏菌优化算法
李得恺1, 张长胜1, 杨雪松1
1.昆明理工大学 信息工程与自动化学院 昆明 650504
通讯作者:

张长胜,硕士,副教授,主要研究方向为复杂工业过程建模、智能优化算法.E-mail:122832170@qq.com.

作者简介:

李得恺,硕士研究生,主要研究方向为智能优化算法、图像处理.E-mail:2531026098@qq.com.

杨雪松,硕士研究生,主要研究方向为图像处理、智能优化算法.E-mail:2305307269@qq.com.

收稿日期: 2023-05-12 接受日期: 2023-07-29
资助项目: 国家自然科学基金项目(No.51665025)资助
摘要

针对黏菌优化算法(Slime Mould Algorithm, SMA)的寻优过程存在收敛效率较低、容易陷入局部最优解等问题,文中提出融合多策略改进的黏菌优化算法(Improved SMA Fused with Multi-strategy, MISMA).引入Halton序列,丰富初始种群的多样性,提升算法寻优的遍历性和收敛精度.融入差分变异思想,改进算法的全局位置更新公式,强化全局探索能力,增强算法的持续寻优性能.糅合改进收敛因子和精英选择机制的局部搜索策略,提升算法的局部开采能力,更好地平衡算法的全局探索与局部开发进程.基于动态边界的透镜成像学习策略改善个体的质量,加强算法反早熟及摆脱局部最优解的能力.在13个基准函数及部分CEC2014测试函数上的数值仿真实验表明,MISMA具有较强的鲁棒性.此外,在光伏电池组件模型参数优化实验上进一步验证MISMA在处理实际工程优化问题时的优越性及适用性.

关键词: 黏菌优化算法(SMA); Halton序列; 差分变异; 收敛因子; 透镜成像学习; 动态边界
中图分类号:TP301.6
Improved Slime Mould Algorithm Fused with Multi-strategy
LI Dekai1, ZHANG Changsheng1, YANG Xuesong1
1. Faculty of Information Engineering and Automation, Kunming University of Science and Technology, Kunming 650504
Corresponding author:
ZHANG Changsheng, master, associate professor. His research interests include complex industrial process modeling and intelligent optimization algorithms.

About Author:
LI Dekai, master student. His research interests include intelligent optimization algorithms and image processing.
YANG Xuesong, master student. His research interests include image processing and intelligent optimization algorithms.

Fund:National Natural Science Foundation of China(No.51665025)
Abstract

The slime mould algorithm(SMA) yields low convergence efficiency and is easily dropped into local shackles. To address these shortcomings, an improved slime mould algorithm fused with multiple strategies(MISMA) is proposed.The Halton sequence is introduced to enrich the diversity of the initial population, and consequently the ergodicity and convergence precision of the algorithm are improved.The differential variation idea is employed to modify the global position update equations and enhance the global exploration capability and the continuous optimization performance.The local search strategy combining convergence factor and elite selection mechanism is ameliorated to improve the local development capacity of the algorithm. Thus, the global search performance and local exploitation capability of the algorithm are well balanced. The lens imaging learning strategy based on dynamic boundary is proposed to improve the individual quality and the capability of the algorithm avoiding prematurity and getting rid of local constraints.Numerical simulation experiments of 13 benchmark functions and some CEC2014 test functions show the strong robustness of MISMA.Moreover, the superiority and applicability of MISMA for dealing with practical engineering optimization problems are verified through parameter optimization experiments of the PV module model.

Key words: Slime Mould Algorithm(SMA); Halton Sequence; Differential Mutation; Convergence Factor; Lens Imaging Learning; Dynamic Boundary

在人工智能及大数据时代背景下, 大规模工程优化问题的复杂化计算亟需解决, 而面对高维、非线性和局部多极值全局优化问题时, 传统优化方法的求解效果并不理想.为了解决这一困境, 学者们提出结合蒙特卡洛式和启发式寻优的元启发式算法, 兼顾全局探索性能和局部开发能力, 能在一定时间或精度内实现对复杂问题最优解的探寻.

根据搜索机理可将结合蒙特卡洛和启发式寻优的元启发式算法大致归为三类.1)基于进化机制.例如:遗传算法[1]通过模拟生物进化时染色体中遗传物质进行的选择、交叉和变异等操作迭代更新解集合, 确定最优解.2)基于物理现象或数学模型.例如, 万有引力搜索算法[2]和正弦余弦算法[3]分别根据万有引力定律、正弦余弦函数完成搜索过程摹仿.3)基于群体智能.例如, 粒子群优化算法[4]模拟鸟群的捕食行为, 构建迭代寻优机制, 搜寻问题最优解.

Li等[5]提出黏菌优化算法(Slime Mould Algori-thm, SMA), 是一种基于群体智能实现的元启发式算法, 通过模拟黏菌的觅食过程实现优化目的.SMA简单、容易实现、调节参数较少、寻优精度较高, 一经提出便引起学者们的广泛关注, 目前已在电力系统最优无功功率调度[6]、图像分割[7]及特征参数识别[8]等诸多工程实践中得到应用.然而在解决众多优化问题, 尤其对于具有多局部极值、高维较复杂的问题时, SMA存在算法收敛速度较慢和容易陷入局部最优极值等缺点.

为了改善SMA的综合寻优性能, 学者们进行大量的改进.1)引入优秀算子.Naik等[9]提出ESMA(Equilibrium SMA), 引入均衡优化算法中的“平衡池思想”, 强化算法的搜索性, 规避局部最优解.Naik等[10]提出AOSMA(Adaptive Opposition SMA), 在位置更新中使用最优个体替换一个随机个体, 确保利用阶段的最大化, 同时自适应采取反向学习策略, 丰富种群的多样性.Tang等[11]提出MSMA, 增加种群多样性, 并使用螺旋搜索策略, 帮助SMA摆脱局部最优.2)与其它优势算法结合.Ö rnek等[12]将正余弦算法融入SMA, 加强SMA的全局最优搜索和逃离局部最优极值的能力.Houssein等[13]提出SMA-AGDE(SMA Combined to Adaptive Guided Differential Evolution Algorithm), 将AGDE融入SMA, 采用其变异策略增强SMA的局部搜索能力和群体的多样性, 避免算法过早收敛.3)改进寻优机制及参数动态调整策略.Naik等[14]提出LSMA(Leader SMA), 借鉴“头狼思想”改进阶段位置更新方程, 利用决策层最优黏菌个体的优势信息引导群体演化, 强化算法的全局探索性能, 提高收敛精度.Ö rnek等[12]提出基于对数的非线性衰减a参数, 控制策略协调算法探索和开采能力.

上述研究分别从不同角度剖析SMA, 但鲜有研究针对SMA寻优演化过程单一、缺乏变异机制而极易导致算法陷入局部最优解的固有缺陷进行改进, 也未聚焦最优解更新过程中的劣质解对SMA迭代寻优的影响, 且部分研究中改进算法的时间复杂度远超SMA.此外, SMA在求解高维多峰的复杂优化问题时的优化性能仍不够理想.

基于上述分析, 本文从种群初始化、全局探索、局部开发和跳出局部最优这四个角度改进SMA, 提出融合多策略改进的黏菌优化算法(Improved SMA Fused with Multi-strategy, MISMA).引入Halton序列, 丰富初始种群的多样性, 提升算法寻优的遍历性和收敛精度.融入差分变异思想, 改进算法的全局位置更新公式, 强化全局探索能力, 增强算法的持续寻优性能.糅合改进收敛因子和精英选择机制的局部搜索策略, 提升算法的局部开采能力, 更好地平衡算法的全局探索与局部开发进程.基于动态边界的透镜反向学习策略改善个体的质量, 加强算法反早熟及摆脱局部最优解的能力.在13个基准函数及部分CEC-2014测试函数上的数值仿真实验表明, MISMA具有较强的鲁棒性.此外, MISMA优化辨识的光伏电池组件模型最优参数组具有最小的均方根误差值, 进一步验证MISMA在处理实际工程优化问题时的优越性及适用性.

1 黏菌优化算法

黏菌优化算法搜索空间的解表示黏菌个体的位置, 拟优化目标抽象为黏菌位置的优劣程度, 个体位置的更新过程模拟黏菌的移动行为, 并经历接近食物、包围食物和抓取食物三个阶段.

阶段1)接近食物.黏菌根据空气中的气味逼近食物, 食物浓度越高, 黏菌重量越大; 反之, 黏菌重量减轻, 转向探索其它区域.该阶段的数学描述如下:

Xi, j(t+1)=

Xbest, j(t)+vb(WXA, j(t)-XB, j(t)), r< pvcXi, j(t), r≥p

p=tanh|S(i)-DF|, i=1, 2, …, N. (1)

其中:t表示当前代标识; X表示黏菌位置; Xbest, j表示当前代最优黏菌个体在第j维的位置; XA、XB表示第t次迭代时随机选择的黏菌个体; vb模拟黏菌种群中个体信息的交互过程, vb~U(-a, a, 1, d), 服从[-a, a]的均匀分布; vc模拟黏菌对自身的保留, vc~U(-b, b, 1, d), 服从[-b, b]的均匀分布; r表示[0, 1]内的随机数; N表示黏菌种群的规模; S(i)表示第i个黏菌的适应度值; DF表示全局最优黏菌的适应度值; W表示黏菌随机个体的权重因子.

阶段2)包围食物.黏菌联结多个食物源, 并在食物源之间建立粗细不一的静脉网络.当静脉接近食物源时, 黏菌体内发出的信号刺激内部生物振荡器产生传播波, 促进静脉的细胞质流动.接触到的食物浓度越高, 波信号越强, 细胞质流动越快, 静脉越厚, 反之静脉越薄.此阶段的数学描述如下:

Xi, j(t+1)=

r1(ub-lb)+lb, r1< zXbest, j(t)+vb(WXA, j(t)-XB, j(t)), r2< pvcXi, j(t), r2≥p(2)

其中:ub、lb分别表示搜索空间的上界和下界; r1、r2均表示[0, 1]内的随机数; 转换概率z调节算法的全局搜索和局部搜索, 文献[5]的参数实验中已验证, z=0.03时, 算法的寻优表现最佳, 故本文同样设置

z=0.03.

阶段3)抓取食物.振荡器产生传播波, 改变脉络中的细胞质流动.通过W、vb、vc模拟振荡频率及静脉厚度, 黏菌在食物浓度低时缓慢接近食物, 找到优质食物时更快接近并抓取食物.W的表达式如下:

W(SmellIndex(i))= 1+rlg(bF-S(i)bF-wF+1), 1≤i≤N21-rlg(bF-S(i)bF-wF+1), N2< i≤N

其中:bF表示当前代中最优适应度值, wF表示当前代中最差适应度值; SmellIndex=sort(S), 表示排序后的适应度值; r表示[0, 1]内均匀随机数; vb的取值范围为[-a, a]; vc的取值范围为[-b, b],

a=arctan⁡arctanh(1-tMax_iter)

b=1-(tMax_iter)

Max_iter表示最大迭代次数.

2 基于多策略改进的黏菌优化算法

依据算法的仿生原理可知, SMA的寻优机制存在的不足严重制约其寻优性能, 本文综合多种策略改进SMA.

2.1 基于Halton序列的种群初始化

针对SMA采用rand随机初始化种群, 容易导致种群多样性不足、算法搜索速度较慢的问题, 本文采用统计学的拟蒙特卡洛方法中的低差异序列Halton[15]初始化黏菌种群.Halton产生具有特定规则分布的确定性超均匀分布序列, 并载波至解空间, 使个体的分布更均匀, 提高初始解的覆盖率; 同时增加初始种群的多样性和算法的全局探索性, 提升算法规避局部极值的能力和搜索效率.

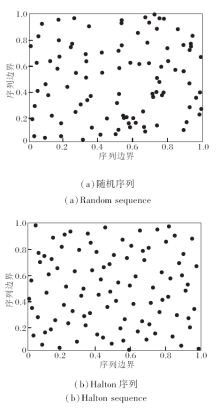
随机序列与以3和5为基的Halton序列的二维分布对比结果如图1所示.由图可知, 相比随机序列, Halton序列并未出现序列值重叠的现象, 表明将其载波至初始空间, 可增加多样性, 有效提升初始种群的质量.

图1 二维初始序列分布Fig.1 Initial sequence distribution in two dimensions

Halton序列的产生过程如下.给定整数n表示成某个质数p的数位和形式, 并将这些数位倒序后依次放置于小数点后, 组成以p为基的形式, 由此重构出一组[0, 1]内的均匀分布且无重复的序列.

n在d维空间的Halton序列值如下所示:

H(n)=[φ 1(n), φ 2(n), …, φ d(n)]. (3)

其中:任意整数

n=∑i=0mbipi=bmpm+bm-1pm-1+…+b1p1+b0∈ [1, N],

质数p≥ 2, 常数bi∈ [0, 1, …, p-1], φ (n)表示反序函数,

φ (n)=(0.b0b1…bm)p=∑i=0mbip-i-1= b0p-1+b1p-2+…+bmp-m-1.

2.2 融入差分变异策略的全局搜索

式(2)中新个体在全局范围内通过随机方式产生, 并且个体缺乏对种群中最优个体良好经验的继承和学习机制, 个体进化具有较强的盲目性, 导致搜索全局最优解的计算量进一步增加, 降低算法收敛速度.针对这一缺陷, 本文基于差分进化算法中的经典算子DE/best/2思想, 在SMA的全局搜索部分融入差分变异策略.一般而言, SMA在全局搜索时具有较大的搜索步长, 有利于加快寻优速度, 但容易使算法在执行过程中跳过全局最优解, 降低算法搜索速度和收敛精度.故引入权重因子δ 控制算法的演化速度, 同时利用贪婪机制对比新旧个体适应度值用于获取较优解.经变异处理后的全局搜索策略如下:

Xnew, j(t+1)=Xi, j(t)+δ r(Xbest, j(t)-Xi, j(t)+XC, j(t)-XD, j(t)), (4)

Xi, j(t+1)=Xnew, j(t+1), f(Xnew, j(t+1))≤f(Xi, j(t+1))Xi, j(t+1), f(Xnew, j(t+1))> f(Xi, j(t+1))(5)

其中, C、D分别为当前种群随机选取个体的下标值;

δ =δ 0-tMax_iter,

根据调试经验建议设置δ 0的取值范围为1~1.5.

从式(4)可以看出:在可行域范围内进行全局扰动的基础上, 引入的两组差异矢量可进一步增加种群个体间的差异性, 提升算法对多维空间的探索能力.另外, 在算法初始阶段, 个体间距较大, 权重简化为δ 0·rand, 此时搜索步长较长, 算法能够在全局范围内进行寻优, 一定程度上提高算法的全局探索能力, 防止算法早熟收敛.在算法迭代后期, 个体间距较小, 步长大幅缩小, 权重简化为(δ 0-1)rand, 保证算法在当前位置的邻域范围内深度挖掘.

2.3 结合改进收敛因子和优质解选取机制的局部搜索

式(1)中r< p时的局部搜索扰动项

vb(WXA-XB)

降低算法的搜索效率; r≥ p时的局部精细搜索过程利用父代中的所有个体进行更新, 未聚焦于最优解的邻域附近, 造成深度开采的不足; 调节收敛因子a平衡全局探索和局部开发.针对上述分析, 本文分别改进两个局部搜索过程:在r< p时融入凹形下降型(Concave Descending Form, CaDF)改进收敛因子aCaDF, 动态调整算法由全局搜索向局部开采的过渡过程, 在迭代前期快速收敛至最优解附近, 在迭代后期小幅逼近最优解, 并去掉W、利用Xbest取代XB.在r≥ p时采用优势解选择机制, 加速SMA收敛并提高收敛精度.改进后的局部搜索为:

Xi, j(t+1)=Xbest, j(t)+vb(XA, j(t)-Xbest, j(t)), r< pvcXSmellIndex(B), j(t), r≥p(6)

其中:XSmellIndex(B)表示按优选机制挑选的优势个体位置, 下标值B为[1, Num]内的整数,

Num=Ceil((1-N2)⋅tMax_iter+N2)

Ceil(·)表示取整; 改进后的vb取值范围为[-aCaDF, aCaDF], 服从[-aCaDF, aCaDF]的均匀分布,

aCaDF=eMax_iter-t/Max_iter-1e-1k(7)

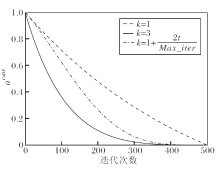
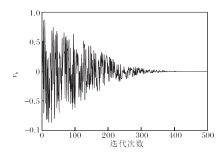
在算法迭代初期, 种群内个体的差异性较大, 根据非线性递减概率规则r< p, MISMA采用式(6)中r< p时的表达式进行局部寻优的概率较大, 此时MISMA充分利用历史最优信息指导搜索过程, 促进搜索精度提升.在算法演化后期, 个体间的差异性降低, 数值p减小, MISMA利用式(6)中r≥ p时的表达式表示的局部搜索过程在小范围内精细搜索最优解, 此时个体继承和学习优势个体的良好经验, 并对当前代的最优个体的邻域范围进行深度挖掘, 从而提高寻优精度.改进收敛因子aCaDF及相应的震荡系数vb变化曲线分别如图2和图3所示.

图2 aCaDF变化曲线Fig.2 Variation of aCaDF

图3 vb变化曲线Fig.3 Variation of vb

2.4 基于动态边界透镜反向学习的局部解改进策略

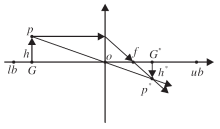
在SMA最优解更新过程中, 如果局部最优解劣于全局最优解, 继续将父代最优解保留为全局最优解, 而不对未进入下一轮迭代的局部最优解进行任何改善, 继续迭代, 由此增加算法搜索全局最优解的计算量, 降低收敛速度, 容易造成算法的收敛精度不高.为了解决此不足, 本文提出融入动态边界的透镜反向学习策略, 改进淘汰的局部最优解, 即在算法进入下次迭代之前, 若父代个体的质量未得到改善, 执行动态边界透镜反向学习策略, 改进当前代中未进入下一次迭代的最优解.透镜成像反向学习策略由龙文等[16]根据凸透镜成像的原理而提出, 并通过调整缩放因子动态获取新个体, 改善迭代过程中的种群质量, 进一步降低算法陷入局部最优解的几率.策略原理如图4所示.

图4 透镜成像反向学习策略原理图Fig.4 Schematic diagram of opposition-based learning for lens imaging

图4所示二维空间内的单个元素G为横轴上高度为h的物体p的投影, 位于0.5(lb+ub)处(原点o)放置一个焦距为f的凸透镜, 反向元素G*的求取过程模拟p通过透镜所呈高度为h*的倒像p*向X轴投影, 则透镜成像反向学习策略的数学模型如下:

0.5(ub+lb)-GG*-0.5(ub+lb)=hh*,

其中, 缩放因子γ=h(h*)-1.进一步, 有

G*=ub+lb2+ub+lb2γ-Gγ.

将其推广至d维空间, 同时结合动态边界跟踪搜索模式产生新个体, 未进入下次迭代的局部最优解:

Xnew, j(t+1)=ub'j+lb'j2+ub'j+lb'j2γ-Xpbest, j(t)γ, (8)

其中, Xpbest表示在第j维空间更新的反向位置, 动态上界ub'=max(Xi), 动态下界lb'=min(Xi).若更新后的新解优于父代最优个体, 将其更新为全局最优解, 否则继续保留.

由此可以看出:融入透镜反向学习改进的局部解更新策略在充分利用本次迭代的计算资源的前提下, 增强算法的局部逃逸性能, 强化算法的全局搜索能力, 进一步提高寻优精度.其次, 将透镜反向学习策略与动态边界跟踪搜索模式结合以保存搜索经验, 将个体定位在逐步缩小的搜索区域中, 产生的新个体位置距全局最优个体Xbest更近, 避免种群个体的质量较差导致的算法的收敛速度变慢的问题.另外, 改进策略是对劣质局部最优解自身信息的突变, 该操作不受迭代过程的影响, 无论在迭代前期还是迭代后期均能使个体有效跳出当前位置, 强化算法对局部最优解的逃逸能力.

2.5 算法步骤

根据2.1节~2.4节描述的算法改进策略, 本节给出MISMA的具体步骤.

1)设置算法种群数量N、最大迭代次数M、空间维度d等初始参数.

2)采用Halton序列初始化种群, 生成N× d维矩阵.

3)算法进入循环阶段.返回超出搜索空间的个体, 计算每个黏菌个体的适应度值并排序.

4)按适应度值更新最优黏菌位置.若子代最优个体适应度值小于父代最优个体, 更新, 否则按式(8)生成反向个体, 重新对比适应度值并更新最优个体.

5)按式(7)更新改进非线性收敛因子aCaDF.

6)若r< z, 按式(2)和式(4)执行全局搜索, 并按照式(5)更新适应度值较优的种群个体.

7)若r> z, 按式(6)执行局部搜索, 记录每代的最优个体位置及其适应度值.

8)若当前迭代次数小于最大迭代次数, 重复执行3)~7), 直至算法达到最大迭代次数, 输出最优个体的位置及适应度值.

2.6 时间复杂度分析

2.1节~2.4节系改进策略的有机融合, 构成MISMA的主要框架.这些策略实现简单, 但改善效果显著, 在不同进程中相互协调SMA的整体性能.下面分析SMA和MISMA的时间复杂度.

在SMA中, 算法的种群规模设为N, 求解问题的维数设为d, 依据算法描述和时间复杂度计算规则, 假设目标函数为f(x), 初始化参数时间为t0, 每维产生随机数的时间为t1, 则种群初始化阶段的时间复杂度表示如下:

T1=O(t0+Nt1d)=O(d).

在进入迭代后, 边界计算时间为t2, 适应度值计算时间为f(d), 排序时间为t3, 对比并更新最优适应度值和最优解的时间为t4, 更新每维权重的时间为t5, 则该阶段时间复杂度表示如下:

T2=O(N(f(d)+t2)+t3+t4+(lgN)t5d)=O(f(d)+d).

在循环搜索阶段, 全局搜索按式(2)进行全局搜索的计算时间为t6, 局部搜索更新参数p、vb和vc的时间为t7, 产生随机数的时间为t8, 当r< p时, 每维按照式(2)更新个体位置所需时间为t9, 当r≥ p时, 每维按照式(2)更新个体位置所需时间为t10.该阶段时间复杂度表示如下:

T3=O(Nt6+N(t7+3t8d+t9d)+Nt10d)= O(d).

故SMA的时间复杂度为:

T(d)=T1+Max_iter(T2+T3)=O(d+f(d)).

在MISMA中, 初始参数设置、目标函数适应度值求解排序、参数更新的时间复杂度与SMA保持一致.在种群初始化阶段, 每维按照式(3)执行Halton序列初始化的时间为w1, 则该阶段的时间复杂度为:

T'1=O(t0+Nw1d)=O(d).

在进入迭代后、循环搜索前, 按照式(8)执行局部解改进策略所需时间为w2, 则该阶段的时间复杂度为:

T'2=O(N(f(d)+t2)+t3+t4+w2+f(d)+t5)= O(f(d)).

在循环搜索阶段, 全局搜索产生步长因子δ 的时间为w3, 执行差分变异全局搜索策略的时间为w4, 采用贪婪策略选取较优位置的时间为f(d)+w5, 局部搜索改进参数vb的更新时间为w6, 当r< p时, 按式(6)更新个体位置所需时间为w7, 当r≥ p时, 按式(6)更新个体位置所需时间为w8, 则该阶段时间复杂度为:

T'3=O(Nt6+N(w3+w4+f(d)+w5)+N(w6+w7)d+Nw8d)= O(d+f(d)).

根据上述分析, MISMA的总时间复杂度为:

T'(d)=T'1+Max_iter(T'2+T'3)= O(d+f(d)).

综上所述, MISMA未增加额外的时间复杂度, 二者的时间复杂度属于同一数量级, 执行效率相同.

3 仿真实验及结果分析
3.1 基准测试函数及测试环境

为了检验MISMA的性能, 本文选取13个基准测试函数进行算法寻优测试, 基准测试函数的相关信息如表1所示.单峰函数主要用于检验算法的收敛效率和局部开采能力, 多峰函数主要用于检验算法跳出局部最优解的逃逸能力和全局探索性能.

表1 测试函数相关信息 Table 1 Information of test functions

仿真测试环境包括:Intel(R)Core(TM)i5-8400CPU@2.80 GHz、16.0 GB内存、64位Windows10操作系统, MatlabR2019(b).

MISMA的公共参数设置均与SMA保持一致, 步长因子初值δ 0=1.5, 缩放因子γ由0随迭代次数线性递增至200.所有算法的通用条件设置相同:N=30, Max_iter=500.所有对比算法分别独立运行30次, 规避寻优过程出现的偶然性误差.

3.2 改进策略有效性分析

为了验证改进策略分别对SMA的性能提升效果, 定义如下4种对比算法:基于Halton序列改进的黏菌优化算法(Improved SMA Based on Halton, HI-SMA)、融入全局搜索策略的黏菌优化算法(SMA Based on Global Search, GSSMA)、结合新局部搜索策略的黏菌优化算法(SMA Combined with New Lo-cal Search, NLSMA)、基于透镜成像学习策略的改进黏菌优化算法(Improved SMA Based on Lens Imaging Learning, ILSMA).将上述4种算法与SMA、MISMA进行实验对比.限于篇幅, 选取6个具有不同特征的基准函数, 检验改进策略的有效性.具体实验结果如表2所示, 表中黑体数字表示最优值, 反映算法对搜索空间的有效探索.

表2 改进策略的有效性实验结果 Table 2 Results of validity experiment of improved strategies

由表2可知, 4种改进策略均能有效提升SMA的寻优性能, 4种改进后的算法或于各项寻优指标上寻到最优值0, 或以一定的数量级优势取胜于SMA.HISMA均获得不差于甚至优于SMA的寻优结果, 说明利用Halton序列初始化黏菌种群能有效改善种群多样性, 提升算法的寻优精度.除了在函数f12上GSSMA的表现略弱于SMA以外, 在其它函数上GSSMA均优于SMA, 表明融入基于差分变异的全局搜索策略对于SMA全局探索和寻优效率的改善力度明显.在单峰函数上, NLSMA在计算性能方面均优于SMA, 表明改进局部搜索过程提升SMA的局部开采能力和收敛速度.在多峰函数上, 除了在函数f9上ILSMA计算性能与SMA持平以外, 在其余函数上ILSMA的计算性能明显优于SMA, 佐证局部解改进策略对SMA局部逃逸能力的强化作用.进一步地, MISMA综合4种改进策略的优势, 寻优性能表现出全方位的显著提升.在单峰函数f1、 f4上, MISMA在各项指标上均寻到最优值0, 在函数f6上, MISMA性能高出SMA至少9个数量级.在多峰函数f12、 f13上, MISMA也表现出明显优势.并且MISMA的运行速度具有明显优势, 运行时间均优于SMA.这说明MISMA具有优秀的寻优性能, 也表明MISMA 未增加额外的时间复杂度, SMA和MISMA的时间复杂度属于同一数量级.

为了直观展示MISMA的性能优势, 图5给出6种算法的动态收敛曲线.限于篇幅, 仅给出6个变化明显的函数收敛曲线, 同时, 取函数适应度值以10为底的对数, 以便分析收敛趋势.

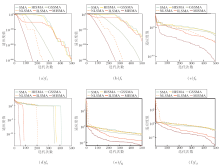图5 各算法在6个测试函数上的函数收敛曲线Fig.5 Function convergence curves of different algorithms with 6 test functions

从图5可以看出, 相比SMA, Halton序列产生的确定性超越均匀分布序列, 使HISMA的初始个体分布更均匀, 提高算法的搜索速度和规避局部极值的能力.虽然SMA与HISMA收敛曲线基本重合, 但是HISMA收敛速度不低于SMA, 在函数f9上HISMA收敛速度快于SMA, 且HISMA平行于横轴的曲线即局部搜索时长明显短于SMA.相比SMA, 两组差异矢量进一步增加GSSMA种群个体间的差异性, 在搜索过程中几乎没有出现停滞, 相比SAM, GSSMA的收敛速度和全局探索能力在函数f1、 f4上提升明显.相比SMA, 凹形下降型收敛因子aCaDF使NLSMA在迭代前期快速收敛至最优解附近, 并在迭代后期小幅逼近最优解.除了函数f6、 f12、 f13以外, NLSMA均快于SMA完成收敛过程, 并在迭代前期已能快速收敛至最优解附近, 且在收敛过程中保持阶梯式递降.相比SMA, 执行动态边界透镜反向学习策略使ILSMA加强算法的局部搜索能力, 收敛精度具有较明显的提升.从函数f6、 f12、 f13上可观察到ILSMA的收敛曲线斜率大于SMA, 相比其他3种改进策略下的SMA, 收敛精度占优.

最后, 综合所有改进策略的MISMA在6个测试函数上取得最优的收敛效率和收敛精度, 相比SMA, MISMA快速收敛至最优解, 对全局空间的探测、对局部空间的开采和逃离局部最优解、对迭代过程中每代解的利用能力都得到明显提升.但改进后的MISMA也存在不足, 在函数f12上, MISMA的收敛曲线仍有多段平行于横轴, 主要是由于算法搜索到的值均局限于某个值附近, 说明其逃离局部最优解的能力还存在一定局限.在函数f6、 f12、 f13上, MISMA几乎与其余算法同时完成收敛, 说明MISMA虽然提升全局探测能力和收敛精度, 但收敛效率仍存在一定的局限性.

上述分析验证本文的4个改进策略对于提升SMA寻优性能的有效性, 各改进策略对于SMA寻优性能的改善各有侧重, 但单一策略对于整体提升SMA性能的力度有限, MISMA综合4种改进策略的优势, 寻优性能表现出全方位的显著提升, 说明本文对SMA的改进措施的有效性.

3.3 MISMA优越性验证

3.3.1 寻优性能对比分析

为了充分检验MISMA的优越性, 将MISMA与ESMA[9]、AOSMA[10]、MSMA[11]、LSMA[14]在相同测试环境下进行对比分析, 具体结果如表3所示, 表中黑体数字表示最优值.

表3 各算法在13个测试函数上的性能对比 Table 3 Performance comparison of different algorithms with 13 functions

由表3可知, MISMA在13个测试函数的平均值和标准差指标上获得11个最优结果, 显然, 相比同系算法, MISMA在SMA综合寻优性能改善方面具有显著优势.对于单峰函数:MISMA在函数f1、 f2、 f3、 f4上的平均值和标准差均能得到理论最优值0; 在函数f5和f7上, MISMA在平均值和标准差上的表现略差于MSMA, 但依然优于其余3种算法.在函数f7上, MISMA寻优的平均值和标准差领先其余算法6~10个数量级.由4种算法在7个单峰函数上的寻优表现可知, MISMA的局部开采能力和收敛效率优于对比算法.对于多峰函数, 各算法在函数f8上的平均值寻优表现差距较小, 但MISMA在标准差上优于其它算法5~7个量级, 收敛至-12 569.486 6.在函数f9、 f10、 f11上, 各算法的函数计算性能持平.在函数f12、 f13上, MISMA在平均值和标准差上领先其余算法3~11个量级.由此说明, MISMA在多峰函数的寻优表现依旧卓越, 具有优良的全局探索性能和局部极值逃逸性能.

5种算法在6个测试函数上的寻优动态收敛曲线如图6所示.由图可知, MISMA在不同类型的函数上均表现出优良的求解精度和收敛速度.对于单峰函数, MISMA的收敛速度最快, 保持较强的持续收敛特性.在函数f6上, 其它算法虽表现有小幅度的持续收敛, 但后期均处于不同程度的停滞状态, 而MISMA在迭代后期依然保持强劲的开采势头.对于多峰函数, MISMA在函数f9上的收敛速度差于MSMA, 但依旧领先于ESMA、LSMA和AOSMA.在函数f12、 f13上, MISMA在收敛末期依然保持优秀的持续寻优趋势, 在迭代后期能有效跳出局部最优, 继续寻优, 收敛精度明显优于其它算法.

图6 各算法在6个测试函数上的寻优收敛曲线Fig.6 Convergence curves of different algorithms with 6 test functions

综上所述, 相比ESMA、AOSMA、MSMA和LSMA, MISMA表现出较佳的局部开采性能和收敛精度, 并能在较短迭代寻优进程中搜索到函数较优值, 同时具有突出的局部最优解逃逸能力和全局搜索性能, 保证其能快速逃离局部最优解, 逼近全局最优解, 进一步佐证MISMA具有优越的综合寻优性能.

3.3.2 CEC2014测试函数上的性能分析

为了进一步检验MISMA在求解不同复杂优化问题时的优越性和适用性, 本文选取CEC2014测试集[17]上的单峰函数、多峰函数、混合函数、复合函数进行分析.

选取的函数信息如表4所示.

表4 CEC2014测试函数相关信息 Table 4 Information of CEC2014 test functions

本文选取混合改进策略的黑猩猩优化算法(Chimp Optimization Algorithm Based on Hybrid Im-provement, SLWChOA)[17]、NMPA(Nonlinear Marine Predator Algorithm)[18]、HPSOBOA(Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimi-zation)[19]、PSOGWO(Hybrid Algorithm of Particle Swarm Optimization and Grey Wolf Optimizer)[20]、CSGWO(Cuckoo Search Grey Wolf Optimization)[21]作为对比算法.实验中各算法的实验测试环境和通用参数设置与3.1节一致, 关键参数设置参见各源文献.

各对比算法在8个函数上的实验结果如表5所示, 表中黑体数字表示最优值.由表可知, MISMA在CEC2014函数上求解得到6个最优结果.对于单峰函数, MISMA在函数CEC01上的寻优精度和稳定性低于NMPA, 但在函数CEC02上表现最优.对于多峰函数, 虽然MISMA在函数CEC08上的稳定性差于HPSOBOA, 但其收敛精度均最优.对于混合函数, MISMA在函数CEC19上的寻优结果略差于NMPA, 但在函数CEC18上表现最优.对于复合函数, MISMA的寻优性能均表现最佳, 标准差均为0, 佐证MISMA在CEC2014函数上仍然具备优良的寻优性能.

表5 各算法在8个CEC2014测试函数上的性能对比 Table 5 Performance comparison of different algorithms with 8 CEC2014 functions
4 光伏电池组件参数优化问题

太阳能发电系统因廉价环保得到广泛应用, 但其实际性能受环境因素影响, 需要搭建数据驱动模型, 精确优化辨识组件参数, 以便评估光伏系统的性能.

由于传统的机械方法难以应对高度非线性的数值优化问题, 因此, 本文通过MISMA分别对单、双二极管光伏(Photovoltaic, PV)模型[22]参数进行优化辨识, 验证算法的工程适用性.

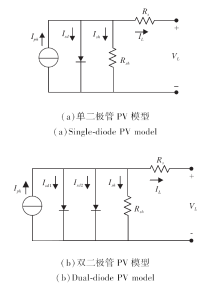
单、双二极管PV模型参数的优化目的是为了减小输出电流计算值 IL*与实际值IL的均方根误差.单二极管PV模型包括光生电流Iph、反向饱和电流Isd、并联电阻Rsh、串联电阻Rs、理想系数n这5个待优化参数.双二极管PV模型需辨识参数为光生电流Iph、反向饱和电流 Isd1和 Isd2、并联电阻Rsh、串联电阻Rs、理想系数n1和n2.二者的等效电路分别如图7所示.

图7 单双二极管PV模型等效电路图Fig.7 Equivalent circuit diagram of single-diode and dual-diode PV models

单、双二极管PV模型的数学描述如下:

$\begin{aligned} & f\left(I_{p h}, I_{s d}, R_{s h}, R_s, n\right)= \\ & I_{p h}-I_d-I_{s h}-I_L= \\ & I_{p h}-I_{s d}\left(\exp \left(\frac{q\left(V_L+I_L R_s\right)}{n k T}\right)-1\right)-\frac{V_L+I_L R_s}{R_{s h}}-I_L, \\ & f\left(I_{p h}, I_{s d 1}, I_{s d 2}, R_{s h}, R_s, n_1, n_2\right)= \\ & I_{p h}-I_{d 1}-I_{d 2}-I_{s h}-I_L= \\ & I_{p h}-I_{s d 1}\left(\exp \left(\frac{q\left(V_L+I_L R_s\right)}{n_1 k T}\right)-1\right)- \\ & I_{s d 2}\left(\exp \left(\frac{q\left(V_L+I_L R_s\right)}{n_2 k T}\right)-1\right)-\frac{V_L+I_L R_s}{R_{s h}}-I_L, \end{aligned}$

其中, Id为二极管电流, T为电池温度, VL为输出电压, Ish为并联电阻电流, 玻尔兹曼常数值

k=1.380 648 52× 1023,

电子电荷

q=1.602 176 46× 1019 C,

Iph∈ [0, 1], Isd∈ [0, 1], n∈ [1, 2].

Rsh∈ [0, 100], Rs∈ [0, 1].

实验过程使用的实际输出电流IL和电压VL数据源于文献[23], 将MISMA与NMPA、PSOGWO、CSGWO、SMA、SLWChOA、HPSOBOA置于相同环境下, 各自独立运行30次, 得出一组最优参数组合.各算法的通用参数设置与3.1节一致, 并于牛顿迭代法思想下构建收敛精度α 小于10-4的输出电流目标约束:

IL*=IL- f(IL)f'(IL), | IL*-IL|< α ,

RMSE= 1N(∑s=1N[IL, S*-IL, S]2)

其中, N为实测数据量, s为相应组数据.

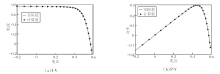
各算法在单、双二极管PV模型上的参数辨识结果及其对应的均方根误差(Root Mean Squared Error, RMSE)分别如表6和表7所示, 单、双二极管PV模型的特性曲线分别如图8和图9所示.

表6 各算法在单二极管PV模型上的优化结果 Table 6 Optimization results of different algorithms for single-diode PV model
表7 各算法在双二极管PV模型上的优化结果 Table 7 Optimization results of different algorithms for dual-diode PV model

图8 单二极管PV 模型特性曲线Fig.8 Characteristic curves of single-diode P-V model

图9 双二极管PV 模型特性曲线Fig.9 Characteristic curves of dual-diode PV model

由表6可知, MISMA在单二极管PV模型上的RMSE值最小, RMSE=7.7365e-04, 辨识的最优参数组合

[Iph, Isd, Rsh, Rs, n]=[0.7608, 0.3066, 52.1493, 0.0366, 1.4759].

观察图8可知:I-V和P-V特性曲线与实测数据高度吻合, 表明MISMA对单二极管PV模型组件参数的辨识效果优越.

由表7可知, MISMA在双二极管PV模型上的RMSE值同样为最小,

RMSE=7.6614e-04,

优化得出的最优参数组合

[Iph, Isd, Rsh, Rs, n]=[0.7608, 0.4190, 0.1314, 53.2859, 0.0374, 1.7168, 1.4128].

同时, 由图9可见, 通过MISMA优化后得出的I-V和P-V特性曲线与实测数据高度吻合.

综上所述, 对于单、双二极管PV模型, 经MIS-MA优化辨识后得出的最优参数组能保证其在各项评估结果上处于较优水平, 优化效果具有一定优势, 侧面验证MISMA的工程适用性及优越性.

5 结束语

针对SMA收敛效率较低和容易陷入局部最优解的缺陷, 本文提出融合多策略改进的黏菌优化算法(MISMA).利用Halton序列初始化种群, 引入基于差分变异算法相关思想, 更新个体的全局位置公式, 采用糅合自适应收敛因子和精英选择机制的局部搜索策略, 提出基于动态边界的透镜成像反向学习策略, 设计改进局部最优个体等改进策略.在13个基准测试函数、部分CEC2014函数及光伏电池组件模型参数寻优实验上检验算法性能, 结果表明, MISMA寻优性能提升显著, 具有一定的优越性, 在处理实际优化问题时的适用性较强.但是, MISMA逃离局部桎梏的能力仍有一定的局限性, 在某些测试函数上性能表现略弱, 综合寻优性能仍有一定的提升空间, 这需要在未来研究中进一步改进, 并尝试将其应用于更多样性的实际工程优化问题中.

本文责任编委 何 清

Recommended by Associate Editor HE Qing

参考文献
[1] GALLETLY J E. An Overview of Genetic Algorithms. Kybernetes, 1992, 21(6): 26-30. [本文引用:1]
[2] RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA: A Gravitational Search Algorithm. Information Sciences, 2009, 179(13): 2232-2248. [本文引用:1]
[3] MIRJALILI S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowledge-Based Systems, 2016, 96: 120-133. [本文引用:1]
[4] KENNEDY J, EBERHART R. Particle Swarm 0ptimization // Proc of the International Conference on Neural Networks. Washington, USA: IEEE, 1995: 1942-1948. [本文引用:1]
[5] LI S M, CHEN H L, WANG M J, et al. Slime Mould Algorithm: A New Method for Stochastic Optimization. Future Generation Compu-ter Systems, 2020, 111: 300-323. [本文引用:2]
[6] WEI Y Y, ZHOU Y Q, LUO Q F, et al. Optimal Reactive Power Dispatch Using an Improved Slime Mould Algorithm. Energy Reports, 2021, 7: 8742-8759. [本文引用:1]
[7] CHEN X W, HUANG H, HEIDARI A A, et al. An Efficient Multilevel Thresholding Image Segmentation Method Based on the Slime Mould Algorithm with Bee Foraging Mechanism: A Real Case with Lupus Nephritis Images. Computers in Biology and Medicine, 2022, 142. DOI: 10.1016/j.compbiomed.2021.105179. [本文引用:1]
[8] ZHENG J L, XIE Y J, HUANG X P, et al. Balanced Version of Slime Mould Algorithm: A Study on PEM Fuel Cell System Parameters Identification. Energy Reports, 2021, 7: 3199-3209. [本文引用:1]
[9] NAIK M K, PANDA R, ABRAHAM A. An Entropy Minimization Based Multilevel Colour Thresholding Technique for Analysis of Breast Thermograms Using Equilibrium Slime Mould Algorithm. Applied Soft Computing, 2021, 113. DOI: 10.1016/j.asoc.2021.107955. [本文引用:2]
[10] NAIK M K, PANDA R, ABRAHAM A. Adaptive Opposition Sli-me Mould Algorithm. Soft Computing, 2021, 25(22): 14297-14313. [本文引用:2]
[11] TANG A D, TANG S Q, HAN T, et al. A Modified Slime Mould Algorithm for Global Optimization. Computational Intelligence and Neuroscience, 2021. DOI: 10.1155/2021/2298215. [本文引用:2]
[12] ÖRNEK B N, AYDEMIR S B, DÜZENLI T, et al. A Novel Version of Slime Mould Algorithm for Global Optimization and Real World Engineering Problems: Enhanced Slime Mould Algorithm. Mathematics and Computers in Simulation, 2022, 198(C): 253-288. [本文引用:2]
[13] HOUSSEIN E H, MAHDY M A, BLONDIN M J, et al. Hybrid Slime Mould Algorithm with Adaptive Guided Differential Evolution Algorithm for Combinatorial and Global Optimization Problems. Expert Systems with Applications, 2021, 174. DOI: 10.1016/j.eswa.2021.114689. [本文引用:1]
[14] NAIK M K, PANDA R, ABRAHAM A. Normalized Square Diffe-rence Based Multilevel Thresholding Technique for Multispectral Images Using Leader Slime Mould Algorithm. Journal of King Saud University-Computer and Information Sciences, 2022, 34(7): 4524-4536. [本文引用:2]
[15] BANGYAL W H, BATOOL H, AHMED J, et al. An Improved Particle Swarm Optimization Algorithm with Chi-Square Mutation Strategy. International Journal of Advanced Computer Science and Applications, 2019, 10(3): 481-491. [本文引用:1]
[16] 龙文, 伍铁斌, 唐明珠, 等. 基于透镜成像学习策略的灰狼优化算法. 自动化学报, 2020, 46(10): 2148-2164.
(LONG W, WU T B, TANG M Z, et al. Grey Wolf Optimizer Algorithm Based on Lens Imaging Learning Strategy. Acta Electronica Sinica, 2020, 46(10): 2148-2164. ) [本文引用:1]
[17] 何庆, 罗仕杭. 混合改进策略的黑猩猩优化算法及其机械应用. 控制与决策, 2023, 38(2): 354-364.
(HE Q, LUO S H. Chimp Optimization Algorithm Based on Hy-brid Improvement Strategy and Its Mechanical Application. Control and Decision, 2023, 38(2): 354-364. ) [本文引用:2]
[18] SADIQ A S, DEHKORDI A A, MIRJALILI S, et al. Nonlinear Marine Predator Algorithm: A Cost-Effective Optimizer for Fair Power Allocation in NOMA-VLC-B5G Networks. Expert Systems with Applications, 2022, 203. DOI: 10.1016/j.eswa.2022.117395. [本文引用:1]
[19] ZHANG M J, LONG D Y, QIN T, et al. A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems. Symmetry, 2020, 12(11). DOI: 10.3390/sym12111800. [本文引用:1]
[20] AL-TASHI Q, KADIR S J A, RAIS H M, et al. Binary Optimization Using Hybrid Grey Wolf Optimization for Feature Selection. IEEE Access, 2019, 7: 39496-39508. [本文引用:1]
[21] BAI Q C, LI H. The Application of Hybrid Cuckoo Search-Grey Wolf Optimization Algorithm in Optimal Parameters Identification of Solid Oxide Fuel Cell. International Journal of Hydrogen Energy, 2022, 47(9): 6200-6216. [本文引用:1]
[22] YU K J, LIANG J J, QU B Y, et al. Multiple Learning Backtra-cking Search Algorithm for Estimating Parameters of Photovoltaic Models. Applied Energy, 2018, 226(C): 408-422. [本文引用:1]
[23] EASWARAKHANTHAN T, BOTTIN J, BOUHOUCH I, et al. Non-linear Minimization Algorithm for Determining the Solar Cell Parameters with Microcomputers. International Journal of Solar Energy, 1986, 4(1): 1-12. [本文引用:1]