设G=(V, ε )表示一个无向图, 其中,

V={v₁, v₂, …, v_N}

表示N个节点的集合, 包括l个标记样本

$\begin{aligned} D_{l}= & \left\{\left(x_{1}, y_{1}\right), \left(x_{2}, y_{2}\right), \cdots, \left(x_{l}, y_{l}\right), \right. \\ & \left.y_{i} \in\{1, 2, \cdots, C\}\right\}, \end{aligned}$

C表示样本的类别, 和u个无标记样本

D_u={(x_l+1), (x_l+2), …, (x_l+u)},

通常, l≪u.ε ⊆V× V表示节点之间的边集.X∈ R^{N× F}表示节点的特征矩阵, F表示特征维度, Y表示节点的标记矩阵.

A=[a_ij]∈ R^{N× N}

表示节点的邻接矩阵.

D=diag(d₁, d₂, …, d_N)

表示A的度矩阵,

d_i= ∑ja_ij

表示顶点i的度.

图半监督学习的目标是学习一个函数f, 最终输出标记矩阵 Y︿.

图神经网络的目标是学习一个编码器

f(X, A)∈ R^{N× F'},

以图的特征和结构作为输入, 产生低维的节点嵌入, 即F'≪F.GCN的卷积层传播公式为

$\boldsymbol{H}^{(l+1)}=\sigma\left(\widetilde{\boldsymbol{D}^{-\frac{1}{2}}} \widetilde{\boldsymbol{A}} \widetilde{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{H}^{(l)} \boldsymbol{W}^{(l)}\right) $

其中, A~=A+I_N表示无向图G的邻接矩阵A和单位矩阵I_N的和, D~表示 A~的度矩阵, W^(l)表示权重矩阵, H^(l)表示第l层激活矩阵, σ (· )表示非线性激活函数, 例如

ReLU(· )=max(0, · ).

本文提出基于层次对比学习的半监督节点分类算法(SSC-HCL), 框架如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 SSC-HCL结构图Fig.1 Structure of SSC-HCL

SSC-HCL将原始图G=(X, A)的结构和特征作为输入, 采用GCN对图进行编码, 在学习的过程中, 将不同层次上得到的嵌入表示作为不同的视图, 用作对比学习.同时, 使用半监督对比损失, 最大化多个视图上学得表示的一致性, 通过迭代优化学习节点的表示.

具体地, SSC-HCL(以三层为例)通过在图G上应用GCN, 得到第1层~第3层视图表示:

$\begin{aligned} Z^{1} & =\sigma\left(\widehat{A} \boldsymbol{X} \boldsymbol{W}^{0}\right), \\ Z^{2} & =\sigma\left(\widehat{A} \boldsymbol{Z}^{1} \boldsymbol{W}^{1}\right), \\ Z^{3} & =\sigma\left(\widehat{A} \boldsymbol{Z}^{2} \boldsymbol{W}^{2}\right), \end{aligned}$

其中,

$\widehat{\boldsymbol{A}}=\widetilde{\boldsymbol{D}}^{-\frac{1}{2}} \widetilde{\boldsymbol{A}} \widetilde{\boldsymbol{D}}^{-\frac{1}{2}}$

表示归一化邻接矩阵.然后, 将层次视图设计为对比视图, 以增大正例对的相似性、降低负例对的相似性为目的, 改进图的嵌入表示.

半监督对比损失同时利用大量的无标记样本和少量的标记样本, 为仅使用无标记样本的对比学习提供丰富的监督信息, 帮助模型学习更好的节点表示, 进一步提高模型性能.在学习的过程中, 使用评分函数衡量节点编码特征的相似度, 目标是尽可能地增大同一类别的节点之间的相似度, 尽可能地减小不同类别的节点之间的相似度, 指导学习过程.半监督对比损失分为两部分:监督对比损失和无监督对比损失.

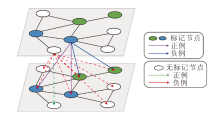
SSC-HCL的半监督对比损失机制如图2所示.使用x_i表示视图中的节点, 如果x_i为标记节点, x_i的正例为与它具有同类的标记节点, 负例为与它具有不同类的标记节点, 即图2中的紫色箭头和蓝色箭头指向的节点分别表示节点x_i的正例和负例.如果x_i为无标记节点, x_i的正例为另一个视图上它本身, 负例为除x_i之外的其它节点, 即图2中的绿色箭头和红色箭头指向的节点分别表示节点x_i的正例和负例.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 半监督对比损失机制示意图Fig.2 Schematic diagram of semi-supervised contrastive loss mechanism

无监督对比损失表示如下:

l~ucs= 12n∑i=1n( lucs(x_i)+ lucs+1(x_i)),

其中, lucs和 lucs+1分别表示第s层和第s+1层次中对于无标记节点x_i的成对的无监督对比损失.通过内积衡量节点表示之间的相似度, 得到 lucs(x_i), 即将正例对之间的相似度和负例对之间的相似度进行对比. lucs(x_i)可以形式化地表示为

$l_{u c}^{s}\left(x_{i}\right)=-\lg \left[\frac{\exp \left(\left\langle\boldsymbol{z}_{i}^{s}, \boldsymbol{z}_{i}^{s+1}\right\rangle\right)}{\exp \left(\left\langle\boldsymbol{z}_{i}^{s}, \boldsymbol{z}_{i}^{s+1}\right\rangle\right)+\sum_{j \neq i} \exp \left(\left\langle\boldsymbol{z}_{i}^{s}, \boldsymbol{z}_{j}^{s}\right\rangle\right)+\sum_{j \neq i} \exp \left(\left\langle \boldsymbol{z}_{i}^{s}, \boldsymbol{z}_{j}^{s+1}\right\rangle\right)}\right],$

其中, zis和 zis+1表示从不同的视图中学习得到的节点x_i的第i行的表示, < · > 表示内积.

lucs+1(x_i)的计算方法与 lucs(x_i)类似, 可以形式化地表示为

$l_{u c}^{s+1}\left(x_{i}\right)=-\lg \left[\frac{\exp \left(\left\langle\boldsymbol{z}_{i}^{s+1}, \boldsymbol{z}_{i}^{s}\right\rangle\right)}{\exp \left(\left\langle\boldsymbol{z}_{i}^{s+1}, \boldsymbol{z}_{i}^{s}\right\rangle\right)+\sum_{j \neq i} \exp \left(\left\langle\boldsymbol{z}_{i}^{s+1}, \boldsymbol{z}_{j}^{s+1}\right\rangle\right)+\sum_{j \neq i} \exp \left(\left\langle\boldsymbol{z}_{i}^{s+1}, \boldsymbol{z}_{j}^{s}\right\rangle\right)}\right], $

同时, 为了充分利用稀缺但有价值的标记样本, 使用监督对比损失为学习节点表示提供额外的监督信号.监督对比损失表示如下:

l~scs= 12l∑i=1l( lscs(x_i)+ lscs+1(x_i)).

lscs(x_i)和 lscs+1(x_i)可以形式化地表示为

$l_{s c}^{s}\left(x_{i}\right)=-\lg \left[\frac{\sum_{k=1}^{l} I I_{\left[y_{i}=y_{k}\right]} \exp \left(\left\langle\boldsymbol{z}_{i}^{s}, \boldsymbol{z}_{k}^{s+1}\right\rangle\right)}{\sum_{k=1}^{l} I I_{\left[y_{i}=y_{k}\right]} \exp \left(\left\langle\boldsymbol{z}_{i}^{s}, \boldsymbol{z}_{k}^{s+1}\right\rangle\right)+\sum_{j=1}^{l} I I_{\left[y_{i} \neq y_{j}\right]} \exp \left(\left\langle\boldsymbol{z}_{i}^{s}, \boldsymbol{z}_{j}^{s+1}\right\rangle\right)}\right], $

$l_{s c}^{s+1}\left(x_{i}\right)=-\lg \left[\frac{\sum_{k=1}^{l} I I_{\left[y_{i}=y_{k}\right]} \exp \left(\left\langle\boldsymbol{z}_{i}^{s+1}, \boldsymbol{z}_{k}^{s}\right\rangle\right)}{\sum_{k=1}^{l} I I_{\left[y_{i}=y_{k}\right]} \exp \left(\left\langle\boldsymbol{z}_{i}^{s+1}, \boldsymbol{z}_{k}^{s}\right\rangle\right)+\sum_{j=1}^{l} I I_{\left[y_{i} \neq y_{j}\right]} \exp \left(\left\langle\boldsymbol{z}_{i}^{s+1}, \boldsymbol{z}_{j}^{s}\right\rangle\right)}\right], $

其中, II_{[· ]}表示指示函数, 在[· ]内为真和假时分别取值为1和0.

半监督对比损失结合无监督对比损失和监督对比损失, 表示如下:

lsscs= l~ucs+ l~scs.(1)

使用交叉熵损失衡量网络的实际输出与真实标记之间的差异, 即

$l_{c e}=-\sum_{i=1}^{l} \sum_{i=1}^{C} Y_{i j} \ln \left(\widehat{Y}_{i j}\right), $ (2)

其中, Y_ij表示节点x_i的真实标记, Y︿ij表示节点x_i的第i个样本在第j个位置的预测标记.

结合半监督对比损失和交叉熵损失, 得到整体的网络输出, 总体的目标损失函数表示如下:

l=λ ∑s=1klsscs+l_ce, (3)

其中, λ > 0表示半监督对比损失和交叉熵损失之间的相对权重, k表示第s层和第s+1层上的半监督对比损失.

最终, 第i个节点的预测函数表示如下:

y~i=arg maxj∈[1, C]Y︿ij.

SSC-HCL的详细训练过程如算法1所示.

算法1 SSC-HCL(以三层为例)

输入 特征矩阵X, 邻接矩阵A, 标记矩阵Y, 迭代次数N

输出 未标记节点的标记

初始化 随机初始化模型参数

For epoch=1 to N do

通过GCN得到第1层的嵌入表示Z¹

通过GCN得到第2层的嵌入表示Z²

通过GCN得到第3层的嵌入表示Z³

由式(1)计算第1层和第2层上的半监督对比损失 lssc1

由式(1)计算第2层和第3层上的半监督对比损失 lssc2

计算总的半监督对比损失 lssc1+ lssc2

由式(2)计算交叉熵损失l_ce

由式(3)计算总体目标损失l

根据梯度下降方法, 更新参数l

End for

预测未标记节点的标记

为了验证本文算法的有效性, 在Cora^[33]、CiteSeer^[33]、PubMed^[33]、Amazon Photo^[34]这4个基准数据集上进行实验, 数据集信息如表1所示.Cora、CiteSeer、PubMed为引文网络数据集, 节点表示文档, 边表示文档之间的引用关系, 每个文档都由一个词袋向量表示相应的词存在或不存在.Amazon Photo数据集是亚马逊产品联合购买数据集, 节点表示商品, 边表示两种商品经常被同时购买, 节点特征表示产品评论, 类别标签由产品的类别给出.

表1

Table 1

表1(Table 1)

表1 实验数据集信息 Table 1 Experimental dataset information 名称 类别数 节点数 边数 特征维度 Cora 7 2708 5429 1433 CiteSeer 6 3327 4732 3703 PubMed 3 19717 44338 500 Amazon Photo 8 7487 119043 745

表1 实验数据集信息 Table 1 Experimental dataset information

在Cora、CiteSeer、PubMed数据集上, 本文使用与Yang等^[35]相同的训练集、验证集、测试集划分方式, 即每类随机抽取20个节点作为标记数据进行训练, 500个节点用于验证, 1 000个节点用于测试.在Amazon Photo数据集上, 每类随机抽取30个节点作为标记数据进行训练, 随机抽取30个节点用于验证, 其余节点用于测试.

本文选择如下对比方法.

1)DeepWalk^[12].基于图嵌入的方法, 通过随机游走学习节点的嵌入表示.

2)Chebyshev^[13].基于图卷积的方法, 把CNN扩展到非欧数据上.

3)GATs^[14].使用注意力机制学习邻居节点的权重, 对邻居节点的特征加权求和, 为不同的节点分配不同的权重.

4)文献[15]方法.传统的基于图的半监督学习方法, 通过节点之间的边传播标签, 将标签分配给未标记节点.

5)GCN^[20].对图数据进行操作的经典的图卷积神经网络.

6)DGI^[25].最大化图局部和全局的互信息, 学习节点表示.

7)文献[26]方法.最大化图的多视图编码表示之间的互信息, 学习节点表示.

8)GMI^[27].对比输入图和每个节点的隐藏表示之间的相关性, 学习节点表示.

9)GRACE^[28].利用节点级对比目标的无监督图表示学习框架.

本节计算各方法10次运行的平均分类准确率以评估性能.各方法在4个数据集上的结果如表2所示, 表中黑体数字表示最优值.由表可见, SSC-HCL优于对比方法, 在Cora、CiteSeer、PubMed、Amazon Photo数据集上与次佳方法的分类准确率相比, 分别提升0.8%、0.6%、0.5%和1.2%.因此可以看出, 利用不同层次进行对比学习, 能够更好地保留图的节点特征和拓扑信息, 学得更好的表示, 从而验证SSC-HCL的有效性.

表2

Table 2

表2(Table 2)

表2 各方法在4个数据集上的分类准确率对比 Table 2 Classification accuracy comparison of different models on 4 datasets % 方法 Cora CiteSeer PubMed Amazon Photo 文献[15]方法 68.0 45.3 63.0 67.8 DeepWalk 67.2 43.2 65.3 - Chebyshev 81.2 69.8 74.4 74.3 GCN 81.2± 0.5 71.3± 0.4 78.6± 0.4 87.3± 1.0 GATs 82.9± 0.7 72.5± 0.7 78.3± 0.3 86.2± 1.5 DGI 81.2± 0.6 72.9± 0.5 77.6± 0.3 83.1± 0.5 GMI 82.2± 0.8 72.7± 0.4 79.6± 0.4 85.1± 0.1 文献[26]方法 82.8± 0.6 72.9± 0.6 79.3± 0.3 87.3± 0.3 GRACE 82.4± 0.6 71.5± 0.3 79.4± 0.8 81.8± 1.0 SSC-HCL 83.7± 0.7 73.5± 0.6 80.1± 0.7 88.5± 0.8

表2 各方法在4个数据集上的分类准确率对比 Table 2 Classification accuracy comparison of different models on 4 datasets %

为了进一步分析模型深度对分类准确率的影响, 改变模型中编码器的卷积层数, 设置隐藏层维度为128.SSC-HCL和GCN在不同层数上的分类准确率如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同层数对方法性能的影响Fig.3 Influence of different layers on classification performance on 3 datasets

由图3可以看出, 两层GCN编码器的性能最佳, 随着层数的不断增加, 性能下降, 多卷积层可能产生从较远的邻域聚合信息的噪声, 从而降低节点表示的质量和下游节点分类任务的性能.尽管GCN和SSC-HCL的性能都有一定下降, 但SSC-HCL在不同深度下的性能大幅优于GCN.

此外, 进一步研究不同标记数量对方法性能的影响.对于每个数据集, 为每类抽取n个标记样本进行实验, n=10, 15, 20, 25, 30.GCN、DGI、文献[26]方法、GRACE、SSC-HCL在Cora、CiteSeer、PubMed数据集上的分类准确率如表3~表5所示, 表中黑体数字表示最优值.

表3

Table 3

表3(Table 3)

表3 各方法在Cora数据集上不同标记数量下的分类准确率 Table 3 Classification accuracies of different methods with different number of labeled nodes on Cora dataset 方法 n=10 n=15 n=20 n=25 n=30 GCN 73.6% 77.8% 81.2% 83.7% 84.9% DGI 74.9% 78.6% 81.2% 83.2% 83.3% 文献[26]方法 75.6% 79.0% 82.8% 83.4% 84.2% GRACE 74.3% 78.1% 82.4% 83.1% 84.1% SSC-HCL 76.0% 80.3% 83.7% 85.8% 86.1%

表3 各方法在Cora数据集上不同标记数量下的分类准确率 Table 3 Classification accuracies of different methods with different number of labeled nodes on Cora dataset

表4

Table 4

表4(Table 4)

表4 各方法在CiteSeer数据集上不同标记数量下的分类准确率 Table 4 Classification accuracies of different methods with different number of labeled nodes on CiteSeer dataset 方法 n=10 n=15 n=20 n=25 n=30 GCN 65.2% 69.5% 71.3% 70.6% 72.7% DGI 68.7% 71.1% 72.0% 73.1% 73.4% 文献[26]方法 69.1% 71.3% 72.9% 73.2% 73.9% GRACE 68.7% 70.4% 71.5% 71.7% 73.0% SSC-HCL 69.8% 71.9% 73.5% 73.7% 75.0%

表4 各方法在CiteSeer数据集上不同标记数量下的分类准确率 Table 4 Classification accuracies of different methods with different number of labeled nodes on CiteSeer dataset

表5

Table 5

表5(Table 5)

表5 各方法在PubMed数据集上不同标记数量下的分类准确率 Table 5 Classification accuracies of different methods with different number of labeled nodes on PubMed dataset 方法 n=10 n=15 n=20 n=25 n=30 GCN 67.1% 78.1% 78.6% 80.0% 80.3% DGI 70.2% 77.3% 77.6% 80.4% 80.6% 文献[26]方法 70.9% 78.1% 79.3% 80.2% 80.5% GRACE 71.2% 77.9% 79.4% 80.6% 80.8% SSC-HCL 71.8% 78.7% 80.1% 81.0% 81.5%

表5 各方法在PubMed数据集上不同标记数量下的分类准确率 Table 5 Classification accuracies of different methods with different number of labeled nodes on PubMed dataset

由表3~表5可以看出, 随着标记数量的增加, 性能随之上升, 这一结果表明, 样本的标记数量与方法性能相关, 标记数量越高, 分类准确率越高.在3个引文网络数据集上的实验结果表明, SSC-HCL在不同标记数量上的分类准确率均最优.

为了提供更直观地说明, 在Cora数据集上, 给出SSC-HCL、DGI、GMI学得的节点嵌入表示的t-SNE^[36]可视化结果, 具体如图4所示, 图中不同颜色表示不同类别.由图可观察得出, SSC-HCL得到的子簇内较紧凑, 子簇间界限较明显, 不同颜色的子簇间重叠较少.DGI得到的红色子簇和绿色子簇之间重叠部分较多, 且属于同类的黑色子簇之间的距离较远.GMI得到的橙色子簇和黑色子簇之间重叠于左上方, 且属于同类的黑色子簇之间的距离较远.结果表明, SSC-HCL能够得到良好的节点嵌入表示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 各方法在Cora数据集上的t-SNE可视化结果Fig.4 t-SNE visualization of different methods on Cora dataset