郭晟楠,博士,讲师,主要研究方向为时空数据挖掘、深度学习.E-mail:guoshn@bjtu.edu.cn.
作者简介:

唐伟文,硕士研究生,主要研究方向为时空数据挖掘、深度学习.E-mail:tangweiwen@bjtu.edu.cn.

陈 炜,博士研究生,主要研究方向为知识图谱推理与应用.E-mail:w_chen@bjtu.edu.cn.

林友芳,博士,教授,主要研究方向为数据挖掘、机器学习、强化学习、复杂网络、智能技术与系统等.E-mail:yflin@bjtu.edu.cn.

万怀宇,博士,教授,主要研究方向为时空数据挖掘、信息抽取、社交网络挖掘.E-mail:hywan@bjtu.edu.cn.
从历史交通事故数据中探究事故发生的规律,实现准确的路段级交通事故风险预测,可以有效提升交通出行的安全与效率.然而,由于天气、交通状态等多源因素的影响、交通事故之间复杂的时空相关性和事故数据的稀疏性,实现准确的路段级交通事故风险预测面临巨大的挑战.针对上述挑战,文中提出融合时序知识图谱的双层次多视角时空图神经网络模型(Two-Level and Multi-view Spatial-Temporal Graph Neural Network by Incorporating Temporal Knowledge Graph, STGN-TKG).首先,构建交通事故时序知识图谱并设计交通事故时序知识图谱历时嵌入模型,挖掘多源影响因素数据之间的动态、高阶相关性.然后,利用空间图卷积注意力模块和时序表征模块,从两个层次、多个语义视角,充分建模交通事故之间复杂的时空相关性.最后,提出符合实际场景的事故风险传播策略,缓解数据稀疏带来的零膨胀问题.在两个真实的路段级交通事故风险数据集上的实验表明,STGN-TKG在路段级事故风险预测任务中表现较优.
GUO Shengnan, Ph.D., lecturer. Her research interests include spatio-temporal data mining and deep learning.
About Author:
TANG Weiwen, master student. His research interests include spatio-temporal data mining and deep learning.
CHEN Wei, Ph.D.candidate. His research interests include knowledge graph reasoning and application.
LIN Youfang, Ph.D., professor. His research interests include data mining, machine learning, reinforcement learning, complex net-work and intelligent technology and system.
WAN Huaiyu, Ph.D., professor. His research interests include spatio-temporal data mining, information extraction and social network mining.
Exploring the law of accident occurrence from historical traffic accident data and realizing accurate road level traffic accident risk prediction can improve the travel safety and efficiency effectively. However, road level traffic accident risk prediction is faced with great challenges due to the influence of multiple factors, such as weather and traffic state, the complex temporal and spatial correlation between traffic accidents and the sparsity of accident data. To address these issues, a two-level and multi-view spatial-temporal graph neural network by incorporating temporal knowledge graph(STGN-TKG) is proposed. Firstly, a traffic accident temporal knowledge graph is constructed for the first time, and diachronic embedding for traffic accident temporal knowledge graph is designed to mine the high-order and dynamic correlation between multi-source influencing factor data. Then, a spatial graph convolution attention module and a temporal representation module are employed to fully model the complex spatial-temporal correlations between traffic accidents from two levels and multiple views. Finally, an accident risk propagation strategy is proposed to alleviate the zero-inflated issue. The experimental results on two real-world road level traffic accident risk datasets show that STGN-TKG achieves superior performance on the road level accident risk prediction task.
准确预测未来交通事故发生的风险, 可以大幅减少人员伤亡、降低交通事故造成的经济损失, 对市民出行、政府管控都具有重要意义.
围绕这一课题, 路段级的交通事故风险预测尤为重要, 具有实际应用价值.因为, 准确的路段级的事故风险预测, 可以及时为交通参与者提供有针对性的行车建议和预警信息, 保障出行安全.例如, 当预测某个路段的交通事故风险在未来一小时会激增时, 可以对该路段上正在通行的车辆广播安全行车准则, 并对计划通行该路段的车辆发送预警信息.然而, 实现准确的路段级交通事故风险预测面临以下三点挑战.
1)交通事故风险会受到多源因素的动态影响.具体而言, 交通事故风险会同时受到交通状态和已发生的交通事故的影响.天气、温度和兴趣点(Point of Interests, POI)等因素对交通事故的发生也存在一定影响.在这些多源影响因素中:少数是静态的, 如兴趣点的分布; 多数是随时间动态变化的, 如交通状态和天气.相比静态因素, 动态因素与交通事故发生的关系更加紧密.这些影响因素之间不仅存在直接(一阶)相关性, 还存在间接(高阶)相关性, 即影响因素之间的潜在关联.挖掘影响因素之间的动态、高阶相关性及它们对交通事故风险的影响是为实现准确的路段级交通事故风险预测需要解决的首要问题.为了捕捉多源因素的影响, 除了交通事故数据以外, SDAE(Stack Denoise Autoencoder)[1]还考虑从定位数据中获得的人类移动数据, 而SDCAE(Stack Denoise Convolutional Autoencoder)[2]则考虑交通流量数据.RiskOracle[3]、GSNet(Geographical and Se-mantic Spatial-Temporal Network)[4]和RiskSeq[5]同时考虑天气、温度和交通状态数据.
2)交通事故的发生存在复杂的时空相关性.在时间维度上, 路段上发生的历史事故会非线性地影响未来事故的发生.在空间维度上, 事故的发生会受到相邻路段和周围兴趣点的影响, 而且影响程度是随时间动态变化的.因此需要充分建模时空相关性.RiskOracle、GSNet、RiskSeq和DSTGCN(Deep Spatio-Temporal Graph Convolutional Network)[6]采用时空图卷积网络捕捉复杂的时空相关性, 实现准确的交通事故风险预测.
3)由于交通事故的发生是一个小概率事件, 因此经统计得到的全路网的路段级事故风险中会出现大量零值, 导致模型预测值收敛于零值, 即出现零膨胀的问题[7].而收敛于零的预测值对于实际应用是没有意义的.因此, 如何克服交通事故风险数据的稀疏性, 得到具有实际应用意义的预测结果是值得进一步思考和解决的问题.为了缓解或解决零膨胀问题, Wang等[4]提出加权损失函数, 而Wang等[8]提出MVMT-STN(Multi-view Multi-task Spatio-Temporal Networks), 采用多任务学习框架, 考虑粒度之间的空间关联, 共同预测多粒度交通事故风险.
为了解决上述挑战与问题, 本文提出融合时序知识图谱的双层次多视角时空图神经网络模型(Two-Level and Multi-view Spatial-Temporal Graph Neural Network by Incorporating Temporal Knowledge Graph, STGN-TKG).首先, 构建交通事故时序知识图谱, 并设计可以融入秒级时间戳信息的交通事故时序知识图谱历时嵌入模型(Diachronic Embedding for Traffic Accident Temporal Knowledge Graph, DETA), 建模多源影响因素之间的关联性, 并通过预训练的方式得到多源影响因素的深层嵌入表示.然后, 基于多源影响因素的深层嵌入表示和浅层信息, 构建两个层次(深层与浅层)、三个语义视角(路段、兴趣点和事故风险)下的路段关系图, 并采用空间图卷积与注意力捕获交通事故风险的空间相关性, 同时利用循环神经网络和时间注意力捕获交通事故风险的时间相关性.在不同层次、不同语义视角下, 任意图节点通过图卷积可以聚合与传播邻居节点的信息, 获取局部交通子图的交通事故风险语义信息.空间注意力会关注所有路段, 任意路段可以计算注意力分数, 对所有路段的信息进行加权聚合, 从而获取全局的交通事故风险语义信息.此语义信息是双层次多视角的.循环神经网络和时间注意力挖掘交通事故数据中的时间相关性, 完成不同时间步之间交通事故风险语义信息的有效传递.在两个真实的路段级交通事故风险数据集上的实验表明, STGN-TKG在预测未来下一个时间段所有路段的事故风险的任务上达到较佳的预测效果.
城市交通事故预测是智能交通系统建设的重点环节, 学者们取得丰硕的成果.现有的研究方法主要分为两类:传统的机器学习方法和深度学习方法.
传统的机器学习方法中具有代表性的方法是支持向量机(Support Vector Machine, SVM)、负二项式回归和决策树.Sharma等[9]使用带有高斯核的SVM分析城市交通事故.Caliendo等[10]分别采用泊松、负二项式和负多项式的回归模型模拟事故频率.Olutayo等[11]使用决策树分析最易引发交通事故的多种因素.然而, 早期的这些工作都假设交通事故的发生相互独立, 但这种假设在实际中是不满足的.而且这些方法未考虑天气、兴趣点等外部因素对交通事故的影响, 预测准确率并不理想.
近年来, 随着深度学习技术的飞速发展, 学者们提出应用于交通事故预测的深度学习方法.为了挖掘交通事故数据和用户定位数据, Chen等[1]设计SDAE, 学习人类移动的层次特征表示, 用于交通事故预测.为了建模邻近区域的空间依赖性, 在SDAE的基础上, Chen等[2]设计SDCAE.但SDAE和SDCAE都未考虑数据在时间维度上的动态性.Yuan等[12]提出Hetero-ConvLSTM, 捕获交通事故的空间异质性和时间自相关性.Zhou等[3]提出RiskOracle, 使用差分时变图神经网络, 捕获交通流的影响和空间依赖性.Wang等[4]提出GSNet, 同时建模地理空间相关性和语义空间相关性.受限于数据的零膨胀问题, 分钟级事故预测的研究只有RiskOracle和RsikSeq, 路段级事故预测的研究只有DSTGCN.
在现有工作中, 大多数是针对区域级事故风险预测的研究, 针对路段级事故风险预测的研究很少, 但路段级事故风险预测能提供更有针对性的行车建议和更精确的事故预警信息, 是研究交通事故更具有现实意义的方式.上述方法都是从浅层次语义视角(如真实拓扑关系)进行信息的聚合与传播, 未考虑深层次语义视角(如事故之间潜在的关联性), 因此无法充分捕获交通事故发生的规律和模式.
知识图谱(Knowledge Graph, KG)本质上是一个静态的多关系有向图, 形式化表示为
G=\{(u, r, v) \mid u \in E, v \in E, r \in R\},
其中, E表示实体集合, R表示关系集合, (u, r, v)表示头实体-关系-尾实体构成的事实三元组.
知识图谱包含多种类型的实体(节点)和关系(边).因此, 根据图中不同的边, 可得到一个实体的多方面属性.此外, 通过这些不同的关系还可以发现实体之间的高阶相关性.总之, 知识图谱具有较强的表征能力.
知识图嵌入(KG Embedding, KGE)是将知识图谱嵌入低维空间中, 学习实体和关系的表示, 能有效挖掘实体之间的高阶相关性.
针对静态知识图谱嵌入, 已有很多较成熟的解决方案[13, 14, 15], 其中较经典的模型是TransE[16].
为了捕获数据在时间维度上的信息, 关联知识图谱中的三元组与时间戳或时间间隔t, 得到事实四元组(u, r, v, t), 此时静态知识图谱就转换为时序知识图谱(Temporal KG, TKG).TKG全面建模数据的动态性, 应用场景丰富.
近些年, 一些工作将静态知识图谱嵌入模型, 扩展为时序知识图谱嵌入模型.为了扩展TransE, Jiang等[17]在评分函数中加入一个时间戳嵌入.Dasgupta等[18]提出HyTE(Hyperplane-Based Tem-porally Aware KG Embedding), 将嵌入投影到时间戳超平面, 再在投影空间上使用TransE的得分函数计算分数, 用于扩展TransE.Ma等[19]提出ConT, 在评分函数中添加时间戳嵌入, 扩展一些静态知识图谱嵌入模型.当时间戳的数量很大时, 上述模型效率不佳.此外, 由于它们只学习历史时间戳的嵌入, 因此不能推广到未来时间戳.
针对上述不足和受历时词嵌入(Diachronic Word Embeddings)的启发, Goel等[20]提出历时嵌入(Diachronic Embedding, DE), 在给定实体和任意时间戳后, 计算实体的动态表示, 有代表性的模型是DE_SimplE.但DE_SimplE只能提供天级时间粒度的实体表示, 为了获取更细时间粒度的实体表示, 本文在DE_SimplE的基础上添加可以处理秒级时间戳的历时函数, 得到交通事故时序知识图谱历时嵌入模型(DETA).
定义1 路网 路段级事故风险预测研究的地理范围是城市行政区.首先借助Python第三方库OSMnx获取行政区路网, 再对道路路段进行拼接、过滤等预处理, 最终获得长度在500~2 000 m的路段, 路段数为N.
路网可以视为一个有向图
Groad=(V, Eroad, A),
其中,
V={v1, v2, …, vN}
表示路段集合; Eroad⊂V× V表示边集, ei, j∈ Eroad表示路段i与路段j相邻; A∈ RN× N表示路段邻接矩阵
Ai, j=
定义2 路段关系图 浅层次的路段语义视角就是真实的路段邻接关系, 对应的路段关系图表示为
为了方便表述, 所有路段关系图都只由邻接矩阵定义.
浅层次兴趣点和事故风险视角下的路段关系图表示为
定义3 事故风险 根据事故中的伤亡人数, 本文将交通事故分为轻微事故、一般事故和严重事故三种[8], 对应的事故风险值为1、2和3.Y
定义4 时序知识图谱 时序知识图谱可定义为
其中, E表示实体集合; R表示关系集合; T表示时间戳集合, 时间戳精度为秒; φ (· )表示实体到实体类型的映射函数; ϕ (· )表示关系到关系类型的映射函数; A表示实体类型集合; B表示关系类型集合.
给定静态数据Xs和历史T个时间段的动态数据
Xd={
预测未来下一个时间段内的所有路段的事故风险Yτ +1.动态数据和静态数据拼接得到最初输入X.
此处, 静态数据Xs∈ RN× S, 表示兴趣点的分布, S表示静态数据的特征维度.
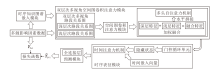
本文提出融合时序知识图谱的双层次多视角时空图神经网络模型(STGN-TKG), 架构图如图1所示.STGN-TKG主要由四部分组成:时序知识图谱嵌入模块、双层次多视角的空间图卷积注意力模块、时序表征模块和预测模块.
输入X后, 模型首先通过时序知识图谱嵌入模块获取多源影响因素的深层历时嵌入, 由此, 构建深层次路段关系图, 同时配合路段物理层面的浅层关系图, 利用双层次多视角的空间图注意力模块捕获交通事故风险数据中的空间信息, 再采用时序表征模块捕获交通事故风险数据中的时间相关性, 最后预测输出所有路段的交通事故风险.
现有关于交通事故风险预测的工作都是从浅层次语义视角进行相关性建模[1, 2, 3, 4, 5], 未从深层次语义视角挖掘不同数据对交通事故深层次的复杂影响.知识图嵌入是将知识图谱嵌入低维空间中, 学习实体和关系的表示, 能有效挖掘实体之间的高阶相关性.因此, 知识图谱嵌入是处理多源数据更佳的方式.考虑到时间的动态性, 本文采用时序知识图谱嵌入.
时序知识图谱嵌入模块首先基于训练集数据构建一个交通事故时序知识图谱, 然后设计可以融入秒级时间戳信息的交通事故时序知识图谱历时嵌入模型(DETA), 建模多源影响因素之间的动态、高阶相关性, 最后通过预训练的方式, 得到多源影响因素的深层嵌入表示.
3.1.1 构建交通事故时序知识图谱
首先, 基于训练集数据构建交通事故时序知识图谱.基于时序知识图谱的定义, 给出交通事故时序知识图谱的定义
G={(u, r, v, t)|u∈ E, v∈ E, r∈ R, t∈ T, φ (u)∈ A, φ (v)∈ A, ϕ (r)∈ B}.
A有6种实体类型, 包括:事故等级与原因实体、交通状态等级实体、出租车服务区域实体、兴趣点实体、天气实体和路段实体.B有9种关系类型, 包括:天气状态关系、交通状态关系、区域相邻关系、路段下游关系、路段交叉关系、区域包含兴趣点关系、区域包含路段关系、路段邻近兴趣点关系和事故发生关系.所有关系都是单向关系, 不区分单向和双向.T只包括训练集中出现过的时间戳.
图2为交通事故时序知识图谱的一个实例, 图中不同的节点表示不同实体, 不同的边表示不同的关系, 边是有向的.
3.1.2 时序知识图谱历时嵌入模型
为了获得秒级时间粒度的历时实体嵌入, 本文设计可以处理秒级时间戳的交通事故时序知识图谱历时嵌入模型(DETA).模型由三部分组成:关系嵌入方法、实体嵌入方法和得分函数.
1)关系嵌入方法.关系r∈ R嵌入表示zr的定义如下:
zr[i]={lr[i], tr[i]}, 1≤ i≤ d, (1)
其中, lr∈ Rd表示正向关系r的可学习向量, tr∈ Rd表示逆反关系
2)实体嵌入方法.实体v∈ E在时刻t作为头实体的历时嵌入表示
$\begin{array}{l} z_{v}^{t}[i]= \\ \left\{\begin{array}{ll} \sum_{j \in P_{t}} a_{v}^{j}[i] \sin \left(w_{v}^{j}[i] j+b_{v}^{j}[i]\right), & 1 \leqslant i \leqslant \gamma d \\ m_{v}[i], & \gamma d< i \leqslant d \end{array}\right. \end{array}$ (2)
其中, γ 表示嵌入中动态部分的比例值, a
设
3)得分函数.给定任意事实四元组f=(u, r, v, t), 得分函数会给出事实发生的概率:
ψ (u, r, v, t)=
其中
得分函数是正向事实四元组与逆向事实四元组语义匹配得分的平均值, 头实体历时嵌入经过关系嵌入的线性映射后得到的嵌入与尾实体历时嵌入越相近, 语义匹配得分越高.
3.1.3 历时嵌入模型预训练
基于构建好的交通事故时序知识图谱对DETA进行预训练.在预训练时, γ 设置为0.32, 历时嵌入维度为100, 训练100轮.对于任意事实四元组f=(u, r, v, t), 将头实体u或尾实体v随机替换为实体集E的其它实体e(e≠ u且e≠ v), 得到Nneg个负样本, 正样本则是本身.最后使用交叉熵损失函数指导模型正确区分正负样本, 即
其中, Θ 表示Nneg个负样本的替换实体集, ψ (· )表示得分函数.
在正式训练时, 给定实体和目标时间段τ +1对应的时间戳, DETA会计算实体的深层历时嵌入.不妨设路段、兴趣点、事故等级与原因在目标时间段τ +1内的深层历时实体嵌入矩阵分别为
为了充分挖掘路段之间的空间相关性对交通事故的影响, 在双层次多视角的空间图卷积注意力模块中设计双层次路段关系图, 包括基于深层历时实体嵌入得到的深层次路段关系图和基于真实世界的语义构建的浅层次路段关系图.此外, 对于每个层次, 同时从路段、兴趣点、事故风险三个语义视角建模路段的邻接关系.构建双层次多视角的路段关系图后, 采用空间图卷积与多头自注意力机制, 捕获交通事故风险的空间相关性.
3.2.1 浅层次路段关系图
在真实世界的语义空间中, 路段存在物理层面的浅层相关性, 对事故风险有直接影响.
浅层次路段语义视角下的路段关系图直接基于路网中路段的真实邻接关系构建, 即
在兴趣点语义视角下, 计算的分布是路段附近的兴趣点分布, 而在事故风险语义视角下, 计算的分布是训练集上路段的事故风险分布.具体计算过程如下:
$\begin{aligned} A_{* }^{s}(i, j)=1- & J S\left(\boldsymbol{R}_{* }^{i}, \boldsymbol{R}_{* }^{j}\right), \\ J S\left(\boldsymbol{R}_{* }^{i}, \boldsymbol{R}_{* }^{j}\right)= & \frac{1}{2} \sum_{1 \leqslant l \leqslant L}\left(R_{* }^{i}(l) \ln \left(\frac{2 R_{* }^{i}(l)}{R_{* }^{i}(l)+R_{* }^{j}(l)}\right)+\right. \\ & \left.R_{* }^{j}(l) \ln \left(\frac{2 R_{* }^{j}(l)}{R_{* }^{i}(l)+R_{* }^{j}(l)}\right)\right), \end{aligned}$
其中, * ∈ {risk, poi}, Ri* ∈ RL和Rj* ∈ RL表示路段i和路段j在特定语义视角下的特征分布.
可以提前计算浅层次路段关系图.
3.2.2 深层次路段关系图
为了基于知识图谱得到实体嵌入, 从路段、兴趣点、事故风险三个语义视角分别构建深层次路段关系图, 需要先计算路段和兴趣点之间的关系(即转移矩阵)T
基于转移矩阵和时序知识图谱嵌入模块输出的深层历时实体嵌入矩阵, 可以求出路段在不同语义视角下的动态嵌入, 再以自适应[22]的方式构建不同语义视角下的深层次路段关系图.具体操作如下:
$\begin{array}{l} \boldsymbol{A}_{\text {road }}^{d}=\operatorname{softxmax}\left(\operatorname{ReLU}\left(\left(\boldsymbol{E}_{\tau+1}^{r}\right)^{\mathrm{T}} \boldsymbol{E}_{\tau+1}^{r}\right)\right), \\ \boldsymbol{A}_{\mathrm{poi}}^{d}=\operatorname{softxmax}\left(\operatorname{ReLU}\left(\left(\boldsymbol{M}_{r}^{p}\right)^{\mathrm{T}} \boldsymbol{M}_{r}^{p}\right)\right), \\ \boldsymbol{A}_{\text {risk }}^{d}=\operatorname{softxmax}\left(\operatorname{ReLU}\left(\left(\boldsymbol{M}_{r}^{f}\right)^{\mathrm{T}} \boldsymbol{M}_{r}^{f}\right)\right), \end{array}$
其中, M
M
ReLU(· )表示激活函数.
采用自适应的方式构建路段关系图, 可以让模型感知交通事故对路网的动态影响, 从而实现更准确的事故风险预测.
3.2.3 空间图卷积注意力模块
构建好双层次多视角的路段关系图后, 本文使用两层的图卷积进行空间信息的聚合与传播, 即
其中, * ∈ {road, risk, poi}, Ψ ∈ {d, s}, W0, b0, W1、b1表示可学习参数, 不同路段关系图有不同的可学习参数,
获取到不同层次、不同视角下的图卷积输出后, 首先对相同视角、不同层次的路段表示进行加权融合:
X* =w* Xs* +Xd* ,
其中, w* 表示可学习参数, 初始值为0.5.
然后, 水平拼接不同语义视角下的路段表示, 得到
X'=Xroad‖ Xpoi‖ Xrisk∈ RT× N× (3× D).
空间图卷积只是独立建模路段在不同语义空间中的局部空间相关性, 为了挖掘路段在不同语义空间之间的全局空间相关性, 本文采用多头自注意力机制(Multi-head Attention, MHA)[23]进行进一步处理.该过程可表述为
其中, W
多头注意力机制的输入特征维度与输出特征维度一样, 因此, 模块最终输出$\widetilde{\boldsymbol{X}} \in \mathbf{R}^{T \times N \times(3 \times D)} \text {. }$
除了空间相关性, 交通事故数据中也存在明显的时间相关性, 包括短期相关性和长期相关性.本文采用GRU(Gated Recurrent Unit)建模数据在时间上的长短期相关性, 隐藏状态
其中,
H={h1, h2, …, hT}∈
其中, hi∈
为了更深刻地建模时间依赖性, 并捕获历史时间段对目标时间段的动态影响, 本文引入时间注意力机制[24].注意力分数
a=softmax(ReLU(HWX+Eτ +1WE+ba))∈ RT,
其中, WX、WE和ba表示可学习参数, Eτ +1表示目标时间段的时间嵌入向量.
基于注意力分数, 对每个时间段的GRU输出进行加权聚合, 即
基于最终表示
$\widehat{\boldsymbol{Y}}_{\tau+1}=\operatorname{MLP}(\widehat{\boldsymbol{X}}) \in \mathbf{R}^{N}$
关于损失函数, 本文选择均方误差(Mean Squared Error, MSE), 计算公式如下:
$\text { Loss }=\frac{1}{N}\left(\boldsymbol{Y}_{\tau+1}-\widehat{\boldsymbol{Y}}_{\tau+1}\right)^{2} \text {. }$ (5)
模型训练包括预训练与正式训练, 都使用Adam(Adaptive Moment Estimation)优化算法[25]进行参数学习.时序知识图谱嵌入模块需要进行预训练, 式(4)会指导DETA在交通事故时序知识图谱上进行充分训练, 完成预训练的DETA能产生蕴含动态、高阶相关性的历时实体嵌入.在正式训练时, 式(5)会指导STGN-TKG在路段级交通事故风险数据集上进行充分训练, DETA的参数也会进行微调, 以便更好地适应事故风险数据集.
基于第三方库OSMnx和纽约市公开城市数据(https://opendata.cityofnewyork.us), 本文构建两个真实的路段级交通事故风险数据集:布鲁克林数据集和曼哈顿数据集, 具体时间跨度为2019年1月1日至2019年12月31日.两个数据集的统计情况如表1所示.
| 表1 数据集统计信息 Table 1 Statistics of datasets |
为了缓解零膨胀问题, 本文提出事故风险传播策略:在任意时间段内, 计算每个路段的事故风险后, 对于风险值不为零的路段, 将其风险值进行辐射性广播, 即
ris
其中, risk
当路段上发生事故时, 事故不仅会影响本路段的风险值, 还会对通过路段邻接关系影响相邻路段的事故风险值, 即事故的影响会通过路网扩散.先前关于交通事故风险预测的工作在计算事故风险时, 只考虑事故对自身路段(区域)的影响, 忽略对其它路段(区域)的影响, 这样的风险计算方式显然不准确.而事故风险传播策略会以指数衰减的形式在路网中传播事故的影响, 这是符合实际场景需求的, 因此事故风险传播策略不仅可以缓解零膨胀问题, 还可以让事故风险的计算方式更合理准确.
数据集按时间顺序以6∶ 2∶ 2的比例划分为训练集、验证集和测试集.时间段粒度是小时, 一天划分为h=24个时间段, 一周观测w=7天.构造样本时T取值为7, 其中p=3, q=4, 样本标签是未来一个小时内所有路段的事故风险值.事故风险传播策略中k=5.经过参数搜索, 模型在两个数据集上的重要超参数设置如表2所示.
| 表2 超参数设置 Table 2 Hyperparameter settings |
本文使用如下3个指标综合评估模型的性能.考虑到预测任务是回归问题, 本文使用均方根误差(Root MSE, RMSE)衡量回归误差.受相关论文启发[3, 4, 26], 本文研究任务也可以视为排序问题, 因此采用召回率(Recall)和平均精度均值(Mean Average Precision, MAP)评估模型对高风险路段的排序误差.评价指标计算公式如下:
其中:S表示测试集样本数; Y(i)和
RMSE关注预测的准确性, 值越小越好, 而Recall和MAP关注高风险路段的召回率和平均精度, 值越大越好.在事故风险预测中, 高风险路段的预测结果更受关注, 也更具有应用价值, 因为高风险路段预测准确比低风险路段预测准确的影响更大, 因此Recall和MAP指标更具有参考意义.
为了进一步检验模型在事故发生概率较高的高峰时段的预测性能, 本文还评估模型在高峰时段的预测性能.经过对训练集数据进行统计分析, 确定高峰时段集合为{14, 15, 16, 17, 18, 19}, 相应的指标值符号为RMSE* 、Recall* 、MAP* .
本文将STGN-TKG与如下7个基准模型进行对比.
1)HA(Historical Average).将样本输入中事故风险值序列的均值作为预测结果.
2)MLP.由多层全连接层组成, 隐藏层之间设置激活函数, 进行转换与激活.
3)SDCAE[2].堆叠多个去噪卷积层, 捕获地理空间特征, 预测城市尺度上的交通事故风险.
4)GSNet[4].能有效地从地理和语义两方面捕捉复杂的时空关系, 用于交通事故风险预测.
5)AGCRN(Adaptive Graph Convolutional Re-current Network)[22].基于两个增强图卷积的自适应模块和循环神经网络, 自动捕获交通序列中时空相关性.
6)GRU[27].经典的时间序列预测模型, 可以有效捕获数据在时间维度上的非线性依赖关系.
7)ConvLSTM(Convolutional LSTM)[28].结合CNN(Convolutional Neural Network)和LSTM(Long Short Term Memory), 可以对空间依赖性和时间依赖性进行建模.
各对比模型在布鲁克林、曼哈顿数据集上的实验结果如表3和表4所示, 表中黑体数字表示最佳值, 斜体数字表示次优值.
| 表3 各模型在布鲁克林数据集上的预测性能 Table 3 Prediction performance of different models on Brooklyn dataset |
| 表4 各模型在曼哈顿数据集上预测性能 Table 4 Prediction performance of different models on Manhattan dataset |
表3和表4结果表明, STGN-TKG在几乎所有场景下都取得最佳值.由于HA无法捕捉复杂的时空相关性, 性能明显低于深度学习方法.MLP结构简单, 无法充分捕获时空相关性.GRU只考虑时间相关性, 却忽略空间相关性.SDCAE只通过CNN提取局部空间相关性, 却忽略时间相关性.因此, 这些模型的预测效果都不太理想.ConvLSTM同时考虑时间相关性和空间相关性, 相比MLP和GRU, 指标值有不小的提升.GSNet能充分捕获多语义时空相关性, 所以在Recall和MAP指标上表现较优, 但由于其未能从深层语义视角进行信息的聚合与传播, 导致RMSE指标很差.AGCRN虽然能自适应地选择最佳空间模式, 并有效建模时间相关性, 但不能从多个语义视角建模空间关系, 因此预测效果不如STGN-TKG.
总之, 所有基准模型都只是在浅层语义上对时空相关性进行建模和捕捉, 无法学习和应用动态的高阶语义信息, 并进一步提高预测性能.而在浅层次路段关系图的基础上, STGN-TKG能借助DETA产生的历时实体嵌入构建深层次路段关系图, 进而采用空间图卷积注意力模块和时序表征模块同时对浅层语义和深层语义时空相关性进行有效挖掘与提取, 因此取得最佳的预测效果.
为了验证STGN-TKG中设计的核心模块是否对预测效果有提升作用, 设计如下3个模型变体.
1)-TKG.移除时序知识图谱嵌入模块, 随机初始化向量(torch.nn.Embedding)替换深层历时嵌入.
2)-DepthGCN.移除深层次空间图卷积组件, 包括深层次路段关系图的构建.
3)-SpatialAttn.移除全局空间注意力组件, 即不使用多头自注意力机制.
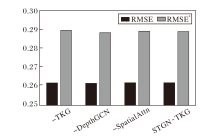
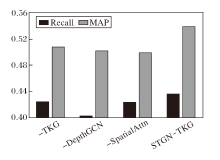
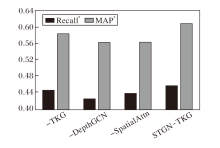
在曼哈顿数据集上开展消融实验, 结果如图3~图5所示.由图可见, 在RMSE指标上, 三种变体与完整模型非常接近, 但在另外两个指标上, 完整模型优势明显.
对比-TKG和完整模型可以得出, 时序知识图谱嵌入模块计算的深层历时嵌入蕴含实体的动态性和实体之间的高阶相关性, 从而优于自适应嵌入方式.-DepthGCN和完整模型的实验结果说明深层次图卷积能有效利用基于深层历时嵌入构建的深层次路段关系图进行事故空间信息的聚合与传播.-SpatialAttn和完整模型的实验结果则表明多头自注意力机制能捕获路段在不同语义空间之间的全局空间相关性.
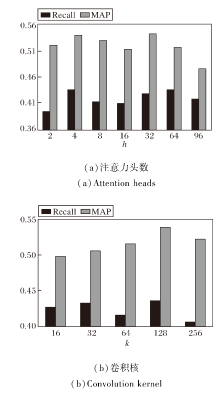
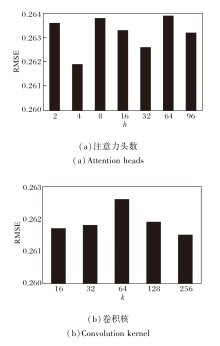
为了研究不同超参数对模型性能的影响, 选择对模型性能影响较大的两个超参数, 即图卷积核和注意力头数进行实验.实验在曼哈顿数据集上开展, 除了注意力头数与卷积核, 其余超参数设置与最优超参数一致.实验结果如图6和图7所示, 图中对比预测所有时段的指标值.
由图6可知, MAP和Recall指标虽然有稍许上下波动, 但整体都呈现出先增后减的变化趋势.由图7可知, RMSE指标变化波动较小, 注意力头数改变时整体呈现先减后增的变化趋势, 卷积核改变时呈现明显的先增后减趋势.
综合三种指标可知, 注意力头数取值为4或卷积核取值为128时, 模型性能最优.
为了探究事故风险传播策略的有效性, 在曼哈顿数据集上开展实验, 对比使用与不使用事故风险传播策略时的指标值, 具体如表5所示, 表中-AUG表示不使用事故风险传播策略.模型超参数设置相同.
| 表5 是否使用事故风险传播策略的模型性能对比 Table 5 Performance comparison of models with or without accident risk propagation strategy |
由表5可见, 虽然RMSE指标稍微变差了一些, 但Recall和MAP指标有大幅提升, 说明事故风险传播策略不仅缓解数据零膨胀问题, 而且使交通事故风险的计算方式更合理, 更符合实际场景, 进而使模型能更准确地预测高风险路段, 显著提升模型的整体性能.
本文提出融合时序知识图谱的双层次多视角时空图神经网络模型(STGN-TKG).首先, 为了充分建模多源数据的动态性并挖掘多源数据中的高阶相关性, 构建交通事故时序知识图谱, 并设计交通事故时序知识图谱历时嵌入模型(DETA), 进行预训练, 获得多源数据的深层嵌入表示.然后, 设计双层次多视角的空间图卷积注意力模块, 从深浅两个层次, 以及路段、兴趣点和事故风险三个语义视角进行空间信息的聚合与传播, 并采用门控循环单元与时间注意力捕获时间相关性.为了缓解零膨胀问题, 提出事故风险传播策略.最后, 在两个真实的路段级交通事故风险数据集上的实验验证STGN-TKG的优越性.针对零膨胀问题, 本文只提出事故风险传播策略, 只能缓解此问题而并未解决, 因此, 如何设计一种有效的解决方案是进一步提升模型事故风险预测性能的研究方向之一.
本文责任编委 陶卿
Recommended by Associate Editor TAO Qing
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|