基于耦合协调种群状态评估的差分进化算法

引用本文

封全喜, 金培源, 岑健铭, 艾武, 林彬. 基于耦合协调种群状态评估的差分进化算法. 模式识别与人工智能, 2023,36(8): 733-748
FENG Quanxi, JIN Peiyuan, CEN Jianmin, AI Wu, LIN Bin. Differential Evolution Algorithm Based on Coupling and Coordinating Population State Assessment. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(8): 733-748. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202308006
Permissions

《模式识别与人工智能》编辑部

基于耦合协调种群状态评估的差分进化算法

封全喜^1,², 金培源¹, 岑健铭¹, 艾武^1,², 林彬^1,²

1.桂林理工大学理学院桂林 541004

2.桂林理工大学广西高校应用统计重点实验室桂林 541004

通讯作者:

林彬,博士研究生,副教授,主要研究方向为计算机视觉.E-mail:linbin@glut.edu.cn.

作者简介:

封全喜,博士,教授,主要研究方向为智能计算、机器学习及其应用.E-mail:fqx9904@163.com.

金培源,硕士研究生,主要研究方向为智能计算.E-mail:minkewhale@foxmail.com.

岑健铭,硕士研究生,主要研究方向为智能计算.E-mail:cenjianming0819@foxmail.com.

艾武,博士,副教授,主要研究方向为机器学习及其应用.E-mail:aiwu818@gmail.com.

收稿日期: 2023-03-27 接受日期: 2023-08-30

资助项目: 国家自然科学基金项目(No.62166015,62166013)

摘要

差分进化算法是一种基于群体内个体之间差异的全局随机搜索算法,其中变异算子是差分进化算法的重要组成部分,不同的变异算子适用于不同的种群分布情况.为了有效识别种群的进化状态,文中提出基于耦合协调种群状态评估的差分进化算法,计算四个不同等级目标函数值和个体间距离的耦合协调度,评估种群在迭代过程中所处的进化状态.根据评估结果将种群状态分为搜索、平衡、收敛三种进化状态,并针对不同的进化状态构造相应的变异算子池.此外,通过自适应调节Powell方法,提升算法的收敛速度.最后,在CEC2017测试函数集上的数值实验验证文中算法的有效性.

关键词: 差分进化算法; 耦合协调度; 变异算子; 进化状态; 自适应Powell方法

中图分类号:TP18

Differential Evolution Algorithm Based on Coupling and Coordinating Population State Assessment

FENG Quanxi^1,², JIN Peiyuan¹, CEN Jianmin¹, AI Wu^1,², LIN Bin^1,²

1. College of Science, Guilin University of Technology, Guilin 541004

2. Guangxi Colleges and Universities Key Laboratory of Applied Statistics, Guilin University of Technology, Guilin 541004

Corresponding author:
LIN Bin, Ph.D. candidate, associate professor. His research interests include computer vision.

About Author:
FENG Quanxi, Ph.D., professor. His research interests include intelligent computing, machine learning and its applications.
JIN Peiyuan, master student. Her research interests include intelligent computing.
CEN Jianming, master student. His research interests include intelligent computing.
AI Wu, Ph.D., associate professor. His research interests include machine learning and its applications.

Fund:National Natural Science Foundation of China(No.62166015,62166013)

Abstract

Differential evolution is a global stochastic search algorithm based on the differences between individuals within a population. The mutation operator is an important component of the differential evolution algorithm, and different mutation operators are suitable for different population distributions. To effectively identify the evolutionary state of the population, a differential evolution algorithm based on coupling and coordinating population state assessment(CCPDE) is proposed. The evolutionary state of the population in the iteration process is evaluated by calculating the coupling coordination degree between four different levels of fitness values and individual distances. The population is classified based on the evaluation results into three evolutionary states: search, balance and convergence, and corresponding mutation operator pools are constructed for different evolutionary states. In addition, the convergence speed of CCPDE is accelerated by adaptive adjustment of the Powell method. Numerical experiments on CEC2017 test functions show the effectiveness of CCPDE.

Key words: Key Words Differential Evolution Algorithm; Coupling Coordination Degree; Mutation Operator; Evolutionary State; Adaptive Powell's Method

文章图片

差分进化(Differential Evolution, DE)是Storn等^[1]提出的一种简单且功能强大的进化算法.算法基于种群内个体之间的差异性进行迭代, 具有较强的全局搜索能力, 现已成功应用于许多工程领域, 包括:无人机路径规划^[2]、斜拉桥索力优化^[3]、系统功率分配^[4]、飞行控制率评估^[5]、激光熔覆工艺参数优化^[6]等.

差分进化算法主要由变异、交叉、选择三个算子构成.变异算子是差分进化算法的重要组成部分, 不同的变异算子迭代效果不同.因此, 在算法迭代过程中, 需要选择合适的变异算子.针对此问题, 学者们提出多种不同的变异算子及其选择策略.常见的变异算子选择策略都是基于概率模型提出的.Qin等^[7]提出SaDE(Self-Adaptive DE), 根据各变异算子的前期迭代效果计算后验概率, 并依据概率值选择合适的变异算子.Liu等^[8]提出HHDE(Historical and Heuristic DE), 基于个体历史成功经验和其当前状态信息动态选择变异算子和控制参数.Pan等^[9]提出SspDE(DE Algorithm with Self-Adaptive Trial Vector Generation Strategy and Control Parameters), 设计变异算子列表, 存放上一代变异成功的变异算子, 并据此计算选择概率.

此外, 还有学者提出基于多策略共存的变异算子选择策略.Wang等^[10]提出CoDE(Composite DE), 算法中每个个体采用多个不同类型的变异算子, 产生多个候选个体, 并选择适应度值高的个体进入下一代.Wang等^[11]在CoDE的基础上, 提出C²oDE(Constrained CoDE), 采用三种不同变异算子, 其中两个算子侧重收敛性能, 一个算子侧重搜索性能.此外将可行性准则和ε 约束方法进行搭配, 进而选择合适的个体进入下一代.数值实验表明该算法是一种有效的算法.还有学者通过种群划分方式, 分别为不同类型的种群分配不同的变异算子.Wu等^[12]提出MPEDE(Multi-population Based Ensemble DE), 将种群分为三个规模相同的指标种群和一个奖励子种群, 并为每个指标种群分配不同的变异算子.每隔一定代数后, 根据三个变异算子的迭代效率, 将性能最优的变异算子分配给奖励子种群.

近年来, 也有学者基于种群的分布信息选择变异算子.Liu等^[13]提出TSDE(DE with a Two-Stage Optimization Mechanism), 利用迭代过程中前期注重全局搜索和后期注重局部收敛的特点, 将迭代过程均衡划分为两个阶段, 分别设计变异算子池.Zhou等^[14]提出DEMS(DE with Multi-stage Strategies), 利用种群中个体间的平均距离将迭代过程划分成搜索、平衡和收敛三个阶段, 不同阶段分别使用不同类型的变异算子.Zhan等^[15]提出APSO(Adaptive Particle Swarm Optimization), 计算种群中所有个体之间的欧氏距离, 评估种群的分布情况, 并针对不同的分布情况采用不同的变异算子.Yu等^[16]提出ADE(Adaptive DE), 利用种群中最优个体与其它个体之间的欧氏距离评估种群的分布情况.考虑到计算所有个体之间欧氏距离的计算复杂度较高, Zhan等^[17]提出ADDE(Adaptive Distributed DE), 利用种群中最优个体和中间个体评估种群的分布情况.Li等^[18]提出DEET, 计算所有个体距离与目标函数值的相关性, 评估种群进化状态.

上述种群状态评估算法取得良好的效果, 表明根据种群个体的分布信息和目标函数值评估种群状态, 再选择合适变异算子, 有助于提升差分进化算法的性能.然而, 部分种群状态评估算法只是单纯使用最优个体或中位数个体以评估种群状态, 导致种群状态评估不准确.还有部分种群状态评估算法即使利用种群分布信息和目标函数值, 也仅仅以最优个体作为参照评估种群状态, 容易导致评估结果不稳定.还有部分种群状态评估算法利用种群中所有个体, 导致算法的计算复杂度较高.

为了有效评估种群状态, 本文提出基于耦合协调种群状态评估的差分进化算法(DE Algorithm Based on Coupling and Coordination Population State Evaluation, CCPDE), 计算四个不同等级目标函数值和个体间距离的耦合协调度, 评估种群在迭代过程中所处的进化状态.根据评估结果将种群状态分为搜索、平衡、收敛三种进化状态, 并针对不同的进化状态构造相应的变异算子池.此外, 通过自适应Powell方法^[19], 提升算法的收敛速度.最后, 在CEC2017测试函数集上的数值实验验证本文算法的有效性.

1 差分进化算法

差分进化算法是一种新兴的进化计算技术, 最初用于解决切比雪夫多项式问题, 后来逐渐发展成为解决复杂优化问题的有效技术.差分进化算法是一种基于群体智能的全局随机搜索算法, 具有控制参数较少、容易实现、优化效果稳健等优点.在算法迭代过程中, 差分进化算法特有的记忆能力有助于算法动态跟踪当前搜索情况, 调整搜索策略.

与其它进化算法类似, 差分进化算法的迭代过程中不需要借助问题的特征信息, 适应于求解各种类型的复杂优化问题.算法主要通过种群内个体间的差异产生下一代种群.

相比其它进化算法, 差分进化算法基于种群的全局搜索策略、差分变异操作和“ 一对一” 的竞争选择策略.算法主要由变异、交叉和选择这三个基本操作组成.

变异算子是差分进化算法的重要组成部分, 根据向量之间的差异提升种群的多样性.不同的变异算子具有不同的性能.下面列出7种常见的变异算子.

1)DE/rand/1:

$v_{i}^{g}$ = $x_{r_{1}}^{g}$ +F· ( $x_{r_{2}}^{g}$ - $x_{r_{3}}^{g}$ ).

2)DE/best/1:

$v_{i}^{g}$ = $x_{best}^{g}$ +F· ( $x_{r_{1}}^{g}$ - $x_{r_{2}}^{g}$ ).

3)DE/best/2:

$v_{i}^{g}$ = $x_{best}^{g}$ +F· ( $x_{r_{2}}^{g}$ - $x_{r_{3}}^{g}$ )+F· ( $x_{r_{4}}^{g}$ - $x_{r_{5}}^{g}$ ).

4)DE/current-to-rand/1:

$v_{i}^{g}$ = $x_{i}^{g}$ +F· ( $x_{r_{1}}^{g}$ - $x_{i}^{g}$ )+F· ( $x_{r_{2}}^{g}$ - $x_{r_{3}}^{g}$ ).

5)DE/current-to-best/1:

$v_{i}^{g}$ = $x_{i}^{g}$ +F· ( $x_{best}^{g}$ - $x_{i}^{g}$ )+F· ( $x_{r_{1}}^{g}$ - $x_{r_{2}}^{g}$ ).

6)DE/current-to-pbest/1^[20]:

$v_{i}^{g}$ = $x_{i}^{g}$ +F· ( $x_{pbest}^{g}$ - $x_{i}^{g}$ )+F· ( $x_{r_{1}}^{g}$ - $x_{r_{2}}^{g}$ ).

7)DE/current-to-ci_mbest/1^[21]:

$\begin{array}{l} \boldsymbol{v}_{i}^{g}=\boldsymbol{x}_{i}^{g}+F \cdot\left(\boldsymbol{x}_{\text {ci_mbest }}^{g}-\boldsymbol{x}_{i}^{g}\right)+F \cdot\left(\boldsymbol{x}_{r_{1}}^{g}-\boldsymbol{x}_{r_{2}}^{g}\right), \\ \boldsymbol{x}_{c i \_m b e s t}^{g}{ }^{g}=\sum_{k=1}^{m} w_{k} \boldsymbol{x}_{k}^{g}, \\ w_{k}=\frac{m-k+1}{1+2+\cdots+m}, k=1, 2, \cdots, m . \end{array}$

其中: $v_{i}^{g}$ 表示第g代的第i个变异向量; F∈ [0, 1]表示缩放因子; r₁、r₂、r₃、r₄、r₅表示在{1, 2, …, NP}中随机选择且互不相等的整数, NP表示种群规模; $x_{best}^{g}$ 表示最优个体; $x_{pbest}^{g}$ 表示从NP× p个较优个体中随机选择的个体, p为[0, 1]区间内均匀分布随机数; $x_{ci_mbes t^{i}}^{g}$ 表示种群中目标函数值排名前m个个体的线性组合向量, m表示从[1, i]区间内随机选择的一个整数; w_k表示组合向量的权重.

交叉算子按一定概率将变异个体 $v_{i}^{g}$ 与父代个体 $x_{i}^{g}$ 进行重组, 生成实验向量:

$\begin{array}{l} \boldsymbol{u}_{i}^{g}=\left(u_{i, 1}^{g}, u_{i, 2}^{g}, \cdots, u_{i, D}^{g}\right), \\ u_{i, j}^{g}=\left\{\begin{array}{ll} v_{i, j}^{g}, & \operatorname{rand}_{j}(0, 1)< C R \text { 或 } j=j_{\text {rand }} \\ x_{i, j}^{g}, & \text { 其它 } \end{array}\right. \end{array}$

其中, D表示函数维数, j_rand表示{1, 2, …, D}中的一个随机整数, CR表示交叉概率.

选择算子采用一对一的“ 贪婪” 选择方式, 将实验向量 $u_{i}^{g}$ 和父代个体 $x_{i}^{g}$ 两两对比, 选择目标函数值较优的个体进入下一代, 即

$x_{i}^{g + 1}$ = $\{\begin{array}{l} u_{i}^{g}, & f (u_{i}^{g}) \leq f (x_{i}^{g}) \\ x_{i}^{g}, & f (u_{i}^{g}) > f (x_{i}^{g}) \end{array}$

其中, $x_{i}^{g + 1}$ 表示第g+1代的第i个个体, f(· )表示个体的目标函数值.

2 基于耦合协调种群状态评估的差分进化算法

差分进化算法是一种群体智能进化算法, 其“ 贪婪” 的选择算子有助于算法在迭代过程中不断进行优胜劣汰.在迭代过程中, 差分进化算法通常利用某些个体或某些群体, 如最优个体、最优子种群等信息引导种群朝着更好的方向进化.然而, 这些进化方式由于种群状态的不同而呈现多样化.

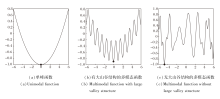
根据解的近似最优性原理可知, 优良解之间具有相似结构^[22].此原理广泛应用于提升进化算法的性能, 特别是具有较大山谷结构的优化问题.连续优化问题的搜索空间可以大致分为三类:单峰函数、有大山谷结构的多模态函数和无大山谷结构的多模态函数^[18].这3种不同类型函数的极值点分布如图1所示.

	Figure Option View Download New Window
	图1 三种不同类型函数的极值点示意图Fig.1 Schematic diagrams of extreme points for 3 different types of functions

由图1可知, 第一个函数只有一个驻点, 即单峰函数的极值点.因此, 采用最优个体作为基向量, 有助于提高最优解的精度和算法的收敛速度.第二个函数为有大山谷结构的多模态函数, 解空间包含多个结构明显的局部极值点, 但总体上看呈现大山谷结构.在这种情况下, 虽然最优个体仍然能较好地指导种群进化, 但为了避免种群陷入局部最优解, 应选择特定的最优群体作为基向量较为合适.第三个函数为无大山谷结构的多模态函数, 解空间具有多个局部极值点且分布结构不明显, 这种情况使用全局搜索性能更强的变异算子搜索更有希望的区域, 避免算法陷入局部最优解.

基于上述分析可知, 差分进化算法的进化过程中种群状态会动态变化.本文将上述三种情况分别记为收敛状态、平衡状态和搜索状态.根据“ 没有免费午餐” 定理^[23], 每个变异算子都有自己特定的适用范围.因此, 如何针对不同种群状态选择合适的变异算子是一个极具挑战的任务.

因此, 本文首先利用耦合协调度模型度量种群的分布情况, 将种群进化状态分为搜索、平衡、收敛三种情况, 再根据不同的进化状态, 分别设计不同的变异算子池.

2.1 基于耦合协调度模型的种群进化状态识别

耦合协调度模型常用于分析事物的协调发展水平, 由耦合度和协调度两部分构成.耦合度的概念源于物理学领域^[24], 一般用于刻画多个指标之间相互影响的程度, 已广泛应用于社会科学领域^{[25, 26]}.协调度指耦合相互作用关系中良性耦合程度的大小, 可体现协调状况的好坏.

本文使用耦合协调度模型评估目标函数值与个体距离两个指标之间的关系, 从而多角度度量当前种群进化状态, 减少种群进化状态的误判.根据统计学中四分位数概念, 本文以上四分位数、中位数、下四分位数3个分割点, 将排序后种群分为4个等级的子种群, 再通过耦合协调度模型计算种群的进化状态.具体步骤如下.

1)将种群中所有个体按目标函数值的优劣排序, 并根据排序结果将种群均分成4个不同等级的子种群, 分别记为POP₁、POP₂、POP₃、POP₄.

2)从4个子种群POP₁、POP₂、POP₃、POP₄中分别随机抽取4个个体 $X_{1, i_{1}}$ 、 $X_{2, i_{2}}$ 、 $X_{3, i_{3}}$ 、 $X_{4, i_{4}}$ , 它们的目标函数值分别记为 $f_{1, i_{1}}$ 、 $f_{2, i_{2}}$ 、 $f_{3, i_{3}}$ 、 $f_{4, i_{4}}$ , 计算个体两两之间目标函数值的差:

$\begin{array}{l} \Delta f_{k, j}=\left|f_{k, i_{k}}-f_{j, i_{j}}\right|, \\ k=1, 2, 3, 4, j=1, 2, 3, 4 . \end{array}$ (1)

Δ f_k_,_j标准化后得

$U_{1_{k, j}}$ =1- $\frac{Δ f_{k, j}}{\max_{k, j} (Δ f_{k, j})}$ , k=1, 2, 3, 4, j=1, 2, 3, 4, (2)

其中, $\max_{k, j}$ (Δ f_k_,_j)表示个体间目标函数值差值Δ f_k_,_j的最大值.

3)计算4个个体 $X_{1, i_{1}}$ 、 $X_{2, i_{2}}$ 、 $X_{3, i_{3}}$ 、 $X_{4, i_{4}}$ 两两之间的欧氏距离:

d_k_,_j= ${(X_{k, i_{k}} - X_{j, i_{j}})}_{2}$ , k=1, 2, 3, 4, j=1, 2, 3, 4.(3)

同样, d_k_,_j标准化后得

$U_{2_{k, j}}$ =1- $\frac{d_{k, j}}{\max_{k, j} (d_{k, j})}$ , k=1, 2, 3, 4, j=1, 2, 3, 4, (4)

其中 $\max_{k, j}$ (d_k_,_j)表示个体间欧氏距离d_k_,_j的最大值.

4)计算4个个体 $X_{1, i_{1}}$ 、 $X_{2, i_{2}}$ 、 $X_{3, i_{3}}$ 、 $X_{4, i_{4}}$ 两两之间的耦合协调度:

$\begin{array}{l} C C D_{k, j}=\sqrt{C_{k, j} T_{k, j}}, \\ C_{k, j}=2\left[\frac{U_{1_{k, j}} U_{2_{k, j}}}{\left(U_{1_{k, j}}+U_{2_{k, j}}\right)^{2}}\right]^{\frac{1}{2}}, \\ T_{k, j}=\beta_{1} U_{1_{k, j}}+\beta_{2} U_{2_{k, j}}, \end{array} $ (5)

k=1, 2, 3, 4, j=1, 2, 3, 4.

其中:C_k_,_j表示第k个个体与第j个个体的耦合度; T_k_,_j表示第k个个体与第j个个体的协调度; 本文令

β ₁=β ₂= $\frac{1}{2}$ .

5)计算每个个体之间的耦合协调度平均值, 即种群状态评估值:

$\theta=\frac{1}{16} \sum_{k=1}^{4}\left(\sum_{j=1}^{4} C C D_{k, j}\right) . $ (6)

并依据θ 将进化种群划分成如下3种状态.

(1)当θ ≤ 1-μ 时, 说明4个不同等级个体之间的总体耦合协调度值较低, 即4个个体分布较分散, 此时种群处于搜索状态.

(2)当1-μ < θ < μ 时, 说明4个不同等级个体之间分布有聚合有分散, 此时种群处于平衡状态.

(3)当θ ≥ μ 时, 说明四个不同等级的个体处于聚合情况, 即目标函数值和距离均较接近, 此时种群处于收敛状态.

μ 为给定的阈值, 范围在[0.5, 1)内.

2.2 变异算子池

在完成种群状态的评估之后, 需要根据不同进化状态设计合适的变异算子池, 具体设计方式如下.

1)搜索状态变异算子池

{DE/rand/1, DE/best/2, DE/current-to-rand/1}.在搜索状态下, 需要增强算法的全局搜索能力, 故应选择搜索性能较优的变异算子.在所有的变异算子中, DE/rand/1为较常用的一种.相比DE/rand/1, DE/best/2包含2个不同的差分向量, 具有更好的全局探索能力.DE/current-to-rand/1在解决旋转问题时具有较好表现.因此本文选择DE/rand/1、DE/best/2、DE/current-to-rand/1这3个变异算子组成搜索状态的变异算子池.

2)平衡状态变异算子池

{DE/current-to-pbest/1, DE/current-to-ci_mbest/1}.在平衡状态下, 种群个体聚集和分散情况不明显, 此时应同时关注算法的搜索性能和收敛性能.DE/current-to-pbest/1利用表现较优的个体作为目标向量, 引导种群向优秀个体进化, 能有效平衡算法搜索和收敛性能.DE/current-to-ci_mbest/1集成多个优秀个体的信息, 以此作为目标向量, 引导种群向有前途的方向进化, 是近年来表现较优的一种变异算子.因此, 本文选择DE/current-to-pbest/1和DE/current-to-ci_mbest/1两个算子组成平衡状态的变异算子池.

3)收敛状态变异算子池

{DE/best/1, DE/current-to-best/1}.在收敛状态下, 种群已聚集在某一局部区域, 此时应该提升算法的收敛速度和解的精度.故本文选择DE/best/1和DE/current-to-best/1两个算子组成收敛状态的变异算子池.

2.3 自适应Powell方法

Powell共轭梯度下降法^[27]是一种直接优化方法.从一个初始点出发, 轮流对每个方向进行双向搜索, 直到满足最优性条件.

考虑到差分进化算法的局部搜索能力较弱, 本文引入自适应Powell方法^[19], 每隔固定代数G执行一次此方法, 进行局部搜索, 提升CCPDE搜索效率.自适应Powell方法自适应调节Powell方法的容忍度ε 和步长δ .第j维的步长为:

δ _j= $\frac{0.001 \overset{m}{\sum_{i = 1}} (x_{i, j} - x_{best, j})}{NP \cdot 10 %}$ , (7)

其中, NP· 10%表示计算步长解的数目, x_i表示第i个个体, x_best表示种群的最优解.

自适应Powell方法基于迭代次数自适应调整Powell方法的搜索过程, 并通过混合外推技术结合逆黄金分割法与抛物线插值方法, 从而优化种群中个体.

自适应Powell方法伪代码如算法1所示.

算法1 自适应Powell方法^[19]

给定初始点x₀, D维的单位矩阵E, 容忍度ε ,

搜索步长δ =(δ ₁, δ ₂, …, δ _D)

WHILE |f(x₀)-f(x_D₊₁)|< ε 未满足

δ = $\frac{2 δ}{3}$ , x₀=x_D₊₁

FOR k=1∶ D

令g(λ )=f(x_k_-1+λ E_k)

结合逆黄金分割法和逆抛物线插值法, 构造混合外推法

以δ _k为初始步长, 寻找包含λ ₂的区间[λ ₁, λ ₃], 使得g(λ ₂)< g(λ ₁), g(λ ₂)< g(λ ₃)用Brent's搜索方法寻找函数g(λ )在区间[λ ₁, λ ₃]上的最优值λ

令x_k=x_k_-1+λ E_k

FOR j=1 to D-1

E_j=E_j₊₁

END FOR

E_D=x_D-x₀, g(λ )=f(x_D+λ E_D)

同样构造λ 的区间[λ ₁, λ ₃], 用Brent's搜索方法寻找函数g(λ )最优值λ

x_D₊₁=x_D+λ _DE_D

END FOR

END WHILE

2.4 本文算法步骤

为了充分利用种群的个体间距离和目标函数值, 有效评估种群进化状态并选择合适的变异算子, 本文提出基于耦合协调度种群状态评估的差分进化算法(CCPDE), 伪代码如算法2所示.

算法2 CCPDE

输入最大评价次数MaxFES, 种群大小NP, 状态阈值μ , 缩放因子F, 交叉概率CR, 固定代数G, 容忍度ε

输出种群中最优解

初始化种群POP, Gen=0, FES=NP

WHILE FES< MaxFES

Gen=Gen+1

按目标函数值将种群分为4个子种群.从子种群中分别随机选择一个个体, 通过式(1)~式(6)计算耦合协调度, 得到种群进化状态评估值θ

IF θ ≤ 1-μ

{DE/rand/1, DE/current-to-rand/1, DE/best/2}中随机选择一个变异算子, 对当前种群POP执行变异操作

ELSE IF 1-μ < θ < μ

{DE/current-to-pbest/1, DE/current-to-ci_mbest/1}中随机选择一个变异算子, 对当前种群POP执行变异操作

ELSE

{DE/best/1, DE/current-to-best/1}中随机选择一个变异算子, 对当前种群POP执行变异操作

END IF

交叉、选择、更新参数

FES=FES+NP

IF mod(Gen, G)=0

ε = $\frac{ε}{FES}$

根据式(7)计算δ

随机产生正整数k∈ {1, 2, …, NP}

x₀=x_best+rand(0, 1)· (x_best-x_k)

以x₀为初始点, 调用算法1中的Powell方法, 产生新的解y

利用y代替种群中的最差解

END IF

END WHILE

由算法2可知, CCPDE的步骤具体如下:首先, 初始化种群以及设置各参数.再利用耦合协调度评估种群的进化状态.然后, 根据种群所处的进化状态选择相应的变异算子池.最后, 每隔固定代数, 利用Powell方法更新种群, 直到迭代终止, 输出最优解.

3 实验及结果分析

3.1 测试函数与参数设置

本文使用CEC2017测试集^[28]验证算法性能.CEC2017测试集包含30个测试函数, F1~F3为单峰函数, F4~F10为多峰函数, F11~F20为混合函数, F21~F30为复合函数.

本文选择目标函数值误差均值和标准差度量算法性能.每个测试函数独立运行25次, 以25次目标函数值误差均值作为最终结果, 目标函数值的最大计算次数

MaxFES=10000D,

其中D表示函数维数.

通过Wilcoxon符号秩检验和Friedman检验对数值实验结果进行检验分析, 显著性水平为0.05.对比结果中优于、劣于、相似分别表示CCPDE的数值结果显著优于、劣于和相似于对比算法的数值结果.

所有算法均在Windows 11, Intel(R) Core(TM) i5-11300H@3.10 GHz, 16 GB of RAM环境上进行数值实验, 在matlabR2020b上编码实现.

3.2 与常见差分进化算法对比结果

为了验证CCPDE的有效性, 在CEC2017测试集上进行数值实验.选择如下对比算法:TSDE^[13], EPSDE(DE Algorithm with Ensemble of Parameters and Mutation and Crossover Strategies)^[29], FADE(Fitness-Based Adaptive DE)^[30], CJADE(Chaotic- Local-Search-Based JADE)^[31], IMODE(Improved Multi-operator DE)^[32].

对比算法参数设置与原文献一致.CCPDE的F和CR参数值采用JADE^[19]的自适应参数调整方案, 状态参数阈值μ 设置为0.8.

6种算法在CEC2017测试函数上的Wilcoxon符号秩检验的对比结果如表1~表3所示, 测试函数的维度分别为10、30、50.

由表1~表3中结果可知, CCPDE的整体性能均优于其它对比算法, 特别是在维数为30和50的测试函数上, 综合性能明显优于其它算法.

表1 各算法在10维测试函数下的误差均值对比 Table 1 Comparison of mean error values of different algorithms with 10D test functions

表2 各算法在30维测试函数下的误差均值对比 Table 2 Comparison of mean error values of different algorithms with 30D test functions

表3 各算法在50维测试函数下的误差均值对比 Table 3 Comparison of mean error values of different algorithms with 50D test functions

为了进一步分析6种算法的收敛性和鲁棒性, 以维数为30的测试函数为例, 绘制6种算法在F1、F5、F13、F21测试函数的收敛曲线图和箱线图, 具体如图2所示.由(a)可以看出:CCPDE的收敛性与CJADE较接近, 优于其它4种算法; CCPDE的鲁棒性与TSDE、EPSDE较接近, 优于FADE, 稍劣于CJADE.由于CJADE倾向于算法的收敛性, 因此在单峰函数上表现较优, 而CCPDE由于使用多个变异算子, 更倾向于提升算法的综合性能.在(b)中, CCPDE性能明显优于其它5种算法.在(c)中, CCPDE的收敛性能与FADE较接近, 另外根据箱线图可看出, CCPDE所得最优值优于其它算法.在(d)中, IMODE的收敛性能最优, 而观察箱线图可以看出, CCPDE的鲁棒性优于FADE、TSDE、EPSDE和IMODE.

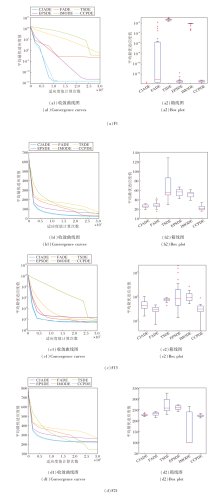	Figure Option View Download New Window
	图2 各算法在4个测试函数上的收敛曲线图和箱线图Fig.2 Convergence curves and box plots of different algorithms on 4 test functions

综合上述分析结果可知, 对于各种不同类型的测试函数, CCPDE的收敛性、鲁棒性和解的精度等综合性能都较优.

3.3 与其它进化算法对比结果

为了进一步验证CCPDE的有效性, 选择如下对比算法.

1)CSsin^[33].改进的布谷鸟搜索算法, 设计线性概率调整的双搜索策略, 用于平衡布谷鸟搜索算法的搜索性和收敛性, 并通过种群规模减轻计算负担.

2)PPSO(Proactive Particles in Swarm Optimi-zation)^[34].自动调节性能的粒子群优化算法, 利用模糊逻辑, 动态确定惯性权重、认知因素和社会因素的最佳设置.

3)CGO(Chaos Game Optimization)^[35].新型元启发式算法.

4)AGBSO^[36].基于替代搜索模式的头脑风暴算法, 基于网格搜索, 将搜索空间划分为更小的搜索空间进行算法搜索.

5)CMA-ES(Evolutionary Optimization Strategy Based on the Derandomized Evolution Strategy with Covariance Matrix Adaption)^[37].基于去随机化进化策略和协方差矩阵适应的新型进化算法.

实验中这5种算法的参数设置与其原文献相同, 在CEC2017测试集上进行对比分析.

各算法在30个测试函数上求解的目标函数误差均值和标准差如表4所示, 表中黑体数字表示最优值.

表4 6种进化算法在30维测试函数上的误差均值对比 Table 4 Comparison of mean error values of 6 evolutionary algorithms with 30D test functions

观察表4中结果可知, 对于单峰函数, CMA-ES表现最优, CCPDE次优.对于多峰函数, CCPDE表现与AGBSO接近, 优于其它4种进化算法.对于混合函数, CCPDE的数值结果明显优于其它5种进化算法.对于复合函数, CSsin在F21、F23~F27测试函数上的数值结果最优.CCPDE在F29、F30测试函数上的结果最优.

根据上述分析, 在CEC-2017测试集的30个测试函数上, CCPDE总体性能优于5种进化算法.

进一步给出6种进化算法误差均值的Friedman秩和排名, 具体如表5所示.由表可知, CCPDE的Fridman秩值为1.97, 明显优于其它算法.秩排名第二和第三的分别是AGBSO与CSsin, Fridman秩值为3.36和3.47, 较接近.秩排名第六位的是PPSO, 秩值为4.38, 明显差于其它算法.由此可知, 相比其它进化算法, CCPDE具有一定优势.

表5 6种进化算法的Friedman检验结果 Table 5 Friedman test results of 6 evolutionary algorithms

3.4 与其它种群状态评估方法对比结果

为了进一步验证耦合协调度种群评估方法的有效性, 本节使用DEMS^[14]、ADDE^[17]、DEET^[18]替换CCPDE中的耦合协调度评估方法, 在30维CEC2017 测试函数上开展数值实验, 误差均值和标准差如表6所示, 表中黑体数字表示最优值.

表6 CCPDE与其它种群状态评估方法的误差均值对比 Table 6 Comparison of mean error values between CCPDE and other population state assessment methods

函数	DEET-CCPDE	ADDE-CCPDE	DEMS-CCPDE	CCPDE
F1	1.65e-14± 7.87e-15	4.38e-14± 1.96e-14	4.55e-14± 4.16e-14	4.43e-14± 1.80e-14
F2	7.75e+07± 3.86e+08	3.32e-10± 1.01e-09	5.26e+06± 2.63e+07	4.85e-11± 1.89e-10
F3	3.01e+03± 6.96e+03	4.98e+01± 2.27e+02	3.83e+03± 9.81e+03	4.82e+00± 2.19e+01
F4	2.61e+01± 2.94e+01	2.25e+01± 2.94e+01	2.38e+01± 2.98e+01	1.98e+01± 2.96e+01
F5	2.00e+01± 5.46e+00	3.84e+01± 2.09e+01	1.91e+01± 6.08e+00	2.07e+01± 6.76e+00
F6	8.64e-14± 4.96e-14	1.09e-13± 2.27e-14	1.14e-13± 0.00e+00	1.05e-13± 3.15e-14
F7	4.66e+01± 4.41e+00	6.18e+01± 1.36e+01	5.83e+01± 9.61e+00	4.63e+01± 5.37e+00
F8	2.12e+01± 6.67e+00	3.76e+01± 1.12e+01	1.99e+01± 5.59e+00	1.95e+01± 5.87e+00
F9	8.22e-01± 1.29e+00	1.63e+00± 2.77e+00	1.89e-01± 4.04e-01	2.15e-02± 3.90e-02
F10	1.69e+03± 3.52e+02	1.78e+03± 4.14e+02	1.76e+03± 2.84e+02	1.57e+03± 3.36e+02
F11	1.78e+01± 1.22e+01	9.26e+01± 4.31e+01	2.88e+01± 4.28e+01	1.33e+01± 6.12e+00
F12	1.02e+03± 4.41e+02	1.58e+03± 1.67e+03	2.02e+03± 3.92e+03	9.32e+02± 3.29e+02
F13	3.35e+01± 2.94e+01	2.61e+02± 1.26e+02	1.61e+02± 1.55e+02	2.64e+01± 1.34e+01
F14	3.39e+03± 8.85e+03	1.32e+02± 5.23e+01	2.81e+03± 7.28e+03	1.14e+02± 4.47e+02
F15	1.67e+01± 1.37e+01	1.68e+02± 1.36e+02	3.98e+01± 5.70e+01	1.83e+01± 2.09e+01
F16	3.23e+02± 1.75e+02	3.38e+02± 2.31e+02	3.41e+02± 1.45e+02	2.86e+02± 1.59e+02
F17	5.54e+01± 2.83e+01	1.10e+02± 8.50e+01	6.23e+01± 4.18e+01	5.72e+01± 3.74e+01
F18	1.28e+04± 1.51e+04	8.70e+02± 3.60e+03	2.65e+04± 3.41e+04	7.34e+01± 5.00e+01
F19	1.31e+01± 5.99e+00	7.97e+01± 4.90e+01	2.99e+01± 2.85e+01	1.30e+01± 4.73e+00
F20	8.47e+01± 6.65e+01	9.13e+01± 7.64e+01	8.55e+01± 5.98e+01	9.47e+01± 6.13e+01
F21	2.20e+02± 5.50e+00	2.37e+02± 9.31e+00	2.23e+02± 5.36e+00	2.21e+02± 5.69e+00
F22	1.00e+02± 9.10e-14	1.00e+02± 2.08e-13	1.00e+02± 1.86e-13	1.00e+02± 2.30e-13
F23	3.69e+02± 9.47e+00	3.93e+02± 1.56e+01	3.72e+02± 8.12e+00	3.71e+02± 6.31e+00
F24	4.40e+02± 4.55e+00	4.67e+02± 1.47e+01	4.56e+02± 9.13e+00	4.35e+02± 4.97e+00
F25	3.88e+02± 7.66e+00	3.87e+02± 2.95e+00	3.86e+02± 1.57e+00	3.87e+02± 2.46e+00
F26	1.17e+03± 8.49e+01	1.50e+03± 1.67e+02	1.24e+03± 3.23e+02	1.15e+03± 7.46e+01
F27	5.02e+02± 8.24e+00	5.07e+02± 9.37e+00	5.04e+02± 6.09e+00	5.02e+02± 5.76e+00
F28	3.36e+02± 5.37e+01	3.38e+02± 6.29e+01	3.40e+02± 6.14e+01	3.48e+02± 5.60e+01
F29	4.54e+02± 2.05e+01	4.71e+02± 4.72e+01	4.57e+02± 4.60e+01	4.49e+02± 2.44e+01
F30	2.90e+03± 1.20e+03	2.19e+03± 1.71e+02	4.48e+03± 3.27e+03	2.20e+03± 1.72e+02
优于	5	19	12
劣于	3	0	0
相似	22	11	18

表6 CCPDE与其它种群状态评估方法的误差均值对比 Table 6 Comparison of mean error values between CCPDE and other population state assessment methods

实验中DEET-CCPDE表示在状态评估阶段使用DEET的评估方法, 其余算法内容与CCPDE一致.同样, ADDE-CCPDE、DEMS-CCPDE为ADDE和DEMS的评估方法与CCPDE结合形成的算法.由表6中结果可知, 耦合协调度种群状态评估方法能提升算法的性能.

为了进一步衡量状态评估方法的优劣, 给出4种算法的Friedman秩排名, 具体如表7所示.由表可知, CCPDE的秩为1.70, 表现最优, 排名第二的是DEET-CCPDE, 其次是DEMS-CCPDE和ADDE-CCPDE.

表7 CCPDE和3种种群状态评估方法的Friedman检验结果 Table 7 Friedman test results of CCPDE and 3 population state assessment methods

ADDE的评估方法仅基于目标函数值排名最优和中位数这两个特定个体的距离, 容易出现误判.DEMS的评估方法计算种群中每个个体两两之间距离的平均值, 评估效果略优于ADDE.DEET同时考虑种群分布、目标函数值的影响, 但是仅以最优解作为参照, 会出现评估不准确的情况.相比而言, 耦合协调度评估方法虽然只计算四个个体之间耦合情况, 但四个个体分别来自于不同等级的子种群, 取样均匀, 且耦合协调度模型能够综合考虑种群个体的分布与目标函数值.

综合上述结果可知, 在CCPDE中, 基于耦合协调度的种群评估方法优于其它3种种群状态评估方法, 4种种群状态评估方法的数值结果也进一步验证此结果.

3.5 参数敏感性分析

为了分析状态参数阈值μ 对CCPDE性能的影响, 本节主要探讨μ 对进化状态划分的影响.为了选择CCPDE的最优状态参数阈值, 本节将μ 固定在[0.5, 0.9]区间, 步长设置为0.1, 算法独立运行25次, 测试函数维数设为10、20、30.5个不同阈值相应算法的Friedman检验结果如表8所示, 表中黑体数字表示最优值.

表8 不同维度下μ 值改变后的Friedman检验结果 Table 8 Friedman test results after altering μ in different dimensions

由表8结果分析可知:在测试函数维数为10、30, μ =0.8时, 均值排名最优; 在测试函数维数为50, μ =0.7时, 均值排名最优, 秩排名为2.12.由此可知, 当μ =0.8时, 算法的总体性能最佳.

4 结束语

差分进化算法在迭代过程中的种群状态是动态变化的, 不同的种群状态对于变异算子的要求不同.如何有效评估种群状态, 并选择合适的变异算子, 是本文研究的重点.本文提出基于耦合协调种群状态评估的差分进化算法(CCPDE).首先, 从不同等级的子种群中随机选取四个个体, 通过耦合协调度计算不同等级目标函数值和不同距离个体的聚散程度, 评估当前种群所属状态, 并根据评估状态将种群进化分为搜索、平衡和收敛三种状态.然后, 对于不同的进化状态, 从相应的变异算子池选择对应的变异算子进行种群迭代.最后, 在迭代过程中, 利用自适应Powell方法, 在固定代数进行局部搜索, 加快算法收敛速度.为了验证本文算法的有效性, 基于CEC2017测试函数集, 先后进行与改进差分进化算法、其它进化算法、不同种群状态评估方法的对比数值实验, 以及参数敏感性分析实验.实验结果表明:1)相比其它种群状态评估方法, CCPDE的基于耦合协调度种群评估方法充分考虑种群个体分布和目标函数值关联关系, 性能优于其它三种种群状态评估方法; 2)当CCPDE的状态参数阈值μ 设置为0.8时, 算法总体性能较优; 3)相比改进差分进化算法和进化算法, CCPDE的鲁棒性、收敛性较优, 能够有效处理不同类型问题的函数, 存在显著优势.综合所有数值实验可知, 本文算法是一种有效的算法.今后考虑将CCPDE融入约束差分优化、多目标优化等复杂实际问题中.

本文责任编委付俊

Recommended by Associate Editor FU Jun

参考文献

文献选项

[1]	STORN R, PRICE K. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization, 1997, 11(4): 341-359. [本文引用:1]
[2]	YU X B, JIANG N J, WANG X M, et al. A Hybrid Algorithm Based on Grey Wolf Optimizer and Differential Evolution for UAV Path Planning. Expert Systems with Applications, 2023, 215. DOI: 10.1016/j.eswa.2022.119327. [本文引用:1]
[3]	GUO J J, GUAN Z G. Optimization of the Cable Forces of Completed Cable-Stayed Bridges with Differential Evolution Method. Structures, 2023, 47: 1416-1427. [本文引用:1]
[4]	GUO X F, YANG Q, ZHENG H R, et al. Optimization of Power Distribution for Electrothermal Anti-Icing Systems by Differential Evolution Algorithm. Applied Thermal Engineering, 2023, 221. DOI: 10.1016/j.applthermaleng.2022.119875. [本文引用:1]
[5]	李爱军, 王景, 李佳, 等. 基于差分进化算法的飞行控制律评估. 模式识别与人工智能, 2014, 27(3): 256-262. (LI A J, WANG J, LI J, et al. Clearance of Flight Control Law Based on Cultural Differential Evolution Algorithm. Pattern Recognition and Artificial Intelligence, 2014, 27(3): 256-262. ) [本文引用:1]
[6]	杜彦斌, 周志杰, 许磊, 等. 基于灰色关联分析与自适应混沌差分进化算法的激光熔覆工艺参数优化方法. 计算机集成制造系统, 2022, 28(1): 149-160. (DU Y B, ZHOU Z J, XU L, et al. Laser Cladding Process Para-meter Optimization Method Based on Grey Relational Analysis and ACDE Algorithm. Computer Integrated Manufacturing Systems, 2022, 28(1): 149-160. ) [本文引用:1]
[7]	QIN A K, HUANG V L, SUGANTHAN P N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417. [本文引用:1]
[8]	LIU X F, ZHAN Z H, LIN Y, et al. Historical and Heuristic-Based Adaptive Differential Evolution. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2019, 49(12): 2623-2635. [本文引用:1]
[9]	PAN Q K, SUGANTHAN P N, WANG L, et al. A Differential Evolution Algorithm with Self-Adapting Strategy and Control Parameters. Computers and Operations Research, 2011, 38(1): 394-408. [本文引用:1]
[10]	WANG Y, CAI Z X, ZHANG Q F. Differential Evolution with Composite Trial Vector Generation Strategies and Control Parameters. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 55-66. [本文引用:1]
[11]	WANG B C, LI H X, LI J P, et al. Composite Differential Evolution for Constrained Evolutionary Optimization. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2019, 49(7): 1482-1495. [本文引用:1]
[12]	WU G H, MALLIPEDDI R, SUGANTHAN P N, et al. Differential Evolution with Multi-population Based Ensemble of Mutation Stra-tegies. Information Sciences, 2016, 329: 329-345. [本文引用:1]
[13]	LIU Z Z, WANG Y, YANG S X, et al. Differential Evolution with a Two-Stage Optimization Mechanism for Numerical Optimization // Proc of the IEEE Congress on Evolutionary Computation. Wa-shington, USA: IEEE, 2016: 3170-3177. [本文引用:2]
[14]	ZHOU X G, ZHANG G J, HAO X H, et al. Differential Evolution with Multi-stage Strategies for Global Optimization // Proc of the IEEE Congress on Evolutionary Computation. Washington, USA: IEEE, 2016: 2550-2557. [本文引用:2]
[15]	ZHAN Z H, ZHANG J, LI Y, et al. Adaptive Particle Swarm Optimization. IEEE Transactions on Systems, Man, and Cybernetics (Cybernetics), 2009, 39(6): 1362-1381. [本文引用:1]
[16]	YU W J, SHEN M, CHEN W N, et al. Differential Evolution with Two-Level Parameter Adaptation. IEEE Transactions on Cyberne-tics, 2014, 44(7): 1080-1099. [本文引用:1]
[17]	ZHAN Z H, WANG Z J, JIN H, et al. Adaptive Distributed Differential Evolution. IEEE Transactions on Cybernetics, 2020, 50(11): 4633-4647. [本文引用:2]
[18]	LI Y, LI G H. Differential Evolutionary Algorithm with an Evolutionary State Estimation Method and a Two-Level Selection Mechanism. Soft Computing, 2020, 24(15): 11561-11581. [本文引用:3]
[19]	FENG Q X, LIU S Y, ZHANG J K, et al. Improved Biogeography-Based Optimization with Rand om Ring Topology and Powell's Method. Applied Mathematical Modelling, 2017, 41: 630-649. [本文引用:4]
[20]	ZHANG J Q, SANDERSON A C. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958. [本文引用:1]
[21]	ZHENG L M, ZHANG S X, TANG K S, et al. Differential Evolution Powered by Collective Information. Information Sciences, 2017, 399: 13-29. [本文引用:1]
[22]	MORITA M, OCHIAI H, TAMURA K, et al. Multi-point Search Combinatorial Optimization Method Based on Neighborhood Search Using Evaluation of Big Valley Structure // Proc of the IEEE International Conference on Systems, Man, and Cybernetics. Washington, USA: IEEE, 2015: 2835-2840. [本文引用:1]
[23]	WOLPERT D H, MACREADY W G. No Free Lunch Theorems for Optimization. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67-82. [本文引用:1]
[24]	KEDEM O, CAPLAN S R. Degree of Coupling and Its Relation to Efficiency of Energy Conversion. Transactions of the Faraday Society, 1965, 61: 1897-1911. [本文引用:1]
[25]	CHENG M L, LI Q, WEN Z G. Coupling Coordination Degree Analysis and Driving Factors of Innovation Network and ECO-Efficiency in China. Environmental Impact Assessment Review, 2023, 99. DOI: 10.1016/j.eiar.2022.107008. [本文引用:1]
[26]	SONG M J, ZHAO Y, LIANG J, et al. Spatial-Temporal Variability of Carbon Emission and Sequestration and Coupling Coordination Degree in Beijing District Territory. Cleaner Environmental Systems, 2023, 8. DOI: 10.1016/j.cesys.2022.100102. [本文引用:1]
[27]	POWELL M J D. Restart Procedures for the Conjugate Gradient Method. Mathematical Programming, 1977, 12(1): 241-254. [本文引用:1]
[28]	AWAD N H, ALI M Z, SUGANTHAN P N, et al. Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Bound Constrained Real-Parameter Numerical Optimization. Technical Report. Singapore, Singapore: Nanyang Technological University, 2016. [本文引用:1]
[29]	MALLIPEDDI R, SUGANTHAN P N. Differential Evolution Algorithm with Ensemble of Parameters and Mutation and Crossover Strategies // Proc of the International Conference on Swarm, Evolutionary, and Memetic Computing. Berlin, Germany: Springer, 2010: 71-78. [本文引用:1]
[30]	XIA X W, GUI L, ZHANG Y L, et al. A Fitness-Based Adaptive Differential Evolution Algorithm. Information Sciences, 2021, 549: 116-141. [本文引用:1]
[31]	GAO S C, YU Y, WANG Y R, et al. Chaotic Local Search-Based Differential Evolution Algorithms for Optimization. IEEE Transactions on Systems, Man, and Cybernetics(Systems), 2021, 51(6): 3954-3967. [本文引用:1]
[32]	SALLAM K M, ELSAYED S M, CHAKRABORTTY R K, et al. Improved Multi-operator Differential Evolution Algorithm for Solving Unconstrained Problems // Proc of the IEEE Congress on Evolutionary Computation. Washington, USA: IEEE, 2020. DOI: 10.1109/CEC48606.2020.9185577. [本文引用:1]
[33]	SALGOTRA R, SINGH U, SAHA S, et al. Improving Cuckoo Search: Incorporating Changes for CEC 2017 and CEC 2020 Benchmark Problems // Proc of the IEEE Congress on Evolutionary Computation. Washington, USA: IEEE, 2020. DOI: 10.1109/CEC48606.2020.9185684. [本文引用:1]
[34]	TANGHERLONI A, RUNDO L, NOBILE M S. Proactive Particles in Swarm Optimization: A Settings-Free Algorithm for Real-Para-meter Single Objective Optimization Problems // Proc of the IEEE Congress on Evolutionary Computation. Washington, USA: IEEE, 2017. DOI: 10.1109/CEC.2017.7969538. [本文引用:1]
[35]	TALATAHARI S, AZIZI M. Chaos Game Optimization: A Novel Metaheuristic Algorithm. Artificial Intelligence Review, 2021, 54(2): 917-1004. [本文引用:1]
[36]	CAI Z H, GAO S C, YANG X, et al. Alternate Search Pattern-Based Brain Storm Optimization. Knowledge-Based Systems, 2022, 238. DOI: 10.1016/j.knosys.2021.107896. [本文引用:1]
[37]	HANSEN N, MÜLLER S D, KOUMOUTSAKOS P. Reducing the Time Complexity of the Derand omized Evolution Strategy with Covariance Matrix Adaptation(CMA-ES). Evolutionary Computation, 2003, 11(1): 1-18. [本文引用:1]

1997

0.0

... 差分进化(Differential Evolution, DE)是Storn等^[1]提出的一种简单且功能强大的进化算法 ...

2023

0.0

... 算法基于种群内个体之间的差异性进行迭代,具有较强的全局搜索能力,现已成功应用于许多工程领域,包括:无人机路径规划^[2]、斜拉桥索力优化^[3]、系统功率分配^[4]、飞行控制率评估^[5]、激光熔覆工艺参数优化^[6]等 ...

2023

0.0

2023

0.0

2014

0.0

2022

0.0

2009

0.0

... Qin等^[7]提出SaDE(Self-Adaptive DE),根据各变异算子的前期迭代效果计算后验概率,并依据概率值选择合适的变异算子 ...

2019

0.0

... Liu等^[8]提出HHDE(Historical and Heuristic DE),基于个体历史成功经验和其当前状态信息动态选择变异算子和控制参数 ...

2011

0.0

... Pan等^[9]提出SspDE(DE Algorithm with Self-Adaptive Trial Vector Generation Strategy and Control Parameters),设计变异算子列表,存放上一代变异成功的变异算子,并据此计算选择概率 ...

2011

0.0

... Wang等^[10]提出CoDE(Composite DE),算法中每个个体采用多个不同类型的变异算子,产生多个候选个体,并选择适应度值高的个体进入下一代 ...

2019

0.0

... Wang等^[11]在CoDE的基础上,提出C²oDE(Constrained CoDE),采用三种不同变异算子,其中两个算子侧重收敛性能,一个算子侧重搜索性能 ...

2016

0.0

... Wu等^[12]提出MPEDE(Multi-population Based Ensemble DE),将种群分为三个规模相同的指标种群和一个奖励子种群,并为每个指标种群分配不同的变异算子 ...

2016

0.0

... Liu等^[13]提出TSDE(DE with a Two-Stage Optimization Mechanism),利用迭代过程中前期注重全局搜索和后期注重局部收敛的特点,将迭代过程均衡划分为两个阶段,分别设计变异算子池 ...

... 选择如下对比算法:TSDE^[13],EPSDE(DE Algorithm with Ensemble of Parameters and Mutation and Crossover Strategies)^[29],FADE(Fitness-Based Adaptive DE)^[30],CJADE(Chaotic- Local-Search-Based JADE)^[31],IMODE(Improved Multi-operator DE)^[32] ...

2016

0.0

... Zhou等^[14]提出DEMS(DE with Multi-stage Strategies),利用种群中个体间的平均距离将迭代过程划分成搜索、平衡和收敛三个阶段,不同阶段分别使用不同类型的变异算子 ...

... 4 与其它种群状态评估方法对比结果为了进一步验证耦合协调度种群评估方法的有效性,本节使用DEMS^[14]、ADDE^[17]、DEET^[18]替换CCPDE中的耦合协调度评估方法,在30维CEC2017 测试函数上开展数值实验,误差均值和标准差如表6所示,表中黑体数字表示最优值 ...

2009

0.0

... Zhan等^[15]提出APSO(Adaptive Particle Swarm Optimization),计算种群中所有个体之间的欧氏距离,评估种群的分布情况,并针对不同的分布情况采用不同的变异算子 ...

2014

0.0

... Yu等^[16]提出ADE(Adaptive DE),利用种群中最优个体与其它个体之间的欧氏距离评估种群的分布情况 ...

2020

0.0

... 考虑到计算所有个体之间欧氏距离的计算复杂度较高,Zhan等^[17]提出ADDE(Adaptive Distributed DE),利用种群中最优个体和中间个体评估种群的分布情况 ...

2020

0.0

... Li等^[18]提出DEET,计算所有个体距离与目标函数值的相关性,评估种群进化状态 ...

... 连续优化问题的搜索空间可以大致分为三类:单峰函数、有大山谷结构的多模态函数和无大山谷结构的多模态函数^[18] ...

2017

0.0

... 此外,通过自适应Powell方法^[19],提升算法的收敛速度 ...

... 考虑到差分进化算法的局部搜索能力较弱,本文引入自适应Powell方法^[19],每隔固定代数G执行一次此方法,进行局部搜索,提升CCPDE搜索效率 ...

... 算法1 自适应Powell方法^[19] ...

... CCPDE的F和CR参数值采用JADE^[19]的自适应参数调整方案,状态参数阈值#cod#x003bc ...

2009

0.0

... 6)DE/current-to-pbest/1^[20]: ...

2017

0.0

... 7)DE/current-to-ci_mbest/1^[21]: ...

2015

0.0

... 根据解的近似最优性原理可知,优良解之间具有相似结构^[22] ...

1997

0.0

... 定理^[23],每个变异算子都有自己特定的适用范围 ...

1965

0.0

... 耦合度的概念源于物理学领域^[24],一般用于刻画多个指标之间相互影响的程度,已广泛应用于社会科学领域^[25,26] ...

2023

0.0

... 耦合度的概念源于物理学领域^[24],一般用于刻画多个指标之间相互影响的程度,已广泛应用于社会科学领域^[25,26] ...

2023

0.0

... 耦合度的概念源于物理学领域^[24],一般用于刻画多个指标之间相互影响的程度,已广泛应用于社会科学领域^[25,26] ...

1977

0.0

... 3 自适应Powell方法Powell共轭梯度下降法^[27]是一种直接优化方法 ...

2016

0.0

... 1 测试函数与参数设置本文使用CEC2017测试集^[28]验证算法性能 ...

2010

0.0

2021

0.0

2021

0.0

2020

0.0

2020

0.0

... 1)CSsin^[33] ...

2017

0.0

... 2)PPSO(Proactive Particles in Swarm Optimi-zation)^[34] ...

2021

0.0

... 3)CGO(Chaos Game Optimization)^[35] ...

2022

0.0

... 4)AGBSO^[36] ...

2003

0.0

... 5)CMA-ES(Evolutionary Optimization Strategy Based on the Derandomized Evolution Strategy with Covariance Matrix Adaption)^[37] ...