基于属性加权的概念认知学习模型

引用本文

梁涛巨, 林艺东, 林梦雷, 王启君. 基于属性加权的概念认知学习模型. 模式识别与人工智能, 2023,36(8): 749-763
LIANG Taoju, LIN Yidong, LIN Menglei, WANG Qijun. Weighted Attributes-Based Concept-Cognitive Learning Model. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(8): 749-763. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202308007
Permissions

《模式识别与人工智能》编辑部

基于属性加权的概念认知学习模型

梁涛巨^1,^2,³, 林艺东^1,^2,³, 林梦雷^1,^2,³, 王启君^1,^2,³

1.闽南师范大学数学与统计学院漳州 363000

2.闽南师范大学数字福建气象大数据研究所漳州 363000

3.闽南师范大学福建省粒计算及其应用重点实验室漳州 363000

通讯作者:

林艺东,博士,副教授,主要研究方向为不确定性理论及其应用.E-mail:yidong_lin@yeah.net.

作者简介:

梁涛巨,硕士研究生,主要研究方向为粒计算、概念认知学习.E-mail:liangtaoju22@163.com.

林梦雷,硕士,教授,主要研究方向为不确定性理论及其应用.E-mail:menglei36@126.com.

王启君,硕士研究生,主要研究方向为粒计算、概念认知学习.E-mail:wqj_1106@163.com.

收稿日期: 2023-07-05 接受日期: 2023-08-31

资助项目: 国家自然科学基金项目(No.12201284)、福建省自然科学基金项目(No.2022J05169,JAT210255)、闽南师范大学校长基金项目(No.L22130)

摘要

现有概念认知学习模型往往存在忽略属性与决策间的相关性、涉及的概念空间存在冗余性、学习效果有限等问题.因此,文中提出面向属性加权的概念认知学习模型(Weighted Attributes-Based Concept-Cognitive Learning Model, WACCL).首先,探讨属性与决策之间的相关性,提出属性的加权机制.考虑到概念空间冗余性问题,探索不同概念的地位,实现概念空间压缩.然后,结合概念间的相似性,实现概念聚类,为线索的学习提供依据.最后,在13个数据集上的实验验证WACCL的有效性.

关键词: 概念认知学习; 模糊概念; 属性加权; 概念聚类

中图分类号:TP182

Weighted Attributes-Based Concept-Cognitive Learning Model

LIANG Taoju^1,^2,³, LIN Yidong^1,^2,³, LIN Menglei^1,^2,³, WANG Qijun^1,^2,³

1. School of Mathematics and Statistics, Minnan Normal University, Zhangzhou 363000

2. Institute of Meteorological Big Data-Digital Fujian, Minnan Normal University, Zhangzhou 363000

3. Fujian Key Laboratory of Granular Computing and Application, Minnan Normal University, Zhangzhou 363000

Corresponding author:
LIN Yidong, Ph.D., associate professor. His research interests include uncertain theories and application.

About Author:
LIANG Taoju, master student. His research interests include granular computing and concept-cognitive learning.
LIN Menglei, master, professor. His research interests include uncertain theories and application.
WANG Qijun, master student. Her research interests include granular computing and concept-cognitive learning.

Fund:National Natural Science Foundation of China(No.12201284), Natural Science Foundation of Fujian Province(No.2022J05169,JAT210255), President Foundation of Minnan Normal University(No.L22130)

Abstract

In the existing concept-cognitive learning models, correlations among attributes and decisions are ignored, the concept space involved is redundant and the learning effectiveness is poor. Aiming at these problems, a weighted attributes-based concept-cognitive learning model(WACCL) is proposed in this paper. Firstly, the relevance of attribute-decision is discussed, and a weighting mechanism for attributes is proposed. With the consideration of the concept space redundancy, the positions of different concepts are explored and the compression of the concept space is achieved. Subsequently, conceptual clustering is implemented by combining similarities between concepts to provide a basis for learning clues. Finally, the effectiveness of WACCL is demonstrated by experiments on 13 datasets.

Key words: Key Words Concept-Cognitive Learning; Fuzzy Concept; Weighted Attributes; Conceptual Clustering

文章图片

认知计算作为人工智能的重要组成部分, 是模拟人类大脑认知过程的计算机系统.认知计算旨在解决生物系统中不确定、不精确和不完整的问题^[1].经过多年发展, 认知学习现已成为实现认知计算的有利工具之一, 广泛应用于认知心理学^[2]、机器学习^{[3, 4]}、信息科学^{[5, 6, 7, 8]}、分类任务^{[9, 10, 11, 12]}等领域.

形式概念分析(Formal Concept Analysis, FCA)^{[13, 14]}是一种数据分析工具, 为揭示数据中的隐藏关系和潜在知识提供重要的数学基础, 在知识表示与发掘、信息检索、对象分类等领域具有广泛的应用前景.

概念是FCA研究的基本单元, 为了提升对数据和信息的理解能力, 学者们研究来自不同关系的概念, 如模糊概念^[15]、三支概念^[16]、多尺度概念^[17]和加权概念^[18].

概念作为人类认知的基本构筑单位, 在认知计算中扮演着重要角色.于是学者们开始将FCA融入认知计算中, 提出概念认知学习.概念认知学习模拟人类学习特点, 关注如何通过经验和学习过程获取、组织和应用概念.在抽象层和机器层^[19], 概念认知学习被认为是采用一定的方法学习未知概念和概念结构, 如概念聚类^[20]和模仿人类认知过程^[21].

为了提高概念学习的效率和灵活性, Li等^[21]在认知计算的角度上讨论基于粒计算的概念学习.Niu等^[22]结合局部粒概念, 提取全局粒概念, 并且实现多源数据的信息融合.李金海等^[23]研究概念渐进式认知机理, 讨论在不完全条件下概念的获取问题.

为了处理解决问题的基本技能被忽视的问题, Xie等^[24]将一般信息粒转化为基于能力的充分必要信息粒, 从能力视角提出Cb-CCLM(Competence-Based Concept-Cognitive Learning Model).

随着新的信息和经验的累积, 个体需要不断调整和更新概念的分类方式, 以更好地理解和应对新的情景和任务.为了衡量概念结构的稳定性, Zhang等^[3]基于属性拓扑的概念树表示概念, 降低概念认知过程的复杂性.Mi等^[9]提出用于动态分类的概念认知计算系统, 提高决策者在动态环境下对问题解决的反应能力.

为了克服个体认知和认知环境的限制, Yuan等^[10]结合隶属度和非隶属度, 设计ILMPFTC(Incre-mental Learning Mechanism Based on Progressive Fuzzy Three-Way Concept).Xu等^[25]从概念运动视角研究概念的进化机制, 增强双向概念学习在概念学习中的灵活性和进化能力.

概念聚类是概念认知学习的基本方法之一, 目的是使相似概念越近、相异概念越远.概念分类和概念生成是概念聚类的两个关键任务.Mi等^[6]结合属性和对象信息, 提出FCLM(Fuzzy-Based Concept Learning Model), 用于概念分类和概念发现.Xu等^[11]考虑注意力对概念聚类的影响, 提出MA-CLM(Multi-attention Concept-Cognitive Learning Model), 提高分类效率.

一般来说, 通过概念加权, 可以根据个人的喜好和要求选择有用的信息.Singh等^[26]在计算概念前研究属性权重之间的相关性.Zhang等^[12]在决策信息中探讨条件属性的权重信息, 设计DMPWFC(Dynamic Updating Mechanism Algorithm Based on Progressive Weighted Fuzzy Concept).然而生活中存在着不同决策下属性权重不同的情况, 权重的差异反映不同决策类下属性的不同重视程度.在不同决策任务中, 属性被分配不同的权重, 以提高概念认知学习的准确性.

因此, 受文献[11]和文献[12]的启发, 本文利用属性与决策之间的相关性, 提出基于属性加权的概念认知学习模型(Weighted Attributes-Based Con-cept-Cognitive Learning Model, WACCL).首先, 利用属性与决策之间的相关性, 刻画属性在各决策中的影响作用, 探讨概念的重要性度量.然后, 通过概念的重要性, 在不同决策类下生成K-决策概念空间.为了降低概念认知的复杂性和提高学习效率, 通过概念聚类获得具有更强泛化能力的伪概念, 进行概念预测.最后, 通过实验验证WACCL的可行性、有效性及准确性.

1 相关知识

由于现实中的许多分类任务是使用模糊数据描述的, 因此本节主要回顾模糊形式背景及其相关的定义.

定义1^[15] 设三元组(U, A, $\tilde{I}$ )为模糊形式背景, 其中,

U={x₁, x₂, …, x_m},

表示非空有限对象集,

A={a₁, a₂, …, a_n},

表示非空有限属性集,

$\tilde{I}$ ∶ U× A→ [0, 1],

即对∀ x∈ U, a∈ A, 都存在一个隶属函数

μ (x, a)∈ [0, 1],

记μ (x, a)为 $\tilde{I}$ (x, a).

L^A为A上所有的模糊集合, 对

∀ X⊆2^U, $\tilde{B}$ ⊆L^A,

对象学习算子

$\tilde{F}$ ∶ 2^U→ L^A

和属性学习算子

$\tilde{G}$ ∶ L^A→ 2^U

定义如下:

$\begin{array}{l} \widetilde{F}(X)(a)=\bigwedge_{x \in X} \widetilde{I}(x, a), a \in A, \\ \widetilde{G}(\widetilde{B})=\{x \in X: \forall a \in A, \widetilde{I}(x, a) \geqslant \widetilde{B}(a)\} . \end{array}$

若

$\tilde{F}$ (X)= $\tilde{B}$ , $\tilde{G}$ ( $\tilde{B}$ )=X,

称序对(X, $\tilde{B}$ )为模糊概念, X和 $\tilde{B}$ 分别称为(X, $\tilde{B}$ )的外延和内涵.对∀ x∈ U, ( $\tilde{G}$ $\tilde{F}$ (x), $\tilde{F}$ (x))称为模糊粒概念^[23].给定一个对象x, 利用对象学习算子和属性学习算子可以获得其对应的模糊粒概念.

对

$\left(X_{1}, \widetilde{B}_{1}\right) \in L(U, A, \tilde{I}), \quad\left(X_{2}, \widetilde{B}_{2}\right) \in L(U, A, $\tilde{I})

可定义偏序关系

$\left(X_{1}, \widetilde{B}_{1}\right) \leqslant\left(X_{2}, \widetilde{B}_{2}\right) $

当且仅当X₁⊆X₂或 ${\tilde{B}}_{2}$ ⊆ ${\tilde{B}}_{1}$ , 称(X₁, ${\tilde{B}}_{1}$ )为(X₂, ${\tilde{B}}_{2}$ )的子概念, (X₂, ${\tilde{B}}_{2}$ )为(X₁, ${\tilde{B}}_{1}$ )的超概念.

定义2^[15] 设(U, A, $\tilde{I}$ )为模糊形式背景, (U, D, J)为经典形式背景, (U, A, $\tilde{I}$ , D, J)称为模糊决策形式背景, 其中,

D={d₁, d₂, …, d_k}

为决策属性集,

$\tilde{I}$ ∶ U× A→ [0, 1], J∶ U× D→ {0, 1}, A∩ D=Ø .

对∀ x∈ U, 有且仅有一个d∈ D, 使得

J(x, d)=1.

根据D可将U划分为

U\D={C₁, C₂, …, C_k}.

定义3^[21] 设(U, A, $\tilde{I}$ , D, J)为模糊决策形式背景, 则决策类C_i(i=1, 2, …, k)对应的决策模糊粒概念空间Q_i(i=1, 2, …, k)表示为

Q_i={( $\tilde{G}$ $\tilde{F}$ (x), $\tilde{F}$ (x))|x∈ C_i}.

本文讨论的概念均为模糊概念, 后面不再突出“ 模糊” 二字.

例1 表1为一个模糊决策形式背景, 包含10个对象和2个条件属性.该模糊决策形式背景中有2个决策, 则对象集划分为2个决策类:

${{\text{}}_{1}}=\left\{ {{x}_{1}}, {{x}_{2}}, \cdots , {{x}_{8}} \right\}$, ${{\text{}}_{2}}=\left\{ {{x}_{9}}, {{x}_{10}} \right\}$.

表1 模糊决策形式背景 Table 1 Fuzzy decision formal context

决策粒概念空间

$\begin{align} & {{\text{}}_{1}}=\left\{ \left( \left\{ {{x}_{1}} \right\}, \left\{ 0.70, 0.46 \right\} \right); \left( \left\{ {{x}_{2}} \right\}, \left\{ 0.77, 0.38 \right\} \right) \right.; \\ & \begin{matrix} {} & \begin{matrix} {} & \left( \left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{3}} \right\}, \left\{ 0.63, 0.26 \right\} \right); \left( \left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{4}} \right\}, \right. \\\end{matrix} \\\end{matrix} \\ & \begin{matrix} {} & {} & \left. \left\{ 0.61, 0.31 \right\} \right) \\\end{matrix}; \left( \left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}} \right\}, \left\{ 0.56, 0.21 \right\} \right); \\ & \begin{matrix} {} & {} & \left( \left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{3}}, {{x}_{4}}, {{x}_{6}} \right\}, \left\{ 0.40, 0.24 \right\} \right) \\\end{matrix}; \\ & \begin{matrix} {} & {} & \left( \left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{7}} \right\}, \left\{ 0.48, 0.15 \right\} \right); \\\end{matrix} \\ & \begin{matrix} {} & {} & \left. \left( \left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{8}} \right\}, \left\{ 0.44, 0.21 \right\} \right) \right\} \\\end{matrix}, \\ & {{\text{}}_{2}}=\left\{ \left( \left\{ {{x}_{9}} \right\}, \left\{ 0.67, 0.09 \right\} \right); \left. \left( \left\{ {{x}_{10}} \right\}, \left\{ 0.24, 0.27 \right\} \right) \right\} \right.. \\ \end{align}$

后面使用C₁~C₁₀依次表示上述10个概念.

2 构建K-概念空间

在购买商品的决策问题中, 会有价格导向决策、品质导向决策及功能导向决策等.对于不同决策任务, 属性可能会被分配到不同的权重, 灵活地调整属性权重可以更好地处理复杂的信息.为了提高属性在不同决策任务中的灵活性, 本文建立属性与类别之间的相关性描述, 提出基于属性加权的概念认知学习模型(WACCL).模型结合属性权重, 刻画概念的重要性.然后, 选择重要性较高的概念, 减少概念空间的冗余性.最后, 建立概念聚类机制, 进一步提高概念认知学习的效率.

定义4 设(U, A, $\tilde{I}$ , D, J)为模糊决策形式背景, 属性a∈ A与对象x∈ U的相关程度为 $\tilde{I}$ (x, a), 则将属性a与决策类C_i的相关性定义为

${\tilde{I}}_{i}$ (a)= $\frac{1}{| C_{i} |} \sum_{x_{j} \in C_{i}} \tilde{I}$ (x_j, a).

属性与决策类的相关性表示属性对决策的预测能力或影响程度, 反映不同属性对于决策的重要性和贡献程度.在进行决策时, 属性权重可以帮助识别更具有影响力的属性, 以实现个性化决策和提高决策的准确性.下面结合属性与类别的相关性, 给出属性权重的定义.

定义5 设(U, A, $\tilde{I}$ , D, J)为模糊决策形式背景.对于决策类C_i, 属性a_j(j=1, 2, …, n)的权重定义为

ω _ij= $\frac{{\tilde{I}}_{i} (a_{j})}{\overset{n}{\sum_{k = 1}} {\tilde{I}}_{i} (a_{k})}$ .

显然, 每个属性在不同决策中被分配到不同的权重, 反映该属性在不同分类任务中的重要性.记权重矩阵:

ω = $(\begin{array}{l} ω_{11} & ω_{12} & \dots & ω_{1 n} \\ ω_{21} & ω_{22} & \dots & ω_{2 n} \\ ︙ & ︙ & ︙ \\ ω_{k 1} & ω_{k 2} & \dots & ω_{kn} \end{array})$ ,

其中ω _ij为属性a_j在决策类C_i下的权重.

例2 (接例1) 由定义5可得权重矩阵

ω = $(\begin{array}{l} 0.67 & 0.33 \\ 0.72 & 0.28 \end{array})$ .

定义6 设(U, A, $\tilde{I}$ , D, J)为模糊决策形式背景, 若(X, $\tilde{B}$ )为决策粒概念空间Q_i中的概念, 则(X, $\tilde{B}$ )的贡献值定义为

Cva(X, $\tilde{B}$ )= $\overset{n}{\sum_{j = 1}}$ ω _ij $\tilde{B}$ (a_j).

例3 (接例2) 决策粒概念空间Q₁中所有概念的贡献值分别为

Cva(C₁)=0.6208, Cva(C₂)=0.6413, Cva(C3₎=0.5079, Cva(C4₎=0.5110, Cva(C5)₌0.4445, Cva(C6)₌0.3472, Cva(C7)=₀.3711, Cva(C8)=₀.3641.

在概念空间中, 不同概念以贡献值体现类重要程度, 概念的贡献值越高, 它在概念空间中越显著.选择贡献值较高的概念可以降低概念空间的复杂性, 提高学习效率.

算法1 构建K-概念空间

输入模糊形式背景(U, A, $\tilde{I}$ , D, J), 阈值K

输出 K-概念空间Q^K

Q^K← Ø ; U=C₁∪ C₂∪ …∪ C_k

for i=1∶ k

$Q_{i}^{K}$ ← Ø

for x∈ C_i

构造粒概念( $\tilde{G}$ $\tilde{F}$ (x), $\tilde{F}$ (x))

根据定义6计算贡献值Cva( $\tilde{G}$ $\tilde{F}$ (x), $\tilde{F}$ (x))

if Cva( $\tilde{G}$ $\tilde{F}$ (x), $\tilde{F}$ (x))≥ K then

$Q_{i}^{K}$ ← ( $\tilde{G}$ $\tilde{F}$ (x), $\tilde{F}$ (x))

end

Q^K=Q^K∪ $Q_{i}^{K}$

end

定义7 对于决策粒概念空间Q_i, 给定阈值K(0≤ K≤ 1), K-决策概念空间定义为:

$\text{}_{i}^{K}=\left\{ \left( X, \tilde{B} \right)\in {{\text{}}_{i}}, \right.\left. Cva\left( X, \tilde{B} \right)\ge K \right\}.$

阈值K为概念贡献值的一个临界值, 不仅可以筛选贡献值较高的概念, 还可以控制概念空间中的概念数量.阈值过高会导致重要的概念被错误删除, 而阈值过低会导致概念空间过于庞大和冗余, 需要根据特定的任务和领域对阈值进行调整和优化.

算法1总结K-概念空间的构建过程.显然, 不同的决策将Q^K划分为k个K-决策概念空间.

例4 (接例3) 设阈值K=0.4, K-决策概念空间

$Q_{1}^{K}$ ={C₁, C₂, C₃, C₄, C₅}.

3 基于属性加权的概念聚类

根据现代范畴理论^[27]基本思想, 同一范畴内的各个成员都由家族相似性联系在一起, 而人们对事物的分类和认知是基于抽象的范畴, 不是基于单个特征.概念聚类将相似事物归为一类, 是形成范畴的过程.在概念认知学习中, 核心概念是具有重要性和代表性的概念.因此, 核心概念可以作为现代范畴理论中原型的一种表现形式, 即最典型或最常见的代表^[28].下面给出概念空间中的核心概念定义.

定义8^[11] 设M为K-决策概念空间 $Q_{i}^{K}$ (i=1, 2, …, k)的概念子集, 若存在概念(X, $\tilde{B}$ )∈ M且对

∀ (X_i, ${\tilde{B}}_{i}$ )∈ M,

有

Cva(X, $\tilde{B}$ )≥ Cva(X_i, ${\tilde{B}}_{i}$ ),

称(X, $\tilde{B}$ )为概念子集M的核心概念.

在认知心理学中, 邻接概念用于解释人类思维和语言理解中概念之间的关系和联系.如果两个概念的外延有交集, 那么这两个概念之间存在一定的联系.

定义9^[11] 设(X₁, ${\tilde{B}}_{1}$ ), (X₂, ${\tilde{B}}_{2}$ )为 $Q_{i}^{K}$ 中任意两个概念, 若

X₁∩ X₂≠ Ø ,

称(X₁, ${\tilde{B}}_{1}$ )和(X₂, ${\tilde{B}}_{2}$ )互为邻接概念.

在概念聚类中, 概念的相似度可以用来划分概念簇.在描述概念之间相似性时, 不仅要关注对象信息, 还要关注对概念分类和聚类分析同样重要的属性信息.下面给出概念之间相似性度量的定义.

设(U, A, $\tilde{I}$ , D, J)为模糊决策形式背景, 对于

∀ (X, $\tilde{B}$ )∈ $Q_{i}^{K}$ ,

|X|表示概念(X, $\tilde{B}$ )的对象基数.

定义10 设(X₁, ${\tilde{B}}_{1}$ )、(X₂, ${\tilde{B}}_{2}$ )为 $Q_{i}^{K}$ 中任意两个概念, 则它们的相似度定义为

θ ^{1, 2}= $\frac{| X_{1} ⋂ X_{2} |}{| X_{1} ⋂ X_{2} | + \partial_{1} | X_{1} - X_{2} | + \partial_{2} | X_{2} - X_{1} |}$ ,

其中,

∂ ₁=Cva(X₁, ${\tilde{B}}_{1}$ ), ∂ ₂=Cva(X₂, ${\tilde{B}}_{2}$ ).

θ ^{1, 2}的值越大, 两个概念相似性越强.

定义11 设G为 $Q_{i}^{K}$ 的一个子概念空间, 如果如下3个条件成立:

1)(X_s, ${\tilde{B}}_{s}$ )为G的核心概念, 且

∀ (X_i, ${\tilde{B}}_{i}$ )∈ G,

都为(X_s, ${\tilde{B}}_{s}$ )的邻接概念,

2)若(X_s, ${\tilde{B}}_{s}$ )为G的核心概念, 则对

∀ (X_i, ${\tilde{B}}_{i}$ )∈ G,

有θ ^s^,ⁱ≥ β ,

3)一个概念只存在一个概念簇里面, 则称G为K- β 概念簇.下面简称G为概念簇.

在概念认知学习中, 将概念簇的概念进行抽象化, 形成具有更强泛化能力的伪概念是常用手段之一.伪概念是基于已有概念进行抽象化和泛化得到的, 它们不是真正的概念, 只是特殊情形下有用的概念.

此外, 伪概念的泛化能力可能会受特定学习环境的影响, 需要进行进一步的实验以评估其泛化能力的有效性.

定理1 对于 $Q_{i}^{K}$ , 当β 增大时, 概念簇G的概念基数不变或减小.

证明阈值β 增大时, 与G中核心概念相似度大于β 的概念会不变或变少, 因此G的概念基数不变或减小.

对于概念簇G, r=|G|表示G中的概念基数, 对∀ (X_i, ${\tilde{B}}_{i}$ )∈ G, (X_i, ${\tilde{B}}_{i}$ )的权重定义为

v_i= $\frac{Cva (X_{i}, {\tilde{B}}_{i})}{\overset{r}{\sum_{j = 1}} Cva (X_{j}, {\tilde{B}}_{j})}$ .

定义12 设G为K- β 概念簇, (X_s, ${\tilde{B}}_{s}$ )为G中的核心概念, 若对∀ (X_i, ${\tilde{B}}_{i}$ )∈ G, 有

$\begin{array}{l} X_{p}=X_{s} \cup_{i=1}^{r} X_{i}, \\ \widetilde{B}_{p}=\left(\widetilde{B}_{p}\left(a_{1}\right), \widetilde{B}_{p}\left(a_{2}\right), \cdots, \widetilde{B}_{p}\left(a_{n}\right)\right), \end{array}$

其中,

${\tilde{B}}_{p}$ (a_j)= $\overset{r}{\sum_{i = 1}}$ v_i ${\tilde{B}}_{i}$ (a_j), j=1, 2, …, n,

则称(X_p, ${\tilde{B}}_{p}$ )为由概念簇G诱导的伪概念.

算法2 生成伪概念

输入概念子集M, 核心概念(X_s, ${\tilde{B}}_{s}$ ), 阈值β

输出概念簇G, 伪概念(X_p, ${\tilde{B}}_{p}$ )

for (X_i, ${\tilde{B}}_{i}$ )∈ M

if X_i∩ X_s≠ Ø

根据定义10计算相似度θ ^s^,ⁱ

if θ ^s^,ⁱ≥ β then

G ← (X_i, ${\tilde{B}}_{i}$ )

end

通过定义12得到伪概念(X_p, ${\tilde{B}}_{p}$ )

算法2总结从一个概念子集得到伪概念的过程.概念聚类将相似的概念聚类在一个簇中, 从而减少概念空间的维度, 提高概念认知学习的效率.下面给出基于属性加权的概念聚类过程.

算法3 基于属性加权的概念聚类

输入 K-概念空间Q^K, 阈值β

输出伪概念空间D

D← Ø ; Q^K= $Q_{1}^{K}$ ∪ $Q_{2}^{K}$ ∪ …∪ $Q_{k}^{K}$

for i=1∶ k

M= $Q_{i}^{K}$ ; D_i← Ø

while |M|> 0

G=Ø ; 找出M的核心概念(X_s, ${\tilde{B}}_{s}$ )

通过算法2得到概念簇G和伪概念(X_p, ${\tilde{B}}_{p}$ )

M= $Q_{i}^{K}$ \G; D_i← (X_p, ${\tilde{B}}_{p}$ )

end

D=D∪ D_i

end

K-决策概念空间 $Q_{i}^{K}$ 中概念聚类的过程如图1所示.由图可看出, 概念簇并不是同时生成的, 它们之间是有先后顺序的, 概念簇中核心概念贡献值越大则该概念簇越先生成.

	Figure Option View Download New Window
	图1 概念聚类算法流程图Fig.1 Flow chart of conceptual clustering

例5 (接例4) 设阈值β =0.4, 则K-决策概念空间 $Q_{1}^{K}$ 划分为3个部分:

{C₂, C₃, C₄}→ {C₁}→ {C₅},

对于概念簇{C₂, C₃, C₄}, 用伪概念表示为

({1, 2, 3, 4}, {0.6779, 0.3217}).

4 概念预测

概念预测指在给定一些信息的情况下, 根据已有的知识和经验, 预测与这些信息相关的概念和类别.

在K-概念空间完成概念聚类后, 得到伪概念空间:

D= $[\begin{array}{l} D_{1} \\ D_{2} \\ ︙ \\ D_{k} \end{array}]$ = $[\begin{array}{l} (X_{1, p_{1}}, {\tilde{B}}_{1, p_{1}}) & (X_{1, p_{2}}, {\tilde{B}}_{1, p_{2}}) & \dots & (X_{1, p_{m (1)}}, {\tilde{B}}_{1, p_{m (1)}}) \\ (X_{2, p_{1}}, {\tilde{B}}_{2, p_{1}}) & (X_{2, p_{2}}, {\tilde{B}}_{2, p_{2}}) & \dots & (X_{2, p_{m (2)}}, {\tilde{B}}_{2, p_{m (2)}}) \\ ︙ & ︙ & ︙ \\ (X_{k, p_{1}}, {\tilde{B}}_{k, p_{1}}) & (X_{k, p_{2}}, {\tilde{B}}_{k, p_{2}}) & \dots & (X_{k, p_{m (k)}}, {\tilde{B}}_{k, p_{m (k)}}) \end{array}]$ , (1)

其中,

m(i)=|D_i|

表示D_i中的伪概念基数, D_i为由决策为i所有伪概念组成的伪概念空间.

定理2 设Q^K为K-概念空间, D为由Q^K生成的伪概念空间, |D|为D中的伪概念基数, k为决策个数, 则

k≤ |D|≤ |Q^K|.

证明从式(1)显然有

|D|≤ |Q^K|.

由于每个K-决策概念空间通过聚类都会生成至少一个伪概念, 故|D|≥ k.综上所述,

k≤ |D|≤ |Q^K|

可证.

定理3 设(U, A, $\tilde{I}$ , D, J)为模糊决策形式背景, $Q^{K_{1}}$ 和 $Q^{K_{2}}$ 为不同阈值下的K-概念空间, $D^{K_{1}}$ 和 $D^{K_{2}}$ 分别为由 $Q^{K_{1}}$ 和 $Q^{K_{2}}$ 生成的伪概念空间, 若K₁> K₂, 在阈值β 相等的情况下, 有

| $D^{K_{1}}$ |≤ | $D^{K_{2}}$ |.

证明由K₁> K₂可得,

$Q^{K_{1}}$ ⊆ $Q^{K_{2}}$ .

对于

∀ (X, $\tilde{B}$ )∈ $Q^{K_{2}}$ - $Q^{K_{1}}$ ,

在概念聚类后会有如下3种情况:

1)(X, $\tilde{B}$ )全为邻接概念, 此时,

| $D^{K_{1}}$ |=| $D^{K_{2}}$ |;

2)(X, $\tilde{B}$ )全为核心概念, 此时,

| $D^{K_{1}}$ |< | $D^{K_{2}}$ |;

3)(X, $\tilde{B}$ )部分为核心概念, 此时,

| $D^{K_{1}}$ |< | $D^{K_{2}}$ |.

综上所述, | $D^{K_{1}}$ |≤ | $D^{K_{2}}$ |可证.

概念预测可以通过不同的方法实现, 本文通过欧氏距离描述物体之间的相似性.

定义13 设(U, A, $\tilde{I}$ , D, J)为模糊决策形式背景, x_r为新样本, 其相对于 $\tilde{I}$ 的隶属值为 ${\tilde{B}}_{r}$ , 则样本x_r与伪概念空间D_i最小距离的定义为

$E_{i}\left(x_{r}, p_{s}\right)=\min _{s \in S}\left(\sum_{j=1}^{n} \omega_{i j}\left(\widetilde{B}_{r}\left(a_{j}\right)-\widetilde{B}_{i, p_{s}}\left(a_{j}\right)\right)^{2}\right)^{\frac{1}{2}}, $

其中S={1, 2, …, m(i)}.

对于一个新样本, 算法4给出概念预测的过程.值得一提的是, 基于属性加权的分类实质上是一个多分类的过程, 而不是多标签的过程.

算法4 基于属性加权的概念认知学习模型(WACCL)

输入伪概念空间D, 新增对象x_r

输出 x_r的类别标签l

for 每个伪概念空间D_i∈ D

根据定义13, 计算得到最小距离E_i(x_r, p_s)

end

l=arg $\min_{i = {1, 2, \dots, k}}$ E_i(x_r, p_s)

返回类别标签l

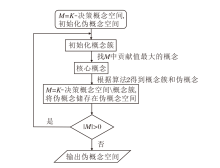
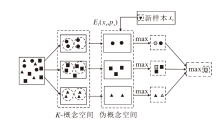
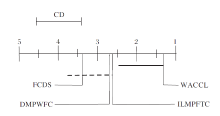
因此, 基于属性加权的概念认知学习模型(WACCL)主要包括3个部分: 构建K-概念空间、构造伪概念空间、概念泛化.WACCL的简化框架如图2所示, 考虑3个决策类的数据集.首先根据认知算子和阈值K构建K-概念空间; 然后进行概念聚类, 得到伪概念空间; 最后对新样本进行预测并输出类别.

	Figure Option View Download New Window
	图2 WACCL简化框架Fig.2 Simplified framework of WACCL

在第一阶段, 构建K-概念空间需要识别所有概念, 时间复杂度为O(|U|).在第二阶段, 最不理想的情况下, 即每个概念簇都只有一个概念时, 时间复杂度为O(|Q^K|).在第三阶段, 需要识别所有的伪概念并进行概念预测, 时间复杂度为O(|D|).整个过程总的时间复杂度为

O(|U|+|Q^K|+|D|).

5 实验及结果分析

5.1 实验设置

为了验证本文模型(WACCL)的可行性、有效性及学习效果, 选择如下概念认知学习算法进行对比: ILMPFTC^[10]、DMPWFC^[12]、决策重要度的动态更新机制(Incremental Learning Mechanism for Fuzzy Concept Based on Decision Signification, FCDS)^[29].

从UCI知识库上选择13个数据集用于数值仿真实验, 数据集具体信息如表2所示.

表2 实验数据集信息 Table 2 Description of experimental datasets

针对每个数据集, 利用

$\begin{array}{l} \widetilde{R}\left(x_{i}, a_{j}\right)= 0.8\left(\frac{f\left(x_{i}, a_{j}\right)-\min \left(f\left(a_{j}\right)\right)}{\max \left(f\left(a_{j}\right)\right)-\min \left(f\left(a_{j}\right)\right)}\right)+0.1 . \end{array}$

进行模糊化处理, 使属性值域为[0.1, 0.9], 其中, f(x_i, a_j)为x_i对属性a_j的隶属值, max(f(a_j))和min(f(a_j))分别表示属性a_j中所有对象的最大隶属值和最小隶属值.需要说明的是, 值域为[0.1, 0.9]是为了避免DMPWFC中出现log₂0的情形, 因此通过 $\tilde{R}$ (x_i, a_j)将隶属值归一化为[0.1, 0.9].

在实验中, 对每个数据集进行划分, 80%的数据用于训练模型, 剩下的数据平均分为10份, 逐次添加到测试集上, 以此评估WACCL的分类性能.

实验在个人计算机上的Matlab2016b上实现, 计算机的配置为Intel(R) Core(TM) i5-8265U CPU@1.60 GHz, 8 GB内存.

5.2 参数分析

在实验中, WACCL的参数K、 β 的选择范围为[0, 1], K的步长为0.01, β 的步长为0.1.ILMPFTC、DMPWFC、FCDS的参数δ 选择范围为[0, 1], 步长为0.01.

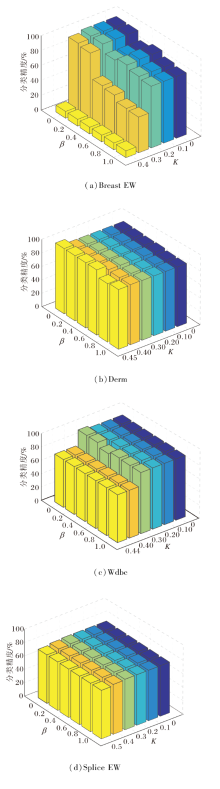
选取Breast EW、Derm、Wdbc、Splice EW数据集进行参数分析.对于参数K, 若取值过大会导致概念空间中所有概念被删除掉, 故选择范围为[0, 0.5], 步长为0.1.部分数据集在K=0.5时无法输出结果, 此时取K能达到的最大值.而参数β 选取范围为[0, 1], 步长为0.2.

当参数变化时, WACCL分类精度的可视化结果如图3所示.显然, K在[0, 0.3]时, 分类精度几乎没有变化, 这是因为大部分概念的贡献值都大于或等于0.3.由于删除概念会改变概念空间中的概念数量, 从而对分类精度造成一定的影响, 所以K在[0.3, 0.5]区间中, WACCL的分类精度变化相对较大.参数β 在某些数据集上变化不会对分类精度造成影响, 而对于大部分数据集, 分类精度会随K的增大而减小.

	Figure Option View Download New Window
	图3 参数对WACCL分类精度的影响Fig.3 Influence of parameters on classification accuracy of WACCL

在Breast EW数据集上参数的变化对分类精度影响较大, 当K=0.4时, 分类精度较低, 说明过大的K值会导致重要的概念被错误删除, 该数据集上K的最优值范围为[0, 0.3], β 的最优值范围为[0, 0.2].

在Derm数据集上, K的最优值在0.45左右, β 的最优值范围为[0, 0.6].在Wdbc数据集上, K的最优值在0.3左右, β 的最优值范围为[0, 0.2].在Splice EW数据集上, 参数变化对分类精度影响较小, 说明参数在此数据集上的灵敏度较低.

5.3 分类性能对比

在实验中, 各算法选择的参数都为近似最优, WACCL在13个数据集上的参数选择如表3所示.

表3 WACCL在各数据集上的参数选择 Table 3 Parameter settings for different datasets of WACCL

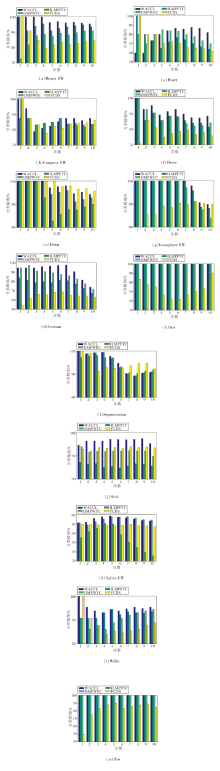
各算法在13个数据集上的分类精度对比如表4所示, 表中黑体数字为最优值.由表可见, WACCL在12个数据集上的分类精度最高, 尤其在Iris、Zoo数据集上分类精度达到100%.同时WACCL在13个数据集上的平均分类精度也最高, 相比ILMPFTC, 平均分类精度提高3.46%, 相比DMPWFC, 平均分类精度提高4.43%, 相比FCDS, 平均分类精度提高9.94%.

表4 各算法在13个数据集上的分类精度 Table 4 Classification accuracy of different algorithms on 13 datasets %

各算法10次分类精度对比如图4所示, 随着数据的逐次添加, 4种算法在大部分数据集上的分类精度呈下降趋势.从图中可以看出WACCL在Breast EW、German、Horse、Ionosphere EW、Iris、Sick、Wdbc、Zoo数据集上几乎每次分类精度都最高.由表4和图4结果可说明AWFC的分类机制优于对比算法.

	Figure Option View Download New Window
	图4 各算法10次分类精度对比Fig.4 Accuracy comparison of different algorithms classifying for 10 times

在信息检索中, 往往会关心检索的信息中用户感兴趣的比例、用户感兴趣的信息中有多少被检索, 查全率和查准率可以更好地适用此类需求.

对于二分类问题, 将样例根据其真实类别与学习器预测类别的组合划分为真正例(True Positive, TP)、假正例(False Positive, FP)、真反例(True Negative, TN)、假反例(False Negative, FN)4种情形, 则样例总数表示为TP+FP+TN+FN.

分类结果的混淆矩阵如表5所示.

表5 分类结果混淆矩阵 Table 5 Confusion matrix of classification results

查准率P与查全率R分别定义为

$\begin{array}{l} P=\frac{T P}{T P+F P}, \\ R=\frac{T P}{T P+F N} . \end{array}$

F1值为查全率和查准率的调和平均, 定义为

F1= $\frac{2 \times P \times R}{P + R}$ .

在执行多分类任务时, 会有多个混淆矩阵, 为了在多个混淆矩阵上综合考察查准率和查全率, 直接的做法是在各混淆矩阵上分别计算查全率和查准率, 再计算平均值, 从而得到宏查准率(macro-P)、宏查全率(macro-R)以及相应的宏F1(macro-F1).具体公式如下:

$\begin{array}{l} \text { macro- } P=\frac{1}{n} \sum_{i=1}^{n} P_{i}, \\ \text { macro- } R=\frac{1}{n} \sum_{i=1}^{n} R_{i}, \\ \text { macro-F } 1=\frac{2 \cdot \text { macro- } P \cdot \text { macro- } R}{\text { macro }-P+\text { macro }-R} . \end{array}$

WACCL、ILMPFTC、DMPWFC和FCDS在13个数据集上的查准率和查全率如表6所示, 表中黑体数字表示最优值.由表可知, WACCL在8个数据集上的查全率和查准率都大于或等于其它算法, 在Derm、German、Wdbc数据集上取得最大的查准率, 在Ionosphere EW数据集上的查全率最大.

表6 各算法在13个数据集上的查准率和查全率对比 Table 6 Comparison of precision and recall of different algorithms on 13 datasets %

4种算法在13个数据集上的F1值对比如表7所示, 表中黑体数字表示最优值.由表可见, WACCL在9个数据集上取得最大值.

表7 各算法在13个数据集上的F1值对比 Table 7 F1 value comparison of different algorithms on 13 datasets %

查准率、查全率和F1值都说明WACCL具有优越的综合性能.

5.4 统计检验

为了进一步验证各算法的分类性能, 本节首先验证WACCL、ILMPFTC、DMPWFC、FCDS的差异是否显著.在此选用Friedman检验^[30]对其进行验证.定义如下:

$\chi_{F}^{2}=\frac{12 N}{k(k+1)}\left(\sum_{i=1}^{k} R_{i}^{2}-\frac{k(k+1)^{2}}{4}\right) $

其中, N为数据集个数, k为算法个数, R_i为所有数据集上第i种算法平均排名.

F遵循自由度为k-1和(k-1)(N-1)的Fisher分布.

F= $\frac{(N - 1) χ_{F}^{2}}{N (k - 1) - χ_{F}^{2}}$ ,

WACCL、ILMPFTC、DMPWFC、FCDS的分类精度排名如表8所示, 表中黑体数字表示最优值.由表可见, WACCL在9个数据集上排名第一, 说明此算法的分类结果更准确.

表8 各算法的分类精度排名 Table8 Classification accuracy rank of different algorithms %

选用α =0.1, F检验的临界值F=2.243.根据Friedman检验的定义, 计算可得F=9.853, 大于临界值, 说明算法性能具有差异性.所以, 使用Bonferroni-Dunn进行后续检验^[31].平均序值差别的临界值域为:

CD_α=q_α $\sqrt[]{\frac{k (k + 1)}{6 N}}$ ,

其中, N为数据集个数, k为算法个数, q_α为Tukey分布的临界值.

当

k=4, N=13, α =0.1

时, q₀_.₁=2.291, 则CD₀_.₁=1.160.若两种算法的距离超过临界值, 说明两种算法存在显著性能差异.

各算法的Bonferroni-Dunn测试图如图5所示.由图可以直观看到, WACCL与其它3种算法的平均排名的差值都大于临界值, 由此可知WACCL与其它3种算法差异显著.

	Figure Option View Download New Window
	图5 各算法的Bonferroni-Dunn测试图Fig.5 Bonferroni-Dunn test of different algorithms

5.5 十折交叉验证

为了更进一步验证WACCL分类的有效性和准确性, 选取Breast EW、Congress EW、German、Ionos-phere EW、Iris、Segmentation、Sick、Wdbc数据集, 进行十折交叉验证法验算.各算法10次分类精度对比如表9所示, 表中黑体数字表示最优值.

表9 各算法十折交叉验证结果 Table 9 Ten-fold cross-validation results of different algorithms %

由表9可以看出, WACCL在8个数据集上的分类精度最高:相比ILMPFTC, 平均分类精度提高2.98%; 相比DMPWFC, 平均分类精度提高6.2%; 相比FCDS, 平均分类精度提高4.06%.分类结果显示WACCL分类的有效性和准确性最优.

6 结束语

面向模糊决策形式背景, 本文提出基于属性加权的概念认知学习模型(WACCL).模型认为每个属性在不同决策中的作用不一样, 通过概念聚类的方法压缩概念空间中概念的数量, 使学习更高效.最后通过实验分析说明WACCL的有效性和实用性.实际上, WACCL只讨论概念的生成和概念分类, 未涉及动态更新的问题, 如何实现新增对象后与原来概念空间之间的动态概念学习是值得研究的关键问题.此外, 目前概念认知学习的研究集中在属性是单一尺度的情况下, 因此多尺度的概念认知学习方法将是今后的工作重心之一.

本文责任编委张燕平

Recommended by Associate Editor ZHANG Yanping

参考文献

文献选项

[1]	WANG Y X. On Cognitive Computing. International Journal of Software Science and Computational Intelligence, 2011, 1(3): 1-15. [本文引用:1]
[2]	FELDMAN J. The Simplicity Principle in Human Concept Learning. Current Directions in Psychological Science, 2003, 12(6): 227-232. [本文引用:1]
[3]	ZHANG T, LI H H, LIU M Q, et al. Incremental Concept-Cognitive Learning Based on Attribute Topology. International Journal of Approximate Reasoning, 2020, 118: 173-189. [本文引用:2]
[4]	SHI Y, MI Y L, LI J H, et al. Concept-Cognitive Learning Model for Incremental Concept Learning. IEEE Transactions on Systems, Man and Cybernetics(Systems), 2018, 51(2): 809-821. [本文引用:1]
[5]	KUZNETSOV S O. Machine Learning and Formal Concept Analysis // Proc of the International Conference on Formal Concept Analysis. Berlin, Germany: Springer, 2004: 287-312. [本文引用:1]
[6]	MI Y L, SHI Y, LI J H, et al. Fuzzy-Based Concept Learning Me-thod: Exploiting Data with Fuzzy Conceptual Clustering. IEEE Transactions on Cybernetics, 2022, 25(1): 582-593. [本文引用:2]
[7]	WANG Y X. On Concept Algebra: A Denotational Mathematical Stru-cture for Knowledge and Software Modeling. International Journal of Cognitive Informatics and Natural Intelligence, 2008, 2(2): 1-19. [本文引用:1]
[8]	GUO D D, JIANG C M, SHENG R X, et al. A Novel Outcome Eva-luation Model of Three-Way Decision: A Change Viewpoint. Information Sciences, 2022, 607: 1089-1110. [本文引用:1]
[9]	MI Y L, QUAN P, SHI Y, et al. Concept-Cognitive Computing System for Dynamic Classification. European Journal of Operational Research, 2022, 301(1): 287-299. [本文引用:2]
[10]	YUAN K H, XU W H, LI W T, et al. An Incremental Learning Mechanism for Object Classification Based on Progressive Fuzzy Three-Way Concept. Information Sciences, 2022, 584: 127-147. [本文引用:3]
[11]	XU W H, CHEN Y Q. Multi-attention Concept-Cognitive Learning Model: A Perspective from Conceptual Clustering. Knowledge-Based Systems, 2022, 252. DOI: 10.1016/j.knosys.2022.109472. [本文引用:5]
[12]	ZHANG C L, TSANG E C C, XU W H, et al. Incremental Concept-Cognitive Learning Approach for Concept Classification Oriented to Weighted Fuzzy Concepts. Knowledge-Based Systems, 2023, 260. DOI: 10.1016/j.knosys.2022.110093. [本文引用:4]
[13]	WILLE R. Restructuring Lattice Theory: An Approach Based on Hierarchies of Concepts // RIVAL I, ed. Ordered Sets. Berlin, Germany: Springer, 1982: 445-470. [本文引用:1]
[14]	GANTER B, WILLE R. Formal Concept Analysis: Mathematical Foundations. Berlin, Germany: Springer, 1999. [本文引用:1]
[15]	SHAO M W, LEUNG Y, WANG X Z, et al. Granular Reducts of Formal Fuzzy Contexts. Knowledge-Based Systems, 2016, 14: 156-166. [本文引用:3]
[16]	QI J J, WEI L, YAO Y Y. Three-Way Formal Concept Analysis // Proc of the International Conference on Rough Sets and Know-ledge Technology. Berlin, Germany: Springer, 2014: 732-741. [本文引用:1]
[17]	CHEN D X, LI J J, LIN R D. Formal Concept Analysis of Multi-scale Formal Context. Journal of Ambient Intelligence and Huma-nized Computing, 2020, 11: 5315-5327. [本文引用:1]
[18]	LI J L, HE Z Y, ZHU Q L. An Entropy-Based Weighted Concept Lattice for Merging Multi-source Geo-Ontologies. Entropy, 2013, 15(6): 2303-2318. [本文引用:1]
[19]	YAO Y Y. Interpreting Concept Learning in Cognitive Informatics and Granular Computing. IEEE Transactions on Systems, Man, and Cybernetics(Cybernetics), 2009, 39(4): 855-866. [本文引用:1]
[20]	PÉREZ-SUÁREZ A, MARTÍNEZ-TRINIDAD J, CARRASOOO-CHOA J A. A Review of Conceptual Clustering Algorithms. Artificial Intelligence Review, 2019, 52(2): 1267-1296. [本文引用:1]
[21]	LI J H, MEI C L, XU W H, et al. Concept Learning via Granular Computing: A Cognitive Viewpoint. Information Sciences, 2015, 298: 447-467. [本文引用:3]
[22]	NIU J J, HUANG C C, LI J H, et al. Parallel Computing Techniques for Concept-Cognitive Learning Based on Granular Computing. International Journal of Machine Learning and Cybernetics, 2018, 9(3): 1785-1805. [本文引用:1]
[23]	李金海, 米允龙, 刘文奇. 概念的渐进式认知理论与方法. 计算机学报, 2019, 42(10): 2233-2250. (LI J H, MI Y L, LIU W Q. Incremental Cognition of Concepts: Theories and Methods. Chinese Journal of Computers, 2019, 42(10): 2233-2250. ) [本文引用:2]
[24]	XIE X X, XU W H, LI J J. A Novel Concept-Cognitive Learning Method: A Perspective from Competences. Knowledge-Based Systems, 2023, 265. DOI: 10.1016/j.knosys.2023.110382. [本文引用:1]
[25]	XU W H, GUO D D, QIAN Y H, et al. Two-Way Concept-Cognitive Learning Method: A Fuzzy-Based Progressive Learning. IEEE Transactions on Fuzzy Systems, 2023, 31(6): 1885-1899. [本文引用:1]
[26]	SINGH P K, CHERUKURI A K, LI J H. Concepts Reduction in Formal Concept Analysis with Fuzzy Setting Using Shannon Entropy. International Journal of Machine Learning, 2017, 8(1): 179-189. [本文引用:1]
[27]	ROSCH E, MERVIS C B. Family Resemblances: Studies in the Internal Structure of Categories. Cognitive Psychology, 1975, 7(4): 573-605. [本文引用:1]
[28]	UNGERER F, SCHMID H. An Introduction to Cognitive Linguistics. 2nd Edition. London, UK: Routledge, 2013. [本文引用:1]
[29]	王启君, 林艺东, 林梦雷, 等. 基于决策重要度的概念认知学习模型. 模式识别与人工智能, 2022, 35(9): 816-826. (WANG Q J, LIN Y D, LIN M L, et al. Concept-Cognitive Lear-ning Model Based on Decision Significance. Pattern Recognition and Artificial Intelligence, 2022, 35(9): 816-826. ) [本文引用:1]
[30]	FRIEDMAN M. A Comparison of Alternative Tests of Significance for the Problem of m Rankings. The Annals of Mathematical Statistics, 1940, 11(1): 86-92. [本文引用:1]
[31]	DEMŠAR J. Statistical Comparisons of Classifiers over Multiple Data Sets. The Journal of Machine Learning Research, 2006, 7: 1-30. [本文引用:1]

2011

0.0

... 认知计算旨在解决生物系统中不确定、不精确和不完整的问题^[1] ...

2003

0.0

... 经过多年发展,认知学习现已成为实现认知计算的有利工具之一,广泛应用于认知心理学^[2]、机器学习^[3,4]、信息科学^[5,6,7,8]、分类任务^[9,10,11,12]等领域 ...

2020

0.0

... 为了衡量概念结构的稳定性,Zhang等^[3]基于属性拓扑的概念树表示概念,降低概念认知过程的复杂性 ...

2018

0.0

2004

0.0

2022

0.0

... Mi等^[6]结合属性和对象信息,提出FCLM(Fuzzy-Based Concept Learning Model),用于概念分类和概念发现 ...

2008

0.0

2022

0.0

2022

0.0

... Mi等^[9]提出用于动态分类的概念认知计算系统,提高决策者在动态环境下对问题解决的反应能力 ...

2022

0.0

... 为了克服个体认知和认知环境的限制,Yuan等^[10]结合隶属度和非隶属度,设计ILMPFTC(Incre-mental Learning Mechanism Based on Progressive Fuzzy Three-Way Concept) ...

... 1 实验设置为了验证本文模型(WACCL)的可行性、有效性及学习效果,选择如下概念认知学习算法进行对比: ILMPFTC^[10]、DMPWFC^[12]、决策重要度的动态更新机制(Incremental Learning Mechanism for Fuzzy Concept Based on Decision Signification, FCDS)^[29] ...

2022

0.0

... Xu等^[11]考虑注意力对概念聚类的影响,提出MA-CLM(Multi-attention Concept-Cognitive Learning Model),提高分类效率 ...

... 因此,受文献[11]和文献[12]的启发,本文利用属性与决策之间的相关性,提出基于属性加权的概念认知学习模型(Weighted Attributes-Based Con-cept-Cognitive Learning Model, WACCL) ...

... 定义8^[11] 设M为K-决策概念空间 QiK(i=1,2,…,k)的概念子集,若存在概念(X, B~)#cod#x02208 ...

... 定义9^[11] 设(X₁, B˙1),(X₂, B˙2)为 QiK中任意两个概念,若 ...

2023

0.0

... Zhang等^[12]在决策信息中探讨条件属性的权重信息,设计DMPWFC(Dynamic Updating Mechanism Algorithm Based on Progressive Weighted Fuzzy Concept) ...

1982

0.0

... 形式概念分析(Formal Concept Analysis, FCA)^[13,14]是一种数据分析工具,为揭示数据中的隐藏关系和潜在知识提供重要的数学基础,在知识表示与发掘、信息检索、对象分类等领域具有广泛的应用前景 ...

1999

0.0

2016

0.0

... 概念是FCA研究的基本单元,为了提升对数据和信息的理解能力,学者们研究来自不同关系的概念,如模糊概念^[15]、三支概念^[16]、多尺度概念^[17]和加权概念^[18] ...

... 定义1^[15] 设三元组(U,A, I~)为模糊形式背景,其中, ...

... 定义2^[15] 设(U,A, I~)为模糊形式背景,(U,D,J)为经典形式背景,(U,A, I~,D,J)称为模糊决策形式背景,其中, ...

2014

0.0

2020

0.0

2013

0.0

2009

0.0

... 在抽象层和机器层^[19],概念认知学习被认为是采用一定的方法学习未知概念和概念结构,如概念聚类^[20]和模仿人类认知过程^[21] ...

2019

0.0

... 在抽象层和机器层^[19],概念认知学习被认为是采用一定的方法学习未知概念和概念结构,如概念聚类^[20]和模仿人类认知过程^[21] ...

2015

0.0

... 在抽象层和机器层^[19],概念认知学习被认为是采用一定的方法学习未知概念和概念结构,如概念聚类^[20]和模仿人类认知过程^[21] ...

... 为了提高概念学习的效率和灵活性,Li等^[21]在认知计算的角度上讨论基于粒计算的概念学习 ...

... 定义3^[21] 设(U,A, I~,D,J)为模糊决策形式背景,则决策类C_i(i=1,2,…,k)对应的决策模糊粒概念空间Q_i(i=1,2,…,k)表示为 ...

2018

0.0

... Niu等^[22]结合局部粒概念,提取全局粒概念,并且实现多源数据的信息融合 ...

2019

0.0

... 李金海等^[23]研究概念渐进式认知机理,讨论在不完全条件下概念的获取问题 ...

... U,( G~F~(x), F~(x))称为模糊粒概念^[23] ...

2023

0.0

... 为了处理解决问题的基本技能被忽视的问题,Xie等^[24]将一般信息粒转化为基于能力的充分必要信息粒,从能力视角提出Cb-CCLM(Competence-Based Concept-Cognitive Learning Model) ...

2023

0.0

... Xu等^[25]从概念运动视角研究概念的进化机制,增强双向概念学习在概念学习中的灵活性和进化能力 ...

2017

0.0

... Singh等^[26]在计算概念前研究属性权重之间的相关性 ...

1975

0.0

... 3 基于属性加权的概念聚类根据现代范畴理论^[27]基本思想,同一范畴内的各个成员都由家族相似性联系在一起,而人们对事物的分类和认知是基于抽象的范畴,不是基于单个特征 ...

2013

0.0

... 因此,核心概念可以作为现代范畴理论中原型的一种表现形式,即最典型或最常见的代表^[28] ...

2022

0.0

1940

0.0

... 在此选用Friedman检验^[30]对其进行验证 ...

2006

0.0

... 所以,使用Bonferroni-Dunn进行后续检验^[31] ...