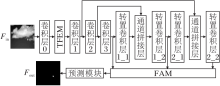
本文提出高阶微分方程启发的红外小目标检测网络(HODE-Net), 网络结构如图1所示, 图中, F_in表示来自SIRST数据集的输入红外图像, F_out表示由语义分割网络生成的分割结果.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 HODE-Net结构图Fig.1 Structure of HODE-Net

HODE-Net在U-Net的基础上进行改进, 添加目标特征增强模块(TFEM)、四阶Adams方程引导的特征融合模块(FAM)和预测模块.骨干网络为ResNet-20再加两个转置卷积层, 各层详细信息如表1所示.TFEM使用不同感受野的特征对原始特征进行补偿, 旨在增强目标和抑制背景, 提供特征提取主网络更有利的特征.四阶Adams引导的FAM用于融合和学习U-Net中低层、中层和高层的不同尺度信息, 获取丰富的上下文信息, 弥补下采样操作容易丢失的细节特征.预测模块包含顺次连接的卷积层、归一化层、ReLU激活层、随机失活层和卷积层, 获得红外小目标检测结果.

表1

Table 1

表1(Table 1)

表1 骨干网络的详细信息 Table 1 Details of backbone network 层 输出尺寸 骨干网络 卷积层0 480× 480 3× 3卷积, 16 卷积层1 转置卷积层2_2 480× 480 480× 480 (3× 3卷积, 16)× 3 (3× 3卷积, 16)× 3 卷积层2 转置卷积层1_2 240× 240 240× 240 (3× 3卷积, 32)× 3 (3× 3卷积, 32)× 3 卷积层3 120× 120 (3× 3卷积, 64)× 3 转置卷积层1_1 240× 240 3× 3卷积, 32 转置卷积层2_1 480× 480 3× 3卷积, 16

表1 骨干网络的详细信息 Table 1 Details of backbone network

单一尺度的特征包含的信息是有限的, 因此需要挖掘多尺度特征间的内在联系.利用不同尺度的特征进行交互指导可以达到这一目的, 但如果只是简单使用交互相关进行层级间的特征融合往往效果不佳.低级特征一般具有更高的分辨率、更详细的位置信息和边缘信息, 即小目标的大部分细节信息都包含在低级特征中.而高级特征一般含有的背景噪声更小、语义信息更丰富, 因此多尺度特征进行融合可得到同时具有丰富细节信息和高级语义信息的特征.

现有多尺度特征融合方法大多是通过相乘、相加和通道拼接等方式, 利用特征之间的互补性进行融合, 得到的融合特征具有各尺度特征的优点.例如:FC3-Net^[15]中的F-MFC将下采样阶段每层的输入与输出的不同尺度特征进行特征融合, 获取i层特征与i+1层特征, i层特征为低级特征, i+1层特征为中级特征, i+1层特征进行下采样得到高级特征, 将从不同层提取特征不断补偿进中级特征, 得到的融合特征传播到深层网络中.CFC(Cross-Level Feature Correlation)将上采样阶段三层输出的不同尺度特征进行特征融合, 利用高级特征抑制中层特征中的背景噪声, 获得纯净的目标特征, 再与低层次特征进行融合, 但同时不可避免地产生冗杂信息, 大幅影响网络检测性能, 导致虚警率较高.

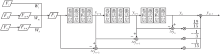
针对上述问题, 本文提出的四阶Adams引导的特征融合模块(FAM), 将下采样阶段最后一层的输出与上采样阶段两层的输出进行特征融合, 利用自适应权重因子进行特征融合, 减少冗杂信息的产生, 并且利用四阶Adams方法启发式网络加强目标特征, 去除产生的冗杂信息, 最终获得噪声更小、细节信息和语义信息更丰富的特征.FAM结构如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 FAM结构图Fig.2 Structure of FAM

FAM输入是具有3个不同维度、不同语义层次的特征, 即细节信息丰富但语义特征较弱的中级特征F_m和低级特征F_l、缺乏细节信息但语义特征较强的高级特征F_h.首先, 将不同尺度特征统一尺度, 以便后续融合, 通过上采样操作将所有不同尺度的特征映射到低层特征尺度, 调整为与低层特征相同尺度的特征:

F_{m→ l}=Upsample(F_m),

Fh_{→ l=}Upsample(Fh₎,

其中Upsample(· )表示上采样操作.统一尺度后的三层特征图, 经过大小为1× 1的卷积层, 得到初始因子:

ω _l=Conv(F_l),

ω m₌Conv(Fm_{→ l)},

ω h=_Conv(Fh→ _l),

其中Conv(· )表示卷积操作.

然后, 为了抑制特征融合带来的背景混叠现象, 引入自适应学习各尺度特征融合的特征权重因子:

$\begin{array}{l} \theta_{l}=\frac{e^{\omega_{l}}}{e^{\omega_{h}}+e^{\omega_{m}}+e^{\omega_{l}}}, \\ \theta_{m}=\frac{e^{\omega_{m}}}{e^{\omega_{h}}+e^{\omega_{m}}+e^{\omega_{l}}}, \\ \theta_{h}=\frac{e^{\omega_{h}}}{e^{\omega_{h}}+e^{\omega_{m}}+e^{\omega_{l}}}, \\ \theta_{l}+\theta_{m}+\theta_{h}=1 . \end{array}$

θ _l、θ _m、θ _h的取值范围都在[0, 1]内.该权值反映网络对不同级别特征映射的需求.

对获得不同权重的不同层次特征图进行聚合, 得到抗混叠特征:

F_f=θ _lF_l+θ _mF_{m→ l}+θ _hF_{h→ l}.

抗混叠特征F_f包含丰富的上下文信息, 语义特征较强、细节信息丰富, 有利于提高检测性能.

在抑制背景混叠的同时也会削弱小目标区域特征, 因此再采用四阶Adams方法启发式网络进行更深层的学习, 使多尺度特征图具有更详细准确的特征.四阶Adams方法启发式网络借鉴数学领域的思想改进网络结构, Weinan等^[18]观察ResNet和常微分方程(Ordinary Differential Equations, ODE)之间的关系, 将深层神经网络嵌入离散动力系统, 确定ResNet和ODE的离散化之间的相似性.Chen等^[19]利用神经常微分方程(Neural ODE, NODE), 解释普通微分方程的一阶欧拉离散法, 用于构建神经网络, 动态调整不同输入的结构或参数, 进一步提升性能.

具体来说, 此类方法利用有限差分方程实现ODE的离散化, 其中偏导数可以使用一组近似差分代替.由于四阶Adams隐式方程的ODE精度高于欧拉方法, 本文的四阶Adams方法启发式网络采用四阶Adams隐式方程求解的ODE设计得到.网络由三个残差块组成, 每个残差块的结构为顺序连接的卷积层-激活层-卷积层-激活层, 卷积层的卷积核大小为3× 3, 填充和步长均为1, 激活函数均采用ReLU函数, 具体设计过程如下.

四阶Adams隐式公式可表示为

y_n+1=y_n+ h24(9f_n+1+19f_n-5f_n-1+f_n-2).

定义

f=y-x,

并令h=1, 得

$\begin{aligned} y_{n+1}= & y_{n}+\frac{9}{24}\left(y_{n+1}-x_{n+1}\right)+\frac{19}{24}\left(y_{n}-x_{n}\right)- \\ & \frac{5}{24}\left(y_{n-1}-x_{n-1}\right)+\frac{1}{24}\left(y_{n-2}-x_{n-2}\right) . \end{aligned}$ (1)

将x_n、y_n看作某一模块的输入和输出, x_n也表示前一模块的输出y_n-1, 即x_n=y_n-1, 类似地,

x_n+1=y_n, x_n-1=y_n-2, x_n-2=y_n-3,

则式(1)可改写为

y_n+1= 3415y_n- 2415y_n-1+ 615y_n-2- 115y_n-3. (2)

为了方便深度神经网络的训练, 采用残差学习的思想, 使用Δ y_n表示y_n和y_n-1之间的残差, 即

Δ y_n=y_n-y_n-1,

类似地,

Δ y_n-1=y_n-1-y_n-2,
Δ yn_-2=yn_-2-yn_-3,

则式(2)可改写为

y_n+1=y_n+ 1915Δ y_n- 13Δ y_n-1- 115Δ y_n-2.

上式建立y_n+1、y_n、y_n-1、y_n-2和y_n-3这五项之间的关系, 将上述方程应用于3个残差中, 构建更强大的可解释网络.高阶差分方程计算四阶Adams方法启发式网络的输入特征和输出特征之间的残差, 再在输出特征中进行补偿, 在更多特征项之间建立联系, 减少信息在网络传播过程中的流失, 具有更强的特征提取能力和更高效的特征复用.在FAM中, 四阶Adams方法启发式网络可以作为一个信息瓶颈以抑制高频噪声, 同时通过反传播梯度加强目标特征.

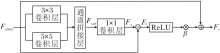
在特征提取主网络之前, 目标特征增强模块(TFEM)对原始特征图进行增强目标、抑制背景噪声的初步处理, 具体结构如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 TFEM结构图Fig.3 Structure of TFEM

TFEM首先使用大小为3× 3的卷积层Conv_{3× 3}和5× 5的卷积层Conv_{5× 5}, 从不同空间大小提取特征信息, 越小的卷积核越倾向于关注小尺度的特征.两个卷积层得到的特征在通道维度上串联, 得到合并特征:

F_cat=Cat[Conv_{3× 3}(F_enter), Conv_{5× 5}(F_enter)],

其中Cat(· )表示Concat连接.通过一个1× 1的卷积层Conv_{1× 1}进行融合, 得到多尺度特征:

F_s=Conv_{1× 1}(F_cat).

然后, 将多尺度特征与原始特征进行差分, 获得多尺度增益:

F_Δ =F_s-F_enter.

通过线性标度增强有用的多尺度特征, 可在抑制背景噪声的同时增强目标特征.最后, 利用增强后的多尺度特征对原始特征映射进行补偿, 得到具有丰富小目标特征的特征图, 便于后续网络检测的红外小目标的信息更加完整.具体特征图为:

F_i=β ReLU(F_Δ )+F_enter,

其中, ReLU(· )表示ReLU激活函数, β 表示线性放大因子.

本文实验使用公开可用的SIRST数据集^[8].数据集包含427幅红外图像和480个具有精确注释的实例, 并将50%的图像作为训练集, 30%的图像作为验证集, 20%的图像作为测试集.本文使用ACM^[13]和ALCNet^[14]中的数据集划分方法, 确保数据集的一致性.此外, 文中所有对比实验和消融实验都以相同的方式划分数据集, 确保实验的公平性.

本文使用交并比(Intersection over Union, IoU)、归一化交并比(Normalization IoU, nIoU)、受试者工作特性曲线(Receiver Operating Characteris-

tic Curve, ROC)、检测率(P_d)和虚警率(F_a)这5个评价指标.IoU、nIoU定义为

$\begin{array}{l} I o U=\frac{T P}{T+P-T P}, \\ n I o U=\frac{1}{N} \sum_{i=1}^{N}\left(\frac{T P(i)}{T(i)+P(i)-T P(i)}\right), \end{array}$

其中, T表示真值像素, P表示预测为正确的像素, TP表示预测为正确且是真值的像素数量.nIoU是专门为红外小目标检测设计的指标, 更适合评估红外小目标检测的性能.

P_d表示被预测为正确的真值占总真值的比例:

P_d= TPTP+FN,

其中FN表示预测为错误且是真值的像素数量.F_a表示被正确预测的假值占总假值的比例:

F_a= FPFP+TN,

其中, FP表示预测为正确且是假值的像素, TN表示预测为错误且是假值的像素,

P_d也称作真阳性率(True Positive Rate, TPR), F_a也称作假阳性率(False Positive Rate, FPR), ROC曲线描述真阳性率与假阳性率之间的动态关系.

本文实验使用AdaGrad作为优化器, 学习速率为0.05, 权值初始化策略采用He等^[20]提出的一种鲁棒初始化方法.

训练过程共包含3 000个迭代周期, 权值衰减为10^-4, 批次大小为32.

HODE-Net采用无需预训练的随机初始化, 在保证网络性能的前提下, 实现网络轻量化.

本节对HODE-Net的各模块进行消融实验, 验证各模块对提高网络性能的有效性.

在相同的实验参数下, 将FAM分别应用于FPN^[11]和U-Net上, 研究FAM对红外小目标检测任务检测性能的影响, 结果如表2所示.从表中可以看到, 在加入FAM后, 网络检测性能有明显提升, 相比单一FPN, 加入FAM后网络的IoU和nIoU值分别提升3.83%和4.05%.相比单一U-Net, 加入FAM后网络的IoU和nIoU值分别提升4.68%和4.50%.综上所述, FAM能够合理利用特征信息, 具有较高的特征提取能力, 可大幅提升网络性能.

表2

Table 2

表2(Table 2)

表2 各模块对方法性能的影响 Table 2 Effect of different modules on method performance 模块 IOU nIOU IOU增益 /% nIOU增益 /% FPN 0.702 0.700 - - FPN+FAM 0.729 0.728 3.83 4.05 FPN+FAM+TFEM 0.744 0.739 6.08 5.71 U-Net 0.708 0.702 - - U-Net+FAM 0.741 0.733 4.68 4.50 U-Net+FAM+TFEM 0.753 0.745 6.35 6.12 ACM+FPN 0.723 0.716 - - ACM+FPN+TFEM 0.739 0.732 2.21 2.23 ACM+U-Net 0.715 0.712 - - ACM+U-Net+TFEM 0.730 0.724 2.15 1.77

表2 各模块对方法性能的影响 Table 2 Effect of different modules on method performance

将TFEM分别应用于ACM+U-Net、ACM+FPN、U-Net+FAM和FPN+FAM上, 进行四组消融实验, 结果如表2所示.由表中可得到, 加入TFEM后网络的IoU和nIoU值均得到较大提升, 验证TFEM对提升网络性能的有效性.

从表2还可得到, 相比单一FAM, FAM和TFEM共同应用于网络上, 性能提升更多.相比单一FPN, 加入FAM和TFEM后网络的IoU和nIoU值分别提升6.08%和5.71%, 相比单一U-Net, 加入FAM和TFEM后网络的IoU和nIoU值分别提升6.35%和6.12%.同时可以得到, 相比FPN+FAM+TFEM, U-Net+FAM+TFEM的IoU和nIoU值更高, 因此选择U-Net作为基础网络的性能更优.

上述实验结果能够验证FAM和TFEM二者相辅相成, TFEM在基础网络前进行特征初步处理, FAM在基础网络后有效融合多尺度特征, 进而达到增强有用信息、抑制无用信息、消除干扰信息的效果.

FAM的特征可视化结果如图4所示.对比抗混叠特征、低级特征、中级特征和高级特征可以发现, 抗混叠特征包含的背景噪声最少且目标特征最清晰.对比FAM的输出特征与抗混叠特征可发现, 抗混叠特征在经过更深层的学习之后, 目标区域得到增强, 输出特征具有更详细准确的目标特征.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 FAM特征可视化结果Fig.4 Feature visualization results of FAM

在TFEM中, β 为线性放大因子, β 值对重构特征图的质量具有较大影响.定义β =0, 1, 2, 3, 4, 相应的HODE-Net的IoU和nIoU值如表3所示.

表3

Table 3

表3(Table 3)

表3 β 不同时HODE-Net的指标值对比 Table 3 Index value comparison of HODE-Net with different β β IOU nIOU 0 0.717 0.709 1 0.733 0.728 2 0.753 0.745 3 0.737 0.722 4 0.739 0.725

表3 β 不同时HODE-Net的指标值对比 Table 3 Index value comparison of HODE-Net with different β

由表3可以得到, 相比β =0, 当β =1时, HODE-Net的IoU和nIoU值均有所提高, 说明放大多尺度目标特征确实能提升检测性能.特别地, 当β =2时, IoU和nIoU值均达到最大值, 检测性能最优, 当β =3, 4时, IoU值提高, nIoU值降低, 这是由于在β 值较高时, 进一步放大多尺度目标信息的同时也会放大与红外小目标物理特性相似的高亮噪声, 从而导致nIoU值下降.

本节选择如下对比网络:Top-hat^[2], 文献[3]网络, ILCM^[4], MPCM^[5], IPI^[6], NIPPS^[7], PSTNN^[9], FPN^[11], ACM^[13], ALCNet^[14], FC3-Net^[15], CHF-Net^[16], GAU(Gated Attention Unit)^[21], SK(Selective Ker-nel)^[22].各网络的IoU、nIoU、P_d和F_a结果如表4所示.

表4

Table 4

表4(Table 4)

表4 各网络的指标值对比 Table 4 Index value comparison of different networks 网络 IOU nIOU Pd/% Fa 传统网络 Top-hat 文献[3]网络 ILCM MPCM IPI NIPPS PSTNN 0.220 0.193 0.186 0.357 0.466 0.473 0.325 0.352 0.207 0.259 0.445 0.607 0.602 0.292 91.63 84.26 85.96 82.25 80.39 87.52 80.43 14580× 10-6 7984× 10-6 6492× 10-6 89× 10-6 79× 10-6 62× 10-6 43.60× 10-6 基于FPN的 网络 FPN SK GAU ACM 0.702 0.673 0.701 0.723 0.700 0.672 0.687 0.716 94.21 96.33 93.78 96.27 17.40× 10-6 58.93× 10-6 25.24× 10-6 15.49× 10-6 基于U-Net 的网络 U-Net SK GAU ACM ALCNet FC3-Net CHFNet HODE-Net 0.708 0.667 0.685 0.715 0.722 0.742 0.745 0.753 0.702 0.659 0.677 0.712 0.719 0.725 0.731 0.745 97.04 96.67 95.16 95.48 98.45 99.09 97.74 99.28 27.60× 10-6 50.41× 10-6 45.15× 10-6 10.4× 10-6 23.82× 10-6 6.684× 10-6 8.69× 10-6 5.932× 10-6

表4 各网络的指标值对比 Table 4 Index value comparison of different networks

由表4可知, HODE-Net的指标值显著高于其它网络, 检测性能最优.

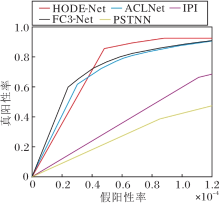
当数据集上的正样本和负样本之间存在不平衡时, ROC是一种平衡评估方法, 反映IoU和nloU在固定阈值下的分割性能.ALCNet、PSTNN、FC3-Net、IPI、HODE-Net的ROC曲线如图5所示.由图可以看出, HODE-Net的性能最优.由此表明HODE-Net可大幅提升红外小目标检测性能.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 各网络的ROC曲线Fig.5 ROC curves of different networks

目前性能最优的GAU、ACM、ALCNet、FC3-Net、CHFNet与HODE-Net在SIRST数据集上检测的部分视觉结果如图6所示.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 各网络在SIRST数据集上的可视化结果Fig.6 Visualization results of different networks on SIRST dataset

从图6可以看出, 对于真实红外图像, 现有网络都能检测出小目标, 但检测的小目标与标签真实值仍具有较大差异, 并且出现虚警现象, 而HODE-Net的视觉结果明显更优, 能够检测与标签真实值相似的轮廓, 保留小目标的角度和细节信息.综上所述, HODE-Net的视觉效果较优.