基于变分贝叶斯对比网络的非参数图像聚类方法

引用本文

张胜杰, 王一飞, 向旺, 薛迪展, 钱胜胜. 基于变分贝叶斯对比网络的非参数图像聚类方法. 模式识别与人工智能, 2023,36(9): 832-841
ZHANG Shengjie, WANG Yifei, XIANG Wang, XUE Dizhan, QIAN Shengsheng. Nonparametric Image Clustering Based on Variational Bayesian Contrastive Network. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(9): 832-841. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202309006
Permissions

《模式识别与人工智能》编辑部

基于变分贝叶斯对比网络的非参数图像聚类方法

张胜杰¹, 王一飞¹, 向旺¹, 薛迪展², 钱胜胜²

1.郑州大学河南先进技术研究院郑州 450003

2.中国科学院自动化研究所多模态人工智能系统全国重点实验室北京 100190

通讯作者:

钱胜胜,博士,副研究员,主要研究方向为数据挖掘、多媒体内容分析.E-mail:shengsheng.qian@nlpr.ia.ac.cn.

作者简介:

张胜杰,硕士研究生,主要研究方向为多媒体内容分析.E-mail:zsj2021@gs.zzu.edu.cn.

王一飞,硕士研究生,主要研究方向为计算机视觉、自然语言处理.E-mail:wang_fei@gs.zzu.edu.cn.

向旺,硕士研究生,主要研究方向为多媒体内容分析.E-mail:202022592017676@gs.zzu.edu.cn.

薛迪展,博士研究生,主要研究方向为机器学习、跨模态学习、多媒体内容分析.E-mail:xuedizhan17@mails.ucas.ac.cn

收稿日期: 2023-07-06 接受日期: 2023-09-20

资助项目: 国家自然科学基金项目(No.62276257)资助

摘要

非参数图像聚类中聚类簇数是未知的,需要模型自动发现.虽然一些现有的贝叶斯方法可以自动推断聚类簇数,但由于计算成本过高或过于依赖已学习到的特征,在大规模图像数据集上并不可行.因此,文中提出基于变分贝叶斯对比网络的非参数图像聚类方法.首先,利用ResNet提取图像特征.然后,提出深度变分迪利克雷过程混合优化方法,自动推断聚类数量,可直接嵌入端到端的深度模型,并可与特征提取器进行联合优化.最后,提出极化对比聚类学习,利用极化标签去噪策略对标签进行去噪和极化处理,并利用极化标签与数据增强预测标签进行对比学习,联合优化图像特征提取器和分类器.在三个基准数据集上的实验表明,文中方法性能较优.

关键词: 非参数图像聚类(NIC); 贝叶斯方法; 对比聚类; 极化标签; 变分方法

中图分类号:TP18

Nonparametric Image Clustering Based on Variational Bayesian Contrastive Network

ZHANG Shengjie¹, WANG Yifei¹, XIANG Wang¹, XUE Dizhan², QIAN Shengsheng²

1. Henan Institute of Advanced Technology, Zhengzhou University, Zhengzhou 450003

2. State Key Laboratory of Multimodal Artificial Intelligence Systems, Institute of Automation, Chinese Academy of Sciences, Beijing 100190

Corresponding author:
QIAN Shengsheng, Ph.D., associate professor. His research interests include data mining and multimedia content analysis.

About Author:
ZHANG Shengjie, master student. His research interests include multimedia content analysis..
WANG Yifei, master student. His research interests include computer vision and natural language processing.
XIANG Wang, master student. His research interests include multimedia content analysis.
XUE Dizhan, Ph.D. candidate. His research interests include machine learning, cross-modal learning and multimedia content analysis.

Fund:National Natural Science Foundation of China(No.62276257)

Abstract

The number of clusters in nonparametric image clustering is unknown and it needs to be discovered by the model automatically. Although some existing Bayesian methods can automatically infer the number of clusters, they are not feasible on large-scale image datasets due to the high computational costs or over-reliance on learned features. Therefore, nonparametric image clustering based on variational Bayesian contrastive network is proposed in this paper. Firstly, image features are extracted by ResNet. Secondly, deep variational Dirichlet process mixture is put forward to automatically infer the number of clusters, and it can be directly embedded into end-to-end deep models and jointly optimized with feature extractors. Finally, polarized contrast clustering learning is presented, and the denoising strategy with polarized label is utilized to denoise and polarize the labels. The polarized labels and data augmented predicted labels are employed for comparative learning to jointly optimize image feature extractors and clustering model. Experiments on three benchmark datasets show that the performance of the proposed method is superior.

Key words: Nonparametric Image Clustering(NIC); Bayesian Algorithm; Contrastive Clustering; Polarizing Label; Variational Method

文章图片

图像聚类^{[1, 2, 3, 4]}旨在图像类别标签不可用的情况下, 将图像聚为不同的簇, 这是一项重要的无监督学习任务.由于深度学习^[5]的出现, 深度图像聚类已成为图像聚类研究的主要领域之一.然而, 绝大多数现有的深度图像聚类^{[6, 7, 8]}关注有参数的图像聚类任务(Parametric Image Clustering, PIC), 即聚类数量作为先验信息已经给出, 但在实际情况中, 聚类数量往往是未知的.在聚类数量未知的情况下, 有参数的聚类方法明显达不到相当的效果.因此, 本文将研究重心聚集在一个更具有现实意义的任务上, 即非参数图像聚类(Nonparametric Image Clustering, NI-C)^{[9, 10]}.在NIC中, 聚类数量被定义为K, 值未知.

贝叶斯方法是针对NIC的传统解决方法, 其中迪利克雷过程混合方法(Mixtures of Dirichlet Proce-sses)^[11]由于其坚实的数学基础和高效的实践性能引起学者们的广泛关注.然而, 对于迪利克雷过程混合方法, 传统的蒙特卡洛马尔可夫链采样方法^{[12, 13]}十分耗时.因此, 为了提高效率, 变分方法^{[14, 15, 16]}将预测问题转化为优化问题.

但是, 现有的针对迪利克雷过程混合的变分方法需要在整个数据集上进行优化, 如果在大规模数据集^{[17, 18]}上, 计算开销非常大.此外, 现有的大多数贝叶斯方法, 包括DeepDPM^[19], 遵循迪利克雷过程混合方法的思想, 并在深度学习的框架中使用一种分离/融合的机制以发现聚类数量, 分开进行特征学习与聚类.但是最近的深度聚类研究^{[7, 8, 20, 21]}表明, 联合训练特征与分类器可以有效促进性能提升, 从而提高聚类性能.针对上述问题, 如何构建一个能够扩展到大规模数据集的高效非参聚类方法, 并且与深度学习方法在一个端到端的框架中无缝嵌入是解决非参数聚类的关键点之一.

最近, 对比学习方法^{[22, 23]} 能够有效学习样本的特征表示, 在深度聚类任务中引起持续关注.对比学习的思想是构造样本对:如果两个样本对是正样本对, 认为是相似的两个样本, 将其距离拉近; 否则, 如果两个样本对是负样本, 认为两个样本是不相似的样本, 将其距离拉远.Zhong等^[20]提出DRC(Deep Robust Clustering), 研究交互信息与对比学习之间的内在关系, 将交互信息最大化转化为最小化对比损失.Li等^[7]提出CC(Contrastive Clustering), 同时优化实例和簇级对比损失, 从实例样本视角和聚类视角进行优化.Zhong等^[8]提出GCC(Graph CC), 设计基于图拉普拉斯对比损失和基于图的对比学习策略, 学习更多的判别特征和更紧凑的聚类分配.然而, 现有的对比聚类方法和大多数其它深度聚类方法依赖于已经给出的聚类数量, 数据增强产生的随机噪声影响对比学习的稳定性和效率.此外, 在当前的研究中, 常忽略预测的聚类标签会倾向于接近某个独热编码这一现象.因此, 如何利用对比聚类中产生的噪声和聚类标签接近某个独热编码的特性, 增强对比学习的效率和判别能力是提高非参数聚类的性能表现的关键点之一.

因此, 本文提出基于变分贝叶斯对比网络的非参数图像聚类方法, 可以自动搜索聚类数量, 并将聚类模型与对比学习整合进一个端到端的框架中.首先, 提出深度变分迪利克雷过程混合优化方法(Deep Variational Dirichlet Process Mixture, DVDPM), 优化迪利克雷过程高斯混合模型的变分推理损失, 自动发现新的聚类簇.本文的变分推理损失基于变分分布和后验分布的Kullback-Leibler(KL)散度, 能够在一个批次内优化, 进而可扩展到大规模数据集上.同时, 变分推理损失可以与其它设计好的损失进行联合优化, 如对比损失, 使DVDPM能够自动发现新簇, 并无缝嵌入到深度学习方法中.然后, 提出极化对比聚类学习方法, 高效学习图像特征和分类器.设计的极化标签去噪策略利用预测标签和生成的极化标签间的噪声对整个模型进行优化.为了能够让极化标签与预测标签进行对比优化, 提出极化对比损失, 能够有效优化模型并拟合数据.在三个基准数据集上的实验表明, 本文方法性能较优.

1 基于变分贝叶斯对比网络的非参数图像聚类方法

1.1 任务描述

假设一个数据集

O={x₁, x₂, …, x_N},

包含N幅图像, 其中x_i表示第i幅图像, 由RGB组成的张量表示.

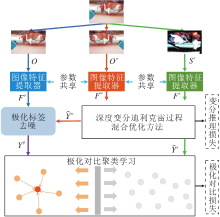
图像聚类任务旨在预测聚类标签 ${y_{i}}_{i = 1}^{N}$ , 其中y_i表示第i幅图像的标签.在参数图像聚类中, 聚类数量K是给出的, 然而在非参数图像聚类中, K是未知的, 需要被发现.

1.2 整体框架

本文提出基于变分贝叶斯对比网络的非参数图像聚类方法, 总体框图如图1所示.

	Figure Option View Download New Window
	图1 本文方法框架图Fig.1 Framework of the proposed method

本文方法由如下部分构成:

1)图像特征提取器.对于给定的输入图像, 使用ResNet^[24]进行图像特征提取.

2)深度变分迪利克雷过程混合优化方法(DVD-

PM).对于得到的图像特征, 使用DVDPM优化迪利克雷过程高斯混合模型.

3)极化对比聚类学习.通过极化标签去噪策略生成去噪的极化标签, 并与预测标签通过极化对比学习损失进行优化.

本文方法首先使用共享参数的图像特征提取器分别对原始图像集O、数据增强图像集O^w和数据增强图像集S^s进行特征提取, 分别得到F^o, F^w, F^s.再对F^w、F^s使用DVDPM, 得到预测标签 ${\overset{︿}{Y}}^{w}$ 与 ${\overset{︿}{Y}}^{s}$ . ${\overset{︿}{Y}}^{s}$ 使用变分推理损失对DVDPM进行优化.最后, 通过F^o计算聚类中心, 得到预测标签 ${\overset{︿}{Y}}^{w}$ 对应索引的极化标签Y^p, 与 ${\overset{︿}{Y}}^{s}$ 在标签空间进行极化对比聚类学习.

1.3 图像特征提取器

为了更好地得到图像的细粒度特征表示, 本文使用ResNet^[24]进行图像特征的细粒度特征信息提取.图像特征提取器如下所示:

f_i=AvgPool(ResNet(x_i, θ ))∈ R²⁰⁴⁸.

其中:ResNet(· )输出为一个49× 2 048维的数组; AvgPool(· )为平均池化函数, 可以将数组转化为2 048维的向量; θ 为ResNet的参数.

为了提高模型训练的效率, 本文使用与DeepDPM相同的MoCo(Momentum Contrast)^[23]对ResNet进行无监督的预训练.

1.4 深度变分迪利克雷过程混合优化方法

为了发现聚类数量, 并将聚类方法与特征学习方法融入一个统一的深度学习框架中, 本文提出深度变分迪利克雷过程混合优化方法(DVDPM).

在迪利克雷过程混合模型^[11]中, { $η_{1}^{*}$ , $η_{2}^{*}$ , …}表示混合权重, z_n表示与第n个输入数据特征h_n关联的混合成分的赋值变量.整个过程可描述为如下断棒构造过程:

1)Draw v_i|α ~Beta(1, α ), i∈ N⁺.

2)Draw $η_{i}^{*}$ |G₀~G₀, i∈ N⁺.

3)对于第n个数据点:

(1)Draw z_n|{v₁, v₂, …}~Mult(π (v)),

其中

π (v)=v_i $\overset{i - 1}{\prod_{j = 1}}$ (1-v_j);

(2)Draw h_n|z_n~p(h_n| $η_{z_{n}}^{*}$ ).

其中:Mult(· )表示多项式分布, G₀表示一个非原子概率分布.

在DPGMM中, p(h_n| $η_{z_{n}}^{*}$ )是一个多元高斯分布, 由参数

$η_{z_{n}}^{*}$ ={ $μ_{z_{n}}$ , $Σ_{z_{n}}$ }

构成, 如h_n~N( $μ_{z_{n}}$ , $Σ_{z_{n}}$ ).由于深度神经网络可以在表示空间中学习线性尺度, 不同维度也被认为是独立的, 因此本文采用各向同性高斯以简化计算, 如

$Σ_{z_{n}}$ =diag( $σ_{z_{n}}^{2}$ , $σ_{z_{n}}^{2}$ , …, $σ_{z_{n}}^{2}$ ).

此外, G₀为一个正态伽马分布,

G₀=NormalGamma(μ ₀, c, a, b).

因此, 基于上述推断, 可以将高斯分布的参数表示为

( $μ_{z_{n}}$ , $Σ_{z_{n}}$ )~NormalGamma(μ ₀, c, a, b).

在迪利克雷过程混合模型的先验下, 无法直接计算后验分布, 需要近似推断方法, 因此引入马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)采样方法^{[12, 13]}.然而, 由于数据点是串行生成的, MCMC的采样效率低下, 尤其是在大规模数据集上, 采样缓慢.变分推理提供一种确定性和高度并行的算法以逼近似然性和后验.

DVDPM通过推导DPGMM(Dirichlet Process Gaussian Mixture Model)^[25]的深度变分推理损失以优化整个模型, 并且可以无缝嵌入到深度神经网络中.

但下面两个缺点导致现有的变分推理方法^{[14, 15, 16]}不适用于本文的任务:1)必须同时对所有数据进行聚类, 这在大型数据集(如本文实验中的数据集)上不可行, 因为内存和计算成本过高; 2) 很难与基于批处理的深度学习训练方式结合.

为了解决上述问题, DVDPM参数化迪利克雷和高斯混合, 可以单独预测每个观测的高斯分配概率, 降低内存和计算成本, 并使其可以以批处理的方式进行训练.此外, DVDPM的参数和输入可以通过具有特定目标的损失函数的反向传播算法联合优化.考虑DPGMM的参数

θ ={α , μ ₀, c, a, b},

隐变量

w={v, η ^*, z},

观察值

H={h₁, h₂, …, h_n},

使q_γ(w)为变分参数y作为索引的分布簇, 目标是最小化q_γ(w)和隐变量的后验分布p(w|h)的KL散度:

KL(q_γ(w)‖ p(w|H, θ ))=E_q[ln q_γ(w)]-E_q[ln p(w, H|θ )]+ln p(H|θ ).

在本文使用q作为期望的下标时, 省略变分参数γ .上式的最小化可以替换为对数边缘似然ln p(h|θ )下界的最大化:

ln p(H|θ )≥ E_q[ln p(w, H|θ )]-E_q[ln q_γ(w)],

其中差值为q_γ和p之间的KL散度.

由于本文方法是基于DPGMM的断棒构造, 可以扩展变分下界并进行优化.本文需要一个近似于无限维随机测度G分布的变分分布簇, 可用无穷集合

v={v₁, v₂, …}

和η 表示.由于特定数据集通常包含有限簇, 本文采用截断值T足够大(在实现中比K大得多, 以避免K的信息泄漏)的断棒构造.因此, q(v_T=1)=1, 意味着当t> T时, 混合比例π _t(v)=0.本文参数化截断的v={v₁, v₂, …, v_T_-1}.对于截断的高斯混合, 参数

η ^*={ $η_{1}^{*}$ , $η_{2}^{*}$ , …, $η_{T}^{*}$ }={(μ 1_,Σ 1₎, (μ 2_,Σ 2₎, …, (μ T_,Σ T₎}.

在观测到高斯分量后, h_n的赋值概率

q_γ(z_n=i)∝ N(h_n|μ _i, Σ _i).

所有的变分参数

γ ={v₁, …, v_T_-1, μ ₁, …, μ _T, Σ ₁, …, Σ _T}.

再计算变分下界的所有项.为了将DVDPM整合进深度学习, 得到变分损失:

$\begin{aligned} L_{\mathrm{var}}(H)= & -E_{q}[\ln p(v \mid \alpha)]- \\ & E_{q}\left[\ln \left(\eta^{* } \mid \mu_{0}, c, a, b\right)\right]- \\ & \sum_{n=1}^{N}\left(E_{q}\left[\ln p\left(z_{n} \mid v\right)\right]+\right. \\ & \left.E_{q}\left[\ln p\left(h_{n} \mid z_{n}, \eta^{* }\right)\right]\right)+ \\ & E_{q}\left[\ln q_{\gamma}\left(v, \eta^{* }, z\right)\right] . \end{aligned}$

因此, 可以将L_var添加到最终损失函数中, 并联合优化模型.对于大多数候选簇, 后验概率π _i(v)迅速缩减到接近0, 可用簇的数量将其减少到接近K.

为了简化表示, 表示概率向量:

q(z_n)=DVDPM(h_n)∈ R^T.

DVDPM伪代码如下.

算法1 DVDPM

输入原始数据集O, 数据增强集O^w,

数据增强集S^s, 截断值T, 损失系数λ ,

温度系数τ _s, 学习率l, 批量大小bs

输出优化后的ResNet参数θ ,

优化后的迪利克雷过程高斯混合模型参数

v, η ^*, 原始数据集O样本的类别标签Y

随机初始化迪利克雷过程高斯混合模型参数v, η ^*;

for $|\frac{o}{bs}|$ do:

从原始数据集O、数据增强集O^w、数据增强集

S^s分别随机采样bs个样本x_bs, $x_{bs}^{w}$ , $x_{bs}^{s}$ ;

计算嵌入特征f_bs, $f_{bs}^{w}$ , $f_{bs}^{s}$ ;

计算预测标签 ${\hat{y}}^{w}$ , ${\hat{y}}^{s}$ ;

利用嵌入特征f_bs和预测标签 ${\hat{y}}^{w}$ 进行极化去噪

标签策略, 得到伪标签 $y_{bs}^{p}$ ;

优化ResNet参数θ 和迪利克雷过程高斯混合模

型参数v, η ^*;

end for

for $|\frac{o}{bs}|$ do:

从原始数据集O随机采样bs个样本x_bs;

计算嵌入特征f_bs;

计算预测标签y_bs;

Y=Y∪ y_bs;

end for

return ResNet参数θ , 迪利克雷过程高斯混合模型参

数v, η ^*, 原始数据集的预测标签Y

1.5 极化对比聚类学习

为了联合训练DVDPM中的图像特征提取器和分类器, 本文提出极化对比聚类学习.

首先, 使用数据增强, 生成一个增强图像集:

O^w= ${x_{i}^{w}}_{i = 1}^{N}$ .

然后, 与原始图像集相似, 利用图像特征提取器提取数据增强图像集的特征 ${f_{i}^{w}}_{i = 1}^{N}$ .为了简洁表示, 定义

F^o= ${f_{i}}_{i = 1}^{N}$ , F^w= ${f_{i}^{w}}_{i = 1}^{N}$ .

从F^w获得聚类标签的方式如下:

${\overset{︿}{Y}}^{w}$ ={ ${\hat{y}}_{i}^{w}$ | ${\hat{y}}_{i}^{w}$ =DVDPM(W $f_{i}^{W}$ +b), i=1, 2, …, N}, (1)

其中, ${\hat{y}}_{i}^{w}$ 为 $x_{i}^{w}$ 的预测标签, W∈ R^d^{× 2048}, b∈ R^d为线性层的可训练参数.

1.5.1 极化标签去噪

现有的针对对比视觉表征学习的工作^{[22, 23]}通常将两个不同数据增强的特征进行对比学习.本文尝试在标签空间使用对比学习, 但是预测标签会产生额外的噪声.此外, 已正确聚类的标签更倾向于接近某个独热向量, 这会提高不同簇的判别程度.因此, 本文提出基于原始图像特征F^o和数据增强图像集的预测标签 ${\overset{︿}{Y}}^{w}$ 极化标签以及去噪标签Y^p的对比标签学习去噪方法.

由于数据增强增加数据样本的泛化性却不改变其类别标签, 数据增强集S^s应趋于接近数据增强集O^w生成的伪标签, 即“ 聚类预测标签接近某个独热编码” .这一现象对于非参数聚类是有利的, 因为在本文提出的深度变分迪利克雷过程混合优化与极化对比聚类过程中, 聚类数会逐渐收敛至真实聚类数量K, 导致数据增强集O^w生成的伪标签的可信性逐渐增高.

基于K-means算法^[26], 首先, 选择每个簇的 $\frac{N}{\overset{︿}{K}}$ 个最高置信度的样本和对应的特征组成支持集, 支持集的第k个簇为:

$\begin{array}{l} H_{k}=\left\{f_{i} \mid i \in \operatorname{argtopk}\left(\widehat{\boldsymbol{Y}}_{:, k}^{w}, \frac{N}{\widehat{K}}\right)\right\}, \\ k=1, 2, \cdots, \widehat{K}, \end{array}$

其中, $\overset{︿}{K}$ 表示预测的聚类数量, ${\overset{︿}{Y}}_{∶, k}^{w}$ 表示 ${\overset{︿}{Y}}^{w}$ 矩阵的第k列,

argtopk $({\overset{︿}{Y}}_{∶, k}^{w}, \frac{N}{\overset{︿}{K}})$

返回 $\frac{N}{\overset{︿}{K}}$ 个来自 ${\overset{︿}{Y}}_{∶, k}^{w}$ 的每个簇最高置信度的样本索引.

然后, 去噪聚类中心计算表示如下:

δ _k= $\frac{\overset{︿}{K}}{N} \sum_{f_{i}}$ f_i, k=1, 2, …, $\overset{︿}{K}$ .

通过计算特征 ${f_{i}}_{i = 1}^{N}$ 以及聚类中心 ${δ_{k}}_{i = 1}^{\overset{︿}{K}}$ 的余弦相似性, 选择 $\frac{N}{\overset{︿}{K}}$ 个距离聚类中心的样本以及极化标签

${y_{i}^{k} \in R^{T}}_{i = 1}^{\frac{N}{\overset{︿}{K}}}$ ,

其中 $y_{ik}^{k}$ =1且 $y_{ij}^{k}$ =0(j≠ k).表示集合

S={ $x_{1}^{1}$ , …, $x_{\frac{N}{\overset{︿}{K}}}^{1}$ , …, $x_{1}^{\overset{︿}{K}}$ , …, $x_{\frac{N}{\overset{︿}{K}}}^{\overset{︿}{K}}$ }

为所有聚类中心的距离最近的集合的集.对应的极化标签定义为

Y^p={ $y_{1}^{1}$ , …, $y_{\frac{N}{\overset{︿}{K}}}^{1}$ , …, $y_{1}^{\overset{︿}{K}}$ , …, $y_{\frac{N}{\overset{︿}{K}}}^{\overset{︿}{K}}$ }.

为了简化表示, 同样定义

Y^p= ${y_{i}^{p}}_{i = 1}^{N}$ .

1.5.2 极化对比学习

在得到极化去噪标签Y^p之后, 将极化去噪标签Y^p与预测标签进行对比学习.在图像集S上应用另外一种数据增强方式, 得到数据增强图像集:

S^s= ${x_{i}^{s}}_{i = 1}^{N}$ .

通过特征提取器得到增强图像的特征

F^s= ${f_{i}^{s}}_{i = 1}^{N}$ .

然后, 通过DVDPM计算特征的预测标签:

${\overset{︿}{Y}}^{s}$ ={ ${\hat{y}}_{i}^{s}$ | ${\hat{y}}_{i}^{s}$ =DVDPM(W $f_{i}^{s}$ +b), i=1, 2, …, N}.

上式使用和式(1)相同的DVDPM(· )和W, b.为了更加有效地将Y^p与 ${\overset{︿}{Y}}^{s}$ 进行对比学习, 提出极化对比损失, 用于在标签空间进行优化.

由于相同样本的标签应该具有一致性, 在极化标签与预测标签之间的极化对比损失为:

$L_{c o n}^{s a}=-\frac{1}{N} \sum_{i=1}^{N} \ln \left(\frac{\exp \left(\frac{\cos \left(y_{i}^{p}, \hat{y}_{i}^{s}\right)}{\tau_{s}}\right)}{\sum_{j=1}^{T} \exp \left(\frac{\cos \left(y_{i}^{p}, \hat{y}_{j}^{s}\right)}{\tau_{s}}\right)}\right), $

其中, cos(· , · )表示余弦相似度, τ _s表示温度系数.

1.6 优化损失

总体的优化损失:

L=λ L_var+L_con. (2)

其中, L_var在两个数据增强图像集上进行计算, λ 用于平衡两个损失项的系数.

2 实验及结果分析

2.1 实验环境

本文使用STL-10^[27]、ImageNet-dog^[28]、Tiny-Ima-geNet^[29]作为基准数据集进行训练和测试.STL-10数据集包含10个类别的图像, 每类包含500幅训练图像和800幅测试图像.ImageNet-dog数据集是ImageNet数据集^[28]的一个子集, 包含15种狗的类别.Tiny-ImageNet数据集是一个具有挑战性的数据集, 包含ImageNet数据集的200个子类, 由100 000幅训练图像和10 000幅测试图像构成.具体数据集信息如表1所示.

表1 实验数据集信息 Table 1 Description of experimental datasets

采用3个标准度量评估聚类性能, 包括准确度(Accuracy, ACC)、归一化互信息(Normalized Mutual Information, NMI)和调整兰德系数(Adjus-ted Rand Index, ARI).

本文利用PyTorch实现所有实验, 并采用Adam(Adaptive Moment Estimation)优化器^[30], 初始学习率l=0.005.基于文献[8]和文献[19]的工作, 本文采用ResNet^[24]的两个变体作为图像特征提取器的主干, 即ResNet18和ResNet34.截断值T在Tiny-ImageNet数据集上设置为256, 在其它两个数据集上设置为128.批量大小设置为256.对于数据增强集O^w, 使用标准翻转和移位作为增强方法.对于数据增强集S^s, 主要应用一个复杂的增强组合^[8], 包括Cutout增强、RandAugment增强、Random Horizontal Flip增强和Random Crop增强.在3个数据集上, 设置L_var的损失系数λ =1e-5, 设置温度系数τ _s=1.

2.2 实验结果对比

本文选择9种参数图像聚类方法(PIC)和4种非参数图像聚类方法(NIC)进行对比, 其中聚类数量在PIC中为已知信息, 但在NIC方法中为未知信息.

1)PIC方法.

(1)DAC(Deep Adaptive Clustering)^[1].结合特征学习和聚类的算法.

(2)DCCM(Deep Comprehensive Correlation Mi-

ning)^[4].

(3)PICA(Partition Confidence Maximisation)^[6].

(4)CC^[7].基于对比学习的深度图像聚类.

(5)GCC^[8].基于构图的对比学习聚类算法.

(6)DRC^[20].基于对比学习的深度鲁棒聚类.

(7)DSEC(Deep Self-Evolution Clustering)^[31].

(8)IDFD(Instance Discrimination and Feature

Decorrelation)^[32].

(9)EDESC^[33].

2)NIC方法.

(1)GCC-NIC.GCC在本文NIC设置下的变体, 由修改分类器的参数聚类数量得到.在STL-10、ImageNet-dog数据集上, 本文将GCC-NIC的聚类数量K设置为32; 在Tiny-ImageNet数据集上, 本文将GCC-NIC的聚类数量K设置为256.

(2)DeepDPM^[19].使用一个分裂/融合网络, 并提出一个损失计算函数.

(3)文献[26]方法.使用肘部法则优化簇类发现的K-means算法.

(4)DBSCAN(Density Based Spatial Clustering of Applications with Noise)^[34].比较有代表性的非贝叶斯的基于密度的聚类算法.

各方法在3个数据集上的指标值对比结果如表2~表4所示, 表中黑体数字表示最优值, 斜体数字表示次优值.

表2 各方法在STL-10数据集上的指标值对比 Table 2 Index value comparison of different methods on STL-10 dataset

表3 各方法在ImageNet-dog数据集上的指标值对比 Table 3 Index value comparison of different methods on ImageNet-dog dataset

表4 各方法在Tiny-ImageNet数据集上的指标值对比 Table 4 Index value comparison of different methods on Tiny-ImageNet dataset

观察表1~表3中的数据可得到如下结论.

1)本文方法在3个数据集上性能显著优于4种NIC方法.相比性能最优的DeepDPM, 本文方法在STL-10、ImageNet-dog、Tiny-ImageNet数据集上分别实现0.027、0.183和0.052的ACC提升.这表明本文方法可以在特征学习和聚类的联合框架内准确找到聚类数, 并将数据分类到不同的簇中.

2)相比PIC方法(给出聚类数量), 本文方法仍然可以获得具有竞争力的性能.特别地, 相比GCC, 本文方法在STL-10、ImageNet-dog、Tiny-ImageNet数据集上分别实现0.027、0.073和0.023的ACC提升.这表明本文方法可以在未知聚类数量的情况下有效聚类图像, 这显著提升本文方法的实用性.

3)GCC-NIC的性能明显低于GCC和本文方法, 这表明NIC是一项具有挑战性的任务, 当前的PIC方法无法直接解决NIC问题.然而, 本文的DVDPM可以在训练期间自动搜索聚类数, 促进非参数聚类.

2.3 消融实验结果

为了验证本文方法的有效性, 设计如下变式.

1)CE.仅使用交叉熵损失函数进行优化.

2) $L_{con}^{sa}$ .仅使用极化对比损失进行优化.

3)CE+L_var.使用交叉熵损失函数和变分推理损失进行优化.

4) $L_{con}^{sa}$ +L_var.本文的优化项.

本文方法的不同变式在STL-10、ImageNet-dog数据集上的指标值对比如表5所示, 表中黑体数字表示最优值.

表5 模型的不同变式在2个数据集上的性能对比 Table 5 Performance comparison of different variants of the proposed method on 2 datasets

变式	STL-10		ImageNet-dog
变式	NMI	ACC	NMI	ACC
CE	0.627	0.631	0.471	0.501
$L_{con}^{sa}$	0.685	0.716	0.468	0.532
CE+L_var	0.751	0.803	0.478	0.574
$L_{con}^{sa}$ +L_var	0.808	0.877	0.490	0.589

表5 模型的不同变式在2个数据集上的性能对比 Table 5 Performance comparison of different variants of the proposed method on 2 datasets

由表5可得如下结论.

1)仅使用CE或 $L_{con}^{sa}$ 对本文方法进行优化时, $L_{con}^{sa}$ 的表现优于CE, 但是整体低于与变分推理损失L_var一起优化的性能.这是因为L_var能够自动发现聚类数量, 提高聚类表现.

2)相比CE+L_var, $L_{con}^{sa}$ +L_var的表现更优.这是因为极化对比去噪策略与变分推理损失更契合, 更优于交叉熵损失函数与变分推理损失的契合度.

2.4 聚类可视化

为了进一步验证本文方法的特征学习与聚类效果, 进行聚类可视化的定性分析.由于DeepDPM的特征是由MoCo提取的, 并未在训练过程中联合学习特征, 因此本节将本文方法与GCC在STL-10数据集上进行对比.

为了公平对比, 将GCC引入NIC设置, 并将聚类数K设置为32, 而本文的截断值T设置为128.

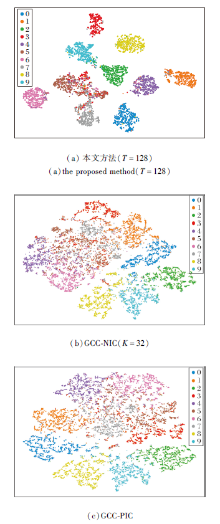
本文方法和GCC-NIC由t-SNE^[35]生成的可视化聚类效果如图2所示.从图2(a)和(b)中可以观察到, 本文方法更具有判别性, 几乎将每类特征都聚成簇, 而GCC-NIC几乎将所有特征混合在一起, 由此验证本文方法在NIC设置下联合学习特征的高效性.

	Figure Option View Download New Window
	图2 3种方法的可视化聚类结果Fig.2 Visualization results of 3 methods

同时, 为了展示本文方法聚类效果的先进性, 将本文方法与在PIC设置下的GCC进行可视化聚类对比.图2(c)为GCC-PIC由t-SNE生成的可视化聚类效果.

从图2(a)和(c)中可以观察到, 本文方法依然具有较强的判别性, 而GCC-PIC的聚类簇之间并没有较清晰的界限, 同时较多的聚类簇混杂在一起.从(b)和(c)中可以观察到, 相比GCC-NIP, GCC-PIC有更清晰的聚类效果, 这也印证现有PIC方法无法在NIC设定下媲美PIC方法这一结论.

2.5 敏感性分析

为了进一步验证本文方法的稳定性, 进行特征提取器敏感性分析, 选取ResNet-18、ResNet-34、ResNet-50网络, 本文方法在不同深度的ResNet上的准确率对比如图3所示.

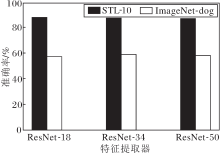	Figure Option View Download New Window
	图3 特征提取器不同时本文方法在2个数据集上的准确率对比Fig.3 Accuracy comparison of the proposed method with different feature extractors

由图3可知, 本文方法在不同深度的ResNet上实现相当的性能, 表明本文方法在不同的特征提取器上的表现具有稳定性.

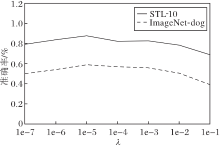
为了进一步探究式(2)损失项λ L_var中超参数λ 的敏感性, 本节设计λ 在STL-10、ImageNet-dog数据集上的敏感性实验, 结果如图4所示.由图可知, 当λ 逐渐增大, 推理聚类数量逐渐减少时, 对应的准确率先增大后减小.上述观察结果揭示在非参数聚类中选择合适参数的重要性.

	Figure Option View Download New Window
	图4 λ 不同时本文方法在2个数据集上的准确率对比Fig.4 Accuracy comparison of the proposed method with different λ on 2 datasets

2.6 运行效率分析

本节分析NIC方法的运行效率.DBSCAN、GCC-NIC、DeepDPM和本文方法在STL-10、ImageNet-dog数据集上的运行时间如表6所示.从表可看出, 本文方法显著提升运行效率, 由此也验证方法的高效性.同时也证实当前NIC方法在本文的较大规模数据集上并不适用, 验证本文方法在较大规模数据集上的可靠性.本文将贝叶斯方法与对比学习相结合以提高NIC性能, 是较新颖的NIC方式.

表6 各方法在2个数据集上的运行时间对比 Table 6 Running time comparison of different methods on 2 datasets s

3 结束语

本文提出基于变分贝叶斯对比网络的非参数图像聚类方法.首先, 通过推导迪利克雷过程高斯混合模型的变分推理损失, 提出深度变分迪利克雷过程混合优化方法, 自动推断聚类数量, 并无缝集成到端到端的深度模型中.然后, 提出极化对比聚类学习, 利用极化标签去噪策略, 对比极化标签和预测标签, 有效学习图像特征和分类器.在3个基准数据集上的实验表明, 本文方法性能较优.今后将在非参数文本聚类和非参数多视图聚类等其它应用上研究本文方法.

本文责任编委陈松灿

Recommended by Associate Editor CHEN Songcan

参考文献

文献选项

[1]	CHANG J L, WANG L F, MENG G F, et al. Deep Adaptive Image Clustering // Proc of the IEEE International Conference on Compu-ter Vision. Washington, USA: IEEE, 2017: 5880-5888. [本文引用:2]
[2]	JI X, HENRIQUES J F, VEDALDI A. Invariant Information Clus-tering for Unsupervised Image Classification and Segmentation // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 9865-9874. [本文引用:1]
[3]	WANG J Y, ZHU X T, GONG S G, et al. Attribute Recognition by Joint Recurrent Learning of Context and Correlation // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2017: 531-540. [本文引用:1]
[4]	WU J L, LONG K Y, WANG F, et al. Deep Comprehensive Correlation Mining for Image Clustering // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2019: 8149-8158. [本文引用:2]
[5]	LECUN Y, BENGIO Y, HINTON G. Deep Learning. Nature, 2015, 521(7553): 436-444. [本文引用:1]
[6]	HUANG J B, GONG S G, ZHU X T. Deep Semantic Clustering by Partition Confidence Maximisation // Proc of the IEEE/CVF Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 8846-8855. [本文引用:2]
[7]	LI Y F, HU P, LIU Z T, et al. Contrastive Clustering. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(10): 8547-8555. [本文引用:4]
[8]	ZHONG H S, WU J L, CHEN C, et al. Graph Contrastive Clus-tering // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2021: 9204-9213. [本文引用:6]
[9]	CARREIRA-PERPINAN M A. Fast Nonparametric Clustering with Gaussian Blurring Mean-Shift // Proc of the 23rd International Conference on Machine Learning. Palo Alto, USA: AAAI, 2006: 153-160. [本文引用:1]
[10]	NGUYEN T V, PHUNG D, NGUYEN X, et al. Bayesian Nonparametric Multilevel Clustering with Group-Level Contexts // Proc of the 31st International Conference on Machine Learning. Palo Alto, USA: AAAI, 2014: 288-296. [本文引用:1]
[11]	ANTONIAK C E. Mixtures of Dirichlet Processes with Applications to Bayesian Nonparametric Problems. The Annals of Statistics, 1974, 2(6): 1152-1174. [本文引用:2]
[12]	MACEACHERN S N. Estimating Normal Means with a Conjugate Style Dirichlet Process Prior. Communications in Statistics-Simulation and Computation, 1994, 23(3): 727-741. [本文引用:2]
[13]	ESCOBAR M D, WEST M. Bayesian Density Estimation and Infe-rence Using Mixtures. Journal of the American Statistical Association, 1995, 90(430): 577-588. [本文引用:2]
[14]	BLEI D M, JORDAN M I. Variational Methods for the Dirichlet Process // Proc of the 21st International Conference on Machine Learning. Palo Alto, USA: AAAI, 2004. DOI: 10.1145/1015330.1015439. [本文引用:2]
[15]	BLEI D M, JOURDAN M I. Variational Inference for Dirichlet Pro-cess Mixtures. Bayesian Analysis, 2006, 1(1): 121-143. [本文引用:2]
[16]	WANG Z Y, NI Y, JING B Y, et al. DNB: A Joint Learning Framework for Deep Bayesian Nonparametric Clustering. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(12): 7610-7620. [本文引用:2]
[17]	DENG J, DONG W, SOCHER R, et al. ImageNet: A Large-Scale Hierarchical Image Database // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2009: 248-255. [本文引用:1]
[18]	KRIZHEVSKY A. Learning Multiple Layers of Features from Tiny Images. Master Dissertation. Toronto, Canada: University of Toronto, 2009. [本文引用:1]
[19]	RONEN M, FINDER S E, FREIFELD O. DeepDPM: Deep Clustering with an Unknown Number of Clusters // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 9851-9860. [本文引用:3]
[20]	ZHONG H S, CHEN C, JIN Z M, et al. Deep Robust Clustering by Contrastive Learning[C/OL]. [2023-06-11]. https://arxiv.org/pdf/2008.03030.pdf. [本文引用:3]
[21]	XU J, TANG H Y, REN Y Z, et al. Multi-level Feature Learning for Contrastive Multi-view Clustering // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 16030-16039. [本文引用:1]
[22]	CHEN T, KORNBLITH S, NOROUZI M, et al. A Simple Framework for Contrastive Learning of Visual Representations // Proc of the 37th International Conference on Machine Learning. San Diego, USA: JMLR, 2020: 1597-1607. [本文引用:2]
[23]	CHEN X L, FAN H Q, GIRSHICK R, et al. Improved Baselines with Momentum Contrastive Learning[C/OL]. [2023-06-11]. https://arxiv.org/abs/2003.04297. [本文引用:3]
[24]	HE K M, ZHANG X Y, REN S Q, et al. Deep Residual Learning for Image Recognition // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 770-778. [本文引用:3]
[25]	GÖRÜR D, RASMUSSEN C E. Dirichlet Process Gaussian Mixture Models: Choice of the Base Distribution. Journal of Computer Science and Technology, 2010, 25(4): 353-664. [本文引用:1]
[26]	MCQUEEN J B. Some Methods of Classification and Analysis of Multivariate Observations. Proceedings of the Berkeley Symposium on Mathematical Statistics and Probability, 1967, 5(1): 281-297. [本文引用:2]
[27]	COATES A, NG A Y, LEE H. An Analysis of Single-Layer Networks in Unsupervised Feature Learning // Proc of the 14th International Conference on Artificial Intelligence and Statistics. Palo Alto, USA: AAAI, 2011: 215-223. [本文引用:1]
[28]	KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet Cla-ssification with Deep Convolutional Neural Networks. Communications of the ACM, 2017, 60(6): 84-90. [本文引用:2]
[29]	LE Y, YANG X. Tiny ImageNet Visual Recognition Challenge[C/OL]. [2023-06-11]. http://cs231n.stanford.edu/reports/2015/pdfs/yle_project.pdf. [本文引用:1]
[30]	KINGMA D P, BA J. Adam: A Method for Stochastic Optimization[C/OL]. [2023-06-11]. https://arxiv.org/pdf/1412.6980.pdf. [本文引用:1]
[31]	CHANG J L, MENG G F, WANG L F, et al. Deep Self-Evolution Clustering. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(4): 809-823. [本文引用:1]
[32]	TAO Y L, TAKAGI K, NAKATA K. Clustering-Friendly Representation Learning via Instance Discrimination and Feature Decorrelation[C/OL]. [2023-06-11]. https://arxiv.org/abs/2106.00131. [本文引用:1]
[33]	CAI J Y, FAN J C, GUO W Z, et al. Efficient Deep Embedded Subspace Clustering // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 21-30. [本文引用:1]
[34]	ESTER M, KRIEGEL H P, SANDER J, et al. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise // Proc of the 2nd International Conference on Knowledge Discovery and Data Mining. Palo Alto, USA: AAAI, 1996: 226-231. [本文引用:1]
[35]	VAN DER MAATEN L, HINTON G. Visualizing Data Using t-SNE. Journal of Machine Learning Research, 2008, 9: 2579-2605. [本文引用:1]

2017

0.0

... 图像聚类^[1,2,3,4]旨在图像类别标签不可用的情况下,将图像聚为不同的簇,这是一项重要的无监督学习任务 ...

... (1)DAC(Deep Adaptive Clustering)^[1] ...

2019

0.0

... 图像聚类^[1,2,3,4]旨在图像类别标签不可用的情况下,将图像聚为不同的簇,这是一项重要的无监督学习任务 ...

2017

0.0

... 图像聚类^[1,2,3,4]旨在图像类别标签不可用的情况下,将图像聚为不同的簇,这是一项重要的无监督学习任务 ...

2019

0.0

... 图像聚类^[1,2,3,4]旨在图像类别标签不可用的情况下,将图像聚为不同的簇,这是一项重要的无监督学习任务 ...

... ning)^[4] ...

2015

0.0

... 由于深度学习^[5]的出现,深度图像聚类已成为图像聚类研究的主要领域之一 ...

2020

0.0

... 然而,绝大多数现有的深度图像聚类^[6,7,8]关注有参数的图像聚类任务(Parametric Image Clustering, PIC),即聚类数量作为先验信息已经给出,但在实际情况中,聚类数量往往是未知的 ...

... (3)PICA(Partition Confidence Maximisation)^[6] ...

2021

0.0

... 但是最近的深度聚类研究^[7,8,20,21]表明,联合训练特征与分类器可以有效促进性能提升,从而提高聚类性能 ...

... Li等^[7]提出CC(Contrastive Clustering),同时优化实例和簇级对比损失,从实例样本视角和聚类视角进行优化 ...

... (4)CC^[7] ...

2021

0.0

... 但是最近的深度聚类研究^[7,8,20,21]表明,联合训练特征与分类器可以有效促进性能提升,从而提高聚类性能 ...

... Zhong等^[8]提出GCC(Graph CC),设计基于图拉普拉斯对比损失和基于图的对比学习策略,学习更多的判别特征和更紧凑的聚类分配 ...

... 基于文献[8]和文献[19]的工作,本文采用ResNet^[24]的两个变体作为图像特征提取器的主干,即ResNet18和ResNet34 ...

... 对于数据增强集S^s,主要应用一个复杂的增强组合^[8],包括Cutout增强、RandAugment增强、Random Horizontal Flip增强和Random Crop增强 ...

... (5)GCC^[8] ...

2006

0.0

... 因此,本文将研究重心聚集在一个更具有现实意义的任务上,即非参数图像聚类(Nonparametric Image Clustering, NI-C)^[9,10] ...

2014

0.0

... 因此,本文将研究重心聚集在一个更具有现实意义的任务上,即非参数图像聚类(Nonparametric Image Clustering, NI-C)^[9,10] ...

1974

0.0

... 贝叶斯方法是针对NIC的传统解决方法,其中迪利克雷过程混合方法(Mixtures of Dirichlet Proce-sses)^[11]由于其坚实的数学基础和高效的实践性能引起学者们的广泛关注 ...

... 在迪利克雷过程混合模型^[11]中,{ η1#cod#x0002A ...

1994

0.0

... 然而,对于迪利克雷过程混合方法,传统的蒙特卡洛马尔可夫链采样方法^[12,13]十分耗时 ...

... 在迪利克雷过程混合模型的先验下,无法直接计算后验分布,需要近似推断方法,因此引入马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)采样方法^[12,13] ...

1995

0.0

... 然而,对于迪利克雷过程混合方法,传统的蒙特卡洛马尔可夫链采样方法^[12,13]十分耗时 ...

2004

0.0

... 因此,为了提高效率,变分方法^[14,15,16]将预测问题转化为优化问题 ...

... 但下面两个缺点导致现有的变分推理方法^[14,15,16]不适用于本文的任务:1)必须同时对所有数据进行聚类,这在大型数据集(如本文实验中的数据集)上不可行,因为内存和计算成本过高 ...

2006

0.0

... 因此,为了提高效率,变分方法^[14,15,16]将预测问题转化为优化问题 ...

2022

0.0

... 因此,为了提高效率,变分方法^[14,15,16]将预测问题转化为优化问题 ...

2009

0.0

... 但是,现有的针对迪利克雷过程混合的变分方法需要在整个数据集上进行优化,如果在大规模数据集^[17,18]上,计算开销非常大 ...

2009

0.0

... 但是,现有的针对迪利克雷过程混合的变分方法需要在整个数据集上进行优化,如果在大规模数据集^[17,18]上,计算开销非常大 ...

2022

0.0

... 此外,现有的大多数贝叶斯方法,包括DeepDPM^[19],遵循迪利克雷过程混合方法的思想,并在深度学习的框架中使用一种分离/融合的机制以发现聚类数量,分开进行特征学习与聚类 ...

... 基于文献[8]和文献[19]的工作,本文采用ResNet^[24]的两个变体作为图像特征提取器的主干,即ResNet18和ResNet34 ...

... (2)DeepDPM^[19] ...

0.0

... 但是最近的深度聚类研究^[7,8,20,21]表明,联合训练特征与分类器可以有效促进性能提升,从而提高聚类性能 ...

... Zhong等^[20]提出DRC(Deep Robust Clustering),研究交互信息与对比学习之间的内在关系,将交互信息最大化转化为最小化对比损失 ...

... (6)DRC^[20] ...

2022

0.0

... 但是最近的深度聚类研究^[7,8,20,21]表明,联合训练特征与分类器可以有效促进性能提升,从而提高聚类性能 ...

2020

0.0

... 最近,对比学习方法^[22,23] 能够有效学习样本的特征表示,在深度聚类任务中引起持续关注 ...

... 现有的针对对比视觉表征学习的工作^[22,23]通常将两个不同数据增强的特征进行对比学习 ...

0.0

... 最近,对比学习方法^[22,23] 能够有效学习样本的特征表示,在深度聚类任务中引起持续关注 ...

... 为了提高模型训练的效率,本文使用与DeepDPM相同的MoCo(Momentum Contrast)^[23]对ResNet进行无监督的预训练 ...

... 现有的针对对比视觉表征学习的工作^[22,23]通常将两个不同数据增强的特征进行对比学习 ...

2016

0.0

... 对于给定的输入图像,使用ResNet^[24]进行图像特征提取 ...

... 3 图像特征提取器为了更好地得到图像的细粒度特征表示,本文使用ResNet^[24]进行图像特征的细粒度特征信息提取 ...

... 基于文献[8]和文献[19]的工作,本文采用ResNet^[24]的两个变体作为图像特征提取器的主干,即ResNet18和ResNet34 ...

2010

0.0

... DVDPM通过推导DPGMM(Dirichlet Process Gaussian Mixture Model)^[25]的深度变分推理损失以优化整个模型,并且可以无缝嵌入到深度神经网络中 ...

1967

0.0

... 基于K-means算法^[26],首先,选择每个簇的 NK︿个最高置信度的样本和对应的特征组成支持集,支持集的第k个簇为: ...

... (3)文献[26]方法 ...

2011

0.0

... 1 实验环境本文使用STL-10^[27]、ImageNet-dog^[28]、Tiny-Ima-geNet^[29]作为基准数据集进行训练和测试 ...

2017

0.0

... 1 实验环境本文使用STL-10^[27]、ImageNet-dog^[28]、Tiny-Ima-geNet^[29]作为基准数据集进行训练和测试 ...

... ImageNet-dog数据集是ImageNet数据集^[28]的一个子集,包含15种狗的类别 ...

2023

0.0

... 1 实验环境本文使用STL-10^[27]、ImageNet-dog^[28]、Tiny-Ima-geNet^[29]作为基准数据集进行训练和测试 ...

0.0

... 本文利用PyTorch实现所有实验,并采用Adam(Adaptive Moment Estimation)优化器^[30],初始学习率l=0 ...

2020

0.0

... (7)DSEC(Deep Self-Evolution Clustering)^[31] ...

0.0

... Decorrelation)^[32] ...

2022

0.0

... (9)EDESC^[33] ...

1996

0.0

... (4)DBSCAN(Density Based Spatial Clustering of Applications with Noise)^[34] ...

2008

0.0

... 本文方法和GCC-NIC由t-SNE^[35]生成的可视化聚类效果如图2所示 ...