本文中, 分别使用Cⁿ表示n维复空间, Rⁿ表示n维实空间, Pcn表示曲率为-c的n维复庞加莱模型, Dcn表示具有 1c半径的n维复开球, R Pcn表示曲率为-c的n维实庞加莱模型, 当n=1时可以被省略.另外, 使用黑体大写字母(如X)表示矩阵, 使用黑体小写字母(如x)表示向量, 使用斜体字母(如x)表示标量.

本文的理论涉及复空间与实空间运算, 因此简单介绍复空间的基本内积和范数操作.

令

C∋x=x₁+ix₂=(x₁, x₂)=x^R∈ R²,

则x^R表示x转化为实空间上数据的表示.当y∈ C时, x和y内积表示为

< x, y> = xy-,

其中

y-=y₁-iy₂

表示y的共轭复数.另外, x的范数定义为

$ |x|=\sqrt{x_{1}^{2}+x_{2}^{2}}=\sqrt{x \bar{x}}=\left\|\boldsymbol{x}^{\mathbf{R}}\right\|, $

其中, |· |表示复数的模或复向量的范数, |· |表示实空间上向量的范数.此外, 也可得

< x, y> +< x, y> =2x^R· y^R,

其中x^R· y^R表示实向量的内积.

该结论可以直接扩展到高维空间.具体地, 对于高维空间, 当x∈ Cⁿ, y∈ Cⁿ表示复向量, 即

x=(x₁, x₂, …, x_n)∈ Cⁿ

时, x∈ Cⁿ可以使用2n维实向量x^R∈ R²ⁿ等价表示, 则

|x|= < x, x>=|x^R|.

另外, 根据

< x, y> =x₁ y-1+x₂ y-2+…+x_n y-n,

也可以推出

< x, y> +< y, x> =2x^R· y^R,

其中x^R· y^R表示x^R和y^R的内积.

双曲空间是具有负常数曲率的黎曼流形, 可以使用多个不同的等距同构模型表示, 这些双曲模型包括庞加莱模型、克莱因模型及洛伦兹模型等^[24].类似于向量空间为欧氏空间提供加、减等基本操作, 莫比乌斯陀螺矢量空间为庞加莱模型提供基本操作算子^[25].下面对庞加莱模型、克莱因模型、洛伦兹模型、庞加莱模型对应的莫比乌斯陀螺矢量空间进行简单介绍.

n维庞加莱模型^{[15, 24, 25]}

Pcn=( Dcn, gPc(z))

可以表示为一个具有黎曼度量 gPc(z)的黎曼流形, 其中,

Dcn={z∈ Cⁿ|c|z|²< 1, c> 0},

表示n维半径为 1c的开球, -c表示庞加莱模型的曲率.另外, 由于

|z|= < z, z>=|z^R|,

庞加莱模型也可表示为

R Pcn=( Bcn, gRPc(z^R)),

其中,

Bcn={z^R∈ Rⁿ|c|z^R|²< 1, c> 0},

且

gRPc(z^R)=4 (1-c=zR=2)-2I_n

表示黎曼度量.

n维克莱因模型可定义为( Kcn, gKc(u)), 其中,

Kcn={u∈ Rⁿ|c|u|²< 1, c> 0},

并且

gKc(u)= (1-c=u=2)-1Iⁿ+ (1-c=u=2)-2u· u,

Kcn表示半径为 1c的开球.

n维洛伦兹模型^[15]是一个位于n+1维闵可夫斯基空间Rⁿ⁺¹中的超曲面, 对于v∈ Rⁿ⁺¹, q∈ Rⁿ⁺¹, 闵可夫斯基内积可以表示为

v* q=v gLcq^T,

其中

gLc=diag(-1, (1ⁿ)^T).

给定负常数曲率-c, 则洛伦兹模型定义为

Lcn={v= (v0, v1, …, vn)T∈ Rⁿ⁺¹|cv* v=-1, v₀> 0}.

这些双曲空间上的模型之间是等距同构的, 相互之间可以转换^[15].例如, 庞加莱模型上的任意点z^R与克莱因模型上唯一对应的u之间的坐标可通过

$\begin{array}{l} \mathbf{R P}_{c}^{n} \rightarrow \mathbf{K}_{c}^{n}: \boldsymbol{u}=\frac{2 z^{R}}{1+c\left\|z^{R}\right\|^{2}}, \\ \mathbf{K}_{c}^{n} \rightarrow \mathbf{R P}_{c}^{n}: \boldsymbol{z}^{R}=\frac{\boldsymbol{u}}{\mathbf{1}+\sqrt{\left(1-c\|\boldsymbol{u}\|^{2}\right.}} \end{array}$

进行转换.而庞加莱模型上的任意点z和洛伦兹模型上唯一对应的点v=(v₀, h)的相互转换公式为

$\begin{array}{l} \mathbf{R P}_{c}^{n} \rightarrow \mathbf{L}_{c}^{n}: \boldsymbol{v}=\left(\frac{1}{\sqrt{c}}\left(\frac{1+c\left\|z^{R}\right\|^{2}}{1-c\left\|z^{R}\right\|^{2}}\right), \frac{2 z^{R}}{1-c\left\|z^{R}\right\|^{2}}\right), \\ \mathbf{L}_{c}^{n} \rightarrow \mathbf{R P}_{c}^{n}: z^{R}=\frac{\boldsymbol{h}}{1+\sqrt{c} v_{0}} . \end{array}$

双曲空间模型之间的等距同构变换意味着只需要在其中一个模型上设计算法.与双曲神经网络和双曲核函数等现有工作一致^{[13, 23]}, 本文主要利用庞加莱模型设计双曲算法.

莫比乌斯陀螺空间是一个具有莫比乌斯陀螺距离的度量空间, 为庞加莱模型提供代数形式^[26].

∀ z_i∈ P_c, z_j∈ P_c,

莫比乌斯加法定义为^{[26, 27]}

z_i􀱇_c z_j= zi+zj1+c< zj, zi>.

类似地, 莫比乌斯减法定义为^{[26, 27]}

z_i􀱉_c z_j=z_i􀱇_c(-z_j)= zi-zj1-c< zj, zi>.

莫比乌斯陀螺距离定义为^{[26, 27]}

d⊖c(z_i, z_j)=|z_j􀱉_c z_i|= zi-zj1-c< zj, zi>.

莫比乌斯陀螺距离的定义可以拓展到高维空间^[28], 即当z_i∈ Pcn, z_j∈ Pcn时

d⊖c(z_i, z_j)=|z_j􀱉_c z_i|= zi-zj1-c< zj, zi>. (1)

另外, 莫比乌斯陀螺矢量空间上的陀螺测地线即为庞加莱模型上的测地线, 庞加莱测地线距离可以由莫比乌斯陀螺距离推断而来, 即

$\begin{aligned} d\left(z_{i}, z_{j}\right)= & \frac{2}{\sqrt{c}} \tanh ^{-1}\left(\sqrt{c} d_{\ominus_{c}}\left(z_{i}, z_{j}\right)\right)= \\ & \frac{2}{\sqrt{c}} \tanh ^{-1}\left(\sqrt{c}\left|z_{j} \Theta_{c} z_{i}\right|\right), \end{aligned}$

其中z_i∈ Pcn, z_j∈ Pcn.

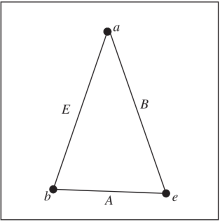
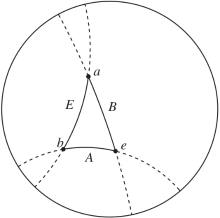
图1和图2分别表示欧氏空间对应的向量空间与庞加莱模型对应的莫比乌斯陀螺矢量空间^[26].

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 向量空间Fig.1 Vector space

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 莫比乌斯陀螺矢量空间[26]Fig.2 Mö bius gyrovector space[26]

图1表示常见的向量空间以及向量空间上的三角形, a、b、e分别表示三角形的三个顶点, A、B、E分别表示顶点对应的边, 则三条边的长度分别为

d(A)=|b-e|, d(B)=|e-a|, d(E)=|a-b|.

双曲空间中也有类似的性质.如图2所示, 在双曲空间设定下, 莫比乌斯陀螺矢量空间上垂直于边界的圆弧(虚线)表示庞加莱模型上的“ 直线” , 即测地线.实线部分表示测地线构成的“ 莫比乌斯陀螺三角形” , 其中, a、b、e分别表示三角形的三个顶点, A、B、E分别表示顶点对应的边, 则莫比乌斯陀螺三角形上的边“ 长度” , 即莫比乌斯陀螺距离分别为

$\begin{array}{l} d_{\Theta_{c}}(A)=\left|b \ominus_{c} e\right|, \\ d_{\Theta_{c}}(B)=\left|e \ominus_{c} a\right|, \\ d_{\Theta_{c}}(E)=\left|a \Theta_{c} b\right| . \end{array}$

受到这些理论的启发, 本文构造基于莫比乌斯陀螺空间上的核方法.

径向基核是欧氏空间中经典的核函数之一, 只依赖于参数之间的距离大小, 最常用的径向基核是高斯核和拉普拉斯核^[29].高斯核为

$k^{\text {Gauss }}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\exp \left(-\frac{\left|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right|^{2}}{2 \xi^{2}}\right), \xi> 0, $

其中x_i∈ Cⁿ, x_j∈ Cⁿ, |x_i-x_j|表示x_i、x_j之间的欧氏距离, ξ > 0表示高斯核的带宽.可使用双曲测地线距离代替欧氏距离构造双曲高斯核.然而文献[23]的工作表明, 直接使用测地线距离构造的高斯核函数不是正定的.

本文使用莫比乌斯陀螺距离代替欧氏距离, 构造双曲高斯核函数.具体地, 该双曲高斯核表示为

$\begin{aligned} k^{\mathrm{MGauss}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)= & \exp \left(-\frac{d_{\Theta_{c}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)^{2}}{2 \xi^{2}}\right)= \\ & \exp \left(-\frac{1}{2 \xi^{2}}\left|\frac{\boldsymbol{z}_{i}-\boldsymbol{z}_{j}}{1-c\left\langle\boldsymbol{z}_{j}, \boldsymbol{z}_{i}\right\rangle}\right|^{2}\right), \\ \xi> 0, & \end{aligned}$ (2)

其中, z_i∈ Cⁿ, z_j∈ Cⁿ, d⊖c(z_i, z_j)表示z_i、z_j之间的莫比乌斯陀螺距离.本文将该核函数称为莫比乌斯高斯核.

2.1.1 正定性证明

下面证明莫比乌斯高斯核的正定性.首先给出正定核函数和负定核函数的定义^[30].

定义1(正定核函数和负定核函数) 令Z表示一个非空集合.对于任意z_i∈ Z, z_j∈ Z和有限个λ ₁∈ C, λ ₂∈ C, …, λ _m∈ C, 如果核函数k∶ (Z× Z)→ C满足

$\sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j} k\left(z_{i}, z_{j}\right) \geqslant 0$

则核函数k称为正定核.反之, 若核函数满足

$\sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j} k\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right) \leqslant 0, $

且

$\sum_{i=1}^{m} \lambda_{i}=0, $

则核函数k称为负定核.

给定正定核和负定核的定义之后, 定理1建立两者之间的联系^[26].

定理1^[26] 令Z表示一个非空集并且

k∶ (Z× Z)→ C

是一个核函数.Φ (z_i, z_j)表示z_i、z_j的函数, 当且仅当Φ (z_i, z_j)是负定时, 核函数

k(z_i, z_j)=exp(-γ Φ (z_i, z_j))

对于所有γ > 0是正定的.

而对于莫比乌斯空间, 其本身与再生核希尔伯特空间存在联系^[31], 具体如下.令

$\mathbf{D}_{c}^{n}=\left\{\boldsymbol{z} \in \mathbf{C}^{n}: c\|\boldsymbol{z}\|^{2}< 1, c> 0\right\}$

表示半径为 1c的开球, 则对于∀ z_i∈ Dcn, z_j∈ Dcn, 存在一个有关核函数的度量:

$\delta^{\mathbf{D}_{c}^{n}}\left(z_{i}, z_{j}\right)=\sqrt{1-\left|\left\langle\hat{k}_{z_{i}}, \hat{k}_{z_{j}}\right\rangle\right|^{2}}, $

其中

k̂z= kzkz

表示规格化核函数.当该核函数

kDcn(z_i, z_j)= 11-c< zj, zi>

时, 度量 δDcn(z_i, z_j)可简化为

$\begin{aligned} \delta^{\mathbf{D}_{c}^{n}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)= & \sqrt{1-\frac{\left(1-c\left\langle\boldsymbol{z}_{i}, \boldsymbol{z}_{i}\right\rangle\right)\left(1-c\left\langle\boldsymbol{z}_{j}, \boldsymbol{z}_{j}\right\rangle\right)}{\left|1-c\left\langle\boldsymbol{z}_{j}, \boldsymbol{z}_{i}\right\rangle\right|^{2}}}= \\ & \sqrt{c}\left|\frac{\boldsymbol{z}_{i}-\boldsymbol{z}_{j}}{1-c\left\langle\boldsymbol{z}_{j}, \boldsymbol{z}_{i}\right\rangle}\right| \end{aligned}$

故

δDcn(z_i, z_j)= c d⊖cn(z_i, z_j),

即 Dcn上的度量与莫比乌斯陀螺距离具有一致性^[30].因此具有度量 δDcn(z_i, z_j)的开球 Dcn就是庞加莱模型.将

δDcn(z_i, z_j)= c d⊖cn(z_i, z_j)

代入式(2), 莫比乌斯高斯核可写成

$\begin{aligned} k^{\mathrm{MGauss}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right) & =\exp \left(-\frac{\delta^{\mathbf{D}_{c}^{n}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)^{2}}{c \xi^{2}}\right)= \\ & \exp \left(-\frac{1}{c \xi^{2}}\left(1-\mid\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}||^{2}\right)\right), \right. \end{aligned}$ (3)

其中, ξ > 0, c> 0.

因此, 证明莫比乌斯高斯核的正定性可以转化为证明等式(3)中的核函数的正定性.根据定理1, 由于

1cξ2> 0,

要证明式(3)的正定性, 只需证明如下引理1.

引理1 函数

$\begin{aligned} \Phi:\left(\mathbf{D}_{c}^{n} \times \mathbf{D}_{c}^{n}\right) \rightarrow & \mathbf{C}: \Phi\left(z_{i}, z_{j}\right)= \\ & \delta^{\mathbf{D}_{c}^{n}}\left(z_{i}, z_{j}\right)^{2}= \\ & \left.1-|| \frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right\rangle\left.\right|^{2} \end{aligned}$

是负定的.

证明 1)证明核函数

kDcn(z_i, z_j)= 11-c< zj, zi>

的正定性.根据麦克劳林公式, 核函数

kDcn(z_i, z_j)= 11-c< zj, zi>

可以转换为

kDcn(z_i, z_j)= ∑l=0∞c^l< z_i, z_j> ^l,

即正定核函数 < zi, zj> l的组合形式.则

$\begin{aligned} \sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j} k^{\mathbf{D}_{c}^{n}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)= & \sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j}\left(\sum_{l=0}^{\infty} c^{l}\left\langle\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right\rangle^{l}\right)= \\ & \sum_{l=0}^{\infty} c^{l}\left(\sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j}\left\langle\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right\rangle^{l}\right), \end{aligned}$

由于c^l> 0且

$\begin{array}{l}\sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j}\left\langle\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right\rangle^{l} \geqslant 0, \end{array}$

因此

$\begin{array}{l} \sum_{l=0}^{\infty} c^{l}\left(\sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j}\left\langle\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right\rangle^{l}\right) \geqslant 0, \end{array}$

则

$\begin{array}{l} k^{\mathbf{D}_{c}^{n}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)=\frac{1}{1-c\left\langle\boldsymbol{z}_{j}, \boldsymbol{z}_{i}\right\rangle} \end{array}$

为正定核函数.

2)证明

< kziDcnkziDcn, kzjDcnkzjDcn> 2

的正定性.由于

$\begin{array}{l} \left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|> 0, \left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|> 0, \\ \sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j}\left(\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right) \geqslant 0 \end{array}$

成立,

$\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right\rangle$

是正定的, 则

$\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right\rangle$

也是正定的.因此

$\left|\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\mid k_{z_{j}}^{\mathbf{D}_{c}^{n} \mid}}\right\rangle\right|^{2}=\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\mid k_{z_{j}}^{\mathbf{D}_{c}^{n} \mid}}\right\rangle \overline{\left|\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\mid k_{z_{i}}^{\mathbf{D}_{c}^{n} \mid}}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\mid k_{z_{j}}^{\mathbf{D}_{c}^{n} \mid}}\right\rangle}$

仍然是正定的^[27], 即

$\sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j}\left|\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\mid k_{z_{i}}^{\mathbf{D}_{c}^{n} \mid}}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right\rangle\right| \geqslant 0$

3)证明

$\left.\Phi\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)=1-|| \frac{k_{z_{i}}^{\mathbf{D}_{n}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right\rangle\left.\right|^{2}$

是条件负定的.在

∑i=1nλ _i=0

时,

$\begin{array}{l} \sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j} \Phi\left(z_{i}, z_{j}\right)= \\ \sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j}\left(1-\left|\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right\rangle\right|^{2}\right)= \\ \left(\sum_{i=1}^{n} \lambda_{i}\right)\left(\sum_{j=1}^{n} \bar{\lambda}_{j}\right)-\sum_{\substack{i=1 \\ j=1}}^{m} \lambda_{i} \bar{\lambda}_{j} \mid\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \left.\frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right|^{2}=\right. \\ -\sum_{\substack{j=1 \\ i=1}}^{n} \lambda_{i} \bar{\lambda}_{j}\left|\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n} \mid}\right|}\right\rangle\right|^{2}< 0, \end{array}$

因此

$\left.\Phi\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)=1-|| \frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \frac{k_{z_{j}}^{\mathbf{D}_{n}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right\rangle\left.\right|^{2}$

是负定的^[26], 引理1得证. 证毕.

综上所述, 在证明引理1后, 根据定理1和等式(3), 可以证明莫比乌斯高斯核是正定的.

2.1.2 实数空间上的莫比乌斯高斯核

莫比乌斯高斯是定义在复庞加莱模型上的, 但是实际的机器学习任务多数是在实数空间上进行的, 因此本文将该核函数转换为实数空间上的运算.

类似莫比乌斯加法的实运算^[26], 也可以在实数空间上表示莫比乌斯减法.令z_i∈ C, z_j∈ C, zRi∈ R², zRj∈ R²表示将其转换到实空间上的向量, 则实数空间上的莫比乌斯减法可以由如下公式推断:

$\begin{array}{c} \mathbf{C}^{n} \ni \boldsymbol{z}_{i} \ominus_{c} \boldsymbol{z}_{j}= \\ \frac{z_{i}-\boldsymbol{z}_{j}}{1-c\left\langle\boldsymbol{z}_{j}, \boldsymbol{z}_{i}\right\rangle}= \\ \frac{\left(1-c\left\langle\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right\rangle\right)\left(\boldsymbol{z}_{i}-\boldsymbol{z}_{j}\right)}{\left(1-c\left\langle\boldsymbol{z}_{j}, \boldsymbol{z}_{i}\right\rangle\right)\left(1-c\left\langle\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right\rangle\right)}= \\ \frac{\left(1-c\left\langle\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right\rangle-c\left\langle\boldsymbol{z}_{j}, \boldsymbol{z}_{i}\right\rangle+c\left\|\boldsymbol{z}_{j}\right\|^{2}\right) \boldsymbol{z}_{i}-\left(1-c\left\|\boldsymbol{z}_{i}\right\|^{2}\right) \boldsymbol{z}_{j}}{1-c\left\langle\boldsymbol{z}_{i}, z_{j}\right\rangle-c\left\langle\boldsymbol{z}_{j}, \boldsymbol{z}_{i}\right\rangle+c^{2}\left|z_{i}\right|^{2}\left|z_{j}\right|^{2}}= \\ \frac{\left(1-2 c \boldsymbol{z}_{i}^{\mathbf{R}} z_{j}^{\mathbf{R}}+c\left\|\boldsymbol{z}_{j}^{\mathbf{R}}\right\|^{2}\right) z_{i}^{\mathbf{R}}-\left(1-c\left\|\boldsymbol{z}_{i}^{\mathbf{R}}\right\|^{2}\right) \boldsymbol{z}_{j}^{\mathbf{R}}}{1-2 c \boldsymbol{z}_{i}^{\mathbf{R}} z_{j}^{\mathbf{R}}+c^{2}\left\|\boldsymbol{z}_{i}^{\mathbf{R}}\right\|^{2}\left\|\boldsymbol{z}_{j}^{R}\right\|^{2}}= \\ \boldsymbol{z}_{i}^{\mathbf{R}} \ominus_{c} z_{j}^{\mathbf{R}} \in \mathbf{R}^{2} . \end{array}$ (4)

该结论可以拓展到高维空间, 即当

z_i∈ Cⁿ, z_j∈ Cⁿ, zRi∈ R²ⁿ, zRj∈ R²ⁿ,

式(4)仍然成立.令

zRi∈ RPcn, zRj∈ RPcn

为n维实庞加莱模型上的数据, 则式(1)中定义的莫比乌斯陀螺距离可以转变为实空间上的如下运算:

$\begin{array}{l} d_{\ominus_{c}}^{\mathbf{R}}\left(z_{i}^{\mathbf{R}}, z_{j}^{\mathbf{R}}\right)=\left\|z_{j}^{\mathbf{R}} \ominus_{c} z_{i}^{\mathbf{R}}\right\|= \\ \left\|\frac{\left(1-2 c z_{i}^{\mathbf{R}} z_{j}^{\mathbf{R}}+c\left\|z_{j}^{\mathbf{R}}\right\|^{2}\right) z_{i}^{\mathbf{R}}-\left(1-c\left\|z_{i}^{\mathbf{R}}\right\|^{2}\right) z_{j}^{\mathbf{R}}}{1-2 c z_{i}^{\mathbf{R}} z_{j}^{\mathbf{R}}+c^{2}\left\|z_{i}^{\mathbf{R}}\right\|^{2}\left\|z_{j}^{\mathbf{R}}\right\|^{2}}\right\|, \end{array}$ (5)

代入式(2), 可得实庞加莱球上的莫比乌斯高斯核:

$k^{\mathrm{MGauss}}\left(z_{i}^{\mathbf{R}}, z_{j}^{\mathbf{R}}\right)=\exp \left(-\frac{d_{\Theta_{c}}^{\mathbf{R}}\left(z_{i}^{\mathbf{R}}, z_{j}^{\mathbf{R}}\right)^{2}}{2 \xi^{2}}\right)=\exp \left(-\frac{\left\|\left(1-2 c z_{i}^{\mathbf{R}} z_{j}^{\mathbf{R}}+c\left\|z_{j}^{\mathbf{R}}\right\|^{2}\right) z_{i}^{\mathbf{R}}-\left(1-c\left\|z_{i}^{\mathbf{R}}\right\|^{2}\right) z_{j}^{\mathbf{R}}\right\|^{2}}{2 \xi^{2}\left(1-2 c z_{i}^{\mathbf{R}} z_{j}^{\mathbf{R}}+c^{2}\left\|z_{i}^{\mathbf{R}}\right\|^{2}\left\|z_{j}^{\mathbf{R}}\right\|^{2}\right)^{2}}\right), \xi> 0 .$

在欧氏空间中, 拉普拉斯核可写为

$\begin{array}{l} k^{\text {Lap }}\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\exp \left(-\frac{\left|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right|}{\xi}\right), \\ \xi> 0 \end{array}$

其中, x_i∈ Cⁿ, x_j∈ Cⁿ, 且 xi-xj表示x_i、x_j之间的欧氏距离, ξ > 0表示拉普拉斯核参数.类似莫比乌斯高斯核, 本文使用莫比乌斯陀螺距离代替欧氏距离, 可得到如下莫比乌斯拉普拉斯核:

$\begin{array}{l} k^{\mathrm{MLap}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)=\exp \left(-\frac{d_{\Theta_{c}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)}{\xi}\right), \\ \xi> 0 . \end{array}$ (6)

代入

δDcn(z_i, z_j)= c d⊖cn(z_i, z_j),

可得到莫比乌斯拉普拉斯核:

$\begin{array}{l} k^{\mathrm{MLap}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)= \\ \quad \exp \left(-\frac{1}{\sqrt{c} \xi} \sqrt{1-\mid\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \left.\frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\left|k_{z_{j}}^{\mathbf{D}_{c}^{n}}\right|}\right|^{2}\right.}\right) . \end{array}$

2.2.1 正定性证明

定理2^[26] 如果k∶ (Z× Z)→ C为一个负定核函数并满足k(z_i, z_j)≥ 0, 则对于0< α < 1, k^α 仍然是负定的.

结合定理1、引理1和定理2, 由于

1- < kziDcnkziDcn, kzjDcnkzjDcn> 2

是负定的, 令α = 12, 可得

$\begin{array}{c} \sqrt{1-\mid\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{n}^{n}}}{\left|k_{z_{i}}^{\mathbf{D}_{c}^{n}}\right|}, \left.\frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\mid k_{z_{j}}^{\mathbf{D}_{c}^{n} \mid}}\right|^{2}\right.}= \\ \left(1-\left|\left\langle\frac{k_{z_{i}}^{\mathbf{D}_{c}^{n}}}{\mid k_{z_{i}}^{\mathbf{D}_{c}^{n} \mid}}, \frac{k_{z_{j}}^{\mathbf{D}_{c}^{n}}}{\mid k_{z_{j}}^{\mathbf{D}_{c}^{n} \mid}}\right\rangle\right|^{2}\right)^{\alpha} \end{array}$

也是负定的, 进而可得莫比乌斯拉普拉斯核也是正定的.

2.2.2 实数空间上的莫比乌斯拉普拉斯核

对于式(6), 使用式(5), 即实数空间上的莫比乌斯陀螺距离 dR⊖c( zRi, zRj)代替复空间设定下的距离 d⊖c(z_i, z_j), 可得到实数空间上的莫比乌斯拉普拉斯核:

$\begin{array}{l} k^{\mathrm{MLap}}\left(z_{i}, z_{j}\right)=\exp \left(-\frac{d_{\Theta_{c}}^{\mathbf{R}}\left(z_{i}^{\mathbf{R}}, z_{j}^{\mathbf{R}}\right)}{\xi}\right)= \\ \exp \left(-\frac{\left\|\left(1-2 c z_{i}^{\mathbf{R}} z_{j}^{\mathbf{R}}+c\left\|z_{j}^{\mathbf{R}}\right\|^{2}\right) z_{i}-\left(1-c\left\|z_{i}^{\mathbf{R}}\right\|^{2}\right) z_{j}^{\mathbf{R}}\right\|}{\xi\left(1-2 c z_{i}^{\mathbf{R}} z_{j}^{\mathbf{R}}+c^{2}\left\|z_{i}^{\mathbf{R}}\right\|^{2}\left\|z_{j}^{\mathbf{R}}\right\|^{2}\right)}\right), \\ \xi> 0 . \end{array}$

其中, zRi∈ R Pcn, zRj∈ R Pcn.

本文在Facebook^[32]、PIT^[33]、Wiki^[34]、Amazon Electronics Computers(AEC)^[35]、Cora ML^[36]这5个社交网络数据集上进行实验.

1)Facebook数据集.2007年收集的用于表示4类蓝色认证的Facebook页面网络之间互相喜欢关系.本文在实验中选择频率最高的前2 489个节点.

2)PIT数据集.马里兰大学信息和网络动力学实验室收集的数据集, 实验中保留614个样本和3个类别.

3)Wiki数据集.2007年从英文维基百科收集的文章网络.在实验中保留2 123个样本和10个类别.

4)AEC数据集.亚马逊共同购买图^[37]的一部分, 节点表示商品, 边表示商品一起购买.实验中选择样本数最多的3类, 并按比例随机抽取2 500个样本.

5)Cora ML数据集.从Cora数据集^[38]中提取的图.实验中保留2 507个节点和5个类别.

对于每个数据集, 分别利用庞加莱嵌入算法^[11]和Deepwalk^[39]将其嵌入2、5、10和25维双曲空间和欧氏空间, 再用不同的核函数支持向量机对样本进行分类.

本文选用如下评价指标:多分类精度的均值(Average Multiple Classification Accuracy, ACC)、ROC(Receiver Operating Characteristic Curve)曲线下面积(Area Under Curve, AUC)和平均查准率-查全率曲线下面积(Area Under Precision-Recall Curve, AUPR).

为了保证方法的泛化性, 减少过拟合, 各算法都分别在每个数据集不同维度的双曲嵌入和欧氏嵌入上至少进行10轮二次交叉验证, 再求其平均值和方差.另外, 实验结果中也给出每种算法在每个指标上取得最好效果的次数(记为Top1 Times).

为了体现本文方法的莫比乌斯高斯核 (k^MGauss)、莫比乌斯拉普拉斯核(k^MLap)有效性, 选择现有的双曲核和欧氏核进行对比, 对比函数包括双曲空间上的核函数与欧氏空间上的核函数.

双曲核函数包括由Fang等^[23]定义在庞加莱模型上的Hyperbolic RBF Kernel, Hyperbolic Laplace Kernel, Hyperbolic Binomial Kernel, Hyperbolic Tan-gent Kernel.在这些核函数中^[23],

$f(z)=\tanh ^{-1}(\sqrt{c}\|z\|) \frac{z}{\sqrt{c}\|z\|}, c> 0, $

其中z∈ R Pcn.另外, 本文还对比由Cho等^[22]定义在洛伦兹模型上的Hyperbolic Polynomial Kernel, Hyper-bolic SVM.上述6个双曲核函数的具体形式如下.

1)Hyperbolic RBF Kernel^[23].

$\begin{array}{l} k^{\mathrm{HGauss}}\left(\boldsymbol{z}_{i}, \boldsymbol{z}_{j}\right)=\exp \left(-\frac{\left\|f\left(\boldsymbol{z}_{i}\right)-f\left(\boldsymbol{z}_{j}\right)\right\|^{2}}{2 \xi^{2}}\right), \\ \xi> 0, \boldsymbol{z}_{i} \in \mathbf{R P}_{c}^{n}, \boldsymbol{z}_{j} \in \mathbf{R} \mathbf{P}_{c}^{n} . \end{array}$

2)Hyperbolic Laplace Kernel^[23].

$\begin{array}{l} k^{\text {HLap }}=\exp \left(-\frac{\left\|f\left(\boldsymbol{z}_{i}\right)-f\left(\boldsymbol{z}_{j}\right)\right\|}{\xi}\right), \\ \xi> 0, \boldsymbol{z}_{i} \in \mathbf{R P}_{c}^{n}, \boldsymbol{z}_{j} \in \mathbf{R} \mathbf{P}_{c}^{n} . \end{array}$

3)Hyperbolic Binomial Kernel^[23].

$\begin{array}{l} k^{\mathrm{HBin}}=\left(1-\left\langle f\left(\boldsymbol{z}_{i}\right), f\left(\boldsymbol{z}_{i}\right)\right\rangle\right)^{-\alpha}, \\ \alpha> 0, \boldsymbol{z}_{i} \in \mathbf{R} \mathbf{P}_{c}^{n}, \boldsymbol{z}_{j} \in \mathbf{R} \mathbf{R}_{c}^{n} . \end{array}$

4)Hyperbolic Tangent Kernel^[23].

$\begin{array}{l} k^{\mathrm{HTang}}=\left\langle f\left(\boldsymbol{z}_{i}\right), f\left(\boldsymbol{z}_{i}\right)\right\rangle, \\ \boldsymbol{z}_{i} \in \mathbf{R} \mathbf{R}_{c}^{n}, \boldsymbol{z}_{j} \in \mathbf{R} \mathbf{P}_{c}^{n} . \end{array}$

5)Hyperbolic Polynomial Kernel^[22].

$\begin{array}{l} k^{\mathrm{HPloy}}= \\ \frac{k^{E}\left(g\left(\boldsymbol{v}_{i}\right), g\left(\boldsymbol{v}_{j}\right)\right)-1}{\sqrt{\left(1-k^{E}\left(g\left(\boldsymbol{v}_{i}\right), g\left(\boldsymbol{v}_{i}\right)\right)\right)\left(1-k^{E}\left(g\left(\boldsymbol{v}_{j}\right), g\left(\boldsymbol{v}_{j}\right)\right)\right)}}, \\ k^{E}\left(\boldsymbol{v}_{i}, \boldsymbol{v}_{j}\right)=\left(\boldsymbol{v}_{i}, \boldsymbol{v}_{j}\right)^{\alpha}, \end{array}$

α > 0表示多项式的次数,

$\begin{array}{l} \boldsymbol{v}=\left(v_{0}, v_{1}, \cdots, v_{n}\right) \in \mathbf{L}^{n}, \\ g(\boldsymbol{v})=\left(\frac{v_{1}}{v_{0}}, \frac{v_{2}}{v_{0}}, \cdots, \frac{v_{n}}{v_{0}}\right), \end{array}$

表示将v的坐标从洛伦兹模型映射到Klein模型上.

6)Hyperbolic SVM^[22].双曲线性SVM, 优化目标k^HLinear为

$\begin{array}{l} \min _{\boldsymbol{w} \in \mathbf{R}^{n+1}}\left(-\frac{1}{2} \boldsymbol{w} * \boldsymbol{w}+\beta \sum_{i=1}^{m} l\left(\boldsymbol{w} * \boldsymbol{z}^{i}\right)\right), \\ \text { s. t. } \boldsymbol{w} * \boldsymbol{w}< 0, \end{array}$

其中

l(· )=max(0, sinh^-1(1)-sinh^-1(· )),

* 表示闵可夫斯基内积, zⁱ∈ Lⁿ表示嵌入在洛伦兹模型上的样本, w表示决定分类超平面的法向量, β > 0表示一个常数.HLinear可以看作是双曲线性核.

欧氏空间上的核函数包括Gaussian Kernel^[29], Laplace Kernel^[40], Polynomial Kernel^[29].函数具体形式如下.

1)Gaussian Kernel^[29].

$\begin{array}{l} k^{\mathrm{EGauss}}=\exp \left(-\frac{\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right\|^{2}}{2 \xi^{2}}\right), \\ \xi> 0, \boldsymbol{x}_{i} \in \mathbf{R}^{n}, \boldsymbol{x}_{j} \in \mathbf{R}^{n} . \end{array}$

2)Laplace Kernel^[40].

$\begin{array}{l} k^{\text {ELap }}=\exp \left(-\frac{\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right\|}{\xi}\right) \\ \xi> 0, \boldsymbol{x}_{i} \in \mathbf{R}^{n}, \boldsymbol{x}_{j} \in \mathbf{R}^{n} \end{array}$

3)Polynomial Kernel^[29].

$\begin{array}{l} k^{\mathrm{EPloy}}=\left(\gamma \boldsymbol{x}_{i} \boldsymbol{x}_{j}+1\right)^{\alpha}, \\ \gamma> 0, \alpha> 0, \boldsymbol{x}_{i} \in \mathbf{R}^{n}, \boldsymbol{x}_{j} \in \mathbf{R}^{n} . \end{array}$

本文还进行显著性测试, 将所有对比函数与k^MLap在显著性水平0.05下进行成对t检验.在每个结果后面使用• /* 来表明是否k^MLap显著优于或劣于对比函数, • 表示显著优于对比函数, * 表示显著劣于对比函数.

对于每个核函数, 本文利用SVM在每个数据集上进行图节点分类.对比的核函数中, k^HPoly是不定的, 其余都是正定的.对于正定核, 利用凸优化求解SVM^[41], 对于双曲多项式核, 利用Kreǐ n SVM^[42]求解.

另外, 对于k^MLap和k^MGauss, 参数ξ 采用交叉验证, 从集合{2^-6, 2^-5, …, 2⁶}中选取.相应地, k^HGuass、k^HLap、k^EGauss、k^ELap也是如此.对于k^HPoly, 多项式次数α 固定为2.对于k^EPloy, γ 从集合{0.01, 0.1, 1, 10}中选择, α 固定为2.另外, k^MGauss、k^MLap、k^HGauss、k^HLap、k^HTang、k^HBin中的曲率参数c也通过交叉验证从集合{2^-6, 2^-5, …, 2⁶}中获取.

各对比函数在6个数据集上的ACC、AUC和AUPR指标值对比如表1~表3所示, 表中黑体数字表示最优值.由表可见, k^MLap和k^MGauss在不同指标上的Top1 Times最大, 性能最佳, t检验结果也表明该结果具有统计学意义.

表1

Table 1

表1(Table 1)

表1 各核函数在5个数据集上的平均ACC对比 Table 1 Average ACC comparison of different kernel functions on 5 datasets 数据集 维度 庞加莱嵌入/% 欧几里得嵌入/% kMGauss kMLap kHGauss kHLap kHTang kHBin kHPoly kHLinear kEGauss kELap kEPoly Facebook 2 83.8 (± 0.6) 83.8 (± 0.7) 74.3• (± 1.0) 74.8• (± 1.2) 63.3• (± 0.6) 67.5• (± 1.3) 66.6• (± 2.8) 61.5• (± 0.3) 67.0• (± 0.4) 67.3• (± 0.3) 66.0• (± 0.5) 5 88.4 (± 0.7) 88.7 (± 0.4) 87.2• (± 0.8) 87.9• (± 0.6) 88.6• (± 0.6) 86.0• (± 1.2) 81.6• (± 1.1) 62.6• (± 0.6) 84.7• (± 0.6) 85.6• (± 0.7) 82.5• (± 0.8) 10 88.4 (± 0.5) 89.0 (± 0.5) 88.2• (± 0.7) 88.5• (± 0.5) 74.0• (± 0.8) 88.4 (± 1.4) 86.5• (± 1.1) 66.5• (± 1.6) 86.8• (± 0.8) 86.7• (± 0.6) 86.4• (± 0.4) 25 88.2 (± 0.7) 88.9 (± 0.4) 88.0• (± 0.5) 88.2• (± 0.5) 85.8• (± 0.5) 89.6* (± 1.0) 88.9 (± 0.6) 74.1• (± 2.2) 87.9• (± 0.6) 88.1• (± 0.6) 88.5 (± 0.6) PIT 2 63.6 (± 1.2) 64.5 (± 1.7) 60.5• (± 1.6) 62.6 (± 2.0) 49.8• (± 1.9) 55.0• (± 3.0) 51.3• (± 0.7) 53.1• (± 1.7) 60.0• (± 1.6) 60.9• (± 2.1) 51.3• (± 0.8) 5 67.2 (± 1.5) 67.7 (± 2.0) 66.3 (± 2.1) 67.2 (± 2.0) 49.5• (± 1.8) 67.4 (± 2.1) 52.8• (± 1.3) 51.1• (± 0.9) 62.1• (± 2.3) 63.8• (± 1.5) 56.2• (± 1.3) 10 66.8 (± 1.7) 67.3 (± 2.2) 67.0 (± 1.9) 66.8 (± 3.5) 51.6• (± 1.5) 68.3 (± 2.1) 59.3• (± 1.6) 53.4• (± 1.5) 65.0 (± 1.3) 66.6± (1.8) 65.4• (± 2.0) 25 66.3 (± 2.1) 67.2 (± 1.7) 66.4 (± 1.9) 67.0 (± 1.2) 53.3• (± 1.4) 67.0 (± 1.5) 60.8• (± 1.7) 51.1• (± 1.1) 62.1• (± 2.7) 63.2• (± 2.3) 66.1 (± 1.5) Wiki 2 54.7 (± 1.4) 54.9 (± 2.6) 41.4• (± 2.3) 43.1• (± 1.6) 18.7• (± 1.8) 33.0• (± 1.7) 17.0• (± 2.5) 21.9• (± 1.1) 23.7• (± 1.0) 24.4• (± 1.1) 18.4• (± 1.0) 5 67.3 (± 0.9) 68.8 (± 1.7) 65.1• (± 1.1) 66.3 (± 1.6) 30.5• (± 3.9) 60.5• (± 1.3) 58.4• (± 1.2) 31.4• (± 1.7) 57.6• (± 1.4) 58.5• (± 1.4) 45.5• (± 1.8) 10 68.5 (± 1.3) 70.6 (± 0.9) 67.4• (± 0.9) 68.2• (± 1.4) 38.4• (± 3.4) 64.7• (± 2.1) 62.0• (± 0.4) 32.5• (± 0.8) 65.6• (± 1.5) 65.2• (± 1.5) 57.8• (± 2.3) 25 70.0 (± 1.0) 71.6 (± 1.2) 69.7 (± 1.0) 69.8 (± 1.3) 59.9• (± 0.7) 66.1• (± 0.8) 67.5• (± 1.6) 41.0• (± 1.0) 68.6• (± 1.5) 68.1• (± 1.3) 64.6• (± 1.5) AEC 2 78.1 (± 0.9) 78.7 (± 0.8) 74.8• (± 1.3) 75.9• (± 0.8) 66.0• (± 1.2) 72.2• (± 1.5) 61.4• (± 7.0) 56.1• (± 0.3) 72.3• (± 1.6) 72.3• (± 1.3) 64.9• (± 4.8) 5 85.9 (± 1.1) 85.7 (± 0.7) 85.1 (± 1.0) 85.1 (± 1.4) 75.9• (± 1.4) 84.1• (± 0.9) 79.1• (± 0.8) 64.4• (± 2.1) 79.0• (± 0.8) 79.2• (± 0.6) 71.6• (± 3.3) 10 88.3 (± 0.7) 87.9 (± 0.5) 87.6 (± 0.7) 87.6 (± 0.5) 82.0• (± 0.6) 87.1• (± 1.2) 86.7• (± 1.1) 71.9• (± 1.6) 85.0• (± 0.8) 84.4• (± 0.9) 80.0• (± 3.2) 25 87.7 (± 0.9) 87.8 (± 0.6) 87.1• (± 0.7) 87.0• (± 0.7) 85.4• (± 0.4) 87.5• (± 0.7) 87.7 (± 0.8) 77.0• (± 1.3) 86.8• (± 0.7) 86.8• (± 0.6) 83.4• (± 1.2) Cora ML 2 70.2 (± 0.6) 71.3 (± 0.4) 67.9• (± 0.6) 69.0• (± 0.7) 38.2• (± 1.6) 58.7• (± 1.3) 47.8• (± 0.4) 44.8• (± 1.4) 57.0• (± 0.7) 57.7• (± 0.6) 45.9• (± 2.0) 5 83.9 (± 0.8) 84.2 (± 0.3) 82.7• (± 0.9) 83.3 (± 0.5) 62.7• (± 1.5) 80.7• (± 1.1) 72.5• (± 1.7) 61.7• (± 1.6) 70.7• (± 0.8) 71.5• (± 0.6) 58.2• (± 0.9) 10 85.2 (± 0.5) 85.4 (± 0.2) 84.3 (± 0.6) 85.0 (± 0.6) 72.3• (± 0.9) 83.7• (± 0.5) 80.8• (± 0.6) 68.2• (± 1.6) 76.2• (± 0.8) 77.2• (± 0.8) 71.5• (± 1.1) 25 85.0 (± 0.6) 85.7 (± 0.8) 84.9 (± 0.4) 75.2• (± 0.7) 79.2• (± 0.4) 84.9 (± 0.6) 83.5• (± 0.9) 74.3• (± 1.3) 79.0• (± 0.7) 78.4• (± 0.5) 75.9• (± 1.3) 均值 76.9 77.5 74.8 75.4 60.1 72.6 67.6 55.9 69.9 70.3 65.0 Top1 Times 2 17 0 0 0 2 0 0 0 0 0

表1 各核函数在5个数据集上的平均ACC对比 Table 1 Average ACC comparison of different kernel functions on 5 datasets

表2

Table 2

表2(Table 2)

表2 各核函数在5个数据集上的平均AUC对比 Table 2 Average AUC comparison of different kernel functions on 5 datasets 数据集 维度 庞加莱嵌入/% 欧几里得嵌入/% kMGauss kMLap kHGauss kHLap kHTang kHBin kHPoly kHLinear kEGauss kELap kEPoly Facebook 2 90.5 (± 0.4) 92.6 (± 0.3) 84.1• (± 1.8) 86.1• (± 0.3) 61.6• (± 5.9) 77.6• (± 1.3) 64.1• (± 3.0) 64.5• (± 1.4) 76.1• (± 1.7) 81.0• (± 0.8) 70.5• (± 2.6) 5 95.6 (± 0.3) 96.0 (± 0.3) 94.2• (± 0.3) 95.4• (± 0.4) 74.7• (± 4.6) 92.4• (± 0.8) 89.0• (± 0.4) 73.5• (± 1.1) 92.2• (± 0.6) 93.9• (± 0.5) 91.2• (± 0.3) 10 96.7 (± 0.2) 96.6 (± 0.3) 94.7• (± 0.6) 95.9• (± 0.4) 81.1• (± 4.3) 93.3• (± 0.3) 92.2• (± 0.4) 84.9• (± 1.0) 94.4• (± 0.5) 95.1• (± 0.2) 93.4• (± 0.4) 25 96.5 (± 0.3) 96.7 (± 0.4) 95.1• (± 0.4) 96.1• (± 0.4) 91.6• (± 0.3) 94.0• (± 0.4) 94.3• (± 0.4) 90.2• (± 0.4) 95.9• (± 0.4) 96.3• (± 0.4) 94.8• (± 0.7) PIT 2 71.9 (± 1.6) 74.2 (± 1.5) 67.4• (± 1.6) 72.0• (± 1.8) 49.2• (± 2.2) 64.1• (± 2.5) 53.8• (± 1.5) 63.4• (± 0.9) 64.5• (± 2.5) 68.1• (± 1.9) 54.3• (± 2.7) 5 76.3 (± 2.2) 77.2 (± 1.7) 74.1• (± 2.1) 76.5 (± 2.1) 49.8• (± 1.5) 76.2 (± 2.4) 58.4• (± 3.1) 62.2• (± 1.6) 71.8• (± 2.7) 74.9 (± 2.8) 65.2• (± 1.3) 10 76.4 (± 1.4) 77.5 (± 1.9) 76.0• (± 1.2) 77.1 (± 1.5) 53.2• (± 4.9) 77.2 (± 2.0) 65.5• (± 2.2) 65.2• (± 1.8) 73.9• (± 3.3) 77.2 (± 1.6) 72.8• (± 1.5) 25 76.9 (± 1.3) 76.9 (± 1.7) 75.8• (± 1.3) 76.9 (± 1.1) 58.0• (± 2.1) 74.9 (± 3.2) 69.7• (± 1.0) 65.9• (± 3.4) 72.0• (± 3.7) 74.9• (± 2.4) 73.5• (± 1.2) Wiki 2 85.8 (± 0.7) 88.5 (± 1.6) 76.9• (± 0.8) 82.9• (± 0.7) 48.7• (± 4.2) 75.3• (± 1.7) 52.2• (± 3.1) 57.9• (± 0.7) 64.6• (± 2.3) 72.2• (± 0.7) 62.7• (± 2.7) 5 92.0 (± 0.5) 93.2 (± 0.6) 89.9• (± 0.4) 91.8• (± 0.3) 68.5• (± 3.8) 86.3• (± 1.5) 79.8• (± 2.6) 78.6• (± 0.9) 85.3• (± 0.8) 88.4• (± 0.6) 81.6• (± 2.0) 10 93.3 (± 0.3) 93.9 (± 0.1) 91.5• (± 0.3) 93.0• (± 0.2) 75.7• (± 3.0) 88.4• (± 0.4) 87.9• (± 1.9) 80.1• (± 0.5) 90.4• (± 0.5) 92.4• (± 0.3) 89.3• (± 0.9) 25 92.6 (± 0.5) 94.5 (± 0.3) 92.0• (± 0.5) 93.6• (± 0.4) 83.3• (± 3.0) 89.1• (± 0.5) 89.1• (± 1.9) 84.4• (± 0.4) 91.4• (± 0.5) 92.6• (± 0.3) 89.3• (± 0.4) AEC 2 86.4 (± 0.4) 87.5 (± 0.5) 83.3• (± 0.7) 86.2• (± 0.5) 74.0• (± 3.6) 78.0• (± 6.1) 68.1• (± 7.9) 69.5• (± 0.8) 81.4• (± 1.2) 82.1• (± 0.9) 77.2• (± 4.8) 5 95.0 (± 0.4) 95.5 (± 0.4) 93.9• (± 0.5) 94.9• (± 0.5) 81.0• (± 6.7) 92.4• (± 0.8) 89.5• (± 0.5) 84.0• (± 0.7) 89.3• (± 0.3) 90.5• (± 0.5) 85.6• (± 4.3) 10 96.8 (± 0.3) 96.8 (± 0.2) 96.2• (± 0.4) 96.7 (± 0.2) 92.5• (± 0.4) 94.6• (± 0.9) 94.9• (± 0.6) 89.9• (± 0.6) 95.1• (± 0.4) 95.2• (± 0.4) 92.1• (± 0.7) 25 96.5 (± 0.4) 96.8 (± 0.3) 95.9• (± 0.3) 96.1• (± 0.5) 93.9• (± 0.3) 94.9• (± 0.6) 95.3• (± 0.6) 91.0• (± 0.2) 96.6• (± 0.4) 96.1• (± 0.3) 92.8• (± 0.9) Cora ML 2 87.2 (± 0.3) 89.8 (± 0.3) 85.8• (± 0.4) 88.5• (± 0.5) 57.8• (± 3.0) 85.2• (± 0.4) 61.9• (± 4.0) 70.9• (± 0.2) 76.9• (± 0.7) 79.7• (± 1.0) 62.8• (± 3.9) 5 94.8 (± 0.2) 95.7 (± 0.2) 93.8• (± 0.5) 95.2• (± 0.4) 86.6• (± 0.1) 93.5• (± 0.3) 88.7• (± 0.3) 86.1• (± 0.1) 88.1• (± 0.6) 90.0• (± 0.3) 85.4• (± 2.1) 10 96.0 (± 0.2) 96.4 (± 0.3) 95.3• (± 0.3) 96.1 (± 0.3) 88.7• (± 0.1) 94.9• (± 0.3) 93.6• (± 0.3) 88.4• (± 0.1) 92.1• (± 0.3) 93.0• (± 0.2) 90.1• (± 0.4) 25 96.0 (± 0.2) 96.6 (± 0.2) 95.7• (± 0.3) 96.6 (± 0.3) 93.0• (± 0.1) 95.6• (± 0.4) 95.6• (± 0.3) 91.7• (± 0.3) 93.6• (± 0.4) 93.6• (± 0.2) 91.6• (± 0.9) 均值 89.7 90.6 87.4 89.4 73.1 85.9 79.1 77.1 84.3 86.4 81.8 Top1 Times 3 19 0 1 0 0 0 0 0 0 0

表2 各核函数在5个数据集上的平均AUC对比 Table 2 Average AUC comparison of different kernel functions on 5 datasets

表3

Table 3

表3(Table 3)

表3 各核函数在5个数据集上的平均AUPR对比 Table 3 Average AUPR comparison of different kernel functions on 5 datasets 数据集 维度 庞加莱嵌入/% 欧几里得嵌入/% kMGauss kMLap kHGauss kHLap kHTang kHBin kHPoly kHLinear kEGauss kELap kEPoly Facebook 2 80.3 (± 0.7) 82.3 (± 0.7) 63.8• (± 2.1) 68.5• (± 1.3) 36.7• (± 3.3) 49.8• (± 3.7) 39.3• (± 2.2) 37.5• (± 0.4) 55.5• (± 2.4) 60.7• (± 0.8) 47.2• (± 3.5) 5 90.3 (± 0.6) 90.7 (± 0.4) 87.2• (± 0.9) 89.1• (± 0.5) 51.4• (± 3.0) 82.6• (± 1.9) 74.7• (± 0.8) 56.4• (± 1.2) 82.2• (± 0.6) 83.9• (± 0.7) 75.8• (± 0.6) 10 91.3 (± 0.4) 91.3 (± 0.4) 88.1• (± 0.6) 89.9• (± 0.6) 64.6• (± 2.5) 84.4• (± 0.8) 83.5• (± 1.0) 70.4• (± 2.3) 87.3• (± 1.0) 88.3• (± 0.3) 82.5• (± 1.2) 25 91.7 (± 0.3) 91.7 (± 0.5) 89.3• (± 0.5) 90.7• (± 0.7) 83.0• (± 0.7) 87.0• (± 1.2) 87.5• (± 1.1) 80.3• (± 0.7) 88.8• (± 0.7) 89.8• (± 0.8) 84.9• (± 1.8) PIT 2 56.7 (± 2.1) 57.3 (± 2.5) 49.2• (± 2.4) 53.3• (± 2.3) 33.8• (± 1.4) 46.2• (± 1.2) 36.5• (± 1.4) 46.3• (± 0.6) 47.4• (± 2.1) 50.0• (± 1.6) 37.0• (± 1.8) 5 60.6 (± 2.8) 61.9 (± 1.8) 59.1• (± 1.7) 61.1 (± 2.6) 33.6• (± 0.9) 58.1• (± 2.5) 40.5• (± 2.2) 45.5• (± 2.1) 54.6• (± 2.3) 58.1• (± 1.4) 47.7• (± 1.1) 10 60.9 (± 2.6) 61.7 (± 2.4) 60.4 (± 1.5) 61.2 (± 2.5) 37.7• (± 3.4) 59.9• (± 2.0) 48.4• (± 2.5) 47.9• (± 2.0) 57.1• (± 2.7) 59.5 (± 2.3) 55.7• (± 2.0) 25 61.4 (± 1.8) 60.9 (± 2.8) 59.9 (± 1.8) 61.8 (± 1.9) 40.3• (± 1.5) 57.2• (± 1.9) 52.9• (± 1.6) 47.6• (± 2.4) 56.3• (± 2.2) 59.3 (± 2.3) 56.8• (± 1.7) Wiki 2 65.5 (± 1.2) 67.8 (± 1.0) 48.8• (± 1.4) 54.5• (± 1.1) 11.2• (± 0.8) 42.1• (± 1.0) 14.3• (± 2.2) 12.3• (± 0.4) 27.5• (± 1.4) 33.1• (± 1.0) 23.2• (± 0.8) 5 77.2 (± 0.8) 77.8 (± 1.0) 72.5• (± 0.8) 75.4• (± 0.7) 38.4• (± 3.5) 60.7• (± 1.4) 59.7• (± 1.2) 53.1• (± 1.1) 66.1• (± 0.9) 69.0• (± 0.7) 55.2• (± 1.7) 10 79.6 (± 0.4) 80.1 (± 0.4) 76.3• (± 0.9) 77.9• (± 0.6) 50.9• (± 1.6) 66.7• (± 0.6) 68.3• (± 0.9) 57.1• (± 0.9) 74.9• (± 1.1) 76.7• (± 0.6) 62.9• (± 0.9) 25 78.4 (± 0.7) 80.8 (± 0.7) 77.1• (± 0.8) 79.3• (± 0.7) 60.2• (± 1.2) 68.2• (± 1.0) 71.9• (± 0.9) 61.6• (± 1.1) 77.3• (± 1.3) 78.7• (± 0.6) 65.1• (± 1.1) AEC 2 78.6 (± 0.6) 79.0 (± 0.6) 73.1• (± 2.1) 76.4• (± 0.8) 58.3• (± 1.7) 71.0• (± 0.9) 56.9• (± 7.2) 55.6• (± 0.6) 67.5• (± 2.2) 68.6• (± 1.2) 58.8• (± 4.5) 5 91.6 (± 0.6) 91.9 (± 0.5) 89.9• (± 0.9) 91.2• (± 0.8) 69.2• (± 4.3) 86.3• (± 1.6) 78.8• (± 1.3) 70.5• (± 0.6) 81.0• (± 0.7) 82.7• (± 0.6) 74.0• (± 3.6) 10 94.3 (± 0.5) 94.1 (± 0.4) 93.3• (± 0.7) 93.9 (± 0.4) 86.4• (± 0.5) 90.2• (± 2.1) 91.3• (± 1.1) 82.5• (± 0.9) 91.2• (± 0.9) 91.4• (± 0.7) 84.4• (± 1.9) 25 93.9 (± 0.5) 94.3 (± 0.3) 92.9• (± 0.5) 93.4• (± 0.6) 90.2• (± 0.5) 90.8• (± 2.5) 92.1• (± 0.8) 86.5• (± 0.6) 92.2• (± 0.6) 93.1• (± 0.4) 85.5• (± 1.7) Cora ML 2 72.9 (± 0.6) 75.7 (± 0.9) 69.9• (± 0.6) 72.9• (± 0.7) 34.4• (± 1.6) 65.5• (± 0.7) 39.4• (± 2.4) 44.2• (± 0.7) 55.8• (± 1.1) 57.9• (± 0.7) 37.0• (± 3.2) 5 88.6 (± 0.4) 89.6 (± 0.3) 86.7• (± 1.0) 88.5• (± 0.7) 71.3• (± 0.2) 84.1• (± 0.7) 77.4• (± 0.5) 72.2• (± 0.4) 75.6• (± 0.7) 77.6• (± 0.5) 66.1• (± 1.4) 10 90.2 (± 0.3) 90.8 (± 0.4) 89.0• (± 0.7) 90.5 (± 0.3) 77.5• (± 0.2) 87.8• (± 0.5) 85.5• (± 0.4) 78.4• (± 0.3) 82.0• (± 0.7) 83.5• (± 0.6) 75.7• (± 0.8) 25 90.5 (± 0.5) 91.3 (± 0.4) 89.9• (± 0.5) 91.1 (± 0.3) 84.5• (± 0.3) 88.9• (± 0.7) 88.9• (± 0.4) 83.2• (± 0.6) 84.9• (± 0.9) 84.9• (± 0.3) 79.3• (± 2.5) 均值 79.7 80.6 75.8 78.0 55.7 71.4 64.4 59.5 70.3 72.3 62.7 Top1 Times 5 16 0 0 0 0 0 0 0 0 0

表3 各核函数在5个数据集上的平均AUPR对比 Table 3 Average AUPR comparison of different kernel functions on 5 datasets

对比现有双曲核, 发现本文的核函数在不同的评价指标上都有显著提升.相比k^HGauss、k^HLap、k^HTang、k^HBin和k^HPoly, 在ACC评价指标上, k^MLap分别提升2.7%、2.1%、17.4%、4.9%和9.9%, 在AUC指标上, k^MLap分别提升3.2%、1.2%、17.5%、4.7%和11.5%, 在AUPR指标上, k^MLap分别提升4.8%、2.6%、24.9%、9.2%和16.2%.k^MLap性能的提升, 验证利用莫比乌斯陀螺距离构造的核函数, 能够减小将数据映射到切空间上造成的扭曲, 提升核函数的映射能力.对比k^HPoly的性能优越性验证k^MLap的自适应能力.另外, 对比双曲线性分类, 发现所有的双曲核函数都具有明显的性能提升, 这说明双曲核函数的有效性.

对比欧氏空间上对应的核函数, 发现k^MGauss和k^MLap提升更加显著.相比k^EGauss, k^MGauss在ACC、AUC和AUPR指标上分别提升7.0%、5.4%和9.4%, 相比k^ELap, k^MLap在ACC、AUC和AUPR指标上分别提升 7.2%、4.2%和8.3%.这不仅表明本文方法的有效性, 也验证双曲空间具有更强大的表征能力.

另外, 对于k^MGauss和k^MLap, 很低的维度就能达到与高维相差不大的效果, 而欧氏空间中核函数的分类效果明显地随着嵌入维度的升高而提升, 即使在25维也很难达到与双曲嵌入相当的效果.这个结论进一步验证双曲空间对于层次结构数据的强大表征能力.

为了充分探讨庞加莱模型曲率参数c对于MGauss和MLap的影响, 在Facebook、Terrorist、Wiki、AEC、Cora ML数据集的10维庞加莱嵌入上利用核SVM进行图节点分类.

核函数在不同评价指标上的分类性能变化如图3~图5所示.由图可以观察到:1)在不同的指标上, MGauss和MLap变化趋势都很接近, 这主要取决于核函数形式的相似性, 两者都是基于莫比乌斯陀螺距离的径向基核.2)当c较小时, MGauss和MLap在不同指标上都较平稳, 能得到较优性能, 这说明核函数的鲁棒性.3)当c值过大时, 不同指标下的分类性能都有所下降, 这说明庞加莱模型的曲率确实会影响核函数的性能, 因此把c作为核函数的参数有助于提高核函数的自适应能力.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 c不同时MGauss和MLap在5个数据集上的ACC指标对比Fig.3 ACC comparison of MGauss and MLap with different c on 5 datasets

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 c不同时MGauss和MLap在5个数据集上的AUC指标对比Fig.4 AUC comparison of MGauss and MLap with different c on 5 datasets

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 c不同时MGauss和MLap在5个数据集上的AUPR指标对比Fig.5 AUPR comparison of MGauss and MLap with different c on 5 datasets

另外, 注意到当c很小时, MGauss和MLap趋向于Gaussian Kernel和Laplace Kernel, 但是由表1~表3中的结果可知, 在欧氏映射数据上利用Gaussian Kernel和Laplace Kernel效果与在双曲映射数据上利用MGauss和MLap的对比进一步说明双曲空间能更好地表征层次结构数据.另外, 虽然MGauss和MLap在c值趋向于0时趋向Gaussian Kernel和Laplace Kernel, 也许在双曲映射数据上直接利用Gaussian Kernel和Laplace Kernel也能取得较优效果, 但是在双曲空间上利用欧氏方法本身是不合理的.而 MGauss和MLap既符合双曲几何的设定, 又有足够好的性能, 是处理层次结构数据更好的选择.