引用本文
张珉, 梁美玉, 薛哲, 管泽礼, 潘圳辉, 赵泽华. 基于结构增强的异质数据联邦学习模型正则优化算法. 模式识别与人工智能, 2023,36(9): 856-865
ZHANG Min, LIANG Meiyu, XUE Zhe, GUAN Zeli, PAN Zhenhui, ZHAO Zehua. Regularization Optimization Algorithm for Heterogeneous Data FederatedLearning Model Based on Structure Enhancement. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2023,36(9): 856-865.  
Doi: 10.16451/j.cnki.issn1003-6059.202309008
Permissions
Copyright©2023, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于结构增强的异质数据联邦学习模型正则优化算法
张珉1,2, 梁美玉1,2, 薛哲1,2, 管泽礼1,2, 潘圳辉1,2, 赵泽华1,2
1.北京邮电大学 计算机学院 北京 100876
2.北京邮电大学 智能通信软件与多媒体北京市重点实验室北京 100876
通讯作者:

梁美玉,博士,教授,主要研究方向为人工智能、数据挖掘、多媒体信息处理、计算机视觉等.E-mail:meiyu1210@bupt.edu.cn.

作者简介:

张 珉,硕士研究生,主要研究方向为联邦学习.E-mail:zm_zhangmin@bupt.edu.cn.

薛 哲,博士,副教授,主要研究方向为机器学习、数据挖掘、多模态/多视图学习、突发事件检测与分析等.E-mail:xuezhe@bupt.edu.cn.

管泽礼,博士研究生,主要研究方向为联邦学习、图神经网络、机器学习.E-mail:guanzeli@bupt.edu.cn.

潘圳辉,博士研究生,主要研究方向为联邦学习、机器学习.E-mail:JerryPan@bupt.edu.cn.

赵泽华,硕士研究生,主要研究方向为联邦学习中的高效通信.E-mail:ZeHuaZhao@bupt.edu.cn.

收稿日期: 2023-07-13 接受日期: 2023-09-30
资助项目: 国家自然科学基金项目(No.62192784、U22B2038、62172056、62272058)、中国人工智能学会-华为MindSpore学术奖励基金项目(No.CAAIXSJLJJ-2021-007B)资助
摘要

联邦学习中由于不同客户端本地数据分布异质,在本地数据集上训练的客户端模型优化目标与全局模型不一致,导致出现客户端漂移现象,影响全局模型性能.为了解决非独立同分布数据带来的联邦学习模型性能下降甚至发散的问题,文中从本地模型的通用性角度出发,提出基于结构增强的异质数据联邦学习模型正则优化算法.在客户端利用数据分布异质的本地数据进行训练时,以结构化的方式采样子网络,并对客户端本地数据进行数据增强,使用不同的增强数据训练不同的子网络学习增强表示,得到泛化性较强的客户端网络模型,对抗本地数据异质带来的客户端漂移现象,在联邦聚合中得到性能更优的全局模型.在CIFAR-10、CIFAR-100、ImageNet-200数据集上的大量实验表明,文中算法性能较优.

关键词: 联邦学习; 非独立同分布(Non-IID); 数据异质性; 客户端漂移; 正则化
中图分类号:TP391
Regularization Optimization Algorithm for Heterogeneous Data FederatedLearning Model Based on Structure Enhancement
ZHANG Min1,2, LIANG Meiyu1,2, XUE Zhe1,2, GUAN Zeli1,2, PAN Zhenhui1,2, ZHAO Zehua1,2
1. School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876
2. Beijing Key Laboratory of Intelligent Telecommunication Software and Multimedia, Beijing University of Posts and Telecommunications, Beijing 100876
Corresponding author:
LIANG Meiyu, Ph.D., professor. Her research interests include artificial intelligence, data mining, multimedia information processing and computer vision.

About Author:
ZHANG Min, master student. Her research interests include federated learning.
XUE Zhe, Ph.D., associate professor. His research interests include machine learning, data mining, multimodal/multi-view learning and emergency detection and analysis.
GUAN Zeli, Ph.D. candidate. His research interests include federated learning, graph neu-ral network and machine learning.
PAN Zhenhui, Ph.D. candidate. His research interests include federated learning and machine learning.
ZHAO Zehua, master student. His research interests include efficient communication in federated learning.

Fund:National Natural Science Foundation of China(No.62192784,U22B2038,62172056,62272058), CAAI-Huawei Mind-Spore Open Fund(No.CAAIXSJLJJ-2021-007B)
Abstract

In federated learning, due to the heterogeneous distribution of local data among different clients, the optimization objectives of client models trained on local datasets are inconsistent with the global model, leading to client drift and affecting the performance of global model. To address the issue of performance decline or even divergence in federated learning models caused by non-independently and identically distributed data, a regularization optimization algorithm for heterogeneous data federated learning model based on structure enhancement(FedSER) is proposed from the perspective of the generality of local models. While training on local data with heterogeneous distributions, clients sample subnetworks in a structured manner. Local data of client are augmented, and different subnetworks are trained with the augmented data to learn enhanced representations, resulting in more generalized client network models. The models counteract the client drift caused by the heterogeneity of local data and achieve a better global model in federated aggregation. Extensive experiments on the CIFAR-10, CIFAR-100 and ImageNet-200 datasets demonstrate the superior performance of FedSER.

Key words: Federated Learning; Non-Independently and Identically Distributed(Non-IID); Data Heterogeneity; Client Drift; Regularization

联邦学习[1]使大量客户端能够在不损害数据隐私的情况下实现对机器学习模型的协作训练.在联邦学习设置中, 参与的客户端通常部署在各种环境中, 或者由不同的用户或机构拥有[2, 3].因此, 每个客户端本地数据的分布可能有很大差异(即数据异构性).

这种在联邦学习中参与设备之间的数据非独立同分布(Non-Independently and Identically Distributed, Non-IID)使联邦学习的模型优化具有挑战性[4, 5, 6].每个客户端在自己的本地数据上训练模型, 优化各自的局部目标.然而, 局部收敛点可能无法较好地符合全局模型的目标(即在中央服务器上的聚合学习后的模型).因此, 客户端模型经常偏离理想的全局优化点, 过拟合其局部目标.当产生客户端漂移现象时, 全局聚合模型的性能会受到影响.

目前学者们已提出许多针对联邦学习中数据异质性问题的解决方案, 包括FedProx[7]、SCAFFOLD(Stochastic Controlled Averaging for Federated Lear-ning)[8]、FedDC(Federated Learning Algorithm with Local Drift Decoupling and Correction)[9]和FedIR[10].这些方法引入局部优化约束, 限制局部模型更新时与全局模型之间的差异.另外一些方法, 包括Fed-Nova[11]、FedMA(Federated Matched Averaging)[12]、FedAvgM(Federated Averaging with Server Momen-tum)[13]和CCVR(Classifier Calibration with Virtual Representations)[14], 改进全局聚合阶段, 使全局模型接近全局最优.还有一些方法引入共享数据集的方式, 如FedRep(Federated Representation Learning)[15]和FedMix(Federated Mixup)[16], 使客户端本地模型除了学习本地数据的分布特征以外, 还学习部分共享数据的分布特征.尽管上述方法在性能上有一定提升, 但仍无法解决客户端上数据分布异质性带来的因客户端模型漂移而导致的全局模型性能下降问题.

首先, 在局部训练阶段或全局聚合阶段引入约束的方法, 虽然限制局部模型和全局模型在训练时更接近, 但在抑制漂移的同时, 也固有地限制本地模型的收敛潜力, 使本地模型在每轮通信中学习到的信息较少, 抑制本地模型的学习能力.因此相比经典的基线方法[17], 许多当前的联邦学习优化算法并不能在不同的数据Non-IID设置中提供稳定的性能改进.其次, 引入共享数据集的方式虽然使各客户端学到相同的数据分布特征, 但这种方式从根本上违背联邦学习分布式训练以及保护客户端本地数据隐私的初衷.

在集中训练范式中, 网络的泛化能力已得到较好研究[18], 目的是对抗模型过拟合的问题.即使在训练数据和测试数据符合相似数据分布的标准设置中, 如果未采取预防措施, 模型仍会对训练数据过拟合.当训练数据和测试数据分布不同时, 这种效应会进一步增强.因此学者们引入各种正则化技术, 加强在训练过程中的学习通用性和保持适当的测试性能.同样, 在联邦学习中, 客户端本地数据分布存在异质性, 导致局部模型更新过程中产生相互冲突的优化目标, 降低整体的模型性能.因此, 在存在数据异构性时, 提高模型的通用性应是主要关注的问题之一.在训练期间提高本地学习模型的通用性将缓解本地客户端模型受异质数据的影响程度, 使客户端的优化目标更接近整体的优化目标.

受模型正则化方法[19]的启发, 本文考虑降低联邦学习中异质数据分布带来的影响, 提出基于结构增强的异质数据联邦学习模型正则优化算法(Regularization Optimization Algorithm for Heterogeneous Data Federated Learning Model Based on Structure Enhancement, FedSER).在客户端利用异质的本地数据进行训练时, 以结构化的方式采样子网络.使用不同的增强数据训练不同的子网络学习增强表示, 促进本地模型的通用性, 得到的客户端模型具有更强的泛化性能, 可对抗本地数据异质带来的客户端漂移问题, 从而提升全局聚合模型的性能.在各种联邦设置的多个数据集上的实验表明, FedSER可达到较优的全局模型精度.

1 相关工作

联邦学习是一种分布式机器学习范式, 可在不泄露数据隐私的情况下协作多方客户端进行机器学习模型的训练.FedAvg(Federated Averaging)[17]是联邦学习提出的最初解决方案, 其思想是在服务器端生成初始化的全局模型并下发给各个客户端节点, 客户端节点利用全局模型初始化自己的本地模型, 并使用随机梯度下降算法(Stochastic Gradient Descent, SGD)在本地数据集上进行多个轮次的迭代训练, 各客户端基于本地数据集训练的本地模型上传给服务器端节点, 服务器端根据各客户端数据量大小对本地模型加权平均, 聚合新的全局模型.然而在现实场景中, 参与联邦训练的客户端节点可能是不同的用户设备或机构[20], 由于用户使用习惯不同或机构用户群体不同等原因, 客户端上的本地数据存在数据Non-IID的情况.Li等[6]通过实验证实传统的FedAvg在数据Non-IID下面临全局模型收敛缓慢、模型性能偏离最优解等问题.

为了解决联邦学习中由于数据Non-IID导致的全局模型精度下降问题, 现有研究工作[21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31]可大致总结为两个方向:1)通过数据增强的方式, 对客户端节点的本地数据集进行数据增强, 或通过部分共享数据集, 降低数据分布之间的异质程度.2)通过对训练过程添加约束, 限制客户端本地模型与全局模型相差过大.Yoon等[16]提出FedMix, 通过一种现象级但简单的数据增强方法Mixup[25], 对异质的本地数据进行数据增强, 不需要在设备之间直接共享本地原始数据, 在数据高度Non-IID的联邦设置下, FedMix在联邦学习的基准数据集上表现出显著的改进性能.Collins等[15]为了缓解不同本地数据分布的异质程度, 提出FedRep, 对每个客户端上的本地数据进行特征映射, 将映射结果上传服务器, 由服务器整合映射结果, 将整合后的结果再下发给各客户端, 客户端在执行本地模型更新时, 先基于公共的数据映射数据集进行训练, 再基于其本地数据集进行训练.

然而, 通过节点间共享数据映射缓解数据异质性程度的方法仍在本质上暴露本地的数据特征, 存在隐私泄露的风险.Li等[7]提出FedProx, 在本地训练过程中增加本地模型与全局模型之间的约束, 构建本地模型与全局模型的差异作为惩罚项约束, 并加入本地模型训练的损失函数中, 使本地模型与全局模型更接近, 缓解本地模型的漂移问题, 得到聚合性能更好的全局模型.Gao等[9]提出FedDC, 使用局部漂移变量, 弥补局部模型与全局模型之间的差异, 在参数水平施加一致性约束.Li等[26]提出MOON(Model Contrastive Federated Learning), 为了处理客户端之间数据分布的异构性, 利用模型间的相似性, 采用对比学习[27]的方法, 将局部模型尽可能相似于全局模型, 缩小与上一轮训练中局部模型的相似性, 以此限制局部客户端模型的优化方向, 与全局模型更一致, 解决客户端之间的数据分布异构问题.

然而上述方法未考虑各个客户端异构性的数据分布, 直接强制本地模型与全局模型趋同, 虽然在一定程度上抑制本地模型漂移, 但也客观限制本地模型的学习能力, 不具有较好的通用性.

深度神经网络在训练中容易出现对训练样本过拟合的情况, 导致训练的模型泛化能力不佳.通常采用对训练样本进行数据增强或在网络梯度中添加噪声等方式以缓解过拟合现象[32], 提高训练模型的通用性.梯度增强[19]是一种对深度神经网络进行正则化的方法, 通过网络本身产生有意义的梯度偏差, 而不仅仅是添加随机噪声.假设训练样本为一幅图像, 一个具有良好通用性的网络应对其随机变换(如随机旋转、随机裁剪等)后的图像识别为同一图像.梯度增强利用变换的训练样本对一组子网络的表示进行正则化, 这些子网络是根据网络宽度(即每层的信道数)从整个网络中随机采样, 子网络以权重共享的方式进行训练, 完成后得到最终的全网络表示.通过子网络从不同的转换中学到不同的表示, 得到泛化性更好、通用性更强的全网络表示.

现有的直接对客户端更新加以限制的方法虽然减轻客户端漂移的程度, 使本地更新更接近于全局模型, 但也阻碍本地模型充分学习少量异构甚至同质数据的能力.对于本地客户端数据分布异质性未知的联邦学习来说, 限制本地模型的学习能力并不理想.

2 基于结构增强的异质数据联邦学习模型正则优化算法
2.1 算法框架

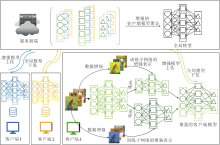
本文提出基于结构增强的异质数据联邦学习模型正则优化算法(FedSER), 整体框架如图1所示.FedSER包括客户端模型更新和服务器聚合两部分.服务器负责协调整个联邦训练过程中模型的分发和聚合, 客户端基于本地数据更新本地模型.为了缓解客户端模型漂移问题, 采用模型结构化增强的方式训练本地模型.

图1 FedSER框架图Fig.1 Framework of FedSER

2.2 问题定义

联邦学习不同于传统分布式机器学习集中收集数据的工作模式, 其数据产生于客户端本地, 不同客户端的本地数据集之间的数据分布通常服从Non-IID.FedSER的目的是缓解由于不同客户端本地数据分布异质导致的客户端模型漂移问题, 得到聚合后性能有所保证的全局模型.

定义 Non-IID 分别从客户端i、 j中抽取服从分布(x, y)~Pi(x, y)和(x, y)~Pj(x, y)的数据样本, 如果

Pi(x, y)≠ Pj(x, y),

称客户端i和客户端j的本地数据是服从Non-IID.

在客户端本地数据服从Non-IID的情况下, 传统的联邦学习算法往往面临模型精度损失的问题.每个客户端在自己的本地数据上训练模型, 优化各自的局部目标, 假设参与联邦学习的每个客户端k上拥有本地数据集Dk, 数据样本个数为nk, 则第k个客户端的经验损失函数为:

fk(θ )= Ε(x, y)~Dk[lk(θ ; (x, y))],

其中, (x, y)~Dk表示客户端k上的数据集服从数据分布Dk, θ 表示神经网络参数, lk通常表示交叉熵损失.然而, 由于不同客户端上的数据服从Non-IID, 即

Di(x, y)≠ Dj(x, y),

客户端上的局部收敛点不能较好地符合全局模型的目标, 因此, 客户端模型偏离理想的全局优化点, 过拟合其局部目标.若最终目标是优化如下函数:

arg minθ[F(θ )∶ = ∑k∈K( nknfk(θ )]],

其中, F(θ )表示全局损失函数, fk(θ )表示客户端k的损失函数, n表示全部样本数量, nk表示客户端k的样本数量, 则当产生客户端漂移现象时, 全局聚合模型的性能会受到影响.

2.3 本地模型结构增强

面对由于不同客户端上Non-IID数据带来的全局模型精度损失问题, 本文提出利用子网络梯度增强的方法, 对客户端模型进行结构正则化训练, 得到通用性更强的客户端模型, 抵抗异质的局部数据分布带来的局部客户端漂移问题.具体来说, 为了得到泛化效果更优的局部模型, 训练本地模型时, 先基于本地数据对局部模型进行训练后, 对局部模型的全网络按结构采样不同的子网络, 再使用经过增强变换的数据样本对子网络重新训练, 重新训练的子网络可以学到变换后的表示.这样, 更大的子网络总是以权重共享的方式训练更小的子网络, 因此可利用在更小的子网络中学到的表示.经过多轮迭代训练, 得到具有多样化表示的完整网络.

子网络通过网络宽度这种结构化的方式采样.令客户端全网络模型参数为θ , 全网络中一层的模型参数为θ l, 以卷积层举例, θ l∈ Rc1×c2×k×k.其中, l表示模型层, c1表示输入的通道数, c2表示输出的通道数, k表示卷积核的大小.采样子网络的宽度ω ∈ [α , 1.0], 其中α 表示采样宽度的下界.子网络的参数为θ ω , 则子网络的宽度为全网络宽度的ω × 100%, 子网络相对应层的模型参数 θlω∈ Rωc1×ωc2×k×k.

在每次迭代训练中, 使用原始数据训练全网络, 这与常规训练过程相同.再对n个子网络进行采样, 其中n表示采样子网络的个数.使用经过增强变换的数据对子网络进行训练, 使子网络学到更通用的增强数据表示.最后利用累积全网络和子网络的损失更新模型的权值.客户端模型的损失函数定义为

L=LCE(Fθ (x), y)+μ ∑i=1nLKD( Fθwi(Ti(x)), Fθ (x)),

其中, Fθ 表示全网络模型, Fθωi表示采样宽度为ω i的子网络, Ti(· )表示对输入执行的变换操作(如分辨率缩放), μ 表示n个子网络上的交叉熵损失LCE和KL散度损失LKD求和之间的平衡参数.每个子网络的宽度ω i是从下界α 和1.0(全宽)之间的均匀分布中采样.本地客户端模型结构增强算法的伪代码如算法1所示.

算法1 客户端模型结构增强算法

输入 全局网络模型F(θ ), 训练样本{x, y},

随机变换T, 子网络个数n,

子网络宽度下界α

输出 本地模型Fk(θ )

function ClientRegularization(Fk(θ ), x)

训练全网络

前向传播:outputf=Fθ (x)

计算损失:lossf=criterion(output, y)

正则化子网络

for 子网络i 从1 ~ n

采样子网络:subneti=Sample(Fθ , α )

固定批归一化层的均值和方差

使用经过变换的训练样本进行前向传播:

outputi=subneti(Ti(x))

使用软标签outputf计算子网络的损失:

lossi=criterion(outputi, outputf)

end for

计算总损失:L=lossf+ ∑i=1nlossi

计算梯度, 反向传播

end function

以这种结构正则化方式训练的增强客户端模型会具有更好的模型通用性, 对于联邦学习中不同客户端上数据分布异质的场景, 客户端模型的通用性更强意味着模型对异质的数据分布具有一定的鲁棒性, 缓解客户端模型的漂移现象, 在全局模型聚合时可得到聚合后性能更优的全局模型.另外, 子网络的训练是通过增强之后的数据, 使用数据增强的方式训练子网络, 可在一定程度上平衡不同节点间数据分布的差异, 提高最终模型的表现.

2.4 联邦客户端正则优化算法

基于上述的本地模型结构增强的优化方法, 本文面向联邦学习中的数据异质性场景, 提出FedSER.FedSER设计为一种基于FedAvg的简单有效的方法, 旨在局部训练中得到泛化性更强的客户端模型, 抵抗由于本地异质数据分布带来的客户端模型漂移现象, 缓解全局模型聚合时的性能下降程度.

正式训练前, 在服务器端进行全局模型参数的初始化, 并下发给所有的客户端, 对其本地模型进行初始化.参与联邦训练的客户端首先基于本地数据集完成一轮前向传播, 再根据网络宽度随机采样n个子网络, 由随机变换后的增强样本对每个子网络进行表示增强的训练, 完成本地模型的正则优化, 上传本轮更新的模型梯度给服务器, 由服务器聚合全部更新的本地模型, 完成全局模型的更新, 不断迭代, 直至达到全局模型收敛.

FedSER具体步骤如算法2所示.

算法 2 FedSER

输入 联邦通讯轮次T, 客户端本地的批大小B,

每轮参与通讯的客户端数量K,

客户端本地更新轮次E, 学习率η

输出 全局联邦模型θ global

服务器端执行

初始化联邦模型 θglobal0

for 轮次t 从 0 ~ T - 1

将全局模型参数θ global传给每个客户端k

for 客户端k∈ K

客户端更新: θkt← ClientUpdate(k, θ t)

end for

全局模型更新: θglobalt+1← ∑k=1K( nkθktn)

end for

return θ global

客户端执行

使用全局模型参数θ 初始化本地模型θ k

for 迭代次数 e 从0 ~ E -1

for 每个本地数据集批次b={x, y}

Fk(θ )← ClientRegularization(Fk(θ ), x)

end for

将Fk(θ )回传到服务器

end for

由于FedSER对FedAvg只进行轻量级修改, 在本地模型训练过程中对模型进行结构化正则训练操作, 使得到的本地模型对异质数据具有更好的通用性.FedSER对于联邦聚合方面未有所改动, 因此可轻松集成其它基于服务器端聚合时优化的算法, 实现优化方法的即插即用.

3 实验及结果分析
3.1 实验数据集

本文在CIFAR-10、CIFAR-100、ImageNet-200这3个联邦学习常用的数据集上进行实验.CIFAR-10数据集包含10类, 50 000个训练样本和10 000个测试样本.CIFAR-100数据集包含100类, 50 000个训练样本和10 000个测试样本.ImageNet-200数据集包含200类, 每类有500个训练样本、50个验证样本和50个测试样本.

在CIFAR-10数据集上, 采用卷积神经网络(Convolutional Neural Network, CNN)作为基础的编码器, 包括2个5× 5的卷积层, 2× 2的最大池化层以及2个全连接层, 以ReLU函数作为激活函数.

在CIFAR-100数据集上, 采用ResNet-50作为基础的编码器.

对于所有的数据集, 采用两层的MLP(Multi-layer Perceptron)作为映射头, 映射头的输出维度默认设置为256.为了公平起见, 所有的对比算法和FedSER采用相同的模型架构.

3.2 实验环境

本文选用如下对比算法:FedProx[7], FedDC[9], FedMix[16], FedAvg[17], MOON[26].评价指标采用准确率(Accuracy).

采用狄利克雷分布生成类间的Non-IID数据划分, 设有C个类别标签, K个客户端, 每个类别标签的样本按不同比例划分在不同的客户端上.设矩阵X∈ Rc× k表示类别标签分布矩阵, 其行向量xc∈ Rk表示类别c在不同客户端上的概率分布向量, 该随机向量在服从的狄利克雷分布pc~Dir(β )中采样, 使客户端k上c类实例数的比例为pc, k, 其中, Dir(β )表示具有浓度参数为β 的狄利克雷分布(β 默认为0.5).基于上述划分策略, 每个客户端在一些类上可能只有少量数据或无数据.将客户端数量默认设置为10, 每类在各个客户端上的数据分布可视化如图2所示.

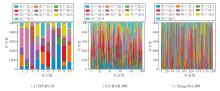图2 使用Non-IID(β =0.5)划分的每个客户端上的数据分布可视化结果Fig.2 Visualization of Non-IID data distribution on each client(β =0.5)

实验平台为4个RTX-2080Ti GPU, 采用PyTorch作为机器学习训练库.对所有算法采用SGD优化器, 学习率设为0.01, SGD的权值衰减设置为0.000 01, 动量设置为0.9.

3.3 不同算法性能分析

对于FedProx、MOON和FedSER, 均有超参数μ 平衡其增加的损失项, 因此对所有算法都采取最优μ 值, FedProx中μ =0.000 1, MOON中μ =1.0, FedSER中μ =1.75.在FedSER中, 采样子网络的个数n=2, 采样宽度下界α =0.8.

各算法在3个数据集上的准确率对比如表1所示, 表中C=16表示客户端数量为16,

C=64× 0.25(100)

表示客户端总数为64, 每次选取25%的客户端参与训练, 总通讯轮次为100.

表1 各算法在3个数据集上的准确率对比 Table 1 Accuracy comparison of different algorithms on 3 datasets

由表1可见, 在具有数据异质的联邦场景下, FedAvg准确率最低, 每种对模型加以正则优化的方法都能在一定程度上缓解数据异质性带来的精度损失问题.特别地, FedSER在每个数据集上都性能最佳.在CIFAR-10数据集上, 当客户端数量为16时, 相比FedAvg, FedSER有2.9%的准确率提升, 相比性能表现次佳的MOON, FedSER也有1.7%的准确率提升.当随机采样64个客户端中的25%参与联邦训练时, 相比表现次优的FedMix, FedSER有3.3%的准确率提升.

在CIFAR100数据集上, 客户端数量设置为16时, 相比性能次优的MOON, FedSER提升1.7%的准确率.在客户端数量为32时, 相比表现次优的FedMix, FedSER提升1.8%的准确率.在ImageNet-200数据集上, 相比在两种设置下均为表现次佳的MOON, FedSER仍有约2%的准确率提升.这是由于直接对客户端更新加以限制的方法虽然减轻客户端漂移的程度, 使本地更新更接近于全局模型, 但也阻碍本地模型充分学习少量异构甚至同质数据的能力.

在数据Non-IID的设置下对所有算法进行性能对比分析.随着数据异质性程度的降低, 客户端漂移带来的影响应变得不那么显著, 在CIFAR-100数据集上对比各算法的准确率, 具体如表2所示.由表可见, 所有算法在非数据异质性下性能均有所提升, 但相比Non-IID数据下的实验结果, FedProx、MOON和FedMix在没有数据异质的情况下性能提升是有限的, 只有1%~2%的准确率提升, 而FedSER在两种设置下准确率提升约3.8%.这是由于FedProx等在优化本地模型时强制其与全局模型的优化方向接近, 阻碍本地模型充分学习少量异质数据甚至同质数据分布的能力.而FedSER从结构而非数据的角度进行优化, 使本地模型学习到的表示更通用, 从而缓解数据异质带来的影响, 因此具有更好的泛化性和通用性.

表2 各算法在CIFAR-100测试集上的准确率对比 Table 2 Accuracy comparison of different algorithms on CIFAR-100 test set
3.4 消融实验

首先分析不同的数据异质性程度对算法性能的影响.选取客户端的数量为16时, 在CIFAR-100数据集上, 具体消融实验结果如表3所示.

表3 数据异质性程度不同时的准确率对比 Table 3 Accuracy comparison of 6 algorithms with different degrees of data heterogeneity

所有实验参数设置与3.3节实验设置相同, 只有数据分布Dir(β )有所改变, β 值越小表示数据分布的异质性越强.从表3中结果可看出, 在不同数据异质性设置下, FedSER具有稳定的最优性能, 有较明显的精度提升, 并且随数据同质性增强, 精度提升最明显.

下面分析每轮通信中不同的本地迭代次数对算法性能的影响.设置每轮通信中本地迭代次数E=10, 20, 30.在CIFAR-100数据集上, 各算法的准确率对比如表4所示.由表可见, 随着每轮中E的增加, 大部分算法性能均有所提升, FedProx在E=20时表现最佳.FedSER在不同的本地训练轮次中的实验结果均最优, 说明FedSER带来的全局模型性能提升在不同的联邦场景的设置下具有一定的鲁棒性.

表4 本地训练轮次不同时的准确率对比 Table 4 Accuracy comparison of 6 algorithms with different local training epochs

需要指出的是, 每轮通信中在本地训练的轮次越多, 越能使模型学到更多知识, 越能提升性能.但在联邦学习中, 客户端往往是计算和存储资源有限的边缘, 一味通过增加本地训练轮次的方法以提升模型性能会导致客户端的计算代价急剧上升, 违背联邦学习的资源约束限制, 并且通过这种方式带来的性能提升是有限的.

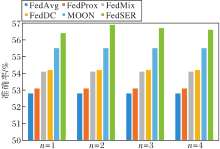
最后, 分析本地模型正则化时采样不同的子网络个数对算法性能的影响, 当采样子网络的个数n=1, 2, 3, 4时, 在CIFAR-100数据集上选取16个参与客户端, 各算法准确率对比如图3所示.子网络个数选取不同主要影响客户端模型经过不同子网络增强训练后的泛化程度, 实验结果表明选取不同的子网络个数都可在不同程度上提升算法性能.在n=2时, 算法性能最佳, 这是因为当采样子网络个数过少时, 对客户端模型的正则优化不够, 客户端漂移现象仍然存在; 当子网络个数过多时, 会导致优化后的客户端模型泛化性更强, 但不能充分学习本地数据分布特征.因此, n=2是一个综合性能更优的选择, 既通过子网络的增强训练避免客户端的漂移, 又能较好地拟合本地数据分布, 得到总体性能最优的模型性能.

图3 子网络个数不同时的准确率对比Fig.3 Accuracy comparison of 6 algorithms with different number of subnetworks

4 结束语

本文面向联邦学习中由于数据异质性带来的全局模型性能损失问题, 提出基于结构增强的异质数据联邦学习模型正则优化算法(FedSER).基于本地模型结构正则化的方法, 在客户端利用异质的本地数据进行训练时, 以结构化的方式采样子网络, 使用不同的增强数据训练不同的子网络学习增强表示, 促进本地模型的通用性, 得到的客户端模型具有更强的泛化性, 可对抗本地数据异质带来的客户端漂移现象, 提升全局聚合模型的性能.FedSER是在客户端层面做出的改进, 今后将考虑结合联邦学习中的通信资源约束, 在全局模型聚合层面上做出优化和探索.

本文责任编委 吴 飞

Recommended by Associate Editor WU Fei

参考文献
[1] KAIROUZ P, MCMAHAN H B, AVENT B, et al. Advances and Open Problems in Federated Learning[J/OL]. [2023-06-20]. https://arxiv.org/abs/1912.04977. [本文引用:1]
[2] BANABILAH S, ALOQAILY M, ALSAYED E, et al. Federated Learning Review: Fundamentals, Enabling Technologies, and Fu-ture Applications. Information Processing and Management, 2022, 59(6). DOI: 10.1016/j.ipm.2022.103061. [本文引用:1]
[3] LI T, SAHU A K, TALWALKAR A, et al. Federated Learning: Challenges, Methods, and Future Directions. IEEE Signal Proce-ssing Magazine, 2020, 37(3): 50-60. [本文引用:1]
[4] ZHU H Y, XU J J, LIU S Q, et al. Federated Learning on Non-IID Data: A Survey. Neurocomputing, 2021, 465: 371-390. [本文引用:1]
[5] ZHANG L, SHEN L, DING L, et al. Fine-Tuning Global Model via Data-Free Knowledge Distillation for Non-IID Federated Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 10164-10173. [本文引用:1]
[6] LI Q B, DIAO Y Q, CHEN Q, et al. Federated Learning on Non-IID Data Silos: An Experimental Study // Proc of the IEEE 38th International Conference on Data Engineering. Washington, USA: IEEE, 2022: 965-978. [本文引用:2]
[7] LI T, SAHU A K, ZAHEER M, etal. Federated Optimization in Heterogeneous Networks[C/OL]. [2023-06-20]. hhttps://arxiv.org/abs/1812.06127. [本文引用:3]
[8] KARIMIREDDY S P, KALE S, MOHRI M, et al. SCAFFOLD: Stochastic Controlled Averaging for Federated Learning[C/OL]. [2023-06-20]. https://arxiv.org/pdf/1910.06378.pdf. [本文引用:1]
[9] GAO L, FU H Z, LI L, et al. FedDC: Federated Learning with Non-IID Data via Local Drift Decoupling and Correction // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 10102-10111. [本文引用:3]
[10] HSU T M H, QI H, BROWN M. Federated Visual Classification with Real-World Data Distribution // Proc of the 16th European Conference on Computer Vision. Berlin, Germany: Springer, 2020: 76-92. [本文引用:1]
[11] WANG J Y, LIU Q, LIANG H, et al. Tackling the Objective Inconsistency Problem in Heterogeneous Federated Optimization // Proc of the 34th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2020: 7611-7623. [本文引用:1]
[12] WANG H, YUROCHKIN M, SUN Y K, et al. Federated Learning with Matched Averaging[C/OL]. [2023-06-20]. https://arxiv.org/abs/2002.06440. [本文引用:1]
[13] HSU T M H, QI H, BROWN M. Measuring the Effects of Non-identical Data Distribution for Federated Visual Classification[C/OL]. [2023-06-20]. https://arxiv.org/pdf/1909.06335.pdf. [本文引用:1]
[14] LUO M, CHEN F, HU D P, et al. No Fear of Heterogeneity: Classifier Calibration for Federated Learning with Non-IID Data[C/OL]. [2023-06-20]. https://arxiv.org/pdf/2106.05001.pdf. [本文引用:1]
[15] COLLINS L, HASSANI H, MOKHTARI A, et al. Exploiting Shared Representations for Personalized Federated Learning[C/OL]. [2023-06-20]. https://arxiv.org/pdf/2102.07078.pdf. [本文引用:2]
[16] YOON T, SHIN S, HWANG S J, et al. FedMix: Approximation of Mixup under Mean Augmented Federated Learning[C/OL]. [2023-06-20]. https://arxiv.org/abs/2107.00233. [本文引用:3]
[17] MCMAHAN H B, MOORE E, RAMAGE D, et al. Communication-Efficient Learning of deep networks from Decentralized Data[C/OL]. [2023-06-20]. https://arxiv.org/pdf/1602.05629.pdf. [本文引用:3]
[18] LI L, GAO K, CAO J, et al. Progressive Domain Expansion Network for Single Domain Generalization // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 224-233. [本文引用:1]
[19] YANG T, ZHU S, CHEN C. GradAug: A New Regularization Method for Deep Neural Networks[C/OL]. [2023-06-20]. https://arxiv.org/abs/2006.07989v2. [本文引用:2]
[20] YANG Q, LIU Y, CHEN T J, et al. Federated Machine Learning: Concept and Applications. ACM Transactions on Intelligent Systems and Technology, 2019, 10(2). DOI: 10.1145/3298981. [本文引用:1]
[21] HUANG W K, YE M, DU B. Learn from Others and Be Yourself in Heterogeneous Federated Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 10133-10143. [本文引用:1]
[22] OH S, PARK J, JEONG E, et al. Mix2FLD: Downlink Federated Learning after Uplink Federated Distillation with Two-Way Mixup. IEEE Communications Letters, 2020, 24(10): 2211-2215. [本文引用:1]
[23] RAMÉ A, SUN R, CORD M. MixMo: Mixing Multiple Inputs for Multiple Outputs via Deep Subnetworks // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2021: 803-813. [本文引用:1]
[24] YUN S, HAN D, CHUN S, et al. CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features // Proc of the IEEE/CVF International Conference on Computer Vision. Wa-shington, USA: IEEE, 2019: 6022-6031. [本文引用:1]
[25] ZHANG H Y, CISSE M, DAUPHIN Y N, et al. Mixup: Beyond Empirical Risk Management[C/OL]. [2023-06-20]. https://arxiv.org/abs/1710.09412. [本文引用:2]
[26] LI Q B, HE B S, SONG D. Model-Contrastive Federated Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pat-tern Recognition. Washington, USA: IEEE, 2021: 10708-10717. [本文引用:3]
[27] CHEN T, KORNBLITH S, NOROUZI M, et al. A Simple Framework for Contrastive Learning of Visual Representations // Proc of the 37th International Conference on Machine Learning. San Diego, USA: JMLR, 2020: 1597-1607. [本文引用:2]
[28] ELAYAN H, ALOQAILY M, GUIZANI M. Deep Federated Learning for IoT-Based Decentralized Healthcare Systems // Proc of the International Wireless Communications and Mobile Computing. Washington, USA: IEEE, 2021: 105-109. [本文引用:1]
[29] FRABONI Y, VIDAL R, KAMENI L, et al. Clustered Sampling: Low-Variance and Improved Representativity for Clients Selection in Federated Learning[C/OL]. [2023-06-20]. https://arxiv.org/abs/2105.05883. . [本文引用:1]
[30] CHEN M Z, SHLEZINGER N, POOR H V, et al. Communication-Efficient Federated Learning. Proceedings of the National Academy of Sciences, 2021, 118(17). DOI: 10.1073/pnas.202478911. [本文引用:1]
[31] CHENG A D, WANG P S, ZHANG X S, et al. Differentially Private Federated Learning with Local Regularization and Sparsification // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 10112-10121. [本文引用:1]
[32] QIAO F C, PENG X. Uncertainty-Guided Model Generalization to Unseen Domains // Proc of the IEEE/CVF Conference on Compu-ter Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 6786-6796. [本文引用:1]