陈恩红,博士,教授,主要研究方向为机器学习、数据挖掘、社会网络、个性化推荐系统.E-mail:cheneh@ustc.edu.cn.
作者简介:
刘子瑞,硕士研究生,主要研究方向为数据挖掘、智慧教育.E-mail:liuzirui@mail.ustc.edu.cn. 
吴金泽,硕士,工程师,主要研究方向为自然语言处理、智慧教育、联邦学习.E-mail:hxwjz@mail.ustc.edu.cn.

姚方舟,博士研究生,主要研究方向为教育数据挖掘、数据采样.E-mail:fangzhouyao@mail.ustc.edu.cn.

刘淇,博士,教授,主要研究方向为数据挖掘、知识发现、机器学习方法及其应用.E-mail:qiliuql@ustc.edu.cn.

沙晶,硕士,工程师,主要研究方向为自然语言处理、智慧教育.E-mail:jingsha@iflytek.com.

王士进,博士,高级工程师,主要研究方向为语音技术、自然语言处理、智慧教育.E-mail:sjwang3@iflytek.com.

苏喻,博士研究生,副教授,主要研究方向为数据挖掘、图像识别.E-mail:yusu@hfnu.edu.cn.
计算机自适应测验旨在根据学生历史表现为学生选择合适的题目,快速有效地测量学生的真实能力.然而在智能教育场景下,现有自适应测验策略仍存在目标复杂和知识稀疏等问题.为此,文中构建用于智能场景的可精准测评学生知识能力的面向序列诊断的强化计算机自适应测验方法,包括基于序列诊断的学生模拟器和学生画像模型,并针对真实场景中自适应测验的目标复杂性,设计薄弱点准确率、预测表现耦合、自适应测验时长、测验异常率和测验的难度结构这5个评价指标.进一步地,提出基于强化学习的计算机自适应测验选题策略,利用双通道自注意力学习及矛盾学习模块缓解知识稀疏的问题.真实数据上的实验表明,文中选题策略不仅可高效测量学生真实能力,还可优化学生的作答体验,同时选择的题目也具有一定的可解释性,从而为智能教育场景下的计算机自适应测验提供一个可行方案.
CHEN Enhong, Ph.D., professor. His research interests in-clude machine learning, data mining, social network and personalized recommender system.
About Author:
LIU Zirui, Master student. His research interests include data mining and intelligent education.
WU Jinze, Master, engineer. His research interests include natural language processing, intelligent education and federated learning.
YAO Fangzhou, Ph.D.candidate. Her re-search interests include educational data mi-ning and data sampling.
LIU Qi, Ph.D., professor. His research inte-rests include data mining, knowledge disco-very, machine learning method and application.
SHA Jing, Master, engineer. His research interests include natural language processing and intelligent education.
WANG Shijin, Ph.D., senior engineer. His research interests include speech techno-logy, natural language processing and intelli-gent education.
SU Yu, Ph.D. candidate, associate professor. His research interests include data mining and image identification.
Computerized adaptive testing is designed to select appropriate questions for students based on their historical performance, thereby measuring their actual ability quickly and effectively. However, in intelligent education scenarios, the existing selection strategy of traditional computerized adaptive testing is still faced with some problems such as target complexity and knowledge sparseness. To solve these problems, a computerized adaptive testing method based on reinforcement learning for series diagnosis is proposed in this paper to accurately assess students' knowledge proficiency for intelligent scenarios. A student simulator and a student portrait model based on series diagnosis model are adopted. To address the complexity of computerized adaptive testing goals in real-world scenarios, five evaluation indicators are designed, including accuracy of weak points, coupling of prediction performance, adaptive testing duration, testing anomaly rate and testing difficulty structure. Furthermore, a selection strategy for reinforcement learning based computerized adaptive testing is proposed. The dual-channel self-attention learning module and the contradiction learning module are utilized to ameliorate knowledge sparseness problem. Experiments on real datasets show that the proposed selection strategy not only efficiently measures students' actual abilities, but also optimizes their answering experience. The selected questions exhibit a certain level of interpretability, and the method provides a feasible solution for computerized adaptive testing in intelligent education scenarios.
智能教育是通过对学生学习能力、认知水平的研究和分析, 选择合适的教育资源, 为学生量身定制教育计划与目标的教育方式[1].因此智能教育能为学生提供更丰富的教育资源以及更自由的学习环境[2].为了满足这个需求, 智能教育场景中往往需要对学生整体知识的掌握程度进行诊断, 为后续试题的推荐与学习提供依据, 因此计算机自适应测验(Computerized Adaptive Testing, CAT)[3]得到应用.CAT是个性化在线教育中一种前沿的测验方式, 其目标是高效诊断考生对于所需掌握概念的知识水平, 减少测验时间.
CAT根据对学生能力的当前估计, 为其选择最合适的题目.具体可分为两步.1)基于学生当前作答情况实时更新学生的知识状态.2)根据知识状态为每位学生自动选择合适的题目.相比传统的纸笔考试, CAT具有高效节约、施测灵活和安全性高等优势, 现已广泛用于各种标准化考试, 如GRE(Gra-duate Record Examination)[4].
然而, 现有CAT的研究主要是基于认知诊断模型进行的, 完全忽略学生作答之间的序列性.在真实的智能教育场景, 如基于智能终端或智能教育应用中, 不同能力的学生测验需求往往是不同的, 优秀的学生希望去做一些难题以提升自己, 而学习能力较一般的学生希望通过作答简单题以查漏补缺[5].如果不考虑学生以往的能力, 使用传统的自适应测验框架, 可能会使学生花费大量的时间在不必要测验的题目上, 从而大幅降低学生的积极性[6].同时, 现有自适应测验方法通常独立测验学生在某个知识概念上的掌握程度, 因此自适应测验在智能教育场景应用时面临着如下问题.
1)目标复杂.现有CAT选题策略主要目标只包括诊断模型的准确率, 然而在智能教育场景下, 模型不仅需要关注对学生能力测量的准确性, 还需要关注学生做题难度的变化趋势、学生答题的时长等会影响学生的作答体验和积极性的因素[6].
2)知识稀疏.真实的智能教育场景下知识点数量较多, 而学生做题数量有限, 大多数情况下一个章节包含的知识点数大于测试的题目数, 因此在测验中选择的知识点相比知识点总量是稀疏的.同时, 考虑到学生答题存在猜测和失误的可能, 并且每道题的难度不同, 通常仅测验一道题目无法充分判断一个知识点是否掌握.若不考虑知识点之间的关联, 在知识稀疏的场景下想要对每个知识点进行测验是不现实的.
针对上述问题, 本文主要研究在智能教育场景下的计算机自适应测验方法, 尝试建模学生作答之间的序列性, 并通过强化学习[7], 构建用于实现自适应测验选题策略的模型.具体而言, 首先提出用于智能教育场景的面向序列诊断的强化计算机自适应测验方法, 包括基于序列诊断的学生模拟器、用于诊断学生知识点掌握程度的学生画像模型以及自适应测验的选题策略.在此基础上提出包括学生画像的薄弱点准确率、预测表现耦合、自适应测验时长、测验异常率和测验的难度结构这5个针对选题策略的评价指标, 评估模型效果以及保证学生在该选题策略下的作答体验.进一步, 提出基于强化学习的计算机自适应测验(Reinforcement Learning Based CAT, RCAT)选题策略, 利用矛盾学习构建知识点之间的关联, 使用双通道性能学习以及矛盾学习的机制, 建模复杂的智能教育环境, 同时利用深度Q网络(Deep Q-Network, DQN)[8]学习选题策略, 得到一个通过估计学生的预测累计奖励值以分配题目的CAT选题策略.最后, 在学生模拟器的环境下进行大量实验, 对RCAT选题策略进行敏感性测试以及消融实验, 并从模型效果、学生作答体验等角度对其进行评估, 由此验证RCAT选题策略的有效性.
知识追踪[9]根据学生以往的答题序列, 对学生的知识掌握情况进行建模, 并预测学生对知识的掌握程度.知识追踪的定义是通过分析学生的学习记录, 预测学生的后续表现, 学习记录可包含学生回答题目的信息, 如题目的知识点、题目难度、题目类型以及题目作答正确与否.
随着在线教育的普及, 知识追踪的重要性逐渐提高.最早的知识追踪模型是贝叶斯知识追踪(Bayesian Knowledge Tracing, BKT)[10], 利用隐马尔可夫模型对学生的知识边缘状态建模.随着计算机和深度学习的快速发展, 深度神经网络能有效提取特征这一特点被认为适用于对学生复杂的认知过程建模.Piech等[11]提出DKT(Deep Knowledge Tra-cing), 利用循环神经网络(Recurrent Neural Net-works, RNN)对学生的知识状态建模.之后, Zhang等[12]提出DKVMN(Dynamic Key-Value Memory Networks), 基于记忆增强神经网络, 存储潜在的知识点, 更新学生的相关知识水平.Nakagawa等[13]提出GKT(Graph-Based Knowledge Tracing), Tong等[14]提出SKT(Structure-Based Knowledge Tracing), 分别利用图神经网络(Graph Neural Networks, GNN)对知识点中存在的图结构以及对知识追踪过程中知识点之间的影响建模.
此外, 为了在知识追踪中提高模型的深度学习能力, 有研究者将注意力机制引入知识追踪模型中, 如AKT(Attentive Knowledge Tracing)[15]、SAKT(Self AKT)[16]和CKT(Convolutional Knowledge Tracing)[17].
在一些场景中, 模型无法实时收集学生真实的交互数据, 可使用知识追踪对学生的作答记录进行序列诊断, 从而模拟不同学生的作答结果.
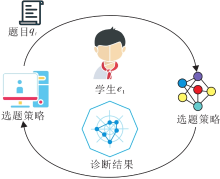
CAT分为如图1所示的两步.
1)计算机根据当前学生的能力自动从题库中选择合适的题目给学生作答.
2)在学生作答完成之后, 计算机重新诊断学生的能力水平.两步交替进行, 直至达到某个预先设定好的终止规则为止[3].
CAT的系统构建一般包括如下步骤:题库建设、选题策略、被试特质水平估计和测验终止规则[18].选题策略是自适应测验中最重要的一步, 目标是选出对学生测验最有价值的题目.下面将介绍几种较有效的选题策略.
最早提出的一种选题策略是:若学生答对当前题目, 为其分配一个更难的题目; 若学生答错当前题目, 为其分配一个相对简单的题目.然而这种“ 量身定制式测验” [19]的选题策略只考虑试题难度和学生的匹配程度, 未考虑学生的测验效率还受题目的区分度和猜测参数影响, 于是Lord[20]提出MIC(Maxi-mum Information Criterion)选题策略.MIC选题策略会选择当前学生能力估计值下具有最大信息量的题目.信息量的度量方式也有很多种, 较著名的是Fisher信息量和基于KL散度的平均全域信息量[21].
随着计算机的快速发展, 对学生能力的诊断方式逐渐呈现多样化和复杂化, 简单的选题策略无法高效判断作答题目对学生能力诊断的有效性.因此很多研究致力于将深度学习融入CAT的选题策略中.
借鉴主动学习思想, Bi等[22]提出MAAT(Model-Agnostic Adaptive Testing), 提供对任何一种学生能力诊断方式都可行的选题方案, 这种选题策略并不基于神经网络的训练.而BOBCAT(Bilevel Optimiza- tion-Based CAT)[23]和NCAT(Neural CAT)[24]是完全由模型选择题目的自适应测验框架, 通过学生的答题数据对模型进行训练, 并利用模型给学生分配题目.
然而主流模型使用的评价方式是通过认知诊断模型进行的, 未考虑学生测验过程的序列性, 因此在智能教育等学生具有较长历史作答记录的场景下表现并不突出.
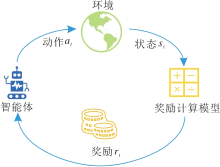
强化学习(Reinforcement Learning, RL)[7]是一种对智能体进行训练并让其按照要求进行一系列决策的机器学习方法, 工作流程如图2所示.
智能体的目标是学习一个可使预期累计奖励最大的策略.早期的强化学习是Bellman[25]提出的利用动态规划解决马尔可夫决策过程(Markov Deci-sion Process, MDP), 令MDP成为定义强化学习问题的最普遍形式.
之后, Watkins等[26]提出Q-Learning, 成为目前最广泛使用的强化学习方法之一, 但该模型存在状态数过多等问题.
随着深度学习的发展, DQN[8]利用深度卷积神经网络拟合Q函数, 为解决状态数过多这一问题提供思路.
由于计算机性能的飞速发展, 深度强化学习在各领域都有不错的表现, 如游戏AI[27], 甚至智能体可在一些领域达到和人类相当的水平, 如围棋中的AlphaGo等.
CAT是一种基于学生与电脑交互的测验方式, 从图1与图2中可看出, CAT形式上与强化学习接近.在以往的研究中, RL能在自适应测验中表现出不错性能, 但是由于难以在不同的场景下定义奖励, RL在自适应测验领域的研究并不广泛.
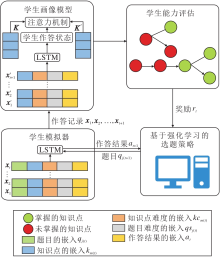
本文提出智能教育中面向序列诊断的强化计算机自适应测验方法, 整体流程如图3所示.整体模型分为学生模拟器、学生画像模型和基于强化学习的选题策略三部分.学生模拟器负责根据学生以往的表现模拟学生在自适应测验中的作答情况; 学生画像模型负责根据学生的作答结果为学生进行能力诊断; 基于强化学习的选题策略负责根据学生当前表现为学生选择合适的题目进行测验.
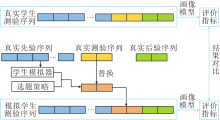
学生的在线学习通常可分为三个阶段:历史作答阶段、当前学习内容的测验阶段和巩固练习阶段.本文学生的在线学习通常以章节为阶段, 因此当前学习内容为学生当前学习的章节, 而学生的作答序列也可按照这三个阶段分别划分为先验序列、测验序列与后验序列.本文提出的自适应测验框架作用于测验阶段的序列.
如图4所示, 先验序列是学生在学习当前章节之前的作答记录, 测验序列是学生在进入当前章节后作答的少量测验题, 后验序列是学生在测验之后在这个章节下进行巩固练习的作答记录.在本文方法中, 先验序列用于训练学生模拟器, 利用训练好的学生模拟器与自适应测验选题策略产生学生模拟测验序列.真实的测验序列作为一个基线的选题策略, 与上述方法产生的模拟测验序列进行对比.后验序列用于计算学生的知识点掌握程度.可根据学生的知识点掌握程度分别评估根据真实测验序列以及模拟测验序列得到的画像模型, 基于模拟测验序列的画像模型的性能越优于基于真实测验序列的画像模型, 选题的策略越优.
在自适应测验的实验环境中, 利用选题策略为学生选择题目后, 无法直接获取学生对这些题目的作答结果.因此, 本文首先通过先验序列学习一个学生模拟器, 模拟学生对自适应测验选择题目的作答结果, 从而生成模拟测验序列.
具体地, 对于任意一位学生, 先验序列中的答题记录为x1, x2, …, xT,
xt=(qj(t), km(t), qsj(t), kcm(t), at).
其中: j(t)表示时刻t学生作答题目的编号; m(t)表示时刻t学生作答知识点的编号; qj(t)表示时刻t学生作答的题目; km(t)表示题目对应的知识点; qsj(t)=1, 2, 3, 4, 5, 表示题目对应的难度; kcm(t)=1, 2, 3, 4, 5, 表示知识点对应的难度, 难度共分为5档, 数字越大表示难度越低; at∈ {0, 1}, 表示学生回答该题目的结果, 学生答对该题目值为1, 否则值为0.对于xt中的每个参数, 使用嵌入方法将其表示为一个向量qj(t), km(t), qsj(t), kcm(t), at, 并连接为一个向量:
${{\mathbf{x}}_{\mathbf{t}}}={{\mathbf{q}}_{\mathbf{j(t)}}}\oplus {{\mathbf{k}}_{\mathbf{m(t)}}}\oplus \mathbf{q}{{\mathbf{s}}_{\mathbf{j(t)}}}\oplus \mathbf{k}{{\mathbf{c}}_{\mathbf{m(t)}}}\oplus {{\mathbf{a}}_{\mathbf{t}}}, $
加入长短记忆神经网络(Long Short-Term Memory, LSTM)[28]中,
ht, ct=LSTM(ht-1, ct-1, xt).
利用得到的隐藏状态ht作为时刻t学生能力的表征, 输出
${{o}_{t+1}}={{\mathbf{W}}^{\mathbf{T}}}({{\mathbf{h}}_{\mathbf{t}}}\oplus {{\mathbf{q}}_{\mathbf{j}(\mathbf{t+1})}}\oplus {{\mathbf{k}}_{\mathbf{m}(\mathbf{t+1})}})+b$
考虑到学生在不掌握的题目上仍可蒙对, 以及在掌握的题目上依然有做错的可能性, 因此对每个题目qi引入猜测参数gi和失误参数si, gi、si为学生模拟器中需要学习的参数.猜测参数gi表示学生未掌握题目i但答对该题目的概率, 而失误参数si表示学生掌握题目i但答错该题目的概率[29].则学生在时刻t+1能否答对题qj(t+1)的概率为:
yt+1=σ ((1-sj(t+1))ot+1+gj(t+1)ot+1).
模型损失函数为:
LR=-
学生模拟器可根据自适应测验选择的题目生成模拟测验序列, 以便学生画像模型根据作答序列对学生进行能力诊断.学生画像模型是一个知识点粒度下的模型, 目标是诊断学生对各知识点的掌握状态.与学生模拟器不同, 学生画像模型独立于学生作答的题目信息, 只包括学生作答题目的知识点, 以及知识点和题目的难度.具体而言, 模型输入为学生作答记录中的先验序列x1, x2, …, xT和模拟测验序列xT+1, xT+2, …两部分的结合, xt 定义与2.2节相同, 仍然作为学生在时刻t的作答记录, 但在嵌入连接过程中不考虑题目信息qj(t), 即
${{\mathbf{{x}'}}_{\mathbf{t}}}={{\mathbf{k}}_{\mathbf{m}(\mathbf{t})}}\oplus \mathbf{q}{{\mathbf{s}}_{\mathbf{j}(\mathbf{t})}}\oplus \mathbf{k}{{\mathbf{c}}_{\mathbf{m}(\mathbf{t})}}\oplus {{\mathbf{a}}_{\mathbf{t}}}, $
再将序列输入双层双向长短记忆神经网络(Bi-directional LSTM, Bi-LSTM):
其中,
l=1, 2,
学生的作答状态如下:
$\mathbf{state}=(\overset{\to }{\mathop{\mathbf{h}_{\mathbf{1}}^{(\mathbf{2})}}}\, , \cdots , \overset{\to }{\mathop{\mathbf{h}_{\mathbf{T}}^{(\mathbf{2})}}}\, )\oplus ((\overset{\leftarrow }{\mathop{\mathbf{h}_{\mathbf{1}}^{(\mathbf{2})}}}\, , \cdots , \overset{\leftarrow }{\mathop{\mathbf{h}_{\mathbf{T}}^{(\mathbf{2})}}}\, )).$
为了强化作答记录中相关知识点的交互关系, 在画像模型中引入注意力机制[30].具体地, 求出作答序列中已作答题目的所有知识点向量构成的矩阵:
K=(km(1), km(2), …, km(T)),
其中km(t)表示学生在时刻t作答的题目对应的知识点qj(t).当前章节ci下所有知识点的嵌入向量构成的矩阵:
K'=(k1, k2, …,
对K'、K、state使用注意力机制[30]:
state'=Attention(K', K, state),
其中, Attention函数的定义为
Attention(Q, K, V)=softmax(
Attention函数会求出矩阵Q和矩阵K的相似度, 并根据相似度将矩阵V对应的值加权求和.画像模型中使用该模块旨在学习学生已作答的题目对应的知识点与要预测的知识点之间的关联信息.
将state'和当前章节下的所有知识点向量K'以及对应的难度向量Kd'结合, 最终输出对每个知识点是否掌握的预测结果:
$p=\sigma ({{\mathbf{W}}^{\mathbf{T}}}(\mathbf{stat{e}'}\oplus (\mathbf{{K}'}+\mathbf{K{d}'}))+b)$
在后验序列中, 对于当前章节ci下每个知识点k∈
对于所有的可被观测到是否掌握的知识点, 最终的损失函数为:
${{L}_{k}}=-\sum\limits_{i=1}^{K}{{{Y}_{i}}\log p+(1-{{Y}_{i}})\log (1-p)}.$
在实际的智能教育场景中, 自适应测验在选择题目的过程中不仅要关注学生能力测验的准确性, 还要考虑学生的作答体验, 分配的题目既要符合测验的逻辑, 又不能影响学生的答题积极性.
2.4.1 学生画像的薄弱点准确率
在智能教育中, 更快找出学生未掌握的知识点能更高效地为学生提供相应的帮助, 因此正确预测一个薄弱知识点相比正确预测一个掌握的知识点更重要.因此, 本文提出学生画像模型中的薄弱点准确率.薄弱点准确率定义为被预测为学生未掌握的知识点中学生实际未掌握的知识点的比例:
Acc=
其中, FN、TN和混淆矩阵[31]中的定义相同, FN表示学生掌握的知识点中被预测为未掌握的知识点的个数, TN表示学生未掌握的知识点被预测为未掌握知识点的个数.该指标作为衡量画像模型性能的最重要指标之一, 同时也是衡量自适应测验选题策略优劣的重要指标.
2.4.2 预测表现耦合
在智能教育场景下的自适应测验中, 学生测验作答的题目不可能覆盖当前章节的所有知识点, 如果学生在一次测验中作答10道题, 答对9题, 而对学生知识点掌握程度的画像结果是学生在15个知识点上只掌握5个知识点, 这显然会影响学生的作答体验.因此本文提出预测表现耦合, 度量学生答题情况与学生能力诊断结果之间的差距.
预测表现耦合是指学生在题目上的平均作答分数和画像模型给出的已掌握知识点的占比之差的绝对值:
Dis=
其中, ci表示第i位学生测验的章节,
预测表现耦合越低, 表明学生的作答结果与学生画像给出的知识点诊断结果越接近, 学生作答体验越优.
2.4.3 自适应测验时长
在智能教育中, 测评时长是影响学生答题积极性的重要因素, 过长的作答时间会导致学生的答题积极性降低, 可能会出现随意作答的情况, 最终影响测验的效果.本文希望利用测验时长衡量模型优劣, 然而无法直接估计每位学生的测验时间, 因此本文根据题目难度、类型及教研老师的经验制定不同题目所需的作答时间表(见表1), 并使用测验的所有题目时长之和作为每位学生自适应测验的时长.
| 表1 不同难度与类型的题目的作答时长 Table 1 Response time for questions of different difficulties and types s |
2.4.4 测验异常率
过多的题目或过长的测验时间都可能影响学生的积极性, 而过少的题目或过短的测验时间会影响画像的准确性, 导致对学生能力的诊断缺乏说服力, 因此本文提出测验异常率, 规范选题策略.
本文为不同规模的章节针对测验题目和测验时间设计不同的合理范围, 如表2所示.若某位学生的答题数量和答题时长不在合理范围内, 说明测验选题策略对于该学生存在异常, 测验异常率为选题策略在所有学生测验中异常的比例:
$\begin{align} & Abnormal=1-\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\, \underset{j=1}{\overset{3}{\mathop \sum }}\, \mathbb{I}[(k{{c}_{i}}\in {{K}^{j}})\cap (nu{{m}_{i}}\in {{N}^{j}}) \\ & \cap (tim{{e}_{i}}\in {{T}^{j}})], \\ \end{align}$
其中:kci、numi、timei分别表示学生i测验章节下知识点个数、答题数量以及答题时长; Kj、Nj、Tj表示表2中情况j下的章节下知识点个数、题目范围、时长范围的范围; I[· ]表示示性函数, 当满足函数中的条件时值为1, 不满足值为0.
| 表2 不同规模的章节对应的合理测验题量与时长 Table 2 Appropriate amount of questions and time for testing corresponding to chapters of different scales |
2.4.5 测验的难度结构
良好的学生作答体验不仅需要合适的时长和题量, 还需要与学生能力匹配的试题难度.如果学生上一题作答难题答错, 下一题给它分配更难的题目, 或上一题答题答对, 下一题分配一道相对简单的题目, 都会影响学生的作答体验, 同时也会影响对学生能力诊断的效率.测验的难度结构这一指标旨在衡量选题策略选择题目的难度变化情况和学生作答情况的一致程度:
$\begin{align} & Consist=\underset{i=0}{\overset{N}{\mathop \sum }}\, \frac{1}{({{T}_{i}}-1)N}\underset{t=2}{\overset{{{T}_{i}}}{\mathop \sum }}\, {{g}_{t}}, \\ & {{g}_{t}}=\mathbb{I}[({{a}_{t-1}}=0)\cap (q{{s}_{j(t)}}\ge q{{s}_{j(t-1)}})] \\ & +\mathbb{I}[({{a}_{t-1}}=1)\cap (q{{s}_{j(t)}}\le q{{s}_{j(t-1)}})], \\ \end{align}$
其中, qsj(t)表示题目qj(t)的难度, I[· ]的定义与2.4.4节相同, 表示示性函数.当学生i在时刻t作答题目难度变化合适时, gt=1, 否则, gt=0.
经过2.4节对测试指标的说明, 智能教育场景下自适应测验目标复杂度量化问题已得到形式化的定义.本节介绍如何在智能教育场景下定义自适应测验的强化学习任务, 并提出基于强化学习的计算机自适应测验(RCAT)选题策略, 利用多目标奖励的方式对2.4节中的评价指标进行优化以解决自适应测验目标复杂的问题, 同时利用对知识点的矛盾学习缓解知识稀疏的问题.
2.5.1 自适应测验任务在强化学习中的定义
具体地, 一个强化学习任务包括< S, A, P, R> 这4个元素.S表示所有状态的集合, 在自适应测验中sT∈ S表示自适应测验选题策略为学生在时刻1, 2, …, T分配的T个题目与学生的作答情况组成的序列
$\{({{q}_{j(1)}}, {{a}_{1}}), ({{q}_{j(2)}}, {{a}_{2}}), \cdots , ({{q}_{j(T-1)}}, {{a}_{T-1}})\}$.
A表示所有动作的集合, 自适应测验中A表示题库中所有题目的集合, At为在选择t题之后, 仍可以选择的题目集合.
在状态st下执行动作qj(t)后状态变为st+1的概率为P(st+1|st, qj(t)), 即在状态st下执行动作qj(t)后, 学生i作答情况at+1的概率为P(at+1|st, qj(t)).
为了解决目标复杂的问题, 本文设计一个包括多个目标的奖励, 包括学生在状态st+1的画像准确率提升值、预测表现耦合的下降值以及学生在状态st+1时出现测验超时异常的惩罚, 即
其中:Dis(t)和2.4节的定义相同, 表示当前学生答完t题后的预测表现耦合; Punish表示分配题目总作答时间超出2.4.4节中最大合适时间的惩罚, 以保证RCAT选题策略在不同的测验题目下尽可能将选择的题目时长控制在一个合适的范围内, 从而实现学生测验题数不固定情况下的个性化自适应测验选题.
由于学生画像模型可能会判断题目作答结果较好的学生掌握该章节下所有知识点, 不存在薄弱点, 对于这样的学生, 模型将无法计算其薄弱点准确率, 因此Acc(t)设计为学生答完t题后画像模型的整体准确率, 用于近似画像的薄弱点准确率.由此, 本文可通过强化学习对2.4节提出的评价指标进行优化, 解决自适应测验目标复杂的问题, 提升学生的作答体验.
2.5.2 强化学习网络框架
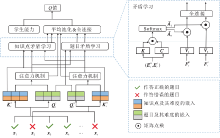
基于多目标奖励的设计, 本文提出缓解自适应测验目标复杂这一问题的方法, 然而自适应测验仍面临知识点稀疏的问题.为了解决这一问题, 基于上述强化学习的定义, 利用注意力神经网络在DQN的框架下实现自适应选题策略算法.RCAT选题策略结构如图5所示, 由NCAT[24]中提出的双通道性能学习模块、矛盾学习模块、学生答题前的能力诊断模块以及策略模块组成.RCAT选题策略首先利用双通道性能学习模块, 分别对学生答对以及答错的题目进行学习, 提取学生的表现信息.再利用矛盾学习模块提取学生答题记录中间的矛盾, 减少猜测或失误带来的影响, 同时利用知识点之间的矛盾信息缓解知识稀疏的问题.最后通过策略模块得到Q值, 并利用Q-learning优化模型.
学生在测验中可能会因为未掌握某一个知识点而答错多道题, 可认为它答错的题目间存在共性, 这些共性潜在反映学生在知识点上的掌握能力.若模型能提取这些共性信息, 可根据这些信息为学生选择更合适的试题, 从而实现个性化试题推荐.本文使用双通道自注意力学习实现这一目标.
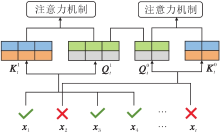
双通道自注意力学习对学生当前作答记录中答对试题和答错试题分别使用自注意力机制进行学习.双通道自注意力学习模块流程如图6所示, 对于学生的作答序列, 可将其分为答对和答错的两个序列,
将注意力机制的处理结果
矛盾学习旨在模拟学生在作答过程中存在的猜测或失误的行为.如果因为学生答对一道较难的题目就在后续分配题目的过程中给学生分配更难的题目, 而不考虑学生是否有可能因为猜测答对该题, 会导致学生的答题记录有效性降低, 从而使画像的准确性降低.此外, 学习知识点之间的矛盾信息可让模型更好地选择未测验的知识点, 有助于缓解自适应测验过程中出现的知识稀疏问题.
因此本文希望通过对题目以及知识点进行矛盾学习, 发掘学生在答题过程中出现的矛盾, 为学生推荐更合适的题目.
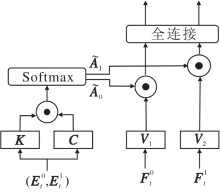
矛盾学习模块流程如图7所示, 矛盾学习使用注意力机制学习正确题目(图中
其中, m1表示已答题序列中答对题目数量, m0表示已答题序列中未答对题目的数量.
同样地, 对每个题目对应的知识点也进行矛盾学习.对
相关性越高, 说明这些题目或知识点之间越容易出现猜测或失误的现象.
对这4个矩阵的题数维度求均值, 得到矛盾学习的输出向量:
将矛盾学习中得到的向量
$\mathbf{s}=MLP(\mathbf{F}_{\mathbf{t}}^{\mathbf{q0}}\oplus \mathbf{F}_{\mathbf{t}}^{\mathbf{q1}}\oplus \mathbf{F}_{\mathbf{t}}^{\mathbf{k0}}\oplus \mathbf{F}_{\mathbf{t}}^{\mathbf{k1}}\oplus \mathbf{F}_{\mathbf{t}}^{\mathbf{v0}}\oplus \mathbf{F}_{\mathbf{t}}^{\mathbf{v1}})$.
再结合学生的能力信息h, 预测在状态st下集合At中每道题目qi的预测累计奖励Q(st, qi).令
Q(st, · )=(Q(st, q1), Q(st, q2), …, Q(st,
则预测累计奖励:
$Q({{s}_{t}}, \cdot )=MLP(\mathbf{s}\oplus \mathbf{h})$
由于题目数众多, 搜索空间非常大, 为了保证模型性能和学生的作答体验, 对选题进行如下约束.首先, 所有题目均只能被选择一次, 并且相同知识点下的题目最多只能被选择两题; 其次, 除非上一题的难度为“ 一般” , 否则, 上一题答错, 下一道题难度要低于上一题; 上一题答对, 下一道题难度要高于上一题.为了保证测验的题目难度变化不会过大, 要求选择的题目难度与上一题相比变化不能超过两级.
在学生作答完第t题后, 利用上述约束, 可从题目集合At-1中筛选满足条件的题目集合At, 选题策略将计算集合At中每道题目被选择后的预期累计奖励Q值, 并从集合At中选择可得到最大预期累计奖励的题目作为下一道测验的题目.
选题策略的学习方式是利用Q-learning进行的.具体地, 在采样过程中, 使用€ -贪婪策略, 即每次选题会以一个递减的概率€ 在集合At中随机选择一道题, 以1-€ 的概率在集合At中选择Q值最大的题目.刚开始采样时, € 趋近于1, 即完全随机抽取题目给学生作答, 随着采样轮数的增加, € 逐渐递减至0, 即完全依靠预测值Q进行题目选择.在每次采样后, 作答记录会放入内存池M 中, 并从内存池中抽取样本进行训练.损失函数为:
智能教育场景下RCAT选题策略步骤如算法1所示.
算法1 RCAT选题策略
初始化测验序列s0={};
初始学生能力h0=LSTM(XT);
初始答题数和答题时间n← 0, time← 0;
while True do
(Q0, Q1, …,
i=arg max{Q0, Q1, …, Q|A|}; //选题策略
time← time+Ti;
if Abnormal(time, n, case) then
break;
end
an, hn+1← Simu(hn, qi); //学生模拟器进行作答
sn+1← sn∪ (qi, an);
n← n+1;
end
输出 Ke← PORTRAIT(sn); //画像模型
在算法中, 学生模拟器也可被看作一位真实的学生.对于每位学生, RCAT首先通过学生模拟器为学生生成一个初始能力值.在学生每轮测验中, 学生模拟器首先将学生的能力值以及学生在当前题目的作答结果提供给选题策略.然后, 选题策略根据学生的初始能力值以及学生当前测验记录选择RCAT选题策略输出Q值最大的题目作为最合适的题目, 选题策略对该题目进行观测, 若题目量已超过测验需求的最小值, 并且该题目分配给学生会导致测验异常, 结束测验, 否则将该题目分配给学生.最后, 在学生的测验结束后, 学生模拟器和选题策略将学生的全部作答记录传输给学生画像模型, 为学生生成当前章节的能力诊断.通过这种方法, RCAT选题策略会为学生选择使画像模型更准确、学生作答体验与画像结果更接近、时间更合适、学生作答体验更优的题目.
为了验证本文方法的有效性, 使用由科大讯飞智学网系统提供的真实数据集MATH.实验数据选取学生在初中数学学科上的在线学习数据.
在预处理部分, 删除先验数据小于100条、测验数据小于5条或大于20条、后验数据小于5条的数据.同时删除测验章节下所有知识点在后验数据中出现次数都小于3条的数据, 以保证学生数据可以进行画像.为了保证测验试题的质量, 题库中删除区分度小于0.4的题目和知识点.经过筛选后, 数据集最终包含64 748条数据, 共有83个章节, 1 521个知识点, 48 157个题目, 每条数据平均包含179.35条作答记录, 平均每个章节的知识概念为18.33条, 平均每个知识概念的题目为33.34道.
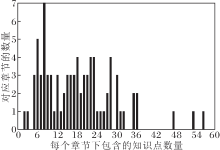
章节下知识点的数量直方图如图8所示, 由图可看出大多数的章节知识点个数都在12题以上, 一个章节最多的知识点数达到56, 而最大的合适题数为12题, 小于章节的平均知识点数, 这说明知识稀疏问题确实是一个需要考虑的问题.每个知识点平均包含33.34道题目, 说明即使在选定知识点的情况下, 仍有很多题目可选择, 因此对题目进行筛选是可行的.每个知识点下的题目众多, 想要判断一个知识点是否掌握, 选择不同的题目效率也会不同, 因此对题目进行定量筛选是有必要的.
为了验证RCAT选题策略的有效性, 选取如下基准选题策略为学生选择题目.
1)Real.真实的作答记录在学生模拟器上的结果.学生真实的作答记录训练得到的学生画像模型表示画像模型本身的性能.
2)Random.随机分配合适的题数及题目让学生模拟器进行作答, 表示最简单的CAT选题策略.
3)MAAT-R.基于规则的CAT选题策略, 使用MAAT[22]中EMC(Expected Model Change)模块, 每次筛选使模型期望变化较大的题目, 同时提出利用题目区分度筛选题目、设计知识点传播规则等方式优化MAAT知识点选择部分, 在智能教育这一特定场景下是一种有效的数据驱动策略.
在MATH数据集上, 将90%的学生数据作为训练集, 10%的学生数据作为测试集.在训练集中取出90%的学生数据进行强化学习训练, 剩下10%的学生数据进行验证, 最终利用测试集的学生在多个评价指标上评估模型.学生模拟器中题目表征设计为768维向量, 知识点表征、题目难度表征、知识点难度、答题记录表征均设计为200维向量, 先验作答记录长度为150, 激活函数使用LeakyRelu函数, 参数为0.3, 模型输出与分配的题目数相同, 为学生答对当前题目的概率.学生画像模型的所有表征也均设计为200维向量, RNN为双层双向长短记忆循环神经网络, 网络隐藏层大小为表征向量的一半, 即100维向量.网络输出大小与学生当前章节下包含的知识点数相同, 每个输出表示掌握对应知识点的概率.
在RCAT选题策略(https://github.com/Liuz-rui/RCAT)中, 题目表征设计为128维向量, 知识点表征、题目难度表征、知识点难度、答题记录表征均设计为50维向量, 使用单头注意力机制, 学生初始状态表征与学生模拟器的隐藏层均为200维向量, 隐藏层大小为512维, 学习率为0.001, 训练轮数为5 000轮.
所有实验均由Pytorch实现, 使用NVIDIA Tesla M40显卡的Linux服务器集群进行训练.
本节从自适应测验的实际应用出发, 采用在2.4节中提出的薄弱点准确率、预测表现耦合、自适应测验时长、测验异常率、测验的难度结构等评价指标, 与基础的选题策略进行对比实验.
MATH数据集上各策略的不同指标值对比如表3所示, 表中黑体数字表示最优值.由表可以看出, RCAT选题策略在学生模拟器的环境下, 大部分评价指标都高于其它策略.相比MAAT-R, RCAT选题策略在准确率上提升0.64%, 在预测表现耦合上降低11.50%, 在测验的难度结构上提升15.25%, 测验异常率降低11.53%.尽管测验时长相比真实情况中每位学生测验时间平均增加30 s, 但是异常率的降低说明真实的学生作答记录中有部分学生的答题数是不足的, RCAT选题策略的时间是在合理范围内变动的.
| 表3 各策略的5个指标值对比 Table 3 Comparison of 5 indexes among different strategies |
实验结果表明兼顾复杂目标的强化学习选题策略能够在知识稀疏的场景下更好地保障选题的效率和效果, 实现多目标的协同优化.
在强化学习中, 不同的奖励会对强化学习的结果造成较大影响, 因此对奖励函数中多个目标的权重进行超参数调优.对于RCAT, 选取不同的奖励组合进行实验, λ =0, 0.01, 0.05, 0.1, 0.2, 0.5, 超出时间的惩罚取为0.2.在 MATH数据集上λ 不同时各指标值如表4所示, 表中黑体数字表示最优值.由表可以看出, 薄弱点准确率、预测表现耦合以及自适应测验时长在不同的奖励组合下具有不同的表现, 说明不同的奖励组合对不同指标的提升存在影响.随着λ 逐渐增大, 薄弱点准确率和超时惩罚的占比逐渐降低, 薄弱点准确率、自适应测验时长和测验异常率会出现小幅下降, 但预测表现耦合有较大提升.在λ =0.2时, 预测表现耦合才达到3.2节中随机选题策略在预测表现耦合上的表现, 而当λ =0.5时, 模型在预测表现耦合上已超过基于规则的自适应测验选题策略, 达到领先地位.实验表明, 利用多目标的奖励机制, 可解决CAT在智能教育场景下目标复杂的问题.
| 表4 不同的奖励组合下的自适应测验的指标值对比 Table 4 Index value comparison of adaptive testing with different reward combinations |
为了验证RCAT选题策略每个模块的有效性, 进行消融实验.RCAT选题策略的主要奖励函数以及核心评估指标是薄弱点准确率和预测表现耦合, 因此对各模块进行消融实验时只考虑这两项指标.RCAT选题策略共包括3个模块:双通道自注意力学习(Double-Channel Self-Attention Learning)模块、题目矛盾学习(Question Contradiction Learning)模块、知识点矛盾学习(Knowledge Concept Contradiction Learning)模块, 分别记为A模块、QC模块、KC模块.分别移除这3个模块, 移除A模块记为RCAT-A, 其余同.按照与3.2节相同的实验设置进行训练与评估, 结果如表5所示, 表中黑体数字表示最优值.
| 表5 消融实验结果 Table 5 Results of ablation experiment |
由表5可见, RCAT-A仅捕捉学生作答题目或知识点表现的矛盾, 未直接利用双通道自注意力机制, 使薄弱点准确率降低以及预测表现耦合升高.RCAT-KC和RCAT-QC在直接使用双通道自注意力机制的同时, 仅使用一个矛盾学习模块, 均影响模型在薄弱点准确率和预测表现耦合上的性能.RCAT选题策略的表现在两个指标上具有领先地位, 这说明3个模块对于模型都是有效且有必要的.
如图8所示, 由于包含8个知识点的章节最多, 相对具有代表性, 本文从中随机选取一个章节, 并随机选取一名学困生、一名学中生和一名学优生, 考察三者在不同选题策略下的表现.其中, 学困生指在先验序列中答题正确率在20%至50%之间的学生, 学中生指在先验序列中答题正确率在50%至80%之间的学生, 学优生指在先验序列中答题正确率在80%以上的学生.
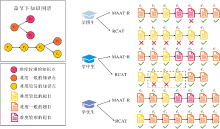
图9为3位学生在测验序列的答题记录以及该章节下知识点图谱.如图所示, RCAT选题策略为不同能力的学生分配不同难度的题目, 同时在学生给出相同作答表现后, RCAT选题策略依然可根据学生能力和学生的答题情况为学生分配不同知识点的题目, 如RCAT选题策略在学中生和学优生都答对知识点e4后为学优生分配知识点e1下的题目.这说明RCAT选题策略实现在智能教育场景下对不同能力学生的个性化选题. 而MAAT-R为学中生和学优生分配的知识点是完全相同的, 说明MAAT-R在选题时不能自适应调整知识点, 只能根据学生能力为学生从固定的知识点中选择合适的题目.
从图9中可看出, 相同学生在不同选题策略上的表现也存在不同.具体地, 对于学困生, 同样测验知识点e1, RCAT选题策略选择的题目测验学生对该知识点存在缺陷, 而MAAT-R选择的题目没有测验, 同时RCAT选题策略测验学困生知识点e4、e5、e8均未完全掌握, 而在MAAT-R中, 均未测验知识点e4、e5.这说明RCAT选题策略更能发现学生的问题, 同时这也符合本研究在2.4.1节中提出的更快找出学生未掌握的知识点这一测验目标, 因此RCAT选题策略在智能教育场景下是有效且存在优势的.
此外, RCAT选题策略在为学中生分配题目时, 先为学生分配知识点e4, 学生答对后为学生分配后继知识点e8, 当学生未答对知识点e8下的题目时, RCAT选题策略为学生选择知识点e8的前驱知识点e6, 答错之后又测验知识点e6的前驱知识点e5, 在学生答对知识点e5下的题目后, RCAT选题策略为学生分配知识点图谱上另一棵树上的知识点e1.可以看出, RCAT选题策略可实现从知识点e8到知识点e6再到知识点e5这一对答错题目的反向溯源过程, 当反向溯源搜索到知识点e5并且学生答对该知识点下的题目后, RCAT选题策略能读取该信息并判断已搜索到未掌握的知识点, 转去测验图谱中另一棵数上的知识点e1.该结果表明强化学习模型中对知识点的矛盾学习确实为模型提供知识点的关联信息, 降低智能教育场景下知识稀疏问题的影响, 也反映强化学习选题策略在智能教育场景下的优越性.
当然从测验中也可看出, RCAT选题策略仍然存在一些问题:RCAT选题策略在为学生选题的过程中, 可能会存在反复测验知识点的问题, 如在对学困生进行测验时, 第1题和第8题考查的都是知识点e5, 这会降低CAT的可解释性, 也可能会影响学生的答题体验.
本文针对智能教育场景下的CAT进行研究, 并按照CAT的流程设计面向序列诊断的强化计算机自适应测验方法.首先, 为了解决传统自适应测验无法考虑学生作答记录序列性的问题, 设计基于序列诊断的学生模拟器和诊断学生知识点掌握程度的学生画像模型.然后, 为了保证CAT结果的准确性以及学生的作答体验, 设计多种评价指标.针对这些指标, 提出基于强化学习的计算机自适应(RCAT)选题策略, 将知识点表征、题目难度表征、知识点难度表征、学生初始能力加入强化学习模型中, 并利用双通道注意力机制以及矛盾学习的机制, 缓解CAT中目标复杂以及知识稀疏的问题.最后, 在真实数据集上进行的大量实验表明, RCAT选题策略存在多个方面的优越性, 同时案例分析证实RCAT选题策略的有效性与可解释性.
本文提出的CAT框架仍存在进一步的改良空间.今后可考虑在基于强化学习的选题策略中加入更多的知识点信息, 如知识点的图谱信息等.其次, 在选题策略中设计更详细的规则, 减少反复测验同个知识点的问题.此外, 还可优化学生模拟器以及学生画像模型自身的性能.
本文责任编委 吴飞
Recommended by Associate Editor WU Fei
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|