ServeDB的工作流程遵循图1所示的基于证明的查询完整性验证框架.ServeDB使用密钥生成、验证数据结构构建、查询陷门生成、密文查询与完整性验证这5种算法描述整个工作流程.密钥生成算法与验证数据结构构建算法运行在数据拥有者侧, 在每个数据集上执行一次.数据上传、私密共享密钥与验证数据结构的密码学摘要主要涉及数据传输, 实现方式与算法无关, 因此不再进一步介绍和分析.查询陷门生成算法运行在客户端侧, 根据用户给出的明文查询范围生成密文查询陷门.密文查询算法运行在云服务器中, 根据客户端提交的查询陷门, 在验证数据结构SVETree上进行密文查询, 返回密文查询结果与完整性证明.完整性验证算法运行在客户端侧, 根据完整性证明对解密后的明文查询结果进行校验.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 基于证明的查询完整性验证框架Fig.1 Proof-based query integrity authentication framework

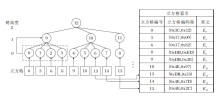
ServeDB验证数据结构SVETree的构建过程可进一步分解为图2所示的5步.首先, 立方体编码系统(Cube Coding System, CCS)生成步骤对数据集的值域空间进行从粗到细的多粒度网格划分, 划分过程如图3所示.立方体编码系统的第l层将数据集值域的每个维度均匀划分为2^l个区间, 将整个d维值域空间均匀划分为2^ld个网格(即立方体), 每个立方体覆盖特定范围内的数据记录.SVETree的立方体编码系统需要确保:每个立方体覆盖的记录数均小于等于用户给定的记录数阈值参数τ ; 如果当前层次数不能满足要求, 增加立方体编码系统层次数, 直到满足阈值要求或达到最大层次数.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 验证数据结构SVETree构建流程图Fig.2 Construction of authentication data structure SVETree

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 二维立方体编码系统网格划分过程Fig.3 Grid partitioning of two-dimensional cube encoding system

然后, 记录编码生成步骤为数据集上的每条记录, 按照立方体编码系统的网格划分方案, 计算记录在每层所属的立方体, 将所属立方体标识的哈希值作为此记录在该层的立方体编码.假设立方体编码系统共L层, 经过编码的每条记录将对应L个立方体编码.立方体编码隐藏记录的原始数据取值, 用于密文查询与完整性证明生成过程.该步骤同时对记录的明文属性进行加密, 生成密文数据记录.

验证数据结构SVETree是一棵平衡二叉树, 二叉树的每个叶节点对应数据集上的一条密文记录.平衡二叉树构建步骤将根据密文数据记录创建一棵满足上述条件的平衡二叉树结构, 并维护叶节点与密文记录的对应关系.

二叉树编码步骤为二叉树中的每个树节点生成布隆过滤器.布隆过滤器存储每个树节点覆盖的所有叶子节点对应记录的全部立方体编码.布隆过滤器用于指导密文查询与完整性证明生成.以图2中平衡二叉树结构为例, 黄色节点覆盖4个叶子节点, 分别对应密文记录R₃、R₂、R₁、R₄, 黄色节点的布隆过滤器将存储这4条记录的全部立方体编码.

最后, 验证信息生成步骤采用类似Merkle Hash Tree的方式, 自底向上地根据每个树节点的布隆过滤器内容、密文记录的数字签名与子节点的哈希签名, 为每个树节点生成哈希签名.最终二叉树根节点的哈希签名是整个验证数据结构的密码学摘要.上述生成方式保证对树节点中任意内容的篡改均会使根节点哈希签名发生变化, 从而使验证者可通过检查哈希签名以检测树节点的内容是否被篡改.

在图1的ServeDB整体工作流程中, 验证数据结构构建算法需要处理全部数据集, 执行开销与数据集规模密切相关, 密钥生成算法的执行开销仅与密钥长度相关, 查询陷门生成、密文查询、完整性验证的执行开销主要受范围查询条件与查询结果规模的影响.

因为客户端触发的查询次数较多, 因此之前的研究工作着重于降低查询过程中密文查询与完整性验证算法的执行开销, 忽略验证数据结构构建算法对整个系统的数据可扩展性的制约.如果无法在可接受的时空开销下生成验证数据结构, ServeDB将难以实现大规模数据集的密文范围查询完整性验证.

在真实数据集上的执行时间分解实验表明:验证数据结构构建过程是ServeDB处理大规模数据集的性能瓶颈所在.在真实数据集foursquare2014^[25]上运行ServeDB的完整执行流程, 保持查询范围占数据集值域空间的1‰ (随机选取5组查询, 每组查询执行5次, 查询相关步骤取平均用时), 各步骤的执行用时情况如表1所示.由表可见, ServeDB在验证数据结构构建步骤上花费的执行时间占总执行时间的99.5%, 远高于其它步骤.在更大规模的gowalla^[26]、ebird^[27]、foursquare2015^[28]数据集上, 构建验证数据结构的执行时间已超过6 h.当缩小查询范围时, ServeDB中报道的密文查询与完整性验证的时间可降至1 s以下^[19].根据表2中的实验数据推算, 假设ServeDB验证数据结构构建时间随数据集规模呈线性增长, 当数据集规模达到1亿条时, 验证数据结构的构建用时将高达60 h.

表1

Table 1

表1(Table 1)

表1 foursquare2014数据集上ServeDB工作流程各步骤执行时间 Table 1 Execution time of each step of ServeDB workflow on foursquare2014 dataset s 工作流程 执行时间 密钥生成(数据拥有者) 0.00001 验证数据结构构建(数据拥有者) 1744.4 查询陷门生成(客户端) 0.006 密文查询(云服务器) 2.9 完备性验证(客户端) 5.8

表1 foursquare2014数据集上ServeDB工作流程各步骤执行时间 Table 1 Execution time of each step of ServeDB workflow on foursquare2014 dataset s

表2

Table 2

表2(Table 2)

表2 foursquare2014数据集上验证数据结构SVETree构建过程各步骤执行时间 Table 2 Execution time of each step of SVETree construction on foursquare2014 dataset s 验证数据结构构建步骤 执行时间 立方体编码系统生成 1.1 记录编码生成 9.6 平衡二叉树构建 0.3 二叉树编码 1668.8 验证信息生成 18.7

表2 foursquare2014数据集上验证数据结构SVETree构建过程各步骤执行时间 Table 2 Execution time of each step of SVETree construction on foursquare2014 dataset s

为了发掘构建过程性能瓶颈所在, 进一步对图2中SVETree构建过程中各步骤的执行时间进行分解, 结果如表2所示.由表可见, 整个执行时间的98.3%花费在二叉树编码步骤.该步骤的主要任务是将密文记录的立方体编码插入二叉树各节点的布隆过滤器中.而插入布隆过滤器过程的99.9%的执行时间花费在根据HMAC哈希函数计算立方体编码在布隆过滤器中对应比特位置, 布隆过滤器的比特置位开销仅占0.1%.上述实验数据表明, 二叉树编码步骤是整个验证数据结构构建过程的核心性能瓶颈所在, 而该步骤的计算开销几乎全部来自HMAC哈希函数计算.

经过提取关键操作与适当简化, 二叉树编码步骤呈现算法1所示的4层循环结构.

算法1 SVETree构建过程的二叉树编码步骤

输入 SVETree平衡二叉树结构T, 验证私钥sk,

立方体编码系统CCS, 哈希私钥HK

输出 编码后二叉树结构T

FOR n∶ =T.nodes() DO

FOR 树节点n覆盖的每个叶节点leaf DO

record∶ =GetCorrespondingRecord(leaf);

FOR l∶ =1 to CCS.L DO

//对于记录在CCS层次l的立方体编码

code∶ =record.cube_codes[l];

//布隆过滤器使用r个比特存储每个编码

FOR i∶ =1 to r DO

// 计算编码对应比特位置hash_pos

hash_key = HMAC(HK[i], code);

hash_ pos = HMAC(n.rand_v, hash_key);

n.bloom_ filter.SetBit (hash_pos);

END FOR

END FOR

END FOR

END FOR

最外层循环遍历二叉树中的每个树节点, 次外层循环遍历该树节点覆盖的所有叶子节点leaf, 次内层循环遍历叶子节点对应记录在CCS每层的立方体编码code, 最内层循环根据HMAC哈希函数为立方体编码计算其在布隆过滤器中的比特位置, 并将相关比特置1.假设SVETree的二叉树T的高度为H、叶节点数量(等于数据集记录数量)为N, 最外层两重循环执行次数为O(HN).假设立方体编码系统有L层、一个编码在布隆过滤器中使用r个比特存储, 最内层两重循环总执行次数为O(Lr).综上所述, HMAC哈希函数的总计算次数为O(rLHN), 其中r为用户给定的系统超参数.

SVETree性能优化应关注于降低HMAC函数计算次数O(rLHN).由于r为用户指定参数, 因此可从另外3个参数出发, 探索可能的优化方向.

1)优化1(降低立方体编码系统层数L).一种可能的思路是在进行立方体划分时, 使数据记录在值域空间内均匀分布, 从而以更少的层数满足划分阈值τ 的要求.

2)优化2(降低SVETree树高度H).一个可能的途径是增加SVETree中树节点分支数量, 从二叉树增长为K叉树.对于|D|条数据记录, K叉SVE-Tree的高度可降低为log_K D.

3)优化3(降低SVETree叶节点数量N).因为立方体编码是以立方体为单位生成, 属于同个立方体的不同数据记录具有相同的立方体编码, 在云服务器端进行密文查询与完整性证明生成时是不可区分的.因此可在SVETree中将具有相同编码的叶节点合并, 从而减少SVETree树节点数量.

CubeTree验证数据结构以平衡多叉树为基础, 为树中每个节点附加布隆过滤器, 用于指导密文查询与完整性证明生成, 采用类似Merkle Hash Tree的签名方式检测数据篡改.CubeTree的构建流程如算法2所示.

算法2 CubeTree 构建流程

输入 明文数据集D, 加密密钥SK, 验证密钥sk,

哈希密钥HK, 分位数参数γ ,

立方体记录数阈值参数τ , 树节点分支数K,

布隆过滤器哈希函数数量r

输出 归一化参数U, CubeTree验证数据结构T

1.D', U∶ =QuantileBasedNormalization(D, γ ); //基于分位数归一化的数据重分布(优化1)

2.CCS∶ =GenerateCubeCodingSystem(D', τ ); //立方体编码系统生成

3.C∶ =ConstructCubeCells(D', CCS, SK); //构建立方格索引

4.T∶ =GenerateTreeStructure(C, K); //生成平衡K叉树基础结构(优化2, 优化3)

5.T∶ =EncodeTree(T, C, sk, HK, r); // K叉树结构编码

6.T∶ =AddVerificationSignature(T, sk); // 增加验证签名

7.RETURN U, T.

对于输入的明文数据集D, CubeTree构建流程中首先进行基于分位数归一化的数据重分布(优化1), 使数据集上所有记录的各可查询维度取值归一化到[0, 1]区间内, 在归一化的过程中同时使记录在值域空间内的分布更均匀.优化1会生成归一化后的数据集D'以及对应的归一化参数U.数据拥有者在发送密钥给客户端时, 会同时将归一化参数U共享给客户端; 客户端在进行密文查询时, 首先将各维度查询范围采用参数U归一化到[0, 1]区间, 再生成查询陷门.然后, 根据归一化后的数据集D', 生成立方体编码系统CCS.基于CCS与加密密钥SK, CubeTree构建流程为D'生成对应的加密立方格索引结构C, 并进一步以C为基础生成平衡K叉树结构(优化2与优化3).CubeTree构建流程采用与SVETree相同的方式对平衡K叉树进行编码, 为每个树节点生成布隆过滤器.最后, CubeTree构建流程自底向上地为平衡K叉树中所有节点增加验证数字签名, 根节点的哈希签名即为整棵树的密码学摘要.

基于分位数归一化的数据重分布优化方法的目标是降低立方体编码系统在处理不均匀数据集时所需的层次数L, 即对应优化方向1.SVETree在生成立方体编码系统时会对数据值域空间进行均匀网格划分.但当数据记录在值域空间中的分布不均衡(如服从类指数分布、高斯分布等)时, 数据密集区域的网格单元覆盖的记录数量将远超稀疏区域, 如图3中第2层和第3层.此时SVETree必须继续增加立方体编码系统的层次数, 使包含记录数量最多的网格单元也在指定阈值τ 以下.在理想情况下, 如果能使数据完全均衡地分布在整个值域空间中, 所需立方体编码系统层次数L最小.

为了降低数据不均衡分布对立方体编码系统层次数的影响, 可采用自适应网格划分与数据重分布两种思路.自适应网格划分的思路是根据数据分布情况自适应生成划分区间, 使每个网格覆盖的记录数量尽量接近.但此方法要求记录每个层次上所有维度的区间划分点, 当层次数较高(如20层)时, 每个维度需要记录的划分点数量在百万规模, 带来较大的归一化参数U空间开销.因此本文采用基于分位数归一化的数据重分布思路解决此问题, 整体对记录进行均衡化的重分布操作, 各层次依然可采用原有的均匀网格划分方式.

重分布优化的主要过程是:估计数据集在每个可查询维度上的分位数, 根据分位数对原始数据取值进行分段归一化, 从而使各维度取值分布更均衡.首先遍历数据集中的每条记录, 获得整个数据集在每个可查询维度上的最小值min和最大值max.根据指定采样率对数据集进行随机采样, 构成小规模的采样数据集.进行随机采样的目的是为了以较低的开销预估各维度的分位数, 避免全数据集分位数计算.对于每个可查询维度i, 获取采样数据集在该维度上的全部取值, 形成维度值数组V_i, 并将该维度在完整数据集上的最小值min[i]和最大值max[i]也加入V_i中.基于V_i, 计算该维度的最小值、Q分位数与最大值, 形成分位数数组q_i, 其中Q为用户给定的分位数数量, q_i包含Q+2个经过排序的元素.

根据各维度的分位数数组q_i, 进一步将所有记录的取值归一化到[0, 1]区间上.对于数据记录的第i个可查询维度的取值x, 在该维度的分位数数组q_i中查找满足条件

q_i[y]≤ x≤ q_i[y+1]

的最小数组下标y, 计算下标y在分位数数组q_i中的相对位置:

a= y|qi|-1, b= y+1|qi|-1,

其中|q_i|为分位数数组包含的元素数量.使用区间线性归一化方法, 计算x在[0, 1]范围内的归一化值:

norm(x)=a+ x-qi[y]qi[y+1]-qi[y](b-a).

后续步骤将使用归一化后的数据集D'代替原始数据集进行处理.需要注意的是, 客户端的查询范围也应先用相同的分位数数组和公式进行归一化, 再生成查询陷门发送给云服务器进行查询.

图4(a)为分布不均衡的原始数据集, 图中虚线表示数据集上两个维度的分位数位置, (b)为分位数归一化后的数据分布, 记录在值域空间[0, 1]²中的分布更均衡.对于给定的网格划分的阈值τ , 在均衡的数据分布上只需更少的立方体编码层次数L即可满足要求.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 基于分位数归一化的数据重分布效果Fig.4 Effect of quantile-based normalized data redistribution

在不进行数据重分布的SVETree中, 立方体编码系统所需层次数受数据分布的显著影响.在所有数据记录集中分布在同个网格的最差情况下, SVETree的立方体编码系统所需层次数可达用户给出的层次数上限.在应用基于分位数归一化的数据重分布优化后, 将重分布后的归一化值域空间记为[0, 1]^d, 将子空间r⊆[0, 1]^d的体积记为|r|, 将数据集D中被子空间r覆盖的记录集合记为

D(r)={i∈ D|i的可查询维度取值在r的范围内}.

定理1给出在理想化重分布效果下立方体编码系统所需的最小层次数L.

定理1 在数据重分布后的d维值域空间[0, 1]^d中, 如果对于任意体积相同的两个子空间

∀ r⊆[0, 1]^d, r'⊆[0, 1]^d∶ |r|=|r'|,

均有

|D(r)|=|D(r')|,

则立方体编码系统所需的最小层次数

L=「 1d(log₂|D|-log₂τ )⌉.

证明 立方体编码系统的第l层将数据集值域的每个维度均匀划分为2^l个区间, 将整个d维值域空间均匀划分为2^ld个网格(即子空间).因为任意体积相同的子空间包含记录数相同, 所以每个网格包含的记录数为|D|/2^ld.当满足|D|/2^ld≤ τ 时, 有

l≥ 1d(log₂|D|-log₂τ ).

因此立方体编码系统所需最小层次数为

「 1d(log₂|D|-log₂τ )⌉.

ServeDB的验证数据结构SVETree以平衡二叉树为基础.在构建时, 二叉树的每层都需要扫描一遍数据集上所有记录, 并根据记录立方体编码, 利用HMAC哈希值计算布隆过滤器的插入位置, 因此构造开销随二叉树的高度线性增长.

本文采用平衡K叉树代替验证数据结构中的平衡二叉树作为基础数据结构, 增加树节点分支数K以降低整棵树的高度H, K叉树结构同样支持完整性验证所需的遍历、查询与自底向上的哈希签名计算等操作.下面介绍采用自底向上的方式确定性地构造平衡K叉树结构.首先, 为数据集上d条记录(或立方格)创建对应的d个叶节点.然后, 从叶节点所在的第0层出发, 逐层向上迭代以创建中间节点.假如第L层有x个树节点, 则每K个节点为一组, 在第L+1层创建「x/K⌉个父节点, 将其中第L层的第0至K-1个树节点对应第L+1层第0个父节点, 第L层的第K至2K-1个树节点对应下一个父节点, 依次类推.当第L+1层只包含一个父节点时, 停止创建, 此时最后一个创建的节点为树的根节点.

一棵平衡四叉树结构如图5所示, 每个叶节点对应一个立方格, 第0层的9个叶节点将在第1层中对应创建3个父节点, 其中编号为0~3的叶节点对应编号为9的父节点(即第1层的第0个顶点).

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 平衡K叉树结构Fig.5 Balanced K-ary tree structure

定理2 当平衡K叉树的叶节点数量为N时, 平衡K叉树的高度至多为log_KN, 树节点数量为O(N).

证明 根据平衡K叉树的构造过程, 当第L层的树节点数量为x时, 第L+1层的树节点数量为「x/K⌉.根据递推公式, 当第0层的树节点数量为N时, 第L层的树节点数量至少为N/K^L.根节点的存在性要求N/K^L≥ 1, 从而L≤ log_KN.在不考虑节点数向上取整的情况下, 树中不同层包含的树节点数量呈等比数列N, N/K, N/K², …根据等比数列求和公式, 树中包含的节点数为(N-1)K(K-1)^-1, 考虑每层树节点数量的取整误差, 树中包含的节点数上限为

(N-1)KK-1+log_KN,

因此树中节点数量为O(N).

相比SVETree, 采用平衡K叉树并不会显著增加树中节点数量, 反而可降低树的高度, 从而降低验证数据结构的构建开销.

不同叶节点数量下平衡K叉树的高度随分支数K的变化情况如图6所示.由图可知, 当K从2增长为4时, 树高度下降一半, 但当K继续增加时, 树高度的降低效应越来越不明显.因为SVETree中每层树节点的布隆过滤器的总长度相同, 因此减少树的高度可同时减少布隆过滤器的存储开销, 但树节点分支数K的增加可能会导致生成完整性证明所需遍历的节点数量增加, 从而增加验证证明的存储与传输开销.在实践中需要根据应用的具体情况平衡分支数参数K的取值.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 平衡K叉树高度与分支数K的关系Fig.6 Relationship between the height of balanced K-ary tree and the number of branches K

SVETree构建过程计算开销较高的一大原因是其内部存在冗余HMAC哈希计算.SVETree为每条数据记录建立一个对应的叶节点, 并根据叶节点构建上层的平衡二叉树.值得注意的是, 在SVETree采用的立方体编码系统中, 被同个立方体(即网格单元)覆盖的所有数据记录具有相同的立方体编码值.立方体编码系统在每l层对每个维度均匀划分为2^l区间, 相当于将第l-1层的2^l-1个区间进一步均匀切分为2份.因此, 如果2条记录在第l层属于同个立方体, 则在第l-1层至第1层中均属于同个父立方体, 因此2条记录在第l层及以上层次的立方体编码相同.假设立方体编码系统共包含L层, 则2条记录如果在第L层被同个立方体覆盖, 则这2条记录将具有完全相同的立方体编码集.SVETree在构建时需要为2条记录重复计算各自的HMAC哈希值, 带来大量的冗余计算开销.

基于上述观察, 本文提出一种基于立方格索引的密文范围查询完整性方法(CubeTree), 流程如图7所示.CubeTree将归一化后被同个最底层立方体(即最细粒度的立方体)覆盖的所有记录合并为一个立方格(Cube Cell), 将每个叶节点索引一条数据记录变为索引一个立方格.立方格采用键值对的形式表示, 其中键为立方格对应最底层立方体的立方体编码.键值对的值由两部分组成:该立方格在每层的立方体编码, 该立方格覆盖的所有记录归一化之前的原始记录值.立方格中的原始记录会进一步被加密密钥SK加密, 从而得到密文立方格索引.数据拥有者向云服务器上传密文立方格索引, 从而避免向云服务器或其它第三方暴露明文记录.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 CubeTree流程图Fig.7 Flow chart of CubeTree

从原始数据集与归一化数据集构建立方格索引的过程如算法3所述.

算法3 立方格索引构建

输入 立方体编码系统CCS, 归一化数据集D',

原始数据集D, 加密密钥SK

输出 立方格索引C

C∶ =new HashMap< CubeCode, CubeCell> ();

FOR each record r'∈ D' DO

code∶ = GetCubeCode(CCS, r', CCS.L); //获得归一化记录r'在第L层所属立方体的编码值

C[code].records.append(D[r'.ID]); //将原始数据记录加入立方格

END FOR

FOR each cube_key ∈ C.keys DO

rid∶ = C[cube_key].records[0].ID; // 获得一个代表性记录的ID

tr∶ = D'[rid]; // 获得归一化后的代表性记录值

FOR l ∶ = 1 to CCS.L DO

C[cube_key].codes[l]∶ =

GetCubeCode(CCS, tr, l);

END FOR

C[cube_key].data∶ =

Encrypt(C[cube_key].records, SK);

// 对原始数据进行加密

C[cube_key].records.clear();

//去除原始数据以保护隐私

END FOR

RETURN C

算法首先扫描一遍归一化数据集, 借助哈希表, 对所有数据记录按照记录所属最底层立方格的编码code进行分组, 哈希表的键即为立方体编码, 哈希表的值存储属于该立方格的所有原始数据记录.对于分组后的每个立方格, 从立方格中随机选取一条记录作为代表记录, 根据归一化后的记录值, 计算立方格在每层的立方体编码, 存储到立方格的值部分中.然后, 利用加密密钥SK对立方格包含的原始数据记录进行整体加密, 得到密文立方格数据, 并擦除明文数据以保护隐私.如果需要进一步避免暴露每个立方格包含的记录数信息, 可对密文立方格进行长度离散化处理, 即向密文立方格数据的尾部填充一定长度的随机值, 使密文立方格对外显示的数据长度为特定的离散化长度(如以1 KB为单位进行离散化), 从而模糊该立方格包含的具体记录数量.

CubeTree可大幅减少立方格的数量及验证数据结构中对应叶节点的数量, 从而大幅降低HMAC哈希函数计算次数与验证数据结构的存储开销.定理3表明在理想化的重分布效果(见定理1的定义)下, 采用CubeTree后立方格的数量为N/τ , 其中τ 为用户给出的记录数阈值.在理想化数据重分布的情况下, 验证数据结构构建过程中HMAC哈希函数的计算次数从SVETree的O(rLHN)降低为O(rLHN/τ ).

定理3 对于包含N条记录的数据集D, 在数据重分布后的d维值域空间[0, 1]^d中, 如果对于任意体积相同的2个子空间

∀ r⊆[0, 1]^d, r'⊆[0, 1]^d∶ |r|=|r'|,

均有

|D(r) |=|D(r') |,

则立方格数量及验证数据结构中叶节点数量为「N/τ ⌉.

证明 根据定理1, 立方体编码系统所需最小层次数

L=「 1d(log₂N-log₂τ )⌉.

在理想化的重分布效果下, 在第L层中每个立方格中包含的记录数为|D|/2^Ld=τ , 立方格的数量为「N/τ ⌉.根据验证数据结构的构造方法, 每个立方格对应一个叶节点, 因此叶节点的数量也为「N/τ ⌉.

CubeTree的验证信息生成过程为CubeTree的树节点增加布隆过滤器与哈希签名, 查询结果的完整性证明的生成与校验都需要哈希签名的信息.

2.5.1 验证信息生成

CubeTree的编码过程(即为树中的每个节点生成对应的布隆过滤器)与SVETree的过程相同, 在此不再赘述.CubeTree采用类似Merkle Hash Tree的方式, 为经过编码的树节点生成完整性验证所需的数字签名.在叶节点对应立方格数据的哈希值与叶节点布隆过滤器哈希值拼接后, 再利用HMAC机制由验证密钥SK签名生成CubeTree叶节点的哈希签名.所有子节点的哈希签名以及该节点的布隆过滤器的哈希值拼接后, 再利用HMAC机制由验证密钥sk签名生成CubeTree的中间节点的哈希签名.具体示例如图8所示.此种签名方式保证对任意立方格、任意节点的布隆过滤器数据的修改, 都会导致CubeTree根节点的哈希签名发生变化, 从而可用于检测整棵树的数据是否被篡改.由于树节点的哈希签名由验证密钥sk生成, 第三方在不知道密钥的情况下无法伪造哈希签名.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 带有验证信息的CubeTree 结构示例(K=3)Fig.8 Example of CubeTree structure with verification information(K= 3)

2.5.2 完整性证明生成与校验

CubeTree在云服务器侧根据用户提交的查询陷门进行密文查询、生成完整性证明的过程与SVETree类似.用户提交的查询陷门即为查询范围覆盖的立方体编码集合.在云服务器侧, SVETree与CubeTree既是密文查询过程中使用的密文索引, 也同时作为完整性验证中的验证数据结构使用.云服务器在遍历SVETree与CubeTree进行密文查询的过程中, 会同步根据树节点的验证信息生成相应的完整性证明.

对于用户提交的查询陷门, 云服务器侧从CubeTree的根节点出发, 自顶向下递归检查查询陷门集合中的每个立方体编码是否存在于树节点的布隆过滤器中.如果某个编码存在, 该树节点属于密文查询的关键路径, 此时需要将该节点信息(包含布隆过滤器相关片段及树节点的哈希签名)加入完整性证明中, 并递归查询该节点的所有子节点; 如果查询陷门中的立方体编码均不存在于树节点的布隆过滤器, 不再查询该节点的子节点.在递归遍历的过程中, 如果遇到某个叶节点的布隆过滤器存在可匹配的立方体编码, 则该叶节点属于被成功查询的节点, 将叶节点对应的密文立方格加入查询结果中, 叶节点本身加入完整性证明中.

在图8中, 假设查询陷门MQ中存在立方体编码被包含在节点N₁₂的布隆过滤器中, 将节点N₁₂加入完整性证明, 并递归处理N₁₂的所有子节点N₉、N₁₀和N₁₁.假设N₉的布隆过滤器与查询陷门之间不存在匹配的立方体编码, 查询过程终止在该节点.假设叶节点N₄的布隆过滤器与查询陷门中的每个编码匹配, 对应的立方格C₄被包含在查询结果中.在图8中, 假设查询陷门只包含立方格C₄的立方体编码, 则所有被加入完整性证明的节点都以深色底纹标出.

客户端在接收到完整性证明后, 根据查询结果中的密文立方格数据重算对应叶节点的哈希签名, 进而从叶节点出发逐层向上重算至根节点的哈希签名.在图8中, 可根据查询结果中的立方格C₄的数据以及完整性证明中N₄的布隆过滤器内容, 重新计算N₄的哈希签名, 并与证明中的N₄的哈希签名进行比对.如果两者一致, 进一步从N₄逐层向上重算各父节点的哈希签名, 直至重算根节点的哈希签名.将重算的根节点哈希签名与数据拥有者共享的哈希签名进行比对, 便可检测查询结果中C₄的数据以及完整性证明中的相关节点数据是否被篡改.如果数据未被篡改, 进一步对其查询过程的合法性进行检查, 检验查询陷门与树节点布隆过滤器的匹配情况计算是否正确.

定理4 在忽略布隆过滤器误报概率的情况下, 在一个具有n个立方格的CubeTree中, 当与查询陷门匹配的叶节点数量为q时, 完整性证明包含的树节点数量为O(qKlog_Kn).

证明 一个具有n个立方格的CubeTree的高度为log_Kn, 从根节点出发到任意一个匹配的叶节点的路径包含log_Kn个树节点.对于每条路径上的每个节点, 完整性证明都会包含该节点以及该节点的K个子节点, 因此完整性证明中包含的树节点数量至少为O(qKlog_Kn).在忽略布隆过滤器误报概率的情况下, 如果一个节点被包含在完整性证明中, 但该节点不在通往匹配叶节点的路径上, 则查询陷门不会与这个节点的布隆过滤器匹配, 完整性证明不会包含该节点的所有子节点, 因此完整性证明至多包含O(qKlog_Kn)个树节点.

CubeTree与SVETree完整性证明的构建与传输开销均受证明中包含的树节点数量影响.如果查询陷门与CubeTree的q个叶节点的布隆过滤器匹配, 定理4表明CubeTree完整性证明中包含的树节点数量为O(qKlog_Kn).因为SVETree的每个叶节点对应一条记录, 同一查询陷门在SVETree中所能匹配到的叶节点数量q'有可能远大于q(在理想重分布的情况下q'=τ q), 所以SVETree完整性证明中包含的树节点数量远高于CubeTree, 带来较高的证明构建与传输开销.

本节实验将在配有Intel Xeon 6248@2.5 GHz CPU、192 GB内存的Linux服务器上进行, 输入输出文件均存储在服务器挂载的并行文件系统上.服务器的操作系统版本为CentOS 7.6(Linux Kernel 版本5.4), 实验中涉及程序均使用C++实现, 使用GCC 8.3.1编译, 采用OpenSSL库版本1.1.1k进行密码学相关计算.

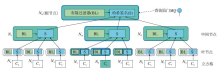
基于验证数据结构CubeTree, 本节实现一个密文范围查询完整性验证原型系统, 系统架构如图9所示.整个系统由数据拥有者、 查询服务器与客户端3个模块组成.3个模块之间的数据交互关系如图9中箭头所示.在3个模块中, 与完整性验证相关的3个子模块以灰色标识, 实验将关注3个子模块的性能表现, 包括子模块执行时间以及子模块间数据传输开销.

图9

	Figure Option ViewDownloadNew Window
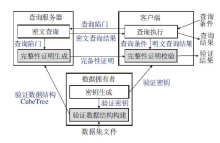	图9 基于CubeTree的密文范围查询完整性验证原型系统架构Fig.9 Structure of encrypted range query integrity authentication prototype system based on CubeTree

实验中同时采用真实数据集与合成数据集.真实数据集选择foursquare2014(简记为fs14)^[25]、gowalla(简记为go)^[26]、ebird(简记为eb)^[27]、foursquare2015(简记为fs15)^[28]、uswildfire(简记为us)^[29]数据集, 具体信息如表3所示.由于在部分实验中ServeDB执行时间较长, 因此从gowalla数据集上随机抽样50万条记录(简记为go^* )、从ebird数据集上随机抽样100万条记录(简记为eb^* )、从foursquare2015数据集上随机抽样300万条记录(简记为fs15^* )参与实验.

表3

Table 3

表3(Table 3)

表3 真实数据集信息 Table 3 Information of real-world datasets 名称 记录数 维度数 数据来源 foursquare2014 8.01× 105 3 签到记录 uswildfire 2.30× 106 3 事件记录 ebird 4.02× 106 2 事件记录 gowalla 6.44× 106 3 签到记录 foursquare2015 3.33× 107 3 签到记录

表3 真实数据集信息 Table 3 Information of real-world datasets

为了测试系统在大规模数据集上的性能表现, 采用随机数生成器生成服从均匀分布(uni)、高斯分布(gau)、指数分布(exp)的合成数据集, 3种分布的倾斜性逐渐增强, 覆盖完全均匀与极度不均衡的情况.如无特别说明, 合成数据集的记录数为200万条, 维度为三维.

如未特别说明, 本节中所有实验采用如下超参数.对于SVETree和CubeTree, 立方体编码系统中每个立方体包含的记录数阈值τ =10 000, 立方体编码系统的最大层次数L=25, 布隆过滤器使用的哈希函数数量r=5, 布隆过滤器以64 KB的固定长度进行分段.CubeTree构建时基于归一化的数据重分布过程的采样率为0.01%, 分位数的最大数量为10 000, 树节点的分支数K=4.

本节的目标是对比ServeDB采用的验证数据结构SVETree与本文的CubeTree在验证数据结构构建、验证数据结构存储、完整性证明生成与校验等阶段的执行开销情况.同时评估CubeTree中采用的3种优化方法(优化1:基于分位数归一化的数据重分布优化.优化2:基于平衡K叉树的数据结构扁平化.优化3:基于立方格索引的验证结构设计)的有效性.

3.2.1 验证数据结构构建用时

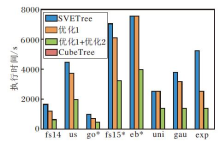
本节对比构建验证数据结构的构建用时情况.实验中测量SVETree构建算法、仅使用优化1的构建算法、同时使用优化1+优化2的构建算法, 以及同时应用3种优化的构建算法(CubeTree)的执行时间, 结果如图10所示.由图可见, 3种优化方法都能起到降低验证数据结构构建用时的效果, 随着优化的不断叠加, 优化效果越来越明显.对于所有数据集的平均情况, 相比SVETree使用优化1可将构建用时平均降低19.5%, 同时使用优化1与优化2可将构建用时平均降低56.7%, 同时使用3种优化可将构建用时平均降低99.4%.

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 验证数据结构构建过程中执行时间对比Fig.10 Execution time comparison of authentication data structure construction

在3种优化方法中, 优化1的效果受数据集分布的倾斜性影响.在均匀分布的合成数据集uni上构建用时仅降低0.2%, 而在分布较倾斜的指数分布数据集exp上构建用时降低51.8%.在优化1的基础上, 优化2在不同数据集上均体现出明显的优化效果, 构建用时在所有数据集上比只使用优化1平均降低45.9%.CubeTree的优化效果最显著, 相比使用优化1+优化2的情况, CubeTree进一步将构建用时平均降低98.7%.在所有数据集上, CubeTree将验证数据结构中树节点的数量平均降低为SVETree的0.58%, 大幅降低验证数据结构的构建开销.

3.2.2 验证数据结构存储开销

本节对比SVETree、CubeTree以及不同优化下验证数据结构占用的存储开销, 具体如图11所示.

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 验证数据结构的存储开销对比Fig.11 Storage cost comparison of authentication data structure

对于所有数据集的平均情况, 相比SVETree, 优化1由于只改变数据分布, 对验证数据结构的存储开销几乎没有影响, 而采用优化2后存储开销平均降低27.2%, 而同时采用3种优化的CubeTree存储开销平均降低85.5%.CubeTree将树节点的数量平均降低99.6%, 从而减少大量的布隆过滤器存储开销.

3.2.3 查询与完整性验证开销

与密文查询过程有关的执行开销包括云服务器侧的查询延迟、云服务器与客户端之间传输完整性证明的通信开销, 以及客户端侧对完整性证明进行校验的时间开销.因为SVETree与CubeTree的密文查询过程与完整性证明生成过程是交织在一起同步进行的, 因此实验中测量的云服务器侧查询延迟也同时是完整性证明的生成用时.

因为密文查询与完整性证明的开销受查询范围与查询结果规模的显著影响, 实验首先分别在fs14、us数据集上测量查询与完整性验证开销随相对查询范围的变化情况.相对查询范围定义为查询范围空间占整个数据集值域空间的比例, 以一个随机采样的数据记录为中心确定.查询范围对查询开销与完整性验证开销的影响如图12所示.由图可见, CubeTree可有效降低查询延时、完整性证明的通信开销与客户端侧的验证用时.对于实验中采用的所有数据集与相对查询范围的平均情况, 相比SVE-Tree, CubeTree的查询延迟平均降低36.7%, 完整性证明的传输开销平均降低99.4%, 完整性证明的校验时间平均降低99.2%.CubeTree包含的树节点数量显著低于SVETree, 而包含在树节点中的布隆过滤器是完整性验证证明生成与传输开销的主要来源, 因此CubeTree完整性证明的相关开销显著低于SVETree.

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 查询范围对查询开销与完整性验证开销的影响Fig.12 Effect of query range on query cost and integrity authentication cost

进一步在随机数据集上评估数据集维度对查询延迟与完整性验证开销的影响.实验中采用随机数生成器生成服从均匀分布(uni)与高斯分布(gau)、包含50万条记录且具有不同维度的数据集, 在相对查询范围为10^-3时, CubeTree与SVETree云服务器侧的查询延时、完整性证明的通信开销与客户端侧完整性证明验证时间如图13所示.由图可见, 对于所有数据集与维度的平均情况, 相比SVETree, CubeTree的云服务器侧查询延迟平均降低85.9%、完整性证明规模平均降低99.8%、客户端侧的完整性证明验证时间平均降低99.8%.实验结果显示查询维度对SVETree与CubeTree的性能具有一定影响, 但没有显著且稳定的变化趋势.

查询与验证开销主要受查询结果数的影响, 在相对查询范围相同的情况下, 当查询维度从2增至5时, 对于高斯分布和均匀分布数据集上的查询结果数量仅分别增至1.98倍和1.05倍, 因此未显著影响查询与验证开销.

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 数据集维度数对查询开销与完整性验证开销的影响Fig.13 Effect of dataset dimension on query cost and integrity authentication cost

近年来提出的密文范围查询完整性验证方法VSRQ^[20]、SAGTree^[21]与VeriRange^[22]均已与Serve-DB对比查询延迟与验证开销, 其中VeriRange提出的时间最晚、相比ServeDB性能提升最明显, 因此本节进一步对比CubeTree与VeriRange.

因为Veri-Range是面向二维范围查询设计、无法支持三维及以上的多属性范围查询, 因此本节实验选择真实数据集上的经度与纬度属性作为二维范围查询条件, 实验中随机采样50万条记录进行实验.

实验中调节VeriRange的网格划分参数λ , 使VeriRange的数据网格可包含的最大记录数量与CubeTree的记录数阈值τ 保持一致, 均不超过25 000条记录.

以VeriRange原文献提供的程序为基础, 跳过密文索引构建过程中的伪数据点添加过程, 保证与CubeTree行为保持一致.程序中采用与CubeTree相同的加密方法与HMAC哈希函数.

3.3.1 数据拥有者端执行开销

在真实数据集上对比CubeTree与VeriRange在数据拥有者侧构建密文索引与验证数据结构的构建开销, 具体如图14所示.

图14

Fig.14

	Figure Option ViewDownloadNew Window
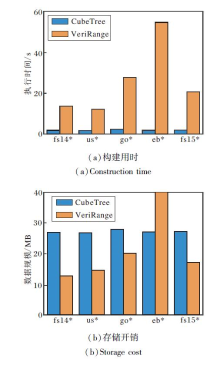	图14 CubeTree与VeriRange密文索引与验证数据结构构建开销对比Fig.14 Comparison of construction overhead of encrypted index and authentication data structure between CubeTree and VeriRange

由图14可见, 相比VeriRange, CubeTree在所有数据集上将构建用时平均降低90.4%, 但CubeTree的存储开销平均增长51.8%.CubeTree以可接受的额外存储开销换取更低的构建用时, 使其具有良好的可扩展性.

3.3.2 查询与验证开销

CubeTree与VeriRange在us、fs14数据集上云服务器端查询延迟与客户端完整性证明的验证开销如图15所示.由图可知, 相比CubeTree, VeriRange的查询延迟在所有查询范围上平均降低99.9%、完整性证明通信开销平均降低34.5%、完整性证明验证时间平均降低99.0%.

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 CubeTree与VeriRange查询延迟与完整性验证开销对比Fig.15 Comparison of query latency and integrity proof verification costs between CubeTree and VeriRange

VeriRange在查询与验证阶段的性能优势来自如下两方面:1)VeriRange直接对数据网格位置标签建立查询索引, 避免CubeTree中采用的布隆过滤器机制, 降低查询与验证阶段所需的计算与存储开销.2)VeriRange将数据网格索引结构PKD树作为查询密钥的一部分发送给客户端存储; 在客户端进行密文查询时, 需要先在本地通过PKD树获取查询范围涉及的所有数据网格位置标签, 再将位置标签作为查询陷门发送至云服务器.VeriRange服务器端查询过程仅需根据位置标签进行轻量的哈希表查询, 并且客户端不需要对查询结果的完备性进行额外验证, 从而大幅降低查询与验证开销.

VeriRange的弊端在于其将原本属于云服务器端的部分密文查询工作, 通过密钥中的PKD树分摊至客户端进行.PKD树的存储开销会受数据集规模与网格划分参数的显著影响, 随着记录数增加、网格划分粒度变细, VeriRange的密钥数据规模将持续增长, 而CubeTree的密钥规模则与数据集记录数无关.

CubeTree与VeriRange在不同数据集上生成的密钥数据规模如图16所示.由图可知, CubeTree的密钥数据规模在所有数据集上平均为VeriRange的3.5%, 且CubeTree的密钥规模不受数据规模影响.

上述实验结果表明, 相比VeriRange, CubeTree在密文索引与验证数据结构构建阶段具有更优的性能优势, 而VeriRange在查询与验证阶段具有较强的优势.

图16

Fig.16

	Figure Option ViewDownloadNew Window
	图16 CubeTree与VeriRange密钥数据规模对比Fig.16 Comparison of private key data sizes between CubeTree and VeriRange

CubeTree的设计思路是将计算开销尽可能分摊至拥有强大算力的云服务器侧进行, 以减轻客户端的计算压力, 因此更适用于云端算力资源丰富而客户端存储开销紧张的场景或是需要三维及以上多维范围查询的应用.而VeriRange的设计思路则是通过使客户端适当分摊密文查询的计算与存储开销, 从而降低查询与验证阶段的整体开销, 因此更适合二维范围查询中云端算力相对紧张而客户端存储资源相对充裕的场景.

CubeTree的构建过程受立方体编码系统中底层立方体包含的最大记录数阈值τ 、树节点的分支数K、基于分位数归一化过程中的采样率与分位数数量等超参数的影响.本节将通过实验评估上述超参数的影响.

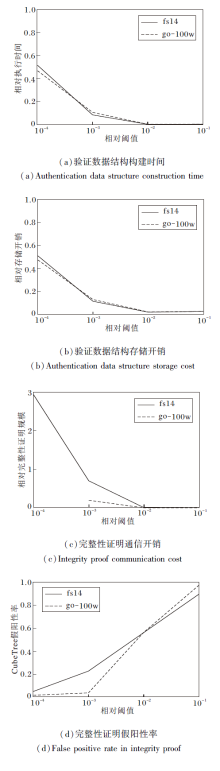
3.4.1 立方体包含记录数阈值

最底层立方体包含的最大记录数阈值τ 影响最底层立方体的覆盖范围与立方体编码系统的层次数, 从而间接影响验证数据结构与完整性证明的相关开销.随着阈值τ 的增加各种开销的变化情况如图17所示.实验中go数据集随机采样100万条记录(简记为go-100w)参与计算, 查询范围占数据集值域空间的1.25× 10^-4.

图17

Fig.17

	Figure Option ViewDownloadNew Window
	图17 立方体记录数阈值τ 对系统性能的影响Fig.17 Effect of cube record threshold τ on system performance

因为不同数据集的执行时间、存储开销差异较大, 为了统一对比不同数据集的情况, 图17将CubeTree的执行时间、存储开销、完整性证明规模换算为与SVETree对应开销的相对值, 并且将阈值τ 换算为相对于数据集记录总数的相对阈值.

由图17可见, 阈值τ 对验证数据结构的构建时间与存储开销的影响趋势高度一致.对于实验中2个数据集的平均情况而言, 随着阈值τ 的上升, 相比SVETree, CubeTree的相对执行时间从49.2%降至0.4%, 相对存储开销从51.2%降至2.6%, 而完整性证明的相对通信开销从292%降低至0.7%.

对于SVETree和CubeTree, 阈值τ 的上升均会使立方体编码系统所需层次数下降、最底层立方体的覆盖范围增加, 每个立方体/立方格内将包含更多的数据记录, 导致完整性证明中包含更多不在查询范围内的假阳性数据记录, 使SVETree的完整性证明假阳性率从平均54.9%升至76.7%, CubeTree的完整性证明假阳性率从平均3.2%升至93.0%.因此在实际应用中应根据具体需求选择合适的阈值参数, 在验证数据结构/完整性证明的计算开销与假阳性率之间取得平衡.

3.4.2 树节点分支数

CubeTree中树节点分支数参数K影响Cube-Tree的构建时间、存储开销以及完整性证明的通信开销.上述开销随树节点分支数K的变化情况如图18所示.

图18

Fig.18

	Figure Option ViewDownloadNew Window
	图18 树节点分支数K对CubeTree性能的影响Fig.18 Effect of the number of tree branches K on CubeTree performance

实验中go数据集随机采样100万条记录参与计算(简记为go-100w), 查询范围占数据集值域空间的1.25× 10^-4.实验结果显示增加分支数K可显著降低验证数据结构的构建时间、存储开销以及完整性证明的规模.但过高的分支数(如K> 64)会导致验证数据结构过于扁平, 在完整性证明中包含更多树节点, 反而增大验证证明规模, 因此需根据应用数据特点选择合适的分支数.

3.4.3 采样率与分位数数量

采样率与分位数数量是CubeTree采用的基于分位数归一化步骤的超参数, 直接影响验证数据结构中立方体编码系统的层次数.层次数越高, 验证数据结构的构建与存储开销越大.实验评估采样率的影响时, 分位数数量固定为1 000; 评估分位数数量的影响时, 采样率固定为0.1.具体结果如图19所示.

图19

Fig.19

	Figure Option ViewDownloadNew Window
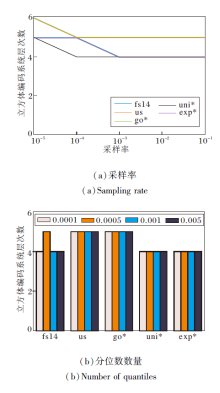	图19 分位数参数对立方体编码系统层次数影响Fig.19 Effect of quantile parameters on the number of levels of cube encoding system

随着采样率的降低, 分位数估计值的准确度下降, 归一化的优化效果变弱, 导致立方体编码系统层次数增加.而对于固定的采样率, 分位数数量的变化并不会显著影响立方体编码系统的层次数.实验表明基于分位数的归一化优化方法对于采样率更敏感, 而对分位数的取值相对不敏感.在计算开销允许的条件下, 可增加采样率以提升分位数估计的精确度.

在服从高斯分布的合成数据集上, 测量SVE- Tree与CubeTree验证数据结构构建过程的构建用时与内存开销随数据集规模的变化情况, 构建用时超过5 h认为超时, 具体结果如图20所示.由图可知, SVETree与CubeTree的构建用时与内存开销均随数据规模呈线性增长.通过对实验数据进行线性拟合估计, SVETree的平均构建速度为383.5条/秒, 而CubeTree的平均构建速度为137 968.2条/秒.SVE- Tree和CubeTree构建过程的内存开销分别是每条记录平均6.5 KB和0.32 KB.

图20

Fig.20

	Figure Option ViewDownloadNew Window
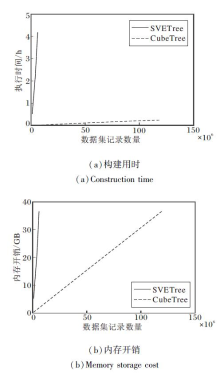	图20 验证数据结构构建过程的数据可扩展性评估Fig.20 Data scalability evaluation of authentication data structure construction process

实验结果表明CubeTree具有良好的数据可扩展性, 可扩展到亿级规模数据集.在相同时间约束下, CubeTree处理的数据规模是SVETree的359.8倍; 在相同内存容量约束下, CubeTree处理的数据规模是SVETree的20.3倍.CubeTree可在850 s、40 GB的时空开销内为1.2亿规模数据集构建验证数据结构, 而SVETree在处理800万规模数据集时所需时间已超过5 h.