基于融合Lasso的非参数加性分位数回归模型

引用本文

付漫侠, 周水生. 基于融合Lasso的非参数加性分位数回归模型. 模式识别与人工智能, 2024,37(1): 58-72
FU Manxia, ZHOU Shuisheng. Nonparametric Additive Quantile Regression Model Based on Fused Lasso. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2024,37(1): 58-72. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202401005
Permissions

《模式识别与人工智能》编辑部

基于融合Lasso的非参数加性分位数回归模型

付漫侠¹, 周水生¹

1.西安电子科技大学数学与统计学院西安 710126

通讯作者:

周水生,博士,教授,主要研究方向为最优化理论与算法、模式识别及应用、智能信息处理、机器学习等.E-mail: sszhou@mail.xidian.edu.cn.

作者简介:

付漫侠,硕士研究生,主要研究方向为最优化计算理论与算法、模式识别及应用.E-mail: 21071212648@stu.xidian.edu.cn.

收稿日期: 2023-10-20 修回日期: 2024-01-17

资助项目: 陕西省自然科学基础研究计划资助项目(No.2024JC-YBMS-051)资助

摘要

加性分位数回归为非线性关系的建模提供一种灵活、鲁棒的方法.拟合加性分位数模型的方法通常使用样条函数逼近分量,但需要先验的选择节点,计算速度较慢,并不适合大规模数据问题.因此文中提出基于融合Lasso的非参数加性分位数回归模型(Nonparametric Additive Quantile Regression Model Based on Fused Lasso, AQFL),是在融合Lasso罚和 l₂罚之间折衷的可对加性分位数回归模型进行估计和变量选择的模型.融合Lasso罚使模型能快速计算,并在局部进行自适应,从而实现对所需分位数甚至极端分位数的预测.同时结合 l₂罚,在高维数据中将对响应影响较小的协变量函数值压缩为零,实现变量的选择.此外,文中给出保证收敛到全局最优的块坐标ADMM算法(Block Coordinate Alternating Direction Method of Multipliers, BC-ADMM),证明AQFL的预测一致性.在合成数据和碎猪肉数据上的实验表明AQFL在预测准确性和鲁棒性等方面较优.

关键词: 分位数回归; 加性模型; 融合Lasso罚; l₂罚

中图分类号:TP181

Nonparametric Additive Quantile Regression Model Based on Fused Lasso

FU Manxia¹, ZHOU Shuisheng¹

1. School of Mathematics and Statistics, Xidian University, Xi'an 710071

Corresponding author:
ZHOU Shuisheng,Ph.D.,professor.His research interests include optimization theory and algorithm, pattern recognition and application, intelligent information processing and machine lear-ning.
About Author:
FU Manxia,Master student.Her research interests include optimization theory and algorithm, pattern recognition and application.

Fund:Natural Science Basic Research Program of Shaanxi Province(No.2024JC-YBMS-051)

Abstract

Additive quantile regression provides a flexible and robust method for modeling non-linear relationships. Methods for fitting the additive quantile models rely on spline functions to approximate components. However, the required prior selection of nodes results in slow computation speed and it renders the methods unsuitable for large-scale data problems. Therefore, a nonparametric additive quantile regression model based on the fused Lasso(AQFL) is proposed in this paper. AQFL leverages a compromise between the fused Lasso penalty and the l₂ penalty for estimating and selecting variables in the additive quantile regression model. The fused Lasso penalty is employed to make the model compute fast and localize adaptively, thereby achieving the prediction for the desired quantile or even extreme quantiles. Additionally, in combination with the l₂ penalty, AQFL compresses the covariate function values with a small impact on the response to zero in high-dimensional data, thereby achieving variable selection. Furthermore, a block coordinate alternating direction method of multipliers(BC-ADMM) algorithm is presented to ensure convergence to the global optimum and demonstrate the prediction consistency of AQFL. Experimental results on synthetic data and ground pork data demonstrate the superiority of AQFL in prediction accuracy and robustness.

Key words: Quantile Regression; Additive Model; Fused Lasso Penalty; l₂ Penalty

文章图片

分位数回归^[1]是一种用于估计感兴趣的条件分位数的鲁棒方法, 对重尾分布具有天然的鲁棒性, 可正确拟合异方差关系, 为响应的条件分布提供全面的分析, 其稀疏度水平可随分位数变化而变化.因此, 分位数回归在研究收入分配、股票价格波动、疾病治疗效果和教育等方面应用广泛.

加性模型的优势在于它可捕捉数据中的复杂关系, 如非线性关系.此外, 可避免维数困扰的问题.维数困扰是指在高维数据中建立全局模型时, 参数估计变得困难或不可靠.通过将模型分解为可加组件, 加性模型可更好地处理高维数据, 使参数估计更稳定、可靠.

受加性模型和广义加性模型工作的启发, de Gooijer等^[2]提出基于核方法建模以估计加性非线性条件分位数模型, 证明对于固定维数p, 加性分位数回归达到与加性均值回归相同的收敛速度, 从而在理论上减轻维数困扰, 但是方法需要对维数p≥ 5的情况进行偏差校正.Gaillard等^[3]通过B样条拟合广义加性分位数模型生成温度情景, 将其插入概率预测负荷模型, 得到电力负荷预测的最佳效果.然而, 此方法需要研究者手动选择平滑参数.Fasiolo等^[4]使用样条基展开拟合响应和感兴趣的分位数之间的平滑关系, 给出条件分位数校准公式, 快速自动估计平滑参数.模型结构类似于广义加性模型, 只在维数较低时进行, 都是使用B样条基函数逼近分量, 样条函数的性能很大程度上取决于节点的选择.Sherwood等^[5]提出QA-SCAD, 利用组惩罚实现超高维加性分位数回归问题估计和变量选择的同时进行.虽然将加性分位数回归模型扩展到超高维问题, 但仍基于B样条函数, 随着维数增加, 计算速度越来越慢.此外, 样条函数的性能很大程度上取决于节点的选择.然而, 节点的选择是主观的, 可能因为选择的不同导致拟合结果的不同.

现有的均值回归模型在理论和计算上的结论无法直接应用在分位数回归上, 因此, 在理论方面, Padilla等^[6]给出分位数回归预测一致性的损失函数.Ye等^[7]在此基础上研究分位数K-NN Fused Lasso, 证明K-NN Fused Lasso接近极小极大收敛速度.在计算方面, Pietrosanu等^[8]研究高维分位数回归问题, 使用ADMM(Alternating Direction Method of Multipliers)^[9] 、MM(Majorize-Minimize) Algorithm^[10]以及Coordinate Descent Algorithm^[11]进行变量选择, 获得估计量.Hochbaum等^[12]开发O(nlogn)次的分位数融合Lasso快速算法.Brantle等^[13]提出Parallelizable ADMM Algorithm, 计算一维数据的k阶分位数趋势滤波估计量.

本文提出基于融合Lasso的非参数加性分位数回归模型(Nonparametric Additive Quantile Regre-ssion Model Based on Fused Lasso, AQFL), 是在融合Lasso罚和l₂罚之间折衷的可对加性分位数回归模型进行估计和变量选择的模型.融合Lasso罚使模型能快速计算, 并在局部进行自适应, 实现对所需分位数甚至极端分位数的预测.同时结合l₂罚, 在高维数据中将对响应影响较小的协变量函数值压缩为0, 实现变量的选择.此外, 本文给出保证收敛到全局最优的块坐标ADMM算法(Block Coordinate Alter-nating Direction Method of Multipliers, BCADMM), 证明AQFL的预测一致性.最后, 在合成数据和碎猪肉数据上的实验表明AQFL在预测准确性和鲁棒性等方面较优.

1 相关工作

传统的回归分析只关注因变量的条件均值, 未充分考虑因变量条件分布的完整特征.相比之下, 分位数回归能分析因变量条件分布的完整特征.因此, 本文希望将一些在均值回归中有效的研究方法推广到加性分位数回归中.

1.1 均值回归

在均值回归模型中, 学者们采用不同的方法构建复杂模型, 其中一种方法是使用协变量的多项式或样条函数引入非线性关系.使用非参数建模的方法拟合均值回归模型也是常见的, 此方法可以更灵活地适应数据的特征, 不需要对模型做出具体的函数形式假设.Tibshirani等^[14]提出的非参数融合Lasso罚模型, 通过响应向量y和有序的单变量x估计向量

θ =(θ ₁, θ ₂, …, θ _n),

其中

θ _i=E[y_i|x_i]=f(x_i) , x1_<x2_<…< xn_.

具体模型表达式如下:

$\min_{θ \in R^{n}} \frac{1}{2} \overset{n}{\sum_{i}} (y_{i} - θ_{i})^{2}$ +λ ‖ Dθ ‖ ₁,

其中, λ > 0为调优参数, 差分矩阵

$D={{\left( \begin{matrix} -1 & 1 & {} & {} \\ {} & \ddots & \ddots & {} \\ {} & {} & -1 & 1 \\\end{matrix} \right)}_{\left( n-1 \right)\times n}}$.

上述方法将部分系数和系数之间的差收缩为0, 得到模型系数的稀疏解和系数差分的稀疏解, 使相邻系数之间更平滑.

Kim等^[15]将讨论扩展到单变量非参数趋势滤波罚模型, 并将趋势滤波罚函数定义为输入数据上的k + 1阶差分算子, 将融合Lasso归纳为k = 0的情况.之后, Tibshirani^[16]将趋势滤波罚与样条方法进行详细对比.研究发现, 相比平滑样条方法, 非参数趋势滤波方法在模型的扩展性、理论分析、算法实现、局部自适应等方面都具有优势.

1.2 加性分位数回归

假设样本 ${x_{i}, y_{i}}_{i = 1}^{n}$ 为随机变量(X, Y)的n个观察值,

x_i=(x_i₁, x_i₂, …, x_ip)∈ R^p

为p维向量.给定分位数τ ∈ (0, 1).加性分位数回归模型有如下形式:

y_i=β ₀(τ )+ $\overset{p}{\sum_{j}}$ f_j(x_ij, τ )+ε _i(τ ).

令

$θ_{ij}^{*}$ =f_j(x_ij, τ ),

省略τ , 则估计的加性分位数回归模型:

y_i=β ₀+ $\overset{p}{\sum_{j}} θ_{ij}^{*}$ +ε _i, i=1, 2, …, n,

其中

${{\beta }_{0}}+\sum\limits_{j=1}^{p}{\theta _{ij}^{* }}={{Q}_{{{y}_{i}}|{{x}_{i}}}}\left( \tau \right), {{Q}_{{{y}_{i}}|{{x}_{i}}}}\left( \tau \right)=\inf \left\{ t:F\left( t\left| {{x}_{i}} \right. \right)\ge \tau \right\}$,

F(y_i $|x_{i}$ )表示x_i条件下y_i的累积分布函数, 随机误差ε _i满足

P(ε _i≤ 0|x_i)=τ .

此外, 令

$\overset{n}{\sum_{i}} θ_{ij}^{*}$ =0,

可提升模型的可识别性.

令

$θ_{j}^{*}$ = $(θ_{1 j}^{*}, θ_{2 j}^{*}, \dots, θ_{nj}^{*})^{T}$ ,

则加性分位数回归的目标是尽可能准确估计 $θ_{j}^{*}$ , 它的优化问题如下所示:

${\hat{θ}}_{j}$ ∈ arg $\min_{θ_{j} \in R^{n}}$ L(θ _j), j=1, 2, …, p,

其中, 损失函数

L(θ _j)= $\overset{n}{\sum_{i}}$ ρ _τ(y_i- $\overset{p}{\sum_{j}}$ θ _ij-β ₀),

非对称绝对偏差函数

ρ _τ(t)=(τ -1{t≤ 0})t.

相比传统的均值回归, 加性分位数回归通过对不同分位数的目标函数进行建模, 捕捉协变量在不同分位数上的非对称性, 有利于处理偏态数据和非线性关系.加性分位数回归可灵活适应于不同的数据分布和模型假设, 不需要对数据的正态分布和模型的线性关系进行假设, 对异常值和离群点具有较好的鲁棒性, 适用于各种类型的数据和问题.此外, 加性分位数回归还可用于构造预测区间, 而均值回归只能提供不同位置的点估计.

2 基于融合Lasso的非参数加性分位数回归模型

拟合加性分位数模型的方法通常使用样条函数逼近分量.但样条函数的性能很大程度上取决于预先选定的节点, 如果节点数量过多或位置选择不当, 可能会出现过拟合现象.此外, 样条函数的计算复杂度相对较高, 特别是在高维数据或复杂形状下, 这可能导致计算时间较长或需要更高的计算资源, 因此本文提出基于融合Lasso的非参数加性分位数回归模型(AQFL).

2.1 模型建立

融合Lasso罚是一种用于变量选择和估计的统计方法, 本文将其应用于非参数加性分位数回归, 提出如下模型:

$\begin{array}{l} \arg \underset{1 \leq j \leq p}{\underset{θ_{j} \in R^{n}}{\min_{β_{0} \in R}}} \overset{n}{\sum_{i}} ρ_{τ} (y_{i} - \overset{p}{\sum_{j}} θ_{ij} - β_{0}) + λ \overset{p}{\sum_{j}} ‖ D P_{j} θ_{j} ‖_{1}, \\ s.t. 1^{T} θ_{j} = 0, \forall j, \end{array}$ (1)

其中,

λ ≥ 0, X_j= $(x_{1 j}, x_{2 j}, \dots, x_{nj})^{T}$ ,

P_j表示将向量X_j从小到大排序的置换矩阵.可将DP_j作为一个整体, 若DP_j的第q行元素

$(D P_{j})_{q, r}$ = $\{\begin{array}{l} - 1, & r = k \\ 1, & r = l \\ 0, & 其它 \end{array}$

则DP_jθ _j的第q个元素

$(D P_{j} θ_{j})_{q}$ =θ _lj-θ _kj .

假设 ${\hat{θ}}_{j}$ 为式(1)的解, 当λ 足够大时, l₁罚项促使

| ${\hat{θ}}_{lj}$ - ${\hat{θ}}_{kj}$ |=0.

非零元素| ${\hat{θ}}_{lj}$ - ${\hat{θ}}_{kj}$ |对应 ${\hat{θ}}_{j}$ 中的节点.因此, ${\hat{θ}}_{j}$ 为数据提供具有自适应选择的节点的分段常数拟合.

此外, 融合Lasso罚函数通过对模型参数施加稀疏性惩罚, 自动选择对目标函数具有重要影响的变量, 从而提高模型的解释能力和泛化能力.这种方法将模型参数推向0附近, 有效减少过拟合的风险.通过稀疏性惩罚, 还可减少异常值和噪声对估计结果的影响, 提高模型的鲁棒性.

在高维数据中, 本文希望对响应影响较小的协变量函数值为0, 进而添加一个l₂罚, 并在两个罚项间折衷.由此得到如下优化问题:

arg $\underset{1 \leq j \leq p}{\underset{θ_{j} \in R^{n}}{\min_{β_{0} \in R}}} \overset{n}{\sum_{i}}$ ρ _τ(y_i- $\overset{p}{\sum_{j}}$ θ _ij-β ₀)+ λ α $\overset{p}{\sum_{j}}$ ‖ DP_jθ _j‖ ₁+λ (1-α ) $\overset{p}{\sum_{j}}$ ‖ θ _j‖ ₂, (2)

其中0≤ α ≤ 1.α 在鼓励θ _j成为分段常数和在整个向量θ _j上使用组Lasso诱导稀疏性之间提供一种权衡^[17], 从而实现模型拟合和变量选择的同时进行.本文称式(2)为AQFL.

2.2 求解算法

首先考虑单个变量时如何求解估计器.当p = 1时, 式(2)改为

$\min_{θ \in R^{n}} \overset{n}{\sum_{i}}$ ρ _τ(y_i-θ _i)+λ α ‖ DPθ ‖ ₁+λ (1-α )‖ θ ‖ ₂. (3)

使用ADMM求解, 将式(3)重写为

$\underset{z \in R^{n}}{\min_{θ \in R^{n}}} \overset{n}{\sum_{i}}$ ρ _τ(y_i-θ _i)+λ α ‖ DPz‖ ₁+λ (1-α )‖ z‖ ₂,
s.t. z=θ .

上式的增广拉格朗日表达式为

L(θ , z, u)= $\overset{n}{\sum_{i}}$ ρ _τ(y_i-θ _i)+λ α ‖ DPz‖ ₁+λ (1-α )‖ z‖ 2₊ $\frac{R}{2}$ θ -z+u‖ 2^, (4)

其中R为更新中控制步长的惩罚参数.通过迭代更新下式以求解式(4):

θ ← arg $\min_{θ \in R^{n}}$ { $\overset{n}{\sum_{i}}$ ρ _τ(y_i-θ _i)+ $\frac{R}{2}$ ‖ θ -z+u‖ ²}, $\begin{array}{l} \end{array} \begin{array}{l} \end{array}$ (5)

z← arg $\min_{z \in R^{n}}$ { $\frac{1}{2}$ ‖ θ +u-z‖ ²+ $\frac{λα}{R}$ ‖ DPz‖ ₁+ $\frac{λ (1 - α)}{R}$ ‖ z‖ ₂}, (6)

u← u+θ -z, (7)

其中u为拉格朗日乘子.式(5)有如下形式的闭式解:

θ _i= $\{\begin{array}{l} z_{i} - u_{i} + \frac{τ}{R}, & y_{i} - z_{i} + u_{i} > \frac{τ}{R} \\ z_{i} - u_{i} + \frac{τ - 1}{R}, & y_{i} - z_{i} + u_{i} < \frac{τ - 1}{R} \\ y_{i}, & 其它 \end{array}$ (8)

式(6)有如下估计^[18]:

z← ${(1 - \frac{λ (1 - α)}{R {‖\tilde{z}‖}_{2}})}_{+} \tilde{z}$ , (9)

其中 $\tilde{z}$ 满足

$\tilde{z}$ ← arg $\min_{\tilde{z} \in R^{n}}$ { $\frac{1}{2} {‖θ + u - \tilde{z}‖}^{2}$ + $\frac{λα}{R} {‖\tilde{DPz}‖}_{1}$ }.

上式可使用现有的求解器, 如R语言中的glmgen包进行计算.

当p > 1时, 使用块坐标下降法得到全局最优解, 步骤如算法1所示.

算法1 BC-ADMM

step 1 初始化 ${\hat{β}}_{0}$ =0, ${\hat{θ}}_{j}$ =0, j = 1, 2, …, p.

step 2 循环

j = 1, 2, …, p, 1, 2, …, p, 1, 2, …, p, …

step 2.1 计算残差

r_j=y- ${\hat{β}}_{0}$ 1- $\sum_{j'} \hat{θ}$ '_j.

step 2.2 由ADMM求解式(3):

step 2.1.1 初始化

$θ_{j}^{(0)}$ =r_j, z⁽⁰⁾=r_j, u⁽⁰⁾=0.

step 2.1.2 循环k=1, 2, …, 直至

‖ $θ_{j}^{(k)}$ - $θ_{j}^{(k - 1)}$ ‖ ₂≤ κ ,

或达到最大迭代次数N_iter.

由式(8)、式(9)及glmgen包和式(7)依次更新 $θ_{j}^{(k)}$ 、z⁽^k⁾和u⁽^k⁾.

step 2.3 计算截距:

${\hat{β}}_{0}$ ← ${\hat{β}}_{0}$ +mean( ${\hat{θ}}_{j}$ ),

并居中

${\hat{θ}}_{j}$ ← ${\hat{θ}}_{j}$ -mean( ${\hat{θ}}_{j}$ ).

step 3 重复step 2, 直至式(2)收敛.

在实践中, 直接采用经验值0.5作为R的取值, 确保研究过程更严谨、可靠^[7].如果达到最大迭代或原始残差 $‖ θ_{j}^{(k)} - θ_{j}^{(k - 1)} ‖_{2}$ 在误差κ 范围内, 停止该过程.在计算中发现, 当设置参数κ =10^-2时, 可显著提升算法的收敛精度和速度.P_j为定义在输入数据第j列上的置换矩阵, j = 1, 2, …, p.由于每个P_j之间是独立的, 使用块坐标下降法对每个变量进行上述计算时不会对响应和各个协变量之间的关系产生影响.

3 参数分析

调优参数λ 的选择至关重要, 本节讨论AQFL的解不全为0的充分条件, 从而得到参数λ 的取值范围, 并给出选择最优模型的两种方法.

3.1 λ 的取值范围

在α = 0, 1时, 分别研究如何选择变量λ 的值, 使AQFL的解

${\hat{θ}}_{j}$ =0, j = 1, 2, …, p

成立, 从而得到λ 的取值范围.

引理1 定义

$\tilde{y}$ =y- $\frac{1}{n}$ 1^Ty1,
V=[ ${P^{T}}_{1}$ , ${P^{T}}_{2}$ , …, ${P^{T}}_{p}$ ],

其中, ${P^{T}}_{j}$ U∈ Rⁿ^{× (}ⁿ^-1)为矩阵DP_j的右逆.当α = 1时, 式(2)的解全为0当且仅当

λ ≥ ‖ V^Tγ (0) $‖_{\infty}$ ;

当α = 0时, 式(2)的解全为0当且仅当

λ ≥ ‖ γ (0)‖ ₂.

其中

γ (0)=(τ -1{ ${\tilde{y}}_{1}$ < 0},
τ -1{ ${\tilde{y}}_{2}$ 0}, …, τ -1{ ${\tilde{y}}_{n}$ 0})T^.

证明若

$\hat{β}$ = $({\hat{β}}^{T}_{1}, {\hat{β}}^{T}_{2}, \dots, {\hat{β}}^{T}_{p})^{T}$

为

$\min_{β \in R^{(n - 1) p}} \overset{n}{\sum_{i}}$ ρ _τ(y_i-(Vβ )_i)+α λ ‖ β ‖ ₁+ (1-α )λ $\overset{p}{\sum_{j}}$ ‖ Uβ _j‖ ₂ (10)

的解, 则式(2)的解 ${\hat{θ}}_{1}$ , ${\hat{θ}}_{2}$ , …, ${\hat{θ}}_{p}$ 满足

${\hat{θ}}_{j}$ = ${P^{T}}_{j}$ U ${\hat{β}}_{j}$ , j = 1, 2, …, p.

当α = 1时, 令

β _j=DP_jθ _j,

则有

θ _j= ${P^{T}}_{j}$ Uβ _j.

令

β = $({β^{T}}_{1}, {β^{T}}_{2}, \dots, {β^{T}}_{p} {)^{T}}_{(n - 1) p}$ ,

得到式(10)的最优性条件

-V^Tγ (β )+λ s(β )=0,

其中

γ (β )=(τ -1{y₁< (Vβ )₁},
τ -1{y₂< (Vβ )₂}, …, τ -1{y_n< (Vβ )_n})^T.

当β _j≠ 0时,

s(β _j)=sign(β _j);

当β _j=0时,

s(β _j)∈ [-1, 1].

若β = 0, 有

-V^Tγ (0)+λ s(0)=0

成立当且仅当

λ ≥ $‖ V^{T} γ (0) ‖_{\infty}$ .

当α = 0时, 式(2)的最优性条件

-γ (θ _j)+λ s(θ _j)=0, j = 1, 2, …, p.

当θ _j≠ 0时,

s(θ _j)= $\frac{θ_{j}}{‖ θ_{j} ‖_{2}}$ ;

当θ _j=0时,

s(θ _j)∈ {g∶ ‖ g‖ ₂≤ 1}.

若θ _j=0, j = 1, 2, …, p,

-γ (0)+λ s(0)=0

成立当且仅当

λ ≥ ‖ γ (0)‖ ₂.

由引理1可得AQFL的解不全为0的充分条件.

推论1 ∀ α ∈ [0, 1], 若式(2)的解不完全为0, 则

λ < min{ $\frac{1}{α} ‖ V^{T} γ (0) ‖_{\infty}$ , $\frac{1}{1 - α}$ ‖ γ (0)‖ ₂}.

推论1的结果给出参数λ 的合适范围.根据推论1的计算结果, 最大值记为λ _max, 这意味着当λ 值超过λ _max时, 整体拟合将达到完全稀疏性(即式(2)的解全为0).

因此, 本文将λ 设置在0.01× λ _max到λ _max之间, 在这个范围内选择合适的稀疏性水平.

3.2 λ 的选择

调优参数λ 的选择是模型估计中一个重要的实际问题, 控制估计器的平滑程度.AQFL的λ 值可通过K折交叉验证或基于贝叶斯信息准则(Bayesian Information Criterion, BIC)选择.分位数回归的BIC^[19]计算公式如下:

BIC(τ )= $\frac{2}{σ} \overset{n}{\sum_{i}}$ ρ _τ(y_i- $\overset{p}{\sum_{j}} {\hat{θ}}_{ij}$ )+ν ln n,

其中, σ > 0, 可经验地选择为

σ = $\frac{1}{2}$ (1-|1-2τ |),

v等于罚项的非零元素的个数^[20].

4 理论分析

均值回归的风险上界是指通过均值回归方法得到的预测值 ${\hat{θ}}_{j}$ 与真实值 $θ_{j}^{*}$ 之间的误差δ 的上界.具体地, 它是通过衡量损失函数 $\frac{1}{n} \overset{n}{\sum_{i}} δ_{i}^{2}$ 的上界以评估均值回归模型的预测能力.此外, 收敛速率也是常提及的一个评估指标, 通常是指在样本数量增加时, 估计值与真实值之间差异的减小速度.较小的风险上界通常意味着更优的模型性能, 而更快的收敛速率意味着模型可更快地逼近真实值.文献[6]在分位数上定义函数

$Δ_{n}^{2}$ (δ )= $\frac{1}{n} \overset{n}{\sum_{i}}$ min{|δ _i|, $δ_{i}^{2}$ },

从而将均值回归上的评估指标推广到分位数回归.它类似于Huber损失函数, 在最小二乘代价函数和l₁范数代价函数之间折衷, 因此对数据中的异常值不太敏感.本文利用这一损失函数证明AQFL存在风险上界, 具有较快的收敛速率.

为了简单起见, 假设y在本节中的均值为0.令{a_n}⊂R, {b_n}⊂R为2个正序列.如果存在常数C> 0和n₀> 0, 使得对n≥ n₀有a_n≤ Cb_n, 记

a_n=O(b_n).

若对于∀ ε > 0, 存在C> 0, 使得

P(a_n≥ Cb_n)< ε

成立, 记

a_n=O_P(b_n);

若

a_n=O_P(b_n), b_n=O_P(a_n),

则记

a_n=Θ (b_n).

首先为加性分位数回归的理论分析做出如下假设1.

假设1 令

$Q_{y_{i} |x_{i}}$ (τ )= $\overset{p}{\sum_{j}} θ_{ij}^{*}$ ,

其中 $θ_{ij}^{*}$ 是有界的.若非零函数的数量是有界的, 即存在常数K, 使得

$\overset{p}{\sum_{j}}$ ‖ $θ_{j}^{*}$ ‖ ₀=K< ¥ ,

则

$\overset{p}{\sum_{j}}$ ‖ DP_j $θ_{j}^{*}$ ‖ ₁=O( $\sqrt[]{n}$ ),

$\overset{p}{\sum_{j}}$ ‖ $θ_{j}^{*}$ ‖ ₁=O( $\sqrt[]{n}$ ).

假设1要求y的第τ 分位数向量 $θ_{j}^{*}$ 存在有界变化, 放缩值 $\sqrt[]{n}$ 来自文献[7].

假设2^[6] 若存在一个常数L > 0, 使得

$‖δ ‖_{\infty}$ ≤ L,

则对于∀ δ ∈ Rⁿ, 存在 $\tilde{f}$ > 0, 使得

$\min_{i = 1, 2, \dots, n}$ $f_{y_{i} |x_{i}}$ ( $\overset{p}{\sum_{j}} θ_{ij}^{*}$ +δ _i)≥ $\tilde{f}$ a.s.,

其中 $f_{y_{i} |x_{i}}$ 为给定x_i时y_i的条件概率密度.

假设2确保y_i对应的分位数是唯一的, 并且累积分布函数在分位数的邻域周围呈一致的线性增长.这是对y_i分布的一个普遍假设, 适用于大多数常见的分布序列.通过上述假设, 有如下定理1成立.

定理1 若假设1和假设2成立, 当α ≤ 1时, 若λ =Θ ( $\sqrt[]{n}$ ), 则至少有1-ε /2的概率使

$Δ_{n}^{2}$ ( $\overset{p}{\sum_{j}}$ ( ${\hat{θ}}_{j}$ - $θ_{j}^{*}$ ))=O_P

成立.特别地, 当α = 1时, 若

λ =Θ ( $\sqrt[]{\ln (n - 1) p} \sqrt[]{\ln n}$ ),

至少有1-ε /2的概率使得

$Δ_{n}^{2}$ ( $\overset{p}{\sum_{j}}$ ( ${\hat{θ}}_{j}$ - $θ_{j}^{*}$ ))= O_P( $\sqrt[]{n^{- 1} \ln n \cdot \ln (n - 1) p}$ )

成立.

定理1表明, 当α = 1时, 模型(2)至少有n^-1^/²的收敛速率(忽略对数因子).随着α 的减小, 收敛速率越来越慢, 但模型仍是收敛的.为了证明定理1, 首先引入定义1.

定义1^[6] 定义经验损失函数:

$\overset{︿}{M}$ (θ )= $\overset{n}{\sum_{i}} {\overset{︿}{M}}_{i}$ (θ _i),

其中

${\overset{︿}{M}}_{i}$ (θ _i)=ρ _τ(y_i-θ _i)-ρ _τ(y_i- $θ_{i}^{*}$ ),

令

M_i(θ _i)=E[ρ _τ(y_i-θ _i)-ρ _τ(y_i- $θ_{i}^{*}$ )],

$\overset{︿}{M}$ 的总体版本变成

M(θ )= $\overset{n}{\sum_{i}}$ M_i(θ _i).

使用定义1中的符号, 考虑M-估计量:

$\hat{θ}$ =arg $\min_{θ \in S \subset R^{np}} \overset{︿}{M}$ (θ ),

且

θ ^*∈ arg $\min_{θ \in R^{np}}$ M(θ ).

假设

θ ^*∈ S⊂R^np,

其中S表示贯穿本节的一般约束集.

定义2^[7] 对集合S⊂R^np, S的次高斯宽度定义为

SGW(S)=E( $\sup_{u \in S} \overset{np}{\sum_{i}}$ s_iu_i),

其中s₁, s₂, …, s_np为独立的1-次高斯随机变量.

令

D_j ∶ = DP_j, j=1, 2, …, p,

将式(2)改写为

arg $\min_{θ \in R^{np}} \frac{1}{n} \overset{n}{\sum_{i}}$ ρ _τ(y_i-(Wθ )_i)+λ Ω (θ ),

其中

$\Omega \left( \theta \right)=\alpha \sum\limits_{j=1}^{p}{{{\left\| {{D}_{j}}{{\theta }_{j}} \right\|}_{1}}}+\left( 1-\alpha \right)\sum\limits_{j=1}^{p}{{{\left\| {{\theta }_{j}} \right\|}_{2}}}, \theta =\left( {{\theta }_{11}}, \text{ }\ldots , \text{ }{{\theta }_{n1}}, \right.\text{ }\ldots , \text{ }{{\theta }_{1p}}, \left. \ldots , \text{ }{{\theta }_{np}} \right)_{np}^{T}, W={{1}^{T}}\otimes {{I}_{n}}$

因此, 构造矩阵

D=diag{D₁, D₂, …, D_p}₍_n_-1)_p_×_np,

其广义逆

D^†=diag{ ${D^{†}}_{1}$ , ${D^{†}}_{2}$ , …, ${D^{†}}_{p}$ },

${D^{†}}_{j}$ 表示D_j的广义逆, 投影矩阵

Ξ =diag{Π ₁, Π ₂, …, Π _p}_np_×_np,

Π _j表示Ker(D_j)上的投影矩阵, 则

D^†D=I_np-Ξ .

本文目标是求出在约束集S中M(· )- $\overset{︿}{M}$ (· )的期望值的上界.结合文献[7]的引理1, 得到如下引理2.

引理2 若假设1和假设2成立, 令δ ∈ R^np, 满足

Δ ²(Wδ )≤ t²,

则

SGW({δ ∶ δ ∈ S, Δ ²(Wδ )≤ t²})≤ ${\tilde{C}}_{1}$ ( $\frac{t^{2}}{\sqrt[]{n}}$ +t)+ ${\tilde{C}}_{2}$ [α $\sqrt[]{\ln (n - 1) p} \sqrt[]{\ln n} \overset{p}{\sum_{j}}$ ‖ Dδ _j‖ ₁+(1-α ) $\sqrt[]{n} \overset{p}{\sum_{j}}$ ‖ δ ‖ ₂],

其中 ${\tilde{C}}_{1}$ 、 ${\tilde{C}}_{2}$ 为正常数.

有了上述定义和引理作为基础, 现可给出定理1的证明.

证明固定μ ∈ [0, 1], 令

$\tilde{δ}$ =μ ( $\hat{θ}$ -θ ^*),

则由 $\hat{θ}$ 的最优性及目标函数的凸性, 有

$\overset{n}{\sum_{i}}$ ρ _τ(y_i- ${(W \tilde{θ})}_{i}$ )+λ Ω ( $\tilde{θ}$ )≤ $\overset{n}{\sum_{i}}$ ρ _τ(y_i- $(W θ^{*})_{i}$ )+λ Ω (θ ^*), (11)

其中 $\tilde{θ}$ =θ ^*+ $\tilde{δ}$ .因此

0≤ λ [Ω (θ ^*)-Ω ( $\tilde{θ}$ )]+A^*^T( $\tilde{θ}$ -θ ^*),

其中,

A^*∶ =(a^*, a^*, …, a^* ${)^{T}}_{np}$ ,
a* ⁼(-1 {1_≤ $\overset{p}{\sum_{j}} θ_{1 j}^{*}$ }τ -1 {2≤ $\overset{p}{\sum_{j}} θ_{2 j}^{*}$ }…, τ -1 {n≤ $\overset{p}{\sum_{j}} θ_{nj}^{*}$ }) ${^{T}}_{n}$

因此

A^*^T( $\tilde{θ}$ -θ ^*)=α A^*^T( $\tilde{θ}$ -θ ^*)+(1-α )A^*^T( $\tilde{θ}$ -θ ^*)=
α A^{* T}(In_p-Ξ +Ξ )( $\tilde{θ}$ -θ ^*)+(1-α )A^{* T}( $\tilde{θ}$ -θ ^*)=
α A^{* T}D^†D( $\tilde{θ}$ -θ ^*)+α A^{* T}Ξ ( $\tilde{θ}$ -θ ^*)+(1-α )A^*^T( $\tilde{θ}$ -θ ^*)^,

其中,

A^*^TD^†D( $\tilde{θ}$ -θ ^*)≤ ‖ A^*^TD^† $‖_{\infty} {‖D (\tilde{θ} - θ^{*})‖}_{1}$ ≤ ‖ A^*^TD^† $‖_{\infty} \overset{p}{\sum_{j}}$ ( ${‖D {\tilde{θ}}_{j}‖}_{1}$ +‖ D $θ_{j}^{*}$ ‖ ₁), A^{* T}Ξ ( $\tilde{θ}$ -θ ^*)≤ ‖ a^{* T}Π ‖ ₁‖ Π $\overset{p}{\sum_{j}}$ ( ${\tilde{θ}}_{j}$ - $θ_{j}^{*}$ )‖ $_{\infty}$ c( $n^{- \frac{1}{2}}$ Δ ²(Wδ )+Δ (Wδ )), A^{* T}( $\tilde{θ}$ -θ ^*)≤ $\overset{p}{\sum_{j}}$ ‖ a^*‖ ₂ ${‖{\tilde{θ}}_{j} - θ_{j}^{*}‖}_{2}$ ≤ ‖ a* ‖ ₂ $\overset{p}{\sum_{j}}$ ( ${‖{\tilde{θ}}_{j}‖}_{2}$ + $‖ θ_{j}^{*} ‖_{2}$ ).

(12)

式(12)可由文献[7]中引理20得到, c为正常数.由文献[21]知, 至少有1-2ε 的概率使得

$‖ A^{* T} D^{†} ‖_{\infty}$ ≤ R₁∶ =c₁ $\sqrt[]{\ln n} \sqrt[]{\ln (n - 1) p}$ ,

‖ a^*‖ ₂≤ R₂∶ =c₂ $\sqrt[]{n}$ ,

其中c₁、c₂均为正常数.因此, 令λ =2R₂, 存在常数C > 0, 使得

μ ( $\hat{θ}$ -θ ^*)∈ A∶ = {δ ∶ Ω (δ )≤ C(Ω (θ ^*)+ $\frac{α R_{1}}{R_{2}}$ ( $n^{- \frac{1}{2}}$ Δ ²(Wδ )+Δ (Wδ ))) } (13)

成立的概率至少为1-2ε .

令 $\hat{δ}$ = $\hat{θ}$ -θ ^*, 假设

Δ ²(W $\hat{δ}$ )> η ².

令

Δ ²(W $\hat{δ}$ )=q²,

设函数

g(t)=Δ ²(tW $\hat{δ}$ ), g∶ [0, 1]→ R.

显然, g为连续函数, 且

g(0)=0, g(1)=q².

则存在 $t_{\hat{δ}}$ , 使得g( $t_{\hat{δ}}$ )=η ².故对于

$\tilde{δ}$ = $t_{\hat{δ}}$ W $\hat{δ}$ , $t_{\tilde{δ}}$ ∈ [0, 1],

有

Δ ²(W $\tilde{δ}$ )=η ²

成立, 其中 $\tilde{δ}$ ∈ A, A为凸集.因此, 结合文献[6]引理13, 有

$\underset{Δ^{2} (W (u - θ^{*})) \leq η^{2}}{\sup_{u \in A,}}$ M(u)- $\overset{︿}{M}$ (u)≥ [M(θ ^*+ $\tilde{δ}$ )- $\overset{︿}{M}$ (θ ^*+ $\tilde{δ}$ )]≥ M(θ ^*+ $\tilde{δ}$ )≥ c₀η ².

由不等式(11)可知,

$\overset{︿}{M}$ (θ ^*+ $\tilde{δ}$ )+λ [Ω (θ ^*+ $\tilde{δ}$ )-Ω (θ ^*)]≤ 0.

因此

$\underset{Δ^{2} (Wδ) \leq η^{2}}{\sup_{δ \in A,}}$ [M(θ ^*+δ )- $\overset{︿}{M}$ (θ ^*+δ )+λ [Ω (θ ^*)-Ω (θ ^*+δ )]]≥ M(θ ^*+δ )≥ c₀η ².

故

{Δ ²(Wδ )≥ η ²}⊂{ $\underset{Δ^{2} (Wδ) \leq η^{2}}{\sup_{δ \in A}}$ [M(θ ^*+δ )- $\overset{︿}{M}$ (θ ^*+δ )+λ [Ω (θ ^*)-Ω (θ ^*+δ )]]≥ c₀η ²}. (14)

令ε ∈ (0, 1), 假设事件

I={μ ( $\hat{θ}$ -θ ^*)∈ A, ∀ μ ∈ [0, 1]}

发生的概率至少为1-ε /2, 则

P{Δ ²(W $\hat{δ}$ )> η ²}≤ P[{ $Δ_{}^{2}$ (W $\hat{δ}$ )> η ²}∩ I]+ $\frac{ε}{2}$ .

因此根据式(14)、马尔可夫不等式和三角不等式,

$\begin{align} & \Pi \left[ \left\{ \Delta _{{}}^{2}\left( W\hat{\delta } \right)> {{\eta }^{2}} \right\}\cap \Im \right] \\ & \le \Pi \left( \left\{ \underset{\delta \in \text{}, \Delta _{{}}^{2}\left( W\delta \right)\le {{\eta }^{2}}}{\mathop{\sup }}\, \left[ M\left( {{\theta }^{* }}+\delta \right)-\hat{M}\left( {{\theta }^{* }}+\delta \right)+\lambda \left[ \Omega \left( {{\theta }^{* }} \right)-\Omega \left( {{\theta }^{* }}+\delta \right) \right] \right]\ge {{c}_{0}}{{\eta }^{2}} \right\}\cap \Im \right) \\ & \le \frac{1}{{{c}_{0}}{{\eta }^{2}}}E\left( {{1}_{\Im }}\underset{\delta \in \text{}, \Delta _{{}}^{2}\left( W\delta \right)\le {{\eta }^{2}}}{\mathop{\sup }}\, \left[ M\left( {{\theta }^{* }}+\delta \right)-\hat{M}\left( {{\theta }^{* }}+\delta \right)+\lambda \left[ \Omega \left( {{\theta }^{* }} \right)-\Omega \left( {{\theta }^{* }}+\delta \right) \right] \right] \right) \\ & \le \frac{1}{{{c}_{0}}{{\eta }^{2}}}E\left( {{1}_{\Im }}\underset{\delta \in \text{}, \Delta _{{}}^{2}\left( W\delta \right)\le {{\eta }^{2}}}{\mathop{\sup }}\, \left[ M\left( {{\theta }^{* }}+\delta \right)-\hat{M}\left( {{\theta }^{* }}+\delta \right) \right] \right)+\frac{\lambda }{{{c}_{0}}{{\eta }^{2}}}E\left( {{1}_{\Im }}\underset{\delta \in \text{}, \Delta _{{}}^{2}\left( W\delta \right)\le {{\eta }^{2}}}{\mathop{\sup }}\, \Omega \left( \delta \right) \right). \\ \end{align}$

定义

H(η )={δ ∈ A∶ Δ (Wδ )≤ η }.

若δ ∈ H(η )且I成立, 则由式(13)可定义

$\mathcal{L}\left( \eta \right)=\left\{ \delta \Omega \left( \delta \right)\le C\left( \Omega \left( {{\theta }^{* }} \right)+\tilde{R}\left( {{n}^{{-1}/{2}\; }}{{\Delta }^{2}}\left( W\delta \right)+\Delta \left( W\delta \right) \right) \right)\Delta \left( \delta \right)\le \eta \right\}$,

则由文献[7]的引理15、引理16和本文引理2可知,

$\begin{align} & \text{}\left[ \left\{ \Delta _{{}}^{2}\left( W\hat{\delta } \right)> {{\eta }^{2}} \right\}\cap \Im \right] \\ & \le \frac{1}{{{c}_{0}}{{\eta }^{2}}}E\left( \underset{\delta \in \mathcal{L}\left( \eta \right)}{\mathop{\sup }}\, \left[ M\left( {{\theta }^{* }}+\delta \right)-\hat{M}\left( {{\theta }^{* }}+\delta \right) \right] \right)+\frac{\lambda }{{{c}_{0}}{{\eta }^{2}}}\underset{\delta \in \mathcal{L}\left( \eta \right)}{\mathop{\sup }}\, \Omega \left( \delta \right) \\ & \le \frac{1}{{{c}_{0}}{{\eta }^{2}}}E\left[ SGW\left( \delta \in \mathcal{L}\left( \eta \right), \Delta _{{}}^{2}\left( W\delta \right)\le {{\eta }^{2}} \right) \right]+\frac{\lambda }{{{c}_{0}}{{\eta }^{2}}}\underset{\delta \in \mathcal{L}\left( \eta \right)}{\mathop{\sup }}\, \Omega \left( \delta \right) \\ & \le \frac{1}{{{c}_{0}}{{\eta }^{2}}}\left( {{C}_{1}}\left( \frac{{{\eta }^{2}}}{\sqrt{n}}+\eta \right)+{{C}_{2}}\left( \alpha \sqrt{\log \left( n-1 \right)p}\sqrt{\log n}\cdot \sqrt{n}+\left( 1-\alpha \right)\sqrt{n}\cdot \sqrt{n} \right) \right)+\frac{\lambda }{{{c}_{0}}{{\eta }^{2}}}C\left( \sqrt{n}+\tilde{R}\left( \frac{{{\eta }^{2}}}{\sqrt{n}}+\eta \right) \right), \\ \end{align}$

其中C₁、C₂、C均为正常数.因此, 当α ≤ 1时, 令λ =2R₂, 取η =c_γ $n^{\frac{1}{2}}$ , 使得

$\text{}\left[ \left\{ {{\Delta }^{2}}\left( W\hat{\delta } \right)> {{\eta }^{2}} \right\}\cap \Im \right]\le \varepsilon $,

成立, 其中常数c_γ> 1.根据文中的符号定义,

$Δ_{n}^{2}$ (W $\hat{δ}$ )=O_P(1).

特别地, 当α =1时, 选择λ =2R₁, 取

η = $c_{\bar{γ}} n^{\frac{1}{4}} [\ln n \cdot \ln {(n - 1) p]}^{\frac{1}{4}}$ ,

有

$Δ_{n}^{2}$ (W $\hat{δ}$ )=O_P( $\sqrt[]{n^{- 1} \ln n \cdot \ln (n - 1) p}$ )

成立, 其中 $c_{\bar{γ}}$ > 1.

5 实验及结果分析

5.1 评估标准

为了评估AQFL和BC-ADMM的性能, 选择人工数据集和真实数据集进行实验.使用加性模型生成一些人工数据集, 这些数据集具有重尾和异方差等特性, 设 $y_{i}^{*}$ 和 ${\hat{y}}_{i}$ (τ )表示第i个测试样本的观测值和预测的τ 分位数值, 其中预测来源于使用训练数据拟合的模型.下面给出具体的评估标准.

1)均方误差(Mean Square Error, MSE):

MSE= $\frac{1}{n} \overset{n}{\sum_{i}} [y_{i}^{*} - {\hat{y}}_{i} {(τ)]}^{2}$ .

2)平均绝对误差(Mean Absolute Error, MAE):

MAE= $\frac{1}{n} \overset{n}{\sum_{i}} |y_{i}^{*} - {\hat{y}}_{i} (τ)|$ .

3)平均检验误差(Mean Check Error, MCE):

MCE= $\frac{1}{n} \overset{n}{\sum_{i}}$ ρ _τ[ $y_{i}^{*}$ - ${\hat{y}}_{i}$ (τ )].

4)真变量(True Vector, TV):正确包含在模型中的非零协变量的数目.

5)非零项(Non-Zero, NZ):预测结果中 ${\hat{f}}_{j}$ 非零的数目.

6)最小比(Proportion Smaller, PS):测试集上响应真实值的最小值和其预测值的比例, PS的值应接近τ .

5.2 合成数据实验

本节选择如下对比方法:QGAM(Quantile Gene-ralized Additive Models)^[4]、QA-SCAD^[5]和FLAM(Fu-sed Lasso Additive Model)^[18], 验证AQFL的优越性.QGAM基于秩为30的三次回归样条基数, 利用qgam包实现.QA-SCAD使用rqPen包实现, 参数设置为a = 3.7, 罚函数为SCAD(Smoothly Clipped Absolute Deviation)罚, 算法选择QICD(Quantile Iterative Coordinate Descent).FLAM使用flam包实现, 采用K折交叉验证选取参数λ .

在所有数据生成的设置中, 协变量分两步生成.首先, 通过 $\tilde{x}$ ~N(0_p, Σ _p)生成n个有p维协变量的观察值, 其中σ _jk为Σ _p的第j行第k列元素, 且

σ _jk= $0 . 5^{|j - k|}$ .

其次, 在向量a= $(a_{1}, a_{2}, \dots, a_{p})^{T}$ ∈ R^p上定义

Φ (a)= ${Φ (a_{1}), Φ (a_{2}), \dots, Φ (a_{p} {)}}^{T}$ ∈ R^p,

其中Φ (· )为标准正太分布的累积分布函数.从而通过x=Φ ( $\tilde{x}$ )生成p维协变量.

5.2.1 低维合成数据实验

从如下3种问题的模型中分别生成500个训练样本, 并从同一模型生成1 000个测试样本.

1)问题1:

y_i= $θ_{i 1}^{*}$ + $θ_{i 2}^{*}$ + $θ_{i 3}^{*}$ + $θ_{i 4}^{*}$ +ε _i, ε _i~N(0, 1).

2)问题2:

y_i= $θ_{i 1}^{*}$ + $θ_{i 2}^{*}$ + $θ_{i 3}^{*}$ + $θ_{i 4}^{*}$ +ε _i, ε _i~0.5t(3).

3)问题3:

y_i= $θ_{i 1}^{*}$ + $θ_{i 2}^{*}$ + $θ_{i 3}^{*}$ + $θ_{i 4}^{*}$ ε _i, ε _i~N(0, 1).

其中,

$θ_{ij}^{*}$ =f_j(x_ij),
i=1, 2, …, n, j=1, 2, 3, 4.

图1为数据的生成图, 其中f_j为分段常数函数或在定义域的某些区域恒定其它区域高度可变的函数, 用于说明AQFL的局部自适应性.进而由问题1~问题3得到服从正态分布、重尾分布和具有异方差性质的数据, 说明AQFL可灵活适应于不同的数据分布和模型假设.将问题1~问题3称为低维设置.问题1和问题2是同方差的, 第τ 分位数

$Q_{(y_{i} |x_{i})}$ (τ )=f₁(x_i₁)+f₂(x_i₂)+f₃(x_i₃)+f₄(x_i₄)+Φ ^-1(τ ),

主要关注中位数τ = 0.5的情况.问题3是异方差的, 第τ 条件分位数

$Q_{(y_{i} |x_{i})}$ (τ )=f₁(x_i₁)+f₂(x_i₂)+ f₃(x_i₃)+f₄(x_i₄)Φ ^-1(τ ),

主要关注分位数τ = 0.9, 0.1的情况.

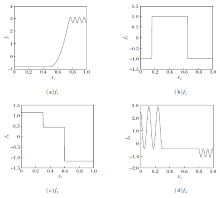	Figure Option View Download New Window
	图1 在低维合成数据实验中用于生成各个协变量的相应函数值的4个真实函数Fig.1 Four real functions for generating respective function values of each covariate in low-dimensional synthetic data experiments

分位数回归方法可直接对分位数进行建模, 但均值回归方法不能提供非中位数的估计值, 所以对于问题3生成的数据, 本文只对比分位数估计器.

为了全面评估AQFL的性能, 本文对3种不同的问题下生成的数据进行模拟实验.在实验中, 使用测试集MSE最小时对应的调优参数λ 评估AQFL.依据定理1结论, 取参数α = 0.5, 0.75, 1, 用于提升模型的收敛性.由于QGAM只适用于低维情况, 所以在低维数据上计算测试集的MSE、MCE和PS值, 对比AQFL、QGAM和FLAM的性能.在对中位数建模时, MAE是MCE的2倍.因此, FLAM通过MAE值除以2得到MCE值.为了可靠评估3个模型的性能, 对每个模型的模拟实验重复运行50次.

在低维情况下, 3个模型在问题1~问题3上的拟合结果如表1所示.由表可知, 在低维数据上, QFAL在α =1时效果最优, 因此本节主要对比α =1时的实验结果.在问题1中, FLAM拟合效果更优的原因是它拟合均值模型, 而AQFL(τ =0.5)拟合中位数模型.因为正态分布的均值是其位置参数, 均值回归在正态分布的数据上通常能够更好地捕捉数据的整体趋势, 从而产生较小的MSE.问题2中AQFL的各指标值都优于其它两个模型, 充分说明相比均值回归模型, 分位数模型更适合具有重尾分布的数据.在问题3的异方差特征的数据中, 相比QGAM, AQFL在不同分位数水平上的拟合效果更优.因此, AQFL在预测方面做得更优.此外, 在区域的一个部分快速变化而在另一个部分恒定的数据上, AQFL比QGAM拟合效果更优, 说明AQFL具有局部自适应性.

表1 低维情况下各模型在3个问题上的拟合结果 Table 1 Fitting results of different models for 3 questions in low dimension

本文使用问题1中的响应生成方式, 即使用参数α = 1和MSE最小时对应的λ 值绘制图2, 对比FLAM、AQFL(τ =0.5)和QGAM(τ =0.5)在4个函数上的预测曲线以及它们重复50次后的标准误差, 其中, AQFL和FLAM使用自举法, 逐点计算标准误差.

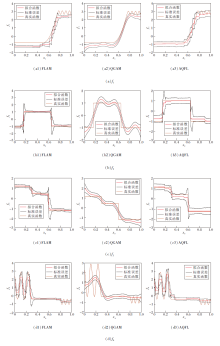	Figure Option View Download New Window
	图2 各模型在4个函数上的拟合曲线及真实曲线对比Fig.2 Comparison of fitted curves and real curves among different models on 4 functions

由图2可见, 对比FLAM和AQFL在0.5分位数时的拟合效果, 直观说明AQFL能够代替均值回归模型.相比AQFL更熟练地适应函数的常量和快速变化区域, QGAM的局部适应性是有限的.因为它施加的惩罚类型使λ 鼓励整个 ${\hat{f}}_{j}$ 为0, 而基函数的数量控制每个 ${\hat{f}}_{j}$ 的灵活性.基函数越少, 函数拟合变量越少; 基函数越多, 函数拟合变量越多.但是, 可改变的数量不能在函数拟合的范围内发生很大的变化, 所以在选定基函数的数量后, QGAM在分段常数型数据(b2)、(c2)上过拟合, 而在局部剧烈变化的数据(a2)、(d2)上欠拟合.

5.2.2 高维合成数据实验

本节考虑在5.2.1节的问题1~问题3上添加96个噪声函数(即f₅=0, f₆=0, …, f₁₀₀=0)的高维设置.为简单起见, 仍记为问题1~问题3, 参数α 和λ 等其它设置与5.2.1节一致, 并在高维数据的计算中增加TV和NZ两个评估标准, 以评估AQFL、QA-SCAD和FLAM预测和变量选择的性能.为了可靠评估3个模型的性能, 对每个模型的模拟实验重复运行50次.

在高维情况下, 3个模型在问题1~问题3上的拟合结果如表2所示.由表可见, 在具有噪声函数的高维数据上, AQFL在α = 0.75时的指标值最优.当α = 1时, AQFL只能将模型参数推向0附近, 无法实现与α < 1的AQFL相当的稀疏性, 这充分说明模型添加l₂罚对变量选择的重要性.而在α = 0.5时, l₂罚函数作用增加, 可能会过度惩罚一些模型参数, 使原本非零的变量整体为0.

表2 高维情况下各模型在3个问题上的拟合结果 Table 2 Fitting results of different models for 3 questions in high dimension

因此, 本节主要对比α = 0.75时的实验结果.FLAM在问题1上拟合效果更优, 这与低维设置中的原因一致.

下面重点关注TV和NZ两个反映模型能否正确进行变量选择的指标.在问题1和问题2中, AQFL、FLAM和QA-SCAD都包含真正的协变量.因为只有4%的变量是真正的非零变量, 而AQFL选择很多实际为0的无关变量, 所以QA-SCAD的NZ值略优于AQFL.可通过类比最小二乘设置中的Lasso来理解这种现象.当使用预测精度MSE选择Lasso的调优参数时, Lasso在模型预测和变量选择上实现的效果通常是不一致的^[22], 故本节选择的调优参数有利于预测, 但不利于变量选择.在异方差数据的问题3中, 对于TV标准, AQFL效果更优, 可正确选择非零变量, 而QA-SCAD会导致系数过度收缩, 不能正确选择非零的变量, 因此AQFL更适合在有维数噪声的高维数据上实现极端分位数的预测和变量选择.

在高维情况下, AQFL、FLAM和QA-SCAD在不同问题上生成响应数据, 共计训练50次, 并对训练时间取平均值, 结果如图3所示.针对问题3的异方差数据, FLAM不能提供非中位数的估计值, 因此只对比AQFL和QA-SCAD的训练时间.由图可见, AQFL在训练时间上处于中等水平.这是因为FLAM只能处理均值回归模型, 而AQFL基于分位数损失函数, 需要更多的迭代步骤找到全局最优解, 导致训练时间增加.在处理加性分位数回归问题时, 相比QA-SCAD, AQFL在3个问题上都具有更高的训练效率.因此, AQFL在实际应用中仍具有一定的优势.

	Figure Option View Download New Window
	图3 高维情况下各模型在不同问题上的训练时间对比Fig.3 Training time comparison of different models for 3 problems in high dimension

5.3 碎猪肉数据实验

为了体现AQFL优势, 在一组真实数据上进行实验, 并与QA-SCAD^[5]进行对比.本文分析来自faraway包中通过测量240个碎猪肉样品的脂肪含量和100通道吸收光谱获得的215个样本, 删除5个具有离群值的观测值, 留下210个样本, 从中随机抽取200个样本作为训练数据, 另外10个样本作为测试数据.由于信道频谱数据高度相关, 所以使用前30个主成分转换预测因子.主成分居中并按比例排列, 使其平均值为0, 标准差为1.使用30个主成分作为协变量对脂肪含量的对数进行拟合.

拟合分位数回归模型需要选择τ .2个τ 值可用于创建一个不需要对误差进行参数假设的预测区间.例如, τ = 0.1, 0.9的模型可用于创建80%的预测区间.如果对整个条件分布感兴趣, 可使用更大范围的τ 值.为了估计整个条件分布, 定义多个τ 值检验AQFL, 取

τ ∈ Τ = {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9}.

参数λ 选择如5.2节所述, 计算过程重复100次.

设y_ij表示测试数据的第i个样本的第j个缩放居中对数值, ${\hat{y}}_{ij}^{τ}$ 表示其对应的第τ 分位数的估计值.文献[5]在真实数据集上定义MCE和分位数偏差(Quantile Bias, QB):

MCE= $\frac{1}{10} \sum_{τ} \overset{10}{\sum_{i}}$ ρ _τ(y_ij- ${\hat{y}}_{ij}^{τ}$ ),
QB= $\sum_{τ} |\frac{1}{1000} \overset{100}{\sum_{j}} \overset{10}{\sum_{i}} 1 (y_{ij} \leq {\hat{y}}_{ij}^{τ}) - τ|$

使用MSE(τ = 0.5)、MAE(τ = 0.5)、MCE(τ ∈ Τ )和QB(τ ∈ Τ )这4个标准评估模型.从5.2.2节实验知α = 0.75时效果最优, 所以表3对比AQFL(α = 0.75)和QA-SCAD的平均值, 由此说明AQFL能够适应不同的数据类型.

表3 AQFL和QA-SCAD在对碎猪肉数据的指标值平均值 Table 3 Mean average index values of AQFL and QA-SCAD on ground pork data

6 结束语

分段型数据在实际数据中很常见, 因此准确估计具有这种结构的数据是一个重要的研究课题, 然而在多元情况下, 缺乏关于分段数据的稳健估计.因此, 本文提出基于融合Lasso的非参数加性分位数回归模型(AQFL), 并给出相应算法, 有效计算优化问题的解, 从理论角度证明模型的预测一致性.在合成数据和真实数据上的实验评估AQFL的性能, 实验表明, AQFL具有较优的鲁棒性和局部适应性, 并且研究结果具有一定的推广价值.

本文责任编委郝志峰

Recommended by Associate Editor HAO Zhifeng

参考文献

文献选项

[1]	KOENKER R, BASSETT G. Regression Quantiles. Econometrica, 1978, 46(1): 33-50. [本文引用:1]
[2]	DE GOOIJER J G, ZEROM D. On Additive Conditional Quantiles with High-Dimensional Covariates. Journal of the American Statistical Association, 2003, 98(461): 135-146. [本文引用:1]
[3]	GAILLARD P, GOUDE Y, NEDELLEC R. Additive Models and Ro-bust Aggregation for GEFCom2014 Probabilistic Electric Load and Electricity Price Forecasting. International Journal of Forecasting, 2016, 32(3): 1038-1050. [本文引用:1]
[4]	FASIOLO M, WOOD S N, ZAFFRAN M, et al. qgam: Bayesian Non-parametric Quantile Regression Modelling in R. Journal of Statistical Software, 2021, 100(9). DOI: 10.18637/jss.v100.i09. [本文引用:2]
[5]	SHERWOOD B, MAIDRNAN A. Additive Nonlinear Quantile Regression in Ultra-High Dimension. Journal of Machine Learning Research, 2022, 23(1): 2741-2787. [本文引用:4]
[6]	PADILLA O H M, CHATTERJEE S. Risk Bounds for Quantile Trend Filtering. Biometrika, 2022, 109(3): 751-768. [本文引用:5]
[7]	YE S S, PADILLA O H M. Non-parametric Quantile Regression via the K-NN Fused Lasso. Journal of Machine Learning Research, 2021, 22: 1-38. [本文引用:7]
[8]	PIETROSANU M, GAO J Y, KONG L L, et al. Advanced Algorithms for Penalized Quantile and Composite Quantile Regression. Computational Statistics, 2021, 36(1): 333-346. [本文引用:1]
[9]	BOYD S, PARIKH N, CHU E, et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Foundations and Trends® in Machine Learning, 2011, 3(1): 1-122. [本文引用:1]
[10]	HUNTER D R, LANGE K. Quantile Regression via an MM Algori-thm. Journal of Computational and Graphical Statistics, 2000, 9(1): 60-77. [本文引用:1]
[11]	WU T T, LANGE K. Coordinate Descent Algorithms for Lasso Pe-nalized Regression. The Annals of Applied Statistics, 2008, 2(1): 224-244. [本文引用:1]
[12]	HOCHBAUM D S, LU C. A Faster Algorithm for Solving a Gene-ralization of Isotonic Median Regression and a Class of Fused Lasso Problems. SIAM Journal on Optimization, 2017, 27(4): 2563-2596. [本文引用:1]
[13]	BRANTLE H L, GUINNESS J, ERIC C C. Baseline Drift Estimation for Air Quality Data Using Quantile Trend Filtering. The Annals of Applied Statistics, 2020, 14(2): 585-604. [本文引用:1]
[14]	TIBSHIRANI R, SAUNDERS M, ROSSET S, et al. Sparsity and Smoothness via the Fused Lasso. Journal of the Royal Statistical Society(Series B), 2005, 67(1): 91-108. [本文引用:1]
[15]	KIM S J, KOH K, BOYD S, et al. l₁ Trend Filtering. SIAM Review, 2009, 51(2): 339-360. [本文引用:1]
[16]	TIBSHIRANI R J. Adaptive Piecewise Polynomial Estimation via Trend Filtering. The Annals of Statistics, 2014, 42(1): 285-323. [本文引用:1]
[17]	YUAN M, LIN Y. Model Selection and Estimation in Regression with Grouped Variables. Journal of the Royal Statistical Society(Series B), 2006, 68(1): 49-67. [本文引用:1]
[18]	PETERSEN A, WITTEN D, SIMON N. Fused Lasso Additive Mo-del. Journal of Computational and Graphical Statistics, 2016, 25(4): 1005-1025. [本文引用:2]
[19]	YU K M, MOVEED R A. Bayesian Quantile Regression. Statistics and Probability Letters, 2001, 54(4): 437-447. [本文引用:1]
[20]	TIBSHIRANI R J, TAYLOR J. Degrees of Freedom in Lasso Pro-blems. The Annals of Statistics, 2012, 40(2): 1198-1232. [本文引用:1]
[21]	STONE C J. The Dimensionality Reduction Principle for Generali-zed Additive Models. The Annals of Statistics, 1986, 14(2): 590-606. [本文引用:1]
[22]	LENG C L, LIN Y, WAHBA G. A Note on the Lasso and Related Procedures in Model Selection. Statistica Sinica, 2006, 16(4): 1273-1284. [本文引用:1]

1978

0.0

... 分位数回归^[1]是一种用于估计感兴趣的条件分位数的鲁棒方法,对重尾分布具有天然的鲁棒性,可正确拟合异方差关系,为响应的条件分布提供全面的分析,其稀疏度水平可随分位数变化而变化 ...

2003

0.0

... 受加性模型和广义加性模型工作的启发,de Gooijer等^[2]提出基于核方法建模以估计加性非线性条件分位数模型,证明对于固定维数p,加性分位数回归达到与加性均值回归相同的收敛速度,从而在理论上减轻维数困扰,但是方法需要对维数p#cod#x02265 ...

2016

0.0

... Gaillard等^[3]通过B样条拟合广义加性分位数模型生成温度情景,将其插入概率预测负荷模型,得到电力负荷预测的最佳效果 ...

2021

0.0

... Fasiolo等^[4]使用样条基展开拟合响应和感兴趣的分位数之间的平滑关系,给出条件分位数校准公式,快速自动估计平滑参数 ...

... 2 合成数据实验本节选择如下对比方法:QGAM(Quantile Gene-ralized Additive Models)^[4]、QA-SCAD^[5]和FLAM(Fu-sed Lasso Additive Model)^[18],验证AQFL的优越性 ...

2022

0.0

... Sherwood等^[5]提出QA-SCAD,利用组惩罚实现超高维加性分位数回归问题估计和变量选择的同时进行 ...

... 2 合成数据实验本节选择如下对比方法:QGAM(Quantile Gene-ralized Additive Models)^[4]、QA-SCAD^[5]和FLAM(Fu-sed Lasso Additive Model)^[18],验证AQFL的优越性 ...

... 3 碎猪肉数据实验为了体现AQFL优势,在一组真实数据上进行实验,并与QA-SCAD^[5]进行对比 ...

... 文献[5]在真实数据集上定义MCE和分位数偏差(Quantile Bias, QB): ...

2022

0.0

... 现有的均值回归模型在理论和计算上的结论无法直接应用在分位数回归上,因此,在理论方面,Padilla等^[6]给出分位数回归预测一致性的损失函数 ...

... 文献[6]在分位数上定义函数 ...

... 假设2^[6] 若存在一个常数L #cod#x0003E ...

... 定义1^[6] 定义经验损失函数: ...

... 因此,结合文献[6]引理13,有 ...

2021

0.0

... Ye等^[7]在此基础上研究分位数K-NN Fused Lasso,证明K-NN Fused Lasso接近极小极大收敛速度 ...

... 5作为R的取值,确保研究过程更严谨、可靠^[7] ...

... 存在有界变化,放缩值 n来自文献[7] ...

... 定义2^[7] 对集合S⊂R^np,S的次高斯宽度定义为 ...

... 结合文献[7]的引理1,得到如下引理2 ...

... 式(12)可由文献[7]中引理20得到,c为正常数 ...

... 则由文献[7]的引理15、引理16和本文引理2可知, ...

2021

0.0

... 在计算方面,Pietrosanu等^[8]研究高维分位数回归问题,使用ADMM(Alternating Direction Method of Multipliers)^[9] 、MM(Majorize-Minimize) Algorithm^[10]以及Coordinate Descent Algorithm^[11]进行变量选择,获得估计量 ...

2011

0.0

2000

0.0

2008

0.0

2017

0.0

... Hochbaum等^[12]开发O(nlogn)次的分位数融合Lasso快速算法 ...

2020

0.0

... Brantle等^[13]提出Parallelizable ADMM Algorithm,计算一维数据的k阶分位数趋势滤波估计量 ...

2005

0.0

... Tibshirani等^[14]提出的非参数融合Lasso罚模型,通过响应向量y和有序的单变量x估计向量 ...

2009

0.0

... Kim等^[15]将讨论扩展到单变量非参数趋势滤波罚模型,并将趋势滤波罚函数定义为输入数据上的k + 1阶差分算子,将融合Lasso归纳为k = 0的情况 ...

2014

0.0

... 之后,Tibshirani^[16]将趋势滤波罚与样条方法进行详细对比 ...

2006

0.0

... _j上使用组Lasso诱导稀疏性之间提供一种权衡^[17],从而实现模型拟合和变量选择的同时进行 ...

2016

0.0

... 式(6)有如下估计^[18]: ...

... 2 合成数据实验本节选择如下对比方法:QGAM(Quantile Gene-ralized Additive Models)^[4]、QA-SCAD^[5]和FLAM(Fu-sed Lasso Additive Model)^[18],验证AQFL的优越性 ...

2001

0.0

... 分位数回归的BIC^[19]计算公式如下: ...

2012

0.0

... v等于罚项的非零元素的个数^[20] ...

1986

0.0

... 由文献[21]知,至少有1-2#cod#x003b5 ...

2006

0.0

... 当使用预测精度MSE选择Lasso的调优参数时,Lasso在模型预测和变量选择上实现的效果通常是不一致的^[22],故本节选择的调优参数有利于预测,但不利于变量选择 ...