李金海,博士,教授,主要研究方向为认知计算、粒计算、大数据分析、概念格、粗糙集.E-mail:jhlixjtu@163.com.
作者简介:

王 坤,硕士研究生,主要研究方向为三元概念分析、并行计算.E-mail:wang_kun@stu.kust.edu.cn.

陈强强,博士研究生,主要研究方向为数据挖掘、机器学习.E-mail:chen_qiangqiang@163.com.
作为形式概念分析的扩展,三元概念分析在高维数据的理论和应用中均取得显著效果.然而,数据量的极速增长导致三元概念的生成算法的时间复杂度呈指数级增长,在现实应用中面临巨大挑战,需要构造并行算法.因此文中提出适用于大规模数据的三元概念分布式并行构造算法,首先给出对象-属性和属性-条件三元概念的相关理论,并证明所有三元概念可通过合并这两种类型的中间概念生成.然后,采用两阶段聚合策略,改进Spark框架中的弹性分布式数据集操作符,有效解决数据倾斜问题,明显提升算法的运行效率.最后,在多个公开数据集上的实验表明,文中算法在海量数据中的三元概念生成过程中表现高效.
LI Jinhai, Ph.D., professor. His research interests include cognitive computing, granular computing, big data analysis, concept lattice and rough set.
About Author:
WANG Kun, Master student. His research interests include triadic concept analysis and parallel computing.
CHEN Qiangqiang, Ph.D. candidate. His research interests include data mining and machine learning.
As an extension of formal concept analysis, triadic concept analysis achieves significant results in both theory and applications of high-dimensional data. However, the time complexity of triadic concept generation algorithms, caused by the rapid growth of data volume, typically grows exponentially, presenting significant challenges in practical applications. Therefore, parallel algorithms are crucial. In this paper, a distributed parallel construction algorithm for triadic concepts suitable for large-scale data is proposed. First, the theories of object-attribute triadic concepts and attribute-condition triadic concepts are provided, and it is proved that all triadic concepts can be generated by merging these two types of intermediate concepts. Second, a two-stage aggregation strategy is employed to improve the resilient distributed dataset operator in the Spark framework. Consequently, the data skew problem is effectively solved and the efficiency of the proposed algorithm is significantly improved. Finally, experiments on multiple public datasets indicate that the proposed algorithm performs efficiently in generating triadic concepts for large datasets.
形式概念分析[1]的主要研究对象为概念, 包括外延与内涵, 具体为确定对象与属性之间的关系[2].现有的生成概念算法主要包括增量算法[3, 4, 5]和批处理算法[6, 7].增量算法是在当前数据生成概念的基础上进行动态更新以得到新概念的方法, 而批处理算法是在完整数据集上进行批次概念构造.随着人工智能的快速发展, 数据量显著增长, 生成概念所需的时空复杂度急剧上升[8].因此, 迫切需要能更高效构建概念的算法.这些研究推动形式概念分析的快速发展, 并促进其在机器学习分类和特征选择等领域的广泛应用[9, 10, 11, 12].
Wille[13]根据实际需求进一步将形式概念分析从二元扩展到三元, 提出三元概念分析, 即把形式概念分析的对象集和属性集拓展为对象集、属性集和条件集, 主要描述它们之间的三元关系[14].三元概念分析继承并推广形式概念分析的方法和技巧, 是处理和分析高维数据的重要框架之一.近年来, 三元概念分析发展迅速, 在理论和应用上均取得一定进展.理论方面的研究主要包含:三元概念构造三元格[13, 14, 15]、三元概念诱导三元规则的生成[16, 17]、三元概念聚类[18, 19]及三元概念结合其它理论的研究[20, 21, 22].应用方面的研究主要有概念认知系统[23]、动态社交网络社团挖掘[24]、文本分类[25]等.
无论是理论研究还是创新应用, 三元概念的构建都是不可或缺的基础问题.因此, 学者们致力于研究三元概念的高效生成算法.李俊余等[26]研究形式概念分析和三元概念分析之间的关系, 并给出三元概念的一种构造方式[27], 之后将布尔矩阵引入三元概念分析中, 探讨如何使用布尔矩阵构造三元概念[28].祁建军等[29]对三元背景和概念三元格提出一种简化方式, 提高三元概念的构造效率.Konecny等[30]在一个高度概括的框架下分析三元概念, 该框架统一涵盖多种潜在的扩展形式.Ananias等[31]提出基于三元组查询识别三元概念的方法, 使三元概念Hasse图的可视化和探索成为可能.Wan等[32]在三元概念分析与形式概念分析之间关系的基础上, 引入粒度属性的概念, 提出多粒度三元背景.
上述三元概念构造方法主要包括:对象-条件三元概念构造方法[28]、枚举法[26]和增量式构造方法[33].这些方法都采用串行方式进行三元概念的构建.由于三元概念分析的诱导算子结构较复杂, 数据量的爆炸式增长将导致串行三元概念构造算法的时间复杂度呈指数级增长, 难以有效处理海量且结构复杂的数据[34].因此, 分布式并行技术在三元概念构造中的应用成为一个重要的研究方向[35].开发高效的分布式并行构造方法已成为三元概念分析研究中的重要课题之一.
一些学者现已将MapReduce计算框架用于形式概念的构建[36, 37].MapReduce框架主要包括Map和Reduce两个阶段, 由于两个阶段之间的数据需要写入磁盘, 导致资源利用率较低.而Spark框架是一种基于内存处理的分布式计算框架[38], 具有处理快速、通用性高、用户友好和兼容性强等特点, 其核心组件之一是弹性分布式数据集.弹性分布式数据集采用一种容错的并行数据结构, 使用户能在多个数据节点上执行各种转换操作(如map、filter、join等)和动作操作(如reduce、collect、count等).尽管Spark框架具有超高的计算性能, 但存在数据混洗[39]过程中因数据不均衡而发生数据倾斜的问题, 因此提高其运行效率是必要的, 具体操作是通过局部聚合和全局聚合降低数据倾斜.
本文研究基于Spark框架的分布式并行算法, 给出临时概念、临时属性-条件三元概念以及过程三元概念的定义, 为了进一步构造全部的三元概念提出对象-属性和属性-条件两种三元概念, 并证明可通过合并这两种类型的三元概念生成所有三元概念.不仅如此, 还设计包含两阶段聚合策略的三元概念分布式并行构造算法, 有效应对数据倾斜问题.最后, 在多节点的分布式集群上运行该算法, 评估其在处理不同规模数据集时的性能表现.
本节介绍三元形式概念分析的基本理论.
定义1[1] 设F=(U, A, I)为形式背景, 其中
$U=\left\{u_{1}, u_{2}, \cdots, u_{l}\right\}, $
表示对象集,
$A=\left\{a_{1}, a_{2}, \cdots, a_{m}\right\}$
表示属性集.I表示笛卡尔积U× A上的二元关系, (u, a)∈ I表示对象u拥有属性a, 或属性a被对象u拥有.
$\forall U_{i} \subseteq U, A_{j} \subseteq A$, 定义如下算子:
$f\left(U_{i}\right)=\left\{a \in A \mid \forall u \in U_{i}, (u, a) \in I\right\}, $
表示Ui中所有对象共同拥有的属性集;
$g\left(A_{j}\right)=\left\{u \in U \mid \forall a \in A_{j}, (u, a) \in I\right\}, $
表示拥有Aj中所有属性的对象集.若
$f\left(U_{i}\right)=A_{j}, g\left(A_{j}\right)=U_{i}, $
则称序对(Ui, Aj)为概念, 其中Ui为概念的外延, Aj为概念的内涵.本文将所有形式概念组成的集合记为Ω .
对于$\forall U_{1} \subseteq U, U_{2} \subseteq U, \forall A_{1} \subseteq A, A_{2} \subseteq A$, 有如下性质成立:
1)$U_{1} \subseteq U_{2} \Rightarrow f\left(U_{2}\right) \subseteq f\left(U_{1}\right), $
2)$A_{1} \subseteq A_{2} \Rightarrow g\left(A_{2}\right) \subseteq g\left(A_{1}\right), $
3)$f\left(U_{1} \cup U_{2}\right)=f\left(U_{1}\right) \cap f\left(U_{2}\right), $
4)$f\left(U_{1} \cap U_{2}\right) \supseteq f\left(U_{1}\right) \cup f\left(U_{2}\right) .$
不仅如此, ∀ (U1, A1)∈ Ω , (U2, A2)∈ Ω , 上述算子满足关系:
$\begin{array}{l} \left(U_{1}, A_{1}\right) \vee\left(U_{2}, A_{2}\right)=\left(g f\left(U_{1} \cup U_{2}\right), A_{1} \cap A_{2}\right), \\ \left(U_{1}, A_{1}\right) \wedge\left(U_{2}, A_{2}\right)=\left(U_{1} \cap U_{2}, f g\left(A_{1} \cup A_{2}\right)\right) . \end{array}$
上述内容介绍形式概念分析的基本理论, 包括属性与对象之间的关系及概念定义.此外给出概念之间的关系, 即随着对象增多, 它们拥有的属性减少; 随着对象减少, 它们拥有的属性增多.
定义2[14] 设T=(U, A, C, Y)为一个三元背景, 其中
U={u1, u2, …, ul}
表示对象集, 每个ui(i≤ l)表示一个对象;
A={a1, a2, …, am}
表示属性集, 每个aj(j≤ m)表示一个属性;
C={c1, c2, …, cn}
表示条件集, 每个ck(k≤ n)表示一个条件.Y为U、A和C之间的三元关系:
Y⊆U× A× C.
若u、a和c具有关系Y, 记为(u, a, c)∈ Y, 表示对象u在条件c下具有属性a.
∀ Ui⊆U, Z⊆Aj× Ck, (* )-诱导算子定义如下:
$\begin{array}{l} U_{i}^{(* )}= \\ \left\{\left(a_{j}, c_{k}\right) \in A_{j} \times C_{k} \mid \forall u_{i} \in U_{i}, \left(u_{i}, a_{j}, c_{k}\right) \in Y\right\}, \\ Z^{(* )}=\left\{u_{i} \in U_{i} \mid \forall\left(a_{j}, c_{k}\right) \in Z, \left(u_{i}, a_{j}, c_{k}\right) \in Y\right\} \end{array}$
当$A_{j} \subseteq A, C_{k} \subseteq C, $定义(i, j, Ck)-诱导算子如下:
$\begin{array}{l} U_{i}^{\left(i, j, C_{k}\right)}= \\ \left\{a_{j} \in A_{j} \mid \forall\left(u_{i}, c_{k}\right) \in U_{i} \times C_{k}, \left(u_{i}, a_{j}, c_{k}\right) \in Y\right\}, \\ A_{j}^{\left(i, j, C_{k}\right)}= \\ \left\{u_{i} \in U_{i} \mid \forall\left(a_{j}, c_{k}\right) \in A_{j} \times C_{k}, \left(u_{i}, a_{j}, c_{k}\right) \in Y\right\} . \end{array}$
例1 表1为一个三元背景T=(U, A, C, Y), 该三元背景描述不同季节中5种植物的状态.5种植物分别为梅花(u1)、蒲公英(u2)、松树(u3)、向日葵(u4)和菊花(u5), 构成对象集{u1, u2, u3, u4, u5}.3种状态分别为花朵(a1)、种子(a2)和叶子(a3), 构成属性集{a1, a2, a3}.4个季节分别为春季(c1)、夏季(c2)、秋季(c3)和冬季(c4), 构成条件集{c1, c2, c3, c4}.表中, 1表示某个植物在特定季节处于某种特定状态, 0表示不处于该状态.
| 表1 三元背景T=(U, A, C, Y) Table 1 A triadic context T=(U, A, C, Y) |
定义3[14] 设T=(U, A, C, Y)为一个三元背景,
Ui⊆U, Aj⊆A, Ck⊆C.
若满足
$\begin{array}{l} U_{i}=\left(A_{j} \times C_{k}\right)^{(* )}, \\ A_{j}=\left(U_{i} \times C_{k}\right)^{(* )}, \\ C_{k}=\left(U_{i} \times A_{j}\right)^{(* )}, \end{array}$
则称(Ui, Aj, Ck)为三元背景T的三元概念, 并称Ui为外延, Aj为内涵, Ck为方式.记T中所有三元概念组成的集合为Ω .
定义4[14] 设T=(U, A, C, Y)为一个三元背景, ∀ Ck⊆C, Ck≠ Ø , 称(U, A, Ck,
$Y_{C_{k}} \subseteq Y \cap(U \times A \times C) .$
特别地, 当|Ck|=1时, 三元子背景退化为二元形式背景.
为了后续并行算法的有效开展, 本节提出临时概念、临时属性-条件三元概念及过程三元概念的定义, 并基于这些概念计算对象-属性三元概念和属性-条件三元概念.同时也表明, 所有三元概念均可通过合并对象-属性三元概念和属性-条件三元概念构造生成.
定义5 设T=(U, A, C, Y)为一个三元背景, C1, C2, …,
$C=\bigcup_{r=1}^{r_{0}} C_{r}, $
且
$C_{r} \cap C_{s}=\emptyset$
对所有的r≠ s均成立, 则称条件集C被划分为r0个互不相交的子集.当r0=n时, 称Tr=(U, A, Cr,
定义6 设Tr=(U, A, Cr,
Bs∈ 2A\Ø , s=1, 2, …, 2|A|-1,
其中|A|表示集合的元素个数, 则称(um, Bs, c)为临时概念, 其中um为对象, Bs为在给定条件c下该对象um拥有的属性.全部临时概念组成的集合记为Ω uc.
定义7 设Tr=(U, A, Cr,
假设(u', A', c)为临时概念, 接下来给出使用临时概念集合Ω uc和由临时概念“ 外延合并” 生成的中间概念Ω 1进一步生成过程三元概念集合Ω 2的构造方法.具体步骤如下.
1)外延合并.将Ω uc中的全部临时概念在条件和内涵相同时合并外延形成新的集合:
$\begin{aligned} \mathcal{U}_{1}= & \left\{\left(\cup\left\{U^{\prime} \mid\left(U^{\prime}, A^{\prime}, c\right) \in \mathcal{U}_{u c}, A^{\prime}=A_{0}^{\prime}\right\}, A_{0}^{\prime}, c_{0}\right) \mid\right. \\ & \left.\forall\left(U_{0}^{\prime}, A_{0}^{\prime}, c_{0}\right) \in \widetilde{U}_{u c}\right\} . \end{aligned}$
2)内涵合并.将Ω 1中所有临时概念在条件和外延相同时合并内涵, 形成新的集合:
$\begin{aligned} \mathcal{U}_{2}= & \left\{\left(U_{0}^{\prime}, \cup\left\{A^{\prime} \mid\left(U^{\prime}, A^{\prime}, c\right) \in U_{1}, U^{\prime}=U_{0}^{\prime}\right\}, c_{0}\right) \mid\right. \\ & \left.\forall\left(U_{0}^{\prime}, A_{0}^{\prime}, c_{0}\right) \in \widetilde{U}_{1}\right\} . \end{aligned}$
因此Ω 2为通过上述两个步骤形成过程三元概念组成的集合.
定理1 设Ω uc为临时概念的集合, 通过外延合并和内涵合并两步操作从集合Ω uc生成的集合Ω 2为过程三元概念.
证明 设∀ U1⊆U, U2⊆U, A1⊆A, A2⊆A, (U1, A1, c)为单条件三元背景Tr的一个过程三元概念.假设
$\left(U_{1}, A_{1}, c\right) \notin U_{2}, $
则一定存在一个过程三元概念(U2, A2, c)满足U1⊆U2或A1⊆A2.
若U1⊆U2且A1=A2, 则∃u∈ U2\U1, 使得(U1∪ {u}, A1, c)构成一个过程三元概念.
若U1=U2且A1⊆A2, 则∃a∈ A2\A1, 使得(U1, A1∪ {a}, c)构成一个过程三元概念.
若U1⊆U2且A1⊆A2, 则这种情况一定经过上述两个步骤生成过程三元概念
$\left(U_{1} \cup\{u\}, A_{1} \cup\{a\}, c\right) .$
在3种情况下假设(U1, A1, c)∉Ω 2导致能构造新的过程三元概念, 而这种构造与初始假设矛盾, 即(U1, A1, c)∈ Ω 2成立.由此定理1得证.
定理1表明, 对于单条件三元背景, 当条件唯一时, 先对相同内涵但不同外延的临时概念求并集, 然后对相同外延但不同内涵的临时概念求并集, 从而计算全部的过程三元概念.根据定义6可知单条件三元背景的临时概念也是生成形式概念的中间结构.
例2 根据定义7和定理1, 计算例1中春天这一条件下的所有单条件三元背景对应的全部过程三元概念:
$\begin{array}{l} \left(\left\{u_{1}, u_{2}, u_{3}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{1}\right\}\right), \\ \left(\left\{u_{2}\right\}, \left\{a_{1}, a_{2}, a_{3}\right\}, \left\{c_{1}\right\}\right) \\ \left(\left\{u_{1}, u_{2}, u_{3}, u_{5}\right\}, \left\{a_{3}\right\}, \left\{c_{1}\right\}\right), \\ \left(U, \emptyset, c_{1}\right) . \end{array}$
类似地, 在条件c2、c3和c4下可计算例1对应的单条件三元背景下的所有过程三元概念的集合.
定义8 设T=(U, A, C, Y)为一个三元背景, 若∀ (U', A')∈
$\begin{array}{l} U^{\prime}=\left(A^{\prime} \times C^{\prime}\right)^{(* )}, \\ A^{\prime}=\left(U^{\prime} \times C^{\prime}\right)^{(* )}, \\ C^{\prime}=\left(U^{\prime} \times A^{\prime}\right)^{(* )}, \end{array}$
则称UA=(U', A', C')为一个对象-属性三元概念.
根据定义7和定义8可知, 当一个过程三元概念的内涵和外延都分别为另一个过程三元概念的内涵和外延的子集时, 合并这些条件就可生成一个对象-属性三元概念, 所有对象-属性三元概念组成的集合记为Ω UA.
例3 例2已得到所有过程三元概念, 依据前述结论, 可进一步计算所有的对象-属性三元概念:
$\begin{array}{l} \left(\left\{u_{1}, u_{2}, u_{3}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{1}\right\}\right), \\ \left(\left\{u_{5}\right\}, \left\{a_{2}\right\}, \left\{c_{4}\right\}\right), \\ \left(\left\{u_{2}\right\}, \left\{a_{1}, a_{2}, a_{3}\right\}, \left\{c_{1}\right\}\right), \\ \left(\left\{u_{1}, u_{2}\right\}, \left\{a_{2}, a_{3}\right\}, \left\{c_{2}\right\}\right), \\ \left(\left\{u_{4}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{2}\right\}\right), \\ \left(\left\{u_{3}, u_{4}\right\}, \left\{a_{2}, a_{3}\right\}, \left\{c_{3}\right\}\right), \\ \left(\left\{u_{5}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{3}\right\}\right), \\ \left(\left\{u_{3}\right\}, \left\{a_{3}\right\}, \left\{c_{1}, c_{2}, c_{3}, c_{4}\right\}\right), \\ \left(\left\{u_{1}, u_{2}, u_{3}, u_{5}\right\}, \left\{a_{3}\right\}, \left\{c_{1}, c_{2}, c_{3}\right\}\right), \\ (U, \emptyset, C), \\ (\emptyset, A, C), \\ \left(\left\{u_{1}\right\}, \left\{a_{1}\right\}, \left\{c_{1}, c_{4}\right\}\right), \\ \left(\left\{u_{1}, u_{2}, u_{3}, u_{4}, u_{5}\right\}, \left\{a_{3}\right\}, \left\{c_{2}, c_{3}\right\}\right) . \end{array}$
定理2 设T=(U, A, C, Y)为三元背景,
$h:\left(U_{i}, A_{j}\right) \mapsto\left(U_{i}, A_{j}, \left(U_{i} \times A_{j}\right)^{(* )}\right), $
定义映射
$h:\left(U_{i}, A_{j}\right) \mapsto\left(U_{i}, A_{j}, \left(U_{i} \times A_{j}\right)^{(* )}\right), $
其中
$\Omega_{C}=\bigcup_{r=1}^{n} \Omega_{C_{r}}, $
则该映射h为一个单射.
证明 首先, 证明映射h的合理性.
$\forall\left(U_{i}, A_{j}\right) \in \Omega_{C}, \exists C_{k} \subseteq C\left(C_{k} \neq \emptyset\right)$
满足
$U_{i}^{\left(i, j, C_{k}\right)}=A_{j}$
且
$A_{j}^{\left(i, j, C_{k}\right)}=U_{i}, $
显然
$C_{k} \subseteq\left(U_{i} \times A_{j}\right)^{(* )} .$
设
$c \in\left(U_{i} \times A_{j}\right)^{(* )}, $
则可推导出
$A_{j}^{\left(i, j, C_{k}\right)} \subseteq A_{j}^{(i, j, c)}$
且
$U_{i}^{\left(i, j, C_{k}\right)} \subseteq U_{i}^{(i, j, c)} .$
故如下等式成立:
$\begin{aligned} U_{i}^{\left(i, j, C_{k}\right)}= & \cap\left\{U_{i}^{(i, j, c)} \mid c \in\left(U_{i} \times A_{j}\right)^{(* )}\right\}= \\ & U_{i}^{\left(i, j, \left(U_{i} \times A_{j}\right)^{(* )}\right)}=A_{j}, \end{aligned}$
$\begin{aligned} A_{j}^{\left(i, j, C_{k}\right)}= & \cap\left\{A_{j}^{(i, j, c)} \mid c \in\left(U_{i} \times A_{j}\right)^{(* )}\right\}= \\ & A_{j}^{\left(i, j, \left(U_{i} \times A_{j}\right)^{(* )}\right)}=U_{i}, \end{aligned}$
因此
$\forall\left(U_{i}, A_{j}\right) \in \Omega_{C}, \left(U_{i}, A_{j}, \left(U_{i} \times A_{j}\right)^{(* )}\right) \in U_{0} .$
然后证明映射h为单射.根据定义方式可直接得到.
定理2表明, 对于Ω C中不同的形式概念而言, 可生成与之对应的三元概念.然而, 对于全部三元概念构成的集合Ω 中却有一部分三元概念并不能通过Ω C集合中的形式概念诱导生成.因此, 该映射h不是满射.
定义9 设Tr=(U, A, Cr,
$U=\bigcup_{v=1}^{v_{0}} U_{v}, $
则集合U被划分为v0个互不相交的子集U1, U2, …,
设Tv, r=(Uv, A, Cr,
定义10 设Tu=(u, A, C, Yu, C)为单对象-多条件三元背景, 若∀ cn∈ C, 满足
$B_{n} \in 2^{A} \backslash \emptyset, $
则称(u, Bn, cn)为临时属性-条件三元概念, 其中u为对象, Bn为在给定对象u时条件cn拥有的属性.
$\forall A^{\prime \prime} \subseteq A, C^{\prime \prime} \subseteq C, $当$\left(A^{\prime \prime}, C^{\prime \prime}\right) \in \Omega_{U_{v}}$时, 称(u, $ A^{\prime \prime}, C^{\prime \prime}$)为一个过程三元概念.
定义11 设T=(U, A, C, Y)为一个三元背景, 若∀ (A″, C″)∈
$\begin{aligned} U^{\prime \prime} & =\left(A^{\prime \prime} \times C^{\prime \prime}\right)^{(* )}, \\ A^{\prime \prime} & =\left(U^{\prime \prime} \times C^{\prime \prime}\right)^{(* )}, \\ C^{\prime \prime} & =\left(U^{\prime \prime} \times A^{\prime \prime}\right)^{(* )}, \end{aligned}$
则称AC=(U″, A″, C″)为一个属性-条件三元概念.
根据(u, A″, C″)和定义11可知, 当一个过程三元概念的内涵和方式都分别包含于另一个过程三元概念的内涵和方式时, 合并它们的对象可生成一个属性-条件三元概念.所有属性-条件三元概念组成的集合记为Ω AC.
例4 基于例1, 并结合定义10和定义11, 可计算所有的属性-条件三元概念Ω AC如下:
$ \begin{array}{l} \left(\left\{u_{1}, u_{2}, u_{3}, u_{5}\right\}, \left\{a_{3}\right\}, \left\{c_{1}, c_{2}, c_{3}\right\}\right), \\ \left(\left\{u_{4}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{2}\right\}\right), \\ \left(\left\{u_{1}, u_{2}, u_{3}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{1}\right\}\right), \\ \left(\left\{u_{2}\right\}, \left\{a_{1}, a_{2}, a_{3}\right\}, \left\{c_{1}\right\}\right), \\ \left(\left\{u_{3}\right\}, \left\{a_{3}\right\}, \left\{c_{1}, c_{2}, c_{3}, c_{4}\right\}\right), \\ \left(\left\{u_{1}, u_{2}\right\}, \left\{a_{2}, a_{3}\right\}, \left\{c_{2}\right\}\right), \\ \left(\left\{u_{1}, u_{2}, u_{3}, u_{4}, u_{5}\right\}, \left\{a_{3}\right\}, \left\{c_{2}, c_{3}\right\}\right), \\ \left(\left\{u_{5}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{3}\right\}\right), \\ \left(\left\{u_{5}\right\}, \left\{a_{2}\right\}, \left\{c_{4}\right\}\right), \\ \left(\left\{u_{3}, u_{4}\right\}, \left\{a_{2}, a_{3}\right\}, \left\{c_{3}\right\}\right), \\ (U, A, \emptyset), \\ \left(\left\{u_{1}\right\}, \left\{a_{1}\right\}, \left\{c_{1}, c_{4}\right\}\right), \\ \left(\left\{u_{2}\right\}, \left\{a_{2}, a_{3}\right\}, \left\{c_{1}, c_{2}\right\}\right) . \end{array}$
定理3 设T=(U, A, C, Y)为三元背景,
$ \forall\left(A_{j}, C_{r}\right) \in \Omega_{U}, \left(\left(A_{j} \times C_{r}\right)^{(* )}, A_{j}, C_{r}\right) \in U, $
定义映射:
$ h:\left(A_{j}, C_{r}\right) \mapsto\left(\left(A_{j} \times C_{r}\right)^{(* )}, A_{j}, C_{r}\right), $
其中
$\Omega_{U}=\bigcup_{v=1}^{l} \Omega_{U_{v}}, $
则该映射为Ω U到Ω 的单射.
证明 具体过程与定理2类似, 故不再赘述.
定理4 设T=(U, A, C, Y)为三元背景,
$\widetilde{V}^{\prime}=\widetilde{U}_{U A} \cup \widetilde{U}_{A C}, $
若∀ (U', A', C')∈ Ω '且(U, A, C)∈ Ω , 映射
$p:\left(U^{\prime}, A^{\prime}, C^{\prime}\right) \mapsto(U, A, C)$
为从Ω '到Ω 的双射.
证明 首先证明映射p为单射.根据定义方式可直接得到.
然后证明映射p为满射.利用反证法, 假设p不是满射, 则∃(U, A, C)∈ Ω , 使得对所有
$\left(U^{\prime}, A^{\prime}, C^{\prime}\right) \in \widetilde{J}^{\prime}, $
都有
$p\left(U^{\prime}, A^{\prime}, C^{\prime}\right) \neq(U, A, C) .$
由定义3可知, 必有A∈
综上可知p为双射.
定理4表明, 所有的三元概念都可通过合并对象-属性三元概念和属性-条件三元概念这两类基本三元概念生成.这意味着在三元关系的框架内, 任何复杂的三元概念都可通过这两种基本类型三元概念的组合进行构建, 从而简化三元概念的构建过程.
例5 通过例3和例4的结果, 以及定理4, 可将所有对象-属性三元概念和属性-条件三元概念合并为最终的三元概念.因此例1计算的最终的三元概念结果如下:
$\begin{array}{l} \left(\left\{u_{1}, u_{2}, u_{3}, u_{5}\right\}, \left\{a_{3}\right\}, \left\{c_{1}, c_{2}, c_{3}\right\}\right), \\ \left(\left\{u_{4}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{2}\right\}\right), \\ \left(\left\{u_{1}, u_{2}, u_{3}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{1}\right\}\right), \\ \left(\left\{u_{2}\right\}, \left\{a_{1}, a_{2}, a_{3}\right\}, \left\{c_{1}\right\}\right), \\ \left(\left\{u_{3}\right\}, \left\{a_{3}\right\}, \left\{c_{1}, c_{2}, c_{3}, c_{4}\right\}\right), \\ \left(\left\{u_{1}, u_{2}\right\}, \left\{a_{2}, a_{3}\right\}, \left\{c_{2}\right\}\right), \\ \left(\left\{u_{2}\right\}, \left\{a_{2}, a_{3}\right\}, \left\{c_{1}, c_{2}\right\}\right), \\ \left(\left\{u_{1}, u_{2}, u_{3}, u_{4}, u_{5}\right\}, \left\{a_{3}\right\}, \left\{c_{2}, c_{3}\right\}\right), \\ \left(\left\{u_{5}\right\}, \left\{a_{1}, a_{3}\right\}, \left\{c_{3}\right\}\right), \\ \left(\left\{u_{5}\right\}, \left\{a_{2}\right\}, \left\{c_{4}\right\}\right), \\ (U, \emptyset, C), \\ \left(\left\{u_{3}, u_{4}\right\}, \left\{a_{2}, a_{3}\right\}, \left\{c_{3}\right\}\right), \\ (\emptyset, A, C), \\ \left(\left\{u_{1}\right\}, \left\{a_{1}\right\}, \left\{c_{1}, c_{4}\right\}\right), \\ (U, A, \emptyset) . \end{array}$
为了更直观地描述三元概念, 通过图1展示例5中的15个三元概念构成的三元图.
图1的上方线图称为方式图, 其中每个圆圈表示一个三元概念的方式, 包含该圆圈所示条件及其右侧连接的圆圈所示的条件.左下方的线图称为内涵图, 每个圆圈表示一个三元概念的内涵, 包含该圆圈所示的属性以及其左上方连接的圆圈所示的属性.右下方的线图称为外延图, 每个圆圈表示一个三元概念的外延, 包含该圆圈所示的对象及其左下方连接的圆圈所示的对象.三元图中间的倒三角区域中的每个圆圈表示一个三元概念, 通过虚线与外延图、内涵图和方式图中的圆圈相连, 分别表示该三元概念的外延、内涵和方式.
经典的形式背景和三元背景都是由0和1布尔值构成, 这样的数据能逐行进行读取操作, 并且不影响合并的结果.算法1描述形式概念分布式构造算法, 其中RDD1表示从分布式存储系统(Hadoop分布式文件系统, HDFS)读取形式背景数据.RDD2表示将形式概念分析中每行具有值1的属性输入PowerFun函数中, 该函数对RDD2中每行数据的值为1的属性集合生成幂集, 具体步骤为使用Spark的弹性分布式数据集(RDD)的map和flatMap算子操作实现.RDD3表示首先通过flatMap算子展开数据, 然后使用reduceByKey和mapToPair转换算子操作, 将具有相同属性的对象合并为键值对.RDD4表示使用reduceByKey和mapToPair转换算子将具有相同对象的属性合并为键值对.Ω 表示补充对象和属性集为空之后的所有形式概念.
算法1 形式概念分布式构造算法
输入 形式背景F=(U, A, I)
输出 形式概念Ω
RDD1← F;
Temp =Ø ;
For each row in RDD1
Temp = Temp ∪ PowerFun(row);
End
RDD2← Temp;
RDD3←
ReduceByKey(MapToPair(FlatMap(RDD2)));
RDD4← ReduceByKey(MapToPair(RDD3));
Ω ← RDD4 ∪ (U, Ø )∪ (Ø , A).
三元概念合并具有单个条件或单个对象的形式概念生成.根据定义6、定义7和定理1, 临时概念和临时属性-条件三元概念可作为形式概念分布式并行构造的基础.
算法2是三元概念分布式并行构造算法.首先, 从HDFS分布式存储系统导入三元背景数据.输入的三元背景通过SeparateFun函数分成单条件三元背景和单对象三元背景, 这些三元背景被转换成二元形式背景之后使用算法1计算形式概念.再向形式概念中添加条件或对象以生成过程三元概念, 并将其存储在RDDOC1或RDDOC2中.然后, 基于定理2~定理4的结论及Spark架构里的广播算子, 生成对象-属性三元概念和属性-条件三元概念.最后, 调用Distinct操作符, 去除重复的三元概念, 获得完整的三元概念集.算法的关键步骤涉及通过执行RDDs的嵌套循环遍历以遍历处理三元概念.这一步不可避免地需要将RDD数据持久化到磁盘上.为此, 利用RDD的广播操作符, 使用广播变量将处理三元概念分发到所有节点进行处理, 通过这种方式增加处理效率和降低数据倾斜.
算法2 三元概念分布式并行构造算法
输入 三元背景T=(U, A, C, Y)
输出 三元概念Ω 0
(RDDOC, RDDCO)← SeparateFun( );
RDDOC1← (Algorithm1(RDDOC), C);
For each pair1 in RDDOC1
For each pair2 in Broadcast(RDDOC1)
If OAFun(pair1)⊆OAFun(pair2)
CFun(pair1)←
CFun(pair1)⊆CFun(pair2);
End
End
End
RDDOC2← Distinct(RDDOC1);
RDDCO1← (Algorithm1(RDDCO), O);
For each pair1 in RDDCO1
For each pair2 in Broadcast(RDDCO1)
If ACFun(pair1)⊆ACFun(pair2)
OFun(pair1)←
OFun(pair1)∪ OFun(pair2);
End
End
End
RDDCO2← Distinct(RDDCO1);
RDDTC← Distinct(RDDCO2∪ RDDOC2);
Ω 0← RDDTC∪ (U, Ø , C)∪ (Ø , A, C).
两阶段聚合包括局部聚合和全局聚合.局部聚合对弹性分布式数据集的键添加随机数进行分区, 从而减少数据倾斜的发生.全局聚合时先消除局部聚合时添加的随机前缀, 再使用聚合算子进行聚合.算法3是两阶段聚合优化三元概念分布式并行算法, 对发生数据倾斜的Reduce阶段进行优化.
算法3 两阶段聚合优化三元概念分布式并行算法
输入 三元背景T=(U, A, C, Y)
输出 三元概念Ω 0
(RDDOC, RDDCO)← SeparateFun( );
For each row in RDDOC(RDDCO)
RDD1=RDD1∪ PowerFun(row);
End
RDD2← MapToPair(FlatMap(RDD1));
For each Key in RDD2
Key← random+Key;
End
RDD3← ReduceByKey(RDD2);
For each Key in RDD3
Key← Key-random;
End
RDD4←
ReduceByKey(MapToPair(FlatMap(RDD3)));
RDD5← ReduceByKey(MapToPair(RDD4));
For each pair1 in RDD5
For each pair2 in Broadcast(RDD5)
If OAFun(pair1)⊆OAFun(pair2) & RDDOC
CFun(pair1)←
CFun(pair1)⊆CFun(pair2);
End
If ACFun(pair1)⊆ACFun(pair2) & RDDCO
OFun(pair1)←
OFun(pair1)∪ OFun(pair2);
End
End
End
RDDOC1(RDDCO1)← Distinct(RDD5);
RDDTC← Distinct(RDDCO1∪ RDDOC1);
Ω 0← RDDTC∪ (U, Ø , C)∪ (Ø , A, C).
基于3.2节构建形式概念和三元概念的分布式并行算法, 下面详细介绍在Spark框架上并行构建形式概念和三元概念的过程.
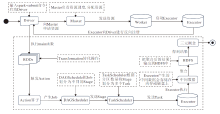
算法4给出详细步骤, 描述从数据输入到最终生成三元概念的整个运行流程, 详细算法流程架构如图2所示.
算法4 Spark框架下三元概念的构建
step 1 应用程序通过spark-submit命令提交到Spark集群, 启动Driver调度和安排作业.
step 2 Driver向集群中的Master节点请求资源.Master节点负责调度和分配资源.一旦做出资源分配决定, 资源分配信息将发送给Worker.
step 3 在Worker节点上启动Executor进程进行向后注册, 表示Executor进程已准备好接收和执行任务.
step 4 主函数在集群上创建一个SparkCon-text, 创建RDD操作符、累加操作符和广播变量操作符.然后在本文的三元概念并行构造算法的基础上生成三元概念.
step 5 Action操作触发计算.
step 6 Action操作的执行生成一个或多个作业, 每个作业表示一系列需要完成的计算任务.这些作业被发送到DAGScheduler.DAGScheduler将每个作业划分为不同阶段, 每个阶段由一组可并行执行的任务组成.
step 7 划分阶段被发送到TaskScheduler.TaskScheduler根据数据分区将每个阶段分解为多个任务, 每个任务对应于阶段中的一部分数据.准备好的任务被发送到各自的Executor进程.
step 8 在接收到任务后, Executor进程并行执行计算任务.Executor生成的中间数据根据需要存储在内存中, 最后对中间数据进行聚合操作.
step 9 计算完成后, 聚合结果输出到HDFS, 得到计算结果, 完成整个Spark作业的执行过程.
实验环境为运行在Linux系统上的Spark集群, 该集群由1个主节点和7个工作节点组成.每个节点系统的配置包括12 GB内存、Intel(R) Xeon(R) Sil-ver 4210R CPU@2.40 GHz处理器、200 GB硬盘, 操作系统为CentOS Linux 7.5.1804, 运行JDK 1.8.0_301版本, 并部署Hadoop 3.3.1环境, 确保高效的分布式计算能力.
Hadoop集群的配置情况如表2所示, 每个节点都有一个唯一的IP地址, 与集群名称一一对应, 并配置Hadoop生态系统环境以支持运行.
| 表2 Hadoop集群配置情况 Table 2 Hadoop cluster configuration |
表2中ZKFC表示ZKFailoverController, RM表示ResourceManager, QP表示QuorumPeerMain, NN表示NameNode, DN表示DataNode, NM表示Node-Manager, JN表示JournalNode.集群配置明确区分每个节点的功能, 从而提升数据处理和存储的效率与灵活性.
实验所选数据集来自UCI机器学习数据库(https://archive.ics.uci.edu/), 该数据集包含丰富的特征和标签, 用于不同的机器学习任务.相关数据的详细信息如表3所示.
| 表3 实验数据集详细信息 Table 3 Detailed information of experimental datasets |
在表3中的原始数据被处理成标准数据集(只包含0和1的离散数据集)的基础上, 进一步将属性集划分为不同组以构建三元背景, 其中每组表示一个条件.
将本文的基于Spark框架的分布式并行构造算法与如下三元概念构造方法进行耗时对比, 包括文献[6]算法、文献[14]算法、文献[33]算法、MapReduce框架(简记为文献[36]算法)、基于待选集的三元概念构造方法(简记为文献[40]算法).其中, 串行算法在配置相同的单台计算机上运行.
各算法在12个数据集上的三元概念生成时间对比如表4所示, 表中-表示无法正常计算三元概念.由表可发现, 随着数据对象集规模的增加, 文献[6]算法、文献[14]算法和文献[36]算法在构建三元概念时的耗时增长迅速.相比文献[40]算法, 本文算法在数据量较小时并未占优, 这是因为在数据量较小时, 资源的调动时间可能超过并行处理带来的性能提升, 从而影响整体效率.然而, 随着数据集规模的扩大, 本文算法的效率显著高于对比算法, 特别是在数据集对象规模增加时, 优势尤为明显.
| 表4 各算法三元概念生成时间对比 Table 4 Time comparison of generating triadic concepts using different algorithms s |
本文算法不仅显著提高三元概念的构造效率, 同时也显著提升形式概念的构建效率.文献[1]算法(串行)、文献[2]算法(并行)、文献[37]算法和本文算法形式概念生成时间对比如表5所示, 表中-表示无法正常计算形式概念.由表可看出, 随着数据集的对象规模的增加, 本文算法的计算效率显著优于文献[37]算法.同时所有分布式并行计算框架生成形式概念的效率均受到属性集规模的显著影响.例如:在Predictive Maintenance、Online Shoppers Purchasing数据集上, Online Shoppers Purchasing数据集的对象数量大于Predictive Maintenance数据集, 但Predictive Maintenance数据集上的属性数量等于Online Shoppers Purchasing数据集.然而, Pre-dictive Maintenance数据集上最终计算时间却高于Online Shoppers Purchasing数据集.
| 表5 各算法形式概念生成时间对比 Table 5 Time comparison of generating formal concepts using different algorithms |
设置节点个数分别为1, 3, 5, 7, 本文算法与文献[36]算法的执行时间如表6所示.由表可见, 本文算法在不同节点的集群上始终表现出优越性能.这得益于Spark框架使用内存机制减少数据传输开销和优化计算性能, 两阶段聚合的策略也大幅消除数据倾斜现象的发生, 从而能更高效地生成三元概念.
| 表6 节点数不同时两种算法执行时间对比 Table 6 Execution time comparison of 2 algorithms with different nodes |
加速比是从单节点开始计算, 再逐渐增至7个节点.由于Linux集群需要两个主节点以实现集群故障切换功能, 其中一个主节点处于备用模式, 不执行计算操作.加速比公式为Sp=T1/Tp, 其中, p表示节点数, T1表示单节点上数据集处理所需的时间, Tp表示p个节点上处理所需的时间.通常加速比越高, 表示集群的并行性能越明显.
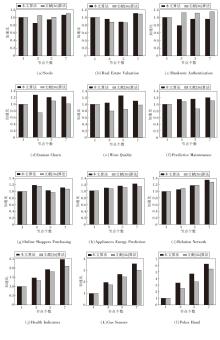
本文算法和文献[36]算法在12个数据集的不同节点集群配置下的加速比变化情况如图3所示.
由图3可见, 文献[36]算法在(a)~(c)中的加速比高于本文算法.MapReduce是基于磁盘的处理框架, 而Spark是基于内存的处理框架.Spark在启动和资源分配上开销更大, 因此对于较小的数据集, MapReduce可能更高效.但是从(d)~(h)可看出, 随着对象数量的增加, 两者之间的性能差距逐渐缩小, 显示出Spark基于内存计算的优势.从(i)开始, 本文算法和文献[36]算法之间的加速比差距越来越显著, 反映出基于内存的Spark技术在处理大数据集时, 优于基于磁盘的MapReduce框架.
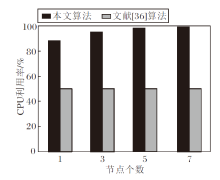
文献[36]算法和本文算法的CPU利用率如图4所示.由图可见, 文献[36]算法的CPU利用率始终保持在50%, 本文算法的利用率不仅高于文献[36]算法, 而且始终超过80%.特别是随着节点个数的增加, 本文算法的CPU利用率也持续上升, 表明本文算法能有效利用CPU资源.
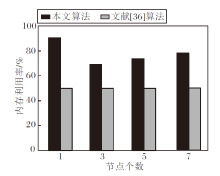
文献[36]算法和本文算法的内存利用率如图5所示.由图可见, 文献[36]算法的内存利用率与其CPU利用率相同, 均为50%.相比之下, 本文算法在单节点上内存利用率超过90%, 为最高值, 并在3~7个节点之间持续上升.这可能是因为Spark在单节点上为串行计算, 所有数据分配任务都在该单节点上运行, 而在3~7个节点之间, 节点间网络通信和数据交换的开销增加, 内存利用率逐渐上升.
本文研究分布式并行三元概念的构建, 设计基于Spark框架的算法, 构建形式概念和三元概念, 并采用两阶段优化策略优化数据倾斜问题.在不同数据集上的增强实验表明:分布式并行算法在概念构建中效率较高, 可有效利用内存和CPU资源.
Spark框架的并行算法性能良好, 但仍存在一些局限性.当属性和条件数量增加时, 如何设计算法避免生成大量无用的临时概念是一个挑战.其次, 设计一种算法优化Spark并行计算框架的内存, 进一步提升内存利用效率亦值得思考.为了实现更高的计算效率, 可利用增强型并行框架Flink, 设计增量式分布式并行算法, 更有效地构建三元概念.今后将考虑基于Flink框架和更合理的分布式数据库开发更高效的并行算法, 进一步提升三元概念的构造效率.
本文责任编委 苗夺谦
Recommended by Associate Editor MIAO Duoqian
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|