宋宝燕,博士,教授,主要研究方向为数据库技术、大数据管理等.E-mail:bysong@lnu.edu.cn.
作者简介:

单晓欢,博士,实验师,主要研究方向为图数据处理技术、知识图谱数据管理等.E-mail:shanxiaohuan@lnu.edu.cn.

蒋建涛,硕士研究生, 主要研究方向为知识图谱数据管理.E-mail:1098406507@qq.com.

陈 泽,博士研究生,主要研究方向为自然语言处理、知识图谱数据管理等.E-mail:chenz1996@outlook.com.
知识图谱推理是解决知识图谱不完整性的重要手段之一.针对现有基于嵌入的推理模型依赖准确事实,可解释性较差,而基于规则的推理模型过于依赖图谱的完整性,数据稀疏时推理性能较低,无法准确表达推理模式.因此文中提出联合规则推理模式和事实嵌入的知识图谱推理模型(Knowledge Graph Reasoning Combining Rule Inference Patterns and Fact Embedding, RPFE).首先,将BoxE作为基础嵌入模型,实现事实的嵌入表示.再设计推理模式差异性函数,辅助嵌入模型捕获不同推理模式的规则,并对规则学习提供直观的嵌入解释.然后,提出事实距离一致性评分函数,强化嵌入表示.最后,优化规则和事实得分,弥补知识图谱高质量事实不足的缺陷,进而提升模型推理的可解释性.在3个公开数据集上的实验表明RPFE在知识图谱推理方面的优越性.
SONG Baoyan, Ph.D., professor. Her research interests include database techniques and big data ma-nagement.
About Author:
SHAN Xiaohuan, Ph.D., experimentalist. Her research interests include graph data processing technology and knowledge graph data management.
JIANG Jiantao, Master student. His research interests include knowledge graph data management.
CHEN Ze, Ph.D. candidate. His research interests include natural language processing and knowledge graph data management.
Knowledge graph reasoning is an essential approach to address the incompleteness of knowledge graphs. The existing embedding-based reasoning models rely on accurate facts and suffer from poor interpretability. Rule-based reasoning models depend on the completeness of knowledge graphs, resulting in low inference performance on sparse data and an inability to express inference patterns accurately. To address these issues, a model of knowledge graph reasoning combining rule inference patterns and fact embedding(RPFE) is proposed. First, BoxE is employed as the base embedding model to achieve the embedding representation of facts. Second, the inference pattern diversity functions are designed to assist the embedding models in capturing the rules of different inference patterns, providing intuitive embedded interpretation for rule learning. Then, the fact distance consistency scoring functions are proposed to enhance the embedding representation. Finally, the rules and fact scores are optimized to compensate the lack of high-quality facts in knowledge graphs and improve the interpretability of the reasoning. Experiments on three public datasets indicate that the RPFE yields excellent performance in knowledge graph reasoning.
知识图谱是一种揭示实体之间关系的语义网络, 以三元组的形式将关联事实进行深度融合[1].随着数据规模的持续增长, 知识图谱中实体和关系的数量也随之呈指数增长态势.然而, 由于网络数据质量参差不齐、爬虫技术限制等多种因素, 大多数知识图谱中的事实并非完整[2], 使智能推荐[3]、智能问答[4]等多样化下游应用的有效性及准确性受到影响.
学者们进而提出知识图谱推理技术, 可根据已知事实信息, 挖掘并推理潜在的未知事实, 实现知识图谱的补全和完善.目前, 通用的图谱推理模型主要包括基于图谱嵌入的图谱推理模型和基于规则的图谱推理模型两类.
基于图谱嵌入的图谱推理模型将实体和关系嵌入向量空间中, 通过不断学习, 捕捉嵌入的相似性[5], 获得潜在的事实.此类模型在稀疏知识图谱中表现良好, 具有高效的推理性能[6], 但学习依赖于图谱中准确的事实, 推理缺乏可解释性[7], 使研究者无法充分了解推理问题和任务, 无法判断推理结果的合理性及推理过程的正确性.
基于规则的图谱推理模型从知识图谱中提取若干个通用规则, 并利用规则推理新的事实.此类模型可提供合乎逻辑和可解释的过程和答案, 生成的规则也具有较好的可泛化性[8], 但其严重依赖知识图谱的完整性, 在稀疏知识图谱中难以学习和推理.
此外, 规则推理模式种类丰富, 现有模型难以对其进行准确表达, 影响规则生成的质量, 进而影响模型的可解释性和准确性.
近年来, 相比获得较高拟合度但无法理解的推理过程及推理结果, 寻求对模型工作机理的直接理解, 以可解释的表达方式产生推理结果的研究成为知识推理的研究重点及难点之一.现有研究考虑结合基于图谱嵌入的图谱推理模型和基于规则的图谱推理模型[9, 10, 11, 12, 13, 14], 在增强可解释性的同时提高推理能力.然而, 此类研究目前仍面临如下挑战.
1)现有研究在对事实嵌入的学习过程中, 未能充分考虑各类规则推理模式, 模型难以捕捉各类规则, 且可解释性较差的问题尚未解决.
2)在稀疏知识图谱中数据缺失严重, 高质量事实的比率较低, 导致难以对规则进行学习, 进而对推理效果及可解释性造成一定影响.
3)嵌入表示仍然过于依赖准确表达的事实, 难以利用学到的规则提升可解释性.
为此, 本文提出联合规则推理模式和事实嵌入的知识图谱推理模型(Knowledge Graph Reasoning Combining Rule Inference Patterns and Fact Embe-dding, RPFE), 充分结合嵌入学习和规则学习, 实现准确、高效且可解释性较强的知识图谱推理.为了避免嵌入模型选取不当导致可解释性下降的问题, 采用基于空间表示的知识图谱嵌入, 同时充分考虑各类规则推理模式, 实现对规则推理模式的准确表达, 进而学习高质量的规则, 有效增强模型学习的可解释性.为了更好地结合嵌入模型与规则推理, 充分利用学到的规则强化提升事实嵌入, 提出推理模式差异性函数, 辅助嵌入模型, 更准确表达推理模式的语义.提出事实距离一致性评分函数, 优化推理的新事实中实体和关系的嵌入, 进而实现可解释性较强且推理性能较高的知识推理.为了解决规则推理模型在数据稀疏情况下效果不理想的问题, 优化规则和事实得分, 将规则置信度与事实评分进行二分类, 并充分利用规则推理的新事实进行迭代训练, 弥补知识图谱高质量事实不足的缺陷, 提升模型推理事实的可解释性.
近年来, 基于图谱嵌入与规则结合的模型成为知识图谱推理的研究热点之一.此类研究主要集中在图谱嵌入模型的选取和规则生成优化两方面.
图谱嵌入模型根据学到的嵌入表示定义评分函数, 并衡量规则的合理性, 主要包括:基于翻译假设模型(Translation-Based Assumption, TBA)、基于线性映射假设模型(Linear Map Assumption, LMA)和基于空间表示模型.
TBA基于距离定义评分函数, 如TransE[15]、RotatE[16]和InverseEF[17]等.此类模型无法捕捉重要的推理模式, 甚至会产生错误的规则.
LMA基于变换相似性定义评分函数, 包括ComplEx[18]、GIE(Geometry Interaction Knowledge Graph Embeddings)[19]和HyGGE[20]等.相比TBA, LMA的可解释性更差.
基于空间表示模型定义嵌入空间中实体、关系能构成事实的语义成立区域, 利用区域判断推理的正确性, 常见的有QUERY2BOX[21]、BoxE[22]等.此类模型能根据关系框的位置状态直观表示各类规则推理模式, 增强在嵌入表征方面的可解释性.
然而现有嵌入模型通常仅利用事实全局得分进行训练, 由于稀疏知识图谱中存在大量的缺失事实, 训练过程中事实依据较少, 进而影响推理的可解释性.
另一方面, 图谱中存在的低质量事实使得在事实的全局训练中嵌入训练效果较差, 难以获得每个实体和关系正确的嵌入表征, 导致学习和推理的准确性和可解释性不佳.
具体规则推理模式和被经典嵌入模型捕获情况如表1所示.
| 表1 规则推理模式主要分类及被经典嵌入模型捕获情况 Table 1 Main classifications of rule inference patterns and results captured by classical embedding models |
在规则生成优化方面, KALE(Embeddings by Jointly Modeling Knowledge and Logic)[12]联合规则学习知识表示, 但要求一次性注入规则, 忽略图谱嵌入和规则之间的交互.RUGE(Rule-Guided Embe-dding)[13]使用的规则来源于已有的规则学习模型, 交互间未涉及规则学习.RulE(Rule Embedding)[14]虽基于RotatE为规则分配嵌入向量, 但忽视规则推理的信息对嵌入学习的作用, 且对嵌入模型的支持性较弱, 不兼容空间表示的嵌入模型.InterERP(Interactions between Embeddings of Entities, Rela-tions and Relation Paths)[23]利用规则构造搜索路径, 在一定程度上增强推理的准确性, 但其对规则头部关系和体部关系的嵌入近似相等, 忽视规则推理模式的实际语义, 模型的可解释性依然有待优化.
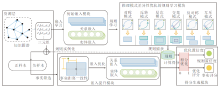
本文提出联合规则推理模式和事实嵌入的知识图谱推理模型(RPFE), 将图谱嵌入和规则推理进行深度融合, 实现对未知事实的高效、准确推理, 并提高推理过程的可解释性, 模型架构如图1所示.
首先, 利用BoxE对知识图谱中事实进行初始嵌入学习, 获得实体及关系的嵌入表征.再设计推理模式差异性优化的规则学习模块, 捕获6种模式的规则[14], 并优化推理模式关系框位置状态的语义表达.然后, 设计事实距离一致性评分函数, 通过强化事实嵌入语义训练, 实现对推理事实的准确表达, 进一步提升规则学习和事实推理的可解释性.最后, 利用不同推理模式下生成的规则, 通过可解释性增强的规则置信度和事实评分优化推理新事实, 对知识图谱进行补充和完善, 并将更新后的知识图谱代入下一轮迭代训练中, 迭代结束后获得最终的推理结果.
由于每个实体在不同事实中表示的含义可能不同, 且不同的嵌入模型捕获推理模式的能力不尽相同, 导致模型对事实语义表示的质量参差不齐, 进而影响推理的准确性.为了解决上述问题, 本文设计并构建RPFE.首先, 采用嵌入表征具有良好可解释性的BoxE[22]作为基础嵌入模型.有别于传统嵌入模型将图谱中的实体和关系均映射为空间中的点, BoxE将实体在不同的事实中编码为不同的点, 关系表示为空间中的区域, 使得表达能力更强, 能更好地捕获隐含在图谱中的推理规则, 同时其关系框的位置状态也能为RPFE捕捉的规则推理模式提供直观的解释.此外, RPFE对其它嵌入模型也具有良好的兼容性.
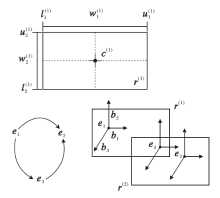
BoxE使用向量ei∈ Rd, bi∈ Rd共同表示实体ei∈ ε 的嵌入, 其中, ei表示实体ei的基准位置, bi表示实体ei的偏移量, 二者共同决定实体在事实下的语义, ε 为实体集.关系ri∈ R嵌入为2个d维方框r(1)∈ Rd, r(2)∈ Rd, 其中R为关系集, r(1)表示关系的入框, r(2)表示关系的出框.l(m)∈ Rd表示关系框的下边界, u(m)∈ Rd表示关系框的上边界, m=1, 2.使用宽度
$ \boldsymbol{w}^{(m)}=\boldsymbol{u}^{(m)}-\boldsymbol{l}^{(m)}+\mathbf{1} $
和方框中心
$ \boldsymbol{c}^{(m)}=\frac{\boldsymbol{l}^{(m)}+\boldsymbol{u}^{(m)}}{2} $
表示关系框的嵌入.如果实体嵌入在框r(m)内, 则事实成立.
图2描述d=2时关系框的表示参数和事实成立时的嵌入表示.
评分函数将三元组得分映射到一个分数, 表示三元组为真的概率:
$ F\left(r\left(e_{1}, e_{2}\right)\right)=\sum_{i=1, 2}\left\|\operatorname{dist}\left(\boldsymbol{e}_{i}^{r\left(e_{1}, e_{2}\right)}, \boldsymbol{r}^{(i)}\right)\right\|_{x}, $ (1)
其中, ‖ · ‖ x表示Lx范数, dist(· )表示BoxE定义的距离函数.
RPFE初始嵌入学习的目标是使事实全局损失最小, 通过最小化损失函数, 学习关系和实体的嵌入:
$ L_{T}=\sum_{r\left(e_{1}, e_{2}\right) \in T \cup T^{\prime}}-\ln \left(1+\tanh \left(y F\left(r\left(e_{1}, e_{2}\right)\right)\right)\right), $
其中, T表示正样本集, T'表示负样本集, tanh(· )表示双曲正切函数, y表示样本标签, 当r(e1, e2)∈ T时, y=-1, 当r(e1, e2)∈ T'时, y=1.
由于仅利用BoxE的最小化事实全局得分的损失进行训练, 难以对不同的规则推理模式进行有针对性地学习, 为此, RPFE定义关系框的差异性, 并利用该差异性设计不同推理模式的专属差异性函数, 通过调整关系框的不同嵌入位置, 捕获不同推理模式的规则, 进而对规则学习提供直观的嵌入解释.
2.2.1 关系框的差异性
本文通过关系框的重叠程度、分离程度和包含状态表示并定义其差异性.
RPFE利用关系框中心点的距离和边框宽度的差异, 衡量两个关系框的重叠程度:
$ P_{o}\left(\boldsymbol{r}_{1}^{(m)}, \boldsymbol{r}_{2}^{(n)}\right)=\left\|\boldsymbol{c}_{1}^{(m)}-\boldsymbol{c}_{2}^{(n)}\right\|_{x}+\left\|\boldsymbol{w}_{1}^{(m)}-\boldsymbol{w}_{2}^{(n)}\right\|_{x}, $
其中m=1, 2, 表示关系的入框或出框.若两个关系框中心点距离越小, 且对应维度边框宽度差异越小, 两框的重叠程度越高.
RPFE利用关系框中心点距离与两框宽度之间的差距, 衡量两个关系框的分离程度:
$ \begin{array}{l} P_{d}\left(\boldsymbol{r}_{1}^{(m)}, \boldsymbol{r}_{2}^{(n)}\right)= \\ \quad\left\|\operatorname{ReLU}\left(\frac{\boldsymbol{w}_{1}^{(m)}+\boldsymbol{w}_{2}^{(n)}}{2}-\left|\boldsymbol{c}_{1}^{(m)}-\boldsymbol{c}_{2}^{(n)}\right|\right)\right\|_{x}, \end{array} $
其中,
$ \operatorname{Re} L U(x)=\max (0, x), $
$ |\cdot| $表示元素的绝对值.若两个关系框中心点的距离与两框宽度之和的一半相差越大, 两框的分离程度越高.
RPFE利用两个关系框上下边界的距离差判定两框是否存在包含状态, 如果一个关系框的下边界大于另一个关系框的下边界, 且一个关系框的上边界小于另一个关系框的上边界, 则该关系框被另一个关系框包含, 关系框
$ \begin{array}{l} P_{c}\left(\boldsymbol{r}_{1}^{(m)}, \boldsymbol{r}_{2}^{(n)}\right)= \\ \quad \| \operatorname{ReLU}\left(\left(\boldsymbol{c}_{2}^{(n)}-\boldsymbol{c}_{1}^{(m)}\right)+\frac{\boldsymbol{w}_{1}^{(m)}-\boldsymbol{w}_{2}^{(n)}}{2}\right)+ \\ \quad \operatorname{ReLU}\left(\left(\boldsymbol{c}_{1}^{(m)}-\boldsymbol{c}_{2}^{(n)}\right)+\frac{\boldsymbol{w}_{1}^{(m)}-\boldsymbol{w}_{2}^{(n)}}{2}\right) \|_{x} . \end{array} $ (2)
关系框
$ \boldsymbol{l}_{j}^{(n)} \leqslant \boldsymbol{l}_{i}^{(m)} \leqslant \boldsymbol{u}_{i}^{(m)} \leqslant \boldsymbol{u}_{j}^{(n)}, $
其中≤ 表示元素小于等于.为了统一参数, 使用关系框的中心和宽度表示上述不等式:
$ \begin{array}{l} \left(\boldsymbol{c}_{j}^{(n)}-\boldsymbol{c}_{i}^{(m)}\right)+\frac{\boldsymbol{w}_{i}^{(m)}-\boldsymbol{w}_{j}^{(n)}}{2} \leqslant \mathbf{0}, \\ \left(\boldsymbol{c}_{i}^{(m)}-\boldsymbol{c}_{j}^{(n)}\right)+\frac{\boldsymbol{w}_{i}^{(m)}-\boldsymbol{w}_{j}^{(n)}}{2} \leqslant \mathbf{0} . \end{array} $
2.2.2 推理模式差异性函数表达及规则学习优化
2.2.2.1 对称推理模式
基于基础嵌入模型, 分析发现对称推理模式嵌入特点, 如果关系ri的入框
ri(x, y)⇒ ri(y, x)
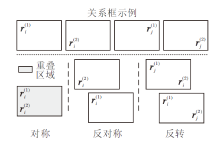
的一条规则, 如图3中对称推理模式所示.
当满足
$ \sigma\left(P_{o}\left(\boldsymbol{r}_{i}^{(1)}, \boldsymbol{r}_{i}^{(2)}\right)\right)-\epsilon \geqslant 0 $
时, 认为规则满足对称推理模式, 其中, σ (· )表示变体Sigmoid函数,
σ (x)=2Sigmoid(x)-1,
$\epsilon$表示捕获规则推理模式的阈值.
对称推理模式利用关系的入框和出框的重叠程度定义其差异性函数, 两框的重叠程度越高越符合该模式, 即
$ s_{p \doteqdot}=P_{o}\left(\boldsymbol{r}_{i}^{(1)}, \boldsymbol{r}_{i}^{(2)}\right) . $
2.2.2.2 反对称推理模式
如果某个关系ri的入框
$ r_{i}(x, y) \Rightarrow \neg r_{i}(y, x), $
如图3中反对称推理模式所示.若在某一维度上, 两个关系框中心点距离大于两框宽度之和的一半时, 说明入框和出框分离, 规则满足反对称推理模式:
$ \sigma\left(P_{d}\left(\boldsymbol{r}_{i}^{(1)}, \boldsymbol{r}_{i}^{(2)}\right)\right)-\epsilon \geqslant 0 . $
当关系ri的入框和出框分离程度越大, 两框有重叠区域的可能性就越小, 越符合该模式语义.因此, 反对称推理模式利用关系框的分离程度定义其差异性函数:
$ s_{p \fallingdotseq}=P_{d}\left(\boldsymbol{r}_{i}^{(1)}, \boldsymbol{r}_{i}^{(2)}\right) . $
2.2.2.3 反转推理模式
如果关系ri的入框
$ r_{i}(x, y) \Leftrightarrow r_{j}(y, x) $
的反转规则:
$ \sigma\left(P_{o}\left(\boldsymbol{r}_{i}^{(1)}, \boldsymbol{r}_{j}^{(2)}\right)+P_{o}\left(\boldsymbol{r}_{i}^{(2)}, \boldsymbol{r}_{j}^{(1)}\right)\right)-\epsilon \geqslant 0 . $
反转推理模式差异性函数考虑两个关系框的入框和出框、出框和入框的重叠程度, 重叠程度越小, 越符合模式语义:
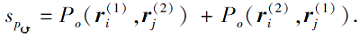
2.2.2.4 层次推理模式
如果存在关系ri的入框
ri(x, y)⇒ rj(x, y)
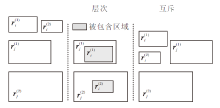
的层次性的规则, 对应的关系框位置状态如图4中层次推理模式所示.层次推理模式利用关系框的包含状态定义其差异性函数, 关系的入框和出框分别被另一个关系的入框和出框包含, 则符合层次模式的语义:
$ s_{P_{\rightrightarrows}}=P_{c}\left(\boldsymbol{r}_{i}^{(1)}, \boldsymbol{r}_{j}^{(1)}\right)+P_{c}\left(\boldsymbol{r}_{i}^{(2)}, \boldsymbol{r}_{j}^{(2)}\right) . $
2.2.2.5 互斥推理模式
如果存在关系ri的入框
$ r_{i}(x, y) \wedge r_{j}(x, y) \Rightarrow \perp $
的互斥性规则, 如图4中互斥推理模式所示.
互斥推理模式差异性函数考虑两个关系框的入框和出框、出框和入框的分离程度, 分离程度越大, 两框有重叠区域的可能性就越小, 即
$ s_{p_{\perp}}=P_{d}\left(\boldsymbol{r}_{i}^{(1)}, \boldsymbol{r}_{j}^{(2)}\right)+P_{d}\left(\boldsymbol{r}_{i}^{(2)}, \boldsymbol{r}_{j}^{(1)}\right) . $ (3)
2.2.2.6 交集推理模式
如果存在关系rk的入框
ri(x, y)∧ rj(x, y)⇒ rk(x, y)
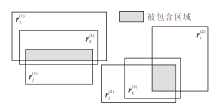
的交集性规则, 如图5所示.
交集推理模式同样利用包含状态对差异性函数进行定义, 得到ri和rj的入框和出框分别相交的区域
$ s_{P_{\boldsymbol{\Pi}}}=P_{c}\left(\boldsymbol{r}_{a}^{(1)}, \boldsymbol{r}_{k}^{(1)}\right)+P_{c}\left(\boldsymbol{r}_{a}^{(2)}, \boldsymbol{r}_{k}^{(2)}\right) . $
BoxE仅由事实得分训练得到的规则学习, 缺乏实体和关系嵌入表征的依据, 导致学到的规则与图谱中的事实可能存在冲突, 进而对事实的推理造成负面影响.为此, RPFE设计事实距离一致性评分, 旨在利用各类规则推理模式强化事实嵌入训练的评分函数, 使利用规则推理的事实能准确表达推理模式的语义, 进而提升事实推理的可解释性.
2.3.1 事实距离一致性
本文利用规则推理的事实中实体嵌入和关系框之间的位置状态定义事实距离一致性评分:
$ \begin{array}{l} d_{\text {in }}\left(\boldsymbol{e}^{r\left(e_{1}, e_{2}\right)}, \boldsymbol{r}^{(m)}\right)= \\ \left\|\operatorname{ReLU}\left(\frac{\boldsymbol{w}^{(m)}}{2}-\left|\boldsymbol{e}^{r\left(e_{1}, e_{2}\right)}-\boldsymbol{c}^{(m)}\right|\right)\right\|_{x}, \\ d_{\mathrm{out}}\left(\boldsymbol{e}^{r\left(e_{1}, e_{2}\right)}, \boldsymbol{r}^{(m)}\right)= \\ \left\|\operatorname{ReLU}\left(\left|\boldsymbol{e}^{r\left(e_{1}, e_{2}\right)}-\boldsymbol{c}^{(m)}\right|-\frac{\boldsymbol{w}^{(m)}}{2}\right)\right\|_{x} \end{array} $
如果e∈ r(m), 则din成立, 使事实中的实体嵌入在关系框内, 同时让二者嵌入距离缩短; 反之dout成立, 使事实中的实体嵌入在关系框外, 同时让二者嵌入距离增大.
2.3.2 各类规则推理模式的事实距离一致性表达
本节设计并定义各类推理模式的事实距离一致性评分, 以实现事实语义的准确表达.
如果关系ri满足对称性, 且∃(x, y)∈ ε 满足关系ri, 则∀ (y, x)∈ ε , 也应满足关系ri.因此, 对称模式的事实距离一致性评分函数如下:
$ s_{t \doteqdot}=\sum_{r_{i}\left(e_{1}, e_{2}\right) \in T}\left(d_{\mathrm{in}}\left(\boldsymbol{e}_{1}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{i}^{(2)}\right)+d_{\mathrm{in}}\left(\boldsymbol{e}_{2}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{i}^{(1)}\right)\right), $
其中, din(
同理, 反转模式的事实距离一致性评分函数如下:
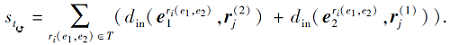
事实中的实体e1的嵌入不仅要在ri的入框内, 还要在rj的出框内.同理e2的嵌入不仅要在ri的出框内, 还要在rj的入框内.
层次和交集模式的事实距离一致性评分函数如下:
$\begin{aligned} s_{t_{\rightrightarrows}}= & \sum_{\substack{r_{i}\left(e_{1}, e_{2}\right) \in T}}\left(d_{\mathrm{in}}\left(\boldsymbol{e}_{1}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{j}^{(1)}\right)+d_{\mathrm{in}}\left(\boldsymbol{e}_{2}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{j}^{(2)}\right)\right), \\ s_{t_{\mathrm{\sqcap}}}= & \sum_{\substack{r_{i}\left(e_{1}, e_{2}\right) \in T \\ r_{j}\left(e_{1}, e_{2}\right) \in T \\ k \neq i, k \neq j}}\left(d_{\mathrm{in}}\left(\boldsymbol{e}_{1}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{k}^{(1)}\right)+d_{\mathrm{in}}\left(\boldsymbol{e}_{2}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{k}^{(2)}\right)+\right. \\ & \left.d_{\mathrm{in}}\left(\boldsymbol{e}_{1}^{r_{j}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{k}^{(1)}\right)+d_{\mathrm{in}}\left(\boldsymbol{e}_{2}^{r_{j}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{k}^{(2)}\right)\right) . \end{aligned} $
利用事实距离一致性对反对称性语义表达的评分函数如下:
$\begin{array}{l} s_{t_{\fallingdotseq}}= \\ \sum_{r_{i}\left(e_{1}, e_{2}\right) \in T}\left(d_{\text {out }}\left(\boldsymbol{e}_{1}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{i}^{(2)}\right)+d_{\text {out }}\left(\boldsymbol{e}_{2}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{i}^{(1)}\right)\right) . \end{array} $
如果事实ri(e1, e2)成立, 那么事实ri(e2, e1)不应成立, e1经过事实作用后的嵌入一方面要在ri的入框内, 另一方面不能在ri的出框内, 同理, e2也是如此.事实距离一致性评分描述事实ri(e1, e2)的头实体e1与关系的出框
互斥性的事实距离一致性要求满足规则头部的实体嵌入都不应出现在其它的关系框中:
$\begin{aligned} s_{t_{\perp}}= & \sum_{\substack{r_{i}\left(e_{1}, e_{2}\right) \in T \\ r_{j}\left(e_{1}, e_{i}\right) \in T \\ k \neq i, k \neq j}}\left(d_{\text {out }}\left(\boldsymbol{e}_{1}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{k}^{(1)}\right)+d_{\text {out }}\left(\boldsymbol{e}_{2}^{r_{i}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{k}^{(2)}\right)+\right. \\ & d_{\text {out }}\left(\boldsymbol{e}_{1}^{r_{1}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{k}^{(1)}\right)+d_{\text {out }}\left(\boldsymbol{e}_{2}^{r_{j}\left(e_{1}, e_{2}\right)}, \boldsymbol{r}_{k}^{(2)}\right) . \end{aligned} $
RPFE利用推理模式差异性函数sp和事实距离一致性评分st, 使模型嵌入得到的规则的损失最小, 通过最小化损失函数强化事实的嵌入表示, 并提升语义信息的可解释性, 具体表示为
$L_{P}=\sum_{f \in F} s_{p}+\sum_{f \in F} s_{t}, $
其中F为具有表1模式的规则集.
规则的生成依赖知识图谱中事实的质量, 而推理事实的准确性又取决于规则的置信度, 因此规则生成及推理事实之间具有相辅相成、相互制约的关系.为此, 本节通过优化规则置信度和事实评分, 识别高质量的规则和事实, 利用候选规则在知识图谱中推理隐藏的事实, 并代入下一轮迭代训练, 提高规则质量及推理事实的准确性.基于文献[24]中提出的规则置信度cf的损失对规则置信度进行学习:
$L_{R}=\sum_{r\left(e_{1}, e_{2}\right) \in T_{f}}\left|e^{-s_{i}}-c_{f}\right|, $
其中, Tf表示规则实例化得到的三元组集, si表示式 (1) 确定的三元组评分.
RPFE将三元组及规则置信度的得分映射到区间[0, 1], 当评分接近0或1时, 模型能明确判定推理事实的正确性并理解推理过程, 提升RPFE的可解释性.利用变体二次函数, 得分接近0和1的事实和规则损失最小, 得分接近0.5的事实或规则损失最大.三元组评分和规则置信度优化的损失函数分别表示为
$\begin{array}{l} L_{T C}=\sum_{r\left(e_{1}, e_{2}\right) \in T_{f}}\left(1-2\left(\sigma\left(s_{i}\right)-0.5\right)^{2}\right), \\ L_{R C}=\sum_{f \in F}\left(1-2\left(c_{f}-0.5\right)^{2}\right), \end{array} $
其中F表示规则集.基于上述优化后的事实评分和规则置信度, 筛选下一轮迭代训练的规则和事实.具体来说, 将置信度大于0.95的规则用于迭代推理事实, 同时过滤评分小于0.3的事实, 得到的事实集记为Tf, 继续进行下一轮迭代训练.补充的负样本T'p融合反对称和互斥两类规则推理模式约束的不可能事实, 确保生成的负样本不是随机的, 为生成样本提供解释依据.
RPFE利用前向链法[5]进行规则实例化, 不断将规则应用到补充推理事实的知识图谱中, 直到无法推理新事实, 完成知识图谱的推理.
为了同时学习事实嵌入表示、规则推理模式生成及捕获事实的可解释嵌入, 框架最小化三元组嵌入、规则推理模式、规则置信度和事实评分的损失, 总体训练目标如下所示:
$\begin{array}{c} \min \left\{\frac{1}{|T|}\left(L_{T}+L_{T C}\right)+\frac{1}{\left|T_{f}\right|} L_{R}+\right. \\ \left.\quad \frac{1}{|F|}\left(L_{P}+L_{R C}\right)\right\} . \end{array} $
RPFE迭代训练的具体步骤如算法1所示.
算法1 RPFE的迭代训练算法
输入 三元组r(h, t)∈ T, 迭代学习总步骤数m
输出 规则集F, 推理后的知识图谱 G'={ε , R, T}
随机初始化实体和关系的嵌入Θ
for M← 1 to m do
for N← 1 to n do
LT← LT-Ñ LT
for end
得到推理模式的规则F和置信度cf
初始化新的事实集Tf← Ø 和负样本集T'
while Ti≠ Ø do
F≒ , F⊥在知识图谱中生成负样本T'i
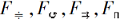 在知识图谱中生成新的事实Ti
在知识图谱中生成新的事实Ti
Tf← Tf∪ Ti\T'i
while end
学习更良好的嵌入LP← LP-Ñ LP
$T \leftarrow T \cup T_{f}$
$\min \left\{\frac{1}{|T|}\left(L_{T}+L_{T C}\right)+\frac{1}{\left|T_{f}\right|} L_{R}+\right. \left.\quad \frac{1}{|F|}\left(L_{P}+L_{R C}\right)\right\}$
for end
return F and G'
本节分析RPFE的时间复杂度和空间复杂度.
1)时间复杂度.RPFE由嵌入学习和规则推理两部分组成.
嵌入学习主要包括三元组的嵌入学习及利用规则推理模式进行优化.在嵌入学习中对三元组学习的时间复杂度为O(|T|d), 其中, |T|表示事实数, d表示嵌入维度.利用规则推理模式对实体和关系的嵌入进行优化的过程中需要从某一实体起始搜索符合规则体的实例, 搜索效率与实体的度密切相关, 因此嵌入优化的时间复杂度为O(|F||ε |ald), 其中, |F|表示规则数, |ε |表示实体数, l表示每条规则的平均长度, a表示每个实体的度的平均数, 从一个实体起始能搜索到符合规则体的最多实例数为al.因此, RPFE嵌入学习的时间复杂度为
O(|T|d+|F||ε |ald).
RPFE在规则推理中使用前向链法进行规则实例化, 时间开销取决于规则数量和每个规则的平均长度, 因此, 规则推理的时间复杂度为
O(|F||ε |al).
综上, RPFE的时间复杂度为
O(|T|d+|F||ε |ald+|F||ε |al).
相比较优的联合嵌入和规则的推理模型(如KALE[12]、RUGE[13]、RulE[14]), RPFE的时间复杂度与其接近.
2)空间复杂度.RPFE仅存储实体和关系的嵌入, 每个关系的嵌入均由一个入框和一个出框表示, 空间开销为O(|ε |d+2|R|d), 其中|R|表示关系数量.RPFE的空间开销取决于实体和关系的嵌入向量.由于关系数远小于实体数, 即|R|≪|ε |, 因此RPFE与现有推理模型 (如KALE、RUGE、BoxE[22])的空间复杂度基本一致, 且低于额外存储规则嵌入的RulE.
本文在Family、WN18RR、FB15k-237这3个常用开放数据集上进行测试实验, 数据集具体信息如表2所示.各数据集上包含表1研究的各类推理模式, Family数据集上主要包括互斥、反对称和反转推理模式, FB15k-237数据集上主要包括对称、反对称和层次推理模式, WN18RR数据集上主要包括对称和反对称推理模式[16].
| 表2 实验数据集信息 Table 2 Information of experimental datasets |
本文实验在CPU为Intel Core i9-12900K, GPU为NVIDIA RTX 3090, 内存128 GB的服务器上完成.在Ubuntu 20.04操作系统中使用Python 3.10.12和PyTorch 2.2.1训练框架进行训练、测试和验证, 优化器为Adam(Adaptive Moment Estimation).PRFE在不同数据集上的配置参数如表3所示.
| 表3 PRFE在不同数据集上的参数配置 Table 3 PRFE parameter configuration on different datasets |
本文的评价指标选取正确三元组推理排名在前N%的占比(Hits@1、Hits@10)和平均倒数排名(Mean Reciprocal Rank, MRR).MRR或Hits@N的值越高, 性能越优.
本节分析RPFE在图谱中对高质量事实可解释的推理能力.实验的目标是推理实体间缺失的关系, 即?(e1, e2).实体和关系嵌入经过双曲正切函数tanh(· )作用, 被映射至[-1, 1]d有界空间中, 其中d表示嵌入维度, 选择L2范数度量向量距离.
本节选取如下对比模型.
1)基于TBA的模型: TransE[15]、RotatE[16], In-verseEF[17].
2)基于LMA的模型:ComplEx[18]、GIE[19]、Hy-GGE[20].
3)基于空间表示的模型:BoxE[22].
4)利用规则学习的模型:RLogic[8]、RNNLo-gic[25].
5)联合嵌入和规则的模型:RUGE[13]、RulE[14]、InterERP[23].
各模型在不同数据集上的推理结果如表4所示, 表中黑体数字表示最优值.由表可见, 基于空间表示模型的性能优于基于TBA的模型和基于LMA的模型, 表明本文选取BoxE作为嵌入模型时效果较优.RPFE的性能显著优于基于嵌入的推理模型, 这是因为RPFE具有对规则充分建模的能力.在FB15k-237、WN18RR数据集上, RPFE的各项指标均优于其它联合嵌入训练和规则的模型, 特别是在推理模式更丰富的FB15k-237数据集上, 这是因为RPFE利用推理模式差异性及事实距离一致性实现对规则的准确建模, 并强化提升嵌入学习质量, 进而推理高质量的事实.
| 表4 各模型在3个数据集上的推理性能对比 Table 4 Reasoning performance comparison of different models on 3 datasets |
在Family数据集上, RPFE虽未取得最优值, 但在各项指标中与RulE相差不大.本文分析RulE具有最优值的原因可能是Family数据集上存在一些依赖于链式推理的事实, 而RulE专门实现对这类推理的嵌入建模.
实验还评估RPFE在FB15k-237数据集上受嵌入维度d、迭代总次数m和捕获推理模式阈值$\epsilon$的影响.
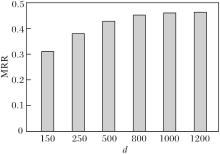
定义d=150, 250, 500, 800, 1 000, 1 200, 其对RPFE的影响如图6所示.由图可知, d=500时推理性能较优, d=1 000时推理性能已接近最优, 因此将d=1 000作为实验设定值, 这得益于RPFE对规则推理模式的良好支持.
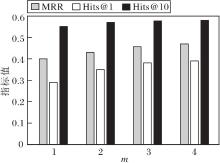
定义m=1, 2, 3, 4, 其对RPFE的影响如图7所示.由图可知, 迭代训练对指标值提升具有明显作用, 这是因为迭代训练中加入高质量事实和更精确的嵌入, 能有效解决图谱稀疏性问题.此外, 随着迭代次数的增加, 生成缺失事实的数量逐渐减少, 指标增长逐渐缓慢.
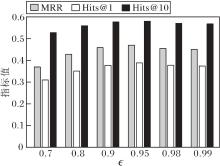
定义$\epsilon$=0.7, 0.8, 0.9, 0.95, 0.98, 0.99, 其对RPFE的影响如图8所示.
由图8可知:当$\epsilon$较小时, RPFE无法准确识别规则的推理模式; 当$\epsilon$> 0.95时, 受嵌入学习精度的影响, RPFE难以捕获更多数量的规则; 当$\epsilon$=0.95时, 评价指标达到最优.因此$\epsilon$=0.95为本文实验设定值.
在常用的FB15k-237数据集上进行消融实验, 验证RPFE各关键模块对模型整体性能的影响.消融实验共包含5种情况:RPFE、删除迭代训练(简记为RPFE-Ite)、删除推理模式差异性和事实距离一致性(简记为RPFE-p-t)、删除事实距离一致性(简记为RPFE-t)、删除规则和事实得分优化(简记为RPFE-L).
各模块消融实验结果如表5所示.由表可得如下结论.
| 表5 消融实验结果 Table 5 Results of ablation experiments |
1)删除迭代训练后模型性能下降明显, 这是因为FB15k-237数据集上关系和事实较丰富, 能学到的规则数量较多, 通过迭代训练可捕获较多有价值的事实和规则, 进而提升推理性能.
2)删除推理模式差异性和事实距离一致性对模型性能影响较大, 原因在于RPFE根据不同推理模式的特点设计推理模式差异性函数和事实距离一致性评分, 实现捕获规则及嵌入表示质量的提升.
3)删除规则和事实得分的优化策略后, Hits@1下降最明显, 这说明优化策略能筛选高质量的规则和推理事实, 有助于提高推理性能.
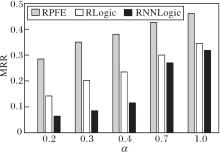
3.4.1 稀疏数据对推理性能的影响
在FB15k-237数据集上抽取一定比例的三元组构造稀疏知识图谱[26], 并研究数据稀疏对规则学习、事实嵌入表征质量及模型推理性能的影响.为了确保公平, 在相同条件下对相关模型进行实验验证.
RPFE、RLogic、RNNLogic在稀疏度α =0.2, 0.3, 0.4, 0.7, 1.0时的推理性能对比如图9所示.由图可发现, RNNLogic对稀疏度的变化最敏感.RPFE和RLogic在α ≥ 0.4时, 随着α 减小推理性能下降缓慢; 当α < 0.4时, 由于数据过于稀疏, 指标值下降较快, 但RPFE的性能始终优于RLogic, 这是因为RPFE在推理过程中不断补充捕获的高质量事实, 弥补在稀疏图谱上规则学习不充分导致推理性能下降的不足.因此, RPFE可应用于稀疏图谱.
3.4.2 噪声数据对推理性能的影响
在FB15k-237数据集上将随机实体替换为原有训练集上的头实体或尾实体, 再将得到的噪声数据加入原始训练集中, 保持测试集和验证集不变, 得到带有噪声三元组的FB15k-237数据集, 并在其上分析RPFE和BoxE的推理性能.
设置噪声比例θ =0%, 10%, 20%, 30%, RPFE和BoxE的推理性能如表6所示, 表中黑体数字表示最优值.由表可见, 随着θ 的增大, MRR值均有所下降.尽管表4中BoxE在FB15k-237数据集上取得最优性能, 但其受噪声影响, 性能下降显著, 而RPFE受噪声的影响相对较小, 在噪声图谱上的性能仍优于BoxE.实验表明RPFE能捕获高质量的事实, 在噪声数据下的稳健性更强.
| 表6 RPFE和BoxE在不同噪声比例下的MRR值对比 Table 6 MRR comparison of RPFE and BoxE with different noise ratios |
为了验证RPFE嵌入模块对不同模型具有良好的兼容性, 在Family数据集上, 采用TransE、Compl-Ex、BoxE作为初始嵌入, 分析RPFE的推理性能, 具体指标值如表7所示, 表中黑体数字表示最优值.
| 表7 嵌入模型不同时RPFE的推理性能对比 Table 7 Reasoning performance comparison of RPFE with different embedding models |
由表7可知, RPFE在3个嵌入模型下均取得较优的推理效果, 说明RPFE具有良好的兼容性和可扩展性.利用BoxE和ComplEx的嵌入推理性能优于TransE的原因在于二者支持Family数据集上的互斥、反对称和反转推理模式, 而TransE难以正确捕获反转推理模式, 导致性能稍差.实验结果显示利用BoxE作为初始嵌入时推理效果最优, 进一步表明RPFE选取BoxE作为嵌入模型的合理性.
本文利用表8中的案例进一步说明RPFE如何推理可解释的高质量事实.
| 表8 案例分析 Table 8 Case analysis |
第1个案例为RPFE在Family数据集上对实体262和263之间的关系推理, 由于存在符合规则头部的事实, 因此可推断husband关系.RPFE优化规则置信度, 使该反转推理模式的规则置信度升高, 可解释性提升, 对于事实嵌入的得分更准确, 事实质量更优.
第2个案例为RPFE在3.4.2节噪声比例为10%的FB15k-237数据集上对两个实体是否具有其它关系的推理.由于两个实体在原数据集上存在一个事实, RPFE利用事实得分的优化策略, 判定该事实为真, 提升图谱中事实的质量, 利用层次推理模式的规则及已有的高质量事实进行推理, 使推理过程具有依据, 由此验证模型具有较强的可解释性.
本文提出联合规则推理模式和事实嵌入的知识图谱推理模型(RPFE), 结合嵌入学习和规则推理, 设计推理模式差异性函数, 捕获不同推理模式的规则, 并对各类推理模式进行专门学习, 提供直观的嵌入解释.本文定义事实距离一致性评分, 优化利用各类模式的规则推理的事实嵌入, 准确表达事实语义.本文还提出迭代学习优化策略, 有效利用规则推理补充和校正知识图谱推理中的事实, 增强模型对新事实的推理能力, 提高规则学习质量, 增强模型学习和推理的可解释性.实验表明, RPFE在3个数据集上推理性能较优, 可有效解决稀疏和低质量数据下推理效果及可解释性较差的问题, 具有良好的理论和实际应用价值.
本文责任编委 欧阳丹彤
Recommended by Associate Editor OUYANG Dantong
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|