任 懿,博士,高级工程师,主要研究方向为强化学习、智能博弈.E-mail:renyi_iscas@126.com.
作者简介: 
侯永宏,博士,教授,主要研究方向为计算机视觉、视频与图像处理、数字通信.E-mail:houroy@tju.edu.cn. 
丁 旺,硕士研究生,主要研究方向为离线强化学习、人工智能.E-mail:2022234138@tju.edu.cn. 
董洪伟,博士,助理研究员,主要研究方向为机器学习、模式识别.E-mail:donghongwei1994@163.com. 
杨松领,硕士研究生,主要研究方向为强化学习、人工智能.E-mail: 2022234112@tju.edu.cn.
针对离线强化学习算法过度依赖数据集样本质量的问题,提出基于优质样本筛选的离线强化学习算法.首先,在策略评估阶段,赋予优势值的样本更高的更新权重,并添加策略熵项,快速识别高质量且在数据分布内概率较高的动作样本,从而筛选更有价值的动作样本.在策略优化阶段,最大化归一化优势函数的同时,保持对数据集上动作的策略约束,使算法在数据集样本质量较低时也可高效利用优质样本,提升策略的学习效率和性能.实验表明,文中算法在MuJoCo-Gym环境的D4RL离线数据集上表现出色,并且可成功筛选更有价值的样本,由此验证其有效性.
REN Yi, Ph.D., senior engineer. His research interests include reinforcement learning and intelligent game.
About Author:
HOU Yonghong, Ph.D., professor. His research interests include computer vision, video and image processing, and digital communication.
DING Wang, Master student. His research interests include offline reinforcement learning and artificial intelligence.
DONG Hongwei, Ph.D., assistant professor. His research interests include machine learning and pattern recognition.
YANG Songling, Master student. His research interests include reinforcement lear-ning and artificial intelligence.
To address the issue of over-reliance on the quality of dataset samples of offline reinforcement learning algorithms, an offline reinforcement learning algorithm based on selection of high-quality samples(SHS) is proposed. In the policy evaluation stage, higher update weights are assigned to the samples with advantage values, and a policy entropy term is added to quickly identify high-quality action samples with high probability within the data distribution, thereby screening out more valuable action samples. In the policy optimization stage, SHS aims to maximize the normalized advantage function while maintaining the policy constraints on the actions within the dataset. Consequently, high-quality samples can be efficiently utilized when the sample quality of the dataset is low, thereby improving the learning efficiency and performance of the strategy. Experiments show that SHS performs well on D4RL offline dataset in the MuJoCo-Gym environment and successfully screens out more valuable samples, thus its effectiveness is verified.
强化学习(Reinforcement Learning, RL)[1]旨在通过智能体与环境的交互学习最佳行为策略.然而, 传统的RL通常需要与环境实时交互, 在某些应用场景下可能成本高昂或应用困难.为了克服这些限制, 离线强化学习(Offline Reinforcement Learning, ORL)[2, 3]作为一种新兴研究方向逐渐受到学术界和工业界的广泛关注.ORL利用丰富的离线数据进行学习和决策, 无需与环境交互, 这些数据可能收集自真实环境, 也可能由模拟器或其它来源生成.ORL在一些关键领域具有重要应用, 如机器人[4]、医疗保健[5]和自动驾驶[6]等.在这些领域中, 利用已有的离线数据进行学习可降低实时交互带来的安全风险, 提高系统的安全性.
ORL的主要挑战在于学习策略和行为策略之间的分布偏移问题.这种差异源于离线数据集的动作覆盖率有限, 导致学到的值函数高估分布外(Out of Distribution, OOD)动作值, 阻碍智能体的性能提升[7].目前大多数ORL算法的主要目标是尽可能减少学习策略与生成数据的行为策略之间的差异, 由此提出各种新机制, 但通常效果并不理想.主要原因是学习策略与行为策略之间的分布偏移会导致策略迭代错误, 从而引入偏差, 并且此偏差会在动态规划过程中传播[8].
为了解决上述问题, 大多数ORL算法都采用保守方法, 约束学习策略与行为策略接近.Kumar等[9]提出BEAR(Bootstrapping Error Accumulation Reduc-tion), 利用最大均值差异(Maximum Mean Discre-pancy, MMD), 确保学习策略接近行为策略.Wu等[10]提出BRAC(Behavior Regularized Actor-Critic), 采取如KL散度、MMD和Wasserstein距离等约束方法, 约束学习策略接近行为策略.Fujimoto等[11]提出BCQ(Batch-Constrained Deep Q-Learning), 将学习策略限制在离线数据集的子集上选择动作, 有效缓解值函数高估问题.Fujimoto等[12]提出TD3+BC, 简单地将行为克隆(Behavior Cloning, BC)项添加到策略优化目标中, 在简单的运动任务中得到较优性能.Wang等[13]提出CRR(Critic-Regularized Regression), 将策略优化目标简化为值过滤回归的形式, 提高模型的泛化性能.Xu等[14]提出SBAC(Soft Behavior Regularized Actor-Critic), 将行为策略的优势值乘以状态边际密度比, 作为新的目标函数, 减小学习策略和行为策略之间的差异, 提升策略优化效率.Peng等[15]提出AWR(Advantage-Weighted Regression), 引入学习策略和行为策略之间的交叉熵损失函数进行策略更新, 并强调最大化优势值, 以有效利用优质样本.Kostrikov等[16]提出IQL(Implicit Q-Learning), 基于期望回归设计一种多步动态规划方法, 完全避免查询OOD样本的值.Xiao等[17]提出InAC(In-Sample Actor-Critic), 添加策略熵正则化项, 鼓励动作选取的多样性, 有效缓解IQL过于保守导致策略容易陷入次优的问题.Garg等[18]提出XQL, 采用极值分析理论, 利用χ 分布直接拟合最优值函数, 解决最大熵强化学习框架下高维动作空间softmax难以计算的问题.
还有方法采用学习一个严格的以真值函数为下界的值函数, 或对未知状态-动作对施加惩罚项等措施.Kumar等[19]提出CQL(Conservative Q-Learning), 将OOD动作的正则项纳入原始贝尔曼误差目标中, 学习保守值函数, 确保学到的Q函数是真实Q函数的下界.Huang等[20]提出ORL-RC(Offline Reinforce-ment Learning with Relaxed Conservatism), 将行为策略正则项添至值函数更新损失中, 进行策略正则化, 有效放宽学到的Q函数和策略的保守性.Kostrikov等[21]提出Fisher-BRC(Behavior Regularized Critic), 使用Fisher分歧正则化作为评论家网络的偏移项, 减少分布偏移问题, 而D-CQL(Density Conservative Q-Learning)[22]估计基于数据集的概率密度函数, 鼓励探索有意义的未知动作.
基于模型的方法通过建立环境模型进行决策, 利用集成方法估计模型的不确定性, 避免在高不确定性的情况下做出决策.这些方法能在面对不同情形时保持一致的决策, 从而提高决策的稳定性.相比之下, 一些方法未明确限制学到的策略, 但仍通过使用行为克隆[23]的一些变体或通过采取单一的策略评估和策略改进[24]解决分布偏移问题.其它更直接的方法基于样本和轨迹分布学习最优策略和最优轨迹分布, 如重要性采样和轨迹优化[25, 26].
然而, 这种保守性往往限制策略的泛化能力, 最终导致性能次优.特别是当离线数据集质量较差时, ORL算法采用的保守性会限制智能体策略的改进[27].为了解决该问题, Peng等[28]提出wPC(Weighted Policy Constraints), 添加优势值的指示函数作为策略约束的权重, 专注于数据集上动作的策略优化, 显著提升智能体在低质量数据集上的性能.但wPC仅简单约束优势函数为正的样本, 而由于离线强化学习数据集样本收集困难、成本较高、样本质量普遍较低、优质数据极少[29], 此时优势函数为正值的动作样本质量仍普遍较低, 筛选的样本质量有限, 导致策略优化后的最优动作概率并不高, 影响策略学习效果.
因此, 为了应对离线强化学习算法过度依赖数据集样本质量的问题, 本文提出基于优质样本筛选的离线强化学习算法(Offline Reinforcement Learning Algorithm Based on Selection of High-Quality Samples, SHS).在策略评估阶段筛选样本, 对优势为正的样本赋予更高的更新权重, 提高样本状态下的平均估计值, 增加优势为正的样本质量.同时基于离线最大熵强化学习框架添加策略熵惩罚项, 识别具有高Q值并在数据分布中概率较高的优质动作样本.在策略优化阶段, 最大化样本优势值以充分利用优质样本, 并沿用wPC保持对数据集上优质动作约束的方法, 使智能体即使在低质量数据集上仍能快速学到优秀策略.SHS有效减轻智能体对离线数据集质量的依赖, 提高智能体在复杂环境中的应对能力, 可较好地应用于实际场景.
设M={s, a, d0, p, r, γ }为一个无限时域马尔可夫决策过程, 其中, s表示智能体的状态, a表示智能体的动作, p表示状态转移概率分布, r表示奖励, d0表示初始状态分布.离线强化学习通过收集的数据集训练离线策略π , 智能体在状态s下采取动作a后, 一直采取策略π 累积获得的折扣期望值:
${{Q}^{\pi }}\left( s,a \right)={{E}_{P,\pi \mid {{s}_{0}}=s,{{a}_{0}}=a}}\left[ \underset{t=0}{\overset{\infty }{\mathop \sum }}\,{{\gamma }^{t}}r\left( {{s}_{t}},{{a}_{t}} \right) \right]$,
其中γ 表示折扣因子.离线强化学习的目标是从固定的数据集D{(st, at, st+1, rt)}中学习一个最大化累积折扣期望值的策略π (a|s), 即
$J\left( \pi \right)=\underset{{{d}_{0}},P,\pi }{\mathop{E}}\,\left[ \underset{t=0}{\overset{\infty }{\mathop \sum }}\,{{\gamma }^{t}}r\left( {{s}_{t}},{{a}_{t}} \right) \right]=\underset{\underset{a\tilde{\ }\pi }{\mathop{s\tilde{\ }{{d}_{0}}}}\,}{\mathop{E}}\,\left[ {{Q}^{\pi }}\left( s,a \right) \right]$.
本质上, 离线强化学习算法需要将策略提升至超越行为策略的级别, 以在实际环境交互中获得更高奖励.然而, 由于面临分布偏移问题, 大多数算法倾向于采取保守主义方法, 使学习策略接近行为策略.因此, 如何平衡策略改进和解决分布偏移问题成为离线强化学习算法需要解决的首要挑战.
TD3+BC[12]结合行为克隆中对数据集动作的惩罚项约束目标策略, 即基于TD3(Twin Delayed Deep Deterministic)优化目标, 添加一个带有权重λ 的行为克隆的正则项(π (s)-a)2, 因此策略优化目标为:
π =arg
其中, D表示数据集采样样本, λ 表示调节策略约束强度的恒定权重因子.TD3+BC结合TD3和行为克隆, 旨在改进学到的策略, 同时约束策略尽可能选择数据集上的动作, 确保策略在数据集上得到改进.然而, 这需要准确的行为克隆, 如果行为克隆不准确, 可能会导致策略训练性能不佳.另外, 由于行为克隆依赖数据集质量, 如果数据集质量较差, TD3+BC也只能学到较差的策略, 导致性能不佳.
wPC[28]将TD3+BC优化目标中策略约束的权重λ 替换为优势值的指示函数, 使策略优化目标的第2项只约束优势值为正的样本, wPC的策略优化目标如下:
J(π )=arg
其中, π (s)表示策略在采样状态s下采取的动作,
$\omega (s, a)=I\left[ \widehat{\text{A}}\left( s, a \right)> 0 \right]=I\left[ {{\widehat{Q}}_{\phi }}\left( s, a \right)-{{\widehat{V}}_{\psi }}\left( s \right)> 0 \right]$,
表示策略约束权重函数, 其目的是约束优势值为正的样本, 放宽对学习策略的不利约束, 同时保留数据集动作的必要约束, 提高算法性能的上限.然而, wPC仅简单地对数据集上优势值为正的动作进行约束.
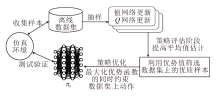
为了解决现有离线强化学习算法对数据集样本质量过于依赖的问题, 本文提出基于优质样本筛选的离线强化学习算法(SHS), 在值函数更新即策略评估阶段严格筛选样本, 并在策略优化阶段高效学习优质样本, 提升策略学习的效率和算法性能的上限.SHS总体框架如图1所示.
首先, 通过采样轨迹从预先收集的离线数据集上提取信息, 利用值网络和Q网络的损失函数进行模型更新.该离线数据集包含智能体在不同状态下采取的动作及其相应的奖励反馈.在策略评估阶段, 旨在提高对智能体在不同状态下的平均值估计.基于离线最大熵强化学习框架添加策略熵惩罚项, 识别那些具有高Q值且在数据分布中频率较高的优质动作样本, 避免对高估的OOD动作进行错误利用.在策略优化阶段, 为了高效利用这些优质样本, 通过最大化归一化的优势函数, 利用已有的经验数据, 优化智能体的策略.特别地, 沿用wPC的思想, 在这一过程中引入策略约束, 确保在数据集上保留优势为正值的动作.通过这种方式, 不仅能提升智能体策略优化的性能和效率, 而且提升总体学习效率和策略的鲁棒性.
为了提高筛选样本的质量, 赋予正优势值的样本更高的更新权重, 以提升样本状态s下的平均估计值Vψ (s), 从而提高优势正值样本的质量.此外, 为了避免对OOD状态值的高估, 在判断优势样本的条件中添加目标策略和行为策略的策略约束正则项D(π b, π θ ), 因此值函数Vψ (s)更新方式如下:
${{L}_{V}}\left( \psi \right)=\left\{ \begin{array}{*{35}{l}} {{E}_{\left( s,a \right)\tilde{\ }D}}[\sigma \left( {{\overset{}{\mathop{Q}}\,}_{\phi }}\left( s,a \right)-{{V}_{\psi }}\left( s \right){{)}^{2}} \right], & {{\overset{}{\mathop{V}}\,}_{\psi }}\left( s \right)\le Q'\left( s,a \right) \\ {{E}_{\left( s,a \right)\tilde{\ }D}}\left[ \left( 1-\sigma \right)\left( {{\overset{}{\mathop{Q}}\,}_{\phi }}\left( s,a \right)-{{V}_{\psi }}\left( s \right) \right){{~}^{2}} \right], & {{\overset{}{\mathop{V}}\,}_{\psi }}\left( s \right)Q'\left( s,a \right) \\ \end{array} \right.$
其中, ψ 表示值网络Vψ 的网络参数,
A(s, a)=Q(s, a)-V(s)
的大小反映当前状态下采取某个动作相对于平均水平动作的优劣程度, 是作为判断是否为优质样本的良好条件.上述更新方法通过赋予高Q值状态样本更大的更新权重系数, 提升平均估计值Vψ (s), 使优势值
达到正值的动作样本需要更高的Q值, 从而达到提高优势正值样本的质量的目的.
为了进一步高效筛选优质样本, 受最大熵强化学习的启发, 本文提出最大熵离线强化学习框架, 对值函数进行约束.通过将强化学习控制问题嵌入图概率模型中, 同时引入一个与奖励相关的二元随机变量Ot, 定义最优性条件:
$p({{O}_{t}}=1|{{s}_{t}}, {{a}_{t}})=\exp \left( \frac{r\left( {{s}_{t}}, {{a}_{t}} \right)}{\mu } \right)$,
其中, μ 表示一个温度参数, Ot表示状态st采取的动作at是否最优, $p\left( {{O}_{t}}=1|{{s}_{t}}, {{a}_{t}} \right)$表示状态st采取的动作at是最优的条件概率.在给定最优变量条件下, 推导最优动作轨迹概率分布$p(\tau |{{O}_{1\, \!:T}})$或最优动作分布$\pi ({{a}_{t}}|{{s}_{t}}, {{O}_{t}})$, 已知最优动作轨迹概率分布p(τ , O1∶ T)满足
$p(\tau |{{O}_{1\, \!:T}})=\rho ({{s}_{1}})\prod\limits_{t=1}^{T}{p\left( {{s}_{t+1}}|{{s}_{t}}, {{a}_{t}} \right)p\left( {{O}_{t}}|{{s}_{t}}, {{a}_{t}} \right)p\left( {{a}_{t}}|{{s}_{t}} \right)}$,
其中, τ 表示智能体轨迹, $p\left( {{a}_{t}}|{{s}_{t}} \right)$表示策略先验分布, 一般使用均匀分布简单表示.
基于变分推理, 引入变分分布推导ELBO(Evi- dence Lower Bound), 推断后验分布$p(\tau |{{O}_{1\, \!:T}})$, 定义变分分布:
$q(\tau )=\rho ({{s}_{1}})\underset{t=1}{\overset{T}{\mathop \prod }}\, p\left( {{s}_{t+1}}|{{s}_{t}}, {{a}_{t}} \right){{\pi }_{\theta }}\left( {{a}_{t}}|{{s}_{t}} \right)$.
因此可将目标函数转化为最小化
$KL(q(\tau )\|p(\tau |{{O}_{1\, \!:T}}))$,
等价于使${{\pi }_{\theta }}\left( {{a}_{t}}|{{s}_{t}} \right)$下的轨迹分布近似为最佳轨迹分布$p(\tau |{{O}_{1\, \!:T}})$, 避免直接求解后验分布$p(\tau |{{O}_{1\, \!:T}})$.因此, 最小化KL散度等于最小化q(τ )的负证据下界, 即
KL(q(τ )‖ p(τ |O1∶ T))=-ELBO(q(τ )).
经过推导, 得出新的目标函数:
$KL(q(\tau )\|p(\tau |{{O}_{1\, \!:T}}))={{E}_{\tau \tilde{\ }{{q}_{\theta }}\left( \tau \right)}}\left[ \underset{t=1}{\overset{T}{\mathop \sum }}\, \left( \ln \left( \frac{{{\pi }_{\theta }}({{a}_{t}}|{{s}_{t}})}{p({{a}_{t}}|{{s}_{t}})} \right)-\frac{r\left( {{s}_{t}}, {{a}_{t}} \right)}{\mu } \right) \right]$.
考虑离线强化学习中先验分布即服从数据集策略分布, 则
p(at|st)=π b(at|st),
因此离线最大熵强化学习中的目标函数满足
$J(\pi )=\arg \underset{\pi }{\mathop{\max }}\, \underset{t=0}{\overset{T}{\mathop \sum }}\, {{E}_{\left( {{s}_{t}}, {{a}_{t}} \right)\tilde{\ }{{\pi }_{\theta }}}}{{\gamma }^{t}}\left[ r({{s}_{t}}, {{a}_{t}})-\mu \ln \left( \frac{{{\pi }_{\theta }}({{a}_{t}}|{{s}_{t}})}{{{\pi }_{b}}({{a}_{t}}|{{s}_{t}})} \right) \right]$.
与SAC(Soft Actor-Critic)[30]不同的是, 离线最大熵强化学习的目标函数不仅包含离线策略的熵项, 还包含行为策略的熵惩罚项, 这迫使目标函数在最大化奖励的同时选择分布内的动作.因此, 值函数遵循如下新的贝尔曼方程:
${{V}^{\pi }}({{s}_{t}})={{E}_{{{a}_{t}}\tilde{\ }\pi ({{a}_{t}}|{{s}_{t}})}}\left[ {{Q}^{\pi }}({{s}_{t}}, {{a}_{t}})-\mu \ln \left( \frac{{{\pi }_{\theta }}({{a}_{t}}|{{s}_{t}})}{{{\overset{}{\mathop{\pi }}\, }_{b}}({{a}_{t}}|{{s}_{t}})} \right) \right]$,
其中
H(π θ (s, a))=-ln π θ (s, a)
能扩大策略的选择空间, 促进多样化的动作选择, 从而在一定程度上缓解离线强化学习算法中常见的过于保守的问题.行为策略熵的惩罚项
-H(π b(s, a))=ln π b(s, a)
能赋予数据集外的动作更低的估计值, 识别具有高Q值并且在数据分布中概率较高的优质动作样本.因此, 值函数遵循如下新的更新方法:
${{L}_{V}}\left( \psi \right)=\left\{ \begin{array}{*{35}{l}} {{E}_{\left( s,a \right)\tilde{\ }D}}[\sigma \left( {{\overset{}{\mathop{Q}}\,}_{\phi }}\left( s,a \right)-{{V}_{\psi }}\left( s \right){{)}^{2}} \right], & {{\overset{}{\mathop{V}}\,}_{\psi }}\left( s \right)\le {{\overset{}{\mathop{Q}}\,}_{\phi }}\left( s,a \right)+\mu \left( \text{ln}~{{\pi }_{b}}\left( s,a \right)-\text{ln}~{{\pi }_{\theta }}\left( s,a \right) \right) \\ {{E}_{\left( s,a \right)\tilde{\ }D}}[\left( 1-\sigma \right)\left( {{\overset{}{\mathop{Q}}\,}_{\phi }}\left( s,a \right)-{{V}_{\psi }}\left( s \right){{)}^{2}} \right], & {{\overset{}{\mathop{V}}\,}_{\psi }}\left( s \right){{\overset{}{\mathop{Q}}\,}_{\phi }}\left( s,a \right)+\mu \left( \text{ln}~{{\pi }_{b}}\left( s,a \right)-\text{ln}~{{\pi }_{\theta }}\left( s,a \right) \right) \\ \end{array} \right.$(1)
其中, π b(s, a)表示行为策略, π θ (s, a)表示学习策略, μ 表示判断是否为优质样本的策略熵惩罚正则化权重.
本文选择添加学习策略和行为策略的策略熵惩罚项作为判断是否为优质样本的约束条件.添加策略熵惩罚项的目的是确保在筛选优质样本时, 避免高估OOD动作值, 以便筛选既具有高价值又在数据分布内概率较高的动作样本.当π b高于π θ 即动作样本在数据分布内的概率较高时, 赋予该动作状态对更高的Q值; 当π b低于π θ 时, 表示该动作样本在数据集概率较小或可能是次优动作, 对其进行惩罚以赋予状态较低的Q值.上述值函数更新方法能提高数据集上优质样本的平均估计值, 筛选既具有高Q值又在数据分布内概率较高的优质动作样本.
在深度强化学习中, 神经网络参数ϕ 的Qϕ (s, a)表示Q函数, 通过最小化时序差分(Temporal Difference, TD)损失
Es, a, r, s'~D[
更新, 利用由
Γ Q(s, a)=r(s, a)+γ
在离线强化学习中, 需要通过采样数据集上样本进行训练, 并根据策略分布π θ 采样动作a'训练Q函数, 目标函数为:
${{L}_{Q}}(\phi )={{E}_{s}}_{, a, r, s'\tilde{\ }D}\left[ \frac{1}{2}{{\left( r\left( s, a \right)+\gamma {{Q}_{{\bar{\phi }}}}\left( s', {{\pi }_{\theta }}\left( \cdot |s' \right) \right)-{{Q}_{\phi }}\left( s, a \right) \right)}^{2}} \right]$, (2)
其中, ϕ 表示Q值网络Qϕ 的网络参数,
${{Q}_{{\bar{\phi }}}}\left( s', {{\pi }_{\theta }}\left( \cdot |s' \right) \right)=\min \left\{ {{Q}_{{{{\bar{\phi }}}_{1}}}}\left( s', {{\pi }_{\theta }}\left( \cdot |s' \right) \right), {{Q}_{{{{\bar{\phi }}}_{2}}}}\left( s', {{\pi }_{\theta }}\left( \cdot |s' \right) \right) \right\}$,
表示Q目标网络取两个独立的Q网络估计的最小值.结合目标网络使用, 可令Q值更新更稳健, 从而提高学习的稳定性和收敛速度.
为了在策略优化阶段更高效地利用优质样本, 最大化归一化优势函数利用经验数据优化策略, 并保留对数据集上优势为正值的动作的策略约束, 专注于数据集上优质动作的策略优化, 防止错误利用高估的OOD动作.此时策略优化目标为:
$\arg \underset{{{\pi }_{\theta }}}{\mathop{\max }}\, {{E}_{(s, a)\tilde{\ }D}}\left[ \frac{\alpha \left( {{\overset{}{\mathop{Q}}\, }_{\phi }}\left( s, {{\pi }_{\theta }}\left( s \right) \right)-{{\overset{}{\mathop{V}}\, }_{\psi }}\left( s \right) \right)}{\frac{1}{{{D}_{C}}}\sum\limits_{\left( s, a \right)\in D}{|{{\overset{}{\mathop{Q}}\, }_{\phi }}\left( s, {{\pi }_{\theta }}\left( s \right) \right)-{{\overset{}{\mathop{V}}\, }_{\psi }}\left( s \right)|}}-\omega (s, a){{({{\pi }_{\theta }}(s)-a)}^{2}} \right]$, (3)
其中, α 表示策略优化目标最大化优势函数的权重, DC表示抽样样本数.随着α 的增大, 策略优化将偏向于更新优势值较高的样本, 并减轻对数据集上动作的约束程度.在目标函数选择过程中, 为了提高策略学习效率, 本文采用最大化归一化优势函数而不是值函数作为策略优化的目标, 这有助于减小目标值方差, 使学习过程更稳定.特别地, 由于在策略评估过程中进行优质样本筛选, 从而提高样本状态下的平均估计值
SHS的伪代码如算法1所示.
算法1 SHS
随机初始化值网络
初始化目标网络
对于训练步数 t=1 to T:
从经验回放池D采样B={(s, a, r, s')}
使用行为克隆方法训练行为策略网络π b
基于式(1)损失函数LV(ψ )训练值网络Vψ
基于式(2)损失函数LQ(ϕ )训练Q值网络Qϕ
基于式(3)损失函数Lπ (θ )训练策略网络π θ
软更新目标网络:
本文在MuJoCo-Gym标准环境中评估SHS的性能.MuJoCo-Gym环境是一个典型的离线强化学习评估环境, 包含各种不同的任务.本文选择Half-cheetah、Hopper、Walker2d这3种环境中的3类数据集, 共计9个数据集进行实验测试.每次实验使用6个随机种子, 训练1× 106步, 每5 000步评估一次, 每次评估运行10个回合.
MuJoCo-Gym环境中的D4RL离线数据集包括Medium、Medium-Replay、Medium-Expert数据集, 每类数据集都模拟不同的部署场景, 数据集版本为2.0.3类数据集信息如表1所示.
| 表1 实验数据集信息 Table 1 Information of experimental datasets |
3类数据集都是包含1× 106步的轨迹对, 每个轨迹对由四元组组成, 包含当前步长的状态、动作、奖励及下一刻步长的状态.在Medium数据集上, 所有轨迹都是由智能体采用SAC策略训练至一半过程时采样后收集的.在Medium-Replay数据集上, 一半的轨迹来自Medium数据收集期间使用的回放缓冲区, 而另一半的轨迹是从Medium数据集采样得到的.在Medium-Expert数据集上, 一半的轨迹是智能体采用已训练好的SAC策略收集的, 其余一半的轨迹是从Medium数据集上采样得到的.
本文选择如下离线RL算法进行对比评估:TD3+BC[12]、IQL[16]、InAC[17]、XQL[18]、CQL[19]、ORL-RC[20]、wPC[28].TD3+BC将行为克隆项添至策略优化目标, 增加对数据集上动作的约束.IQL基于期望回归设计多步动态规划方法, 完全避免查询OOD样本的值.InAC结合SAC和IQL, 添加策略熵正则化项, 鼓励动作选取的多样性.XQL利用χ 分布直接拟合最优值函数.CQL基于原始贝尔曼误差目标添加OOD动作的正则项以学习保守值函数.ORL-RC将行为策略正则项添至值函数更新损失中, 有效放宽学到的Q函数和策略的保守性.wPC对数据集上优势值为正的动作进行约束, 筛选具有价值的高质量样本.
各方法在MuJoCo-Gym任务上的标准平均回报对比如表2所示, 表中黑体数字表示最优值.
| 表2 各算法在MuJoCo-Gym任务上的性能对比 Table 2 Performance comparison of different algorithms on MuJoCo-Gym task |
由表2可见, MuJoCo-Gym任务中SHS在的Me-dium、Medium-Replay数据集上表现优异, 在3类数据集上获得的标准回报总和为779.9, 超过wPC, 同时优于ORL-RC.
IQL、wPC、ORL-RC和SHS在MuJoCo-Gym任务中获得的标准平均回报曲线图如图2所示, 由图可见, SHS取得最优结果.值得注意的是, SHS在Medium、Medium-Replay数据集上的表现超越ORL-RC, 并且收敛速度更快.实际上, SHS在几乎所有数据集上都是收敛速度最快的, 这表明优质样本筛选对策略模型在初始学习阶段的影响尤为显著.SHS通过筛选优质样本进行优先更新, 导致状态值高估, 减少达到优势正值的动作样本, 从而在劣质数据集上算法能快速筛选优质样本进行策略学习.因此, SHS有助于智能体在劣质数据集上快速筛选高质量动作, 显著提升在Medium、Medium-Replay数据集上获得的平均回报.然而, 在Medium-Expert数据集上, SHS效果提升不太显著.这是因为相比Me-dium、Medium-Replay数据集, Medium-Expert数据集包含更多的优质样本, 此时筛选优质样本可能会过滤大量优质样本, 限制智能体的性能提升, 因此SHS在Medium-Expert数据集上表现一般.
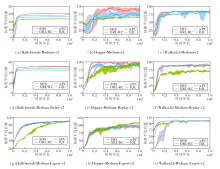 | 图2 各算法在MuJoCo-Gym任务中的标准平均回报曲线Fig.2 Standard average return curves of different algorithms on MuJoCo-Gym task |
为了进一步验证SHS能筛选更优质的样本, 进行优势正值率的对比分析, 优势正值率的计算公式如下:
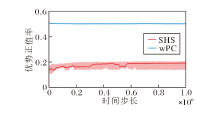
SHS和wPC在Medium数据集上的优势正值率对比如图3所示.
由图3可知, SHS的优势正值率明显低于同为筛选优质样本算法的wPC.具体而言, wPC的优势正值率约为50%, 而SHS的优势正值率约为17%.这是因为相比wPC, SHS对于优质样本的筛选条件更苛刻, 导致满足优势正值标准的样本数量更少, 因此优势正值率较低.实验结果表明, SHS在劣质数据集上筛选更优质的样本进行学习, 成功识别更有价值的样本, 验证其有效性, 并展示其改善学习效率和策略性能的潜力.
为了探索SHS中最大化优势函数的归一化权重 α 和优质样本的更新权重σ 的有效性, 进行消融实验.
首先控制其它超参数不变, 设置α =0.05, 0.01, 0.005, 0.001, α 改变时SHS在MuJoCo-Gym任务中获得的标准平均回报曲线如图4所示.由图可见, 随着α 增大, 算法在Medium、Medium-Replay两种样本质量较差的数据集上获得的标准平均回报明显提升.然而, 当α =0.05时, 算法性能大幅下降, 这是由于过于注重最大化优势函数而忽视对数据集上动作的约束, 算法会错误利用高估的OOD动作, 导致策略迭代错误引入偏差, 使算法性能下降.
再控制其它超参数不变, 设置 σ =0.5, 0.7, 0.9, 1.0, σ 改变时SHS获得的标准平均回报曲线如图5所示.
由图5可知, 随着 σ 增大, 算法获得的标准平均回报有所提升, 但当σ =1时, 即只更新优势值为正的样本, 算法性能明显下降.这是由于低质量样本数据集上优势值为正的样本较少, 智能体仅能学到有限数量的动作, 难以完整地完成整项任务.因此, 在质量较差的数据集上, 适当提高优质样本的更新权重以便更加关注筛选优质样本, 或者提高最大化优势函数的归一化权重以帮助智能体更高效地学习优质样本, 都有助于提升算法性能.这说明优先更新优质样本和最大化优势函数的有效性.然而, 在Medium-Expert专家数据集上, 由于样本是通过优质策略采样而来, 含有大量优质样本, 此时过度筛选优质样本会导致智能体学到的优质样本减少, 难以完全学到所有的优质样本.因此, 在专家数据集上, 优先更新样本对性能提升的效果并不明显.相比之下, 在专家数据集上约束策略学习能更保守地学到更优策略.
经过消融实验后, SHS超参数设置如下:批尺寸大小为256, γ =0.99, σ =0.9, μ =0.1, α =0.01.
为了探索SHS中策略熵惩罚项的有效性, 本文对比有/无策略熵惩罚项对算法性能的影响, 具体标准平均回报曲线如图6所示.由图可见, 添加策略熵惩罚项后, 标准平均回报显著提升, 整体表现更稳定.特别是在Walker2d-Medium数据集上, 无策略熵惩罚项的算法性能出现急剧下降, 出现明显的不稳定性.
 | 图6 有/无策略熵惩罚项时SHS的标准平均回报曲线Fig.6 Standard average return curves of SHS with and without policy entropy penalty term |
这是由于添加策略熵惩罚项能确保在筛选优质样本时, 通过惩罚OOD动作值避免出现高估问题, 筛选既具有高价值又在数据分布内概率较高的动作样本, 因此在改善算法性能和稳定性方面起到关键作用.
实验结果同样表明, 无策略熵惩罚项时的标准平均回报不仅明显低于有策略熵惩罚项时, 而且在训练过程中波动幅度较大.因此, 策略熵惩罚项对于提升算法的稳定性和鲁棒性至关重要.
本文提出基于优质样本筛选的离线强化学习算法(SHS), 在策略评估阶段赋予优质样本更高的更新权重, 使达到正优势值的样本条件更严苛, 并添加策略熵惩罚项, 确保筛选既具有高价值又在数据分布内概率较高的优质样本.在策略优化阶段, 致力于最大化样本的优势值, 专注于数据集上动作的策略优化, 充分利用优质样本, 帮助智能体迅速学到优质动作, 提升策略性能和优化效率.为了评估SHS性能, 在MuJoCo-Gym环境的D4RL数据集上进行实验, 结果表明, SHS在策略学习方面表现出高效和稳健的特点.相比现有的ORL-RC, SHS性能明显更优.SHS可有效减轻对高质量离线数据集的依赖, 使智能体在有限数据或低质量数据环境中仍能进行有效学习, 这将推动离线强化学习向更广泛和实用的方向发展.因此, 今后将考虑针对低质量数据集的学习策略, 提升智能体在实际复杂环境中的性能.
本文责任编委 高阳
Recommended by Associate Editor GAO Yang
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|