给定图G=(V, E), 其中, V表示节点集合, E表示边集合.若e_{i, j}∈ E, 则节点v_i、v_j之间有边相连.A表示图G的邻接矩阵, 若节点v_i、v_j之间有连边, A_ij=1, 否则A_ij=0, 即A描述图G的拓扑结构信息.

对于每个节点v, N_p(v)表示第p阶邻域, N_{≤ p}(v)表示p阶内邻域.

通常, 归一化邻接矩阵

A˜= D-12A D-12,

其中D表示度矩阵.因此, 图G的归一化拉普拉斯矩阵定义为

L=I- A˜,

其中I表示单位矩阵.由于L的实对称性, 可特征分解为UΛ U^T, 其中特征向量矩阵

U=[u₁, u₂, …, u_n]^T,

特征值构成的对角矩阵

Λ =diag[λ ₁, λ ₂, …, λ _n],
λ i_∈ [0, 2], i∈ {1, 2, …, n}.

给定图G上的节点特征矩阵(信号)

X=[x₁, x₂, …, x_n]^T, i∈ {1, 2, …, n},

其中x_i表示第i个节点v_i的特征属性.

此外, 对于节点分类任务, 节点v的类标签

y_v={1, 2, …, C}∈ Y,

其中, Y表示类标签集合, C表示类的个数.

根据谱图理论和图信号处理, 图拉普拉斯矩阵的特征值λ 表示图G拓扑结构信号的频率.给定一个图信号x, 其图傅里叶变换定义为

x̂=U^Tx,

傅里叶逆变换^[36]定义为

x=U x̂.

根据图傅里叶变换和拉普拉斯矩阵的特征分解, 作用于信号x的谱滤波器为:

$\hat{\boldsymbol{g}}(\boldsymbol{L}) \boldsymbol{x}=\sum_{i=1}^{n} \hat{\boldsymbol{g}}\left(\lambda_{i}\right) \boldsymbol{u}_{i} \boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{x}=\boldsymbol{U} \hat{\boldsymbol{g}} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{x}$, (1)

其中

$\begin{array}{l}\hat{\boldsymbol{g}}=\hat{\boldsymbol{g}}(\boldsymbol{\Lambda})=\operatorname{diag}\left[\hat{\boldsymbol{g}}\left(\lambda_{1}\right), \hat{\boldsymbol{g}}\left(\lambda_{2}\right), \cdots, \hat{\boldsymbol{g}}\left(\lambda_{n}\right)\right], \\\boldsymbol{g}=\boldsymbol{U} \hat{\boldsymbol{g}} .\end{array}$

根据卷积定理, 式 (1) 可改写为空间图卷积的形式:

x* _G g=U((U^Tg)☉(U^Tx)),

其中, * _G表示图卷积算子, ☉表示哈达玛乘积.

早期的谱域GNNs直接对拉普拉斯矩阵进行特征分解, 并使用特征向量作为傅里叶基.然而, 谱分解的计算成本较高, 尤其在处理大规模图时问题更突出.为了避免拉普拉斯特征向量的显式计算, 随后的研究尝试使用各类多项式逼近图谱滤波器.可利用切比雪夫多项式将滤波器逼近为^[20]:

$\hat{g}\left(\lambda_{i}\right) \approx \widehat{P}_{K}\left(\lambda_{i}\right)=\sum_{k=0}^{K-1} \alpha_{k} \hat{p}_{k}\left(\lambda_{i}\right)$, (2)

其中, p̂k(· )表示第k个多项式基, α _k表示 p̂k(· )对应的可学习参数.通过调整超参数K确定最短路径, 调整中心节点的聚合邻域, 使模型能进行局部滤波.将式(2)代入式(1), 滤波过程可改写为

$\hat{\boldsymbol{g}}(\boldsymbol{L}) \boldsymbol{x} \approx \sum_{k=0}^{K-1} \alpha_{k} \boldsymbol{U} \hat{p}_{k}(\boldsymbol{\Lambda}) \boldsymbol{U}^{\mathrm{T}} \boldsymbol{x}=\sum_{k=0}^{K-1} \alpha_{k} \hat{p}_{k}(\boldsymbol{L}) \boldsymbol{x},$

节点同配比^[11]和边同配比^[24]是衡量图同配性的常用指标.本文主要关注节点分类任务, 因此仅考虑节点邻域的标签一致性, 故选择节点同配比度量图的同配性.对于图G, 其节点同配比为:

$H_{G}=\frac{1}{V} \sum_{v \in V} h_{N_{1}}(v)$,

其中 hN1(v)表示节点v的一阶邻域同配比.对于节点v, p阶邻域同配比为:

hN≤p(v)= |{m∈N≤p(v)∶ym=yv}||N≤p(v)|,

其中, y_m表示节点m的类标签, y_v表示节点v的类标签.

H_G是面向整个图数据的总体评价指标, h_{N≤ p}(v)作为节点级指标, 用于衡量单个节点的局部邻域同配性.对于图G, 将每个节点的邻域作为一个子图, h_{N≤ p}(v)能反映图中包含的不同子图模式.然而, h_{N≤ p}(v)仅考虑邻域标签的一致性, 忽略邻域标签的随机性.

为了研究局部邻域子图的标签随机性, Zheng等^[13]提出标签熵的概念, 用于度量节点v的邻域标签分布, 定义如下:

$\begin{array}{l}S_{N_{\leqslant p}}(v)= \\\quad-\sum_{y \in Y}\left(\frac{\left|N_{\leqslant p}^{(y)}(v)\right|}{\left|N_{\leqslant p}(v)\right|}+\varepsilon\right) \log _{2}\left(\frac{\left|N_{\leqslant p}^{(y)}(v)\right|}{\left|N_{\leqslant p}(v)\right|}+\varepsilon\right), \end{array}$

其中

N≤p(y)(v)={m∶ m∈ N_{≤ p}(v)∩ y_m=y}.

显然, 邻居节点的标签分布均匀时, 标签熵趋于最大.相反, 如果给定节点的邻居标签都属于同一类别, 标签熵最小.

多分辨率分析(Multiresolution Analysis, MRA)是一种将信号分解为不同分辨率层次的方法, 核心思想是利用逐级细化的子空间序列{V_j}_{j∈ Z}分割有限能量空间L²(R), 其中

V₀⊂V₁⊂…⊂V_j⊂V_j+1⊂…⊂L²(R).

∀ j, {W_j}_{j∈ Z}表示正交补空间序列, 满足

V_j+1=V_j⊕ W_j,

则L²(R)可分解为基础空间V₀和正交补空间{W_j}_{j∈ Z}的直和:

$L^{2}(\mathbf{R})=V_{0} \oplus W_{0} \oplus W_{1} \oplus \cdots$

对于信号函数f(t)∈ L²(R), 以二进制小波为例, MRA展开可通过尺度小波

Φ _{j, k}(t)=Φ (2^jt-k)∈ L²(R)

和母小波

Ψ _{j, k}(t)=Ψ (2^jt-k)∈ L²(R)

唯一表示为

$\begin{aligned}f(t)= & f_{0}(t)+\sum_{j=0}^{\infty} \omega_{j}(t)= \\& \sum_{k} a_{k} \Phi(t-k)+\sum_{j=0}^{\infty} \sum_{k} b_{j k} \Psi\left(2^{j} t-k\right), \end{aligned}$

其中, j表示缩放参数, k表示平移参数, f₀(· )表示f(t)在V₀中的信息分量, ω _j(· )表示f(t)在W_j中的信息分量^[37], a_k表示信号在V₀中的投影系数,

a_k=< f(t), Φ (t-k)> ,

b_jk表示信号在W_j中的投影系数,

b_jk=< f(t), Ψ (2^jt-k)> .

由于V_j-1⊂V_j⊂V_j+1属于严格包含关系, V_j中的尺度小波和W_j中的母小波可通过V_j+1中的尺度小波表示^[35].所以正交补空间W_j的生成母小波Ψ _{j, k}(· )可用尺度小波Φ _{j+1, k}(· )替换表示为

$f(t)=\sum_{k} a_{k} \Phi(t-k)+\sum_{j=0}^{\infty} \sum_{k} b_{j k} \Phi\left(2^{j+1} t-k\right) .$ (3)

因此, 对于定义在空间L²(R)中的信号f(t), 通过多分辨率分析可对其进行逐层分解和重建.

图上信号的平滑度是图信号处理中的一种有效度量方法, 用于衡量图中相邻节点间信号相似的可能性^{[36, 37, 38]}.拉普拉斯矩阵的特征值

λ _i= uTiLu_i

反映其相关特征向量u_i在图上的平滑度^[39], 即与较小特征值关联的特征向量表示具有缓慢变化的低频信号, 而与大特征值关联的特征向量表示具有快速变化的高频信号.

给定图上的信号x, 经过图傅里叶变换U^Tx, 有

x̂=α ₁u₁+α ₂u₂+…+α _nu_n, (4)

其中{α _i }i=1n表示对应特征向量的系数.由于特征向量是归一化且相互正交的, 因此有

u_i uTix̂=α ₁u_i uTiu₁+α ₂u_i uTiu₂+…+α _nu_i uTiu_n= α i_ui_,

故{u_i uTi}i=1n可视为图信号的一组基础滤波器, 与u_i相关的特征值λ _i表示信号在滤波器u_i uTi下的频率成分.

对于具有相似邻域结构模式的局部子图, 频谱变化也趋于相似^[40].通过节点邻域同配比 hN≤p(v)和标签熵 SN≤p(v)的大小, 可将图中节点的邻域划分为不同的局部模式, 并与各个基础滤波器对应.

鉴于这些局部邻域模式的类型数量有限, 本文利用多分辨率分析的思想重建图谱滤波器, 提出简单的分段函数Se gsk(· ), 用于处理拉普拉斯矩阵的特征值, 函数定义如下:

Se gsk(λ )= 1, 2s-1(k-1)≤λ< 2s-1k, 0, 其它

其中, s表示控制分割区间个数的缩放参数, k表示确定区间位置的平移参数.

分段函数Se gsk(· )旨在将图的归一化拉普拉斯矩阵特征值所在区间λ ∈ [0, 2]等分为s个子区间, 并根据特征值的大小, 归入不同的子区间.由此将特征值对应的基础滤波器组合为不同频段的滤波器组.相比小波函数, 分段函数Se gsk(· )通过简单的区间划分实现滤波器重组, 显著降低计算开销.此外, Se gsk(· )通过均匀划分实现对频段的无偏处理, 并将每个子区间内的特征值重置为1, 实现不同频段的均衡初始化.

使用Se gsk(· )代替式(3)中的尺度小波, 关于拉普拉斯矩阵特征值λ 的滤波器表示如下:

$\begin{aligned}\hat{g}(\lambda)= & \sum_{k} a_{k} \operatorname{Seg}_{0}^{k}(\lambda)+\sum_{s=0}^{\infty} \sum_{k} b_{s k} \operatorname{Seg}_{s+1}^{k}(\lambda)= \\& \sum_{s=0}^{\infty} \sum_{k}\left\langle\hat{g}(\lambda), \operatorname{Seg}_{s}^{k}(\lambda)\right\rangle \operatorname{Seg}_{s}^{k}(\lambda) .\end{aligned}$

实际上, 每个图数据的局部邻域子图模式数量是有限的, 因此无需对滤波器进行无限细化, 只需选择合适的缩放参数s对其分割.此外, 由于系数< ĝ(λ ), Se gsk(λ )> 难以直接计算, 本文利用神经网络学习该系数, 此时滤波器 ĝ(λ )可近似表示为

$\begin{aligned}\hat{g}(\lambda) \approx & \sum_{k}\left\langle\hat{g}(\lambda), \operatorname{Seg}_{s}^{k}(\lambda)\right\rangle \operatorname{Seg}_{s}^{k}(\lambda)= \\& \sum_{k} \theta_{k} \operatorname{Seg}_{s}^{k}(\lambda)\end{aligned}$,

其中, θ _k表示通过神经网络学到的权重参数, 对应组合滤波器在第k个频段的权重参数.

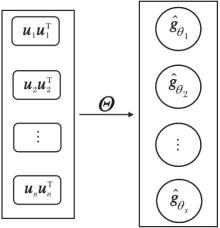
组合滤波器示意图如图1所示.基础滤波器{u_i uTi}i=1n分成s个不相交的子集 U˜1, U˜2, …, U˜s, 满足:

1)当i≠ j时, U˜i∩ U˜j=Ø ,

2) U˜1∪ U˜2∪ …∪ U˜s={u_i uTi}i=1n.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 组合滤波器示意图Fig.1 Schematic diagram of combination filters

每个滤波器子集 U˜i内的基础滤波器通过其对应的可学习权重参数θ _i, 学习特定局部邻域模式子滤波器 ĝθi.因此, 利用分割函数Se gsk(λ )构造谱滤波函数 ĝθ, 即

$\hat{\boldsymbol{g}}_{\theta}=\sum_{k=1}^{s} \Theta_{k k} \operatorname{Seg}_{s}^{k}(\boldsymbol{\Lambda})$, (5)

其中

Θ =diag[θ ₁, θ ₂, …, θ _s]

表示网络可学习参数.对于信号x, ĝθ的滤波过程表示为

$\boldsymbol{U} \hat{\boldsymbol{g}}_{\theta} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{x}=\boldsymbol{U} \sum_{k=1}^{s} \Theta_{k k} \operatorname{Seg}_{s}^{k}(\boldsymbol{\Lambda}) \boldsymbol{U}^{\mathrm{T}} \boldsymbol{x} .$(6)

当s→ +¥ , 式(4)可表示为

U ĝθU^Tx=(θ ₁u₁ uT1+θ ₂u₂ uT2+…+θ _nu_n uTn)x,

其等价于式(1).因此, 其本质上仍是一组针对图的拓扑结构信息进行学习的滤波器, 这些滤波器的参数是在整个图上训练的固定值.实际应用中的图数据通常包括节点特征和图的拓扑结构信息, 而式(6)构造的滤波器组仅针对图的拓扑结构信息进行学习, 并未融合图的节点特征.

图的拓扑结构通过边记录节点之间的连接关系, 这些边也可能因为不同的节点特征而具有不同的属性.因此, 在式(6)构造的组合滤波器的基础上引入节点特征, 学习节点之间的潜在关系, 有助于提高滤波器组在适应局部模式的变化方面的有效性和灵活性.

为了在滤波器的学习过程中整合图的节点特征与拓扑结构信息, 本文在滤波函数中引入一个非线性变换的节点特征矩阵H, 用于自适应引导滤波器组更新权重, 定义如下:

H=σ (XW^* )^T,

其中, W^* ∈ R^{n× s}表示网络可学习参数矩阵, σ (· )表示激活函数.因此, 式(5)中的谱滤波函数 ĝθ可进一步调整为

$\widehat{f}_{\Psi}=\sum_{k=1}^{s} \Psi_{k k} \operatorname{Se}_{s}^{k}(\boldsymbol{\Lambda})$, (7)

其中

Ψ = H˜+Θ ,

H˜表示对角矩阵, 对角元素由节点特征矩阵H的列相加后所得, 即

$\widetilde{\boldsymbol{H}}=\operatorname{diag}\left[\sum_{j=1}^{n} h_{1 j}, \sum_{j=1}^{n} h_{2 j}, \cdots, \sum_{j=1}^{n} h_{s j}\right] .$

因此, 式(7)中 f︿Ψ的滤波过程如下:

$\begin{array}{l}\widehat{\boldsymbol{U} f_{\Psi}} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{x}=\boldsymbol{U} \sum_{k=1}^{s} \Psi_{k k} S e g_{s}^{k}(\boldsymbol{\Lambda}) \boldsymbol{U}^{\mathrm{T}} \boldsymbol{x}= \\\quad \boldsymbol{U} \sum_{k=1}^{s} \widetilde{H}_{k k} S e g_{s}^{k}(\boldsymbol{\Lambda}) \boldsymbol{U}^{\mathrm{T}} \boldsymbol{x}+\boldsymbol{U} \sum_{k=1}^{s} \Theta_{k k} \operatorname{Seg}_{s}^{k}(\boldsymbol{\Lambda}) \boldsymbol{U}^{\mathrm{T}} \boldsymbol{x} .\end{array}$(8)

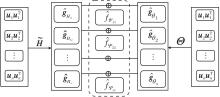
自适应组合滤波器框架如图2所示.在式(8)中, Ψ 可分解为两组滤波器参数Θ 和 H˜.其中, Θ 表示全局共享的参数, 调控面向特定局部邻域模式的滤波器组, 而 H˜表示与节点特征关联的滤波器参数, 指引Θ 关联的滤波器组准确识别具有对应局部邻域模式的节点.通过这种分解方式, 滤波器能更灵活地调整参数, 有效应对复杂的图结构.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 自适应组合滤波器框架图Fig.2 Flowchart of adaptive combination filters

基于2.2节中描述的自适应组合滤波, 描述ACGNN的结构.

首先, 设X⁽⁰⁾∈ R^{n× d}为图节点特征矩阵, 对其进行两次独立的非线性变换, 分别得到

H=σ (X⁽⁰⁾W⁽¹⁾)^T∈ R^{n× s},
$\widetilde{\boldsymbol{X}}^{(0)}=\sigma\left(\boldsymbol{X}^{(0)} \boldsymbol{W}^{(2)}\right) \in \mathbf{R}^{n \times q},$

其中, σ (· )表示激活函数, W⁽¹⁾∈ R^{d× s}、W⁽²⁾∈ R^{d× q}表示网络可学习参数矩阵, s表示Se gsk(· )中的缩放参数, q表示隐藏层维数.H用于在学习滤波器的过程中关联节点特征. X˜输入隐藏空间, 作为特征信号进行训练.

节点特征矩阵在隐藏空间中的信息传播过程描述如下:

X˜1=σ ( Uf︿ΨU^T X˜0),

其中σ (· )表示激活函数.网络输出层为:

Z=softmax( Uf︿ΨU^T X˜1),

其中

$\operatorname{softmax}\left(\boldsymbol{x}_{i}\right)=\frac{\exp \left(\boldsymbol{x}_{i}\right)}{\sum_{j} \exp \left(\boldsymbol{x}_{j}\right)}$.

在训练过程中, 通过最小化所有标记节点的交叉熵误差更新网络参数, 即

$\text { Loss }=-\sum_{i \in y_{L}} \sum_{j=1}^{C} Y_{i j} \ln Z_{i j},$

其中, y_L表示标记节点的集合, Z_ij表示模型将第i个节点分配给j类的预测概率.

ACGNN由组合滤波器和节点特征融合两个模块组成.组合滤波器的计算消耗主要集中在拉普拉斯矩阵的特征分解, 时间复杂度为O(n³), 但在模型处理中将其作为预处理步骤, 有效降低后续计算量.在节点特征融合模块中, 计算的主要开销集中在特征矩阵H的构建, 时间复杂度为O(nds), 其中, n表示节点数, d表示节点的特征维度, s表示缩放参数.由于s≪n, 故节点特征融合模块对整体模型的时间复杂度影响较小.

为了全面评估ACGNN, 在如下8个不同规模的基准数据集上进行实验.1)5个同配图数据集:引文网络数据集Cora、CiteSeer、PubMed^[41], 亚马逊联合采购关系图数据集Computers、Photo^[42].2)3个异配图数据集:维基百科图谱数据集Chameleon、Squirrel^[43], 演员共现网络数据集Actor^[11].数据集统计信息如表1所示.

表1

Table 1

表1(Table 1)

表1 实验数据集统计信息 Table 1 Statistical information of experimental datasets 名称 节点 边 特征维度 类别 同配比 边密度 Cora 2708 5278 1433 7 0.82 1.95 CiteSeer 3327 4552 3703 6 0.71 1.37 PubMed 19717 44324 500 5 0.79 2.25 Computers 13752 245861 767 10 0.80 17.88 Photo 7650 119081 745 8 0.84 15.57 Chameleon 2277 31371 2325 5 0.24 13.78 Squirrel 5201 198353 2089 5 0.21 38.14 Actor 7600 26659 932 5 0.21 3.51

表1 实验数据集统计信息 Table 1 Statistical information of experimental datasets

Cora、CiteSeer、PubMed数据集是3个标准的引文网络数据集, 每个节点表示一篇文章, 边表示节点间存在引用关系.节点特征对应每篇文章的描述词汇, 使用词袋模型编码.

Computers、Photo数据集是亚马逊共同购买图的两个导出子图, 在该类图中, 节点表示商品, 边表示两个商品经常被一起购买, 节点特征对应于产品评价, 使用词袋模型编码, 类别标签由产品类别决定.

Chameleon、Squirrel数据集是2个分别关于变色龙和松鼠主题的维基百科页面网络.节点表示2018年12月的英文维基百科文章, 边表示它们页面之间的相互引用链接.节点特征对应于文章中特定名词的出现情况和平均月流量(2017年10月至2018年11月).

Actor数据集是从电影-导演-演员-编剧网络中导出的仅包含演员的子图, 每个节点表示一个演员.若两个节点之间存在边, 表示二者在同一维基百科页面上共同出现.节点特征对应于维基百科页面中的部分关键词.

本文采用准确率(Accuracy)作为性能评价指标, 定义如下:

Accuracy= TP+TNTP+TN+FP+FN,

其中, TP表示模型将正类样本正确分类为正类, TN表示模型将负类样本正确分类为负类, FP表示模型将负类样本错误分类为正类, FN表示模型将正类样本错误分类为负类.

在8个现实世界数据集上, 采用6∶ 2∶ 2的分割比例, 将节点集随机分成训练集、验证集和测试集, 对每种方法进行全监督学习.通过随机种子随机生成10个随机分裂, 并在相同的分裂上进行评估, 最后, 以95%的置信区间记录每种方法的平均准确率.

为了确保公平性, 所有方法都使用两个卷积单元和一个线性输出层, 用Pytorch进行训练, 权重的初始化遵循Xavier初始化, 使用NVIDIA RTX 4090 GPU加速训练.采用权值衰减L2的Adam(Adaptive Moment Estimation)作为ACGNN训练的优化器.最大训练次数设为1 000, 当验证集损失函数连续200次不下降提前停止训练.所有数据集的失活率设为0.5.对于每个数据集, 在{0.001, 0.005, 0.01, 0.05, 0.1}内搜索最优学习率, 在{16, 32, 64, 128, 256}内搜索最优隐藏层维度, 在{0.000 1, 0.000 5, 0.001}内搜索最优衰减系数.

本文选择如下基线方法进行对比实验.

1)MLP(Multilayer Perceptron).前馈神经网络, 通常包括一个输入层、一个或多个隐藏层以及一个输出层.每层由若干神经元构成, 层与层之间通过全连接的方式相互连接.

2)文献[20]方法.定义图卷积运算, 使用切比雪夫多项式参数化卷积核.

3)GPRGNN^[30].结合自适应广义PageRank与GNN, 将特征传播的每步与可学习的权重关联.

4)BernNet^[31].通过K阶Bernstein多项式逼近图谱滤波器, 并通过设置Bernstein基的系数设计其属性.

5)ChebNetII^[33].基于切比雪夫插值的新型GNNs, 重新考虑切比雪夫多项式近似谱图卷积的问题, 增强原始的切比雪夫多项式近似.

6)GCN(Multi-layer Graph Convolutional Net-work)^[44].通过一阶多项式局部近似谱图卷积, 建立谱方法和空间方法的统一框架.

7)APPNP(Approximate Personalized Propaga-tion of Neural Predictions)^[45].结合PageRank^[46]和神经网络预测, 通过个性化的传播机制, 提高节点分类性能.

8)GATs(Graph Attention Networks)^[47].在节点的单跳邻域中引入多头注意机制, 获得节点表示.

9)FAGCN(Frequency Adaptation Graph Convo-lutional Networks)^[48].频率自适应的图卷积网络, 具有自适应机制, 可在消息传递过程中自适应集成不同信号.

10)Diag-NSD^[49].从拓扑角度, 利用细胞束理论, 为图赋予几何结构, 缓解现有GNNs在处理异配性和过平滑问题时的局限性.

11)GREET(Unsupervised Graph Representa-tion Learning Method with Edge Heterophily Discri-minating)^[50].区分同性边和异性边以学习图表示, 从特征和结构信息中推断边缘同配或异配, 并使用低通滤波器和高通滤波器捕获相应信息.

各方法在8个现实世界数据集上的平均准确率如表2所示, 表中数值表示平均准确率± 95%置信区间, 黑体数字表示最优值, 斜体数字表示次优值.由表可见, ACGNN在Cora、PubMed、Photo、Chameleon、Squirrel数据集上表现最优, 在Computers数据集表现次优, 在CiteSeer、Actor数据集上也表现出与对比方法相当的性能.

表2

Table 2

表2(Table 2)

表2 各方法在8个数据集上的节点分类准确率对比 Table 2 Comparison of node classification accuracy of different methods on 8 datasets % 方法 Cora CiteSeer PubMed Computers Photo Chameleon Squirrel Actor MLP 77.21± 0.79 76.58± 0.88 85.94± 0.22 82.85± 0.38 84.72± 0.34 46.85± 1.51 31.03± 1.18 38.58± 0.56 GCN 87.57± 0.83 79.76± 0.68 86.74± 0.27 86.64± 1.04 88.26± 0.73 59.61± 2.21 46.78± 0.87 33.23± 1.16 文献[20]方法 86.36± 0.53 79.30± 0.41 88.12± 0.47 87.82± 0.76 93.46± 0.32 59.74± 0.61 40.71± 0.33 38.10± 0.45 GATs 88.13± 0.72 80.43± 0.79 87.25± 0.24 85.83± 0.49 92.94± 0.68 63.13± 1.93 44.49± 0.88 33.93± 2.47 GPRGNN 88.57± 0.69 80.12± 0.86 88.46± 0.33 87.20± 0.47 93.85± 0.28 67.28± 1.09 50.15± 1.92 39.92± 0.67 BernNet 88.52± 0.95 80.13± 0.88 88.79± 0.25 88.61± 0.41 93.87± 0.57 68.29± 1.58 51.35± 0.73 41.79± 1.01 FAGCN 88.55± 0.92 83.37± 0.67 88.97± 0.54 89.46± 0.68 93.66± 0.41 60.29± 0.84 43.24± 0.69 39.13± 0.76 ChebNetII 88.71± 0.93 80.53± 0.79 88.93± 0.29 91.27± 0.45 94.06± 0.37 71.37± 1.01 57.72± 0.59 41.75± 1.07 APPNP 88.20± 0.62 80.22± 0.63 87.98± 0.68 88.04± 0.51 90.32± 0.17 51.91± 0.56 34.77± 0.34 38.86± 0.24 Diag-NSD 87.14± 1.06 80.32± 0.56 89.42± 0.43 89.75± 0.54 93.85± 0.27 68.68± 1.73 54.78± 1.81 39.96± 0.59 GREET 88.66± 0.84 80.23± 1.14 88.25± 0.54 88.41± 0.73 93.75± 0.88 68.21± 0.89 54.63± 0.57 39.34± 1.32 ACGNN 88.82± 0.41 80.32± 0.56 90.02± 0.15 91.05± 0.31 94.75± 0.27 73.41 ± 1.29 65.18± 0.80 39.61± 0.22

表2 各方法在8个数据集上的节点分类准确率对比 Table 2 Comparison of node classification accuracy of different methods on 8 datasets %

在异配图上, 不同方法之间的性能差异较大, 特别是在Chameleon、Squirrel数据集上, ACGNN表现出明显优势, 相比次优方法ChebNetII, 准确率分别提升约2.04%和7.46%.这说明ACGNN在处理复杂局部结构模式和图谱信号方面具有明显优势.在同为异配图的Actor数据集上, 各方法的表现都不够理想, 而在同配图数据集上, ACGNN取得3个最优值和1个次优值, 这说明基于特定局部邻域模式和节点特征学习图谱滤波器的方法在同配图数据集上仍然有效.

下面讨论各方法在除了Actor数据集以外的7个数据集上的性能表现.相比MLP, 其余方法在除了Actor数据集以外的7个数据集上均有更优性能, 这归功于GNNs是端到端的训练方式, 并在标签的指导下通过图结构更新节点表示.

另外, 相比基于多项式逼近滤波器的方法(文献[20]方法, GPRGNN, BernNet), ChebNetII在多个数据集取得次优值, 特别是在异配图数据集上具有明显优势.ChebNetII在Chameleon、Squirrel数据集上的准确率分别比文献[20]方法提升11.63%和17.01%, 比GPRGNN提升4.09%和7.57%, 比BernNet提升3.08%和6.37%, 这说明单纯依赖多项式基构造图谱滤波器存在局限性.

虽然ChebNetII使用切比雪夫插值增强多项式逼近性能, 但在Chameleon、Squirrel数据集上的性能仍明显低于ACGNN, 准确率分别降低2.04%和7.46%.这意味着基于多项式的模型在面对异配图数据中的高频信号时存在固有缺陷.

ACGNN在除了Actor数据集以外的7个数据集上的性能均优于Diag-NSD和GREET, 尤其在异配图数据集上具有明显优势.在Chameleon数据集上, ACGNN的准确率分别比DiagNSD和GREET提升4.73%和5.20%, 在 Squirrel数据集上, ACGNN的准确率分别比Diag-NSD和GREET提升10.40%和10.55%.

这表明, ACGNN对基础滤波器进行分段组合设计, 并在滤波器学习过程中融入节点特征, 有利于模型识别局部邻域模式, 捕捉更细致的高频信号, 因此在处理复杂的异配图时表现出一定优势, 具有良好的有效性.

为了验证ACGNN中各模块的有效性, 设计如下3种变体.

1)ACGNN-base.同时移除滤波器组合模块和自适应节点特征模块后的ACGNN变体, 即关闭图2中左右两边的滤波器模块.

2)ACGNN/comb.只移除考虑局部邻域模式的滤波器组合模块后的ACGNN变体, 即关闭图2中右边的滤波器组合模块.

3)ACGNN/adapt.只移除关联节点特征的自适应模块后的ACGNN, 即关闭图2中左边的模块.

为了验证ACGNN各模块面对同配图和异配图时的贡献, 选用3个同配图数据集Cora、CiteSeer、PubMed和3个异配图数据集Chameleon、Squirrel、Actor, 进行消融实验.因为ACGNN-base和ACGNN/comb都移除组合滤波器, 故s设为1, 其它实验参数设置与ACGNN一致, 均采用准确率作为评价指标.

不同变体在6个数据集上的消融实验结果如表3所示, 表中数值表示平均准确率± 95%置信区间, 黑体数字表示最优值, 斜体数字表示次优值.

表3

Table 3

表3(Table 3)

表3 各模块消融实验结果 Table 3 Ablation experiment results of different modules % 方法 Cora CiteSeer PubMed Chameleon Squirrel Actor ACGNN-base 75.58± 1.03 76.73± 0.64 85.60± 0.56 50.07± 0.42 36.33± 0.39 37.21± 0.84 ACGNN/comb 87.95± 0.54 79.35± 0.76 87.86± 0.56 72.65± 1.44 61.84± 1.43 37.36± 0.70 ACGNN/adapt 88.43± 0.62 78.34± 0.65 88.73± 0.36 72.69± 1.03 63.96± 0.52 36.79± 0.55 ACGNN 88.82± 0.41 80.32± 0.56 90.02± 0.15 73.41± 1.29 65.18± 0.80 39.61± 0.22

表3 各模块消融实验结果 Table 3 Ablation experiment results of different modules %

观察表3发现, ACGNN在各数据集上均为最优值.具体地, 在Chameleon、Squirrel、Actor异配图数据集上, ACGNN的准确率比只移除滤波器组合模块的ACGNN/comb分别提升0.76%、3.07%和2.30%, 比只移除节点特征融合模块的ACGNN/adapt分别提升0.6%、3.7%和2.0%.

在Cora、CiteSeer、PubMed同配图数据集上, ACGNN的准确率比ACGNN/comb分别提升0.87%、0.97%和2.16%, 比ACGNN/adapt分别提升0.39%、1.98%和1.29%.由此表明滤波器组合和节点特征融合这两个模块对整体模型性能的提升均具有重要贡献.

更进一步, ACGNN/comb和ACGNN/adapt在除了Actor数据集以外的5个数据集上均优于同时移除两个模块的ACGNN-base.特别是在Chame-leon、Squirrel异配图数据集上, ACGNN/comb的准确率分别比ACGNN-base提升约22.58%、25.51%, 这一提升得益于在滤波器的学习过程中充分考虑节点特征, 能帮助模型准确识别具有对应局部邻域模式的节点, 进行节点级的参数调整, 从而具有更好的节点嵌入表现.在Chameleon、Squirrel数据集上, ACGNN/adapt的准确率分别比ACGNN-base提升约22.62%、27.63%, 这说明对滤波器进行组合后, 方法能考虑异配图中复杂的节点局部邻域模式, 调整不同频率的滤波器, 处理图谱信号, 提高节点嵌入的效果.

需要注意的是, 在Actor数据集上, ACGNN/comb和ACGNN/adapt并未取得令人满意的结果, 甚至ACGNN/adapt的表现低于ACGNN-base.

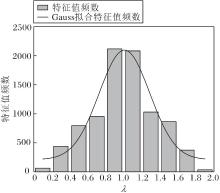
图3描述Actor数据集上拉普拉斯矩阵特征值的分布情况.观察图3可发现, 特征值的分布主要集中在λ =1附近, 而较大特征值或较小特征值占比很少.此外, 在所有特征值中, 有1 135个特征值等于1, 约占特征值总数的15%.这说明Actor数据集对应于一个高度同构的图, 大部分节点具有类似或相同的邻域结构模式^[40].而ACGNN未能充分利用图的同构性特征, 组合滤波器无法通过特征值区分高度同构图的节点邻域结构模式, 从而导致性能受限.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 Actor数据集的特征值分布图Fig.3 Eigenvalue distribution of Actor dataset

下文从图数据的边稠密程度和节点特征维度进行分析.通过计算边密度^[51]

ρ =|E|/|V|,

其中, |E|表示边数, |V|表示节点数, 反映边稠密程度.由表1可知, Actor数据集的边密度为3.5, 略高于Cora等同配图数据集, 但远低于Chameleon、Squirrel等异配图数据集.较低的边密度会限制节点聚合的邻域信息量, 削弱方法在信息聚合中的学习能力.而且, 由表1可知, Actor数据集的特征维度为932, Chameleon、Squirrel数据集的特征维度分别为2 325和2 089, 而较低的特征维度可能使方法更容易出现过平滑问题^[52], 从而影响分类性能.总之, 低边密度、较低的特征维度及高同构特性共同制约GNN模型在Actor数据集上的表现.

本文的缩放参数s决定分割区间数, 可根据图信号的频率分布特性进行调整.通常情况下, 同配图的节点邻域模式数量较少, 可通过较少分割区间数拟合, 而对于异配图, 更多的分割区间数有助于方法拟合更复杂的节点邻域模式, 捕捉更多的细节^[13].

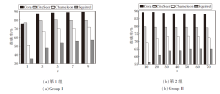
为了验证缩放参数s对ACGNN性能的影响, 实验选取{1, 3, 5, 7, 9}和{10, 20, 30, 40, 50, 60, 70}两组参数, 旨在通过对比不同区间分割数, 分析ACGNN在处理同配图和异配图时, 性能随参数变化的趋势.在Cora、CiteSeer、Chameleon、Squirrel数据集上进行实验, 采用控制变量法, 除了s, 其它实验设置和评价指标与ACGNN一致.具体结果如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 s对ACGNN性能的影响Fig.4 Effect of s on ACGNN performance

观察图4(a) 发现, 随着s的增加, 性能呈现上升趋势.在Cora、CiteSeer同配图数据集上的增加趋势相对平缓, 在Cora数据集上, 准确率在s=9附近达到峰值(88.82%), 在CiteSeer数据集上, 准确率在s=5附近达到峰值(80.32%).在Chameleon、Squirrel异配图数据集上的提升则更加明显, 在Chameleon数据集上, 准确率在s=50附近达到峰值(73.41%), 在Squirrel数据集上, 准确率在s=50附近达到峰值(65.18%).这表明, 通过增大s调节组合滤波器, 可更好地区分不同节点的邻域结构模式, 学到更复杂的滤波器, 从而提升性能.

结合图4(b)发现, 当s≥ 10, 方法在同配图数据集上的性能波动变得很小并很快呈现略微下降的趋势, 而在异配图数据集上的性能在s≥ 10后仍保持明显提升趋势, 但在s≥ 50后也出现略微下降.这种现象与预期一致, 因为同配图数据的节点邻域模式相对简单, 多依赖平滑信息, 而基于过多的分割区间数学习的组合滤波器可能会降低平滑信号的权重, 导致性能下降.相比之下, 异配图数据具有更复杂的节点邻域模式, 对s的变化更敏感, 相对复杂的滤波器能更好地适应这类数据的多样性和复杂性, 但过多的分割区间数也会导致过拟合, 影响方法性能.这种现象表明, 在处理异配图数据时, 选择合适的模型和滤波器组合对于提升方法的泛化能力和实际应用效果具有重要意义.

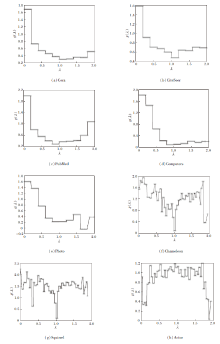
本节通过可视化 ACGNN 在现实世界数据集上学到的滤波器, 进一步验证其有效性.在8个数据集上的滤波器参数可视化结果如图5所示.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 滤波器参数可视化结果Fig.5 Visualization results of filter parameters

由图5可知, 在同配图数据集上, 学到的滤波器整体表现出较强的低通特性.然而, 在同配图上滤波器仍捕捉到部分的高频变化.

结合ACGNN取得的优异性能, 上述情况说明现实世界数据集的滤波器存在局部突变, 而ACGNN的自适应滤波器能有效捕获这些局部突变, 学到更复杂的滤波器.在异配图数据上, 学到的滤波器呈现不同的特点.

在Chameleon、Squirrel数据集上, ACGNN学到类似梳状结构的滤波器.由于ACGNN在这两个数据集上的表现明显优于所有对比方法, 这表明复杂的梳状滤波器能更好地捕捉异配图数据中存在的复杂邻域模式, 捕捉有效的高频信号, 从而提升性能.

综上所述, ACGNN不仅能拟合同配图数据的平滑信号, 而且能在异配图数据中捕捉更复杂的高频信息.