高量子位横场伊辛模型的通用波函数重构

引用本文

丛爽, 林丽敏. 高量子位横场伊辛模型的通用波函数重构. 模式识别与人工智能, 2024,37(12): 1083-1093
CONG Shuang, LIN Limin. Generalized Wave Function Reconstruction of High-Qubit Transverse-Field Ising Model. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2024,37(12): 1083-1093. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202412004
Permissions

《模式识别与人工智能》编辑部

高量子位横场伊辛模型的通用波函数重构

丛爽¹, 林丽敏¹

1.中国科学技术大学自动化系合肥 230022

通讯作者:

丛爽,博士,教授,主要研究方向为先进控制策略、人工神经网络、智能控制、量子系统控制.E-mail:scong@ustc.edu.cn.

作者简介:

林丽敏,硕士研究生,主要研究方向为量子状态重构、深度学习.E-mail:linlimin@mail.ustc.edu.cn.

收稿日期: 2024-11-21 接受日期: 2024-12-31

资助项目: 国家自然科学基金项目(No.62473354)资助

摘要

为了研究重构高维横场伊辛模型中基态波函数的泛化性能,文中提出高量子位通用波函数概率分布重构模型.该模型利用Mamba的自回归特性,同时结合高效采样流程,无需额外标签样本就能自动生成独立训练样本.结合多基态尺度缩放与变分蒙特卡洛优化策略,仅利用少量小区间内的不同物理参数训练高量子位通用波函数的模型权值.在40量子位系统波函数重构的数值仿真实验中,仅需采用外场强度为0.5至1.5的部分值进行权值训练,实现外场强度从0至2的量子态族高精度通用波函数的重构.在量子位从40至80的波函数重构数值仿真实验中,文中模型表现出较好的泛化能力和较高的推理性能,为高量子位系统的基态概率分布提供一种高效精确的通用重构方法.

关键词: 横场伊辛模型; 波函数重构; 高维量子系统; 自回归模型

中图分类号:TP183

Generalized Wave Function Reconstruction of High-Qubit Transverse-Field Ising Model

CONG Shuang¹, LIN Limin¹

1. Department of Automation, University of Science and Technology of China, Hefei 230022

Corresponding author:
CONG Shuang, Ph.D., professor. Her research interests include advanced control strategies, artificial neural networks, intelligent control and quantum system control.

About Author:
LIN Limin, Master student. Her research interests include quantum state reconstruction and deep learning.

Fund:Supported by National Natural Science Foundation of China(No.62473354)

Abstract

A high-dimensional generalized wave function probability distribution reconstruction model is proposed in this paper to investigate the generalization performance of the ground-state wave functions in the reconstructed high-qubit transverse-field Ising model. By leveraging the autoregressive properties of Mamba and combining them with an efficient sampling process, independent training samples can be automatically generated without the need for additional labeled samples. By combining multi-ground-state scaling with the variational Monte Carlo optimization strategy, the model trains the weights of the high-qubit universal wave function using only a small number of different physical parameters within a limited range. In numerical simulation experiments of wave function reconstruction for a 40-qubit system, the model weights are trained using only partial values of external field strength ranging from 0.5 to 1.5, and the model achieves high-precision universal wave function reconstruction of quantum state families with external field strengths ranging from 0 to 2. In numerical simulation experiments of wave function reconstruction for systems with qubits ranging from 40 to 80, the proposed model exhibits better generalization ability and more efficient inference performance, providing an efficient and accurate generalized reconstruction method for the ground-state probability distribution of high-qubit systems.

Key words: Key Words Transverse-Field Ising Model; Wave Function Reconstruction; High-Qubit Quantum System; Autoregressive Model

文章图片

多体量子系统状态的重构是量子多体物理中的基础问题之一, 也是量子信息和量子计算中的研究热点之一.通常采用波函数或密度矩阵描述量子状态, 人们需要通过实验获取数据重构量子态.然而, 传统的量子层析的重构方法需要测量一组随量子位数n指数增长的2ⁿ个完备的测量信息, 随着量子位数的增加, 多体系统的正交基在希尔伯特(Hilbert)空间维度呈指数级增长, 即使凝聚态物理领域的横场伊辛模型(Transverse-Field Ising Model, TFIM)中大量相互作用的自旋粒子只遵循简单的物理定律, 这一空间维度爆炸也会带来系统理论和实验分析的复杂性.

蒙特卡罗方法^[1]和张量网络方法^[2]都是传统上用于处理高维空间的高效数值计算技术, 旨在规避这种复杂性, 虽然在一定程度上可缓解空间维度爆炸的问题, 但仍存在一些限制, 如蒙特卡罗符号问题和张量网络的面积定律纠缠^[3].

近年来, 机器学习几乎在所有领域都产生广泛影响, 同时也激发量子领域和机器学习交叉应用的兴趣, 采用神经网络重构量子多体波函数已成为一个备受关注的研究方向.全连接网络(Fully Connected Network, FCN)和卷积神经网络(Convolutional Neu-ral Network, CNN)是两个典型的监督学习模型, 将量子态重构转化为一个回归问题, 利用额外的带标签的真实数据训练网络, 通过最小化预测输出和真实值之间的误差进行网络权值训练, 尽可能使网络的输出接近真实值.Saito等^[4]提出一种使用FCN计算一维和二维玻色-哈伯德模型(Bose-Hubbard Model)基态的方法, 采用简单的最速下降方法优化具有单个隐藏层的FCN, 结果与精确对角化十分接近.Saito等^[5]又研究FCN和具有多个隐藏层的CNN, 证实只有单个隐藏层的FCN效果优于多个隐藏层的FCN, 并且多层CNN比FCN更有效.Liang等^[6]设计一种全新的卷积神经网络, 解决量子多体问题, 演示通过CNN解决方形晶格上高度受限的1/2自旋J1-J2反铁磁海森堡模型的情况^[6].

横场伊辛模型(TFIM)是一个用于研究量子相变的凝聚态物理模型, 在给定物理参数的情况下, 求解由哈密顿量代表的能量函数为最小值时的基态波函数, 描述一维自旋链或二维方晶格的自旋状态, 其中每个自旋受到邻近自旋之间的相互作用和横向外场的影响^[7].一维TFIM虽然是一个典型的量子自旋系统模型^{[8, 9, 10, 11]}, 其研究结果可用于其它复杂系统, 所以也是本文的研究对象.

求解凝聚态物理模型系统基态的常用数值方法是密度矩阵重整化群(Density Matrix Renormalization Group, DMRG), 核心思想是通过优化局部的低秩张量近似有效处理高量子位系统^[12].由于DMRG在求解一维量子系统中的高效性和精确性, 结果常被用于衡量其它方法准确性的参考标准.

受限波尔兹曼机(Restricted Boltzmann Machine, RBM)是一种生成模型, Carleo等^[8]首次使用受限波尔兹曼机结合变分蒙特卡洛(Variational Monte Carlo, VMC)技术, 用于重构多体哈密顿量基态波函数, 并在一维和二维横场伊辛模型以及海森堡模型中验证方法的可行性和准确性.Carleo等^[9]提出基于深度玻尔兹曼机架构的技术, 用于重构多体量子系统状态, 通过两层隐藏神经元捕捉横场伊辛模型中的量子相关性.

RBM网络中一般采用马尔可夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)^[13]生成样本, 效率较低, 难以进行大规模采样, 因此Barrett等^[13]提出一个高效的采样流程, 本质上具有并行化特性, 计算复杂度与采样的配置种类上限相关, 而非采样的总数量.

循环神经网络(Recurrent Neural Network, RNN)和Transformer^[14]都属于无监督学习模型, 也是自回归模型, 可独立生成符合真实概率分布的样本, 而无需额外的样本输入.在量子态重构应用方面, Hibat-Allah等^[10]提出可重构特定量子态的RNN模型, 具有独特的基于序列的架构和自回归特性, 可用于重构一维和二维自旋模型的基态变分波函数.同时, 该模型的自回归性质允许从波函数中采样, 为估计值的有效计算提供独立样本.不过模型只能表示一个特定的量子态, 自旋模型的物理参数(如外场强度)和量子位数都是固定的.当改变自旋模型的物理参数时, 需要重新从头开始多次对同一个神经网络进行训练, 不具备对变化参数的泛化性.另外, 由于训练的量子位数固定, 无法适应不同位数的量子自旋链.当量子位数变化时, 模型结构会发生变化, 因此难以适应通用的量子态模型.如何重构能适应不同变化参数的通用波函数模型, 仍是一个具有挑战性的研究课题.

Transformer^[14]是近年来提出的一种任务无关模型, 可应用于多种不同的任务或应用场景^{[15, 16, 17, 18]}, 通过自注意力机制和混合位置编码的结合, 在处理不同长度的序列时表现出高度的灵活性和效率.

在量子态重构应用方面, Zhang等^[11]提出TQS(Transformer Quantum State), 通过多基态尺度缩放机制进行训练, 对未训练区域的物理参数和量子位数均具有泛化性.相比特定参数的模型, TQS能使用一个单一模型生成整个相图, 预测实验中训练范围内的场强, 并将这种知识转移到以前未经训练的新系统中.

Transformer核心的自注意力机制能有效捕捉长距离依赖关系, 并支持并行化处理, 因而具有显著提升训练效率和模型性能的能力.不过, Transformer的复杂度与序列长度的平方呈正比, 使其在长序列建模方面需要消耗大量计算资源.另一方面, RNN的复杂度仅与序列长度呈正比, 但不能并行化处理.Gu等^[19]提出Mamba, 以选择性状态空间模型为理论基础, 既有CNN的并行计算优势, 又有RNN的低复杂度和长程感知能力, 旨在解决Transformer在长序列上计算效率低下的问题.在大语言模型任务中, 在参数规模相同时, Mamba表现出优于Transfor-mer的性能, 并且速度提升超过五倍.

为了进一步降低高量子位重构时间的复杂度, 同时提升在小范围数据获取高量子位状态重构的高精度及其泛化能力, 基于Mamba在大语言模型的应用中表现的优越长序列建模能力和高效的推理速度, 本文提出高量子位通用波函数的重构模型(Mamba-Based High-Qubit Generalized Wave Function Reconstruction, Mamba-HQGWR), 不仅适应参数变化, 还具有精度高、泛化能力强的优势.Mamba-HQGWR可实现量子位数n> 40的高量子位波函数的重构.仅需在部分小范围外场强度B_x和量子位数n的情况下进行训练, 便能泛化到训练集外其它不同条件.Mamba-HQGWR能生成一个量子态族, 表征概率分布和相关参数(如外场强度和量子位)的联合分布, 求解的是连续解.设计基于Mamba的无监督高效优化策略, 在变分蒙特卡洛优化策略的基础上, 结合高效采样流程^[14]和多基态尺度缩放机制, 利用Mamba自回归地高效生成训练样本, 无需额外标签样本的输入就能有效计算一维TFIM^[7]基态波函数概率分布的估计值.在n> 40的更高维系统数值实验中, 相比TQS, Mamba-HQGWR在保留并行计算优势的同时, 具备更低的复杂度、更快的推理速度与更优的长序列建模能力.

1 波函数和横场伊辛模型

1.1 量子态的波函数与概率分布之间的关系

在量子领域中, 无法直接通过测量获得未知量子系统的真实状态.与宏观系统不同, 量子系统的测量是一个不可逆的过程, 一旦被测量, 它的状态将永久塌缩到某个确定的本征态上.因此, 为了推断系统的真实状态, 需要重构其波函数.一般波函数|Ψ _f> 的表现形式通常是复数值的, 即

$\left|\Psi_{f}\right\rangle=\sum_{x} e^{i \boldsymbol{\Phi}(\boldsymbol{x})} \sqrt{P_{f}(\boldsymbol{x})}|\boldsymbol{x}\rangle,$

其中, |x> 表示本征态, P_f(x)表示概率分布, Φ (x)表示相位.不过学者们通常更关注量子系统的概率分布而不是相位信息, 研究仅包含正实数P_f (x)的波函数不仅能更直观揭示系统的核心特性, 还为进一步重构完整复数值波函数提供重要的基础和参考.

实数值波函数|Ψ _f> 对由一组本征态组成的量子状态给出概率性的描述.如果量子态以概率分布P_f(x)的概率塌缩到本征态|x> 上, 波函数|Ψ _f> 用|x> 的线性叠加表示, 并且每个本征态的叠加系数与概率分布P(x)的关系式:

$\left|\Psi_{f}\right\rangle=\sum_{x} \psi(\boldsymbol{x})|\boldsymbol{x}\rangle=\sum_{x} \sqrt{P_{f}(\boldsymbol{x})}|\boldsymbol{x}\rangle,$ (1)

其中, ψ (x)表示波函数系数, 由概率分布P_f(x)构成的向量P满足1-范数‖ P‖ ₁=1.

当量子位数为n时, 波函数的概率分布

P_f(x)=P(x₁, x₂, …, x_n)

可由n-1个量子位的概率分布P(x₁, x₂, …, x_n_-1)通过条件概率建模得到, 即

$\begin{array}{l}P\left(x_{1}, x_{2}, \cdots, x_{n}\right)= \\\quad P\left(x_{n} \mid x_{n-1}, \cdots, x_{2}, x_{1}\right) P\left(x_{1}, x_{2}, \cdots, x_{n-1}\right) .\end{array}$

以此类推, 根据概率的乘法公式, 概率分布P_f(x)可由以P(x₁)开始的一系列条件概率相乘得到, 即

P_f(x)=P(x₁)P(x₂|x₁)…P(x_n|x_n_-1, …, x₂, x₁), (2)

其中

x=(x₁, x₂, …, x_n), x_i∈ {0, 1},

表示|x> 中的n位{0, 1}取值,

P(x_i|x_i_-1, …, x₂, x₁)=P(x_i|x_<_i),

表示给定所有x_j(j< i, i≠ 1)时x_i的条件概率.

从式(1)可知, 重构波函数就是重构其概率分布.一旦已知条件概率P(x_i|x_<_i), 就可通过式(2)获得任意可能的概率分布P_f(x)的完整特性.因为条件概率P(x_i|x_<_i)携带历史信息的表达, 而自回归模型与时间序列相关, 所以使用自回归模型求解经典概率P_f(x)是一个合理而自然的选择.

1.2 横场伊辛模型

在凝聚态物理中, 人们一般采用横场伊辛模型(TFIM)^[7]描述一维自旋链的自旋状态, 每个自旋与其相邻的自旋相互作用, 并且受到一个横向磁场的作用.TFIM中的哈密顿量:

$H=-J_{z} \sum_{\langle i, j\rangle} \boldsymbol{\sigma}_{i}^{z} \boldsymbol{\sigma}_{j}^{z}-B_{x} \sum_{i} \boldsymbol{\sigma}_{i}^{x} .$ (3)

其中:J_z表示相邻自旋间的交换耦合强度, B_x表示横向的磁场强度, 两者数值都大于0; $σ_{i}^{z}$ 、 $σ_{i}^{x}$ 分别表示第i个自旋的Pauli矩阵的z和x分量:

$σ_{i}^{x}$ = $[\begin{array}{l} 0 & 1 \\ 1 & 0 \end{array}]$ , $σ_{i}^{z}$ = $[\begin{array}{l} 1 & 0 \\ 0 & - 1 \end{array}]$ .

哈密顿量H对应系统的总能量.哈密顿量的特征值表示物理系统可能具有的能量值, 而相应的本征态表示系统在相应能量下的存在状态.当系统能量最低时, 哈密顿量的特征值最小, 此时的状态称为基态:

H|Ψ > =E₀|Ψ > , (4)

其中, H表示哈密顿量, E₀表示基态能量, |Ψ > 表示基态波函数.

当量子位数n和式(3)中的J_z、B_x是确定值时, 哈密顿量H也是确定的, 将式(1)和式(3)代入式(4), 可得到基态波函数|Ψ > , 再通过表示波函数与概率分布之间关系的式(1), 得到量子系统能量最低、处于基态情况下, 系统在输入物理量J_z和B_x, 以及本征态|x> 情况下的概率分布P(x).

本文旨在设计一个参数化的Mamba-HQGWR, 在输入相应的物理参数下, 使其输出为概率分布P(x).通过不断优化Mamba-HQGWR的参数, 使其尽可能逼近平衡点.一旦平衡点达到, Mamba-HQGWR的输出即为基态波函数概率分布的估计值 $\overset{︿}{P}$ (x).

在式(4)中, 设置不同耦合强度和磁场强度参数可获得不同的基态.一般采用密度矩阵重正化群(DMRG), 对不同的物理参数值求解出式(4)中E₀为最小值时的基态波函数|Ψ > , 每组参数只能得到对应的一个解.本文的任务是:设计一个通用的Mamba-HQGWR, 只利用小范围内数据, 采用高效采样流程和多基态尺度缩放机制优化算法, 训练模型权值, 使训练的模型既能对训练范围外的数据具有泛化能力, 又能对高量子位波函数概率分布具有高精度的重构能力.

2 高量子位通用波函数的重构模型结构设计

一个TFIM是由n个自旋-1/2组成的量子多体系统, 当系统能量最小时, 根据式(1)和式(4), 可使用量子态的概率分布P(x)表示基态波函数.Mamba-HQGWR重构波函数的“ 推理” 过程定义如下.给定自旋配置

x=(x₁, x₂, …, x_n)

和外场强度B_x作为模型输入, 计算模型输出概率分布估计值 $\overset{︿}{P}$ (x), 其耗时为“ 推理时间” .

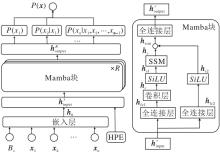
Mamba-HQGWR网络结构如图1所示.输入自旋配置x=(x₁, x₂, …, x_n)和式(3)中的外场强度B_x, 其中x_i表示输入样本的第i个自旋x_i的独热编码, 当x_i为0或1时, x_i取(1 0)或(0 1).

	Figure Option View Download New Window
	图1 Mamba-HQGWR网络结构图Fig.1 Network architecture of Mamba-HQGWR

与原始Mamba块^[19]的直接输入方式不同, Mamba-HQGWR增加输入预处理, 将Mamba块与混合位置编码(Hybrid Positional Encoding, HPE)^[14]结合, 通过HPE操作, 将B_x和x转化为 $h_{input}^{1}$ .这种设计使Mamba块的输入不仅包含外场强度和自旋配置x的信息, 同时引入各自旋x_i的显式位置信息i(i=1, 2, …, n), 从而使模型能更有效捕捉不同量子位之间的关联特性, 并有助于进一步提升高量子位系统波函数概率分布的重构精度.

输入预处理后得到的变量 $h_{input}^{1}$ 进入R个连续的以选择性状态空间模型(Structured State Space Model, SSM)为核心的Mamba块.图1右图是第r个Mamba块的内部结构(1≤ r≤ R), 功能是将输入 $h_{input}^{r}$ 经过Mamba块处理, 转化为具有更深层次高维特征的 $h_{output}^{r}$ .将R个Mamba块逐层叠加的目的是提高模型深度, 增强表达能力.最终, Mamba-HQGWR输出具有条件概率P(x_i|x_<_i)物理性质的 $h_{output}^{R}$ , 实现量子波函数的概率分布重构.

嵌入层是一个线性变换层, 将信息映射到高维空间, 即将外场强度B_x和配置x转换为潜向量:

h₀=W_emb([B_x, x])+b_emb,

其中, W_emb∈ $R^{L \times d_{m}}$ , b_emb∈ $R^{1 \times d_{m}}$ 分别表示嵌入层的权重和偏差, L表示B_x和x的总长度, d_m表示嵌入维度, [· ]表示拼接操作.将h₀加上混合位置编码, 则

$h_{input}^{1}$ =h₀+HPE(pos, j),

其中

$\begin{array}{l}H P E(p o s, j)=\left[P_{L}, P_{F}(p o s, j)\right], \\P_{F}(p o s, 2 j)=\sin \left(\frac{p o s}{10000 \frac{2 j}{d_{m}}}\right), \\P_{F}(p o s, 2 j+1)=\cos \left(\frac{p o s}{10000 \frac{2 j}{d_{m}}}\right), \end{array}$

HPE(· )表示混合位置编码, 包括可学习位置编码P_L与固定的正余弦位置编码P_F(· ), 可学习位置编码P_L表示B_x的位置, 是一组随机初始化的参数, 随训练过程调整, 初始化服从均值为μ 和标准差为σ 的正态分布, 即P_L~N(μ , σ ), pos表示B_x和x_i对应的位置索引, j表示嵌入向量维度.

嵌入层和混合位置编码的输出 $h_{input}^{1}$ 作为第1个Mamba块的输入, Mamba块的详细结构如图1右图所示.以第r个Mamba块为例, $h_{input}^{r}$ 被分成相同的两路方便后续进行残差操作.使用两个不同的全连接层将 $h_{input}^{r}$ 投影到更高维空间, 即

h_fc1=W_fc1 $h_{input}^{r}$ +b_fc1,
hf_c2=Wf_c2 $h_{input}^{r}$ bf_c2,

其中, W_fc1、W_fc2、b_fc1、b_fc2分别表示两个全连接层的权重和偏差, 维度分别为L× d_n和1× d_n, d_n表示投影维度.

为了在各维度间实现信息融合, 以确保每个维度携带更丰富的信息, h_fc1经过卷积层Conv(· ), 得

h_c=Conv(h_fc1).

h_c和h_fc2都要经过激活函数SiLU以增强非线性, 即

$\begin{array}{l}\boldsymbol{h}_{s 1}, \boldsymbol{h}_{s 2}=\operatorname{SiLU}\left(\boldsymbol{h}_{c}\right), \operatorname{SiLU}\left(\boldsymbol{h}_{\mathrm{fc} 2}\right), \\\operatorname{SiLU}(k)=k\left(\frac{1}{1+e^{-k}}\right)\end{array}$

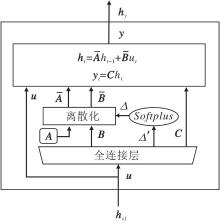
选择性状态空间模型(SSM)是Mamba的核心组件, 以控制领域的状态空间模型为理论依据, 结合选择性的思想, 同时拥有RNN的低复杂度和CNN的并行处理优势.经典的状态空间模型公式为

$\{\begin{array}{l} h_{t} = A h_{t - 1} + B u_{t} \\ y_{t} = C h_{t} \end{array}$

其中, u_t、h_t、y_t表示系统在时刻t的输入、输出和状态, A表示状态转移矩阵, B表示输入影响矩阵, C表示状态到输出的映射矩阵.

SSM对经典的状态空间模型的性能改进主要体现在三个方面:选择性思想、高阶多项式投影算子(High-Order Polynomial Projection Operators, HiPPO)理论和离散化(Discretization), 其网络结构如图2所示.

	Figure Option View Download New Window
	图2 SSM网络结构Fig.2 SSM network architecture

选择性思想是为了使模型更专注输入中对当前任务更重要的部分, 因此模型参数B、C和离散化步长Δ 需要是输入u的函数, 即

[B, C, Δ ']=W_su+b_s,

其中

$\begin{array}{l}\Delta=\operatorname{Softplus}\left(\boldsymbol{W}_{P} \Delta^{\prime}\right), \\\operatorname{Softplus}(k)=\ln \left(1+e^{k}\right), \\\boldsymbol{u}=\left(u_{1}, u_{2}, \cdots, u_{L}\right), \end{array}$

在本文中u=h_s₁, W_s和W_P表示权重, b_s表示偏差.

A是一个在构建新状态时用于捕捉历史信息的矩阵, 决定信息如何随时间的推移进行传递.在控制领域, A还决定系统的稳定性.因此, 为了改进A的性能, SSM中采用HiPPO理论将信号分解为一系列多项式信号, 对越接近当前时刻的信号进行越精确的构建, 而更早的信号则以指数级衰减.因此, 状态h_t能捕捉更多的短时信息, 而对长时信息的捕捉较少.采用HiPPO理论后, A可表示为

A_vk=- $\{\begin{array}{l} {(2 v + 1)}^{\frac{1}{2}} {(2 k + 1)}^{\frac{1}{2}}, & v > k \\ v + 1, & v = k \\ 0, & v < k \end{array}$

为了适应计算机对序列的离散化表示, 需要将连续变量进行离散化处理.SSM中零阶离散化后的状态空间模型公式如下:

$\begin{array}{l}\overline{\boldsymbol{A}}=\exp (\Delta \boldsymbol{A}), \\\overline{\boldsymbol{B}}=(\Delta \boldsymbol{A})^{-1}(\exp (\Delta \boldsymbol{A})-\boldsymbol{I}) \Delta \boldsymbol{B}, \\\left\{\begin{array}{l}h_{t}=\overline{\boldsymbol{A}} h_{t-1}+\overline{\boldsymbol{B}} u_{t} \\y_{t}=\boldsymbol{C} h_{t}\end{array}\right.\end{array}$

其中, $\bar{A}$ 表示A的零阶离散化表示, $\bar{B}$ 表示B的零阶离散化表示, I表示单位矩阵.

SSM通过前一时刻的状态h_t_-1与当前输入u_t进行组合, 生成当前时刻的状态h_t, 这一过程类似于RNN的时间步更新.SSM的最终输出:

y=[y₁, y₂, …, y_L],

在图1右图中表示为h_y.

h_y和h_s₂进行元素相乘, 得

h_ssm=h_y* h_s₂,

其中, * 表示哈德玛乘积(Hadamard Product), 即矩阵对应元素相乘.此操作称为残差操作, 即将输入直接传递到输出, 从而形成“ 跳跃连接(Skip Connection)” .残差能缓解梯度消失问题, 并使深层模型更容易收敛.最终, h_ssm经过一个全连接层得到第r个Mamba块的输出:

$h_{output}^{r}$ =W_fc3h_ssm+b_fc3,

其中W_fc3和b_fc3表示权重和偏差.

因为在SSM中计算h_t时已考虑到之前的状态, 所以适合用于建模条件概率P(x_i|x_<_i).因此, 经过R个Mamba块后输出的 $h_{output}^{r}$ 中每个元素为最终模型重构的条件概率分布P(x_i|x_<_i), 根据式(2)对其进行逐项相乘, 得到波函数的概率分布的估计值 $\overset{︿}{P}$ (x).而且, Mamba中还利用核融合(Kernel Fu-sion)、并行扫描(Parallel Scan)和重算(Re-compu-tation)技术, 相当于在RNN的基础上实现并行化计算.

3 高量子位通用波函数的重构模型参数训练

3.1 训练样本获取

为了达到估计TFIM基态的目标, 在对模型进行训练之前, 必须获得训练样本.因为Mamba是自回归模型, 在给定初始输入后能自动持续地产生独立样本, 所以直接利用Mamba-HQGWR进行训练数据的生成.如果采用传统的马尔可夫链蒙特卡洛方法^[12]进行采样, 将面临采样效率较低及难以满足大规模样本需求等问题.本文基于文献[13]中的采样流程, 设计Mamba-HQGWR自回归生成训练样本的网络, 结构如图3所示.图中, 第1次, Mamba-HQGWR的输入是x₀和训练范围内一个随机的外场强度值B_x, 得到模型输出y₁, 通过二项(Binomial)分布, 得到x₁.x₁返回模型输入, 与x₀和B_x作为模型的第2次输入, 得到x₂.以此类推, 可得到第k次Mamba-HQGWR的输入是部分配置字符串(x₀, x₁, …, x_k_-1)和外场强度值B_x, 输出结果y_k表示x_k为(0 1)或(1 0)的条件概率P(x_i|x_<_i).

	Figure Option View Download New Window
	图3 Mamba-HQGWR生成训练样本的网络结构图Fig.3 Network architecture of Mamba-HQGWR for generating training samples

图3的结构与图1相似, 为同一个网络的两种不同模式, 分别称为采样和推理.推理是指预测给定配置x=(x₁, x₂, …, x_n)的概率分布P(x)的任务, 并且对应于网络的单次前向传递.采样任务是根据网络参数生成样本x.每次迭代中推理和采样的网络参数λ _k相同, 不同的是图3中每次的x_i是由上一时刻输出y_i通过二项分布或多项分布采样得到, 这样循环n次, 得到长度为n的样本x=(x₁, x₂, …, x_n).在图3中的二项分布或多项分布采样主要是用于进行高效采样, 具体执行过程如下:设量子位为i-1(i=1, 2, …, k)时, 自旋配置(x₁, x₂, …, x_i_-1)的种类N_c=2ⁱ^-1, N表示生成样本的总数量.

第1次, 模型输出y₁=( $y_{1}^{0}$ , $y_{1}^{1}$ ), $y_{1}^{0}$ 表示x₁为0的概率, $y_{1}^{1}$ 表示x₁为1的概率, 配置(0)的数量N₁₀=N× $y_{1}^{0}$ , 配置(1)的数量N₁₁=N× $y_{1}^{1}$ , 此时, 生成样本的总数量N=N₁₀+N₁₁.以此类推.

1)当N_c< N_unique时, N_unique表示当前生成的自旋配置种类的数量上限.假设N_c中的某一种自旋配置(x₁, x₂, …, x_i_-1), 该配置出现的次数为N_i.配置(x₁, x₂, …, x_i_-1, 0)的数量N_i₀和配置(x₁, x₂, …, x_i_-1, 1)的数量N_i₁的总和是N_i, 即

N_i=N_i₀+N_i₁.

对于第i个自旋x_i来说, 用模型输出y_i=( $y_{i}^{0}$ , $y_{i}^{1}$ )作为二项分布的采样概率, 随机生成自旋为0和1的样本, $y_{i}^{0}$ 表示x_i为0的概率, $y_{i}^{1}$ 表示x_i为1的概率.配置(x₁, x₂, …, x_i_-1, 0)的数量N_i₀=N_i× $y_{i}^{0}$ , 配置(x₁, x₂, …, x_i_-1, 1)的数量N_i₁=N_i× $y_{i}^{0}$ .

2)当N_c=N_unique时, 为第k次输入, 此时, 2^k≈ N_unique, 将停止生成新的、可能不重复的样本, 而只在现有的自旋配置基础上进一步采样, 把不同的自旋配置样本(x₁, x₂, …, x_k_-1)输入网络中, 得

y_k=( $y_{k}^{0}$ , $y_{k}^{1}$ ),

其中, $y_{k}^{0}$ 表示该样本第k次的自旋为0的概率, $y_{k}^{1}$ 表示该样本第k次的自旋为1的概率.与N_c< N_unique时不同的是, 这里对y_k进行多项分布采样, 仅选择0或1中的一个加入(x₁, x₂, …, x_k_-1).以此方式循环, 直到样本长度为n.

3)当N_c> N_unique时, 与N_c=N_unique相同.

通过上述步骤, 将Mamba自回归生成训练样本与高效采样流程^[14]结合成Mamba-HQGWR的无监督训练样本采样流程.该流程的计算成本为2^k≈ N_unique, 取决于自旋配置种类的数量上限N_unique, 而不是取决于样本总数N, 这意味着通过合理设置N_unique, 既能保证采样配置的多样性, 又能有效控制内存和计算开销.该方法不仅能支持更大规模的采样批次, 还能高效处理大量样本.

3.2 通用优化策略设计

本文在采用变分蒙特卡洛(VMC)优化策略的基础上, 通过对各基态能量的尺度缩放考虑不同基态对通用总基态的影响.

对仅能建模特定量子态(即固定的n和B_x)的自回归模型来说, 将式(3)代入式(4)得到的最小化单个哈密顿量H(n, B_x)的期望能量:

${\hat{e}}_{0}$ = $\frac{< {\overset{︿}{Ψ}}_{λ} | H (n, B_{x}) | {\overset{︿}{Ψ}}_{λ} >}{< {\overset{︿}{Ψ}}_{λ} | {\overset{︿}{Ψ}}_{λ} >}$ , (5)

其中, | ${\overset{︿}{Ψ}}_{λ}$ > 表示特定参数B_x和n下模型预测的试验波函数, < ${\overset{︿}{Ψ}}_{λ}$ | ${\overset{︿}{Ψ}}_{λ}$ > =1.

此时VMC优化策略目标如下.通过对式(5)中 ${\hat{e}}_{0}$ 求一阶偏导, 求 ${\hat{e}}_{0}$ 为最小情况下的量子波函数^[10]:

$\frac{\partial \hat{e}_{0}}{\partial \lambda_{k}}=2 \operatorname{Re}\left(\left\langle\left(E_{\mathrm{loc}}(\boldsymbol{x})-\left\langle E_{\mathrm{loc}}\left(\boldsymbol{x}^{\prime}\right)\right\rangle_{\widehat{P}\left(x^{\prime}\right)}\right) \cdot \frac{\partial \ln (\widehat{\psi}(\boldsymbol{x}))^{*}}{\partial \lambda_{k}}\right\rangle_{\widehat{P}(\boldsymbol{x})}\right)$ . (6)

其中

$E_{\mathrm{loc}}(\boldsymbol{x})=\sum_{x^{\prime}} H\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right) \frac{\widehat{\psi}\left(\boldsymbol{x}^{\prime}\right)}{\widehat{\psi}(\boldsymbol{x})}$ ,

为局部能量估计值, 表示哈密顿量在状态x和x'之间的跃迁矩阵元; λ _k表示模型参数集合; x表示当前的系统状态(如自旋配置), x'表示在哈密顿量作用下可能的状态转变; < · $>_{\overset{︿}{P} (x)}$ 表示对分布 $\overset{︿}{P}$ (x)的期望值; ln( $\overset{︿}{ψ}$ (x))^*表示ln( $\overset{︿}{ψ}$ (x))的共轭.

对模型参数进行寻优的过程如下.首先对初始化的模型进行采样, 将采样获得的数据代入式(6), 计算能量梯度:

g_k= $\frac{\partial {\hat{e}}_{0}}{\partial λ_{k}}$ .

并通过自适应矩估计(Adaptive Moment Estimation, Adam)优化算法^[20]计算模型参数集合的增量:

Δ λ _k=- $\frac{η}{\sqrt[]{{\hat{v}}_{k}} + ϵ} {\hat{m}}_{k}$ ,

其中

${\hat{m}}_{k}$ = $\frac{m_{k}}{1 - β_{1}^{k}}$ ,

表示偏差校正后的一阶矩估计值,

${\hat{v}}_{k}$ = $\frac{v_{k}}{1 - β_{2}^{k}}$ ,

表示偏差校正后的二阶矩估计值,

m_k=β ₁m_k_-1+(1-β ₁)g_k,
$v_{k}=\beta_{2} v_{k-1}+\left(1-\beta_{1}\right) g_{k}^{2},$

η 表示学习率, g_k表示能量梯度, β ₁、 β ₂表示动量估计值的指数衰减率, $\epsilon$ 表示一个非常小的数, 用于防止分母为0.

由增量Δ λ _k得到新的模型参数λ _k₊₁, 直到迭代次数达到最大值.

为了实现通用量子态的高精度波函数重构, 在训练中充分评估并平衡各基态对整体波函数的影响, 通过最小化一组关于n和B_x的哈密顿量

H={H(n, B_x)}

的期望能量 ${\overset{︿}{E}}_{0}$ 以训练Mamba-HQGWR参数^[11]:

$\widehat{E}_{0}=\langle\Psi| म H|\Psi\rangle=\sum_{\left\{n, B_{x}\right\}} \frac{\left\langle\widehat{\Psi}_{\lambda}\right| H\left(n, B_{x}\right)\left|\widehat{\Psi}_{\lambda}\right\rangle}{\left|E_{0}\left(n, B_{x}\right)\right|},$ (7)

其中

|Ψ > = $\oplus_{{n, B_{x}}}$ | ${\overset{︿}{Ψ}}_{λ}$ > ,

表示一组波函数, ⊕表示直和, E₀(n, B_x)表示真实的基态能量, 除以|E₀(n, B_x)|表示衡量不同基态对总基态的影响.由于无法得到精确的基态能量E₀(n, B_x), 采用变分法估计基态能量对其进行近似:

${\tilde{E}}_{0}$ (n, B_x)=< (E_loc(x') $>_{\overset{︿}{P} (x')}$ .

随着优化的进行, 基态能量的估计值 ${\tilde{E}}_{0}$ (n, B_x)越来越接近E₀(n, B_x).

从式(7)可看出, 不同物理参数下的总期望能量 ${\overset{︿}{E}}_{0}$ 是所有单个特定物理参数的期望能量之和.每个哈密顿量H(n, B_x)在优化模型权值时都要乘以 $\frac{1}{| {\tilde{E}}_{0} (n, B_{x}) |}$ 进行尺度缩放.Mamba-HQGWR参数训练的优化策略是在式(6)的基础上引入尺度缩放机制, 通过多基态联合优化提升波函数重构的通用性.此外, 为了避免 ${\tilde{E}}_{0}$ (n, B_x)→ 0引发的数值发散, 实验中将尺度缩放的上限限制为5.

4 实验及结果分析

4.1 实验环境

为了验证Mamba-HQGWR重构波函数的有效性和精确性, 选择基态能量的相对能量误差Δ E作为验证指标.Δ E衡量估计值和真实值之间的相似程度, 值越小, 相似度越高, 精确度越高.通过密度矩阵重正化群(DMRG)得到真实值E₀.DMRG的核心思想是将系统分块, 再通过局部截断逼近以保留重要的自由度^[2].对于一维系统, 总哈密顿量H_DMRG可以写为分块形式:

H_DMRG=H_B⊗I+I⊗H_E+H_I,

其中, H_B表示系统块的哈密顿量, H_E表示环境块的哈密顿量, H_I表示系统块和环境块之间的相互作用项.通过递归扩展得到H_B和H_E, 初始值分别由一个格点表示.H_I表示系统和环境块的边界耦合.DMRG将H_DMRG代入式(4)的H, 求解基态能量E₀, 利用归约密度矩阵的特征值截断, 保留占主导权重的基矢.

相对能量误差:

Δ E= $\frac{| {\overset{︿}{E}}_{0} - E_{0} |}{|E_{0}|}$ × 100%,

其中, ${\overset{︿}{E}}_{0}$ 表示Mamba-HQGWR估计的基态能量, E₀表示使用DMRG对式(4)求解的真实的基态能量值.

实验中, 首先采用图3设计的高效的无监督训练样本自动生成流程, 再采用变分蒙特卡洛优化与多基态能量尺度缩放结合的策略训练Mamba-HQGWR.

模型在1张V100-16GB显卡上进行训练, 使用的Mamba块数量R=6, 整个Mamba-HQGWR的参数量约为6× 10⁴, 最大迭代步数为10⁵, 生成样本总数N=1 000 000, 自旋配置种类的数量上限N_unique=100.

4.2 外场强度B_x∈ [0, 2]的概率分布重构数值实验

为了训练具有通用泛化能力的Mamba-HQG-WR, 分别进行预训练以及预训练完成后模型参数微调.预训练时, 固定式(3)中的J_z=1.0, B_x∈ [0.5, 1.5]中间隔为0.1的随机值, 量子位数n∈ [10, 40]中间隔为2的随机值, 耗时约7 h.预训练完成后, 直接对n=40的高维量子系统进行测试, 此时B_x的范围为未训练区域[0.0, 0.5)∪ (1.5, 2.0]和已训练区域[0.5, 1.5]中间隔0.01的值, 已训练区域中也包含未曾训练过的数据点.

受少样本学习启发^[21], 为了进一步提升精度, 将少数特定情况(n=40, B_x为特定值)对训练的通用模型Mamba-HQGWR继续训练2 000次, 得到特定B_x和n下模型微调的结果.

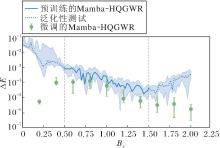
分别对预训练模型和微调模型在不同B_x值上进行泛化能力测试.为了减少系统误差, 提高结果的可靠性和准确性, 在每个B_x值上都进行预训练和微调的各10次重复测试.实验中的相对误差能量Δ E结果如图4所示, 图中, 在同一横坐标B_x值下的不同Δ E数据表示10次测试的误差范围, 蓝色实线为在已训练区域B_x∈ [0.5, 1.5]内测试结果的中位数曲线, 浅蓝色区域为预训练模型泛化能力测试的第10%至第90%的误差范围, 虚线部分表示未训练区域B_x[0.0, 0.5)∪ (1.5, 2.0]内泛化能力测试结果的中位数曲线, 带圆点的绿色误差条表示对预训练模型进行特定情况微调后测试的第10%至第90%的误差范围.图中小于10^-7的数据未显示.

	Figure Option View Download New Window
	图4 B_x∈ [0.5, 1.5]时Mamba-HQGWR的相对误差能量Fig.4 Relative error energy of Mamba-HQGWR with B_x∈ [0.5, 1.5]

从图4可看出, 即使在n=40的高维量子系统, 在只需要输入B_x的情况下, Mamba-HQGWR在已训练区域和未训练区域都具有泛化能力, 误差Δ E基本在10^-3以下.对预训练模型进行微调后, Δ E都有进一步幅度的减小, 并且部分可达到10^-5.由此可证明Mamba-HQGWR能有效学习具有良好泛化特性的量子态族通用波函数.

为了进一步评估Mamba-HQGWR对不同B_x的泛化能力, 在预训练时将上一实验中B_x∈ [0.5, 1.5]中间隔为0.1的随机值, 改变为B_x∈ [0.0, 0.5)∪ (1.5, 2.0]中间隔为0.1中的随机值, 测试时的B_x值为已训练区域[0.0, 0.5)∪ (1.5, 2.0]和未训练区域[0.5, 1.5]中间隔0.01的值.改变训练区域后的预训练模型测试结果如图5所示, 图中蓝色实线、浅蓝色区域、虚线和绿色误差条的含义与图4一致.

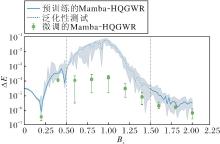	Figure Option View Download New Window
	图5 B_x∈ [0.0, 0.5)∪ (1.5, 2.0]时Mamba-HQGWR的相对误差能量Fig.5 Relative error energy of Mamba-HQGWR with B_x∈ [0.0, 0.5)∪ (1.5, 2.0]

由图5可看出, 不论是训练两侧区域测试中间区域, 还是训练中间区域测试两侧区域, Mamba-HQGWR都能实现B_x∈ [0, 2]的量子态族高精度通用波函数的高精度重构.

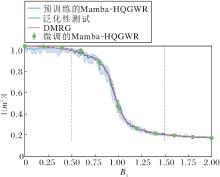
为了从另一个角度表现Mamba-HQGWR的泛化能力, 利用训练后的模型, 在不同外加磁场强度B_x下, 计算量子位数n=40时沿z方向磁化强度的绝对值:

$\left\langle m^{z}\right\rangle=\frac{1}{N} \sum_{i}\left\langle\boldsymbol{\sigma}_{i}^{z}\right\rangle=\frac{1}{N} \sum_{i}\left\langle\widehat{\Psi}_{\lambda}\right| \boldsymbol{\sigma}_{i}^{z}\left|\widehat{\Psi}_{\lambda}\right\rangle,$

其中, | ${\overset{︿}{Ψ}}_{λ}$ > 表示特定参数B_x下, Mamba-HQGWR预训练模型预测的波函数.

Mamba-HQGWR和DMRG的< |m^z|> 与B_x的曲线对比如图6所示.在TFIM中, 当B_x增大时, 系统可能会从有序相过渡到无序相, 即自旋从对齐于z方向过渡到更倾向于沿x方向对齐.可通过图中的磁化强度快速减小或消失体现这种相变点.如图6所示, Mamba-HQGWR的估计值与DMRG计算的真实值很接近, 说明Mamba-HQGWR能正确预测< |m^z|> 与B_x的关系, 有效学到系统的物理特性和波函数分布.此外, 在B_x=1时, 可明显观测到系统发生相变, 进一步验证模型的准确性和泛化能力.

	Figure Option View Download New Window
	图6 Mamba-HQGWR和DMRG沿z方向磁化强度的绝对值< \|m^z\|> 随B_x的变化曲线Fig.6 Curves of absolute value of magnetization < \|m^z\|> along z-direction for Mamba-HQGWR and DMRG as a function of B_x

4.3 量子位数n∈ [40, 80]的概率分布重构数值实验

为了验证Mamba-HQGWR在高量子位系统的泛化能力和高效的推理速度, 将5.1节中B_x∈ [0.5, 1.5], n∈ [10, 40]的预训练模型不进行任何改变, 直接用于不同高量子位系统的测试.测试实验中, 将J_z和B_x固定为1.0, 取n为未训练区域[40, 80]中间隔为2的值, 在相同设置下重复进行10次测试以确保结果可靠性.

Transformer是目前应用广泛的通用模型之一, 本节将Mamba-HQGWR与参数数量几乎相等的基于Transformer的波函数重构模型TQS^[11]进行一样流程的预训练, 预训练时间均约为7 h, 性能对比如图7所示.由图可看出, 从量子位n∈ [10, 80]系统的性能上看, Mamba-HQGWR和TQS在已训练区域n∈ [10, 40]的性能相仿.然而, 在未训练区域n∈ [40, 80], 虽然两者的Δ E随着量子位数的增大都逐渐增大, 但Mamba-HQGWR的增大速度明显小于TQS, 这表明Mamba-HQGWR在高维系统的泛化性能上优于TQS.

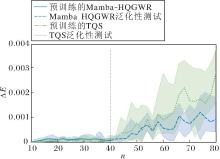	Figure Option View Download New Window
	图7 Mamba-HQGWR与TQS在高维量子系统的泛化能力对比Fig.7 Comparison of generalization ability of Mamba-HQGWR and TQS in high-qubit quantum systems

TQS和Mamba-HQGWR在量子位数n∈ [50, 100]的推理时间对比如表1所示, 表中黑体数字表示最优值, 由表可看出, 虽然TQS和Mamba-HQGWR的训练时间几乎一致, 但随着n的增加, TQS的推理时间呈现近似平方式的增长趋势, 而Mamba-HQGWR的推理时间表现为线性增长, 这主要是由于两个模型的复杂度差异.虽然TQS将传统的量子态层析方法在重构波函数时的复杂度从O(2ⁿ)降至O(n²), 但Mamba-HQGWR的复杂度进一步降至O(n).实验结果显示Mamba-HQGWR具有的计算复杂度与量子位数n呈线性关系, 相比TQS进行高量子位波函数重构时, 复杂度和推理速度随n呈平方增长关系, Mamba-HQGWR具有明显优势, 这使得Mamba-HQGWR具有克服其它模型在时间消耗和空间维度爆炸的能力.相比TQS, Mamba-HQGWR在高维系统泛化能力方面具有明显优势.

表1 TQS和Mamba-HQGWR在量子位不同时的推理时间对比 Table 1 Comparison of inference time between TQS and Mamba-HQGWR with different numbers of qubits s

5 结束语

本文设计高量子位通用波函数概率分布重构模型(Mamba-HQGWR), 并探索其在重构高维多体量子系统中基态波函数的泛化性能.Mamba-HQGWR能直接表示并生成一个量子态族, 更关注概率分布和相关参数(如外场强度和量子位)的联合分布.数值仿真实验表明, 在处理高维量子系统时, Mamba-HQGWR不仅在泛化能力上表现优异, 还展现出较高的计算效率, 能有效应对复杂的量子态重构问题.Mamba-HQGWR有助于二维模型以及复数值波函数的重构, 其多方面的优越性可为量子系统研究在相关领域取得更深入的拓展.

本文责任编委王卓

Recommended by Associate Editor WANG Zhuo

参考文献

文献选项

[1]	FOULKES W M C, MITAS L, NEEDS R J, et al. Quantum Monte Carlo Simulations of Solids. Reviews of Modern Physics, 2001, 73(1): 33-83. [本文引用:1]
[2]	SCHOLLWÖCK U. The Density-Matrix Renormalization Group in the Age of Matrix Product States. Annals of Physics, 2011, 326(1): 96-192. [本文引用:2]
[3]	DE OLIVEIRA N M, PARK D K, ARAUJO I F, et al. Quantum Variational Distance-Based Centroid Classifier. Neurocomputing, 2024, 576. DOI: DOI:10.1016/j.neucom.2024.127356. [本文引用:1]
[4]	SAITO H. Solving the Bose-Hubbard Model with Machine Learning. Journal of the Physical Society of Japan, 2017, 86(9). DOI: DOI:10.7566/JPSJ.86.093001. [本文引用:1]
[5]	SAITO H, KATO M. Machine Learning Technique to Find Quantum Many-Body Ground States of Bosons on a Lattice. Journal of the Physical Society of Japan, 2018, 87(1). DOI: DOI:10.7566/JPSJ.87.014001. [本文引用:1]
[6]	LIANG X, LIU W Y, LIN P Z, et al. Solving Frustrated Quantum Many-Particle Models with Convolutional Neural Networks. Physical Review B, 2018, 98(10). DOI: DOI:10.1103/PhysRevB.98.104426. [本文引用:2]
[7]	PFEUTY P. The One-Dimensional Ising Model with a Transverse Field. Annals of Physics, 1970, 57(1): 79-90. [本文引用:3]
[8]	CARLEO G, TROYER M. Solving the Quantum Many-Body Pro-blem with Artificial Neural Networks. Science, 2017, 355(6325): 602-606. [本文引用:2]
[9]	CARLEO G, NOMURA Y, IMADA M. Constructing Exact Representations of Quantum Many-Body Systems with Deep Neural Networks. Nature Communications, 2018, 9(1). DOI: DOI:10.1038/s41467-018-07520-3. [本文引用:2]
[10]	HIBAT-ALLAH M, GANAHL M, HAYWARD L E, et al. Recu-rrent Neural Network Wave Functions. Physical Review Research, 2020, 2(2). DOI: DOI:10.1103/physrevresearch.2.023358. [本文引用:3]
[11]	ZHANG Y H, DI VENTRA M. Transformer Quantum State: A Multipurpose Model for Quantum Many-Body Problems. Physical Review B, 2023, 107(7). DOI: DOI:10.1103/PhysRevB.107.075147. [本文引用:4]
[12]	BROOKS S, GELMAN A, JONES G, et al. Hand book of Markov Chain Monte Carlo. New York, USA: CRC Press, 2011. [本文引用:2]
[13]	BARRETT T D, MALYSHEV A, LVOVSKY A I. *Autoregressive Neural-Network Wavefunctions for ab initio* Quantum Chemistry*. Nature Machine Intelligence*, 2022, 4(4): 351-358. [本文引用:3]
[14]	VASWANI A, SHAZEER N, PARMAR N, et al. Attention Is All You Need // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 6000-6010. [本文引用:5]
[15]	DOSOVITSKIY A, BEYER L, KULESNIKOV A, et al. An Image Is Worth 16×16 Words: Transformers for Image Recognition at Scale[C/OL]. [2024-11-06]. https://arxiv.org/pdf/2010.11929. [本文引用:1]
[16]	LIU Z, LIN Y T, CAO Y, et al. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2021: 9992-10002. [本文引用:1]
[17]	DONG L H, XU S, XU B. Speech-Transformer: A No-recurrence Sequence-to-Sequence Model for Speech Recognition // Proc of the IEEE International Conference on Acoustics, Speech and Signal Processing. Washington, USA: IEEE, 2018: 5884-5888. [本文引用:1]
[18]	VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph Attention Networks[C/OL]. [2024-11-06]. https://arxiv.org/pdf/1710.10903. [本文引用:1]
[19]	GU A, DAO T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces[C/OL]. [2024-11-06]. https://arxiv.org/pdf/2312.00752. [本文引用:2]
[20]	KINGMA D P, BA J L. Adam: A Method for Stochastic Optimization[C/OL]. [2024-11-06]. https://arxiv.org/pdf/2312.00752. [本文引用:1]
[21]	BROWN T B, MANN B, RYDER N, et al. Language Models Are Few-Shot Learners // Proc of the 34th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2020: 1877-1901. [本文引用:1]

2001

0.0

... 蒙特卡罗方法^[1]和张量网络方法^[2]都是传统上用于处理高维空间的高效数值计算技术,旨在规避这种复杂性,虽然在一定程度上可缓解空间维度爆炸的问题,但仍存在一些限制,如蒙特卡罗符号问题和张量网络的面积定律纠缠^[3] ...

2011

0.0

... DMRG的核心思想是将系统分块,再通过局部截断逼近以保留重要的自由度^[2] ...

2024

0.0

2017

0.0

... Saito等^[4]提出一种使用FCN计算一维和二维玻色-哈伯德模型(Bose-Hubbard Model)基态的方法,采用简单的最速下降方法优化具有单个隐藏层的FCN,结果与精确对角化十分接近 ...

2018

0.0

... Saito等^[5]又研究FCN和具有多个隐藏层的CNN,证实只有单个隐藏层的FCN效果优于多个隐藏层的FCN,并且多层CNN比FCN更有效 ...

2018

0.0

... Liang等^[6]设计一种全新的卷积神经网络,解决量子多体问题,演示通过CNN解决方形晶格上高度受限的1/2自旋J1-J2反铁磁海森堡模型的情况^[6] ...

1970

0.0

... 横场伊辛模型(TFIM)是一个用于研究量子相变的凝聚态物理模型,在给定物理参数的情况下,求解由哈密顿量代表的能量函数为最小值时的基态波函数,描述一维自旋链或二维方晶格的自旋状态,其中每个自旋受到邻近自旋之间的相互作用和横向外场的影响^[7] ...

... 设计基于Mamba的无监督高效优化策略,在变分蒙特卡洛优化策略的基础上,结合高效采样流程^[14]和多基态尺度缩放机制,利用Mamba自回归地高效生成训练样本,无需额外标签样本的输入就能有效计算一维TFIM^[7]基态波函数概率分布的估计值 ...

... 2 横场伊辛模型在凝聚态物理中,人们一般采用横场伊辛模型(TFIM)^[7]描述一维自旋链的自旋状态,每个自旋与其相邻的自旋相互作用,并且受到一个横向磁场的作用 ...

2017

0.0

... 一维TFIM虽然是一个典型的量子自旋系统模型^[8,9,10,11],其研究结果可用于其它复杂系统,所以也是本文的研究对象 ...

... 受限波尔兹曼机(Restricted Boltzmann Machine, RBM)是一种生成模型,Carleo等^[8]首次使用受限波尔兹曼机结合变分蒙特卡洛(Variational Monte Carlo, VMC)技术,用于重构多体哈密顿量基态波函数,并在一维和二维横场伊辛模型以及海森堡模型中验证方法的可行性和准确性 ...

2018

0.0

... 一维TFIM虽然是一个典型的量子自旋系统模型^[8,9,10,11],其研究结果可用于其它复杂系统,所以也是本文的研究对象 ...

... Carleo等^[9]提出基于深度玻尔兹曼机架构的技术,用于重构多体量子系统状态,通过两层隐藏神经元捕捉横场伊辛模型中的量子相关性 ...

2020

0.0

... 一维TFIM虽然是一个典型的量子自旋系统模型^[8,9,10,11],其研究结果可用于其它复杂系统,所以也是本文的研究对象 ...

... 在量子态重构应用方面,Hibat-Allah等^[10]提出可重构特定量子态的RNN模型,具有独特的基于序列的架构和自回归特性,可用于重构一维和二维自旋模型的基态变分波函数 ...

... 通过对式(5)中 ê0求一阶偏导,求 ê0为最小情况下的量子波函数^[10]: ...

2023

0.0

... 一维TFIM虽然是一个典型的量子自旋系统模型^[8,9,10,11],其研究结果可用于其它复杂系统,所以也是本文的研究对象 ...

... 在量子态重构应用方面,Zhang等^[11]提出TQS(Transformer Quantum State),通过多基态尺度缩放机制进行训练,对未训练区域的物理参数和量子位数均具有泛化性 ...

... 的期望能量 E︿0以训练Mamba-HQGWR参数^[11]: ...

... Transformer是目前应用广泛的通用模型之一,本节将Mamba-HQGWR与参数数量几乎相等的基于Transformer的波函数重构模型TQS^[11]进行一样流程的预训练,预训练时间均约为7 h,性能对比如图7所示 ...

2011

0.0

... 求解凝聚态物理模型系统基态的常用数值方法是密度矩阵重整化群(Density Matrix Renormalization Group, DMRG),核心思想是通过优化局部的低秩张量近似有效处理高量子位系统^[12] ...

... 如果采用传统的马尔可夫链蒙特卡洛方法^[12]进行采样,将面临采样效率较低及难以满足大规模样本需求等问题 ...

2022

0.0

... RBM网络中一般采用马尔可夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)^[13]生成样本,效率较低,难以进行大规模采样,因此Barrett等^[13]提出一个高效的采样流程,本质上具有并行化特性,计算复杂度与采样的配置种类上限相关,而非采样的总数量 ...

... 本文基于文献[13]中的采样流程,设计Mamba-HQGWR自回归生成训练样本的网络,结构如图3所示 ...

2017

0.0

... 循环神经网络(Recurrent Neural Network, RNN)和Transformer^[14]都属于无监督学习模型,也是自回归模型,可独立生成符合真实概率分布的样本,而无需额外的样本输入 ...

... Transformer^[14]是近年来提出的一种任务无关模型,可应用于多种不同的任务或应用场景^{[15,16,17,18]},通过自注意力机制和混合位置编码的结合,在处理不同长度的序列时表现出高度的灵活性和效率 ...

... 与原始Mamba块^[19]的直接输入方式不同,Mamba-HQGWR增加输入预处理,将Mamba块与混合位置编码(Hybrid Positional Encoding, HPE)^[14]结合,通过HPE操作,将B_x和x转化为 hinput1 ...

... 通过上述步骤,将Mamba自回归生成训练样本与高效采样流程^[14]结合成Mamba-HQGWR的无监督训练样本采样流程 ...

0.0

2021

0.0

2018

0.0

... Gu等^[19]提出Mamba,以选择性状态空间模型为理论基础,既有CNN的并行计算优势,又有RNN的低复杂度和长程感知能力,旨在解决Transformer在长序列上计算效率低下的问题 ...

0.0

... 并通过自适应矩估计(Adaptive Moment Estimation, Adam)优化算法^[20]计算模型参数集合的增量: ...

2020

0.0

... 受少样本学习启发^[21],为了进一步提升精度,将少数特定情况(n=40,B_x为特定值)对训练的通用模型Mamba-HQGWR继续训练2 000次,得到特定B_x和n下模型微调的结果 ...