生物拓扑语义增强的药物与微生物异质图表征学习

Processing math: 1%

引用本文

郭全明, 郭延哺, 宋胜利, 陈紫豪, 朱昊坤. 生物拓扑语义增强的药物与微生物异质图表征学习. 模式识别与人工智能, 2024,37(12): 1121-1134
GUO Quanming, GUO Yanbu, SONG Shengli, CHEN Zihao, ZHU Haokun. Biological Topology-Semantic Enhanced Heterogeneous Graph Representation Learning for Drug-Microbe Interactions. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2024,37(12): 1121-1134. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202412007
Permissions

《模式识别与人工智能》编辑部

生物拓扑语义增强的药物与微生物异质图表征学习

郭全明¹, 郭延哺^1,², 宋胜利¹, 陈紫豪¹, 朱昊坤¹

1.郑州轻工业大学软件学院郑州 450002

2.东南大学江苏省网络群体智能重点实验室南京 211189

通讯作者:

宋胜利,博士,教授,主要研究方向为智能计算及应用.E-mail:slsong@126.com.

作者简介:

郭全明,硕士研究生,主要研究方向为生物信息计算、人工智能.E-mail:gqm_99@163.com.

郭延哺,博士,副教授,主要研究方向为神经网络理论与应用.E-mail:guoyanbu@gmail.com.

陈紫豪,硕士研究生,主要研究方向为生物信息计算、人工智能.E-mail:c15736774662@163.com.

朱昊坤,硕士研究生,主要研究方向为生物信息计算、人工智能.E-mail:zhuhaokun2000@163.com.

收稿日期: 2024-11-04 接受日期: 2024-12-29

资助项目: 国家自然科学基金项目(No.62403437)、河南省科技攻关项目(No.242102211039)资助

摘要

微生物与药物的相互作用对人体健康具有重要影响.现有关联预测方法未充分建模异质图的内部节点信息,且忽略不同元路径实例蕴含信息的重要性.为此,文中提出生物拓扑语义增强的药物与微生物异质图表征学习方法(Biological Topology-Semantic Enhanced Heterogeneous Graph Representation Learning for Drug-Microbe Interactions, HGRL),提取高阶混合邻域网络嵌入表示,推理微生物与药物间的关联信息.首先,整合微生物与药物相似性及关联数据,构建加权双向异质网络和多视图元路径感知网络.然后,结合变换器门控图网络与贝叶斯高斯混合加权对比学习,提取复杂生物网络的拓扑语义和嵌入特征.基于对抗性负采样的预测结果表明,HGRL在微生物-药物关联预测中性能较优,可作为预测候选药物相关微生物的可靠工具.

关键词: 异质图表征学习; 复杂生物网络; 多视图元路径; 对比学习; 微生物-药物关联预测

中图分类号:TP391

Biological Topology-Semantic Enhanced Heterogeneous Graph Representation Learning for Drug-Microbe Interactions

GUO Quanming¹, GUO Yanbu^1,², SONG Shengli¹, CHEN Zihao¹, ZHU Haokun¹

1. College of Software Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002

2. Jiangsu Provincial Key Laboratory of Networked Collective Intelligence, Southeast University, Nanjing 211189

Corresponding author:
SONG Shengli, Ph.D., professor. His research interests include intelligent computing and applications.

About Author:
GUO Quanming, Master student. His research interests include bioinformatics computation and artificial intelligence.
GUO Yanbu, Ph.D., associate professor. His research interests include neural network theory and applications.
CHEN Zihao, Master student. His research interests include bioinformatics computation and artificial intelligence.
ZHU Haokun, Master student. His research interests include bioinformatics computation and artificial intelligence.

Fund:Supported by National Natural Science Foundation of China(No.62403437), Project of Science and Technology in Henan Pro-vince(No.242102211039)

Abstract

The interaction between microorganisms and drugs significantly impacts human health. In existing association prediction methods, the internal node information of heterogeneous graphs is not adequately modeled and the importance of different meta-path instances is overlooked. Hence, a biological topology-semantic enhanced heterogeneous graph representation learning for drug-microbe interactions(HGRL) method is proposed. High-order mixed neighborhood network embedding representations are extracted to infer microorganism-drug associations. Microorganism-drug similarity and association data are integrated to construct a weighted bidirectional heterogeneous network and a multi-view meta-path aware network. The transformer-gated graph network is combined with Bayesian Gaussian mixture weighted contrastive learning to extract topological semantics and embedding features of complex biological networks. Prediction based on adversarial negative sampling demonstrates that HGRL outperforms existing methods in microorganism-drug association prediction and is a reliable tool for inferring microorganisms associated with candidate drugs.

Key words: Key Words Heterogeneous Graph Representation Learning; Complex Biological Network; Multi-view Meta-Path; Contrastive Learning; Microbe-Drug Association Prediction

文章图片

人体皮肤、胃肠道和口腔等组织中存在细胞、真菌和病毒等微生物群落, 它们在维持人体内部环境稳态中发挥关键作用^[1].在疾病治疗过程中, 微生物可通过影响药物的疗效和毒性, 调节治疗效果; 反之, 药物也可能抑制或杀死体内微生物, 从而引发如糖尿病、心脑血管疾病等复杂病症^[2].传统的湿实验方法周期长、成本高、通量低, 难以满足大规模微生物-药物相互作用研究的需求.因此, 利用智能计算算法研究药物与微生物的相互作用, 对于研发药物、制定治疗方案和实现个体化药物治疗具有重要意义^[3].

近年来人工智能和生物学测序技术的发展, 以及相关微生物和药物数据库的建立, 如MDAD(Mi-crobe-Drug Association Database)数据集^[4]、aBiofilm数据集^[5]、DrugVirus数据集^[6], 使人工智能通过快速计算方法预测微生物与药物之间的相互作用成为可能.

当前, 微生物与药物关联预测的计算方法研究主要包括基于网络相似性的方法和基于机器学习的方法.基于网络相似性的方法构建异质网络, 利用节点之间的相似性推断未知关联.Zhu等^[7]提出HMDAKATZ, 通过微生物和药物的相似性网络构建微生物-药物异质网络, 利用KATZ中心性测度量化异质网络中节点的重要性, 预测它们之间的潜在关联.Wang等^[8]提出MGAVAEMDA, 使用多个数据库建立微生物和药物的特征矩阵, 设计改进的图注意变分自编码器, 用于提取特征, 并利用随机森林模型推理微生物与药物的关系.

近年来, 以图神经网络为代表的机器学习方法因其强大的高阶信息挖掘能力, 在电子信息和生物医学信息处理领域得到广泛应用.在基因-表型关联预测方面, 谭好江等^[9]提出基于多组学数据融合的个性化随机游走算法(Individual Multiple Random Walks, iMRW), 为不同重要程度的节点分配差异化游走步长, 并基于高斯相互作用核的相似性, 预测多源基因-表型关联信息.在药物-药物相互作用预测研究中, 饶晓洁等^[10]提出基于多层次注意力机制和消息传递神经网络的DDI(Drug-Drug Interaction)预测方法, 建模分子中不同原子的贡献, 结合基于分子质心的位置编码, 实现从原子级到分子级的层次化特征学习, 提升药物间相互作用预测的准确性.

在微生物-药物关联预测研究中, 已有多项基于图神经网络的工作.Long等^[11]提出GCNMDA(Graph Convolutional Network Based Framework for Predicting Human Microbe-Drug Associations), 通过图卷积网络预测微生物与药物的相互作用.Long等^[12]提出EGATMDA, 以图注意力网络为基础, 利用分层注意力机制, 从多个生物网络中学习节点嵌入, 进行微生物-药物关联预测.随后, Long等^[13]提出HNERMDA(Heterogeneous Network Embedding Re-presentation Framework for Microbe-Drug Association Prediction), 基于异构网络嵌入表示, 利用metapath-2vec和双分网络推荐算法, 实现微生物与药物之间低维嵌入表示的学习.Tian等^[14]提出SCSMDA(Struc-ture-Enhanced Contrastive Learning and Self-Paced Negative Sampling Strategy for Microbe-Drug Associa-tion Predictions), 采用结构增强的对比学习和自适应优化负采样策略, 预测微生物与药物之间的潜在关联.Deng等^[15]提出Graph2MDA, 学习节点和整个图的潜在表示, 再使用变分图自动编码器预测微生物与药物之间的关联.

鉴于药物与微生物网络的生物实体之间具有的复杂互作用信息, 现有药物与微生物关联计算方法存在的主要挑战包括:1)单一图结构难以挖掘其中高阶关联作用; 2)以传统图卷积网络为基础的计算方法未能充分捕获网络节点中的丰富多模态特征; 3)选择药物微生物的负样本数据时仅随机地从未标记样本集上挑选, 忽略不同负样本对模型预测性能的影响.

针对现有计算方法的不足, 本文以变换器门控图卷积和贝叶斯高斯混合模型(Bayesian Gaussian Mixture Model, BGMM)为基础, 融合加权对比学习和对抗性负采样, 提出生物拓扑语义增强的药物与微生物异质图表征学习方法(Biological Topology-Semantic Enhanced Heterogeneous Graph Representa-tion Learning for Drug-Microbe Interactions, HGRL).首先, 整合药物和微生物多源信息, 构建药物与微生物加权双向异质网络和多视图元路径感知网络.再以相邻节点和元路径信息为基础, 采用变换器门控图卷积网络, 通过多头注意力机制对节点特征进行加权聚合, 自适应地学习节点间的重要性权重, 捕获药物-微生物之间的代表性交互模式.然后, 采用贝叶斯高斯混合加权对比学习, 自动聚类发现负样本结构, 并利用后验概率为不同负样本分配权重, 提升模型对样本对重要程度的区分能力.此外, 引入对抗性负采样方法, 在损失函数梯度方向添加扰动, 生成负样本, 并基于预测概率与标签损失进行模型训练.基于对抗性负采样的预测结果表明, HGRL在微生物-药物关联预测中性能较优, 可作为预测候选药物相关微生物的可靠工具.

1 生物拓扑语义增强的药物与微生物异质图表征学习

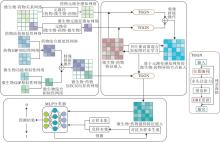
本文提出生物拓扑语义增强的药物与微生物异质图表征学习方法(HGRL), 框架如图1所示.

	Figure Option View Download New Window
	图1 HGRL框架Fig.1 Framework of HGRL

HGRL包含三个核心部分:1)构建药物-微生物加权双向异质网络并设计多视图元路径, 捕获网络语义信息; 2)设计变换器门控图网络, 结合Trans-former的全局建模能力与门控图神经网络的局部特征提取机制进行异质网络表征学习; 3)引入基于贝叶斯高斯混合模型的对比学习框架和对抗性负采样策略, 进行模型优化, 提升预测性能.

1.1 药物-微生物网络构建

1)关联关系网络构建.药物与微生物之间的关联关系表示为二值矩阵A∈ $R^{N_{m} \times N_{d}}$ , 其中, N_m表示微生物数量, N_d表示药物数量.若A_i_,_j=1, 表示微生物m_i与药物d_j关联; 若A_i_,_j=0, 表示该关联是未知状态.

2)相似性网络构建.基于文献[16]方法和SIMCOMP^[17]分别构建微生物功能相似性矩阵MF和药物结构相似性矩阵DS.

为了解决部分微生物或药物缺乏完整功能或结构信息的问题, 本文引入高斯核函数^[18].在微生物-药物关联矩阵A中, 将微生物m_i的第i行A(m_i)和药物d_j的第j列A(d_j)作为它们各自的交互谱, 并基于这些交互谱, 利用高斯核函数计算微生物高斯核相似性矩阵GM和药物高斯核相似性矩阵GD, 定义如下:

GM(m_i, m_j)=exp(-η _m‖ A(m_i)-A(m_j)‖ ²),

GD(d_i, d_j)=exp(-η _d‖ A(d_i)-A(d_j)‖ ²),

其中,

$\eta_{m}=\eta_{m}^{\prime}\left(\frac{1}{N_{m}} \sum_{i=1}^{N_{m}}\left\|\boldsymbol{A}\left(\boldsymbol{m}_{i}\right)\right\|^{2}\right)$ ,

表示微生物的归一化核带宽参数,

$\eta_{d}=\eta_{d}^{\prime}\left(\frac{1}{N_{d}} \sum_{i=1}^{N_{d}}\left\|\boldsymbol{A}\left(\boldsymbol{d}_{i}\right)\right\|^{2}\right)$ ,

表示药物的归一化核带宽参数, η '_m、η '_d表示预先设定的原始带宽参数, 与Van Laarhoven等^[18]提出的高斯核函数一致, 本文中将原始带宽参数同样设为1, 以保持核函数的尺度不变性.

为了综合利用功能相似性和高斯核相似性信息, 提升微生物相似性计算准确性, 对MF和GM进行加权平均, 得到最终微生物相似性网络S_m:

S_m(m_i, m_j)= $\{\begin{array}{l} \frac{MF (m_{i}, m_{j}) + GM (m_{i}, m_{j})}{2}, & MF (m_{i}, m_{j}) \neq 0 \\ GM (m_{i}, m_{j}), & 其它 \end{array}$

此外, 对DS和GD进行加权平均, 构建药物相似性网络S_d:

S_d(d_i, d_j)= $\{\begin{array}{l} \frac{DS (d_{i}, d_{j}) + GD (d_{i}, d_{j})}{2}, & DS (d_{i}, d_{j}) \neq 0 \\ GD (d_{i}, d_{j}), & 其它 \end{array}$

3)加权双向异质网络构建.在相似性计算完成后, 基于已知的药物-微生物交互数据, 构建一个基础交互网络A_het∈ R⁽^M⁺^D^{)× (}^M⁺^D⁾.为了确保网络中关系的双向性和一致性, 对基础交互网络A_het进行对称化处理, 得到对称化交互网络:

A_sym=A_het+ $A_{het}^{T}$ .

然后, 将药物和微生物的相似性信息(分别由S_m和S_d表示)与上述交互信息整合, 构建药物-微生物加权双向异质网络:

S_all= $(\begin{array}{l} S_{m} & 0 \\ 0 & S_{d} \end{array})$ +A_sym.

4)多视图元路径感知网络构建.元路径作为一种语义丰富的异质图模式, 能有效捕捉药物与微生物之间多层次、多角度的拓扑信息^[19].本文设计MDM(微生物-药物-微生物)和DMD(药物-微生物-药物)两种元路径:

$\begin{array}{l}D M D=D \xrightarrow{R_{D M}} M \xrightarrow{R_{M D}} D, \\M D M=M \xrightarrow{R_{M D}} D \xrightarrow{R_{D M}} M, \end{array}$

从微生物和药物两个视角全面表征异构网络中的节点关系, 其中, M表示微生物节点, D表示药物节点, R_MD和R_DM表示微生物与药物之间的关联关系.A表示药物与微生物关联矩阵, 则基于MDM和DMD元路径构建的元路径感知网络可分别表示为

A_MDM=AA^T, A_DMD=A^TA.

这种多视图的建模策略为后续的预测任务提供更丰富的特征表示.

1.2 变换器门控图网络

近年来, 图神经网络在各类结构化数据处理任务中优势显著, 但传统图神经网络面临两个关键局限:1)基于消息传递的架构难以有效建模长程依赖关系, 导致远距离节点间的信息交互受限; 2)节点特征更新缺乏选择性机制, 容易出现过度平滑现象, 损失节点的独特表征.针对这些挑战, 本文提出变换器门控图网络(Transformer-Gated Graph Network, TGGN), 融合Transformer^[20]的全局建模能力与门控图神经网络的局部特征提取机制, 在保持结构敏感性的同时实现高效的长程依赖建模.

TGGN采用分层混合架构, 包含可学习的特征投影、基于图结构的多头注意力机制、图卷积操作和GRU(Gated Recurrent Unit)^[21]门控更新.引入位置编码和层次化残差连接, 实现全局信息交互与局部特征提取的有效平衡.

1)多头注意力机制.TGGN采用稀疏多头注意力机制进行节点间信息交互, 相比传统基于消息传递的图神经网络, 该机制通过自适应注意力权重实现更高效的信息聚合, 能从不同角度捕获药物-微生物的交互模式.例如:某些注意力头关注药物的化学结构特征, 而其它头更注重微生物的功能属性.具体地, 给定节点特征矩阵x∈ $R^{N \times d_{in}}$ , 其中, N表示节点数量, d_in表示输入特征维度.首先通过3个独立的线性变换将特征映射为查询矩阵Q∈ $R^{N \times d_{out}}$ 、键矩阵K∈ $R^{N \times d_{out}}$ 和值矩阵V∈ $R^{N \times d_{out}}$ .在此基础上, 仅在图的边集(i, j)上计算注意力分数, 显著降低计算复杂度.

第h个注意力头下节点对(i, j)的注意力得分为:

$α_{ij}^{h}$ =softmax_j( $\frac{(Q_{i}^{h} \cdot K_{j}^{h})}{\sqrt[]{d_{head}}}$ ),

其中, $Q_{i}^{h}$ 和K $_{j}^{h}$ 分别表示对应节点在第h个头部的查询向量和键向量表示, d_head=d_out/H表示每个注意力头的特征维度.基于softmax归一化后的注意力权重, 通过加权聚合操作整合邻域信息, 即

$z_{i}^{h}=\sum_{j \in N(i)} \alpha_{i j}^{h} V_{j}^{h}$ ,

其中V $_{j}^{h}$ 表示对应节点在第h个头部的值矩阵表示.

最后, 为了充分利用多头机制捕获的多样化特征模式, 拼接各个注意力头的输出, 并通过可学习的线性变换W^O, 融合得到最终的节点嵌入表示:

z_i=concat( $z_{i}^{1}$ , $z_{i}^{2}$ , …, $z_{i}^{H}$ )W^O.

2)图信息传递.为了平衡全局信息交互与局部结构特征提取, TGGN设计基于门控机制的图信息处理模块, 动态调节信息流动, 识别和保留关键的药物-微生物交互特征.在图卷积传播阶段, 给定输入特征矩阵X∈ $R^{N \times d_{out}}$ , 首先通过可学习的权重矩阵W⁽^l⁾∈ $R^{d_{out} \times d_{out}}$ 对节点特征进行变换:

M⁽^l⁾=X⁽^l⁾W⁽^l⁾.

随后, 基于图的边集(i, j)执行消息传递, 采用加法聚合器高效融合邻域信息, 即

$h_{i}^{(l+1)}=\sum_{j \in N(i)} M_{j}^{(l)} .$

TGGN引入GRU门控机制, 增强对节点特征的选择性更新能力.在每层图卷积之后, 当前层的聚合特征M $_{i}^{(l)}$ 结合历史隐藏状态 $h_{i}^{(l)}$ , 通过GRU单元进行自适应更新, 即

$h_{i}^{(l + 1)}$ =GRU(M $_{i}^{(l)}$ , $h_{i}^{(l)}$ ).

3)位置编码与残差连接.与序列数据不同, 图结构数据缺乏天然的位置序列关系.为了准确表征药物-微生物网络中的拓扑距离信息, TGGN采用基于正弦-余弦函数的位置编码, 定义如下:

$\begin{array}{l}P E_{(p o s, 2 i)}=\sin \left(\frac{p o s}{10000^{2 i / d}}\right), \\P E_{(p o s, 2 i+1)}=\cos \left(\frac{p o s}{10000^{2 i / d}}\right), \end{array}$

其中, pos表示节点位置索引, i表示特征维度索引.同时, 考虑特征传递的衰减问题, 结合层正则化^[22], 设计层次化残差连接, 提取生物网络的拓扑信息:

$h_{i}^{(l + 1)}$ =LayerNorm( $h_{i}^{(l)}$ +GNN( $h_{i}^{(l)}$ )).

该连接一定程度上可避免梯度消失问题.

最终, 以基于两种元路径构建的元路径感知网络与初始药物-微生物特征嵌入作为输入, 通过TGGN得到基于元路径的药物-微生物异构节点表示Z^md.通过融合不同元路径获取的结构信息, 模型可更好地理解药物-微生物交互网络中的复杂语义关联, 提升预测性能和模型可解释性.

1.3 模型优化

1)基于贝叶斯高斯混合图对比学习.传统的对比学习方法通常将所有负样本等价对待, 这种处理方式忽视负样本之间的差异性.在微生物-药物关联预测任务中, 不同的负样本对具有不同的信息量和重要性, 某些负样本对可能代表潜在的未发现关联, 而另一些负样本对可能是确定的无关联对.特别地, 生物医学数据普遍具有噪声和不确定性.因此, 本文引入基于贝叶斯高斯混合模型的对比学习框架, 通过自适应负样本加权策略, 提升特征表示的判别性.该框架利用贝叶斯高斯混合模型, 通过自动聚类发现负样本的内在结构, 并利用后验概率对负样本类别进行软分配, 从而更好地捕捉复杂的数据分布特征.

为了在统一的特征空间中进行对比学习, 首先采用双层全连接神经网络, 对微生物的初始嵌入 $H_{m_{i}}^{all}$ 和异构节点嵌入 $Z_{m_{i}}^{md}$ 进行投影.具体地, 通过权重矩阵W₁、W₂, 偏置项b₁、b₂和ELU激活函数σ 进行如下变换:

$\begin{array}{l}\boldsymbol{H}_{m_{i}-}^{\text {all }} \operatorname{Proj}=\boldsymbol{W}_{2} \cdot \sigma\left(\boldsymbol{W}_{1} \cdot \boldsymbol{H}_{m_{i}}^{\text {all }}+\boldsymbol{b}_{1}\right)+\boldsymbol{b}_{2}, \\\boldsymbol{Z}_{m_{i}-}^{m d} \operatorname{Proj}=\boldsymbol{W}_{2} \cdot \sigma\left(\boldsymbol{W}_{1} \cdot \boldsymbol{Z}_{m_{i}}^{m d}+\boldsymbol{b}_{1}\right)+\boldsymbol{b}_{2} .\end{array}$

在投影空间中, 选用余弦相似度作为特征间的度量标准.相比欧氏距离, 余弦相似度更专注于捕捉向量间的方向关系, 不受向量模长影响.投影特征间的双向相似度如下所示:

$\{\begin{array}{l} si m_{HZ} = \exp (\frac{H_{m_{i}}^{all}_Proj \cdot Z_{m_{i}}^{md}_Proj}{‖ H_{m_{i}}^{all}_Proj ‖ ‖ Z_{m_{i}}^{md}_Proj ‖ τ}) \\ si m_{ZH} = si m_{HZ}^{T} \end{array}$

然后利用BGMM对负样本对的相似度进行自动聚类, 捕捉不同负样本对之间的内在差异性.对于相似度值sim_HZ, 其属于第k个高斯成分的后验概率:

$q\left(z=k \mid \operatorname{sim}_{\mathrm{HZ}}\right)=\frac{\pi_{k} N\left(\operatorname{sim}_{\mathrm{HZ}} \mid \boldsymbol{\mu}_{k}, \boldsymbol{\Sigma}_{k}\right)}{\sum_{j=1}^{K} \pi_{j} N\left(\operatorname{sim}_{\mathrm{HZ}} \mid \boldsymbol{\mu}_{j}, \boldsymbol{\Sigma}_{j}\right)},$

其中, π _k表示混合系数, μ _k、Σ _k分别表示第k个高斯分布的均值向量和协方差矩阵.

对比各个高斯成分的均值μ _k, 自动选择均值最小的成分(即相似度较低的负样本), 其后验概率用于构建权重矩阵Q.

进一步地, 将权重矩阵Q与原始相似度矩阵进行元素级乘法运算, 突出具有较大区分度的负样本对的贡献, 进而得到加权相似度矩阵:

$\{\begin{array}{l} si m_{HZ}^{weighted} = si m_{HZ} \cdot Q \\ si m_{ZH}^{weighted} = si m_{ZH} \cdot Q^{T} \end{array}$

基于加权相似度, 采用负对数似然损失函数分别优化微生物和药物的嵌入表示, 得到微生物嵌入整体损失:

$L_{m}^{total}$ =λ $L_{m_{i}}^{HZ}$ +(1-λ ) $L_{m_{i}}^{ZH}$ ,

其中,

$\begin{aligned}L_{m_{i}}^{\mathrm{HZ}} & =-\frac{1}{N} \sum_{i=1}^{N} \ln \left(\sum_{j=1}^{M}\left(\operatorname{sim}_{\mathrm{HZ}}^{\text {weighted }} \cdot \boldsymbol{P}\right)_{i j}+\varepsilon\right), \\L_{m_{i}}^{\mathrm{ZH}} & =-\frac{1}{N} \sum_{i=1}^{N} \ln \left(\sum_{j=1}^{M}\left(\operatorname{sim}_{\mathrm{ZH}}^{\text {weighted }} \cdot \boldsymbol{P}\right)_{i j}+\varepsilon\right), \end{aligned}$

N表示微生物样本总数, M表示每个微生物样本在计算相似性时考虑的正负样本对总数, P表示正样本对指示矩阵, ε 表示极小正数, λ 表示平衡参数.

采用类似的方式学习药物嵌入, 其整体损失函数如下:

$L_{d}^{total}$ =λ $L_{d_{j}}^{HZ}$ +(1-λ ) $L_{d_{j}}^{ZH}$ .

最终, 通过反向传播算法优化可学习参数, 将药物-微生物加权双向异质网络作为TGGN的输入, 学习微生物和药物的最终特征嵌入表示, 记为Z_s.

2)对抗性负采样.在微生物与药物相互作用研究中, 已验证的交互对构成正样本集P, 未验证的潜在联系构成负样本集N.由于负样本数量远大于正样本, 直接随机采样可能导致模型过度关注负样本.为此, 本文提出对抗性负采样方法, 通过对抗训练生成具有挑战性的负样本, 并借鉴自适应负采样策略^[14]进行选择性采样.

给定一个样本的预测概率 $\hat{y}$ 和真实标签y, 损失函数

L( $\hat{y}$ , y)=-[yln $\hat{y}$ +(1-y)ln(1- $\hat{y}$ )].

在损失函数梯度方向添加对抗扰动, 生成对抗样本的预测概率:

${\hat{y}}^{adv}$ = $\hat{y}$ +ε · sign(- $\frac{y}{\hat{y}}$ + $\frac{1 - y}{1 - \hat{y}}$ ),

其中ε 表示扰动强度.将所有对抗样本根据其预测概率的置信度划分为K个区间.每个区间包含一定数量的样本:

$B_{l}=\left\{\hat{y}^{\text {adv }}\left|\frac{l-1}{k} \leqslant\left|\hat{y}^{\text {adv }}\right|< \frac{l}{k}\right\}, l \in[1, k] .\right.$

根据预定义的策略, 从若干区间中选择负样本, 通常选择置信度接近0.5的样本, 表达式如下:

$\begin{array}{l}N_{0}= \left\{\hat{y}_{l, j}^{\mathrm{adv}} \mid l \in[1, k], j \in\left[1, S_{B_{l}}\right] ; l \in \mathbf{N}^{+}, j \in \mathbf{N}^{+}\right\}, \end{array}$

其中,

$S_{B_{l}}=\frac{w_{l}|P|}{\sum_{t} w_{t}}$ ,

表示从第l个区间选择的负样本数量,

w_l= $\frac{1}{h_{l} + α}$ ,

表示第l个区间的归一化采样权重,

α =tan( $\frac{iπ}{2 n}$ ),

表示自适应因子, i表示迭代次数,

$h_{l}=\sum_{\substack{\hat{y}_{l, j}^{\mathrm{adv}} \in B_{l}}} \frac{\left|\hat{y}_{l}^{\mathrm{adv}}\right|}{\left|B_{l}\right|}$ ,

表示第l个区间的平均硬度得分.

最终将采样得到的负样本集N₀与正样本集P组成训练集, 并结合微生物和药物的最终特征嵌入Z_s训练多层感知机分类器.

2 实验及结果分析

2.1 实验设置和评估指标

本文采用MDAD^[4]、aBiofilm^[5]、DrugVirus^[6]这3个微生物与药物数据集, 验证HGRL在关联预测任务上的有效性和鲁棒性.MDAD数据集包括173种微生物和1 373种药物的2 470条经过实验验证的数据关联.aBiofilm数据集包含140种微生物与1 720种药物组成的2 884个微生物-药物关联信息.DrugVirus数据集包含有95种微生物和175种药物构成的933个微生物-药物关联数据.

HGRL采用Glorot初始化方案^[23]、Adam(Adap-tive Moment Estimation)优化器^[24]和余弦退火学习率调度器^[25]进行训练.为了获得最优配置, 采用网格搜索方法优化关键超参数, 通过实验确定最优参数组合:学习率为0.000 6, 余弦退火周期为200, 最小学习率为1e-5, 注意力头数为4, 药物和微生物的嵌入维度以及隐藏层维度均为128.经过1 400个迭代周期的训练后, 性能达到最优.

实验环境如下:PyCharm 2024.1、Python 3.10.8、scikit-learn 1.1.1、scipy 1.9.3、torch 2.1.2、torch-geometric 2.5.3.

硬件配置如下:Intel Xeon Platinum 8255C CPU和NVIDIA RTX 3060 Laptop GPU.

为了评估HGRL在MDAD、aBiofilm、DrugVirus数据集上的性能, 采用五折交叉验证.具体地, 将已知的微生物-药物相互作用对作为正样本, 未发现的潜在相互作用对作为候选负样本.HGRL通过对抗性生成负样本策略, 从候选负样本集上采样与正样本等量的负样本, 构成最终的实验数据集.

在五折交叉验证中, 数据集随机划分为五份, 每次取一份作为测试集, 其余四份作为训练集.本文采用AUC(Area Under the Curve)、AUPRC(Area Under the Precision-Recall Curve)、准确率、Matthews相关系数(Matthews Correlation Coefficient, MCC)和F1分数评估方法性能.

为了降低实验结果的随机性, 对每种方法进行5次独立实验, 并计算各项指标的平均值和标准差.

为了提高研究的透明度和可重复性, 本文的代码和数据集已在Gitee开源:https://gitee.com/gqm_99/HGRL_MDA.

2.2 对比实验

为了确保公平对比, 所有基线方法均采用与HGRL相同的实验设置和评估指标.在数据输入上, 将HGRL构建的微生物相似性网络和药物相似性网络作为所有方法的输入特征, 确保各方法在相同的数据基础上进行预测.

本文选择如下基线方法.

1)GCNMDA^[11].构建药物和微生物的异构网络, 采用基于GCN的框架, 结合条件随机场和注意力机制发现微生物-药物关联.

2)SCSMDA^[14].使用结构增强对比学习和自适应负采样预测微生物-药物关联.

3)GCN(Graph Convolutional Network)^[26].使用图卷积网络处理图结构数据.

4)GAT(Graph Attention Networks)^[27].引入注意力机制的图神经网络, 最初用于预测蛋白质与药物的相互作用.

5)LAGCN(Layer Attention Graph Convolutional Network)^[28].用于预测药物-疾病关联, 结合来自多个图卷积层的嵌入, 使用注意力机制整合这些嵌入, 获得丰富的药物和疾病表示.

6)GSAMDA^[29].采用基于图注意力网络的自编码器(GAT-Based Autoencoder)学习网络中节点的拓扑表示, 并使用稀疏自编码器(Sparse Autoen-coder)学习节点的属性表示.

7)MMGCN(Multi-view Multichannel Attention Graph Convolutional Network)^[30].采用GCN编码器在不同相似性视图中获取miRNA 和疾病的嵌入, 并利用多通道注意力机制增强学习的表示.

8)GACNNMDA^[31].结合基于图注意力网络的自编码器和基于CNN的分类器, 预测潜在的微生物-药物关联.

各方法的AUC和AUPRC结果如表1所示, 表中黑体数字表示最优值.由表可见, HGRL在所有数据集上都取得最优值.

表1 各方法在3个数据集上的性能对比 Table 1 Performance comparison of different methods on 3 datasets

在MDAD数据集上, 相比SCSMDA, HGRL分别提升1.36%和2.97%(p < 0.001), 这种显著的性能提升表明方法能有效捕获复杂的微生物-药物关联模式.在aBiofilm数据集上, 虽然相比次优方法SCSMDA, HGRL在AUC值上的提升幅度相对较小(0.96%, t=6.340, p< 0.001), 但在AUPRC指标上取得显著提升(3.70%, t=19.783, p < 0.001).这种提升幅度的差异主要是由于该数据集上正负样本分布较平衡, 使AUC指标对模型改进的敏感度降低.

在具有挑战性的DrugVirus数据集上, 尽管数据稀疏性和类别不平衡带来更大挑战, HGRL表现仍保持稳定, 较小的标准差(多数指标小于0.01)表明方法在不同数据分布下都具有良好的泛化能力和稳定性.

同时, 由表1可观察到, HGRL在药物-微生物关联预测任务上显著优于传统的图卷积网络(GCN)和图注意力网络(GAT), 在3个数据集上的AUC和AUPRC值均提升约8%.GCN和GAT在处理图数据时, 往往会受到过平滑问题的影响, 即经过多次卷积之后, 节点特征会变得越来越相似, 难以区分不同节点.这是因为它们在聚合邻居信息时, 对所有邻居赋予相同的权重.HGRL通过MDM和DMD两种元路径构建元路径感知网络, 并引入变换器门控图网络(TGGN)融合不同元路径获取的结构信息.TGGN通过多头注意力机制分配不同的权重, 从而更准确地捕获节点之间的差异性, 有效缓解过平滑问题, 更好地保留节点的局部特征, 更有效地捕获节点之间的长程依赖关系.

通过对比学习, HGRL能学到基于元路径的节点语义相似性.融合元路径感知网络与初始药物-微生物特征嵌入, HGRL可更好地理解药物-微生物交互网络中的复杂语义关联.此外, 在传统的图神经网络中, 针对负样本通常采用随机采样.这种随机采样的方式可能导致生成的负样本不够有挑战性, 从而影响方法的学习效果.HGRL采用对抗性负采样, 即通过一个生成器生成更难区分的负样本.生成器会不断尝试欺骗判别器, 而判别器则区分正样本和负样本.这种对抗性的训练过程使方法能学到更鲁棒的特征表示, 提高模型的泛化能力.

综上所述, HGRL充分利用图结构信息, 在与近年来的其它先进方法的对比中, 在AUC和AUPRC指标上均取得最优值, 由此验证方法的有效性.

2.3 消融实验

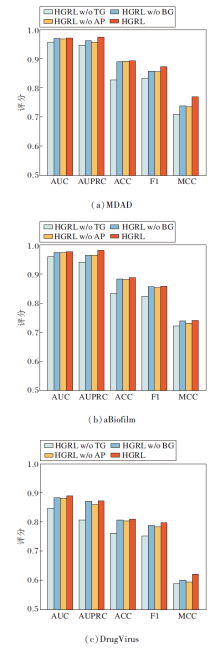
为了评估方法中各组成部分的必要性, 本节考虑逐个移除中的独立组件进行消融实验.选择如下独立组件:变换器门控图组件(简记为TG)、基于贝叶斯高斯混合的对比学习组件(简记为BG)、对抗性负采样组(简记为AP).分别在不包含TG组件的HGRL(HGRL w/o TG)、不包含BG组件的HGRL(HGRL w/o BG)和不包含AP组件的HGRL(HGRL w/o AP)以及HGRL上进行消融实验, 结果如图2所示.

	Figure Option View Download New Window
	图2 不同组件移除对HGRL性能的影响Fig.2 Effect of removing different components on HGRL performance

由图2可看出, 在3个数据集上, HGRL的性能均优于其它模型, 表明TGGN有助于HGRL更好地学习数据特征, 提高预测准确性.基于贝叶斯高斯混合的对比学习(BG)和对抗性负采样组件(AP)在提高模型的泛化能力上也起到重要作用.

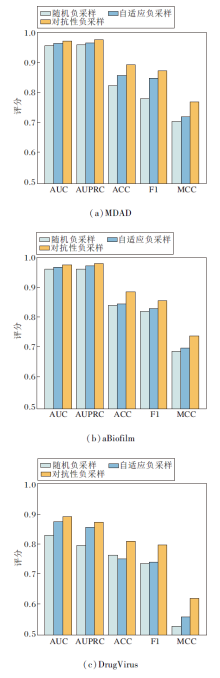
为了更进一步验证对抗性负采样组件的有效性, 在HGRL中分别采用随机负采样、自适应负采样和对抗性负采样这3种策略进行对比实验, 结果如图3所示.由图可见, 在3个数据集上, 采用对抗性负采样的HGRL均取得最优值.实验表明, 相比传统的随机负采样和自适应负采样, 对抗性负采样能生成更具挑战性的负样本, 帮助方法学到更鲁棒的特征表示.这与消融实验结果相互印证, 进一步证实对抗性负采样组件在提升方法性能方面的重要作用.

	Figure Option View Download New Window
	图3 不同负采样策略对HGRL性能的影响Fig.3 Effect of different negative sampling strategies on HGRL performance

2.4 参数敏感性分析

本节旨在评估HGRL对不同超参数设置的敏感性, 主要关注学习率、多头注意力机制头数、嵌入尺寸、区间数(负样本采样时考虑的区间总数)等关键超参数对方法性能(如准确率、F1-Score、AUC等)的影响.

学习率决定方法权重更新的步幅大小, 对模型的收敛性和全局最优解的搜索至关重要.

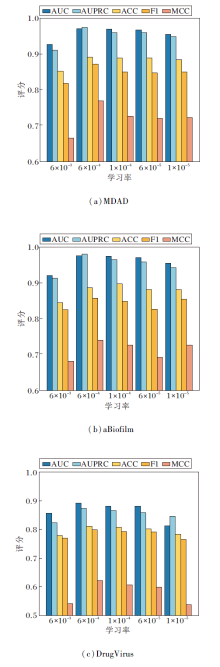
在实验中, 设置学习率为6× 10^-3, 6× 10^-4, 1× 10^-4, 6× 10^-5, 1× 10^-5, 其对HGRL性能的影响如图4所示.

	Figure Option View Download New Window
	图4 不同学习率对HGRL性能的影响Fig.4 Effect of different learning rates on HGRL performance

由图4可发现, 当学习率设为6× 10^-4时, HGRL在AUC、F1-Score等指标上达到最优值.这说明在模型初期, 适中的学习率能保证快速收敛, 同时在后期避免震荡与局部最优陷阱.

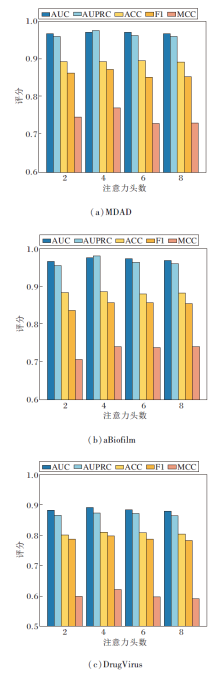
多头注意力机制头数增加可提升方法捕捉数据多样性和复杂模式的能力, 但也会增加计算量和参数量.设置注意力头数为2, 4, 6, 8, 其对HGRL性能的影响如图5所示.

	Figure Option View Download New Window
	图5 不同注意力头数对HGRL性能的影响Fig.5 Effect of different numbers of attention heads on HGRL performance

由图5可见, 当注意力头数设置为4时, HGRL性能达到最优.这说明过少的注意力头数(如2个)难以充分捕获节点间的多维特征关系, 而过多的头数(如6个或8个)会导致注意力机制过度分散, 增加计算开销.

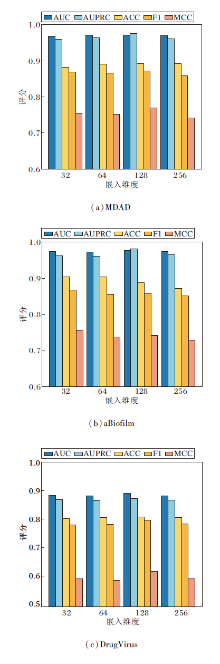
对于图神经网络而言, 嵌入维度直接关系特征表示的丰富性及信息冗余度.本文设定嵌入维度为32, 64, 128, 256, 其对HGRL的影响如图6所示.

	Figure Option View Download New Window
	图6 不同嵌入维度对HGRL性能的影响Fig.6 Effect of different embedding dimensions on HGRL performance

由图6可知, 当嵌入维度从32增至128时, HGRL各项指标值都有所提升.这表明更高的维度可捕获图结构中更复杂的节点间关系.然而, 当嵌入维度超过128时, 性能开始呈现下降趋势.这是因为过大的嵌入维度会引入更多的噪声信息, 使模型在捕获有用特征的同时也学到不相关的冗余信息.

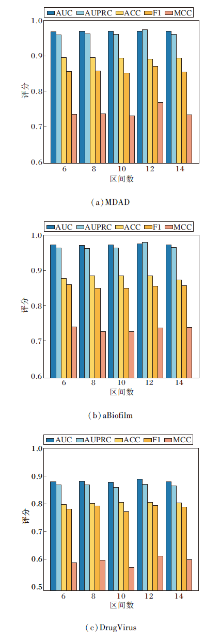
在对抗性负采样方法中, 区间数控制负样本采样的难度与多样性.设置区间数为6, 8, 10, 12, 14, 其对HGRL的影响如图7所示, 由图可观察到, 当区间数为12时, HGRL的AUC和F1-Score值达到最优.这表明在这个采样规模下, 生成的负样本难度适中, 能有效挑战模型的判别能力, 促使模型学到更具区分性的特征表示.

	Figure Option View Download New Window
	图7 不同区间数对HGRL性能的影响Fig.7 Effect of different numbers of bins on HGRL performance

较小的区间数可能导致负样本的多样性不足, 限制模型的学习深度, 过大的区间数则可能引入过多难以区分的负样本, 导致训练不稳定.

为了进一步探索余弦退火学习率调度器的性能影响, 对其关键超参数— — 余弦周期的长度(T_max)和学习率最小值(eta_min)进行敏感性分析.

在MDAD、aBiofilm、DrugVirus数据集上, 设定在T_max∈ [100, 300]和eta_min∈ [1× 10^-6, 1× 10^-4]的参数空间内进行网格搜索, 结果如图8所示.

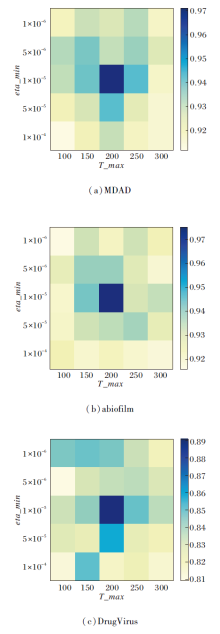	Figure Option View Download New Window
	图8 余弦退火学习率调度器的参数敏感性分析结果Fig.8 Parameter sensitivity analysis of cosine annealing learning rate scheduler

实验表明, 当 T_max=200且eta_min=1× 10^-5时, HGRL的AUC值达到最佳.热力图分析显示, 当eta_min> 5× 10^-5时, 方法性能出现明显下降, 这可能源于较大的最小学习率制约模型的精细调整能力.

同样, T_max偏离200也会导致方法性能降低, 说明合适的周期长度对方法的优化起到至关重要的作用.

3 结束语

为了深入建模节点的高阶特征以及不同元路径之间的交互关系, 本文以变换器门控图网络为基础, 结合贝叶斯高斯混合加权对比学习和对抗性负采样, 提出生物拓扑语义增强的药物与微生物异质图表征学习方法(HGRL).在3个公共数据集上的实验表明, HGRL可自动捕获复杂生物网络的多模态特征, 进一步提升药物与微生物关联分析模型的表达能力和鲁棒性.

鉴于药物与微生物网络的复杂性, 现有药物和微生物间的计算方法研究主要建模生物网络中节点的局部结构信息.今后拟从如下几方面开展药物和微生物关系建模的计算方法的研究.1)研究引入药物和微生物等的物理化学属性, 增强特征表示.2)构建药物、微生物、基因、疾病、circRNA、miRNA、Inc- RNA等组成大规模复杂生物网络数据, 研究复杂网络的动力学特性, 建立高效的大数据挖掘算法, 改进优化模型的性能.3)将HGRL应用于其它生物医学领域的链接预测任务, 如药物相互作用预测、miRNA-疾病关联预测等, 推动电子信息与生物医学、神经科学的交叉研究与发展.

本文责任编委周水庚

Recommended by Associate Editor ZHOU Shuigeng

参考文献

文献选项

[1]	LAI Y P, GALLO R L. AMPed up Immunity: How Antimicrobial Peptides Have Multiple Roles in Immune Defense. Trends in Immunology, 2009, 30(3): 131-141. [本文引用:1]
[2]	MAIER L, PRUTEANU M, KUHN M, et al. Extensive Impact of Non-antibiotic Drugs on Human Gut Bacteria. Nature, 2018, 555(7698): 623-628. [本文引用:1]
[3]	CHO J. Downstream Regulatory Element Antagonist Modulator(DREAM), A Target for Anti-Thrombotic Agents. Pharmacological Research, 2017, 117: 283-287. [本文引用:1]
[4]	SUN Y Z, ZhANG D H, CAI S B, et al. MDAD: A Special Resource for Microbe-Drug Associations. Frontiers in Cellular and Infection Microbiology, 2018, 8. DOI: DOI:10.3389/fcimb.2018.00424. [本文引用:2]
[5]	RAJPUT A, THAKUR A, SHARMA S, et al. aBiofilm: A Resource of Anti-Biofilm Agents and Their Potential Implications in Targeting Antibiotic Drug Resistance. Nucleic Acids Research, 2017, 46(D1): D894-D900. [本文引用:2]
[6]	ANDERSEN P I, IANEVSKI A, LYSVAND H, et al. Discovery and Development of Safe-in-Man Broad-Spectrum Antiviral Agents. International Journal of Infectious Diseases, 2020, 93: 268-276. [本文引用:2]
[7]	ZHU L Z, DUAN G H, YAN C, et al. Prediction of Microbe-Drug Associations Based on KATZ Measure // Proc of the IEEE International Conference on Bioinformatics and Biomedicine. Washington, USA: IEEE, 2019: 183-187. [本文引用:1]
[8]	WANG B, MA F J, DU X X, et al. Prediction of Microbe-Drug Associations Based on a Modified Graph Attention Variational Autoencoder and Rand om Forest. Frontiers in Microbiology, 2024, 15. DOI: DOI:10.3389/fmicb.2024.1394302. [本文引用:1]
[9]	谭好江, 王峻, 余国先, 等. 基于个性化随机游走的基因-表型关联分析. 电子学报, 2024, 52(5): 1619-1632. (TAN H J, WANG J, YU G X, et al. Individual Rand om Walks for Gene-Phenotype Association Analysis. Acta Electronica Sinica, 2024, 52(5): 1619-1632. ) [本文引用:1]
[10]	饶晓洁, 张通, 孟献兵, 等. 基于多层注意力和消息传递网络的药物相互作用预测方法. 自动化学报, 2023, 49(12): 2507-2519. (RAO X J, ZHANG T, MENG X B, et al. Drug-Drug Interaction Prediction Method Based on Multi-level Attention Mechanism and Message Passing Neural Network. Acta Automatica Sinica, 2023, 49(12): 2507-2519. ) [本文引用:1]
[11]	LONG Y H, WU M, KWOH C K, et al. Predicting Human Microbe-Drug Associations via Graph Convolutional Network with Conditional Rand om Field. Bioinformatics, 2020, 36(19): 4918-4927. [本文引用:2]
[12]	LONG Y H, WU M, LIU Y, et al. Ensembling Graph Attention Networks for Human Microbe-Drug Association Prediction. Bioinformatics, 2020, 36(S): i779-i786. [本文引用:1]
[13]	LONG Y H, LUO J W. Association Mining to Identify Microbe Drug Interactions Based on Heterogeneous Network Embedding Representation. IEEE Journal of Biomedical and Health Informa-tics, 2021, 25(1): 266-275. [本文引用:1]
[14]	TIAN Z, YU Y, FANG H C, et al. Predicting Microbe-Drug Associations with Structure-Enhanced Contrastive Learning and Self-Paced Negative Sampling Strategy. Briefings in Bioinformatics, 2023, 24(2). DOI: DOI:10.1093/bib/bbac634. [本文引用:3]
[15]	DENG L, HUANG Y B, LIU X J, et al. Graph2MDA: A Multi-modal Variational Graph Embedding Model for Predicting Microbe-Drug Associations. Bioinformatics, 2022, 38(4): 1118-1125. [本文引用:1]
[16]	KAMNEVA O K. Genome Composition and Phylogeny of Microbes Predict Their Co-occurrence in the Environment. PLoS Computational Biology, 2017, 13(2). DOI: DOI:10.1371/journal.pcbi.1005366. [本文引用:1]
[17]	HATTORI M, TANAKA N, KANEHISA M, et al. SIMCOMP/SUBCOMP: Chemical Structure Search Servers for Network Analyses. Nucleic Acids Research, 2010, 38(S2): W652-W656. [本文引用:1]
[18]	VAN LAARHOVEN T, NABUURS S B, MARCHIORI E. Gaussian Interaction Profile Kernels for Predicting Drug-Target Interaction. Bioinformatics, 2011, 27(21): 3036-3043. [本文引用:2]
[19]	秦海盈, 赵中英, 李建晖, 等. 基于元路径与层次注意力的时序异质信息网络表示学习方法. 模式识别与人工智能, 2021, 34(12): 1093-1102. (QIN H Y, ZHAO Z Y, LI J H, et al. Meta-Path and Hierarchical Attention Based Temporal Heterogeneous Information Network Representation Learning. Pattern Recognition and Artificial Intelligence, 2021, 34(12): 1093-1102. ) [本文引用:1]
[20]	张玉朋, 李香菊, 李超, 等. 基于Transformer与异质图神经网络的新闻推荐模型. 模式识别与人工智能, 2022, 35(9): 839-848. (ZHANG Y P, LI X J, LI C, et al. News Recommendation Model Based on Transformer and Heterogeneous Graph Neural Network. Pattern Recognition and Artificial Intelligence, 2022, 35(9): 839-848. ) [本文引用:1]
[21]	BAI M L, ZHOU Z H, LI J J, et al. Deep Graph Gated Recurrent Unit Network-Based Spatial-Temporal Multi-task Learning for Inte-lligent Information Fusion of Multiple Sites with Application in Short-Term Spatial-Temporal Probabilistic Forecast of Photovoltaic Power. Expert Systems with Applications, 2024, 240. DOI: DOI:10.1016/j.eswa.2023.122072. [本文引用:1]
[22]	WU X Y, AJORLOU A, WANG Y F, et al. On the Role of Attention Masks and LayerNorm in Transformers[C/OL]. [2024-10-20]. https://arxiv.org/abs/2405.18781. [本文引用:1]
[23]	GLOROT X, BENGIO Y. Understand ing the Difficulty of Training Deep Feedforward Neural Networks // Proc of the 13th Internatio-nal Conference on Artificial Intelligence and Statistics. San Diego, USA: JMLR, 2010: 249-256. [本文引用:1]
[24]	REYAD M, SARHAN A M, ARAFA M. A Modified Adam Algorithm for Deep Neural Network Optimization. Neural Computing and Applications, 2023, 35(23): 17095-17112. [本文引用:1]
[25]	ZHANG C, SHAO Y C, SUN H J, et al. The WuC-Adam Algorithm Based on Joint Improvement of Warmup and Cosine Annealing Algorithms. Mathematical Biosciences and Engineering, 2024, 21(1): 1270-1285. [本文引用:1]
[26]	KIPF T N, WELLING M. Semi-Supervised Classification with Graph Convolutional Networks[C/OL]. [2024-10-20]. https://arxiv.org/abs/1609.02907. [本文引用:1]
[27]	VELIČKOVIĆ P, CUCURULL G, CASANOVA A, Graph Attention Networks[C/OL]. [2024-10-20]. https://arxiv.org/abs/1710.10903. [本文引用:1]
[28]	YU Z X, HUANG F, ZHAO X H, et al. Predicting Drug-Disease Associations through Layer Attention Graph Convolutional Network. Briefings in Bioinformatics, 2021, 22(4). DOI: DOI:10.1093/bib/bbaa243. [本文引用:1]
[29]	TAN Y Q, ZOU J, KUANG L N, et al. GSAMDA: A Computational Model for Predicting Potential Microbe-Drug Associations Based on Graph Attention Network and Sparse Autoencoder. BMC Bioinformatics, 2022, 23(1). DOI: DOI:10.1186/s12859-022-05053-7. [本文引用:1]
[30]	TANG X R, LUO J W, SHEN C, et al. Multi-view Multichannel Attention Graph Convolutional Network for miRNA-Disease Association Prediction. Briefings in Bioinformatics, 2021, 22(6). DOI: DOI:10.1093/bib/bbab174. [本文引用:1]
[31]	MA Q, TAN Y Q, WANG L. GACNNMDA: A Computational Model for Predicting Potential Human Microbe-Drug Associations Based on Graph Attention Network and CNN-Based Classifier. BMC Bioinformatics, 2023, 24(1). DOI: DOI:10.1186/s12859-023-05158-7. [本文引用:1]

2009

0.0

... 人体皮肤、胃肠道和口腔等组织中存在细胞、真菌和病毒等微生物群落,它们在维持人体内部环境稳态中发挥关键作用^[1] ...

2018

0.0

... 反之,药物也可能抑制或杀死体内微生物,从而引发如糖尿病、心脑血管疾病等复杂病症^[2] ...

2017

0.0

... 因此,利用智能计算算法研究药物与微生物的相互作用,对于研发药物、制定治疗方案和实现个体化药物治疗具有重要意义^[3] ...

2018

0.0

... 近年来人工智能和生物学测序技术的发展,以及相关微生物和药物数据库的建立,如MDAD(Mi-crobe-Drug Association Database)数据集^[4]、aBiofilm数据集^[5]、DrugVirus数据集^[6],使人工智能通过快速计算方法预测微生物与药物之间的相互作用成为可能 ...

... 1 实验设置和评估指标本文采用MDAD^[4]、aBiofilm^[5]、DrugVirus^[6]这3个微生物与药物数据集,验证HGRL在关联预测任务上的有效性和鲁棒性 ...

2017

0.0

... 1 实验设置和评估指标本文采用MDAD^[4]、aBiofilm^[5]、DrugVirus^[6]这3个微生物与药物数据集,验证HGRL在关联预测任务上的有效性和鲁棒性 ...

2020

0.0

... 1 实验设置和评估指标本文采用MDAD^[4]、aBiofilm^[5]、DrugVirus^[6]这3个微生物与药物数据集,验证HGRL在关联预测任务上的有效性和鲁棒性 ...

2019

0.0

... Zhu等^[7]提出HMDAKATZ,通过微生物和药物的相似性网络构建微生物-药物异质网络,利用KATZ中心性测度量化异质网络中节点的重要性,预测它们之间的潜在关联 ...

2024

0.0

... Wang等^[8]提出MGAVAEMDA,使用多个数据库建立微生物和药物的特征矩阵,设计改进的图注意变分自编码器,用于提取特征,并利用随机森林模型推理微生物与药物的关系 ...

2024

0.0

... 在基因-表型关联预测方面,谭好江等^[9]提出基于多组学数据融合的个性化随机游走算法(Individual Multiple Random Walks, iMRW),为不同重要程度的节点分配差异化游走步长,并基于高斯相互作用核的相似性,预测多源基因-表型关联信息 ...

2023

0.0

... 在药物-药物相互作用预测研究中,饶晓洁等^[10]提出基于多层次注意力机制和消息传递神经网络的DDI(Drug-Drug Interaction)预测方法,建模分子中不同原子的贡献,结合基于分子质心的位置编码,实现从原子级到分子级的层次化特征学习,提升药物间相互作用预测的准确性 ...

2020

0.0

... Long等^[11]提出GCNMDA(Graph Convolutional Network Based Framework for Predicting Human Microbe-Drug Associations),通过图卷积网络预测微生物与药物的相互作用 ...

... 1)GCNMDA^[11] ...

2020

0.0

... Long等^[12]提出EGATMDA,以图注意力网络为基础,利用分层注意力机制,从多个生物网络中学习节点嵌入,进行微生物-药物关联预测 ...

2021

0.0

... 随后,Long等^[13]提出HNERMDA(Heterogeneous Network Embedding Re-presentation Framework for Microbe-Drug Association Prediction),基于异构网络嵌入表示,利用metapath-2vec和双分网络推荐算法,实现微生物与药物之间低维嵌入表示的学习 ...

2023

0.0

... Tian等^[14]提出SCSMDA(Struc-ture-Enhanced Contrastive Learning and Self-Paced Negative Sampling Strategy for Microbe-Drug Associa-tion Predictions),采用结构增强的对比学习和自适应优化负采样策略,预测微生物与药物之间的潜在关联 ...

... 为此,本文提出对抗性负采样方法,通过对抗训练生成具有挑战性的负样本,并借鉴自适应负采样策略^[14]进行选择性采样 ...

... 2)SCSMDA^[14] ...

2022

0.0

... Deng等^[15]提出Graph2MDA,学习节点和整个图的潜在表示,再使用变分图自动编码器预测微生物与药物之间的关联 ...

2017

0.0

... 基于文献[16]方法和SIMCOMP^[17]分别构建微生物功能相似性矩阵MF和药物结构相似性矩阵DS ...

2010

0.0

... 基于文献[16]方法和SIMCOMP^[17]分别构建微生物功能相似性矩阵MF和药物结构相似性矩阵DS ...

2011

0.0

... 为了解决部分微生物或药物缺乏完整功能或结构信息的问题,本文引入高斯核函数^[18] ...

... '_d表示预先设定的原始带宽参数,与Van Laarhoven等^[18]提出的高斯核函数一致,本文中将原始带宽参数同样设为1,以保持核函数的尺度不变性 ...

2021

0.0

... 元路径作为一种语义丰富的异质图模式,能有效捕捉药物与微生物之间多层次、多角度的拓扑信息^[19] ...

2022

0.0

... 针对这些挑战,本文提出变换器门控图网络(Transformer-Gated Graph Network, TGGN),融合Transformer^[20]的全局建模能力与门控图神经网络的局部特征提取机制,在保持结构敏感性的同时实现高效的长程依赖建模 ...

2024

0.0

... TGGN采用分层混合架构,包含可学习的特征投影、基于图结构的多头注意力机制、图卷积操作和GRU(Gated Recurrent Unit)^[21]门控更新 ...

0.0

... 同时,考虑特征传递的衰减问题,结合层正则化^[22],设计层次化残差连接,提取生物网络的拓扑信息: ...

2010

0.0

... HGRL采用Glorot初始化方案^[23]、Adam(Adap-tive Moment Estimation)优化器^[24]和余弦退火学习率调度器^[25]进行训练 ...

2023

0.0

... HGRL采用Glorot初始化方案^[23]、Adam(Adap-tive Moment Estimation)优化器^[24]和余弦退火学习率调度器^[25]进行训练 ...

2024

0.0

... HGRL采用Glorot初始化方案^[23]、Adam(Adap-tive Moment Estimation)优化器^[24]和余弦退火学习率调度器^[25]进行训练 ...

0.0

... 3)GCN(Graph Convolutional Network)^[26] ...

0.0

... 4)GAT(Graph Attention Networks)^[27] ...

2021

0.0

... 5)LAGCN(Layer Attention Graph Convolutional Network)^[28] ...

2022

0.0

... 6)GSAMDA^[29] ...

2021

0.0

... 7)MMGCN(Multi-view Multichannel Attention Graph Convolutional Network)^[30] ...

2023

0.0

... 8)GACNNMDA^[31] ...