在量子理论中, 每个系统可表示为希尔伯特空间中的单位列向量, 在本文中称为状态空间中的状态向量.在不引入观测的前提下, 一个系统可能同时处于多个状态, 由状态空间中多个单位正交的基态向量叠加表示:

$ \boldsymbol{u}=\sum_{i=0}^{m} \alpha_{i} \boldsymbol{e}_{i}$

其中:e_i表示基态向量, 第i个位置为1, 其它位置为0; α _i表示第i个基态向量的概率振幅, 满足

$ \sum_{i=0}^{m}\left|\alpha_{i}\right|^{2}=1$

系统的外积运算表示为uu^T, 内积运算表示为u^Tu, 符合向量的运算规则.给定

u=[1 2]^T, v=[3 4]^T,

张量乘积表示为

u$\otimes$v= 12$\otimes$ 34= 3648.

密度矩阵是描述量子系统的另一种方式, 非对角元素可表示基态向量之间的相互作用.如果当前量子系统处在第i个系统φ _i中的概率为p_i, 密度矩阵定义为

ρ = ∑i=0np_iφ _i φTi,

则密度矩阵是迹为1的正半定算子.当tr(ρ ²)=1时, 密度矩阵表示纯态, 当tr(ρ ²)< 1时, 密度矩阵表示混合态.

量子复合系统是指由两个及以上子系统组成的孤立系统, 复合系统的状态向量和状态空间分别表示为子系统的状态向量和状态空间的张量积形式.对于由n个子系统组成的复合系统Ψ , 通过状态空间H_i中的状态向量ψ _i表示第i个子系统, 则复合系统Ψ 的状态向量为:

Ψ =ψ ₁$\otimes$ψ ₂$\otimes$…$\otimes$ψ _n.

为了减少计算量, 通常采用RDM描述某一子系统的状态, 这一过程与复合系统的张量积过程相反, 通过偏迹运算获得.对于由子系统A和子系统B构成的复合系统ρ ^AB, 子系统A的RDM为:

ρ ^A=tr_B(ρ ^AB)=tr_B(a₁ aT2$\otimes$b₁ bT2)=a₁ aT2tr(b₁ bT2),

其中, tr_B(· )表示子系统B的偏迹操作, a₁、a₂表示子系统A的基态向量, b₁、b₂表示子系统B的基态向量.

本节采用量子测量分析文本匹配的一般过程, 推导语义组合带来的类量子干涉项^[15].首先, 神经网络模型中文本匹配的本质是求解匹配概率.对于匹配文本q和查询文本s, 过程可形式化为条件概率P(q|s).

其次, 将文本匹配形式化为二维实数希尔伯特空间中对系统的观测过程.如图1(a)所示, 向量q表示匹配文本的状态向量, 向量s表示查询文本的状态向量, 由两个基态语义向量w₁和w₂的叠加态表示:

s=α w₁+β w₂,

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 基于投影测量的文本匹配过程Fig.1 Text matching process based on projection measurement

其中α 和β 分别表示w₁和w₂的概率幅度.概率幅度的平方对应单词叠加态塌缩在某一语义基态向量的概率.

若将匹配文本看作测量算子, 可通过观测匹配文本对查询文本的测量结果, 即条件概率值P(q|s)获得塌缩的过程.通过投影测量形式化这一过程, 推导语义组合过程中的量子干涉项信息.

由匹配文本q构成的投影算子通过密度矩阵

M_q=qq^T

进行表示.组成查询文本s的单词w₁和w₂塌缩在匹配文本q上的概率可通过投影测量获得, 即

$ \begin{array}{l} P\left(\boldsymbol{q} \mid \boldsymbol{w}_{1}\right)=\boldsymbol{w}_{1}^{\mathrm{T}} \boldsymbol{M}_{q} \boldsymbol{w}_{1}, \\ P\left(\boldsymbol{q} \mid \boldsymbol{w}_{2}\right)=\boldsymbol{w}_{2}^{\mathrm{T}} \boldsymbol{M}_{q} \boldsymbol{w}_{2} . \end{array}$

如果按照经典概率的方式将词组语义看作单词语义进行机械叠加, 不考虑单词组合过程中的语义组合变化(即单词之间相互独立), 文本匹配过程可表示为

$ \begin{aligned} P(\boldsymbol{q} \mid \boldsymbol{s})= & \alpha^{2} P\left(\boldsymbol{q} \mid \boldsymbol{w}_{1}\right)+\beta^{2} P\left(\boldsymbol{q} \mid \boldsymbol{w}_{2}\right)= \\ & \alpha^{2} \boldsymbol{w}_{1}^{\mathrm{T}} \boldsymbol{M}_{q} \boldsymbol{w}_{1}+\beta^{2} \boldsymbol{w}_{2}^{\mathrm{T}} \boldsymbol{M}_{q} \boldsymbol{w}_{2}, \end{aligned}$(1)

其中α ²和β ²对应于经典概率中发生s的前提下发生w₁和w₂的事件概率.这一条件概率在图1(a)中可表示为将两部分投影结果直接相加.

这种机械性的组合方式忽视由于单词组合带来的语义干涉信息.在测量过程中, 需将词组看作一个整体, 并直接将查询文本s投影到待匹配文本q上(参考图1(b)的投影过程), 则式(1)优化为

$ \begin{array}{l} P^{\prime}(\boldsymbol{q} \mid \boldsymbol{s})= \\ P\left(\boldsymbol{q} \mid \alpha \boldsymbol{w}_{1}+\beta \boldsymbol{w}_{2}\right)= \\ \left(\alpha \boldsymbol{w}_{1}+\beta \boldsymbol{w}_{2}\right)^{\mathrm{T}} \boldsymbol{M}_{q}\left(\alpha \boldsymbol{w}_{1}+\beta \boldsymbol{w}_{2}\right)= \\ \alpha^{2} \boldsymbol{w}_{1}^{\mathrm{T}} \boldsymbol{M}_{q} \boldsymbol{w}_{1}+\beta^{2} \boldsymbol{w}_{2}^{\mathrm{T}} \boldsymbol{M}_{q} \boldsymbol{w}_{2}+\alpha \beta\left(\boldsymbol{w}_{1}^{\mathrm{T}} \boldsymbol{M}_{q} \boldsymbol{w}_{2}+\boldsymbol{w}_{2}^{\mathrm{T}} \boldsymbol{M}_{q} \boldsymbol{w}_{1}\right)= \\ P(\boldsymbol{q} \mid \boldsymbol{s})+\underbrace{2 \alpha \beta \boldsymbol{w}_{1}^{\mathrm{T}} \boldsymbol{M}_{q} \boldsymbol{w}_{2}}_{\text {干濒 }} . \end{array}$

相比式(1), 上式中推导出类量子干涉项, 表达从单词到词组的过程中由于不同维度语义交互带来的额外类量子干涉信息.这一信息会对文本匹配过程中的语义匹配产生影响, 需要在模型设计中充分考虑这类语义信息.

在量子概率空间下进行语义建模具有一些独特的优势和必要性.首先, 量子概率空间是经典概率的推广, 希尔伯特空间下常通过量子叠加和量子纠缠等操作基本远离词语和文本之间的复杂语义关系, 可更全面表达词语之间的相互关联, 提高模型对语义信息的理解能力.其次, 量子干涉理论提供一种新的方式以处理特征之间的相互作用, 有助于提高模型的泛化能力和鲁棒性, 可解决随着任务语义复杂性增强, 建模空间指数级增大的问题.此外, 量子概率空间还具有并行计算的能力, 可加速模型的训练和推理过程.上述特性有望为自然语言处理领域带来新的突破和进展.

模型输入文本匹配对, 由预先训练的标准化词嵌入进行归一化处理, 然后进行表示.查询文本表示为向量序列S={s₁, s₂, …, s_m}, s_i表示S的第i项词向量; 匹配文本表示为向量序列Q={q₁, q₂, …, q_n}, q_j表示Q的第j项词向量.

在文本匹配中, 将词组作为复合系统, 并将复合系统分成两组量子子系统A和B, 状态向量表示为ψ _a和ψ _b, 则复合系统可表示为

ψ =ψ _a$\otimes$ψ _b,

其中, $\otimes$表示张量积运算, 用于建模单词嵌入不同维度间的相互作用, 并捕获所有的语义组合特征.

从词组出发对单词的概率分布进行建模, 技术上通过偏迹操作获得RDM.首先, 以查询文本S为例, 讨论基于两个词形成量子复合系统的情况, 在此基础上可获得1阶RDM(1-Order RDM, 1-RDM).为了求解子系统A的RDM, 需要在复合系统中进行偏迹操作:

ρA1=tr_B(ψ ψ ^T)=tr_B(s_a sTa$\otimes$s_b sTb)=s_a sTatr(s_b sTb),

其中, s_a表示子系统A的基态向量, s_b表示子系统B的基态向量, tr(s_b sTb)=1. 此时RDM退化为系统的密度矩阵, 量子干涉发生在单词s_a的语义交互中.

其次, 讨论由三个词组成的量子复合系统.前两个单词视为量子子系统A, 第三个单词视为量子子系统B.在这种情况下, sa1、 sa2表示子系统A的基态向量, s_b表示子系统B的基态向量, 2阶RDM(2-Order RDM, 2-RDM)表示为

ρA2=tr_B(ψ ψ ^T)=tr_B( sa1sTa2$\otimes$s_b sTb)= sa1sTa2tr(s_b sTb),

其中 sa1sTa2表示两个基态向量的干涉信息项.进一步分析, 假设

$ \begin{array}{l} \boldsymbol{s}_{a_{1}}=\left\{\omega_{1}, \omega_{2}, \cdots, \omega_{d}\right\}, \\ \boldsymbol{s}_{a_{2}}=\left\{\tau_{1}, \tau_{2}, \cdots, \tau_{d}\right\}, \end{array}$

将 sa1sTa2进一步展开, 得

$ \boldsymbol{S}_{a_{1}} \boldsymbol{s}_{a_{2}}^{\mathrm{T}}=\left[\begin{array}{cccc} \omega_{1} \tau_{1} & \omega_{1} \tau_{2} & \cdots & \omega_{1} \tau_{d} \\ \omega_{2} \tau_{1} & \omega_{2} \tau_{2} & \cdots & \omega_{2} \tau_{d} \\ \vdots & \vdots & & \vdots \\ \omega_{d} \tau_{1} & \omega_{d} \tau_{2} & \cdots & \omega_{d} \tau_{d} \end{array}\right]$

其中, 主对角元素ω _iτ _j(i=j)表示经典概率中的语义相似度匹配特征(余弦相似度), 非主对角元素ω _iτ _j(i≠ j)表示不同单词语义基态向量中的干涉项信息.

计算1-RDM和2-RDM的和作为最终的RDM:

ρ _S= ρS1+ ρS2= ∑i=1msaisTai+ ∑i=1m-1∑j=2msaisTaj.(2)

通过式(2), 可获得查询文本和匹配文本的RDM表示ρ _S和ρ _Q.

将ρ _S和ρ _Q相乘, 得到一个二维联合概率表示, 用于构造全局特征文本对之间的信息.计算过程如下:

$ \begin{aligned} \boldsymbol{G}_{S Q}= & \boldsymbol{\rho}_{S} \cdot \boldsymbol{\rho}_{Q}= \\ & \left(\sum_{i=1}^{m} \boldsymbol{s}_{a_{i}} \boldsymbol{s}_{a_{i}}^{\mathrm{T}}+\sum_{i=1}^{m-1} \sum_{j=2}^{m} \boldsymbol{s}_{a_{i}} \boldsymbol{s}_{a_{j}}^{\mathrm{T}}\right) \cdot \\ & \left(\sum_{i=1}^{n} \boldsymbol{q}_{a_{i}} \boldsymbol{q}_{a_{i}}^{\mathrm{T}}+\sum_{i=1}^{n-1} \sum_{j=2}^{n} \boldsymbol{q}_{a_{i}} \boldsymbol{q}_{a_{j}}^{\mathrm{T}}\right)= \\ & \boldsymbol{E}_{S Q}+\boldsymbol{I}_{S}+\boldsymbol{I}_{Q}+\boldsymbol{I}_{S Q}, \end{aligned}$

其中· 表示矩阵的乘法运算.E_SQ表示当前主流匹配模型中使用的经典理论的相似度计算评分:

$\boldsymbol{E}_{S Q}=\left(\sum_{i=1}^{m} \boldsymbol{s}_{a_{i}} \boldsymbol{s}_{a_{i}}^{\mathrm{T}}\right) \cdot\left(\sum_{i=1}^{n} \boldsymbol{q}_{a_{i}} \boldsymbol{q}_{a_{i}}^{\mathrm{T}}\right) .$

I_S表示查询文本s内部的语义干涉信息与匹配单词经典特征信息的交互:

$\boldsymbol{I}_{S}=\left(\sum_{i=1}^{m-1} \sum_{j=2}^{m} \boldsymbol{s}_{a_{i}} \boldsymbol{S}_{a_{j}}^{\mathrm{T}}\right) \cdot\left(\sum_{i=1}^{n} \boldsymbol{q}_{a_{i}} \boldsymbol{q}_{a_{i}}^{\mathrm{T}}\right)$

I_Q表示匹配文本q内部的语义干涉信息与查询单词经典特征信息的交互:

$\boldsymbol{I}_{Q}=\left(\sum_{i=1}^{m} \boldsymbol{s}_{a_{i}} \boldsymbol{s}_{a_{i}}^{\mathrm{T}}\right) \cdot\left(\sum_{i=1}^{n-1} \sum_{j=2}^{n} \boldsymbol{q}_{a_{i}} \boldsymbol{q}_{a_{j}}^{\mathrm{T}}\right)$

I_SQ表示查询文本s和匹配文本q之间语义干涉信息的交互特征:

$\boldsymbol{I}_{S Q}=\left(\sum_{i=1}^{m-1} \sum_{j=2}^{m} \boldsymbol{s}_{a_{i}} \boldsymbol{s}_{a_{j}}^{\mathrm{T}}\right) \cdot\left(\sum_{i=1}^{n-1} \sum_{j=2}^{n} \boldsymbol{q}_{a_{i}} \boldsymbol{q}_{a_{j}}^{\mathrm{T}}\right) .$

提取问答匹配对的联合概率分布特征会失去原始问句和答句的局部匹配特征, 因此本文提出双重特征表示融合全局特征和局部特征信息.

首先, 基于RDM提取局部特征表示.对于ρ _S和ρ _Q, 提取对角元素信息并和原始特征拼接, 得到查询文本和匹配文本的局部特征表示FL_S和FL_Q:

FL_S=[st_S; D_S; ρ _S], FL_Q=[st_Q; D_Q; ρ _Q], (3)

其中, st_{(· )}表示计算密度矩阵的对角线元素的总和, D_{(· )}表示主对角线元素组成的向量, [; ]表示拼接操作.

其次, 利用二维CNN提取全局特征信息G_SQ, 通过池化层得到最终的全局特征向量FG.最后, 结合全局特征向量和局部特征向量, 得到双重特征向量:

F=[FG; FL_S; FL_Q].

在上式中, 由于局部特征提取的主对角线维度与CNN处理后的特征维度并不相同, 因此选择拼接操作融合局部特征与全局特征.

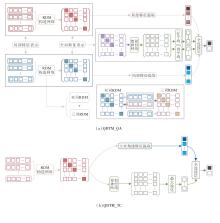
本文提出分别应用于问答任务和文本任务的模型架构(QDTM_QA和QDTM_TC), 核心均为RDM表示, 模型架构如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 QDTM架构图Fig.2 Architecture of QDTM

QDTM_QA在相关性预测模块中, 由式(3)得到的双重特征表示通过全连接层获得二进制标签(0或1)的最终预测匹配得分:

P_i=Softmax(W_i× F_i+b_i),

其中W_i和b_i表示全连接层对应的可学习权值和偏差.在模型训练过程中, 使用交叉熵损失函数训练模型.

文本任务由于只包含单文本, 因此QDTM_TC只包含两个部分:基于RDM的局部特征表示模块, 双重特征提取和融合模块 (如图2(b)所示).由于联合表示模块的缺失, 模型的局部匹配信息来自文本RDM的主对角线之和st_S与对角线元素组成的向量D_S.全局语义信息来自于原始的RDM.最后, 得到的特征为:

F=[st_S; D_S; ρ _S].

QDTM_TC的相关性预测与QDTM_QA相同.

对于文本任务, 本文选择MR^[19]、CR^[20]、SUBJ(https://huggingface.co/datasets/SetFit/subj)、MP-QA^[21]、SST^[22]、TREC^[23]这6个文本分类数据集, 涉及主题分类、问题分类和电影评述等任务.

对于问答任务, 选择WikiQA^[24]、TrecQA^[25]数据集.WikiQA数据集是一个开放域的问答数据集, 数据全部来自微软的查询日志和维基百科.TrecQA数据集上数据均来自TREC-8至TREC-13中的问答数据集.

对于文本任务, 选择如下对比模型.

1)神经网络文本匹配模型:Transformer^[3]、FastText^[25]、文献[26]模型.

2)量子启发的语言模型:NNQLM-I^[8]、NNQLM-II^[8]、C-NNQLM-I(Complex-Valued Neural Network Based QLM-I)^[13]、C-NNQLM-II(Complex-Valued Neu-ral Network Based QLM-II)^[13]、QLM-EE(QLM with Entanglement Embedding)^[27].

对于问答任务, 选择如下对比模型.

1)神经网络问答模型: 文献[28]模型、BLSTM(Bidirectional Long-Short Term Memory)^[29].

2)量子启发语言模型:QLM^[7]、QLM_T(QLM_Trace)^[7]、NNQLM-I^[8]、NNQLM-II^[8]、QINM^[12]、QLM-EE^[27].

本文的模型均基于Python语言、Tensorflow 2.4.0框架构建, 部署于NVIDIA Tesla P40.实验中所有模型都使用50维全局向量词嵌入初始化输入部分, 在训练过程中单词嵌入保持不变, 以保证模型性能的稳定性.

在模型的全局特征提取层, 均使用一层二维卷积层与一层池化层的模型结构.在卷积层, 设置3个不同的卷积尺寸与个数; 在池化层, 选取最大池化方法.将3个卷积核的结果通过最大池化层后, 拼接并输入最后的全连接层.全连接层通过softmax获得最后的预测得分, 并通过argmax获得最后的文本分类结果.

在具体实验中, 设置L2正则化参数为0.000 1, 其余实验参数设置详见表1.

表1

Table 1

表1(Table 1)

表1 实验参数设置 Table 1 Experimental parameter settings 参数 文本分类 问答 MR CR SUBJ MPQA SST TREC TrecQA WikiQA 学习率 0.001 0.001 0.001 0.01 0.001 0.01 0.01 0.02 批量规模 150 128 140 10 140 10 100 140 滤波器数量 80 60 60 60 100 60 120 120 规律器规模 {5, 10, 40} 40

表1 实验参数设置 Table 1 Experimental parameter settings

各模型在文本任务上的准确率对比如表2所示, 表中黑体数字表示最优值.除了QLM-EE以外, 其它实验结果均采用原论文数据, 所有结果均在30维词向量的基础上获得.由表可见, QDTM_TC的性能在MR、CR、SUBJ、MPQA数据集上均超越Fast-Text、文献[26]模型和Transformer等神经网络文本匹配模型, 这表明RDM可有效建模文本中的类量子语义干涉信息, 在局部特征提取方面的性能高于注意力机制、CNN等神经网络提取模块.相比量子语言模型NNQLM-I和NNQLM-II, QDTM_TC性能更优, 这表明本文提出的RDM模块可提取不同语义维度的量子干涉信息, 这种交互而非叠加的语义特征捕获方式优于基于密度矩阵特征提取模块.

表2

Table 2

表2(Table 2)

表2 面向文本任务的QDTM在文本分类数据集上的准确率对比 Table 2 Accuracy comparison of text task-oriented QDTM on text classification datasets 模型 MR CR SUBJ MPQA SST TREC FastText 0.726 0.752 0.867 0.828 0.773 0.736 文献[26]模型 0.769 0.801 0.907 0.845 0.789 0.880 Transformer 0.731 0.762 0.859 0.722 0.753 0.820 NNQLM-I 0.629 0.755 0.866 0.829 0.757 0.732 NNQLM-II 0.748 0.778 0.836 0.832 0.783 0.872 C-NNQLM-I-diag 0.739 0.781 0.896 0.863 0.758 0.887 C-NNQLM-I-flag 0.769 0.794 0.901 0.855 0.802 0.909 C-NNQLM-II-Word 0.751 0.778 0.889 0.847 0.801 0.912 C-NNQLM-II-Dim 0.774 0.799 0.891 0.853 0.781 0.930 QLM-EE 0.717 0.785 0.896 0.809 0.774 0.843 QDTM_TC 0.775 0.801 0.912 0.848 0.795 0.897

表2 面向文本任务的QDTM在文本分类数据集上的准确率对比 Table 2 Accuracy comparison of text task-oriented QDTM on text classification datasets

各模型在问答任务上的平均精度均值(Mean Average Precision, MAP)和平均倒数排名(Mean Reciprocal Rank, MRR)对比如表3所示, 表中黑体数字表示最优值.由表可见, QDTM_QA的性能在WikiQA、TrecQA数据集上都优于经典的神经网络匹配模型(文献[28]模型和BLSTM), 这表明量子启发文本表示和联合概率表示对于问答任务是有效的.在WikiQA数据集上, QDTM_QA性能也优于量子启发语言模型QLM、QLM_T、NNQLM-I、NNQLM-II, 这表明本文提出的双重特征提取模块可改进模型对于局部特征提取不足的问题, 比基于密度矩阵的文本表示更有效.其次, 在TrecQA数据集上, QDTM_QA未达到最佳性能, 劣于NNQLM-II, 这表明由于数据集的差异, 基于RDM的文本表示可能存在冗余信息, 导致实验结果不佳, 有待后续优化.

表3

Table 3

表3(Table 3)

表3 面向问答任务的QDTM在问答数据集上的性能对比 Table 3 Performance comparison of QDTM for Q& A task on Q& A datasets 模型 WikiQA TrecQA MAP MRR MAP MRR 文献[28]模型 0.619 0.628 0.548 0.644 BLSTM 0.608 0.633 0.564 0.630 QLM 0.511 0.515 0.678 0.727 QLM_T 0.511 0.515 0.668 0.728 NNQLM-I 0.546 0.557 0.679 0.753 NNQLM-II 0.650 0.659 0.759 0.825 QLM-EE 0.696 0.700 0.771 0.854 QDTM_QA 0.777 0.804 0.703 0.807

表3 面向问答任务的QDTM在问答数据集上的性能对比 Table 3 Performance comparison of QDTM for Q& A task on Q& A datasets

为了验证模型中RDM文本表示和双重特征架构的有效性, 基于问答任务进行QDTM_QA的消融实验.定义QDTM_QA_D(QDTM_QA with Density Matrix)表示QDTM_QA使用密度矩阵的文本表示方法, QDTM_QA_G(QDTM_QA with Global Fea-ture)表示QDTM_QA只使用全局特征表示, 忽略局部特征表示.

在问答任务上的消融实验结果如表4所示, 表中黑体数字表示最优值.从结果可以看出, QDTM_QA性能高于QDTM_QA_G, 表明在问答任务中应同时考虑全局特征和局部特征, 确保模型性能.同时, QDTM_QA性能也高于QDTM_QA_D, RDM的文本表示方法可全面捕获问答任务中语义交互信息, 有效建模类量子干涉项.QDTM_QA_G和QDTM_QA_D在WikiQA数据集上的性能下降快于在TrecQA数据集上, 说明在小规模数据集上更依赖有效、多层次的语义特征捕获方式.

表4

Table 4

表4(Table 4)

表4 各模型在问答数据集上的消融实验结果 Table 4 Results of ablation experiments of different models on QA datasets 模型 WikiQA TrecQA MAP MRR MAP MRR QDTM_QA 0.777 0.804 0.703 0.807 QDTM_QA_D 0.631 0.651 0.595 0.612 QDTM_QA_G 0.414 0.495 0.587 0.542

表4 各模型在问答数据集上的消融实验结果 Table 4 Results of ablation experiments of different models on QA datasets