刘树栋,博士,副教授,主要研究方向为智能检索与推荐.E-mail:liushudong@zuel.edu.cn.
作者简介:

李丽颖,硕士研究生,主要研究方向为数据挖掘、推荐系统.E-mail:1246926983@qq.com.

陈 旭,博士,讲师,主要研究方向为机器学习、自然语言处理.E-mail:chenxu@whu.edu.cn.
将用户社会关系引入用户-商品评分数据中,构建用户-商品异构关系图,可缓解传统推荐系统面临的数据稀疏性和冷启动问题.但是,由于用户间社会关系的复杂性,聚合不一致的社会邻居可能会降低推荐性能.针对上述问题,文中提出基于自监督三重训练和聚合一致邻居的社会化推荐模型(Social Recommendation Based on Self-Supervised Tri-Training and Consistent Neighbor Aggregation, SR-STCNA).首先,在用户-商品评分数据的基础上,引入用户-用户间的社交关系,在用户-商品异构图中构建多种关系.使用超图表示用户和用户、用户和商品之间的关系.使用自监督三重训练,从未标记的数据中学习用户表示,充分挖掘用户-用户和用户-商品间存在的复杂连接关系.然后,通过用户-商品异构图上的节点一致性得分和关系自注意力,在用户和商品表示学习过程中聚合一致邻居,增强用户和商品嵌入表示能力,提高推荐性能.在CiaoDVD、FilmTrust、Last.fm、Yelp数据集上的实验表明,SR-STCNA性能较优.
LIU Shudong, Ph.D., associate professor. His research interests include intelligent retrieval and reco-mmendation.
About Author:
LI Liying, Master student. Her research interests include data mining and recommender systems.
CHEN Xu, Ph.D., lecturer. His research interests include machine learning and natural language processing.
Integrating user social relationships into user-item rating data to construct a heterogeneous user-item graph can alleviate data sparsity and cold start in traditional recommender systems. However, due to the complexity of user social relationships, aggregating inconsistent neighbors may degrade the recommendation performance. To address this issue, a social recommendation model based on self-supervised tri-training and consistent neighbor aggregation(SR-STCNA) is proposed. Firstly, on the basis of user-item rating data, social relationships among users are introduced and diverse relations within the heterogeneous user-item graph are established. The relationships between users as well as between users and items are presented by a hypergraph. Self-supervised tri-training is employed to learn users' representations from unlabeled data and uncover the complex connectivity between user-user and user-item interactions. Then, the consistent neighbors of users and items are aggregated in the process of their representation learning by the node consistency score and relationship self-attention on the user-item heterogeneous graph. Consequently, the representation ability of users and items is enhanced, thereby improving the recommendation performance. Finally, the experimental results on CiaoDVD, FilmTrust, Last.fm and Yelp datasets validate the superiority of SR-STCNA.
自从矩阵分解技术应用于推荐系统[1], 以协同过滤技术为代表的推荐系统得到快速发展.矩阵分解技术将用户-商品交互数据组织成矩阵形式, 以矩阵乘法为基础, 学习用户和商品的潜在特征, 将以近邻算法为基础的协同过滤中产生相似交互行为的用户具有相似偏好这一启发性假设推广到协同矩阵分解中, 从用户-商品交互的高维稀疏矩阵学习低维稠密用户和商品潜在特征向量, 为推荐系统线下学习和线上部署提供技术手段, 也为以Deep Cro- ssing[2]、NCF(Neural Network-Based Collaborative Filtering)[3]、Wide & Deep[4]为代表的深度神经网络推荐模型提供技术参考.
在推荐系统应用场景中, 与用户有交互记录的商品数往往仅占总商品数极少一部分, 从而使用户-商品交互矩阵中大部分元素为0, 故以矩阵分解为代表的推荐系统首先面临数据稀疏性问题.
此外, 当用户与商品交互次数极少, 甚至是新加入用户时, 用户-商品交互矩阵中不会存在此用户的交互数据, 也不能学习此用户的潜在特征向量, 那么推荐系统无法分析此类用户, 故称此现象为冷启动问题.
为了解决上述问题, 研究人员通过收集用户的上下文信息(如年龄、性别、职业、位置等)[5]或通过多轮对话收集用户偏好信息[6], 用于构建用户偏好模型, 以内容匹配方式为用户提供推荐.
此外, 研究人员还将用户的社交关系信息引入协同过滤等推荐算法中, 产生社会化推荐方法[7], 将产生相似交互行为的用户具有相似偏好的启发性假设进一步推广至具有社交连接的用户可能有相似个性化偏好, 挖掘社会关系对用户偏好影响, 辅助实现社会化协同推荐[8].
Jiang 等[9] 从个体偏好和人际影响两个角度构建用户-用户偏好影响矩阵, 并融入概率矩阵分解中, 从而提高推荐性能.Tang 等[10]计算用户社会关系中直接连接的强弱性和间接连接的弱依赖性, 加权融入矩阵分解过程中.Yu 等[11]提出IF-BPR(Ba-yesian Personalized Ranking with Implicit Friends), 通过元路径计算用户间的相似性, 为用户寻找兴趣相似的隐含好友.
近年来, 随着深度神经网络和图神经网络的快速发展, 社会化推荐研究逐渐转向基于神经网络的社会化推荐模型.与基于矩阵分解的社会化推荐模型[9, 10]和基于异构图的社会化推荐模型[11]一样, 将用户间的社会关系信息融入用户/商品表示学习成为基于神经网络的社会化推荐研究的重要方向之一.
Chen 等[12]提出EATNN(Efficient Adaptive Trans- fer Neural Network), 利用注意力机制, 自适应地为用户学习交互商品与社交关系间的互动作用.Wu 等[13] 提出CNSR(Collaborative Neural Social Recommendation), 通过社交关系表示模块和协同推荐模型的联合学习, 增强社交关系对协同推荐性能的影响力.Fan 等[14]提出GraphRec, 将用户-商品交互图和用户-用户社交关系图构建成一个异构图, 利用用户间的偏好相似性确定它们之间连接的强弱.
Song 等[15]提出DiffNetLG(Diffusion Neural Net- work with Local and Global Implicit Influence), 考虑用户间非直接关联的局部隐含偏好影响因素和在用户间相互共享商品的全局隐式影响因素.Huang 等[16]提出KCGN(Knowledge-Aware Coupled Graph Neural Network), 将商品间内在的知识引入图神经网络社会化推荐模型中, 计算全局图结构的互信息, 学习用户和商品间的高阶关系.Liu 等[17]提出HOSR(High-Order Social Recommender), 在社交网络中利用递归传播表示机制获取用户的高阶邻居.
为了扩大偏好一致好友对社会化推荐的影响, Yu 等[18]提出RSGAN(Reliable Social Recommenda-tion Framework Based on Generative Adversarial Net-work).Quan 等[19]提出GDMSR(Graph Denoising Me-thod for Social Recommendation), 使用自修正课程学习机制和自适应降噪策略, 删除社交关系中无共同偏好的好友关系, 学习更加鲁棒的用户表示.
将用户间的社交关系学习融入用户-商品互动图中, 以图神经网络中的节点聚合表示为基础, 学习对推荐预测更有价值的用户嵌入和商品嵌入, 现已成为基于图神经网络社会化推荐模型研究重点之一.
已有研究方法大都从如下两个方面展开研究.
1)从用户-商品异构图中学习多阶连接, 使图神经网络节点表示学习过程能聚合更多节点信息[20, 21, 22].
2)在用户社交关系图中判别两位用户是否是兴趣偏好一致的强连接, 节点表示学习过程中尽量聚合强连接节点, 剔除兴趣偏好不一致的弱连接[23, 24].
第1类方法虽然能在节点表示学习过程中聚合多阶近邻, 但有可能聚合兴趣偏好不一致的弱连接, 降低节点表示的预测性能.
第2类方法虽然在节点表示学习过程中剔除兴趣偏好不一致的弱连接, 但现有方法也仅从可信赖好友生成[18, 25]或子图对比[19, 23, 26]等角度进行, 未充分利用用户-商品异构网络中的复杂连接与聚合一致邻居.
针对上述问题, 本文提出基于自监督三重训练和聚合一致邻居的社会化推荐模型(Social Recommendation Based on Self-Supervised Tri-Training and Consistent Neighbor Aggregation, SR-STCNA).将用户-商品异构信息网络表示成超图, 获取用户-商品及用户-用户间更复杂的超图连接关系, 定义兴趣偏好一致近邻, 并在超图节点表示学习过程中聚合一致近邻.
具体地, 首先引入用户间的社交关系, 为了表示用户-商品异构图上的多种关系, 使用超图表示用户和用户、用户和商品之间的关系.使用自监督三重训练, 从未标记的数据中学习用户表示, 充分挖掘用户-用户和用户-商品间存在的复杂连接关系.然后, 通过用户-商品异构图上的节点一致性得分和关系自注意力, 在用户和商品表示学习过程中聚合一致邻居, 增强用户和商品嵌入表示能力, 提高推荐性能.在4个公开数据集上的实验表明SR-STCNA性能较优.
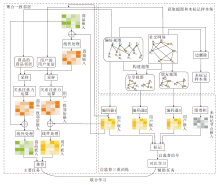
本文提出基于自监督三重训练和聚合一致邻居的社会化推荐模型(SR-STCNA), 整体框架如图1所示.
SR-STCNA由如下3个阶段构成:
1)构建超图和未标记样本集;
2)自监督三重训练;
3)聚合一致邻居.
阶段1包括构建超图和对原始图进行扰动, 其中构建超图是为了生成用户与用户之间多样化的社会关系表示(3位用户之间均为好友关系或2位用户是好友关系并且对相同商品有评分).对原始图进行扰动是为了生成未标记的数据集.
阶段2是自监督三重训练, 通过编码器1获取原始的用户-商品交互图上的用户嵌入和商品嵌入, 通过编码器2和编码器3获取在阶段1得到的2个超图上的用户嵌入, 通过图卷积获得在阶段1得到的未标记数据集上的未标记节点嵌入.利用3个编码器中的其中两个对第3个编码器进行未标记数据集的邻居预测, 如果2个编码器都将未标记节点标记为邻居, 就将这个未标记节点放入第3个编码器的邻居集合中.利用获得的每个编码器的邻居集实现自监督对比学习, 即最大化邻居之间的一致性并最小化非邻居之间的一致性.
阶段3是聚合一致邻居, 利用在阶段2得到的用户-商品交互图上的用户嵌入和商品嵌入进行线性处理, 得到查询嵌入.利用查询嵌入分别对用户邻居和商品邻居进行采样, 并计算邻居的采样权重, 获得用户一致邻居嵌入和商品一致邻居嵌入.最后将获得的邻居嵌入分别与用户嵌入和商品嵌入进行加权聚合, 获得最终的用户嵌入和商品嵌入, 完成推荐任务.
构建超图是为了将普通用户-商品交互和用户-用户社交关系图转换成超图, 使用户和用户之间的关系具有更多样化、更详细的表示和描述.未标记样本集通过边扰动获得损坏的图, 以获得未标记样本集.
1.1.1 构建超图
假设用户集
$ U=\left\{u_{1}, u_{2}, \cdots, u_{m}\right\}, $
m为用户数量, 商品集
$ V=\left\{v_{1}, v_{2}, \cdots, v_{n}\right\}, |v|=n, $
用户-商品交互矩阵
$ \boldsymbol{R}=\left[r_{i j}\right]_{m \times n} \in \mathbf{R}^{m \times n}, $
若用户ui和商品vj有评分, rij=1, 否则rij=0.用户间社交关系矩阵S∈ Rm× m, 如果用户ui、uj有社交关系, sij=1并且sji=1, 否则, sij=0并且sji=0.
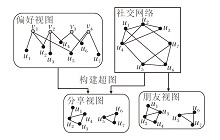
首先将用户-商品交互关系构建成用户-商品交互图Gr, 把用户间社交关系表示成用户-用户社交图Gs, 即图2中的偏好视图和社交网络, 偏好视图后续用于用户、商品初始嵌入学习和自监督未标记样本集的构建.从Gr和Gs中可得到2类三角关系:3位用户彼此均有社交关系(如图2中的u1, u2和u4)和2位用户既有社交关系也对同一件商品有评分(如图2中的u1, u2和v1).基于协同过滤和社会化推荐下启发性假设[7], 如果2位具有社交关系的用户拥有共同的朋友或共同感兴趣的交互商品, 他们就更有可能具有更亲密的关系.因此将上述两个三角关系作为超图.
可通过矩阵运算的方式提取上述两种类型的三角关系.两类三角关系表示的超图中的用户邻接矩阵表示为Enf∈ Rm× m和Ens∈ Rm× m.
首先, 计算用户与其他用户之间存在的三元未闭合的社会关系数量, 三元未闭合的社会关系表示3位用户两两配对, 其中有2对用户一定存在社会关系, 但第3对不一定存在社会关系.三元未闭合的社会关系矩阵:
$ \begin{array}{l} \boldsymbol{E n}_{f}^{\prime}=\boldsymbol{S} \boldsymbol{S}=\left[s_{i j}^{\prime}\right], \\ s_{i j}^{\prime}=\sum_{k=1}^{m} s_{i k} s_{k j}=s_{i 1} s_{1 j}+s_{i 2} s_{2 j}+\cdots+s_{i m} s_{m j}, \end{array}$ (1)
其中, sik表示用户-用户社交矩阵S中的元素, 若sik=1, 表示用户ui、uk有社交关系, 若sik=0, 表示用户ui、uk无社交关系, skj解释同上.
由式(1)可得, 若sikskj=1表示用户ui、uk、uj在社会关系中存在一个三元未闭合的社交关系, 即用户ui、uk有社会关系并且用户uk、uj有社会关系, 但是不能确定用户ui、uj是否存在社会关系.通过En'f可找到任意2位用户ui、uj间的三元未闭合的社会关系个数s'ij.
3位用户彼此均有社交关系的用户邻接矩阵为:
$ \boldsymbol{E n}_{f}=\boldsymbol{E n}_{f}^{\prime} \odot \boldsymbol{S}, $ (2)
其中$\odot $表示矩阵对应元素相乘.Enf可确定用户ui、uj是否可组成三元闭合的社会关系, 即由式(1)计算出的用户ui、uj中的三元未闭合的社会关系个数s'ij.只需要确定ui、uj是否存在社会关系, 如果存在社会关系(sij=1), 那么用户ui、uj的三元闭合的社会关系个数为s'ij, 如果不存在社会关系(sij=0), 用户ui、uj不存在三元闭合的社会关系.
同理, 计算用户与其他用户之间存在的三元未闭合的商品评分关系.三元未闭合的商品评分关系表示在2位用户和1个商品之间, 2位用户对该商品有评分关系, 但是不能确定2位用户之间是否存在社会关系.三元未闭合的商品评分关系矩阵为:
$ \begin{array}{l} \boldsymbol{E n}_{s}^{\prime}=\boldsymbol{R R}^{\mathrm{T}}=\left[r_{i j}^{\prime}\right], \\ r_{i j}^{\prime}=\sum_{k=1}^{n} r_{i k} r_{j k}=r_{i 1} r_{j 1}+r_{i 2} r_{j 2}+\cdots+r_{i n} r_{j n}, \end{array}$
其中, rik表示用户-商品交互矩阵R中的元素, 如果rik=1, 表示用户ui对商品vk有评分, 如果rik=0, 表示用户ui对商品vk无评分, rjk解释同上.
由式(2)可得, 若rikrjk=1, 表示用户ui、商品vk和用户uj在商品评分上存在一个三元未闭合的商品评分关系, 即用户ui对商品vk有评分关系并且用户uj对商品vk有评分关系, 但是不能确定用户ui、uj是否存在社会关系.由En's可找到用户ui、uj中的三元未闭合的商品评分关系个数r'ij.
2位用户既有社交关系也对同一件商品有评分的用户的邻接矩阵为:
$ \boldsymbol{E n}_{s}=\boldsymbol{E n}_{s}^{\prime} \odot \boldsymbol{S}, $ (3)
其中$\odot $表示矩阵对应元素相乘.
r'ijsij表示用户ui、uj中的三元闭合的商品评分关系个数, 即用户ui、uj存在社会关系的前提下, 对相同商品有评分的商品评分关系个数.
将Enf和Ens看作S和R的补充, 通过构建超图拥有3个从不同角度描述用户偏好的视图, 分别表示用户本身的商品偏好、用户和好友有共同好友、用户和好友有共同偏好的商品, 将3个视图分别命名为用户-商品偏好视图、三角社交关系朋友视图和三角关系朋友分享商品视图, 分别表示为Gr、Enf和Ens.
1.1.2 构建未标记样本集
图自监督学习任务需要以边扰动或节点掩藏等方式[27, 28]构建数据增强集.这里以概率ρ 扰动用户分享视图和朋友视图, 创建扰动图:
$ \widetilde{G}=\left(N_{r} \cup N_{s}, P_{\rho} \otimes\left(E_{r} \cup E_{s}\right)\right), $ (4)
其中, ρ 表示边扰动率, 是可调超参数, Nr表示Gr的全部节点, Ns表示Gs的全部节点, Er表示Gr的全部边, Es表示Gs的全部边, $ P \in\{0, 1\}^{\left|E_{r} \cup E_{s}\right|}, P_{\rho} \otimes\left(E_{r} \cup\right.\left.E_{s}\right)$表示以概率ρ 随机丢失Gr和Gs中的边.在扰动图中学习到的用户节点嵌入称作未标记样本嵌入.
自监督三重训练主要步骤如下.
1)利用编码器在偏好视图(用户-商品交互图)上学习用户嵌入和商品嵌入, 以及在上述构建的两个超图上学习用户嵌入和未标记样本集的用户嵌入.
2)层组合.组合多层节点表示, 获得最终用户嵌入.
3)构建自监督信号, 利用自编码器在3个视图上学习到用户嵌入, 根据三重训练的思想[26], 如果其它2个视图均将未标记样本预测为正样本, 将该未标记样本置为第3个视图的正样本, 否则视为负样本.
4)对比学习策略, 对于由上述获取的预测正样本和预测负样本, 最大化与正样本之间的相似性并最小化与负样本之间的相似性, 从而构建三重训练自监督信号.
1.2.1 编码器
使用用户-商品偏好视图和构建的2个超图, 构建3个编码器.采用轻量级图卷积神经网络(Light Graph Convolution Network, LightGCN)[29]作为编码器的基本结构.
首先, 初始化可训练的用户嵌入EU∈ Rm× d和商品嵌入EV∈ Rn× d, 其中, eu∈ EU表示任一用户ui的初始嵌入, ev∈ EV表示任一商品vk的初始嵌入, d表示嵌入向量维数.
从偏好视图Gr上学习偏好视图上第l层用户ui的嵌入:
$ \begin{aligned} \boldsymbol{z}_{u}^{r(l)}= & \sum_{v \in N_{u}^{r}}\left(\frac{1}{\sqrt{\left|N_{u}^{r}\right|} \sqrt{\left|N_{v}^{r}\right|}} \boldsymbol{z}_{v}^{(l-1)}\right)= \\ & \sum_{v \in N_{u}^{r}}\left(\left(\sqrt{\sum_{h=1}^{n} I\left(r_{u h}\right)} \sqrt{\sum_{h=1}^{m} I\left(r_{h v}\right)}\right)^{-1} \boldsymbol{z}_{v}^{(l-1)}\right), \end{aligned}$
商品vk的嵌入:
$ \begin{aligned} \boldsymbol{z}_{v}^{(l)}= & \sum_{u \in N_{v}^{r}}\left(\frac{1}{\sqrt{\left|N_{v}^{r}\right|} \sqrt{\left|N_{u}^{r}\right|}} \boldsymbol{z}_{u}^{r(l-1)}\right)= \\ & \sum_{u \in N_{v}^{r}}\left(\left(\sqrt{\sum_{h=1}^{m} I\left(r_{h v}\right)} \sqrt{\sum_{h=1}^{n} I\left(r_{u h}\right)}\right)^{-1} \boldsymbol{z}_{u}^{r(l-1)}\right) . \end{aligned}$
其中:N
从三角社交关系朋友视图Enf上学习朋友视图上第l层的用户ui的嵌入:
$\begin{array}{l} z_{u}^{f(l)}= \\ \sum_{j \in N_{u}^{f}}\left(\frac{1}{\sqrt{\left|N_{u}^{f}\right|} \sqrt{\left|N_{j}^{f}\right|}} z_{j}^{f(l-1)}\right)= \\ \sum_{j \in N_{u}^{f}}\left(\left(\sqrt{\sum_{h=1}^{m} I\left(s_{u h}^{\prime} s_{u h}\right)} \sqrt{\sum_{h=1}^{m} I\left(s_{h j}^{\prime} s_{h j}\right)}\right)^{-1} z_{j}^{f(l-1)}\right) . \end{array}$
其中:
在式(2)中分别表示三角社交关系朋友视图Enf的邻接矩阵中用户ui(uh)和uh(uj)之间是否存在关系;
从三角关系朋友分享商品视图Ens上学习分享视图上第l层的用户ui的嵌入:
$\begin{array}{l} z_{u}^{s(l)}= \\ \sum_{j \in N_{u}^{s}}\left(\frac{1}{\sqrt{\left|N_{u}^{s}\right|} \sqrt{\left|N_{j}^{s}\right|}} z_{j}^{s(l-1)}\right)= \\ \quad \sum_{j \in N_{u}^{s}}\left(\left(\sqrt{\sum_{h=1}^{m} I\left(r_{u h}^{\prime} s_{u h}\right)} \sqrt{\sum_{h=1}^{m} I\left(r_{h j}^{\prime} s_{h j}\right)}\right)^{-1} z_{j}^{s(l-1)}\right) . \end{array}$
其中:
在三角社交关系朋友视图Enf和三角关系朋友分享商品视图Ens上只负责通过图卷积学习用户嵌入, 并给出预测正样本集, 而在偏好视图Gr上也承担生成推荐的任务, 从而学习用户嵌入和商品嵌入, 并且也需要从扰动图$\widetilde{G}$中学习未标记样本的嵌入.在扰动图$\widetilde{G}$中学习到的用户节点嵌入被用作未标记样本嵌入, 因此从扰动图$\widetilde{G}$中学习第l层的用户ui的嵌入:
$\begin{array}{l} \widetilde{z}_{u}^{(l)}=\sum_{g \in N_{u}^{\tilde{R}}}\left(\left(\sqrt{\left|N_{u}^{\tilde{R}}\right|} \sqrt{\left|N_{g}^{\tilde{R}}\right|}\right)^{-1} \tilde{z}_{g}^{(l-1)}\right)+ \\ \sum_{j \in N_{u}^{\tilde{S}}}\left(\left(\sqrt{\left|N_{u}^{\tilde{S}}\right|} \sqrt{\left|N_{j}^{\tilde{S}}\right|}\right)^{-1} \tilde{z}_{j}^{(l-1)}\right)= \\ \sum_{g \in N_{u}^{R}}\left(\left(\sqrt{\sum_{h=1}^{n} I\left(\tilde{r}_{u h}\right)} \sqrt{\sum_{h=1}^{m} I\left(\tilde{r}_{h g}\right)}\right)^{-1} \tilde{z}_{g}^{(l-1)}\right)+ \\ \sum_{j \in N_{u}^{\tilde{S}}}\left(\left(\sqrt{\sum_{h=1}^{m} I\left(\tilde{s}_{u h}\right)} \sqrt{\sum_{h=1}^{m} I\left(\tilde{s}_{h j}\right)}\right)^{-1} \tilde{\boldsymbol{z}}_{j}^{(l-1)}, \right. \\ \end{array}$
第l层的商品vk的嵌入:
$\begin{array}{l} \left.\tilde{\boldsymbol{z}}_{v}^{(l)}=\sum_{t \in N_{v}^{\tilde{R}}}\left(\sqrt{\left|N_{v}^{\tilde{R}}\right|} \sqrt{\left|N_{t}^{\tilde{R}}\right|}\right)^{-1} \tilde{\boldsymbol{z}}_{t}^{(l-1)}\right)= \\ \sum_{t \in N_{v}^{R}}\left(\left(\sqrt{\sum_{h=1}^{m} I\left(\tilde{r}_{h v}\right)} \sqrt{\sum_{h=1}^{n} I\left(\tilde{r}_{t h}\right)}\right)^{-1} \tilde{z}_{t}^{(l-1)}\right) . \\ \end{array}$
其中:$ \tilde{r}_{u h}$表示扰动的用户-商品交互矩阵$\widetilde{R}$中的元素, 如果$ \tilde{r}_{u h}$=1, 用户ui和商品vh在扰动的用户-商品交互图中有关系, 否则$ \tilde{r}_{u h}$=0, 用户ui和商品vh在扰动的用户-商品交互图中没有关系; $\tilde{s}_{h j}$表示扰动的用户-用户社交矩阵$\widetilde{S}$中的元素, 如果$\tilde{s}_{h j}$=1, 用户uh、uj在扰动的用户-用户社交图中有关系, 否则$\tilde{s}_{h j}$= 0, 用户uh、uj在扰动的用户-用户社交图中无关系; $ N_{v}^{\tilde{R}}$表示在扰动的用户-商品交互图上与用户ui有关系的商品集, $ N_{v}^{\tilde{R}}$表示在扰动的用户-商品交互图上与商品vk有关系的用户集, $ N_{u}^{\tilde{S}}\left(N_{j}^{\tilde{S}}\right)$ 表示在扰动的用户-用户社交图上与用户ui(uj)有关系的用户集; $ \widetilde{\boldsymbol{z}}_{u}^{(0)}$表示用户ui的初始嵌入$\boldsymbol{e}_{u} ; \widetilde{z}_{v}^{(0)}$表示商品vk的初始嵌入ev.
由式(4)可知, 扰动图的邻接矩阵由两个部分组成:扰动的用户-商品交互矩阵
1.2.2 层组合
经过l层图卷积处理后, 对每层的嵌入进行组合, 构建最终的节点嵌入.在偏好视图Gr、三角关系朋友分享商品视图Ens和三角社交关系朋友视图Enf上, 经过l层后的用户ui的嵌入为:
$z_{u}^{t}=\sum_{h=0}^{l}\left(\frac{1}{h+1} z_{u}^{t(h)}\right), $ (5)
偏好视图Gr的商品vk的嵌入为:
$z_{v}=\sum_{h=0}^{l}\left(\frac{1}{h+1} z_{v}^{(h)}\right)$ (6)
其中:t∈ {r, s, f}, 表示3个视图中的其中一个;
$\widetilde{z}_{u}=\sum_{h=0}^{l}\left(\frac{1}{h+1} \widetilde{z}_{u}^{(h)}\right) .$
将学习得到的所有未标记样本ui的嵌入$\tilde{z}_{u}$进行拼接, 得到全部未标记样本的嵌入$\widetilde{\boldsymbol{Z}} \in \mathbf{R}^{m \times d}$.
1.2.3 构建自监督信号
通过在3个视图上执行图卷积, 编码器学习3组用户嵌入.由于每个视图都反映用户偏好的不同方面, 因此可从另外两个视图中寻求自监督信号.给定用户ui, 使用来自其它2个视图的用户嵌入, 预测未标记样本集中为正的样本, 即只有在其它2个视图上都一致将未标记样本标记为正样本, 未标记样本才能在本视图上被标记为正样本, 否则视为负样本.
将各个视图上用户ui的嵌入与未标记样本集上每个节点的嵌入进行余弦相似性计算, 再对所有结果进行Softmax归一化, 得到未标记样本集中每个节点是用户ui的正样本的概率.未标记样本集上的节点是三角关系朋友分享商品视图Ens、三角社交关系朋友视图Enf和偏好视图Gr中用户ui利用自身嵌入在本视图上的正样本的预测概率
$\begin{aligned} \bar{y}_{u+}^{s}= & \operatorname{Softmax}\left(\phi\left(\widetilde{\boldsymbol{Z}}, z_{u}^{s}\right)\right)= \\ & \operatorname{Softmax}\left(\left[\phi\left(\widetilde{z}_{1}, z_{u}^{s}\right), \phi\left(\widetilde{z}_{2}, z_{u}^{s}\right), \cdots, \phi\left(\widetilde{z}_{m}, z_{u}^{s}\right)\right]\right), \\ \bar{y}_{u+}^{f}= & \operatorname{Softmax}\left(\phi\left(\widetilde{\boldsymbol{Z}}, z_{u}^{f}\right)\right)= \\ & \operatorname{Softmax}\left(\left[\phi\left(\widetilde{z}_{1}, z_{u}^{f}\right), \phi\left(\widetilde{z}_{2}, z_{u}^{f}\right), \cdots, \phi\left(\widetilde{z}_{m}, z_{u}^{f}\right)\right]\right), \\ \bar{y}_{u+}^{r}= & \operatorname{Softmax}\left(\phi\left(\widetilde{\boldsymbol{Z}}, z_{u}^{r}\right)\right)= \\ & \operatorname{Softmax}\left(\left[\phi\left(\widetilde{z}_{1}, z_{u}^{r}\right), \phi\left(\widetilde{z}_{2}, z_{u}^{r}\right), \cdots, \phi\left(\widetilde{z}_{m}, z_{u}^{r}\right)\right]\right) . \end{aligned}$
其中:ϕ 表示余弦相似性;
进一步地, 利用另外2个视图上的预测概率, 计算每个未标记样本集上节点是三角关系朋友分享商品视图Ens、三角社交关系朋友视图Enf和偏好视图Gr中用户ui的正样本的预测概率
$\begin{array}{l} y_{u+}^{r}=\frac{1}{2}\left(\bar{y}_{u+}^{s}+\bar{y}_{u+}^{f}\right), \\ y_{u+}^{s}=\frac{1}{2}\left(\bar{y}_{u+}^{r}+\bar{y}_{u+}^{f}\right), \\ y_{u+}^{f}=\frac{1}{2}\left(\bar{y}_{u+}^{s}+\bar{y}_{u+}^{r}\right) . \end{array}$
由此获得在偏好视图Gr上top-K个预测的正样本集
$P_{u+}^{r}=\operatorname{top}-K\left(y_{u+}^{r}\right), $
在三角关系朋友分享商品视图Ens上top-K个预测的正样本集
$P_{u+}^{s}=\operatorname{top}-K\left(y_{u+}^{s}\right), $
在三角社交关系朋友视图Enf上top-K个预测的正样本集
$P_{u+}^{f}=\operatorname{top}-K\left(y_{u+}^{f}\right) .$
1.2.4 对比学习策略
由于把在扰动图$\widetilde{G}$中学习到的用户节点嵌入用作未标记样本嵌入, 因此预测负样本集为全部用户集合中不属于预测正样本集的部分, 表示为{U-
$\begin{array}{l} L_{\text {ssl }}= \\ -\sum_{t \in\{r, s, f\}} \log _{2}\left(\frac{\sum_{p \in P_{u+}^{t}} \psi\left(z_{u}^{t}, \widetilde{z}_{p}\right)}{\sum_{p \in P_{u+}^{t}} \psi\left(z_{u}^{t}, \widetilde{z}_{p}\right)+\sum_{\left.j \in \mid U-P_{u+}^{t}\right\}} \psi\left(z_{u}^{t}, \widetilde{z}_{j}\right)}\right), \end{array}$
其中
$\psi\left(z_{u}^{t}, \widetilde{z}_{p}\right)=\exp \left(\frac{1}{\tau} \phi\left(z_{u}^{t}, \widetilde{z}_{p}\right)\right), $
ϕ (· )∶ Rd× Rd|→ R表示余弦相似性函数, τ 表示自监督损失温度系数.
社会不一致问题是指2位用户之间虽然存在社交连接, 但对商品兴趣偏好并不一致.聚合不一致的社会好友可能会使图神经网络学习到有损推荐性能的节点表示[18, 23].本文利用用户-商品偏好视图中学习的用户嵌入和商品嵌入构建一个查询层.然后利用查询层对邻居进行采样, 获得与节点一致的邻居.最后再将筛选得到的与节点一致的邻居嵌入与节点嵌入进行加权聚合, 以此聚合一致邻居嵌入.
1)嵌入层.连接用户-商品偏好视图和用户社交网络, 构成一个用户-商品异构网络, 利用式(5)和式(6)拼接偏好视图上学习到的用户嵌入
例如, 假设数据集上有5个评级值, 即评分在{1, 2, 3, 4, 5}中, 因此节点之间有6种关系, 即除了用户-用户的社交关系, 还有5种基于评分值的用户-商品评分关系.
2)查询层.针对每对(ui, vk), 利用在偏好视图上的用户初始嵌入eu和商品初始嵌入ev的拼接进行映射, 构建查询嵌入:
$\boldsymbol{q}_{u, v}=\operatorname{Relu}\left(\boldsymbol{W}_{q}^{\mathrm{T}}\left(\boldsymbol{e}_{u} \| \boldsymbol{e}_{v}\right)\right), $
其中, ‖ 表示向量拼接操作, Wq∈ R2d× d表示参数矩阵.
3)邻居采样.为了聚合偏好一致邻居, 可采用邻居采样方法选择那些一致的邻居.查询层中节点zx(用户或商品)的第l层邻居节点
$\operatorname{prob}_{n}^{(l)}=\left(\boldsymbol{z}_{n}^{(l)}, \boldsymbol{q}_{x, n}\right)=\frac{c\left(\boldsymbol{z}_{n}^{(l)}, \boldsymbol{q}_{x, n}\right)}{\sum_{j \in N b_{x}} c\left(\boldsymbol{z}_{j}^{(l)}, \boldsymbol{q}_{x, j}\right)}, $
其中, Nbx表示节点x的第l层邻居节点集, c(
$c\left(\boldsymbol{z}_{n}^{(l)}, \boldsymbol{q}_{x, n}\right)=\exp \left(-\left\|\boldsymbol{q}_{x, n}-\boldsymbol{z}_{n}^{(l)}\right\|_{2}\right) .$
被采样邻居的数量与邻居总数呈正比, 比值设置为γ ∈ [0, 1], 为实验超参数.
每个近邻节点的被采样概率反映它被选中的可能性, 采样概率越高, 选中的可能性越大.
4)关系自注意力.进一步地, 为了区分近邻节点之间不同连接关系, 采用一个关系自注意力模块, 学习这些采样节点的重要性权重.关系自注意力为节点zx的第l层邻居节点
$a_{n}^{(l)}=\frac{\exp \left(\boldsymbol{W}_{a}^{\mathrm{T}}\left(\boldsymbol{z}_{n}^{(l)} \| \boldsymbol{z}_{g}^{(x, n)}\right)\right)}{\sum_{j=1}^{J} \exp \left(\boldsymbol{W}_{a}^{\mathrm{T}}\left(\boldsymbol{z}_{j}^{(l)} \| \boldsymbol{z}_{g}^{(x, j)}\right)\right)}, $
其中, J表示节点zx在第l层采样的邻居总数, Wa表示关系注意力权重,
5)聚合一致邻居.节点zx的第l层聚合一致邻居的节点:
$\boldsymbol{z}_{x}^{(l)}=\operatorname{ReLU}\left(\boldsymbol{W}^{\mathrm{T}}\left(\boldsymbol{z}_{x}^{(l-1)} \| \sum_{j=1}^{J} a_{j}^{(l)} \boldsymbol{z}_{j}^{(l)}\right)\right), $
其中W表示权重矩阵.通过上式可学习到用户和商品聚合一致邻居后最后一层L的嵌入表示
$\hat{r}_{u v}=z_{u}^{(L)} \cdot z_{v}^{(L)} .$
模型学习目标包括两个任务:推荐主任务和基于自监督三重训练的对比学习任务.以贝叶斯个性化排序[31]为基础构建推荐主任务优化目标:
$L_{\text {main }}=\sum_{\substack{v_{k} \in N_{u}^{r} \\ v_{j} \notin N_{u}^{r}}}\left(-\log _{2}\left(\operatorname{sigmoid}\left(\hat{r}_{u v}-\hat{r}_{u j}\right)\right)\right), $
其中
$L=L_{\text {main }}+\beta L_{\mathrm{ssl}}, $
其中, β 表示一个超参数, 用来控制自监督三重训练的强度.
为了验证SR-STCNA性能, 选择CiaoDVD、FilmTrust、Last.fm、Yelp这4个公开社会化推荐的数据集, 数据集的具体信息如表1所示.
| 表1 数据集统计信息 Table 1 Datasets statistics |
本文选取如下2类5个对比模型.
1)图神经网络基本框架模型LightGCN[29].
LightGCN是基于图神经网络的通用推荐模型, 利用用户-商品的接近度学习节点表示并生成推荐.
2)社会化推荐模型.
(1)GDMSR[19].基于图降噪的社会化推荐方法, 为了降低社交网络中的噪声影响, 提出基于自纠正课程学习的自适应降噪策略, 获得更可信的社交近邻.
(2)MHCN(Multi-channel Hypergraph Convolutio-nal Network)[21].基于多通道超图卷积网络的社会化推荐方法, 对用户与超边之间的复杂相关性进行建模.
(3)SEPT(SElf-Supervised Tri-Training)[26].自监督三重训练的社会化推荐方法, 利用超边对用户进行建模, 同时利用自监督三重训练训练模型, 但未聚合一致邻居.
(4)DiffNet++[32].基于增强型扩散网络的社会化推荐方法, 利用扩散模型将用户社交影响力和兴趣偏好融合在一个框架中.
所有的对比模型都按照原论文或源码中的最佳参数设置进行实验分析.SR-STCNA中失活率设置为0.2, Adam(Adaptive Moment Estimation)优化器的学习率设置为0.001, 批尺寸设置为512.在FilmTrust数据集上设置边扰动概率ρ =0.2, 其它3个数据集上设置ρ =0.6.在CiaoDVD数据集上设置邻居采样比γ =0.8, 在FilmTrust数据集上γ =0.4, 在Last.fm数据集上γ =0.4, 在Yelp数据集上γ =0.6.在CiaoDVD、Yelp数据集上设置top-K正样本数为40, 在FilmTrust数据集上top-K正样本数为50, 在Last.fm数据集上top-K正样本数为15.
评价指标选择社会化推荐对比模型[19, 21, 26, 32]中常采用的精确度(Precision)、召回率(Recall)和归一化折损累积增益(Normalized Discounted Cumulative Gain, NDCG), 并截取top-10 作为推荐结果, 因此3个评价指标依次为Precision@10、Recall@10和NDCG@10.
为了更好地学习用户节点和商品节点的嵌入表示, 在模型中使用l层网络聚合节点的高阶邻居节点信息.现探究网络层数l对模型性能的影响.l表示节点所能聚合到的节点信息的范围.在实验中, 为了验证l对模型性能的影响, 在4个数据集上定义l=1, 2, 3, 4, 求得的指标值如表2所示, 表中黑体数字表示最优值.
| 表2 网络层数l对模型性能的影响 Table 2 Effect of network layer l on model performance |
从表2可看出, 当图神经网络层数l=2时, 指标值最高, 而l=3, 4时, Precision@10、Recall@10和NDCG@10的值也会随之减小.通过对二阶邻居节点的信息进行聚合, 可获得更优性能, 但如果将更高阶的邻居节点的信息聚合在一起, 就会在中心节点聚合到更多冗余信息, 导致性能变得不理想.这完全符合目前主流图神经网络框架[29, 33]一般不会聚合超过3层近邻的作法.
用户节点和商品节点的嵌入维数d是模型中一个重要的超参数.为了验证d对性能的影响, 在4个数据集上选取不同d值进行实验, 结果如表3所示, 表中黑体数字表示最优值.
| 表3 节点嵌入维数d对模型性能的影响 Table 3 Effect of node embedding dimension d on model performance |
从表3可看出, 在CiaoDVD数据集上最佳d=110, FilmTrust数据集上最佳d=50, Last.fm数据集上最佳d=100, Yelp数据集上最佳d=90.节点嵌入维数d对于表示节点信息至关重要, 过小将导致节点的信息表示不充分, 过大会导致过拟合问题.
自监督训练强度β 是模型总体学习目标函数L中的超参数, 用于控制自监督训练在联合学习中的影响强度.为了验证β 对性能的影响, 定义β =0, 0.001, 0.002, 0.005, 0.01, 0.02, 0.05, 0.1, 0.5, 在4个数据集上进行实验, 结果如表4所示, 表中黑体数字表示最优值.从表4可看出, CiaoDVD数据集上最佳β =0.002, FilmTrust数据集上最佳β =0.005, Last.fm数据集上最佳β =0.002, Yelp数据集上最佳β =0.001.较小的自监督训练强度β 可使模型得到较优性能, 而较大β 会使得模型性能大幅降低.
| 表4 自监督训练强度β 对模型性能的影响 Table 4 Effect of self-supervised training Intensity β on model performance |
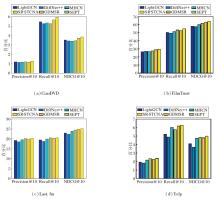
SR-STCNA与5个对比模型在4个数据集上的指标值对比如图3所示.由图可看出, SR-STCNA在4个数据集上总体性能最佳, 这充分说明SR-STCNA在推荐任务上的有效性.在5个对比模型中, DiffNet++性能最差, 这可能与模型参数较多难于训练有关.相比LightGCN, MHCN、SEPT和GDMSR表现更优, 表明将用户社交关系融入图神经网络中对推荐性能是有帮助的.相比MHCN, SEPT和SR-STCNA表现更优, 表明利用自监督三重训练可显著提升推荐性能.
此外, 相比SEPT和GDMSR, SR-STCNA在4个数据集上的Precision@10、Recall@10和NDCG@10值都略优.相比SEPT, SR-STCNA和GDMSR在3个评价指标上都更优, 说明在节点表示学习过程中, 考虑聚合兴趣一致近邻而删除不可信近邻是提高模型推荐性能的有效途径, 这并非实验扰动所致.相比GDMSR, SR-STCNA也有一定优势, 说明在社会化推荐模型聚合兴趣一致邻居比寻找更可信近邻更有效, 原因可能在于很难为所有用户制定统一的信任好友评价指标.
在SR-STCNA中, 构建两个超图视图和一个用户-商品偏好视图, 利用三重训练挖掘自监督信号.本节消融每个视图以研究视图对模型性能的贡献程度.当仅使用偏好视图和一个增强视图时, 模型变为自监督联合训练, 即两个视图相互判断另一个视图的预测正样本集; 当仅使用用户-商品偏好视图时, 模型变为自训练, 即利用自身预测自己的正样本集.使用SS w/o ENS表示仅有用户-商品偏好视图和三角社交关系朋友视图、无三角关系朋友分享商品视图的模型, 使用SS w/o ENF表示仅有用户-商品偏好视图和三角关系朋友分享商品视图、无三角社交关系朋友视图的模型, 使用SS w/o ENS & ENF表示仅有用户-商品偏好视图的模型.因为Light-GCN是SR-STCNA中的基本编码器, 因此将Light-GCN也进行消融实验, 验证所有视图对模型的贡献, 即表示无自监督三重训练模块的模型.为了充分验证聚合一致邻居的有效性, 使用SS w/o CAN 表示没有聚合一致邻居模块的模型.
各模型的具体消融实验结果如表5所示, 表中黑体数字表示最优值.由表可看出, 在4个数据集上使用不同视图的结果均优于LightGCN.在Last.fm、Yelp数据集上, 利用3个视图进行自监督三重训练的效果最优, 因此所有视图都有贡献.在FilmTrust数据集上, 利用2个视图进行自监督联合训练的效果最优.在CiaoDVD数据集上, 利用用户-商品偏好视图进行自训练的效果最优.由FilmTrust、CiaoDVD数据集上消融实验结果可得出, 在模型中利用1个用户-商品偏好视图进行自训练和利用2个视图进行自监督联合训练, 也可以生成较好的自监督信号.增加视图的数量可带来更好地性能提升(如在Last.fm、Yelp数据集上), 但是这个观点并不适用于所有数据集(如在FilmTrust、CiaoDVD数据集上).
| 表5 各模型的消融实验结果 Table 5 Ablation experiment results of different models |
在CiaoDVD数据集上, 三角社交关系朋友视图及三角关系朋友分享商品视图对推荐性能的提升无帮助作用, 可能是在数据集上, 用户数/评分数和用户数/社交关系较少, 用户和商品以及用户和用户的交互数量过少, 导致2个增强视图中包含的信息过少且不准确, 对推荐产生负面影响.在FilmTrust数据集上, 三角关系朋友分享商品视图对推荐性能的提升起到帮助作用, 但是, 三角社交关系朋友视图对推荐性能的提升无帮助作用, 可能是在数据集上, 用户数/社交关系较少, 用户和用户的交互数量过少, 导致三角社交关系朋友视图中包含的信息过少且不准确, 对推荐结果产生负面影响.此外, 未考虑聚合一致邻居的模型SS w/o CAN 在4个数据集上的消融结果表明, 聚合一致邻居确实能提高SR-STCNA的性能.
近年来, 图神经网络逐渐成为机器学习理论与应用领域备受广泛关注核心技术之一, 在多元异构数据间关系表示方面具有强大的学习能力, 而以用户-项目交互数据为主要研究对象的推荐系统, 引入用户上下文信息, 容易构建多种多样的图结构, 如用户-用户社交关系和用户-商品交互数据构成的用户-商品异构图, 用户/商品文本语义信息和用户-商品交互数据构成用户-商品语义图.将图表示学习引入推荐系统中可取得较优的应用效果, 为有效缓解由于新加入用户或用户与商品互动频次较低而导致的冷启动和数据稀疏性问题提供新的思路.本文提出基于自监督三重训练和聚合一致邻居的社会化推荐模型(SR-STCNA), 为了表示用户-商品异构图上的多种关系, 使用超图表示用户和用户、用户和商品之间的关系, 使用自监督三重训练, 从未标记的数据中学习用户表示, 充分挖掘用户-用户和用户-商品间存在的复杂连接关系.然后, 通过用户-商品异构图上的节点一致性得分和关系自注意力, 为用户和商品表示学习过程中聚合一致的邻居, 增强用户和商品嵌入表示能力, 提高社会化推荐性能.在4个公开数据集上的实验表明, SR-STCNA性能较优.本研究对于缓解推荐系统中常见的冷启动和数据稀疏性问题是一次有意义的尝试.将生成式深度学习模型应用到社会化推荐系统中将是今后的研究内容之一.
本文责任编委 林鸿飞
Recommended by Associate Editor LIN Hongfei
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|