引用本文
代星月, 叶海良, 曹飞龙. 社交影响增强的图神经网络推荐方法. 模式识别与人工智能, 2024,37(3): 221-230
DAI Xingyue, YE Hailiang, CAO Feilong. Graph Neural Network Recommendation Based on Enhanced Social Influence. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2024,37(3): 221-230.  
Doi: 10.16451/j.cnki.issn1003-6059.202403003
Permissions
Copyright©2024, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
社交影响增强的图神经网络推荐方法
代星月1, 叶海良1, 曹飞龙1
1.中国计量大学 理学院 应用数学系 杭州 310018
通讯作者:

曹飞龙,博士,教授,主要研究方向为深度学习、神经网络及其应用等.E-mail:icteam@163.com.

作者简介:

代星月,硕士研究生,主要研究方向为深度学习、推荐系统.E-mail:xydai199135@163.com.

叶海良,博士,讲师,主要研究方向为深度学习、图神经网络.E-mail:yhl575@163.com.

收稿日期: 2023-12-16 接受日期: 2024-03-30
资助项目: 国家自然科学基金项目(No.62176244)资助
摘要

随着在线社交平台的发展,社交推荐已成为推荐系统中的一个重要任务.然而,用户间的社交关系通常具有稀疏性,这在一定程度上限制推荐系统的性能.为此,文中提出社交影响增强的图神经网络推荐方法,旨在利用用户之间的隐式社交关系增强社交推荐的效果.首先,分析用户与物品之间的交互数据,揭示隐含的社交关系,重构用户间的社交图.在此基础上,利用互信息最大化方法,有效融合社交图的全局特征与用户的局部特征.同时,将可学习机制融入图注意力网络中,充分捕获用户和物品间的交互信息.最后,提出一种改进的贝叶斯个性化排序损失,为评分预测任务提供准确的用户特征表示和物品特征表示.在3个公开数据集上的实验表明,文中方法性能较优.

关键词: 图神经网络; 表示学习; 互信息最大化; 社交推荐
中图分类号:TP 181
Graph Neural Network Recommendation Based on Enhanced Social Influence
DAI Xingyue1, YE Hailiang1, CAO Feilong1
1. Department of Applied Mathematics, College of Sciences, China Jiliang University, Hangzhou 310018
Corresponding author:
CAO Feilong, Ph.D, professor. His research interests include deep learning, neural network and its applications.

About Author:
DAI Xingyue, Master student. Her research interests include deep learning and recommendation system.
YE Hailiang, Ph.D, lecturer. His research interests include deep learning and graph neural network.

Fund:National Natural Science Foundation of China(No.62176244)
Abstract

With the rapid development of online social platforms, social recommendation becomes a critical task in recommender systems. However, the performance of recommendation systems is limited to some extent due to the sparsity of social relationships between users. Therefore, a graph neural network recommendation method based on enhanced social influence is proposed in the paper, aiming to utilize implicit social relationships between users to enhance social recommendation. The implicit social relationships are revealed, and the social graph among users is reconstructed by analyzing interaction information between users and items. On this basis, global features of the social graph are integrated with local features of users effectively via the mutual information maximization method. A learnable mechanism is integrated into the graph attention network to fully capture the interaction information between users and items. An improved Bayesian personalized ranking loss is designed to provide more accurate user and item feature representations for the rating prediction task. Extensive experiments on three public social recommendation datasets demonstrate the superiority of the proposed method.

Key words: Graph Neural Network; Representation Learning; Mutual Information Maximization; Social Recommendation

社交推荐[1]作为推荐系统中的一个重要任务, 近年来受到学术界[2, 3]的广泛关注.其核心思想是利用用户间的社交联系[4]提高推荐系统的性能.基于同质性假设[5]和社交影响理论[6], 拥有相似兴趣的用户往往表现出相似的行为模式和评价行为, 同时用户的评价也受到其社交圈的影响.

早期的社交推荐方法主要依赖矩阵分解(Matrix Factorization, MF)技术[7].Ma等[8]提出SoRec(Social Recommendation), 分解用户-物品评分矩阵和用户-用户社交关系矩阵, 获取潜在的用户表示和物品特征表示.随后, 基于MF的变体方法不断涌现[9, 10, 11], 这些方法利用用户的社交信息约束矩阵分解过程, 得到更精准的用户嵌入和物品嵌入.Yang等[9]在MF的基础上, 提出TrustMF和TrustPMF, 融入社交邻居的信任影响, 将社交邻居的偏好作为辅助信息, 从而提升推荐的准确性.Jamali等[10]和Ma等[11]将用户的社交关系作为正则项, 约束MF的目标, 使用户的偏好更贴近其社交网络的偏好.然而, 这些基于MF的推荐方法在处理复杂关系时表现相对较弱, 可能影响推荐的准确性.

深度学习凭借强大的非线性特征学习能力, 在推荐系统中逐渐受到广泛关注, 通过学习用户和物品之间的交互关系以及社交关系, 能准确捕获用户和物品的特征表示, 提升社交推荐的性能.Wu等[12]提出DiffNet(Influence Diffusion Neural Network), 通过社交网络上的逐层信息传播过程, 递归融合邻居信息, 学习用户高阶邻居信息.Chen等[13]提出EA-TNN(Efficient Adaptive Transfer Neural Network), 利用神经网络模拟社交域和交互域之间的相互作用.Fan等[14]提出DeepSoR(Deep Neural Network Model on Social Relations for Recommendation), 利用深度神经网络学习社交关系中的非线性用户表示, 并将其与概率矩阵分解(Probabilistic MF, PMF)[15]结合.Zhao等[16]构建SMR-MNRL(Multimodal Network Re-presentation Learning for Social-Aware Movie Recommendation), 结合电影的文本信息、电影海报图像、评分和社交关系等多种模态数据进行推荐.

近年来, 图神经网络(Graph Neural Networks, GNN)因其在处理图数据方面的显著优势, 在社交推荐任务中也取得巨大成功[17].Fan等提出GraphRec(GNN Framework for Social Recommendations)[18]和GraphRec+[19], 利用社交图、用户-物品图和物品-物品图的信息, 全面学习用户和物品的特征表示.Wu等[20]提出DiffNet++, 分析社交网络中的信息传播和用户兴趣的影响, 预测用户行为.Yang等[21]提出ConsisRec, 通过区分一致的用户邻居解决社交不一致问题.Xü 等[22]提出SR-HGNN(Social Recommen-dation Framework with Hierarchical GNN), 旨在准确表达用户的语义信息.Salamat等[23]提出Hetero-GraphRec, 将物品纳入图中生成异构图, 并使用注意机制进行推荐预测.Chen等[24]提出GDSRec(Graph-Based Decentralized Collaborative Filtering for Social Recommendation), 将评分的偏差视为向量, 融入学习用户和物品表示的过程中.上述方法都可有效利用图数据, 提升评分预测[25, 26]的性能.

尽管基于GNN的推荐方法取得一定效果, 但对于社交关系较少的用户, 推荐效果受到一定限制.现有的方法[27]往往直接使用显性的社交关系进行建模, 这可能会对推荐效果产生不利影响.尤其是在用户社交联系较少时, 间接社交关系的利用显得尤为重要.即使用户之间无直接的社交联系, 也可通过识别偏好相近的用户群体以提高推荐质量.为了解决这一问题, Li等[28]提出MFC和MFC+, 将社区关系融入矩阵分解方法中, 发现隐式的社交关系.然而, 在挖掘隐式的社交关系时, 仅考虑社交信息而忽略用户的行为信息(如评分数据)可能导致无法有效提取隐式的社交关系.因此, 在社交推荐中, 综合考虑用户的社交信息和行为信息, 有效挖掘和利用潜在的社交关系显得至关重要, 这将有助于充分利用社交关系, 提高推荐的准确性.

为了解决上述挑战, 本文在Xü 等[22]工作的基础上, 提出社交影响增强的图神经网络推荐方法(GNN Recommendation Based on Enhanced Social In-fluence, GNNES), 利用用户与物品之间的评分数据, 挖掘用户的隐式社交关系.利用互信息最大化方法, 获得蕴含局部信息和全局信息的用户表示, 提升用户在社交域的表征能力.此外, 考虑到用户在交互过程中对不同物品存在偏好差异, 尝试将可学习机制融入图注意力网络, 捕捉用户对不同物品的偏好, 学习用户和物品间不同的交互关系.为了挖掘对用户和物品交互及社交关系的上下文信息, 构建改进的贝叶斯个性化排序(Bayesian Personalized Ranking, BPR)[29]损失函数, 为评分预测任务提供有效的用户特征表示和物品特征表示.

1 社交影响增强的图神经网络推荐方法

在社交推荐场景中, 本文假设用户集

U={u1, …, ui, …, uN},

物品集

V={v1, …, vj, …, vM}.

将用户和物品的评分矩阵$\boldsymbol{R}=\left(r_{i j}\right)_{N \times M}$视为用户和物品的交互图GR={U, V, Er}, 其中, rij表示为用户ui对物品vj的评分, Er表示用户和物品之间的交互关系(评分).用户社交图表示为GS, 其邻接矩阵为T.若用户uj、ui之间存在关系, tij=1, 否则tij=0.基于上述定义, 本文研究的目标是通过用户-物品交互图GR和社交图GS, 预测GR中缺失的评分值.

本文提出社交影响增强的图神经网络推荐方法(GNNES), 整体架构如图1所示.首先, 在重构社交关系图上, 利用互信息最大化的图学习模块, 融合用户在社交网络中的全局特征与局部特征.然后, 设计可学习机制的图注意力网络模块, 学习用户和物品的嵌入表示, 考虑用户和物品之间的交互关系, 为不同邻居学习差异性权重.在获得用户和物品的嵌入表示后, 通过评分预测层, 预测用户评分.最后, 设计一个改进的BPR损失函数, 探索用户-物品交互信息, 为评分预测任务提供有效的特征表示.

图1 GNNES整体架构Fig.1 Overall architecture of GNNES method

1.1 社交图的重构

分析用户对物品的评分数据, 可深入了解用户之间的隐式关系.当两位用户对同一物品表现出相似的喜好时, 表明用户之间存在潜在的社交关联.为了更准确地反映这种关系, 本文重构社交图 Gcs.在图 Gcs中, 节点表示用户, 边表示用户间存在社交关系, 边上的权重反映用户之间的相似性.本文在计算用户间的相似度时, 不仅考虑被用户i、 f共同评价的物品j, 还利用用户i对所有物品的平均评分 r-i, 相似度计算公式如下:

$ S_{i f}=\frac{\sum_{j \in I(i) \cap I(f)}\left(r_{i j}-\bar{r}_{i}\right)\left(r_{f j}-\bar{r}_{f}\right)}{\sqrt{\sum_{j \in I(i) \cap \cap(f)}\left(r_{i j}-\bar{r}_{i}\right)^{2} \sum_{j \in I(i) \cap I(f)}\left(r_{f j}-\bar{r}_{f}\right)^{2}}}, $

其中, I(i)表示与用户i交互的物品集, I(f)表示与用户f交互的物品集.为了保持与邻接矩阵范围的一致, 通过映射函数

f(Sif)=0.5(Sif+1)

将用户相似度Sif的范围从[-1, 1]映射到[0, 1].通过上述方法, 得到相似度矩阵$\boldsymbol{S}=\left(S_{i f}\right)_{N \times N}$, 可作为社交图 Gcs的邻接矩阵, 反映用户间的亲疏关系.

1.2 基于互信息最大化的图学习

在重构的社交图中学习用户节点的特征表示时, 不仅学习用户与其朋友的信息, 还需关注全局社交关系的影响.为此, 本文利用互信息最大化方法[22], 保持用户局部特征与全局社交图特征的一致性.在实现过程中, 采用one-hot编码$e_{\mathrm{s}, \mathrm{u}_{\mathrm{i}} \in\{0, 1\}^{N}}$表示用户ui初始的向量表示, 矩阵形式表示为

$ \boldsymbol{E}_{s}^{0}=\left(\boldsymbol{e}_{s, u_{i}}^{0}\right)_{N \times N} .$

进一步地, 定义消息传播层, 获得每个用户节点的嵌入表示 es, ui, 其矩阵形式表示为

$ \boldsymbol{E}_{s}=\sigma\left(\boldsymbol{D}_{s}^{-\frac{1}{2}} \boldsymbol{S} \boldsymbol{D}_{s}^{-\frac{1}{2}} \boldsymbol{E}_{s}^{0} \boldsymbol{W}_{s}\right), $

其中, σ (· )表示PReLU(Parametric Rectified Linear Unit)非线性激活函数[30], Ws∈ RN× d表示可学习参数矩阵, d表示嵌入维度, Ds表示S的度矩阵,

$ \boldsymbol{D}_{s}=\operatorname{diag}\left(D_{11}, D_{22}, \cdots, D_{N N}\right), $

对角线上元素

$ D_{i i}=\sum_{j=1}^{N} S_{i j} \text {. }$

将用户的嵌入表示 es, ui视为局部表示.为了捕捉在重构社交图上的全局特征表示, 进一步定义全局社交图的特征表示:

$ \boldsymbol{r}_{s}=\operatorname{sigmoid}\left(\frac{\sum_{i=1}^{N} \boldsymbol{e}_{s, u_{i}} D_{i i}}{\sum_{i=1}^{N} \sum_{i=1}^{N} S_{i j}}\right)$

在获得用户的嵌入表示 es, ui和全局图表示rs后, 采用双线性函数作为判别器D(· ), 计算用户的局部表示属于全局图表示的概率分数, 具体定义为

$ D\left(\boldsymbol{e}_{s, u_{i}}, \boldsymbol{r}_{s}\right)=\boldsymbol{e}_{s, u_{i}}^{\mathrm{T}} \boldsymbol{W}_{1} \boldsymbol{r}_{s}, $

其中W1∈ Rd× d表示可学习的变换矩阵.正样本是用户更新后的嵌入表示 es, ui, 而负样本$e_{s, u_{i}}^{n}$是通过对初始用户向量表示$e_{s, u_{i}}^{0}$进行随机打乱而生成的.

通过最小化交叉熵损失优化判别器, 能准确区分正、负样本用户局部-全局特征对, 具体表示为

$ \begin{aligned} L_{\mathrm{MI}}= & -\frac{1}{N_{\mathrm{pos}}+N_{\text {neg }}}\left(\sum_{i=1}^{N_{\mathrm{pos}}} \ln \perp\left(\boldsymbol{e}_{s, u_{i}}, \boldsymbol{r}_{s}\right)+\right. \\ & \left.\sum_{i=1}^{N_{\text {neg }}} \ln \left[1-D\left(\boldsymbol{e}_{s, u_{i}}^{n}, \boldsymbol{r}_{s}\right)\right]\right), \end{aligned}$

其中, Npos表示正样本数量, Nneg表示负样本数量.通过最小化损失函数LMI, 在重构社交图中学习的用户嵌入表示 es, ui融入全局的社交信息, 提高用户对兴趣偏好的感知.

1.3 基于图注意力网络的嵌入学习

为了充分利用用户与物品间的交互信息(评价分数), 本文将可学习机制融入图注意力网络中, 根据用户和物品之间的关联程度, 调整邻居节点特征的重要性, 捕获用户和物品的特征信息.用户ui对物品vj的评价是在1, 2, …, K评分范围内进行的.以本文使用的数据集为例, 评分范围为1, 2, …, 5, 涵盖5个等级, 这些等级反映用户对物品的不同评价.基于这些评分等级, 将交互图GR中物品节点vj细化分解, 形成K个物品节点 vj1, vj2, …, vjK, 使用户和物品之间的多等级关系得以在图 GMR={U, V', Er}上呈现.在图 GMR中, 用户集合U中的节点数为N, 而物品集V'中的节点数为KM, 整个图的总节点数为N+KM.

在多等级交互图 GMR中, 将用户ui的one-hot编码 eui∈ {0, 1}N及物品 vjk的one-hot编码$e_{v_{j}^{k}} \in \mathbf{R}^{K \times M}$作为图卷积网络的输入.为了增强用户的表示, 将从社交图中学习到的用户嵌入表示 es, ui与交互图用户的one-hot编码 eui融合, 得到初始的用户嵌入向量表示:

$ \boldsymbol{e}_{u_{i}}^{0}=\boldsymbol{W}_{2} \cdot \boldsymbol{e}_{u_{i}} \| \boldsymbol{W}_{3} \cdot \boldsymbol{e}_{s, u_{i}}, $

其中, $ \boldsymbol{W}_{2} \in \mathrm{R}^{\frac{d_{t}}{2} \times N}$ , $ \boldsymbol{W}_{3} \in \mathrm{R}^{\frac{d_{t}}{2} \times d}$表示可学习的参数矩阵, dt表示嵌入维度, ‖ 表示拼接操作.相应地, 将物品 evjk编码映射为初始的物品嵌入向量表示:

$ \boldsymbol{e}_{v_{j}^{k}}^{0}=\boldsymbol{W}_{4} \cdot \boldsymbol{e}_{v_{j}^{k}}, $

其中$\boldsymbol{W}_{4} \in \mathrm{R}^{d_{t} \times K M}$表示可学习的参数矩阵.本文通过在用户和物品多等级的交互图上传播信息, 更新用户和物品嵌入向量.

在连接的用户和物品之间进行消息的嵌入传播, 包括消息构建和消息聚合两个主要操作过程.

在消息构建阶段, 针对用户ui, 定义消息构建函数:

$ \boldsymbol{m}_{u_{i}}=\sum_{(j, k) \in N_{i}} \boldsymbol{e}_{v_{j}}^{0}, $

类似地, 物品 vjk的消息构建函数:

$ \boldsymbol{m}_{v_{j}^{k}}=\sum_{i \in N_{j, k}} \boldsymbol{e}_{u_{i}}^{0}, $

其中, Ni表示与用户ui连接的物品集合, Nj, k表示与物品 vjk连接的用户集合.这两个函数分别捕捉与用户连接的物品集合和与物品连接的用户集合的信息, 并融入邻居信息.

在消息聚合阶段, 为了关注和学习不同邻居节点间的重要性差异, 将可学习机制融入图注意力网络中, 设计一个多层感知机网络, 自适应学习注意分数, 更精确地提取重要的邻居特征.具体物品注意分数:

$ \begin{array}{l} a_{v_{j}^{k}}=\operatorname{softmax}\left(\boldsymbol { W } _ { v } ^ { ( 3 ) } \cdot \operatorname { R e L } U \left(\boldsymbol{W}_{v}^{(2)} \cdot\right.\right. \\ \left.\left.\operatorname{ReLU}\left(\boldsymbol{W}_{v}^{(1)} \cdot \boldsymbol{e}_{v_{j}^{k}}^{0}+\boldsymbol{b}_{v}^{(1)}\right)+\boldsymbol{b}_{v}^{(2)}\right)+\boldsymbol{b}_{v}^{(3)}\right) . \end{array}$

其中:$ : W_{v}^{(1)} \in \mathrm{R}^{d_{t} \times d_{t}}, W_{v}^{(2)} \in \mathrm{R}^{d_{t} \times d_{t}}, W_{v}^{(3)} \in \mathrm{R}^{1 \times d_{t}}$, 表示参数矩阵; $ b_{v}^{(1)}, b_{v}^{(2)}, b_{v}^{(3)}$表示偏置.进一步, 定义用户ui的消息聚合函数, 经过第1个传播层后获得的用户ui嵌入表示:

$ \boldsymbol{e}_{u_{i}}^{(1)}=\sigma\left(\boldsymbol{m}_{u_{i} \leftarrow u_{i}}+\sum_{(j, k) \in N_{i}} a_{v_{j}} \boldsymbol{m}_{u_{i}}\right), $

其中σ (· )为PReLU激活函数.考虑用户ui的自连接$m_{u_{i} \leftarrow u_{i}}=e_{u_{i}}^{0}$, 保留用户节点原始的特征信息.

类似地, 物品节点的信息聚合过程表示为

$ \boldsymbol{e}_{v_{j}^{k}}^{(1)}=\sigma\left(\boldsymbol{m}_{v_{j}^{k} \leftarrow v_{j}^{k}}+\sum_{i \in N_{j, k}} a_{u_{i}} \boldsymbol{m}_{v_{j}^{k}}\right), $

其中 mvjk←vjk= evjk0表示物品的自连接.用户注意分数 aui也是通过多层感知机网络计算得到的, 即

$ \begin{array}{l} a_{u_{i}}=\operatorname{softmax}\left(\boldsymbol { W } _ { u } ^ { ( 3 ) } \cdot \operatorname { R e L U } \left(\boldsymbol{W}_{u}^{(2)} \cdot\right.\right. \\ \left.\left.\quad \operatorname{ReLU}\left(\boldsymbol{W}_{u}^{(1)} \cdot \boldsymbol{e}_{u_{i}}^{0}+\boldsymbol{b}_{u}^{(1)}\right)+\boldsymbol{b}_{u}^{(2)}\right)+\boldsymbol{b}_{u}^{(3)}\right) . \end{array}$

其中:$ W_{u}^{(1)} \in \mathrm{R}^{d_{t} \times d_{t}}, W_{u}^{(2)} \in \mathrm{R}^{d_{t} \times d_{t}}, W_{u}^{(3)} \in \mathrm{R}^{1 \times d_{t}}$表示参数矩阵; $ b_{u}^{(1)}, b_{u}^{(2)} 、 b_{u}^{(3)}$表示偏置.这样的设计使模型既捕捉到邻居重要信息的传递, 又能保留节点自身的特征.

基于定义的消息聚合函数, 得到物品节点的嵌入表示和用户节点的嵌入表示.为了学习高阶的语义信息, 堆叠L个消息传播层, 用户(或物品)能逐步获取从邻居节点传播的高阶消息.这一过程表示为

$ \begin{array}{l} \boldsymbol{e}_{u_{i}}^{(l+1)}=\sigma\left(\boldsymbol{m}_{u_{i} \leftarrow u_{i}}^{(l)}+\sum_{(j, k) \in N_{i}} a_{v_{j}^{k}}^{(l)} \boldsymbol{m}_{u_{i}}^{(l)}\right), \\ \boldsymbol{e}_{v_{j}^{k}}^{(l+1)}=\sigma\left(\boldsymbol{m}_{v_{j}^{k} \leftarrow v_{j}^{k}}^{(l)}+\sum_{i \in N_{j, k}} a_{u_{i}}^{(l)} \boldsymbol{m}_{v_{j}^{k}}^{(l)}\right), \end{array}$

其中l=0, 1, …, L-1.通过多层的消息传播, 模型能捕捉到更丰富的节点间关系, 提升推荐的准确性.融合L个消息传播层的输出, 生成用户u和物品 vjk嵌入表示:

$ \begin{aligned} \boldsymbol{E}_{u_{i}} & =\left(\boldsymbol{e}_{u_{i}}^{(1)}\left\|\boldsymbol{e}_{u_{i}}^{(2)}\right\| \cdots \| \boldsymbol{e}_{u_{i}}^{(L)}\right) \\ \boldsymbol{E}_{v_{j}^{k}} & =\left(\boldsymbol{e}_{v_{j}^{k}}^{(1)}\left\|\boldsymbol{e}_{v_{j}^{k}}^{(2)}\right\| \cdots \| \boldsymbol{e}_{v_{j}^{k}}^{(L)}\right) \end{aligned}$

最后, 将不同评分等级的物品特征表示$E_{v_{j}^{1}}, E_{v_{j}^{2}}, \cdots, E_{v_{j}^{K}}$采用平均操作, 得到最终的物品特征表示 Evj.

1.4 评分预测层

在评分预测层中, 将学习到的用户潜在表示 Eui和物品潜在表示 Evj合并到两层全连接网络中, 用于预测评分r'ij, 具体形式为

$ \begin{array}{l} \boldsymbol{E}_{u_{i}, v_{j}}=\boldsymbol{E}_{u_{i}} \| \boldsymbol{E}_{v_{j}}, \\ r_{i j}^{\prime}=\operatorname{ReLU}\left(\boldsymbol{W}_{p}^{2} \operatorname{ReLU}\left(\boldsymbol{W}_{p}^{1} \boldsymbol{E}_{u_{i}, v_{j}}+\boldsymbol{b}_{p}^{1}\right)+\boldsymbol{b}_{p}^{2}\right) . \end{array}$

其中:$ W_{p}^{1} \in \mathrm{R}^{d_{t} \times 2 d_{t}}, W_{p}^{2} \in \mathrm{R}^{1 \times d_{t}}$表示可学习的参数矩阵; $ b_{p}^{1}, b_{p}^{2}$表示偏置项.

1.5 联合损失函数

在图卷积网络中, 为了更准确捕获用户偏好和物品属性, 提出一种改进的BPR损失函数, 旨在优化用户特征表示 Eui和物品特征表示 Evjk.

在用户和物品的交互中, 抽取用户ui非交互物品作为负样本 vjk-, 利用双线性函数计算正样本特征表示$E_{v_{j}^{k}}^{+}$和负样本特征表示$E_{v_{j}^{k}}^{-}$之间的差异, 交互损失函数为:

$ \begin{array}{l} s_{i, j}^{k}=\frac{1}{\tau}\left(\boldsymbol{E}_{u_{i}} \boldsymbol{W}_{1}^{s} \boldsymbol{E}_{v_{j}^{k}}^{\mathrm{T}}-\max \left(\boldsymbol{E}_{u_{i}} \boldsymbol{W}_{1}^{s} \boldsymbol{E}_{v_{j}^{k}}^{\mathrm{T}}\right)\right), \\ L_{i}=-\frac{1}{\varphi\left(\boldsymbol{A}_{i}\right)} \sum_{\left(i, j, k^{+}\right) \in O_{i}} \ln \left(\exp \left(s_{i, j}^{k^{+}}\right)-\exp \left(s_{i, j}^{k^{-}}\right)\right), \end{array}$

其中, $ s_{i, j}^{k^{+}}$表示用户对正样本物品的偏好分数, $ s_{i, j}^{k^{-}}$表示用户对负样本物品的偏好分数, φ (Ai)表示用户和物品交互的邻接矩阵中非零元素的数量, $ W_{1}^{s} \in \mathrm{R}^{d_{t} \times d_{t}}$表示可学习的权重矩阵, τ 表示缩放的超参数, max(· )表示向量中最大的元素, 避免极端值对分数的影响.

在社交关系方面, 定义社交损失函数, 该函数对比用户在社交关系与非社交关系中的特征差异, 优化用户的特征表示.具体地, 从不存在社交关系的用户中抽取负样本 ui-, 利用双线性函数计算正负样本对分数, 具体表示为:

$ \begin{array}{l} s_{i, i^{\prime}}=\frac{1}{\tau}\left(\boldsymbol{E}_{u_{i}} \boldsymbol{W}_{2}^{s} \boldsymbol{E}_{u_{i}^{\prime}}^{\mathrm{T}}-\max \left(\boldsymbol{E}_{u_{i}} \boldsymbol{W}_{2}^{s} \boldsymbol{E}_{u_{i}{ }^{\prime}}^{\mathrm{T}}\right)\right), \\ L_{s}=-\frac{1}{\varphi(\boldsymbol{S})} \sum_{\left(i, i^{+}\right) \in O_{s}} \ln \left(\exp \left(s_{i, i^{+}}\right)-\exp \left(s_{i, i^{-}}\right)\right), \end{array}$

其中, si, i+表示用户的正样本对计算分数, si, i-表示用户的负样本对计算分数, φ (S)表示社交图的邻接矩阵中非零元素的数量, $ W_{2}^{s} \in \mathrm{R}^{d_{t} \times d_{t}}$表示可学习的权重矩阵.

此外, 为了将预测评分与真实评分之间的差异最小化, 在评分预测层采用均方误差作为损失函数, 该损失数学表达式为:

$ L_{R}=\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{M} I_{i j}\left(r_{i j}-r_{i j}^{\prime}\right)^{2} \text {, }$

其中, Iij(· )为指示函数, 当用户和物品之间有交互时, Iij=1, 否则Iij=0.

本文结合改进的BPR损失和评分预测层的损失, 构建一个联合损失函数:

L=LR+λ 1Li+λ 2Ls,

用于平衡不同损失的权重, 其中, λ 1> 0, λ 2> 0, 均为超参数.

2 实验及结果分析
2.1 实验数据集

本文选择Ciao[21]、Epinions[22]、Douban这3个真实的社交推荐数据集, 用于评估方法性能.Ciao数据集的数据来自英国的一个消费者评论网站.Epinions数据集是一个基于社交的产品评论平台的公开数据集.Douban数据集收集于中国豆瓣社交平台.用户可为物品进行打分(分数范围为{1, 2, …, 5}), 也可与他人建立社交关系, 将不同的评分分数视为不同的交互类型.这3个数据集的统计数据如表1所示, 在每个数据集上, 本文按照文献[22]中相同的数据百分比的设置, 将数据分为训练集、验证集、测试集, 分别占总数据x%, 0.5(1-x%), 0.5(1-x%).在实验中, 本文将x设置为60和80.

表1 数据集统计信息 Table 1 Dataset statistics
2.2 实验设置及对比方法

本文在pytorch框架下进行实验, 采用Adam (Adaptive Moment Estimation)优化器[31], 学习率设为0.001.在社交表示学习过程中, 从{250, 500, 1 000, 1 500}中搜索社交关系编码器的最佳嵌入维度.同时, 针对用户和物品交互图, 图关注网络模块的维度在{8, 16, 32, 64}内进行调整.在Ciao数据集上设置超参数λ 1=0.25, λ 2=0.15; 在Epinions数据集上设置λ 1=0.1, λ 2=0.15; 在Douban数据集上设置λ 1=λ 2=0.05.

在实验过程中, 为了提升训练效率, 采用提前停止策略, 如果验证集上的均方根误差(Root Mean Square Error, RMSE)连续5个迭代周期未下降, 停止训练模型.

所有实验均在配备GeForce GTX 1080Ti显卡的工作站上进行.

本文选择均方根误差和平均绝对误差(Mean Ab-solute Error, MAE)作为评估预测精度的指标.RMSE和MAE值越小, 表示预测精度越高.尽管这些指标的相对改进幅度较小, 但之前的研究[32]表明, 即使是小幅度的RMSE或MAE的改进也可能对推荐系统的整体性能产生显著影响.

2.3 对比实验结果

本文选择如下方法作为对比方法:SoRec[8]、TrustMF[9]、SocialMF[10]、文献[11]方法、PMF[15]、GraphRec+[19]、DiffNet++[20]、ConsisRec[21]、SRHG-NN[22]、HeteroGraphRec[23]、GDSRec[24]、Sim-GraphRec(SGR)[33]、SR-AIR(Attentive Implicit Relation Embe-dding for Social Recommendation)[34].

在Ciao、Epinions和Douban数据集上, 采用RMSE和MAE作为性能评价指标, 进行对比实验.在训练集占比分别为80%和60%时, 各方法在测试集上的实验结果如表2和表3所示, 表中黑体数字表示最优值.

表2 各方法在3个数据集上的RMSE对比 Table 2 RMSE comparison of different methods on 3 datasets
表3 各方法在3个数据集上的MAE对比 Table 3 MAE comparison of different methods on 3 datasets

由表2和表3可见, 在2种训练集占比下, GNNES在3个数据集上的RMSE和MAE值都为最优, 由此验证GNNES的有效性.相比传统社交推荐方法, GNNES充分考虑图结构信息, 采用图神经网络编码用户和物品的节点表示, 使GNNES在建模过程中能更全面地利用社交关系, 捕获更丰富的社交信息.相比SR-HGNN, GNNES在建模过程中进一步探索潜在的社交关系, 从而捕获更好的社交信息, 使GNNES在推荐性能上更具优势.相比其它基线方法, GNNES将社交信息整合到图神经网络中.相比消息传递方法(如ConsisRec、HeteroGraphRec、GraphRec++、DiffNet++、SGR、SR-AIR), GNNES在用户的嵌入学习中, 学习用户之间的隐式社交关系和全局信息, 能较全面地理解用户间的联系和影响.

2.4 消融实验结果

为了研究GNNES中不同模块的作用, 在Ciao、Epinions、Douban数据集上进行一系列的消融实验, 验证模块的有效性.

首先, 评估互信息最大化在捕获局部-全局用户嵌入表示上的有效性, 使用两种具有代表性的图神经网络架构替换本文的社交关系编码器:图卷积网络(Graph Convolutional Network, GCN)和图注意力网络(Graph Attention Network, GAT), 分别简记为GNNES-GCN和GNNES-GAT.

各方法的性能对比如图2所示.由图可见, 虽然GCN和GAT在融合用户之间的信息方面均取得较优结果, 但GNNES通过最大化用户依赖的局部表示和全局表示之间的互信息, 进一步提升推荐性能.

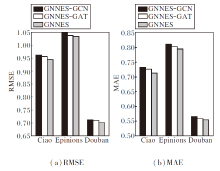图2 基于互信息最大化的图学习模块的消融实验结果Fig.2 Results of ablation experiment of graph learning module based on mutual information maximization

此外, 本文分别验证重构社交关系的影响和改进的BPR损失(Ls和Li)的有效性.一方面, 对比原始的用户关系GNNES-OR和重构后的社交关系GNNES的性能, 结果如图3所示.由图可见, 重构的社交关系有助于提升推荐性能, 隐式的用户关系可有效捕捉不同的用户偏好, 从而有利于学习嵌入表示.

图3 重构社交关系和改进损失的消融实验结果Fig.3 Results of ablation experiment on reconstructing social relationship graph and improving losses

另一方面, 为了验证改进的BPR损失对用户和物品嵌入学习过程的影响, 生成两个变体方法:1)GNNES-REC, 未使用本文设计的BPR损失; 2)GNNES-BPR, 采用传统的BPR损失.3种方法性能对比如图3所示.由图可观察到, 本文设计的改进BPR损失具有较明显的优势.相比GNNES-BPR, GNNES在推荐性能方面具有明显提升.这一结果证实本文改进BPR损失的有效性.

2.5 超参数讨论

首先, 讨论社交关系用户的嵌入维度d.在学习用户的局部-全局嵌入表示中, 经验性地考虑嵌入维度d=250, 500, 1 000, 1 500, 则d对GNNES性能的影响如图4所示.由图可见, 较大维度的数值并不一定具有更优性能, 因为可能存在过拟合问题.因此, 在Ciao、Epinions和Douban数据集上, 维度大小分别设置为500、250和1 000.

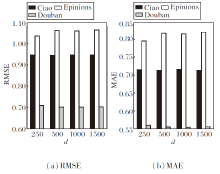图4 社交关系用户嵌入维度d对GNNES性能的影响Fig.4 Effect of social relationship user embedding dimension d on GNNES performance

再讨论交互图中嵌入维度dt.在用户-物品交互图的图注意力网络中讨论不同嵌入维度的影响.考虑嵌入维度dt=8, 16, 32, 64, 则dt对GNNES性能的影响如图5所示.由图可见, 在Ciao、Epinions数据集上, 当dt=16时, 预测精度均最高, 而在Douban数据集上, dt=32时预测精度最佳.因此, 在最终的实验设置中, 在Ciao、Epinions数据集上, 经验性设置dt=16, 在Douban数据集上, 经验性设置dt=32.

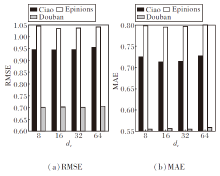图5 用户-物品交互图嵌入维度dt对GNNES性能的影响Fig.5 Effect of embedding dimension dt in user-item interaction graph on GNNES performance

然后, 讨论图注意力网络的层数.增加基于注意力机制的图神经网络的传播层数可提高推荐效果.在层数的选取中, 设计2层、3层、4层, 则层数对GNNES性能的影响如图6所示.

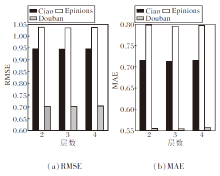图6 图注意力网络层数对GNNES性能的影响Fig.6 Effect of the number of graph attention network layers on GNNES performance

由图6可观察到, 具有3个嵌入传播层的方法获得最优性能.然而, 随着层数的增加, 性能略有下降, 可能因为深度图神经网络会出现过拟合现象.

最后, 讨论改进BPR损失中的参数τ .τ 不同时对GNNES性能的影响如表4所示, 表中黑体数字表示最优值.由表可见, 在3个数据集上, τ =0.15时, 性能最佳.

表4 τ 对GNNES性能的影响 Table 4 Effect of τ on GNNES performance
3 结束语

本文提出社交影响增强的图神经网络推荐方法(GNNES), 挖掘用户间隐式的社交关系, 进一步提升推荐性能.具体而言, 利用用户和物品之间的评分信息重构用户社交图, 采用互信息最大化方法有效提取用户的社交特征.GNNES中包含全局社交图信息和用户局部信息, 可全面反映用户的社交属性.同时, 设计基于可学习机制的图注意力网络模块, 自适应调整不同邻居的权重, 准确捕获重要邻居的信息.最后, 通过联合损失为评分预测任务提供准确的用户特征表示和物品特征表示.在评分预测任务中, 将物品的历史信息融入推荐系统框架中, 有助于推荐系统学习到更丰富的物品语义信息.因此, 如何有效地将用户信息和物品信息整合到推荐系统中, 是今后一个值得研究的课题.

本文责任编委 梁吉业

Recommended by Associate Editor LIANG Jiye

参考文献
[1] CHEN H X, YIN H Z, CHEN T, et al. Social Boosted Recommendation with Folded Bipartite Network Embedding. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(2): 914-926. [本文引用:1]
[2] GUO Z W, YU K P, LI Y, et al. Deep Learning-Embedded Social Internet of Things for Ambiguity-Aware Social Recommendation. IEEE Transactions on Network Science and Engineering, 2022, 9(3): 1067-1081. [本文引用:1]
[3] LI N, GAO C, JIN D P, et al. Disentangled Modeling of Social Homophily and Influence for Social Recommendation. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(6): 5738-5751. [本文引用:1]
[4] 王玙, 高琳. 基于社交圈的在线社交网络朋友推荐算法. 计算机学报, 2014, 37(4): 801-808.
(WANG Y, GAO L. Social Circle-Based Algorithm for Friend Re-commendation in Online Social Networks. Chinese Journal of Computers, 2014, 37(4): 801-808. ) [本文引用:1]
[5] MCPHERSON M, SMITH-LOVIN L, COOK J M. Birds of a Fea-ther: Homophily in Social Networks. Annual Review of Sociology, 2001, 27: 415-444. [本文引用:1]
[6] MARSDEN P V, FRIEDKIN N E. Network Studies of Social Influence. Sociological Methods Research, 1993, 22(1): 127-151. [本文引用:1]
[7] 冷亚军, 陆青, 梁昌勇. 协同过滤推荐技术综述. 模式识别与人工智能, 2014, 27(8): 720-734.
(LENG Y J, LU Q, LIANG C Y. Survey of Recommendation Based on Collaborative Filtering. Pattern Recognition and Artificial Intelligence, 2014, 27(8): 720-734. ) [本文引用:1]
[8] MA H, YANG H X, LYU M R, et al. SoRec: Social Recommendation Using Probabilistic Matrix Factorization // Proc of the 17th ACM International Conference on Information and Knowledge Ma-nagement. New York, USA: ACM, 2008: 931-940. [本文引用:2]
[9] YANG B, LEI Y, LIU J M, et al. Social Collaborative Filtering by Trust. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1633-1647. [本文引用:3]
[10] JAMALI M, ESTER M. A Matrix Factorization Technique with Trust Propagation for Recommendation in Social Networks // Proc of the 4th ACM Conference on Recommender Systems. New York, USA: ACM, 2010: 135-142. [本文引用:3]
[11] MA H, ZHOU D Y, LIU C, et al. Recommender Systems with Social Regularization // Proc of the 4th ACM International Confe-rence on Web Search and Data Mining. New York, USA: ACM, 2011: 287-296. [本文引用:3]
[12] WU L, SUN P J, FU R J, et al. A Neural Influence Diffusion Model for Social Recommendation // Proc of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM, 2019: 235-244. [本文引用:1]
[13] CHEN C, ZHANG M, WANG C Y, et al. An Efficient Adaptive Transfer Neural Network for Social-Aware Recommendation // Proc of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM, 2019: 225-234. [本文引用:1]
[14] FAN W Q, LI Q, CHENG M. Deep Modeling of Social Relations for Recommendation. Proceedings of the AAAI Conference on Artificial Intelligence, 2018, 32(1): 8075-8076. [本文引用:1]
[15] SALAKHUTDINOV R, MNIH A. Probabilistic Matrix Factorization // Proc of the 20th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2007: 1257-1264. [本文引用:2]
[16] ZHAO Z, YANG Q F, LU H Q, et al. Social-Aware Movie Re-commendation via Multimodal Network Learning. IEEE Transactions on Multimedia, 2018, 20(2): 430-440. [本文引用:1]
[17] WANG X, HE X N, WANG M, et al. Neural Graph Collaborative Filtering // Proc of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM, 2019: 165-174. [本文引用:1]
[18] FAN W Q, MA Y, LI Q, et al. Graph Neural Networks for Social Recommendation // Proc of the World Wide Web Conference. New York, USA: ACM, 2019: 417-426. [本文引用:1]
[19] FAN W Q, MA Y, LI Q, et al. A Graph Neural Network Framework for Social Recommendations. IEEE Transactions on Know-ledge and Data Engineering, 2022, 34(5): 2033-2047. [本文引用:2]
[20] WU L, LI J W, SUN P J, et al. DiffNet++: A Neural Influence and Interest Diffusion Network for Social Recommendation. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(10): 4753-4766. [本文引用:2]
[21] YANG L W, LIU Z W, DOU Y T, et al. ConsisRec: Enhancing GNN for Social Recommendation via Consistent Neighbor Aggregation // Proc of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA: ACM, 2021: 2141-2145. [本文引用:3]
[22] XÜ H C, HUANG C, XU Y, et al. Global Context Enhanced Social Recommendation with Hierarchical Graph Neural Network // Proc of the IEEE International Conference on Data Mining. Washington, USA: IEEE, 2020, 701-710. [本文引用:6]
[23] SALAMAT A, LUO X, JAFARI A. HeteroGraphRec: A Heterogeneous Graph-Based Neural Networks for Social Recommendations. Knowledge-Based Systems, 2021, 217. DOI: 10.1016/j.knosys.2021.106817. [本文引用:2]
[24] CHEN J J, XIN X, LIANG X F, et al. GDSRec: Graph-Based Decentralized Collaborative Filtering for Social Recommendation. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(5): 4813-4824. [本文引用:2]
[25] SONG Y Z, YE H L, LI M, et al. Deep Multi-graph Neural Networks with Attention Fusion for Recommendation. Expert Systems with Applications, 2022, 191. DOI: 101016/j. eswa. 2021. 1162
[本文引用:1]
[26] YE H L, SONG Y Z, LI M, et al. A New Deep Graph Attention Approach with Influence and Preference Relationship Reconstruction for Rate Prediction Recommendation. Information Processing and Management, 2023, 60(5). DOI: 101016/j. ipm. 2023. 103
[本文引用:1]
[27] LIU Y, CHEN L, HE X N, et al. Modelling High-Order Social Relations for Item Recommendation. IEEE Transactions on Know-ledge and Data Engineering, 2022, 34(9): 4385-4397. [本文引用:1]
[28] LI H, WU D M, TANG W B, et al. Overlapping Community Re-gularization for Rating Prediction in Social Recommender // Proc of the 9th ACM Conference on Recommender Systems. New York, USA: ACM, 2015: 27-34. [本文引用:1]
[29] DING J T, YU G H, HE X N, et al. Sampler Design for Bayesian Personalized Ranking by Leveraging View Data. IEEE Transactions on Knowledge and Data Engineering, 2021, 33(2): 667-681. [本文引用:1]
[30] HE K M, ZHANG X Y, REN S Q, et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2015: 1026-1034. [本文引用:1]
[31] 邵新茹, 叶海良, 杨冰, 等. 基于三阶段生成网络的图像修复. 模式识别与人工智能, 2022, 35(12): 1047-1063.
(SHAO X R, YE H L, YANG B, et al. Image Inpainting with a Three-Stage Generative Network. Pattern Recognition and Artificial Intelligence, 2022, 35(12): 1047-1063. ) [本文引用:1]
[32] KOREN Y. Factorization Meets the Neighborhood: A Multifaceted Collaborative Filtering Model // Proc of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2008: 426-434. [本文引用:1]
[33] JIA Z H, GAO Q, FAN J. Research on Social Recommendation Model Based on Enhanced Neighbor Perception // Proc of the IEEE International Conference on Systems, Man and Cybernetics. Washington, USA: IEEE, 2022: 3415-3420. [本文引用:1]
[34] MA X T, DONG L Y, WANG Y Q, et al. An Enhanced Attentive Implicit Relation Embedding for Social Recommendation. Data and Knowledge Engineering, 2023, 145. DOI: 10.1016/j.datak.2023.102142. [本文引用:1]