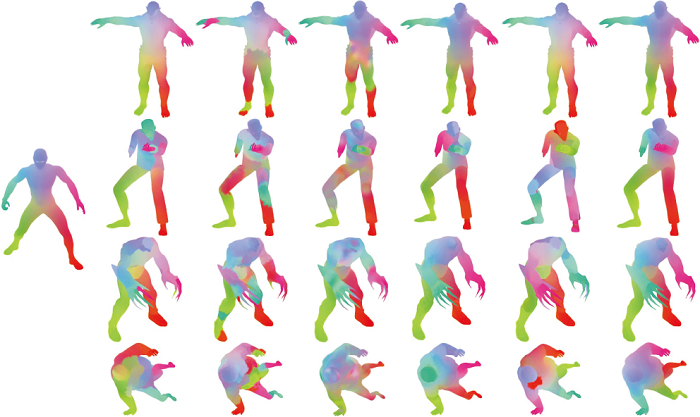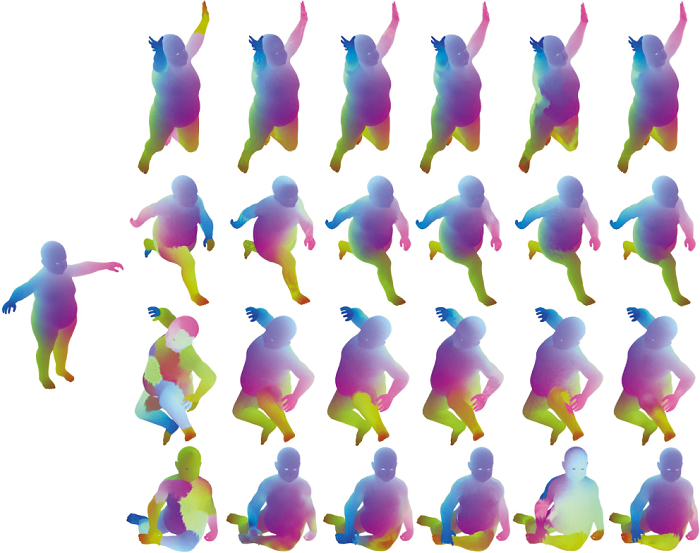为了解决现有非等距三维模型簇对应关系计算算法准确率较低、泛化能力较差的问题, 本文提出采用深度内外特征对齐算法的自监督非等距三维模型簇对应关系计算方法, 总体框架如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 本文方法总体框图Fig.1 Overall framework of the proposed algorithm

本文方法主要由深度内外特征对齐算法和自监督多模型匹配算法(Self-Supervised Multi-shape Ma-tching, SSMM)组成.具体实现步骤如下.

1)将源模型M和目标模型N输入特征提取网络中, 网络采用DiffusionNet^[22], 通过孪生网络形式实现参数共享, 从原始的三维模型中学习特征描述符$\boldsymbol{F}_{\text {init }}^{M}$和$\boldsymbol{F}_{\text {init }}^{N}$.

2)采用内外特征一致性对齐算法自动生成模型对逐点映射结果.利用LMH基作为模型本征信息, 并结合笛卡尔坐标等外部信息嵌入内外积空间, 实现本征信息和外部信息对齐, 利用CPD(Coherent Point Drift)^[23]求解非等距模型对对应关系计算损失函数L_pair, 计算非等距模型对逐点映射结果$\boldsymbol{\Pi}_{\text {pair }}^{M N}$.

3)利用模型对逐点映射结果自监督地训练三维模型簇对应关系计算网络.首先, 将非等距三维模型簇 {Sl}l=1n表示为加权无向完全图, 其中每个模型表示为一个节点, 两个节点之间的权重值为两个模型间内外特征的对齐距离; 然后, 将2)中的模型对逐点映射结果作为自监督训练的数据标签, 利用SPFA(Shortest Path Faster Algorithm)^[24]计算两个节点S_i和S_j在加权无向完全图之间的最短路径, 求解S_i和S_j对应关系计算损失函数$\mathcal{L}_{\text {coll }}$.最后, 联合损失函数$\mathcal{L}_{\text {pair }}$和$\mathcal{L}_{\text {coll }}$, 训练整个网络.

1.2.1 特征提取网络

三维模型对应关系计算的前提是将原始形状的几何模型生成有意义的特征, 特别对于大尺度变形的三维模型, 更需要准确稳定的特征提取算法.本文采用DiffusionNet构建特征提取网络, 不仅可以较好地处理非刚性变换的三维模型, 还对使用离散化表示的三维模型具有较强的鲁棒性.

将非等距三维模型M和N建模为嵌入到R³中的平滑二维黎曼流形, 顶点数分别为n₁和n₂.对三维模型进行离散化处理, 分别把这两个模型的n₁和n₂个顶点坐标保存在矩阵$X \in \mathrm{R}^{\mathrm{n}_{1} \times 3}$和$\boldsymbol{Y} \in \mathrm{R}^{\mathrm{n}_{2} \times 3}$中, 并将X和Y分别输入具有共享权重参数的DiffusionNet模块中, 生成特征 FinitM和 FinitN.

DiffusionNet主要依靠简单的可学习扩散层(Diffusion Layer, DL), 取代模型表面上复杂且昂贵的卷积和池化操作, 基本原理如下.

首先, 在连续的前提下, 将三维模型上的标量场信息u(t)的特征传播建模为热扩散模型, 使用热方程表示如下:

$\Delta_{M} u(t)=\frac{\partial u(t)}{\partial t}, $

其中Δ _M为M的LBO(Laplace-Beltrami Operator).该扩散行为可通过热运算符h_t表示, 定义为

$h_{t}(u(0))=e^{t \Delta_{M}} u(0) \text {, }$

其中u(0)为初始分布.

然后, 在实际情况下, 考虑模型离散状态, 将模型的LBO表示为一个稀疏矩阵:

L=A^-1O=Φ Λ Φ ^TA,

其中, A为面积权重对角矩阵, O为余切权重刚度矩阵, Φ 为保存特征函数的矩阵, Λ 为保存特征值$\left\{\lambda_{i}\right\}_{i=1}^{k}$的对角矩阵.假设U为u的离散化特征, 将DL定义为H_t, 它在学习时间t内扩散到每个离散特征U, 扩散层H_t表示如下:

$H_{t}(\boldsymbol{U})=\boldsymbol{\Phi}\left[e^{-\lambda_{1} t} \quad e^{-\lambda_{2} t} \cdots\right]^{\mathrm{T}} \odot\left(\boldsymbol{\Phi}^{\mathrm{T}} \boldsymbol{A} \boldsymbol{U}\right)$ (1)

其中, ☉为矩阵点乘, 根据$\left[\begin{array}{ll} e^{-\lambda_{1} t} & \left.e^{-\lambda_{2} t} \cdots\right]^{\mathrm{T}} \end{array}\right.$对谱系数Φ ^TAU的逐元素缩放调整可方便表示为时间t的热扩散.式(1)使用稠密线性代数运算(经典的向量和矩阵运算)以求解.

最后, 计算模型曲面上每个点的切平面特征信息的空间梯度内积, 与式(1)的结果馈送到每个点的多层感知机(Multilayer Perceptron, MLP)中, 获得模型特征F_init.

1.2.2 内外特征一致性对齐算法

传统算法大多简单利用笛卡尔坐标等外部特征描述三维模型, 或像FM一样依赖模型谱域本征信息进行计算, 难以保证计算准确率, 因此在不同数据集上效果各异.

本文结合深度学习与内外特征一致性对齐算法^[25], 融合基于局部刚性变换准则^[26]的形变算法, 利用LMH基表示模型的本征特征, 将其与外部信息嵌入内外积空间中, 描述模型对齐过程, 以此计算非等距模型对的对应关系.算法过程如下.

1)在新的内外积空间中描述模型特征.从内外特征的融合入手, 分别构造M和N的LMH基函数$\left\{\boldsymbol{\phi}_{i}^{\mathrm{LMH}}\right\}_{i \geqslant 1}$和$\left \{\boldsymbol{\psi}_{j}^{\mathrm{LMH}}\right\}_{j \geqslant 1}$, 并将LMH基函数前k(k≪n₁且k≪n₂)项保存在矩阵

$\boldsymbol{\Phi}_{k}^{\mathrm{LMH}}=\left(\boldsymbol{\phi}_{1}^{\mathrm{LMH}}, \boldsymbol{\phi}_{2}^{\mathrm{LMH}}, \cdots, \boldsymbol{\phi}_{k}^{\mathrm{LMH}}\right)$

和

$\boldsymbol{\Psi}_{k}^{\mathrm{LMH}}=\left(\boldsymbol{\psi}_{1}^{\mathrm{LMH}}, \boldsymbol{\psi}_{2}^{\mathrm{LMH}}, \cdots, \boldsymbol{\psi}_{k}^{\mathrm{LMH}}\right)$

中.LMH基比LBO基更适合描述模型本征特征的原因在于它既能捕获LBO特征基的全局信息, 也保留模型的局部细节.

定义新的内外积空间, 将模型M和N嵌入该空间中, 特征分别表示为

$\begin{array}{l} \boldsymbol{F}_{k}^{M}=\left(\boldsymbol{\sigma}_{k}^{M}, \boldsymbol{\Phi}_{k}^{\mathrm{LMH}}, \hat{\boldsymbol{n}}_{k}^{M}\right) \in \mathbf{R}^{n_{1} \times(k+6)}, \\ \boldsymbol{F}_{k}^{N}=\left(\boldsymbol{\sigma}_{k}^{N}, \boldsymbol{\Psi}_{k}^{\mathrm{LMH}}, \hat{\boldsymbol{n}}_{k}^{N}\right) \in \mathbf{R}^{n_{2} \times(k+6)}, \end{array}$

其中, n̂kM为 σkM构造的曲面法向量, n̂kN为 σkN构造的曲面法向量,

$\boldsymbol{\sigma}_{k}^{M}=\sum_{i=1}^{\infty}\left(\frac{1}{1+e^{\alpha(i-k)}} \boldsymbol{\phi}_{i}^{\mathrm{LMH}} \boldsymbol{X}\right), $

$\boldsymbol{\sigma}_{k}^{N}=\sum_{i=1}^{\infty}\left(\frac{1}{1+e^{\alpha(i-k)}} \boldsymbol{\psi}_{i}^{\mathrm{LMH}} \boldsymbol{Y}\right) .$

结合模型外部特征和本征特征, 将模型的外部坐标矩阵投射到前k个LMH基上, 在谱域上重建光滑曲面, 是一种可替代外部坐标的模型算子.由于LMH的特征基也是按频率排序的, 所以随着k值的增大, 可获得模型从粗到细的谱表示.

2)对模型M进行变换.根据局部刚性变换准则的形变算法, 采用线性位移和本征函数变换描述内外融合特征形变, 定义为

$\boldsymbol{\sigma}_{k}^{M}+\boldsymbol{\Phi}_{k}^{\mathrm{LMH}} \boldsymbol{\varepsilon}, $

其中ε ∈ R^{k× 3}为形变的位移系数.使用FM描述内部特征变换, 定义为$\boldsymbol{C} \boldsymbol{\Phi}_{k}^{\mathrm{LMH}}$, 其中C为FM矩阵, 由此可得模型M的变换式:

$\boldsymbol{F}_{k}^{M^{\prime}}=\left(\boldsymbol{\sigma}_{k}^{M}+\boldsymbol{\Phi}_{k}^{\mathrm{LMH}} \boldsymbol{\varepsilon}, \boldsymbol{C} \boldsymbol{\Phi}_{k}^{\mathrm{LMH}}, \hat{\boldsymbol{n}}_{k}^{M^{\prime}}\right) \in \mathbf{R}^{n_{1} \times(k+6)}, $

其中$\hat{\boldsymbol{n}}_{k}^{M^{\prime}}$为$\boldsymbol{\sigma}_{k}^{M}+\boldsymbol{\Phi}_{k}^{\mathrm{LMH}} \varepsilon$构造的曲面法向量.

3)采用置换矩阵Π 描述点对点映射P∶ M→ N.为了计算矩阵Π , 使用CPD定义能量函数E_align, 将Π FkM'与 FkN对齐.E_align定义如下:

$\begin{array}{l} E_{\text {align }}\left(\boldsymbol{\Pi} \boldsymbol{F}_{k}^{M^{\prime}}, \boldsymbol{F}_{k}^{N}\right)= \\ \quad D_{\mathrm{KL}}\left(\boldsymbol{F}_{k}^{N}, \boldsymbol{\Pi} \boldsymbol{F}_{k}^{M^{\prime}}\right)+\rho\left\|\Gamma\left(\boldsymbol{F}_{k}^{N}-\boldsymbol{\Pi} \boldsymbol{F}_{k}^{M^{\prime}}\right)\right\|^{2}, \end{array}$

其中, D_KL为连续高斯混合模型分布和狄拉克分布之间的KL散度, ‖ Γ ‖ ²为洁洪诺夫正则化, Γ 为促进平滑的低通运算符, ρ > 0为控制正则化的权重.在能量函数E_align中, 将点对点映射还原问题看作求解概率密度估计问题, 这样保证是可微的, 使算法的标准梯度优化可行.

4)采用基于交替方向乘子算法^[27]的优化策略求解优化问题

$\arg \min _{\boldsymbol{\Pi}, \boldsymbol{C}, \boldsymbol{\varepsilon}} E_{\text {align }}\left(\boldsymbol{\Pi} \boldsymbol{F}_{k}^{M^{\prime}}, \boldsymbol{F}_{k}^{N}\right), $

具体步骤如下.

(1)求解

$\begin{array}{l} \boldsymbol{\Pi}_{0}=\arg \min _{\boldsymbol{\Pi}} E_{\text {align }}\left(\boldsymbol{\Pi} \boldsymbol{F}_{\text {init }}^{M}, \boldsymbol{F}_{\text {init }}^{N}\right), \\ \left(\boldsymbol{C}_{0}, \boldsymbol{\varepsilon}_{0}\right)=\arg \min _{\boldsymbol{C}, \boldsymbol{\varepsilon}} E_{\text {align }}\left(\boldsymbol{\Pi}_{0} \boldsymbol{F}_{\text {init }}^{M}, \boldsymbol{F}_{\text {init }}^{N}\right), \end{array}$

其中 FinitM与 FinitN为特征提取网络学习到的模型特征.

(2)分别求解

$\begin{array}{l} \boldsymbol{\Pi}_{k+1}=\arg \min _{\boldsymbol{\Pi}} E_{\text {align }}\left(\boldsymbol{\Pi} \boldsymbol{F}_{k}^{M^{\prime}}, \boldsymbol{F}_{k}^{N}\right), \\ \left(\boldsymbol{C}_{k+1}, \boldsymbol{\varepsilon}_{k+1}\right)=\arg \min _{\boldsymbol{C}, \boldsymbol{\varepsilon}} E_{\text {align }}\left(\boldsymbol{\Pi}_{k+1} \boldsymbol{F}_{k}^{M^{\prime}}, \boldsymbol{F}_{k}^{N}\right), \end{array}$

k值初始化为0.

(3)重复(2), k值加1, 直到k值到达设定的阈值K为止.

由此得到三维模型之间的映射结果Π pairMN=Π _Κ , C_K和ε _K, 推导出模型M的变换特征:

$\widetilde{\boldsymbol{F}}_{K}^{M^{\prime}}=\left(\boldsymbol{\sigma}_{K}^{M}+\boldsymbol{\Phi}_{K}^{\mathrm{LMH}} \boldsymbol{\varepsilon}_{K}, \boldsymbol{C}_{K} \boldsymbol{\Phi}_{K}^{\mathrm{LMH}}, \hat{\boldsymbol{n}}_{K}^{M^{\prime}}\right) \in \mathbf{R}^{n_{1} \times(k+6)} .$

5)定义深度内外特征对齐算法网络的损失函数:

$\mathcal{L}_{\text {pair }}=\sum_{k=1}^{K} E_{\text {align }}\left(\boldsymbol{\Pi}_{k} \widetilde{\boldsymbol{F}}_{k}^{M^{\prime}}, \boldsymbol{F}_{k}^{N}\right) .$

给定一组非等距模型簇$\left\{S_{l}\right\}_{l=1}^{n}$, 构造为加权无向完全图$G, \left\{S_{l}\right\}_{l=1}^{n}$为G的顶点, 图G中顶点S_i和S_j之间有权重ω _ij, ∀ i∈ {1, 2, …, n}, j∈ {1, 2, …, n}, i≠ j, 权重ω _ij描述S_i与S_j的对齐程度, 因此S_i与S_j的几何结构越相似, 权重ω _ij越小, 反之越大.ω _ij取值为[0, +¥ ].

因为G为无向图, 而S_i到S_j与S_j到S_i的对齐程度是不一样的, 因此取两者的最小值(即两者最相似度量值)作为权重ω _ij, 最大程度减少误差.ω _ij定义如下:

$\begin{array}{l} \omega_{i j}= \\ \quad \min \left\{E_{\text {align }}\left(\boldsymbol{\Pi}_{\text {pair }}^{s_{i} s_{j}} \widetilde{\boldsymbol{F}}_{K}^{s_{i}}, \boldsymbol{F}_{K}^{s_{j}}\right), E_{\text {align }}\left(\boldsymbol{\Pi}_{\text {pair }}^{s_{j} s_{i}} \widetilde{\boldsymbol{F}}_{K}^{s_{j}^{\prime}}, \boldsymbol{F}_{K}^{s_{i}}\right)\right\} . \end{array}$ (2)

循环一致性是三维模型簇对应关系计算的理想属性, 含义是:理想情况下三维模型簇中任意两个模型间的映射结果等于两个模型之间模型匹配组合映射结果的乘积.例如:对于 {Sl}l=1n中一组匹配组合

γ _1i=(S₁, S₂, …, S_i),

根据循环一致性, 可得其匹配组合映射结果

$\boldsymbol{\Pi}_{\text {coll }}^{S_{1} S_{i}}=\boldsymbol{\Pi}_{\text {pair }}^{S_{1} S_{2}} \Pi_{\text {pair }}^{S_{2} S_{3}} \cdots \boldsymbol{\Pi}_{\text {piri }}^{S_{i-1} S_{i}} \text {. }$

在加权无向图中, 可求解这个匹配组合的最短路径, 通过最短路径匹配组合计算的映射结果比两个模型直接对应的结果更精确.本文采用SPFA计算最短路径.SPFA的原理是通过对图进行多次松弛操作, 得到所有可能的最短路径, 再筛选后得到最优解.图G中顶点S_i和S_j之间最短路径γ _ij定义如下:

$\begin{aligned} \left(\gamma_{i j}\right)_{\text {shortest }}= & \left(S_{i}, S_{q}, \cdots, S_{z}, S_{j}\right)_{\text {shortest }}= \\ & \operatorname{SPFA}\left(G, S_{i}, S_{j}\right) . \end{aligned}$

在最短路径γ _ij下三维模型簇映射结果定义为

$\boldsymbol{\Pi}_{\text {coll }}^{S_{i} S_{j}}=\boldsymbol{\Pi}_{\text {pair }}^{S_{i} S_{q}} \cdots \boldsymbol{\Pi}_{\text {pair }}^{S_{z} S_{j}} .$ (3)

定义SSMM的损失函数:

$\mathcal{L}_{\text {coll }}=E_{\text {align }}\left(\boldsymbol{\Pi}_{\text {coll }}^{s_{i} s_{j}} \widetilde{\boldsymbol{F}}_{K}^{s_{i}}, \boldsymbol{F}_{K}^{s_{j}}\right) .$ (4)

损失函数$\mathcal{L}_{\text {coll }}$对深度内外特征对齐算法网络产生的映射结果与最短路径下三维模型簇映射结果的不一致进行惩罚, 修正三维模型簇对应关系计算的循环一致性.

区别于有监督算法, SSMM未使用先验知识, 式(2)~式(4)中的模型间映射结果与模型的内外融合特征完全由深度内外特征对齐算法计算而成, 三维模型簇对应关系计算的训练依据完全由自身算法计算而来, 因此SSMM是一种自监督的方式.

定义总的损失函数:

$\mathcal{L}=\mathcal{L}_{\text {pair }}+\alpha \mathcal{L}_{\text {coll }}, $

其中, α 为加权超参数, 用于平衡正则化项的权重.通过反向传播更新网络模型参数以不断优化损失函数L, 迭代此过程直至网络收敛.

本文方法的编程语言为Python 3.8.8, 运算平台为CUDA-Toolkit 11.3版本, 采用Cudnn8.8.0作为CUDA上深度学习相关的工具库, 深度学习框架为Pytorch-GPU, 版本号为1.11, 硬件支撑为Core i7处理器和NVIDIA GeForce RTX 3080 GPU(12 GB显存)处理器.

实验中设置批处理尺寸大小为53, 使用Adam(Adaptive Moment Estimation)优化器以端到端的方式训练, 训练过程迭代10 000次.k值的阈值K设为30, 这是因为随着k值从0逐渐增至30, 模型对之间的对应关系质量逐步提高, 而超过30的k值不再影响计算结果的优劣.加权超参数α 设为0.6, 原因在于模型簇损失函数$\mathcal{L}_{\text {coll }}$是根据模型对的结果进行自监督启发构建的, 理论上应确保模型对的对应优于模型簇的对应, 因此给予模型对损失函数$\mathcal{L}_{\text {pair }}$更高的权重, 经过优化实验, 发现$\mathcal{L}_{\text {coll }}$权重值设为0.6时效果最优.

本文选择CONSISTENT ZOOMOUT^[14]、ISOMU- SH^[17]、文献[19]算法、文献[28]算法和文献[29]算法进行非等距模型簇对应关系计算的定性对比.CONSISTENT ZOOMOUT将ZOOMOUT与三维模型簇算法结合, 效果显著.ISOMUSH是基于模板的三维模型簇对应关系算法, 和FM也有密切的联系.文献[19]算法是一种基于FM的深度学习算法, 使用Adam优化器训练10 000个迭代周期, 学习率为0.001.文献[28]算法也是基于深度函数映射的非等距三维模型簇对应关系算法, 同样使用Adam优化器训练10 000个迭代周期, 学习率为0.000 2.文献[29]算法是非刚性模型对(两个模型)的对应关系算法, 虽然并不是针对模型簇的算法, 但是采用近似基函数和可扩展上采样算法, 生成的对应关系结果质量较高, 是具有代表性的非刚性模型对应关系算法.

为了和上述模型簇对应关系算法公平对比, 使用算法依次计算模型簇中每个模型对的对应关系结果.

在定量实验中, 为了进一步验证本文方法的有效性, 除了使用上述5种对应关系算法, 还加入经典的对应关系算法ENIGMA^[9]、Smooth Shells^[10]、文献[11]算法、FM^[5]、ZOOMOUT^[15]进行定量对比.

本文选择SMAL^[30]、DEFORM THINGS4D-MA- TCHING(简记为DTM)^[31]、SHERC'16 Topology(简记为SHERC'16T)^[32]、SHERC'19^[33]、FAUST^[34]、SCA- PE^[35]这6个三维模型数据集进行定性实验和定量实验.

SMAL数据集包含13类动物, 共50幅三维图像, 这些图像都是通过扫描动物雕像得到.DTM数据集是一个基于DEFORM THINGS4D数据集^[36]的合成图像数据集, 包含56个动物类别和8个类人类别, 每个类别包含15~50个不同姿态的三维图像.SHERC'16T数据集由25个非刚性变换的三维模型组成, 这些模型中有大量拓扑伪影噪声.SHERC'19数据集由430个具有不同连通性和网格分辨率的人体模型组成, 使用11个不同数据库的44个人类模型.FAUST数据集包括10个不同人体模型, 每个人体以30个不同的动作进行扫描, 得到300个高分辨率三角网格模型.SCAPE数据集由72个具有不同连通性和网格分辨率的人体模型组成, 每个人体模型的动作各异.

本文方法与CONSISTENT ZOOMOUT、ISOMUSH、文献[19]算法、文献[28]算法和文献[29]算法在SMAL数据集上构建的非等距模型簇对应关系结果对比如表1所示, 使用颜色迁移方式(对应点使用相同的颜色)定性评估算法对应关系结果的准确性.图中源模型为马, 目标模型分别为狐狸、狼、牛和狗.由表可见, CONSISTENT ZOOMOUT虽然不是传统的依靠模板模型的三维模型簇对应关系算法, 但依然需要其它的模型间对应关系算法提供初始化模型对的映射矩阵, 容易引入噪声, 因此在4个目标模型的四肢上均出现不连续的斑块, 牛背部的左右对应关系也是错误的.ISOMUSH利用模型簇构造虚拟的公共模型作为模板模型, 但是构造非等距模型簇的公共模板模型是有难度的, 由第3列可看出, 狐狸的可视化效果不平滑, 呈现斑点状且大面积对应失真, 这说明模板模型在狐狸上的匹配是失效的, 同时算法也受模型自身对称性的影响, 其它3个目标模型的左右对应关系结果都是错误的.

表1

Table 1

表1(Table 1)

表1 SMAL数据集上6种算法构建的非等距模型簇对应关系结果 Table 1 Correspondence results of non-isometric shape collections constructed by 6 algorithms on SMAL dataset 源模型 CONSISTENT ZOOMOUT ISOMUSH 文献[19]算法 文献[28]算法 文献[29]算法 本文方法

表1 SMAL数据集上6种算法构建的非等距模型簇对应关系结果 Table 1 Correspondence results of non-isometric shape collections constructed by 6 algorithms on SMAL dataset

文献[19]算法是基于FM的深度学习方法, 从结果可看出, 模型整体对应结果大致正确, 只是狐狸的匹配质量不高, 尾巴、背部等无法正确辨识, 在其它目标模型上也出现一些局部的错误映射, 视觉上呈现局部的不平滑.

文献[28]算法分别从谱域和空间域的角度上计算模型簇的循环一致性, 并融合结果以提高非等距模型对应关系计算准确率.算法总体对应关系较平滑, 但最大的问题在于牛、狗时存在因模型自身对称性导致的错误匹配.与此类似, 文献[29]算法也存在无法区分对称区域的问题, 细节处理不够精细, 模型颜色的“ 断层” 现象更明显, 如狐狸的头部与牛的四肢, 这是因为一旦模型对应关系结果中出现大量噪声, 模型对的对应关系算法就无法像模型簇对应关系算法那样利用多模型的循环一致性消除单个模型对的噪声.

本文方法也存在一些瑕疵, 如狐狸的腹部和狼的脖颈处有些不平滑, 然而相比其它算法, 本文方法对应关系准确率最高, 语义颜色信息也相对最平滑自然, 能有效区分模型对称特性, 解决模型自身对称性影响对应关系计算的问题, 计算出高质量的非等距模型簇的对应关系结果.

各对比算法在DTM数据集上构建的非等距模型簇对应关系结果对比如表2所示, 源模型和目标模型都是类人的合成模型, 源模型为Crypto, 目标模型分别为Drake、Prisoner、Skeletonzombie、Ortiz.

表2

Table 2

表2(Table 2)

表2 DTM数据集上6种算法构建的非等距模型簇对应关系结果 Table 2 Correspondence results of non-isometric shape collections constructed by 6 algorithms on DTM dataset 源模型 CONSISTENT ZOOMOUT ISOMUSH 文献[19]算法 文献[28]算法 文献[29]算法 本文方法

表2 DTM数据集上6种算法构建的非等距模型簇对应关系结果 Table 2 Correspondence results of non-isometric shape collections constructed by 6 algorithms on DTM dataset

由表2可看出, CONSISTENT ZOOMOUT在DTM数据集上受模型自身对称性的影响较小, 算法的更多问题在于对应失真, 初始化参数噪声对算法的影响是致命的.ISOMUSH的4个目标模型的结果都出现模型左右对应错误的现象, 有严重的总体误差, 算法很难处理非等距模型.文献[19]算法的结果局部是平滑的, 但全局并不平滑, 视觉上呈现斑点状, 同时部分模型在全身各个区域也都无法产生正确的对应结果.文献[28]算法的计算结果质量较低, 可视化效果不够平滑, 算法容易受到模型自身对称性的影响, 在第2个模型的左右对应关系和第4个模型的上下对应关系中都存在错误.在文献[29]算法的结果中, 只有第1个模型的匹配质量较高, 其它模型都出现严重失真, 这表明模型对的对应关系算法无法像模型簇算法那样将高质量的对应关系结果用于辅助其它模型的协同一致计算.

本文方法在多模型匹配上, 利用最短路径的循环一致性, 以尽可能多的上下文信息(包括所有训练模型的共同特征和显著几何特性等)实现模型簇对应关系计算, 越多的模型训练可学到越多的形状拓扑结构.即使在一些特殊模型上, 如第2个目标模型, 其右边的断手和左边的完整手都可正确映射到源模型上, 说明本文方法的计算结果在保持良好局部细节的同时总体误差最小.

各对比算法在SHERC'16T数据集上构建的非等距模型簇对应关系结果对比如表3所示.SHERC'16T数据集上的三维模型含有大量的拓扑伪影噪声, 这些噪声是由三维模型的部分重叠造成拓扑合并与变形产生的, 如第1个与第2个目标模型的小腿弯曲造成的表面区域的重叠、第3个和第4个目标模型的手与脚的接触处等.表3中源模型编号为kid00, 目标模型编号分别为kid05、kid09、kid16、kid22.

表3

Table 3

表3(Table 3)

表3 SHERC'16T数据集上6种算法构建的非等距模型簇对应关系结果 Table 3 Correspondence results of non-isometric shape collections constructed by 6 algorithms on SHERC'16T dataset 源模型 CONSISTENT ZOOMOUT ISOMUSH 文献[19] 算法 文献[28] 算法 文献[29] 算法 本文方法

表3 SHERC'16T数据集上6种算法构建的非等距模型簇对应关系结果 Table 3 Correspondence results of non-isometric shape collections constructed by 6 algorithms on SHERC'16T dataset

由表3可看出, CONSISTENT ZOOMOUT在第3个和第4个模型全身各个区域上都无法产生正确的对应结果.ISOMUSH可处理第3个模型的拓扑伪影噪声, 但在第4个模型的区域重叠处对应计算错误, 而且其它模型的局部细节处理不够平滑, 如第1个与第2个模型的两个手掌、手臂处.文献[19]算法结果中大部分模型的对应关系可视化效果较平滑, 但第4个模型的拓扑伪影噪声处理失败, 模型手掌与脚映射到同一个位置.文献[28]算法在处理拓扑伪影噪声方面表现较成功, 但在局部细节方面仍不够平滑, 对应关系的质量也不高.文献[29]算法无法有效处理模型的拓扑伪影噪声, 甚至在第4个模型的各个区域都无法产生正确的对应结果.本文方法虽然也存在一些问题, 如第2个模型和第4个模型大腿处对应效果不平滑, 但对所有模型拓扑伪影噪声处的对应计算大致正确, 整体对应误差最小, 由此说明本文方法可较好地解决拓扑伪影噪声问题.

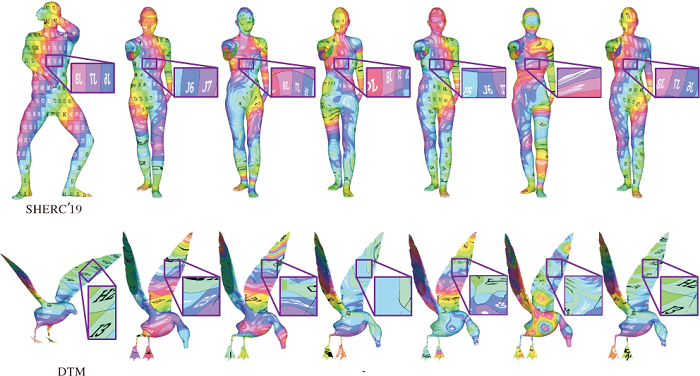
本节通过纹理迁移展示各对比算法在SHERC'19、DTM数据集上构建的对应关系, 具体如表4所示.纹理迁移可直观展示算法双射性的优劣, 反映映射结果的质量.

表4

Table 4

表4(Table 4)

表4 各算法在SHERC'19、DTM数据集上通过纹理迁移得到的对应关系结果 Table 4 Correspondence results of different algorithms presented by texture transfer on SHERC'19 and DTM datasets 数据集 源模型 CONSISTENT ZOOMOUT ISOMUSH 文献[19] 算法 文献[28] 算法 文献[29] 算法 本文方法 SHERC'19 DTM

表4 各算法在SHERC'19、DTM数据集上通过纹理迁移得到的对应关系结果 Table 4 Correspondence results of different algorithms presented by texture transfer on SHERC'19 and DTM datasets

在SHERC'19数据集上, 源模型为男人模型, 编号为33; 目标模型为女人模型, 编号为41.在表4局部的放大框上可看出, 受模型自身对称性结构的影响, CONSISTENT ZOOMOUT和文献[28]算法出现左右颠倒映射的问题, ISOMUSH和文献[19]算法出现大面积的对应失真, 文献[29]算法的结果有严重的总体误差, 而本文方法较好地处理模型自身对称性影响对应关系计算的问题, 目标模型的其它位置也基本没有对应失真.

在DTM数据集上, 源模型为ravenOL, 目标模型为duck.CONSISTENT ZOOMOUT依然出现左右颠倒对应, ISOMUSH、文献[19]算法和文献[28]算法总体误差很大, 特别是文献[19]算法, 在不同数据集上的表现良莠不齐, 说明算法在不同数据集上的泛化能力不足, 文献[29]算法的失真也很严重, 说明该算法并不能处理非等距模型.本文方法映射的连续性最好, 总体映射误差最小, 纹理迁移的结果最接近真实值, 说明双射性优于其它算法.

各对比算法在FAUST、SCAPE数据集上构建的模型簇对应关系结果对比如表5所示.FAUST、SCAPE数据集上存在扫描噪声和模型自身对称性歧义等挑战, 可有效测试算法的性能和准确度.在FAUST数据集上, 源模型编号为tr_reg_083, 目标模型编号为tr_reg_097.在SCAPE数据集上, 源模型编号为mesh007, 目标模型编号为mesh032.

表5

Table 5

表5(Table 5)

表5 各算法在FAUST、SCAPE数据集上构建模型簇对应关系结果 Table 5 Correspondence results of shape collections constructed by 6 algorithms on FAUST and SCAPE dataset 数据集 源模型 CONSISTENT ZOOMOUT ISOMUSH 文献[19] 算法 文献[28] 算法 文献[29] 算法 本文方法 FAUST SCAPE

表5 各算法在FAUST、SCAPE数据集上构建模型簇对应关系结果 Table 5 Correspondence results of shape collections constructed by 6 algorithms on FAUST and SCAPE dataset

由表5可见, CONSISTENT ZOOMOUT、ISOMU- SH和文献[29]算法在2个数据集上都出现模型左右或前后对应错误的情况.虽然文献[19]算法和文献[28]算法在两个数据集上的整体对应关系大致正确, 但是对应关系质量不高, 细节上也不够平滑, 手臂和大腿处存在与周围颜色不连接的区域.本文方法也存在一些瑕疵, 如在SCAPE数据集上右肩膀出现不平滑的颜色断层, 表明出现一些错误的映射分布, 然而本文方法总体准确率最高, 语义颜色信息最平滑自然, 由此说明本文方法具有最强的泛化能力.

本节在SMAL、DTM、SHERC'16T、SHERC'19、FAUST、SCAPE这6个数据集上定量评估各算法计算非等距三维模型簇对应关系的能力.

本文采用PBP(Princeton Benchmark Protocol)^[37]评估不同算法的对应关系精度.具体地, 假设y为目标模型Y上一点, x^* 和x分别为源模型X上与y的真实对应点以及实际对应点, x与y的测地误差e(y)是点x与x^* 的测地距离d_X(x, x^* )在模型X的面积平方根$\sqrt{\operatorname{area}(X)}$上归一化后的结果, 即

$e(y)=\frac{d_{X}\left(x, x^{* }\right)}{\sqrt{\text { area }(X)}} .$

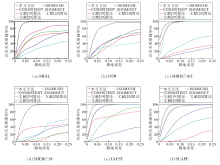
本文方法与CONSISTENT ZOOMOUT、ISOMU-SH、文献[19]算法、文献[28]算法和文献[29]算法在不同数据集上的测地误差曲线如图2所示.测地误差曲线是一种累积分布曲线, 用于指示算法对应关系的性能.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 各算法在6个数据集上的测地误差曲线Fig.2 Geodesic error curves of different algorithms on 6 datasets

由图2可见, 在SMAL数据集上, 本文方法在测地误差为0时对应关系准确率就超过其它5种算法, 并且在测地误差为0.1时达到100%的对应关系准确率, 比效果次优的文献[19]算法准确率提升约10%.在DTM数据集上, 6种算法在测地误差为0.25之前都未达到100%的准确率, 这是因为该数据集是合成图像数据集, 含有大量的拓扑伪影噪声, 而且非等距模型的变形程度很大, 即使测地误差很大时也难以达到完全的正确对应.在SHREC'16T数据集上, 本文方法与文献[19]算法、文献[28]算法的曲线很接近, 在测地误差为0.1时都达到100%的准确率, 然而在测地误差小于0.1时还是有一定的优势, 而且匹配精度也远高于其它3种算法.在SHERC'19数据集上, 本文方法取得最优结果, 准确率比其它3种算法都有较大提升, 比排名次优的文献[19]算法准确率提升约50%.FAUST、SCAPE数据集包含对真实人体的扫描数据, 数据采集过程中可能受到伪影噪声的影响, 本文方法、文献[19]算法和文献[28]算法都能有效处理伪影噪声, 然而, 相比文献[19]算法和文献[28]算法, 本文方法更早达到100%的准确率, 因此, 本文方法的结果更接近于真实情况.

从上述的定量结果可看出, 在非等距三维模型簇对应关系计算上, 本文方法比其它5种算法更精确, 在不同数据集上的计算结果差异更小, 说明泛化能力更强.

为了进一步验证本文方法的性能, 在6个数据集上使用文献[38]提出的度量算法进行定量对比, 指标采用准确度和双射性.算法包括非等距模型簇对应关系算法CONSISTENT ZOOMOUT、ISOMUSH、文献[19]算法、文献[28]算法, 以及模型对的对应关系算法ENIGMA、Smooth Shells、文献[11]算法、FM、ZOOMOUT和文献[29]算法.使用平均测地误差衡量每种算法的准确度, 并通过模型之间复合映射的平均测地误差评估双射性.源模型X与目标模型Y之间的复合映射记为

$\boldsymbol{\Pi}^{X X}=\boldsymbol{\Pi}^{X Y} \boldsymbol{\Pi}^{Y X} .$

各算法在6个数据集上的准确度和双射性对比如表6所示, 表中黑体数字表示最优值.由表可见, 本文方法在所有数据集的测试中都表现出最佳的准确度和双射性, 说明本文方法逐点映射的质量也是最优的.与本文方法最接近的是文献[11]算法和ZOOMOUT, 然而, 文献[11]算法需要标志点的辅助计算, ZOOMOUT的计算结果受初始化参数质量的影响.本文方法能在自动化计算的同时, 实现最优的对应结果.

表6

Table 6

表6(Table 6)

表6 各算法在6个数据集上的准确度和双射性对比 Table 6 Comparison of accuracy and bijectivity of different algorithms on 6 datasets 算法 SMAL DTM SHREC'16T SHERC'19 FAUST SCAPE 准确度 双射性 准确度 双射性 准确度 双射性 准确度 双射性 准确度 双射性 准确度 双射性 CONSISTENT ZOOMOUT 0.078 0.091 0.074 0.094 0.127 0.166 0.153 0.203 0.059 0.084 0.168 0.213 ISOMUSH 0.081 0.111 0.067 0.081 0.142 0.194 0.113 0.137 0.130 0.170 0.045 0.062 文献[19]算法 0.043 0.077 0.069 0.096 0.023 0.048 0.099 0.118 0.038 0.056 0.031 0.059 文献[28]算法 0.101 0.175 0.098 0.178 0.034 0.071 0.083 0.110 0.037 0.058 0.034 0.061 ENIGMA 0.099 0.107 0.101 0.148 0.098 0.144 0.159 0.189 0.148 0.201 0.095 0.149 Smooth Shells 0.037 0.041 0.073 0.094 0.048 0.067 0.069 0.088 0.033 0.062 0.047 0.064 文献[11]算法 0.045 0.063 0.078 0.091 0.032 0.047 0.071 0.094 0.043 0.083 0.035 0.088 FM 0.187 0.243 0.201 0.297 0.243 0.311 0.175 0.241 0.096 0.146 0.093 0.171 ZOOMOUT 0.038 0.076 0.065 0.091 0.049 0.070 0.051 0.088 0.045 0.036 0.027 0.040 文献[29]算法 0.060 0.112 0.071 0.121 0.075 0.131 0.141 0.221 0.050 0.127 0.073 0.146 本文方法 0.021 0.037 0.063 0.071 0.017 0.024 0.050 0.069 0.019 0.031 0.020 0.029

表6 各算法在6个数据集上的准确度和双射性对比 Table 6 Comparison of accuracy and bijectivity of different algorithms on 6 datasets

首先定义如下4种设置:不包含LMH基、不包含SSMM、不包含LMH基和SSMM、包含LMH基和SSMM.在SMAL、DTM、SHREC'16T、SHERC'19数据集上的消融实验结果如表7所示, 表中数据为平均测地误差, 黑体数字表示最优值.

表7

Table 7

表7(Table 7)

表7 本文方法消融实验结果 Table 7 Ablation experiment results of the proposed method 数据集 不包含 LMH基 不包含 SSMM 不包含LMH基 和SSMM 包含LMH基 和SSMM SMAL 0.120 0.091 0.241 0.021 DTM 0.218 0.150 0.306 0.063 SHREC'16T 0.099 0.132 0.196 0.017 SHERC'19 0.186 0.147 0.295 0.050

表7 本文方法消融实验结果 Table 7 Ablation experiment results of the proposed method

由表7可见, 在不包含LMH基的设置下, 本文方法使用LBO基, 平均测地误差明显提高, 这是因为LMH基可结合模型的局部细节和拉普拉斯特征函数获得全局信息, 相比LBO基, 可提高算法对应关系计算的准确率.在不包含SSMM的设置下, 本文方法仅使用深度内外特征对齐算法计算模型对的对应关系, 准确率也有所降低.如果LMH基和SSMM都不使用, 平均测地误差是最高的, 说明算法的不同组成部分相辅相成, 都删除的话会大幅增加平均测地误差.如果同时使用LMH基和SSMM, 平均测地误差最低, 这说明本文方法可有效提高非等距模型簇对应关系计算的准确性.

本节对比本文方法与CONSISTENT ZOOMOUT、ISOMUSH、文献[19]算法、文献[28]算法在SMAL、SHERC'16T、SHERC'19、DTM、FAUST、SCAPE这6个数据集上计算一组非等距模型簇(包含5个非等距模型)对应关系所需的平均运行时间.由于模型对的对应关系算法需要手动依次计算模型簇中每个模型对的对应关系, 因此没有参与模型簇算法对比.CONSISTENT ZOOMOUT和ISOMUSH需要其它算法提供初始化模型对的映射矩阵, 在实验中采用最简单快速的FM生成初始化参数, 因此两种算法实际运行时间要加上FM计算的时间.

各算法运行时间对比如表8所示.由表可见, CONSISTENT ZOOMOUT受模型点数增加的影响较小, 在4种顶点数不同的数据模型上运行时间差不多.ISOMUSH基于模板模型进行计算, 运行时间与模型顶点数呈正比.本文方法、文献[19]算法和文献[28]算法都是基于深度学习的算法, 不需要使用模型对初始化参数, 运行时间不考虑初始化和训练时间, 只计算网络模型的计算测试时间.文献[19]算法通过分类器预测模型到模板的匹配结果, 运行时间是4种算法中最短的.文献[28]算法采用双分支的网络结构, 需要在空间域和谱域上交替优化计算, 运行过程十分耗时.本文方法的运行时间与模型顶点数相关, 实际运行时间仅次于文献[19]算法.由此可看出在计算高质量的非等距三维模型簇对应关系结果的同时, 本文方法在运行时间上也具有优势.

表8

Table 8

表8(Table 8)

表8 各算法在6个数据集上的运行时间对比 Table 8 Runtime comparison of different algorithms on 6 datasets 数据集 顶点数 CONSISTENT ZOOMOUT+FM/s ISOMUSH+FM/s 文献[19]算法/s 文献[28]算法/s 本文方法/s SMAL 5000 116+62 296+62 85 302 102 DTM 8000 112+93 382+93 91 450 161 SHREC'16T 8605 110+104 403+104 92 462 201 SHERC'19 12500 118+130 518+130 120 603 213 FAUST 6890 116+88 312+88 88 391 114 SCAPE 12500 120+139 533+139 125 610 230

表8 各算法在6个数据集上的运行时间对比 Table 8 Runtime comparison of different algorithms on 6 datasets