王文剑,博士,教授,主要研究方向为机器学习、数据挖掘、计算智能.E-mail:wjwang@sxu.edu.cn.
作者简介:

王鑫隆,硕士研究生,主要研究方向为机器学习、图神经网络.E-mail:1757239635@qq.com.

胡 睿,博士研究生,主要研究方向为图表示学习、点云数据分析.E-mail:rynehu@outlook.com.

郭亚梁,硕士研究生,主要研究方向为机器学习、图神经网络.E-mail:591180224@qq.com.

杜航原,博士,副教授,主要研究方向为图表示学习.E-mail:duhangyuan@sxu.edu.cn.

张槟淇,硕士,讲师,主要研究方向为机器学习、数据挖掘.E-mail:843545395@qq.com.
图神经网络通过对图中节点的递归采样与聚合以学习节点嵌入,而现有方法中节点采样与聚合的模式较固定,对局部模式的多样性捕获存在不足,从而降低模型性能.因此,文中提出节点级自适应图卷积神经网络(Node-Level Adaptive Graph Convolutional Neural Network, NA-GCN).设计基于节点重要性的采样策略,自适应地确定各节点的邻域规模.同时,提出基于自注意力机制的聚合策略,自适应地融合给定邻域内的节点信息.在多个基准图数据集上的实验表明,NA-GCN在节点分类任务上具有较优性能.
WANG Wenjian, Ph.D., professor. Her research interests include machine learning, data mining and com-putational intelligence.
About Author:
WANG Xinlong, Master student. His research interests include machine learning and graph neural network.
HU Rui, Ph.D. candidate. His research interests include graph representation learning and point cloud data analysis.
GUO Yaliang, Master student. His research interests include machine learning and graph neural network.
DU Hangyuan, Ph.D., associate profe-ssor. His research interests include graph representation learning.
ZHANG Binqi, Master, lecturer. Her research interests include machine learning and data mining.
Graph neural networks learn node embeddings by recursively sampling and aggregating information from nodes in a graph. However, the relatively fixed pattern of existing methods in node sampling and aggregation results in inadequate capture of local pattern diversity, thereby degrading the performance of the model. To solve this problem, a node-level adaptive graph convolutional neural network(NA-GCN) is proposed. A sampling strategy based on node importance is designed to adaptively determine the neighborhood size of each node. An aggregation strategy based on the self-attention mechanism is presented to adaptively fuse the node information within a given neighborhood. Experimental results on multiple benchmark graph datasets show the superiority of NA-GCN in node classification tasks.
图数据常用于表示非结构化的复杂关系数据, 不遵循欧氏几何空间中的角度和距离规则.图数据在社交网络[1]、生物网络[2]、交通网络[3]等领域都具有广泛的应用.在图数据分析中, 节点分类是最重要的任务之一, 常用于社交网络分析、推荐系统、交通流量预测及化学分子结构预测等.
图神经网络(Graph Neural Networks, GNNs)现已成为处理和分析非欧氏数据的强大工具[4, 5, 6, 7], GNNs通过节点之间的信息传递, 有效捕捉图数据中的依赖关系, 在节点分类任务上具有良好性能.目前大多数节点分类方法是基于图嵌入的表示学习方法[8]或特征工程[9], 这些方法对大规模图数据或复杂的图结构可能存在一定的表示局限性.传统的图嵌入方法往往受限于计算资源和内存容量, 难以有效捕捉全局信息和复杂的结构特征.特征工程通过人工设计以提取节点的特征信息, 但面对高度抽象的图结构时, 很难找到适用的特征表示方法.图嵌入方法和特征工程的局限性导致其节点分类性能较弱.因此, 需要通过在节点之间传递信息并对其进行聚合以学习节点嵌入, 自动捕捉节点之间的复杂关系, 并充分利用图的全局信息和局部信息完成节点分类任务.
近年来, 研究者们针对节点分类GNNs中的嵌入与聚合展开深入研究, 提出一些新的模型, 其中典型代表之一为基于图卷积网络(Graph Convolutional Network, GCN)[10, 11, 12, 13, 14]的方法.值得注意的是, Kipf等[12]提出的GCN可大幅减少参数量并有效降低计算复杂度, 促使许多后续的研究和模型发展.
然而, GCN存在过平滑的问题[15], 特别是在训练深层GCN时, 模型性能急剧下降.为了解决这一问题, Rong等[16]提出DropEdge, 通过随机删除一定比例边的方法降低图的密度, 增加输入数据的多样性, 有效应对GCN面临的过平滑问题.此外, 一些方法引入跳跃连接[17]或残差结构[18, 19], 解决深层GCN的过平滑问题.这些方法采用邻域节点的均值作为聚合策略, 并且均假设图中不同节点的邻域规模是固定的.但这种粗糙的全图学习范式导致模型无法学到局部信息之间的差异性.Li等[20]提出AGCN(Adaptive GCN), 使用自适应性权重矩阵, 根据节点之间的连接关系动态调整卷积层的权重, 有效捕捉不同节点之间的关系.Xu等[21]提出GIN(Graph Isomorphism Network), 一方面提出自适应的特征转换函数, 使网络能灵活调整节点特征的变换, 适应不同的图结构, 另一方面提出选择性地聚合和更新节点特征, 允许节点选择性地保留或丢弃邻域节点的信息, 提高网络对节点特征的建模能力.Veli-č ković 等[22]提出GAT(Graph Attention Networks), 使用注意力机制对目标节点的邻域进行加权, 一定程度上解决GCN中的假设邻域节点同等重要的问题.上述方法致力于精细化每个局部内的操作, 但都未考虑不同局部之间的差异性.
与上述全批训练模型不同的是, Hamilton等[23]提出GraphSAGE(Sample and Aggregate), 通过聚合函数在子图上进行信息传递, 实现对目标节点嵌入的更新.Ying等[24]提出PinSage, 使用重要性采样取代GraphSAGE的均匀采样, 并在聚合中进行重要性加权.邹长宽等[25]提出GraphSage-Degree, 通过节点度中心性对目标节点的邻域进行加权.Chen等[26]减小梯度估计的偏置与方差, 关注采样方法的收敛性.Chen等[27]提出FastGCN, 通过分层采样方式减少处理图数据时所需的内存和计算资源, 从而有效缓解GCN的内存瓶颈问题.Zou等[28]提出LADIES(Layer-Dependent Importance Sampling), 计算邻域节点的重要性作为采样概率, 依概率分层采样固定邻域节点, 在一定程度上缓解邻域爆炸问题.Huang等[29]提出一种自适应分层采样模型, 下层采样均基于上层采样的结果进行, 以此捕捉层之间的相关性, 并通过跳跃连接保持二阶近似. Chiang等[30]提出Cluster-GCN, 通过节点聚类识别关联性较高的邻域节点进行子图采样, 有效提高分批训练的计算效率, 并在一定程度上缓解邻域爆炸问题.Zeng等[31]提出GraphSAINT(Graph Sampling Based Inductive Lear-ning Method), 基于随机游走策略优化子图采样, 减小子图间的方差, 并通过归一化减小训练中的估计偏差.Bai等[32]提出RWT(Ripple Walk Training), 基于随机游走和逐层扩张进行子图采样.Zeng等[33]提出SHADOW-GNN(Decoupled GNN on a Shallow Subgraph), 在子图上训练不同深度的模型, 解耦模型的深度和节点邻域, 有助于缓解过平衡问题.上述基于不同采样策略的方法不必受限于整个图的全局结构, 通常具有较强的局部性和精细化的邻域分析, 但它们仅在局部内进行细粒度操作, 每个局部之间的操作模式都是固定的, 未考虑不同局部之间的差异性.
因此, 为了使模型具有更优的分类性能, 需要构建一种更灵活的自适应图神经网络方法, 在不同局部结构间灵活调整学习策略, 实现对节点特征和图结构的个性化学习, 即模型能自主关注那些对分类任务具有重要性的节点和特征, 减少对与任务无关节点的依赖, 从而提高模型对差异性局部信息的建模能力.这种自适应性模型也符合现实应用的需要.
基于上述分析, 本文从采样和聚合两个方面考虑自适应性, 提出节点级自适应图卷积神经网络(Node-Level Adaptive Graph Convolutional Neural Net-work, NA-GCN), 基于对节点的重要性评估, 设计自适应的采样方法, 进行差异化邻域划分.同时设计自适应的聚合器, 精细化融合不同的局部信息.相比GNN, 这种自适应性有助于网络捕获图不同局部信息中的多样性和差异性, 学习更具判别性和表征性的节点嵌入.在多个基准图数据集上的大量实验表明, NA-GCN的节点分类性能更优.
对于给定图数据集, 可表示为无向无权图G(V, E, X), 其中, V={v1, v2, …, vN}表示节点集合, N表示节点数; E表示边的集合, ${{e}_{ij}}=< {{v}_{i}}$, vj> ∈ E表示节点vi、vj之间的边; X={x1, x2, …, xn}∈ RN× F表示节点特征矩阵, xi∈ RF表示节点vi的F维特征.
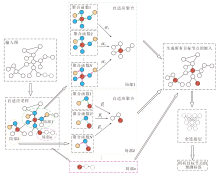
本文提出节点级自适应图卷积神经网络(NA-GCN), 主要由自适应采样和自适应聚合两部分组成, 总体框架如图1所示.
对于给定输入图, NA-GCN首先在自适应采样中根据节点的度为目标节点采样不同规模的邻域.然后, 在自适应聚合中对目标节点及其邻域构成的子图使用多种不同类型的聚合函数进行差异化聚合, 并通过自注意力机制学习每个聚合函数的权重.最后, 生成所有目标节点的嵌入, 并通过全连接层, 使用目标节点的嵌入进行标签预测.
基于谱图理论的视角, 图卷积神经网络的理论基础为图滤波, 基本模型可总结为图(节点)信号的传递和图池化:
Xl+1=G* Xl=Φ (F(Xl)), (1)
其中, G表示卷积算子, * 表示卷积运算符, Φ (· )表示池化, F(· )表示滤波算子, X表示图信号.NA-GCN也处于式(1)描述的理论框架内.
Defferrard等[11]首次利用切比雪夫多项式将式(1)中的G参数化为gθ , 即
Xl+1=G* Xl=Ugθ (Λ )UTXl,
其中, Λ ∈ RN× N表示图谱矩阵, UΛ UT=L表示图上的拉普拉斯信号.进一步, 对gθ (Λ )参数化逼近, 有
${{g}_{\theta }}(\Lambda )=\overset{K-1}{\mathop{\underset{k=0}{\mathop \sum }\, }}\, {{\theta }_{k}}{{\Lambda }^{k}}=\overset{K-1}{\mathop{\underset{k=0}{\mathop \sum }\, }}\, {{\theta }_{k}}{{T}_{k}}\left( \widetilde{\Lambda } \right)$, (2)
其中, ${{T}_{k}}\left( \widetilde{\Lambda } \right)$和θ k分别表示k-阶切比雪夫项及其系数,
$\widetilde{\Lambda }=\frac{2\Lambda }{{{\lambda }_{\text{max}}}}-{{I}_{n}}$,
λ max表示最大谱信号.
GCN[12]最终采用式(2)的二阶截断展开式:
$g{{'}_{\theta }}(\Lambda )\approx {{\theta }_{0}}{{T}_{0}}\left( \widetilde{\Lambda } \right)+{{\theta }_{1}}{{T}_{1}}\left( \widetilde{\Lambda } \right)={{\theta }_{0}}X+{{\theta }_{1}}(L-{{I}_{n}})X$,
再令θ =θ 0=-θ 1, 得
$g{{'}_{\theta }}(\Lambda )\approx \theta {{\widetilde{D}}^{-\frac{1}{2}}}~({{I}_{n}}+A){{\widetilde{D}}^{-\frac{1}{2}}}X$.
不难看出, GCN在进行图滤波运算时仅考虑节点自身及其一阶邻居In+A, 而NA-GCN是针对不同节点对式(2)的自适应阶数展开, 因此GCN可视为NA-GCN的特例.
GCN虽源于图滤波, 但也暗含图卷积神经网络的空间解释, 即式(1)中的第2项.具体地, Φ (· )对应均匀池化${{\widetilde{D}}^{-\frac{1}{2}}}$, F(· )对应一阶信息传递In+A.而GraphSAGE[23]进一步将GCN扩展到面向大图的应用场景中, 并首次形式化图卷积神经网络的空间解释:
$x_{i}^{l+1}=\theta \left( x_{i}^{l}|\underset{N\left( i \right)}{\mathop{\text{max}}}\, (x_{j}^{l}, j\in N(i)) \right)$,
其中, $(\cdot |\cdot )$表示逐通道维度的拼接算子, N(· )表示节点邻域.由于不同邻域内的信息聚合受到邻域内各节点信息间关系的影响, 本文提出一个自适应的聚合策略, 是对GraphSAGE的泛化, 具体内容见1.3节.
大多数GNN并不关注节点在图中的重要性以及图的结构信息, 对所有的节点均传递相同规模的邻域信息(如K跳内所有的邻域特征信息, 或对节点的邻域进行固定采样).本文提出的自适应采样方法根据节点在图中的重要性进行采样.节点在图中的重要性越高, 采样相对越多的邻域节点, 为图中重要性较高的节点聚合越多的邻域信息, 越好捕捉图中重要局部信息.反之, 节点在图中的重要性越低, 采样相对越少的节点.该方法在采样邻域节点时使用均匀采样而不是调整不同邻域节点被采样的概率(如基于重要性采样).这种均匀采样会使网络拥有一定的随机性, 确保其更好的学习能力和泛化能力, 并且不会使网络倾向于选择出现频率较高的节点, 导致对低频但重要的节点学习不足.在一定程度上缓减不同重要性节点学习偏差的问题.这种自适应采样方法使网络既能将注意力放在图中重要性较高的节点上, 又能减轻噪声信息的影响.另一方面, 网络也未完全忽略对边缘信息的学习, 通过差异化地采样图中节点的邻域, 有效控制采样节点的规模, 抑制邻域爆炸现象的发生.
对于每个节点v∈ V, NA-GCN将其作为目标节点并对其邻域进行自适应采样, 生成由内到外K层的子图, 其中位于第k(1≤ k≤ K)层的目标节点v采样Skv个邻域节点, 则
${{S}_{kv}}={{\lambda }_{v}}{{\psi }_{k}}=\frac{{{D}_{v}}}{{{D}_{\text{max}}}}{{\psi }_{k}}$,
其中, λ v表示节点v的采样概率, ψ k表示目标节点v在第k层的最大邻域采样数, Dv表示节点v的度, Dmax表示图中最大节点度数.
考虑到大部分图数据的分布是稀疏的, 即图中部分节点的采样概率λ v非常小, 可能导致无法计算节点在该层的采样数.因此本文为每个目标节点设置概率阈值θ , 即
${{S}_{kv}}=\max \left( \frac{{{D}_{v}}}{{{D}_{\text{max}}}}, \theta \right){{\psi }_{k}}$.(3)
图2为不同局部的目标节点自适应采样示意图, 图中, 虚线划分目标节点采样得到的一阶邻域和二阶邻域, 箭头方向表示采样方向.图中输入图的最大节点度数Dmax=10, 第1层最大邻域采样数ψ 1=7, 第2层最大邻域采样数ψ 1=5, 概率阈值θ =0.3.目标节点v1自适应采样的一阶邻域节点数
S11=max(0.7, 0.3)× 7≈ 5,
对v1的邻域均匀采样5 个节点得到如(a)所示的一阶邻域节点.再通过迭代的方式对v1的一阶邻域节点进行自适应采样, 得到其二阶邻域节点.(b)为边缘节点v2的自适应采样示意图, 采样过程与(a)中重要节点v1的采样过程相同.从图2可直观看到, 对于图中的重要节点和边缘节点, 采样的邻域规模是不同的, 可实现对不同局部的差异性学习.
由于图中节点及其邻域的差异性, 不同的局部信息应使用不同类型的聚合函数[34].本文提出对不同的局部信息使用适应性的聚合函数, 即同时使用平均聚合函数、完全平均聚合函数和最大值池化聚合函数, 并通过自注意力机制学习每个聚合函数的适应性权重.自适应聚合函数:
h=α 1h1+α 2h2+α 3h3, (4)
其中, α 1、α 2、α 3分别表示3种聚合函数的适应性权重, 通过自注意力机制学习得出其值, α 1+α 2+α 3=1.平均聚合函数h1、完全平均聚合函数h2和最大值池化聚合函数h3分别定义如下:
h1=MEAN(hu, ∀ u∈ Smp(v)), (5)
h2=MEAN(hv∪ {hu, ∀ u∈ Smp(v)}), (6)
h3=max({σ (W1hu+b), ∀ u∈ Smp(v)}), (7)
其中, MEAN(· )表示对目标节点v的邻域节点的嵌入hu求均值, Smp(v)表示目标节点v的自适应采样邻域, hv表示目标节点的嵌入, max(· )表示逐元素取最大值, σ 表示非线性激活函数(本文采用ReLU函数), W1表示可学习的权重矩阵, 可通过梯度下降方法进行更新, b表示偏置项.
在邻域信息聚合后, 将目标节点的嵌入与自适应聚合的邻域嵌入进行拼接, 以更新目标节点的嵌入, 拼接方法如下:
hv=σ (W2· CONCAT(hv, h)), (8)
其中, CONCAT(· , · )表示拼接操作, h表示自适应聚合后的邻域嵌入, W2表示可学习的权重矩阵, 也通过梯度下降方法进行更新.
图3为目标节点邻域的自适应聚合示意图, 图中箭头方向表示消息传递的方向.如图所示, NA-GCN通过迭代的方式为节点v聚合不同层的邻域信息, 在第1次迭代中, 节点v的一阶邻域分别根据式(4)~式(8)聚合它们的一阶邻域信息; 在第2次迭代中, 节点v根据式(4)~式(8)聚合其一阶邻域信息.但由于不同局部节点采样的邻域规模不同, 导致不同节点聚合的邻域信息量有所不同, 实现对不同局部的差异性学习.
NA-GCN通过迭代的方式为目标节点聚合不同层的邻域信息以更新其自身嵌入, 迭代过程主要分为3个阶段.1)计算目标节点v在该次迭代过程中的邻域采样数并进行采样; 2)聚合该次迭代过程中采样的邻域信息并与目标节点的嵌入进行拼接; 3)对该次迭代过程中更新的目标节点嵌入进行正则化.在迭代更新后, 算法生成目标节点的最终嵌入.最后, 使用目标节点的最终嵌入进行标签预测.算法主要步骤如算法1所示.
算法1 NA-GCN
输入 图G(V, E, X)
输出 所有目标节点v的类别标签集合L
step 1 初始化节点嵌入$h_{v}^{0}\leftarrow {{x}_{v}}$, ∀ v∈ V, 模型层数K, 第k层最大邻域采样数ψ k, 概率阈值θ , 权重矩阵W1、W2、W3, 偏置项b, L=Ø , 训练轮数T.令当前训练轮数t=1.
step 2 令k=1.
step 3 当k≤ K时, 迭代执行step 3.1~step 3.4.
step 3.1 根据式(3)计算所有目标节点v的第k层自适应采样数Skv, 并进行采样.
step 3.2 根据式(4)~式(7)自适应聚合邻域信息hk.
step 3.3 将目标节点的嵌入与自适应聚合的邻域嵌入进行拼接, 以更新目标节点的嵌入
$h_{v}^{k}=\sigma ({{W}_{2}}\cdot CONCAT(h_{v}^{k-1}, {{h}^{k}}))$.
step 3.4 正则化$h_{v}^{k}=\frac{h_{v}^{k}}{\|h_{v}^{k}{{\|}_{2}}}$, 并令k=k+1.
step 4 生成所有目标节点v的最终嵌入${{z}_{v}}=h_{v}^{k}$.
step 5 计算所有目标节点v的类别概率分布
Pv=softmax(W3· zv).
step 6 使用交叉熵损失函数计算损失值, 并通过Adam(Adaptive Moment Estimation)优化器更新W1、W2、W3和b.
step 7 令t=t+1, 若t≤ T, 转至step 2, 否则转至step 8.
step 8 获取所有目标节点v的类别
yv=arg max(Pv).
step 9 将所有目标节点v的类别加入L中.
step 10 算法结束.
NA-GCN的计算复杂度主要来自于自适应采样和自适应聚合.假设每个批处理中节点v的一阶平均邻域采样数为Sa1, 二阶平均邻域采样数为Sa2, 一阶最大邻域采样数为Sm1, 二阶最大邻域采样数为Sm2, 节点特征维度为d.则对于自适应采样方法, 在最坏的情况下, 时间复杂度为
O(2Sm1+Sm1Sm2+1)≈ O(Sm1Sm2).
但由于图数据中节点度均服从幂律分布, 因此记自适应采样的时间复杂度为O(Sa1Sa2).对于自适应聚合方法, 记一个节点总平均邻域数为Sa, 则其时间复杂度为
O((2Sad)+(Sad2+Sad))≈ O(Sad2).
因此, NA-GCN处理N个节点的总时间复杂度为
O(N(Sa1Sa2+Sad2)).
NA-GCN的时间复杂度与GraphSAGE等相比并没有过度增加, 但却较好地实现差异化学习不同的局部信息.
为了验证NA-GCN的有效性, 在引文网络数据集(Cora、Citeseer、Pubmed[12])和社交网络数据集(Reddit[23]、Flickr[31])上进行实验.数据集统计信息如表1所示.
| 表1 实验数据集 Table 1 Experimental datasets |
Cora数据集是一个常用于节点分类的基准数据集, 包含关于机器学习论文的一些数据信息, 如作者、标题和出版物等.数据集包含2 708篇论文, 分为7类.
Citeseer数据集是计算机领域的学术论文数据集, 包含文献、作者和引用关系等信息.由美国宾夕法尼亚州立大学的计算机科学和工程系创建, 包含3 327篇科技论文, 涉及6个不同的研究领域.
Pubmed数据集是全球最大的生物医学文献数据库之一, 包括来自医学、护理、牙科、兽医等生物医学领域的文献摘要和全文.本文使用的Pubmed数据集包含19 717篇关于糖尿病的科学出版物, 分成3类.
Reddit数据集采集于名为Reddit的公共社交媒体网站, 包含各种社区话题、用户评论、帖子、投票数据、用户个人资料和社区信息等.本文使用的Reddit数据集涉及41类, 232 965篇Reddit博客.
Flickr数据集是一个包含数百万幅图像的大型图像数据集, 主要由Flickr网站上的用户上传和共享的图像组成.本文使用的Flickr社交网络数据集是用户分享图像和视频的社交网络, 共有89 250位用户, 分成7类.
本文采用的性能评价指标主要有准确率(Accu-racy)和Micro-F1分数, 定义如下.
$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}$,
其中, TP表示真正例, FP表示假正例, TN表示真反例, FN表示假反例.
$F{{1}_{micro}}=2\left( \ \ \frac{ \ Precisio{{n}_{micro}\ \ } \ \ \ \ \cdot \ \ \ Recal{{l}_{micro}\ \ }\ \ \ }{ \ \ Precisio{{n}_{micro\ \ }}\ \ + \ \ Recal{{l}_{micro}\ \ \ \ }\ \ } \ \ \right)$,
其中, Precisionmicro表示所有类别精确率的总和, Recallmicro表示所有类别召回率的总和.
在直推式学习任务上与如下10个基线网络进行对比:1)Raw Features.仅基于节点原始特征的逻辑回归分类器.2)MLP(Multilayer Perceptron).由两层神经网络构成的感知机.3)文献[11]网络.使用切比雪夫多项式近似图滤波的算法.4)GCN[12].逐层聚合和更新节点特征的图卷积算法.5)GCN-DSM[14].根据节点相似度选取消息传递的邻域并使用GCN学习节点嵌入.6)GAT-DSM[14].根据节点相似度选取消息传递的邻域并使用GAT学习节点嵌入.7)GAT[22].基于注意力机制聚合邻域节点信息的算法.8)DeepWalk[35].基于深度游走的图嵌入算法.9)Graph-MLP(Simple MLP-Based Graph Learning Framework)[36].在图中不使用消息传递的节点分类算法.10)GATv2[37].基于动态注意力机制聚合邻域节点信息的算法.
在归纳式学习任务上与如下10个基线网络进行对比:1)Random.随机分类器.2)Raw Features.3)GraphSAGE[23].基于采样的图卷积算法(使用mean型聚合函数).4)PinSage[24].基于重要性采样的图卷积算法.5)FastGCN[27].基于分层采样的图卷积算法.6)LADIES[28].基于分层重要性采样的图卷积算法.7)Cluster-GCN[30].通过节点聚类进行子图采样的图卷积算法.8)GraphSAINT[31].基于子图采样策略的高效图神经网络训练算法.9)RWT[32].基于随机游走逐层扩张的子图采样算法.10)Deep-Walk+feature[35].结合原始特征的基于深度游走的图嵌入算法.
在直推式学习任务中, 本文使用Core、 Cite-seer、Pubmed引文网络数据集, 其中每类使用20个节点训练, 在1 000个测试节点上评估网络的预测能力, 在500个额外的节点上测试网络的泛化能力[38].
在归纳式学习任务中, 本文使用Reddit、Flickr社交网络数据集.对Reddit数据集的划分如下:训练集占66%, 验证集占10%, 测试集占24%.对Flickr数据集的划分如下:训练集占50%, 验证集占25%, 测试集占25%.2个数据集的划分方式参考文献[31], 对比网络均遵循各自文献中的设置.
本文使用Mini-batch方式训练NA-GCN, 设置批处理大小为512, 最大迭代轮数为200, 模型层数K=2, 初始学习率为0.001.
实验中所有方法的代码均基于Pytorch框架并使用Adam优化器实现, 每项实验的最终结果均取10次独立重复实验的平均准确率(直推式)或平均Micro-F1分数(归纳式).所有的实验均运行在基于40G RAM和NVIDIA Tesla A100 GPU的Ubuntu 18.04平台上.
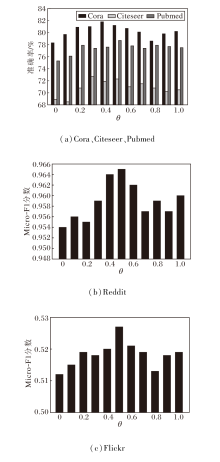
在自适应采样中, θ 的作用是限制采样规模.本文首先考察θ 对节点分类性能的影响.不同数据集上θ 对分类准确率的影响如图4所示.当θ =0时, 表示不对节点邻域的采样比例做任何限制; 当θ =1时, 表示不进行自适应采样, 退化为固定邻域采样.从图可看出, 在5个数据集上节点分类性能都随θ 值的增加呈现先增后减的趋势.当θ 分别为0.4、0.3、0.5、 0.5、 0.5时, NA-GCN在Cora、Citeseer、Pubmed、Reddit、Flickr数据集上的节点分类准确率或Micro-F1分数最高.当θ 较小(如为0)时, 由于图数据的稀疏性, 导致节点度数较低的节点几乎无法采样到邻域节点, 即图中许多边缘节点无法从其邻域中聚合信息, 从而难以生成高质量的节点嵌入, 进而影响节点分类的性能.当θ 较大(如为1)时, 自适应采样的能力受到严重限制, 过度考虑图数据的稀疏性, 在这种情况下, 图中绝大多数节点都无法进行自适应采样, 导致一些小规模数据集上的节点可能采样较大规模的邻域, 引起过拟合和邻域爆炸等问题, 从而导致节点分类性能的下降.
在后续实验中, 本文在Cora、Citeseer、Pubmed、Reddit、Flickr数据集上分别设置θ 为0.4、0.3、0.5、0.5、0.5.
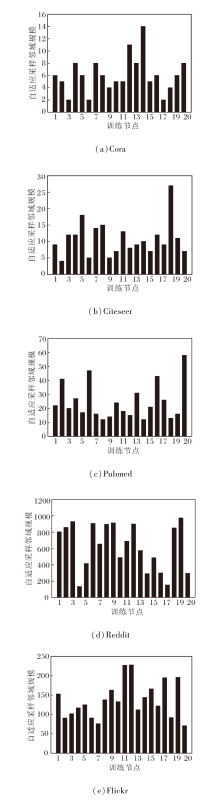
在不同数据集上θ 取上述值时, 1个迭代周期中训练节点的自适应采样结果如图5所示.
图5中对于每个数据集, 均随机选择20个训练节点进行统计.当使用固定邻域采样时, 训练节点采样的邻域节点数量相同, 即采样邻域规模在图中是一条直线.而从图可看出, 每个训练节点均进行差异化的采样过程, 邻域节点数量是不同的.
在直推式学习任务中, NA-GCN与10个基线网络在Cora、Citeseer、Pubmed数据集上的节点分类平均准确率如表2所示, 其中黑体数字表示最优节点分类结果.
| 表2 直推式学习任务上节点分类准确率对比 Table 2 Comparison of node classification accuracy on transductive learning tasks % |
从表2可看到, 相比Raw Features、MLP和Deep-Walk, NA-GCN在Cora、Citeseer、Pubmed数据集上节点分类准确率都有所提升.文献[11]网络、GCN和GAT等图神经网络的性能也明显优于Raw Fea-tures、MLP等传统分类网络和DeepWalk等图嵌入网络.
由表2还可看出, NA-GCN在3个引文网络数据集上的节点分类性能明显优于基线网络, 均实现最优节点分类.值得注意的是, 在Cora、Pubmed数据集上, 相比次优的GAT-DSM, NA-GCN的节点分类性能的提升并不显著(0.1%和0.2%).这是由于Cora数据集上节点规模较小, 限制NA-GCN的自适应采样的性能发挥.而Pubmed数据集上节点特征维度仅有500维, 在直推式学习模式下, 训练节点数目相对较少, 可能无法充分提取更多有效信息.在Citeseer数据集上, NA-GCN的节点分类性能明显更优, 这得益于Citeseer数据集的高维度节点特征信息, 使NA-GCN的自适应聚合得到充分发挥.
在归纳式学习任务中, NA-GCN与10个基线网络在Reddit、Flickr数据集上的平均Micro-F1分数如表3所示, 表中黑体数字表示最优节点分类结果.从表可看到, NA-GCN在2个社交网络数据集上的节点分类性能明显优于各基线网络, 均实现最优节点分类.
| 表3 归纳式学习任务上节点分类Micro-F1分数对比 Table 3 Comparison of node classification Micro-F1 scores on inductive learning tasks |
较大规模社交网络通常具有复杂的拓扑结构, 单一的局部处理模式无法完全适应于社交网络中所有复杂局部信息, 而NA-GCN的自适应能力使其能在不同局部间更灵活地调整学习策略, 有效捕捉网络中节点之间的复杂关系, 更好地适应社交网络的不同局部信息, 从而提升节点分类性能.
为了验证自适应采样和自适应聚合的有效性, 设计NA-GCN的3种变体:标准模型(Base)、仅使用自适应采样(Adaptive Sample, AS)、仅使用自适应聚合(Adaptive Aggregation, AA).NA-GCN及3种变体在5个数据集上的节点分类性能如表4所示, 表中黑体数字表示最优值.由表可知, NA-GCN在5个数据集上的节点分类性能始终优于所有变体.由此验证自适应采样和自适应聚合的有效性.
| 表4 不同设置下的消融实验结果 Table 4 Ablation experiment results under different settings |
为了定量分析NA-GCN与各种对比网络之间的节点分类性能是否存在显著性差异, 使用Friedman检验和成对t检验量化不同实验中不同网络之间的性能差异, 在适用的情况下报告χ 2统计量(或T统计量)和p值.这两种显著性检验是基于不同方法的节点分类性能排名, 本质上是通过Friedman检验整体测试不同方法之间是否存在显著性差异, 后续通过成对t检验分别测试NA-GCN是否优于其它对比网络.由于本文只有5个不同设置的小样本量, 显著性检验有一定的误差和不足, 但仍是评估不同网络相对性能的有效定量分析方法.
直推式学习任务上, 各网络的Friedman检验结果
χ 2=27.538, p=0.002< 0.05,
表明直推式对比实验中不同网络之间的节点分类性能显著不同, 后续成对t检验结果如表5所示.
| 表5 成对t检验结果 Table 5 Results of matched t-test |
从表5中可看到, NA-GCN与GATv2、GAT-DSM、GCN-DSM、GAT、GCN、文献[11]网络、DeepWalk、MLP和Raw Features的节点分类性能显著不同, NA-GCN与Graph-MLP的节点分类性能不存在显著性差异(p=0.104> 0.05).
对于归纳式对比实验, NA-GCN与各种对比网络的节点分类性能不存在显著性差异(p> 0.05), 这是由于数据量较少(2个数据集), 成对t检验的误差较大.
结合节点分类准确性实验结果和显著性检验结果可以看到, NA-GCN性能优于各对比网络.
本文提出节点级自适应图卷积神经网络(NA-GCN), 充分考虑节点的重要性, 借助自适应节点采样和自适应邻域聚合, 可适应性地调整采样和聚合过程, 准确捕捉图结构和节点的特征信息, 有助于更好学习图数据中节点的嵌入, 确保模型能在分类过程中做出更优决策, 进而提升节点分类性能.
NA-GCN在大规模高维数据集上能获得较优的节点分类结果, 但对于节点数量较少或特征维度较低的数据集, 节点分类效果的提升并不明显.为此, 值得进一步研究更精准的采样策略.另外, 在实际应用中, 图数据集可能存在节点标签或图标签的缺失, 采用人工方式获取节点标签或图标签的成本较高, 而机器标注方式难以保证标签的有效性.针对这一问题, 今后将围绕模型在无监督场景或半监督场景下的拓展开展研究.
本文责任编委 郝志峰
Recommended by Associate Editor HAO Zhifeng
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|