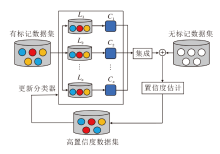
半监督集成学习(SSEL)通过结合特定领域的知识或其它优化算法, 利用半监督学习和集成学习的特性对模型不断迭代更新, 使模型性能不断增强.SSEL框架如图1所示.具体执行步骤如下.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 SSEL框架图Fig.1 Framework of SSEL algorithm

step 1 依据需要划分数据集的特征空间, 利用特定的数据生成策略从数据集D上获取训练集L.

step 2 在训练集L上训练n个不同的基分类器C₁, C₂, …, C_n.

step 3 基分类器C₁, C₂, …, C_n对无标记样本集U上的每个样本U_i(i=1, 2, …, k)进行伪标记的标注, 得到高置信度样本集 U¯.

step 4 高置信度样本集 U¯加入训练集L中.

step 5 从无标记样本集U中删除高置信度样本集 U¯.

step 6 重复step 2~step 5, 直至终止条件.

从SSEL框架中可发现, 划分视图、训练有分歧的分类器、置信度评判及终止是SSEL的关键步骤.

对于多视图任务, 训练有分歧的分类器是通过将数据集划分为不同的特征子空间这一方式进行的, 常见的划分方式有随机划分、均匀划分、有序划分等.对于单视图任务, 可将数据集划分为多个不同的训练子集, 常见策略是选择不同的分类器、优化分类器超参数或Boosting的训练方式等.

置信度评判标准是对无标记样本有效利用的准则, 若置信度评判标准选择恰当, 能最大限度发挥无标记样本的作用, 提升分类器性能.反之, 分类器的性能将在迭代过程中不断下降, 导致过拟合现象的出现.针对不同问题, 置信度评判标准有不同的选择方式, 如分类器的预测概率、数据的相似性结构等.

算法最终停止需要满足终止条件.一种常见的方式是将无标记样本全部打上伪标记, 并加入训练集中, 这种方式可能会引入一些误分类的样本, 导致分类器分类性能的下降.另一种常见的方式是到达指定的迭代次数之后停止训练, 此时会丢弃一些无标记样本.这种方式有利于加快分类器的训练速度, 但不利于提升模型的泛化能力.

在机器学习中, 有多种不同形式的不确定性, 最常见的是模型输出的概率分布.一般而言, 不确定性主要分为模型的不确定性和数据的不确定性.

1)模型的不确定性.模型自身对输入数据的估计可能因为训练不佳、训练数据不够等原因而不准确, 与某一单独的数据无关.因此, 这种不确定性可通过增加训练数据的数量、对数据进行预处理、调节模型的超参数等方式降低不确定性.

2)数据的不确定性.描述数据中内在的噪声, 该噪声无法忽视, 这个现象不能通过增加采样数据以避免.例如, 拍照的手略微颤抖画面就会模糊, 这种数据不能简单的通过增加拍照次数消除.因此, 解决这类问题的方式一般是提升数据采集时的稳定性、使用平滑技术、进行异常值处理或采用特定领域的知识.上述方式虽然不能完全避免“ 噪声” 的影响, 但也能尽量减少这一负面因素对分类器性能的影响.

在机器学习中, 分类风险^[30]是指分类模型对新样本进行分类时可能引入的错误或不确定性, 是评估模型准确性和鲁棒性的重要指标之一.分类风险除了可以帮助预测类别标签以外, 还可以估计模型对样本分类的不确定性.本文使用正态分布刻画分类器对样本进行标注的风险, 即计算样本类间正态分布的交叠面积, 这个交叠面积即为分类风险的值, 以此度量不确定性的标准, 它可用于对比样本所属的不同类之间的相似性.

对于一个m分类任务{P_1i, P_2i, …, P_ni}, i=1, 2, …, m, 对应的概率密度函数为:

${{P}_{i}}(x)=\frac{1}{\sqrt{2\pi }{{\sigma }_{i}}}\exp \left[ -\frac{1}{2}{{\left( \frac{x-{{\mu }_{i}}}{{{\sigma }_{i}}} \right)}^{2}} \right]$.(1)

其中均值和标准差计算如下:

${{\mu }_{i}}=\frac{1}{n}\overset{n}{\mathop{\underset{j=1}{\mathop \sum }\, }}\, {{P}_{ji}}$,

${{\sigma }_{i}}\text{=}\sqrt{\frac{1}{n-1}\overset{n}{\mathop{\underset{j=1}{\mathop \sum }\, }}\, {{({{P}_{ji}}-{{\mu }_{i}})}^{2}}}$.

类u和类v的分类风险可由概率密度函数之间的相交面积进行估计, 即

$Ris{{k}_{uv}}=\underset{-\infty }{\overset{+\infty }{\mathop \int }}\, \min \{{{p}_{u}}(x), {{p}_{v}}(x)\}\text{d}x$.(2)

可通过概率密度函数(式(1))和分类风险(式(2))计算相交区域的面积.

在二分类任务下, 对于某一个无标记样本, 利用多个分类器对其进行预测, 可得到图2所示的分类风险图.若得到图2(a)的分类风险图, 不难看出, 类1和类2的相交区域面积过大, 表明该样本的分类风险较高.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 二分类任务下的分类风险图Fig.2 Classification risk for binary classification

分类风险能表示类间的区分度, 它的区分度越小, 越不利于对无标记样本的类别进行判定.若得到图2(b)的分类风险图, 类1和类2的相交区域面积很小, 说明该样本的分类风险较低, 分类的准确性和稳定性较高, 因此有较大把握确定该样本的类别为类2, 从而使样本能够被正确分类.

在多分类任务下, 假设有3类样本, 对于某一个无标记样本, 利用多个分类器对其进行预测.从图3的高分类风险图中不难看出, 类1和类2、类1和类3以及类2和类3的相交区域面积都很大, 无法判定样本类别.从图4的低分类风险图中可看出, 类1和类2的相交区域面积较大, 类3和类1、类2的相交区域面积较小.由于分类风险表示类间的区分度, 类3与其余两类的区分度较明显, 表明该样本的分类风险较低, 分类的准确性和稳定性较高, 因此将样本类别判定为类3.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 多分类任务下的高分类风险图Fig.3 High classification risk for multi-class classification

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 多分类任务下的低分类风险图Fig.4 Low classification risk for multi-class classification

给定若干分类器, 在极端情况下, 每个分类器对样本的预测概率均为(0.33, 0.34, 0.33), 每个分类器对样本的预测结果均为第2类样本, 那么传统的半监督集成学习算法将样本结果预测为第2类, 并且样本的置信度非常高.事实上, 每个分类器对样本预测的不确定性都非常大, 并无很大把握将其正确分类, 若强行分类会增大误分类风险, 使分类器性能恶化.由图3可知, 分类风险使用正态分布拟合每一类别对应的输出, 根据式(2)计算的类间交叠面积会非常大, 则将该样本判定为低置信度样本, 通过后续迭代重新对其预测, 从而避免出现在不确定性较大的情况下强行分类的现象.

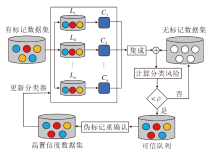
本文提出基于分类风险的半监督集成学习算法(CR-SSEL), 框架如图5所示.具体执行步骤如下.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 CR-SSEL框架图Fig.5 Framework of CR-SSEL

step 1 利用Bootstrap策略获取有标记样本集L, 并训练n个基分类器C₁, C₂, …, C_n.

step 2 基分类器C₁, C₂, …, C_n对无标记样本集中的样本U_i进行预测, 得到样本的不确定性, 然后计算该样本的分类风险, 若它小于设定的置信因子∂ , 加入可信队列Q中, 打上伪标记, 否则加入低置信度样本集U中.

step 3 将可信队列Q中样本分类风险最小的γ × 100%样本加入训练集L中进行训练, 更新分类器C₁, C₂, …, C_n.

step 4 利用更新后的分类器对可信队列Q中剩余样本进行预测, 若样本的分类风险小于设定的置信因子∂ , 且与当前的伪标记一致, 加入训练集L中进行训练, 否则加入低置信度样本集U中, 并将该伪标记擦除.

step 5 重复step 2~step 4, 直至所有的无标记样本集U为Ø .

从上述算法描述可知, CR-SSEL含有两个关键的学习参数:置信因子$\partial$和可信队列阈值γ .$\partial$用于筛选高置信度样本, γ 用于对高置信度样本的伪标记重新确认, 目的是最小化训练过程中样本的不确定性.CR-SSEL的核心是利用分类风险挑选高置信度样本和低置信度样本, 当样本的分类风险越低, 它的概率分布越会呈现出集中于某一类的现象, 而当样本的分类风险越高时, 它的概率分布越会出现难以判断的现象.将高置信度的样本存于可信队列Q中, 低置信度样本加入低置信度样本集U, 便于更新后的分类器对其进行重新预测, 达到对高置信度样本和低置信度样本重复利用的目的.

本文采用的基分类器为神经网络, 神经网络的输出层通过Softmax回归后, 分类结果会转化为概率分布, 那么, 可通过分类结果的概率分布计算样本的分类不确定性.假设存在n个分类器, 有m类样本, 则概率分布

$P=\left[ \begin{array}{* {35}{l}} {{p}_{11}} & {{p}_{12}} & \ldots & {{p}_{1m}} \\ {{p}_{21}} & {{p}_{22}} & \ldots & {{p}_{2m}} \\ \vdots & \vdots & \text{ }\!\!~\!\!\text{ } & \vdots \\ {{p}_{n1}} & {{p}_{n2}} & \ldots & {{p}_{nm}} \\ \end{array} \right]$, (3)

其中

$\overset{m}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, {{p}_{ki}}=1, k=1, 2, \ldots , n$.

将每一类别的概率转化为正态分布, 概率密度函数为:

$\begin{align} & {{f}_{i}}(x)=\frac{2}{\sqrt{2\pi }{{\sigma }_{i}}}\exp \left( -\frac{x-{{\mu }_{i}}}{2\sigma _{i}^{2}} \right) \\ & i=1, 2, \ldots , m, \\ \end{align}$ (4)

其中

${{\mu }_{i}}=\frac{1}{n}\overset{n}{\mathop{\underset{j=1}{\mathop \sum }\, }}\, {{p}_{ji}}$,
${{\sigma }_{i}}\text{=}\sqrt{\frac{1}{n-1}\overset{n}{\mathop{\underset{j=1}{\mathop \sum }\, }}\, {{({{p}_{ji}}-{{\mu }_{i}})}^{2}}}$

累积分布函数为:

${{F}_{i}}(x)=\underset{-\infty }{\overset{x}{\mathop \int }}\, {{f}_{i}}(x)\text{d}x$.

假设第i类样本服从${{X}_{i}}\tilde{\ }N({{\mu }_{i}}, \sigma _{i}^{2})$, 第j类样本服从${{X}_{j}}\tilde{\ }N({{\mu }_{j}}, \sigma _{j}^{2})$, μ _i< μ _j, 则它们的交叠面积

$\begin{align} & \varepsilon =P({{X}_{i}}> c)+P({{X}_{j}}< c)= \\ & 1-{{F}_{i}}(c)+{{F}_{j}}(c)= \\ & 1-\frac{1}{2}erf\left( \frac{c-{{\mu }_{i}}}{\sqrt{2}{{\sigma }_{i}}} \right)+\frac{1}{2}erf\left( \frac{c-{{\mu }_{j}}}{\sqrt{2}{{\sigma }_{j}}} \right) \\ \end{align}$ (5)

其中, erf(· )表示自变量的误差函数,

$c=\frac{1}{\sigma _{i}^{2}-\sigma _{j}^{2}}\left[ {{\mu }_{j}}\sigma _{i}^{2}-{{\sigma }_{j}}\left( {{\mu }_{i}}{{\sigma }_{j}}+{{\sigma }_{i}}\sqrt{{{({{\mu }_{i}}-{{\mu }_{j}})}^{2}}+2\left( \sigma _{i}^{2}-\sigma _{j}^{2} \right)\text{log}\left( \frac{{{\sigma }_{i}}}{{{\sigma }_{j}}} \right)} \right) \right]$

将交叠面积ε 作为分类风险的值.CR-SSEL的伪代码如算法1所示.

算法1 CR-SSEL

输入 有标记数据集L, 无标记数据集U, 分类器C_i(i=1, 2, …, n), 可信队列Q

输出 训练后的分类器C_i(i=1, 2, …, n)

for i=1, 2, …, n do

L_i← BootstrapSample(L)

C_i← Learn(L_i)

end for

while len(U) > 0:

for U_i∈ U do

for i=1, 2, …, m do

构造式(4)

end for

for i=1, 2, …, m do

for j=1, 2, …, n do

计算式(5), 得到ε

end for

if count[i]< ∂ ==m-1:

Q← {U_i, y'}

end if

end for

end for

for i=1, 2, …, Q.size()* γ do

L← Q_i

end for

for i=1, 2, …, Q.size() do

y← predict(Q_i)

if y≠ y'

U← Q_i

end if

end for

end while

下面通过一个具体的示例演示算法1的核心执行过程.设置置信因子∂ =0.35, 可信队列γ =1.0, γ 表示在每轮迭代过程中, 将高置信度样本集上的所有样本用于训练分类器.

无标记样本的标注过程如图6所示.在第1轮迭代过程中, 初始分类器的性能较弱, 如(a)所示, 分类器对样本进行预测, 计算可得样本分类风险值为0.926 1, 此时该样本被判定为低置信度样本.将第1轮迭代过程中筛选的高置信度样本加入训练集中, 分类器对高置信度样本训练.然后进行第2轮迭代训练, 从(b)中容易看出, 此时样本的分类风险为0.755 0, 明显低于上一轮.说明分类器通过对上一轮筛选的高置信度样本训练后性能得到提升, 预测样本更稳定可靠.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 无标记样本的标注过程Fig.6 Labelling process of unlabeled samples

最终, 通过四轮的迭代训练, 样本的分类风险的值为0.173 4, 小于预设的置信因子∂ , 此时样本判定为高置信度样本, 并且类别标签判定为第1类, 将其加入训练集, 用于强化分类器的性能.

通过该示例可知, 在CR-SSEL中, 随着迭代次数的增加以及分类器对高置信度样本的不断训练, 分类器的性能逐渐增强, 直到无标记样本全部被标注完成为止.

下面分析CR-SSEL的时空复杂度.首先, CR-SSEL采用Bootstrap的方式训练分类器, 时间复杂度为O(K), 其中K表示有标记样本个数.其次, CR-SSEL利用多个分类器对无标记样本进行预测, 通过式(3)生成概率密度函数, 并构造类间的分类风险, 时间复杂度为O(k(nm+mm)), 其中, k表示无标记样本数量, n表示分类器个数, m表示样本类别数量.最后, CR-SSEL设置一个可信队列, 对每轮筛选的高置信度样本进行伪标记重确认, 时间复杂度为O(Tk), 空间复杂度为O(k), 其中T表示迭代次数.

进行多轮迭代, 直到无标记样本全部标注完成为止.因此, CR-SSEL总的时间复杂度为

O(K+Tk(nm+mm)+Tk),

空间复杂度为O(k).

本文在挑选的UCI、KEEL数据集上开展实验, 数据集信息如表1所示.数据集划分成类别分布近似一致的70%训练集和30%测试集.为了符合半监督集成学习的实验环境, 去除训练集上一部分有标记样本标签, 作为无标记样本.

表1

Table 1

表1(Table 1)

表1 实验数据集信息 Table 1 Details of experimental datasets 名称 属性个数 样本个数 类别个数 各类别对应样本数 messidor_features 20 1151 2 540, 611 biodeg 42 1055 2 771, 284 Pima 8 768 2 500, 268 Bupa 5 345 2 47, 151 Saheart 10 462 2 302, 160 pop_failures 20 540 2 46, 494 Diabetes 9 768 2 500, 268 Australian 14 690 2 383, 307 Forest 13 523 4 159, 86, 195, 83 vertebral(version 2) 7 620 4 211, 99, 60, 250 coil2000 85 9822 2 9236, 586 magic04 11 19020 2 12332, 6688 Pendigits 17 10579 10 1093, 1101, 1105, 1013, 1105, 1011, 1008, 1107, 1016, 1020

表1 实验数据集信息 Table 1 Details of experimental datasets

实验采取分类精度作为模型的评判标准, 所有结果均是重复10次以上的独立实验的分类精度平均值.

实验中算法使用Python语言实现.在Intel(R) Core(TM) 3.41 GHz i7-6700 CPU以及8 GB内存配置的电脑上进行实验.

本节主要验证分类风险作为置信度的评判标准以及使用可信队列的可行性.选取messidor_fea-tures、pima、biodeg这3个典型数据集, 检验分类风险对CR-SSEL性能的影响.在实验中, 实验结果均是重复10次的独立训练的平均分类精度, 有标记样本占训练样本总量的20%, 分类器个数设置为100.

设定置信因子$\partial$=0.05, 0.10, …, 1.10, 则$\partial$对CR-SSEL性能的影响如图7所示.由图可见, 在messidor_features数据集上, CR-SSEL在∂ =0.25时, 分类精度达到最高值, 并且∂ 取值在0.20~0.45之间时, CR-SSEL拥有较优的分类性能.在pima数据集上, CR-SSEL在∂ =0.40时, 达到最高的分类精度, 并且∂ 取值在0.25~0.50之间时, 分类性能达到较优水平.在biodeg数据集上, CR-SSEL在∂ =0.30时, 分类精度达到最高值, 并且∂ 取值在0.25~0.50之间时, 拥有较高的分类性能.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 置信因子$\partial$对CR-SSEL性能的影响Fig.7 Impact of confidence factor $\partial$ on performance of CR-SSEL algorithm

通过在这3个数据集上的实验结果可知, ∂ 的取值不宜过小, 也不能过大, ∂ 的取值在0.20~0.45之间较合适.当∂ 取值过小时, 只有少数高置信度样本可加入训练集, 若此时这些样本分类错误, 会导致CR-SSEL的分类性能下降, 并持续恶化.当∂ 取值过大时, 初始会有大量无标记样本被打上伪标记, 加入高置信度样本集, 而此时CR-SSEL的分类性能偏弱, 会出现较多的误分类样本, 当利用这类样本对CR-SSEL进行训练时, 也会导致性能下降.

固定置信因子∂ 不变, 设置可信队列阈值γ =0.1, 0.2, …, 1.0, 则γ 对CR-SSEL性能的影响如图8所示.γ 表示在每轮迭代时, 选择分类风险最小的γ × 100%高置信度样本加入训练集, 当γ 设置合理时, 在3个数据集上均能提升CR-SSEL的分类精度, 当γ 设置不当时, 会产生负面作用.由图可看出, γ 对分类精度的影响较明显, 当γ 取值为0.5左右时拥有较高的分类精度, 使用可信队列这种优化方案平均提升1.91%左右的分类精度.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 可信队列阈值γ 对CR-SSEL性能的影响Fig.8 Impact of confidence queue factor γ on performance of CR-SSEL algorithm

综上所述, 本节通过对置信因子∂ 以及可信队列阈值γ 的实验验证, 为CR-SSEL提供有效的参数选择依据, 同时也证实CR-SSEL的可行性.

本节验证分类器个数对CR-SSEL性能的影响, 即集成学习能否进一步提升半监督学习的分类性能.选择在messidor_features、pima、biodeg数据集上进行验证, 有标记样本占训练样本总量的20%, 实验结果均是重复10次独立训练的平均分类精度.

为了验证分类器个数对CR-SSEL性能的影响, 基于3.2节的实验结果, 固定置信因子∂ =0.3, 阈值γ =0.5, 设置分类器个数为20, 40, …, 200.具体实验结果如图9所示, 由图9可发现, 在messidor_features数据集上, 分类器个数设置为100时, CR-SSEL的分类精度到达峰值, 随后略有浮动, 但偏差不大, 最终趋于平稳.在pima数据集上, 随着分类器个数的增加, CR-SSEL的分类精度呈上升态势, 最终收敛.在biodeg数据集上, 当分类器个数到达120时, CR-SSEL的分类精度达到最高值, 最终趋于稳定.

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 分类器个数对CR-SSEL性能的影响Fig.9 Impact of number of classifiers on performance of CR-SSEL algorithm

不难发现, 在3个数据集上, 随着分类器个数的增加, CR-SSEL的分类精度都呈现逐渐提升、最终收敛的趋势, 由此证实CR-SSEL的合理性, 即集成学习对以风险最小化为导向的半监督学习的性能提升是有帮助的.

本节分别选取有标记样本占训练样本总量20%、30%、80%的场景开展对比实验, 其中有标记样本占比20%和30%的场景用于模拟样本标签大量不足的情况.

本文选取如下6种代表性的半监督集成学习算法作为对比算法.

1)基于多视图的半监督集成学习算法:Co- training^[10].

2)基于单视图的半监督集成学习算法:Tri- training^[19]、CST-Voting^[21]、文献[24]算法、Vote- training^[31]、Semi-Bagging^[32].

对比结果为重复10次独立实验的平均分类精度.当有标记样本占比分别为20%、30%、80%时, 各算法的分类精度对比如表2~表4所示, 表中黑体数字表示最优值.由表可观察到, 相比其它算法:有标记样本占比为20%时, CR-SSEL平均精度提高约3.21%; 有标记样本占比为30%时, CR-SSEL平均精度提高约3.11%; 有标记样本占比为80%时, CR-SSEL平均精度提高约2.88%.

表2

Table 2

表2(Table 2)

表2 有标记样本占比为20%时各算法的分类精度对比 Table 2 Comparison of classification accuracies of different algorithms with a labeled sample proportion of 20% 数据集 CR-SSEL Co-training Tri-training Vote-training Semi-Bagging CST-Voting 文献[24]算法 messidor_features 0.7410 0.6965 0.7109 0.6878 0.7196 0.6965 0.7167 Biodeg 0.8513 0.8075 0.8170 0.8107 0.8233 0.8170 0.8256 Pima 0.6796 0.6363 0.6190 0.6277 0.6320 0.6103 0.6592 Bupa 0.5576 0.5096 0.5388 0.5096 0.5480 0.5384 0.5508 Saheart 0.7150 0.6762 0.6834 0.6618 0.6330 0.6546 0.6851 pop_failures 0.9331 0.9012 0.9135 0.9197 0.9259 0.9074 0.9234 Diabetes 0.6897 0.6753 0.6580 0.6492 0.6709 0.6406 0.6756 Australian 0.7322 0.6956 0.7004 0.6908 0.7101 0.7004 0.7104 Forest 0.9103 0.8598 0.8980 0.8535 0.8956 0.8854 0.9066 Vertebral 0.8998 0.8662 0.8853 0.8980 0.8917 0.8535 0.8869 coil2000 0.9420 0.9290 0.9304 0.9297 0.9345 0.9287 0.9321 magic04 0.7603 0.7479 0.7483 0.7492 0.7542 0.7451 0.7529 Pendigits 0.5526 0.4202 0.5170 0.4354 0.5379 0.4234 0.5206 平均值 0.7665 0.7247 0.7400 0.7248 0.7443 0.7231 0.7496

表2 有标记样本占比为20%时各算法的分类精度对比 Table 2 Comparison of classification accuracies of different algorithms with a labeled sample proportion of 20%

表3

Table 3

表3(Table 3)

表3 有标记样本占比为30%时各算法的分类精度对比 Table 3 Comparison of classification accuracies of different algorithms with a labeled sample proportion of 30% 数据集 CR-SSEL Co-training Tri-Training Vote-training Semi-Bagging CST-Voting 文献[24]算法 messidor_features 0.7238 0.6994 0.7081 0.6965 0.6560 0.6936 0.6859 Biodeg 0.8323 0.8044 0.8126 0.8075 0.8194 0.8138 0.8150 Pima 0.6695 0.6320 0.6580 0.6406 0.6363 0.6493 0.6503 Bupa 0.6346 0.5961 0.6057 0.6153 0.6250 0.6057 0.6136 Saheart 0.7004 0.6762 0.6546 0.6690 0.6834 0.6762 0.6816 pop_failures 0.9273 0.9032 0.9163 0.9135 0.9206 0.9169 0.9154 Diabetes 0.7199 0.6017 0.6558 0.6147 0.7056 0.6320 0.6953 Australian 0.7254 0.7004 0.7149 0.6908 0.7048 0.7053 0.7167 Forest 0.9175 0.9044 0.8853 0.8980 0.8789 0.8885 0.9016 Vertebral 0.9054 0.8789 0.8407 0.8821 0.8980 0.8726 0.8924 coil2000 0.9471 0.9331 0.9321 0.9345 0.9368 0.9317 0.9409 magic04 0.7689 0.7520 0.7562 0.7478 0.7629 0.7541 0.7637 Pendigits 0.5861 0.4349 0.5110 0.4568 0.5648 0.4250 0.5609 平均值 0.7737 0.7320 0.7424 0.7359 0.7532 0.7357 0.7564

表3 有标记样本占比为30%时各算法的分类精度对比 Table 3 Comparison of classification accuracies of different algorithms with a labeled sample proportion of 30%

表4

Table 4

表4(Table 4)

表4 有标记样本占比为80%时各算法的分类精度对比 Table 4 Comparison of classification accuracies of different algorithms with a labeled sample proportion of 80% 数据集 CR-SSEL Co-training Tri-Training Vote-training Semi-Bagging CST-Voting 文献[24]算法 messidor_features 0.7245 0.7080 0.7167 0.7196 0.7167 0.7138 0.7126 Biodeg 0.8359 0.8170 0.8256 0.8012 0.8201 0.8264 0.8233 Pima 0.6796 0.6623 0.6580 0.6493 0.6709 0.6493 0.6650 Bupa 0.6826 0.6634 0.6442 0.6730 0.6250 0.6538 0.6712 Saheart 0.7294 0.6618 0.7050 0.6618 0.6906 0.6546 0.6819 pop_failures 0.9390 0.9074 0.9135 0.9247 0.9289 0.9183 0.9296 Diabetes 0.7203 0.7142 0.7056 0.6753 0.6969 0.7012 0.7092 Australian 0.7206 0.6811 0.6763 0.6859 0.7053 0.6714 0.7160 Forest 0.9071 0.8791 0.8725 0.8984 0.8969 0.8862 0.9003 Vertebral 0.9331 0.8931 0.9044 0.8980 0.9108 0.8892 0.9293 coil2000 0.9518 0.9362 0.9372 0.9368 0.9372 0.9369 0.9437 magic04 0.7824 0.7677 0.7609 0.7520 0.7776 0.7565 0.7759 Pendigits 0.5834 0.4322 0.4798 0.4310 0.5760 0.4369 0.5627 平均值 0.7838 0.7479 0.7538 0.7466 0.7656 0.7457 0.7708

表4 有标记样本占比为80%时各算法的分类精度对比 Table 4 Comparison of classification accuracies of different algorithms with a labeled sample proportion of 80%

可通过临界差值(Critical Difference, CD)图进行统计分析, 证实CR-SSEL的良好性能.基于10次实验结果的平均值, 在有标记数据占比为20%、30%、80%时, 13个数据集上的分类精度CD图如图10所示, 图中纵轴表示各算法, 横轴表示算法的平均排序值.

图10

Fig.10

	Figure Option ViewDownloadNew Window
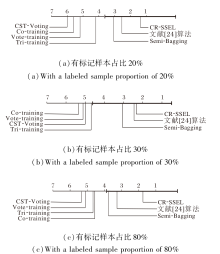	图10 有标记样本占比不同时的分类精度CD图Fig.10 CD diagram for classification accuracy with different labeled sample proportions

对于给定的0.05的显著性水平, 临界差值的数值计算为

$CD={{q}_{0.05}}\times \sqrt{\frac{7\times \left( 7+1 \right)}{6\times 13}}\approx 2.769$,

其中, q_0.05=3.268为Tukey分布的临界值.

从图10可看到, CR-SSEL在3种有标记样本占比的情况下都获得最低的平均排序值, 说明其具有更优的分类性能, 同时分类精度显著优于Tri-trai-ning、Vote-training和CST-Voting.特别地, 当样本标签大量不足(有标记样本占比20%和30%)时, CR-SSEL的分类精度还是显著高于Co-training.

实验结果以及统计分析结论证实CR-SSEL能有效处理半监督学习问题, 具有泛化性能上的优势.