数据增强是解决样本量不足的有效方法之一.增强后的数据将表示一组更全面的可能数据点, 从而最小化训练集和测试集之间的分布差异性, 得到具有更高泛化性能的模型.数据增强方法已在图像、文本等领域中展现出优越性能.对于图像数据来说, 传统数据增强方法包括对图像进行旋转、裁切等几何操作^{[11, 28]}, 但此类增强应考虑图像变化后保留标签的可能性, 对领域具有依赖性^[11].生成式数据增强方法中, You等^[29]提出DPT(Dual Pseudo Trai-ning), 利用扩散模型生成的数据作为带标签的伪图像增强, 对分类器进行训练或微调.而对于文本数据而言, 除了同义词替换、回译等常见方法外, 也可通过对输入数据注入噪声以增强数据^{[30, 31]}.生成式数据增强方法也同样适用于文本数据^{[32, 33]}.Gong等^[32]设计DiffuSeq(A Diffusion Model Designed for Sequence-to-Sequence), 实现较高句子级的多样性.然而, 上述针对图像与文本的数据增强方法利用数据自身的特点, 并依赖于各自领域的专家知识, 因此无法直接适用于表格型数据.

通常利用机器学习的思想设计传统表格型数据增强方法, 这类方法实现简单、速度快, 并且无需构造深度神经网络即可生成新的样本.随机过采样方法^[14] 通过随机复制、重复训练集上的样本以增强数据, 但是相比训练样本, 利用该方法生成的样本变化单一、缺乏多样性, 下游模型容易出现过拟合的现象.Chawla等^[34] 提出SMOTE(Synthetic Minority Over-Sampling Technique), 基于表格型数据的特征空间, 在任意两个训练样本对之间进行多次插值, 生成新的样本, 但是在两个样本中间进行插值的方法容易改变原始训练样本的分布, 给下游模型的训练造成偏差.Chapelle等^[15]提出VRM, 利用噪声注入的方法扰动表格型数据的所有特征, 但该方法未充分考虑表格型数据的特征相对于标签的重要性, 即对重要特征的轻微扰动也会给标签的预测造成显著的影响, 容易造成下游模型的性能下降.此外, 传统表格型数据增强方法在设计时并未充分考虑特征之间的相关性, 生成的数据分布可能与原始数据分布存在差异, 给下游模型的学习带来偏差.

深度神经网络考虑表格型数据特征之间的相关性, 因此, 为了能生成足量且具有多样性的新样本, 研究者考虑利用深度神经网络学习的生成式模型用于表格型数据增强的领域, Xu等^[35] 专为表格型数据设计CTGAN(Conditional Tabular GAN)和TVAE, 用于生成新的样本增强训练数据.Fang等^[13]提出SDAT(Semi-supervised Learning with Data Augmenta-tion for Tabular Data), 主要针对半监督学习任务, 在潜在空间中扰动数据, 并利用VAE重建新的样本.

然而, 有研究通过实验证明, VAE和GAN的生成能力有限, 生成式数据增强方法容易陷入模式崩塌的困境中.扩散模型具有更强大的捕获数据真实分布的能力, 生成的数据能较好地覆盖原始数据的真实分布^{[23, 25]}.

对于生成表格型数据的扩散模型而言, 其生成的样本能较好地模拟表格型数据特征间的联合概率^[25], 因此近年来逐渐成为研究热点之一^{[24, 25, 26, 27]}.但是, 也有研究表明, 用于训练扩散模型的数据信息量越少, 生成的质量越差, 对下游模型的影响越大^[36] , 特别是当训练样本量有限时, 直接利用扩散模型往往难以生成高质量的增强样本.因此, 对于具有有限样本量的表格型数据, 在保持原有表格数据分布和重要信息不变的情况下, 如果能利用有限的训练样本生成足量且具有多样性的数据集, 就可使在给定训练集上训练出来的模型具有良好的泛化性.

对于一个有监督任务而言, 需要找到一个模型f, 描述满足联合分布P(X, Y)的特征X和目标Y之间的关系.设(x, y)~P(X, Y), 为使模型的预测结果f(x)与真实目标y尽可能地接近, 通常使用损失函数l(· , · )度量这一差异.于是, 只需要最小化在所有数据的联合概率P(x, y)上的损失函数l(· , · )的期望便可达到这一目的, 则期望风险:

R(f_θ )=∫ l(f(x), y)dP(x, y).(1)

按照期望风险最小化原则得到的模型是最优模型.但由于数据的真实分布未知, 这个原则通常是理想化的.可利用训练数据集

$D=\{({{x}_{i}}, {{y}_{i}})\}_{i=1}^{N}$

的经验分布近似真实分布, 经验概率P_emp(x, y)可用组合的狄拉克δ 函数表示为

${{P}_{emp}}(x, y)=\frac{1}{N}\overset{N}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, {{\delta }_{{{x}_{i}}}}(x){{\delta }_{{{y}_{i}}}}(y)$.(2)

利用式(2)代替式(1)中数据的真实联合概率P(x, y), 得到经验风险:

${{R}_{emp}}(f)=\int l(f(x), y)\text{d}{{P}_{emp}}(x, y)=\frac{1}{N}\overset{N}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, ~(f(x), y)$.(3)

式(3)成立的前提是样本点等概率.

ERM是现有常见的学习原则之一.Song等^[37]基于ERM提出一致性模型, 加快扩散模型采样的速度, 提高生成样本的质量.Pan等^[38]利用ERM原则构建基于滑动注意力模块的模型, 提高ViT(Vision Transformer)的效率、灵活性、泛化性.

但是直觉上, 最简单达到经验风险最小的方法就是“ 记住” 训练数据, 这虽然能在训练数据上表现出良好的性能, 但也使模型增加一些不必要的结构以“ 记住” 训练数据特有的特征或其本身含有的噪声, 模型存在过拟合的风险.

近年来, 扩散模型以其稳定的训练及高质量的生成结果, 在图像、文本等领域中展现出卓越的性能^{[39, 40, 41, 42]}, 去噪扩散概率模型(Denoising Diffusion Probabilistic Model, 后文简记为DDPM)^[20]是其中一类扩散模型.DDPM首先定义一个前向过程, 用于逐步往原始数据中注入噪声, 直到扩散时间步t=T时, 扰动后的数据分布接近于标准高斯分布.其前向过程通常定义为

${{x}^{t}}=\sqrt{{{\alpha }_{t}}}{{x}^{t}}^{-1}+\sqrt{1-{{\alpha }_{t}}}{{\varepsilon }_{t}}$,

其中, ε _t~N(0, I), $\{{{\alpha }_{t}}\}_{t=1}^{T}$表示一组超参数, x^t表示扩散时间步为t时对应加噪后的数据.若设

${{\bar{\alpha }}_{t}}=\overset{t}{\mathop{\underset{n=0}{\mathop \prod }\, }}\, {{\alpha }_{n}}$,

则给定x⁰, 可得到任意时间步t加噪后的数据:

${{x}^{t}}=\sqrt{{{{\bar{\alpha }}}_{t}}}{{x}^{0}}+\sqrt{1-{{{\bar{\alpha }}}_{t}}}{{\varepsilon }_{t}}$.

模型的逆向过程从标准高斯分布中采样, 在逆扩散时间步方向上执行一条可学习的马尔可夫链, 逐步去除前向过程每步中所加的噪声, 可学习的高斯转移核服从N(x^t-1; μ _θ (x^t, t), σ _tI), 且有

${{\mu }_{\theta }}({{x}^{t}}, t)=\frac{1}{\sqrt{{{\alpha }_{t}}}}\left( {{x}^{t}}-\frac{1-{{\alpha }_{t}}}{\sqrt{1-{{{\bar{\alpha }}}_{t}}}}{{\varepsilon }_{\theta }}({{x}^{t}}, t) \right)$,

${{\sigma }_{t}}\text{=}\frac{1-{{{\bar{\alpha }}}_{t-1}}}{1-{{{\bar{\alpha }}}_{t}}}(1-{{\alpha }_{t}})$,

其中ε _θ 表示一个用于预测时刻t前向过程注入的噪声ε _t的神经网络.

DDPM的优化目标在于最小化双向马尔可夫过程联合分布的KL散度(Kullback-Leibler Diver-gence)以实现, 而Ho等^[20]将其在某一时间步t上的损失函数简化为

$l({{\varepsilon }_{\theta }}({{x}^{t}}, t), {{\varepsilon }_{t}})=\left( {{\varepsilon }_{\theta }}\left( {{x}^{t}}, t \right)-{{\varepsilon }_{t}} \right)_{2}^{2}$.(4)

目前, 现有DDPM的成功得益于图像、文本等数据具有同构的特性, 即均为数值型的特征, 可利用高斯噪声的可加性生成高质量的样本.而表格型数据除了包括数值型特征外, 还包括分类型特征, 因此DDPM需要对分类型特征进行特殊处理, 才能适用于表格型数据.再者, 当训练数据样本量有限时, 训练集上包含的数据信息较少, 可能导致DDPM无法利用有限的信息准确捕获数据真实的分布, 生成的数据质量较差, 容易给下游模型的训练带来偏差.

对于预测模型f∶ X→ Y, X是由{X₁, X₂, …, X_j, …, X_M}构成的M维输入空间, X_j(j=1, 2, …, M)可以为分类型特征, 也可以为数值型特征, Y为输出空间.给定带有标签的表格型数据集

$D=\{({{x}_{i}}, {{y}_{i}})\}_{i=1}^{N}\subseteq X\times Y$,

其中

x_i=(x_i1, x_i2, …, x_ij, …, x_iM)∈ X

为输入样本, y_i∈ Y为对应的标签, N为训练集的样本个数.

对于某预测任务T, 构建预测模型需要的样本数为N_T.当N≪N_T时, 认为对于该预测任务T而言, 数据集D的样本量有限, 无法提供任务T构建模型所需的足量样本.

针对有监督表格型数据训练样本量有限的问题, 如何利用数据增强方法生成数据, 扩充包含有限信息的数据集D, 使其在保证样本量充足的同时, 生成数据更具多样性, 能更好地适应于下游的预测任务, 是本文主要研究的问题.

2.2.1 邻域和邻域分布

邻域风险最小化(VRM)^[15]是关注训练数据邻域分布的风险最小化原则, 依据VRM原则, 可利用先验知识构建训练数据的邻域, 并使用邻域分布估计真实分布.对于ERM而言, 学习算法容易达到这一目的的方法是记忆训练数据, 但这往往会导致利用该原则训练的模型无法在训练数据之外具有较优表现, 不具备良好的泛化性能.区别于ERM, VRM更多地考虑利用数据点邻近区域的数据改进经验概率的估计, 该原则可用于数据增强.为了形式化描述VRM, 需要首先定义邻域和邻域分布.

常用的邻域定义无论是考虑邻域内数据点的数量, 还是考虑邻域中心点到边界的最大距离, 都是以训练数据为基础.与一般的邻域定义不同, 本文的邻域定义不限于训练数据, 而是以问题的样本空间为基础.

定义1 邻域 对于某个预测问题, 其样本空间为X× Y, 给定训练数据集

$D=\{({{x}_{i}}, {{y}_{i}})\}_{i=1}^{N}$,

则训练集上每个输入点x_i的邻域是指样本空间中与x_i密度可达且标签值为y_i的样本集合, 表示为V(x_i), 不同样本点的邻域空间和分布可能不同.

定义2 邻域分布 对于某个预测问题, 其样本空间为X× Y, 给定训练数据集

$D=\{({{x}_{i}}, {{y}_{i}})\}_{i=1}^{N}$,

其邻域分布描述每个输入点的邻域概率, 而邻域概率是每个输入点x_i在其邻域V(x_i)上的概率分布函数, 表示为${{P}_{V\left( {{x}_{i}} \right)}}(x)$.

VRM考虑训练数据周围邻域的样本点, 使模型训练不仅仅局限于训练数据, 在训练数据之外也能达到较优性能.样本点邻域的空间结构和分布可由先验知识或专家知识确定, 也可从数据及相关信息学习得到.依据VRM原则, 可用训练数据点的邻域概率${{P}_{V\left( {{x}_{i}} \right)}}(x)$改进经验分布概率的估计, 得到训练数据(x, y)的邻域分布概率:

${{P}_{V}}(x, y)=\frac{1}{N}\overset{N}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, {{P}_{V\left( {{x}_{i}} \right)}}(x){{\delta }_{{{y}_{i}}}}~(y)$.(5)

根据式(5), 可得到邻域风险:

${{R}_{V}}({{f}_{\theta }})=\int l({{f}_{\theta }}(x), y)d{{P}_{V}}(x, y)=\frac{1}{N}\overset{N}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, l({{f}_{\theta }}(x), {{y}_{i}})d{{P}_{V\left( {{x}_{i}} \right)}}(x)$.(6)

于是, 模型的最优参数可通过最小化邻域风险得到, 即

${{\theta }^{* }}=\arg \underset{\theta }{\mathop{\min }}\, {{R}_{V}}({{f}_{\theta }})$.

基于VRM构建的模型f_{θ *} 不仅仅考虑已有的训练数据, 还考虑训练数据以外邻域分布中的数据, 使模型的训练不再是“ 记住” 数据.相比基于ERM构建的模型, f_θ 具有更优的泛化能力.

2.2.2 邻域构建

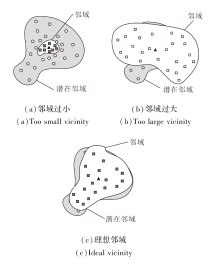
恰当的邻域空间对模型的训练至关重要.邻域太小, 增强后的数据集缺乏多样性; 邻域太大, 容易使训练的模型产生偏差, 如图1(a)、(b)所示.每个输入点的理想邻域应与潜在邻域相近, 如(c)所示.在VRM原则下, 理想模型在性能方面一定程度上依赖于邻域分布与真实分布之间的接近度, 但对于样本量有限的数据来说, 直接从中估计真实分布是很困难的.因此, 邻域的选择需要一些限制.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 不同标识邻域示例Fig.1 Examples of different identified vicinities

对此, Huang等^[43]利用训练样本之外的未标记数据集, 通过惰性随机游走的方式, 自适应调整邻域位置及大小, 以此构建与真实分布接近的邻域分布, 在下游任务中展现出较优性能.但训练数据集之外的数据可能是缺乏的, 尤其是样本有限的情况, 因此该方法只适用于特定的任务之中.

本文考虑训练数据范围之内的样本点, 由于真实分布未知, 邻域分布的选取难以把控, 可从尽可能减小由邻域分布引起的模型偏差方面考虑.

对于表格型数据来说, 根据该类数据的特点, 有如下2个常用的先验知识:1)数据的每个特征对标签预测的贡献是不同的.相关性较强的特征即使受到微小的扰动, 预测结果的影响也是较大的, 相关性较弱的特征受到一定的扰动对于标签预测结果的影响也是微乎其微.2)高斯噪声是常见的噪声.通常可使用高斯噪声对数据进行扰动.

本文结合这2种先验知识, 用于邻域的构建.具体地, 在构建邻域过程中, 可从相关性较弱的特征入手, 对相关性较弱的特征施加高斯噪声扰动以构建输入点的邻域.为了保证输入样本的多样性, 可选择较大的邻域, 即使选择的邻域大于潜在邻域, 由于特征与标签的相关性较弱, 对模型预测结果的影响也是微小的, 从而达到表格型数据增强在不改变表格数据分布与重要信息的情况下扩充样本量的目的.

本文利用互信息作为度量特征与标签之间重要程度的指标, 特征X_j和标签Y之间的互信息定义如下:

$I({{X}_{j}}, Y)={{\int }_{Y}}\underset{{{X}_{j}}}{\mathop \int }\, P({{X}_{j}}, Y){{\log }_{2}}\left( \frac{P\left( {{X}_{j}}, Y \right)}{P\left( {{X}_{j}} \right)P\left( Y \right)} \right)d{{X}_{j}}dY$,

其中, P(X_j, Y)表示X_j与Y之间的联合分布, P(X_j)表示X_j的边缘分布, P(Y)表示Y的边缘分布.通过计算特征与标签之间的互信息, 找出相关性较弱的特征X^w, 对其利用服从$N(0, \sigma _{i}^{2})$的高斯噪声进行扰动, 构建输入点x_i的邻域V(x_i), 其中, $\sigma _{i}^{2}$表示高斯噪声的方差, 用于控制邻域分布的规模, 当σ _i=0时, 式(6)的邻域风险退化为式(3)的经验风险.特别地, 由于表格型数据特征包括数值型与分类型, 在构建邻域时, 当X^w为数值型特征时, 预处理后直接利用高斯噪声扰动弱相关特征以构建邻域分布; 当X^w为分类型特征时, 需先进行One-hot编码转化为数值型特征, 再对转化后的向量组进行高斯扰动, 构建邻域分布.

2.2.3 模型步骤

从2.2.2节构建的邻域分布中采样生成的邻域样本, 尽管可增加样本量, 但对原始数据的扰动相对温和、多样性不足, 仍具有过拟合的风险.生成式数据增强方法常用于捕获数据的真实分布, 生成的数据更具有多样性, 能提高下游任务中预测模型的泛化性能.因此, 本文提出基于邻域分布的去噪扩散概率模型(VD-DDPM), 用于生成新数据.

VD-DDPM的前向过程从t=0到t=T逐步往邻域分布中采样得到的数据${{\tilde{x}}^{0}}$中注入噪声ε ~N(0, I), 直到扰动后的数据分布近似于标准高斯分布.逆向过程从该分布x^T~N(0, I)中采样, 再通过迭代去除噪声还原数据.

VD-DDPM的主要任务是构建预测模型ε _θ , 预测每一时间步注入的噪声ε _t, 即ε _t=ε _θ (x^t, t), 其中θ 表示噪声预测模型的参数.第t步的输入数据x^t的邻域损失定义为

$\begin{align} & {{l}_{V}}({{f}_{\theta }}({{x}^{t}}), \varepsilon )=\int l({{\varepsilon }_{\theta }}({{{\tilde{x}}}^{t}}, t), {{\varepsilon }_{t}})d{{P}_{V\left( {{x}^{t}} \right)}}~({{{\tilde{x}}}^{t}})= \\ & {{E}_{{{P}_{V\left( {{x}^{t}} \right)}}}}({{{\tilde{x}}}^{t}})~[l({{\varepsilon }_{\theta }}({{{\tilde{x}}}^{t}}, t), {{\varepsilon }_{t}})] \\ \end{align}$,

其中${{\tilde{x}}^{t}}$表示原始表格型数据x⁰对弱特征加噪后采样得到的邻域样本${{\tilde{x}}^{0}}$在扩散时间步t上的数据, 则根据式(4), 邻域内样本点的损失函数:

$l({{\varepsilon }_{\theta }}({{\tilde{x}}^{t}}), {{\varepsilon }_{t}})=\left\| {{\varepsilon }_{\theta }}\left( {{{\tilde{x}}}^{t}}, t \right)-{{\varepsilon }_{t}} \right\|_{2}^{2}$,

由此得到邻域风险:

${{R}_{V}}({{\varepsilon }_{\theta }})=\frac{1}{N}\overset{N}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, \int l({{\varepsilon }_{\theta }}({{\tilde{x}}^{t}}, t), {{\varepsilon }_{t}})\text{d}{{P}_{V\left( {{x}_{i}} \right)}}~({{\tilde{x}}^{t}})$.

于是, 可通过寻找一组参数θ ^* , 使邻域风险达到最小, 即

${{\theta }^{* }}=\arg \underset{\theta }{\mathop{\min }}\, {{R}_{V}}({{\varepsilon }_{\theta }})$.(7)

式(7)为邻域风险最小化原则下的去噪扩散概率模型的目标函数.若存在最优参数θ ^* , 使${{R}_{V}}({{\varepsilon }_{{{\theta }^{\text{* }}}}})$最小, 则在这组参数下, 噪声预测器${{\varepsilon }_{{{\theta }^{\text{* }}}}}$可较好地学到与真实加噪的近似, 并且该邻域目标函数可推广到VD-DDPM任意时间步t上, 利用VD- DDPM逆向过程去除噪声, 得到的邻域数据分布可看作是真实数据分布的近似.

为了进一步从理论上探究VD-DDPM的有效性, 下面详细分析该模型中的噪声预测器.不失一般性, 可以只考虑某一时刻t的噪声预测器ε _θ , ${{\tilde{x}}^{t}}$表示x^t邻域内的样本点, ${{\tilde{x}}^{t}}$与x^t之间的关系:

$\begin{align} & {{{\tilde{x}}}^{t}}=\sqrt{{{{\bar{\alpha }}}_{t}}}{{{\tilde{x}}}^{0}}+\sqrt{1-{{{\bar{\alpha }}}_{t}}}{{\varepsilon }_{t}}= \\ & \sqrt{{{{\bar{\alpha }}}_{t}}}({{x}^{0}}+z)+\sqrt{1-{{{\bar{\alpha }}}_{t}}}{{\varepsilon }_{t}}= \\ & \sqrt{{{{\bar{\alpha }}}_{t}}}{{x}^{0}}+\sqrt{1-{{{\bar{\alpha }}}_{t}}}{{\varepsilon }_{t}}+\sqrt{{{{\bar{\alpha }}}_{t}}}z= \\ & {{x}^{t}}+\sqrt{{{{\bar{\alpha }}}_{t}}}z. \\ \end{align}$

其中:z~N(0, Σ ^w)表示仅对弱特征X^w表示后的数据添加均值为0、方差为σ ²的高斯扰动, 其余特征不扰动; ${{\bar{\alpha }}_{t}}$表示去噪扩散概率模型的超参数, 在时刻t为固定值.

通过二阶泰勒公式, 在x^t处展开, 得

$\begin{matrix} & l({{\varepsilon }_{\theta }}({{{\tilde{x}}}^{t}}, t), {{\varepsilon }_{t}})\approx l({{\varepsilon }_{\theta }}({{x}^{t}}, t), {{\varepsilon }_{t}})+ \\ & ({{{\tilde{x}}}^{t}}-{{x}^{t}})G({{x}^{t}})+\frac{1}{2}{{({{{\tilde{x}}}^{t}}-{{x}^{t}})}^{2}}H({{x}^{t}}), \\ \end{matrix}$

其中, G(· )表示l(· , · )的梯度, H(· )表示l(· , · )的海森矩阵.于是, 可得到邻域风险:

$\begin{align} & {{R}_{V}}({{\varepsilon }_{\theta }})=\frac{1}{N}\overset{N}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, \int l({{\varepsilon }_{\theta }}({{{\tilde{x}}}^{t}}, t), {{\varepsilon }_{t}})d{{P}_{V\left( {{x}_{i}} \right)}}~({{{\tilde{x}}}^{t}})\approx \\ & \frac{1}{N}\overset{N}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, ~\int{[l({{\varepsilon }_{\theta }}({{x}^{t}}, t), {{\varepsilon }_{t}})+(}{{{\tilde{x}}}^{t}}-{{x}^{t}})G({{x}^{t}})+ \\ & \frac{1}{2}{{({{{\tilde{x}}}^{t}}-{{x}^{t}})}^{2}}H({{x}^{t}})]d{{P}_{V\left( {{x}_{i}} \right)}}({{{\tilde{x}}}^{t}})= \\ & \frac{1}{N}\overset{N}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, [||{{\varepsilon }_{\theta }}\left( {{x}^{t}}, t \right)-{{\varepsilon }_{t}}||_{2}^{2}+\frac{1}{2}{{{\bar{\alpha }}}_{t}}{{\Sigma }^{w}}H({{x}^{t}})]. \\ \end{align}$ (8)

在上述推导过程中, 由于${{\tilde{x}}^{t}}$是以高斯分布N(0, Σ ^w)采样得到, 故有

$\int{[}({{\tilde{x}}^{t}}-{{x}^{t}})]d{{P}_{V\left( {{x}_{i}} \right)}}({{\tilde{x}}^{t}})=0$,

$\int{{{({{{\tilde{x}}}^{t}}-{{x}^{t}})}^{2}}}d{{P}_{V\left( {{x}_{i}} \right)}}({{\tilde{x}}^{t}})={{\overline{\alpha }}_{t}}{{\Sigma }^{w}}.$

由式(8)可知, 邻域风险由损失函数和一个正则化项构成.在样本量有限时, 该正则化项有益于防止模型训练的过拟合, 有效提高模型的泛化能力, 有助于生成模型更好地捕获真实数据的分布.

本文基于邻域分布的数据增强算法由模型学习算法和数据生成算法两个部分组成.

模型学习算法主要用于训练VD-DDPM.首先利用互信息度量计算D中特征与标签之间的相关性, 再选择相关性较弱的特征X^* 构建邻域分布V(x⁰), 最后在V(x⁰)中采样新的数据集, 用于训练VD-DDPM.模型学习算法过程见算法1, 该算法将输出一个以扩散时间步t和类标签y_i为条件的噪声预测器ε _θ , 用于预测时刻t对应扩散模型前向过程所加噪声ε 的大小.

算法1 VD-DDPM模型学习算法

输入 训练集$D=\{({{x}_{i}}, {{y}_{i}})\}_{i=1}^{N}$, 扩散模型超参数$\{{{\alpha }_{t}}\}_{t=1}^{T}$

输出 噪声预测器ε _θ

计算数据集D中特征与标签之间的互信息, 得到弱相关特征

DO:

从D中采样原始输入点x⁰

在弱相关特征上加噪构建输入点x⁰的邻域V(x⁰)

从邻域V(x⁰)中采样${{\tilde{x}}^{0}}$

t~Uniform({1, 2, …, T})

${{\bar{\alpha }}_{t}}=\overset{t}{\mathop{\underset{n=1}{\mathop \prod }\, }}\, {{\alpha }_{n}}$

ε _t~N(0, I)

梯度下降法更新模型参数

${{\nabla }_{\theta }}{{\left( {{\varepsilon }_{t}}-{{\varepsilon }_{\theta }}\left( \sqrt{{{{\bar{\alpha }}}_{t}}}{{{\tilde{x}}}^{0}}+\sqrt{1-{{{\bar{\alpha }}}_{t}}}{{\varepsilon }_{t}}, t, {{y}_{i}} \right) \right)}^{2}}$

WHILE模型收敛

区别于DDPM, 算法1根据表格型数据的特征构建原始有限样本量数据的邻域, 再从该邻域中进行采样, 训练噪声预测器ε _θ .相比DDPM的训练过程, 算法1不会因为训练样本量有限而导致噪声预测器ε _θ 出现过拟合的问题.对于噪声预测器ε _θ 而言, 其神经网络以标签$\{{{y}_{i}}\}_{i=1}^{N}$为监督信息进行设计, 便于生成时根据指定标签信息生成对应标签类别的新数据; 若对于无监督的生成任务, 可将样本标签y_i看作表格型数据的特征之一与其余特征一并作为网络输入, 算法1同样适用.

数据生成算法主要生成应用于下游任务训练的新数据集, 新数据集服从与真实数据分布相似的邻域分布.训练好VD-DDPM后, 对于不同类别, 分别从简单标准高斯先验中采样并迭代去噪过程, 直到t=0时得到新数据集D_ge.数据生成算法过程如算法2所示.

算法2 VD-DDPM数据生成算法

输入 扩散模型超参数$\{{{\alpha }_{t}}\}_{t=1}^{T}$,

各类别需要的样本数$\{nu{{m}_{c}}\}_{c=1}^{\left| Y \right.\text{ }\!\!~\!\!\text{ }|}$,

训练好的噪声预测模型ε _θ

输出 生成数据集D_ge

D_ge={}

FOR c IN RANGE(|Y|):

FOR i IN RANGE(num_c):

${{x}^{\text{T}}}_{i}\tilde{\ }N(0, I)$

FOR t IN REVERSED(RANGE(T)):

${{\bar{\alpha }}_{t}}=\overset{t}{\mathop{\underset{n=1}{\mathop \prod }\, }}\, {{\alpha }_{n}}$

${{\sigma }_{t}}=\frac{1-{{{\bar{\alpha }}}_{t-1}}}{1-{{{\bar{\alpha }}}_{t}}}~(1-{{\alpha }_{t}})$

z~N(0, I) IF t> 1, ELSE z=0

$x_{i}^{t-1}=\frac{1}{\sqrt{{{{\bar{\alpha }}}_{t}}}}\left( x_{i}^{t}-\frac{1-{{\alpha }_{t}}}{\sqrt{1-{{{\bar{\alpha }}}_{t}}}}{{\varepsilon }_{\theta }}(x_{i}^{t}, t, c) \right)+{{\sigma }_{t}}z$

END FOR

${{D}_{ge}}={{D}_{ge}}\cup (x_{i}^{0}, c)$

END FOR

END FOR

RETURN D_ge

算法2的时间复杂度为O(|Y| num_cT), 其在采样过程中需要对每个样本进行T步的去噪过程, 采样速度较慢.DDPM的时间复杂度与算法2同级别.而基于VAE架构的生成算法(如TVAE)和基于GAN架构的生成算法(如CTGAN)时间复杂度较低, 均为O(|Y| um_c).相比TVAE和CTGAN, 算法2的效率较低, 是未来需要改进的一个方向.

与DDPM的数据生成算法不同, 算法2以数据标签为监督信息, 预测每个扩散步注入的噪声大小, 根据每类指定生成的数量进行新数据的生成, 并将新生成的数据集用于下游任务当中.算法2在设计时考虑监督信息, 可有效避免利用DDPM执行无监督生成任务时可能由于原始训练样本的类别数量不平衡出现生成的新样本类别数量也不平衡的问题, 但算法2同样也可用于无监督任务中.对于VD-DDPM新生成的数据而言, 在下游任务中, 可直接使用生成的数据作为训练集的方法以训练预测模型(简记为VD-DDPM_s), 也可使用生成数据和原始数据混合的方法训练预测模型(简记为VD-DDPM_m).

本文从UCI、KEEL数据库上获取数据, 进行实验评估, 选取的数据集既有只含有数值型特征的数据集, 也有只含有分类型特征的数据集, 还有同时包含数值型特征和分类型特征的数据集.对含缺失值的数据集进行预处理, 若缺失值所在列为数值型特征, 用该列的平均数进行填补; 若缺失值所在列为分类型特征, 用该列的众数进行填补.

本文主要研究样本量有限的表格型数据增强方法, 实验应采用样本量有限的数据集.

由于UCI、KEEL数据库上的数据集样本量差异较大, 为了更准确地刻画实验效果, 从原始数据集上按照一定方式构造样本量有限的训练数据集.一般地, 模型训练所需数据的样本量与特征个数有关, 因此, 根据数据集特征的个数M以及设定的倍数γ 选取样本, 其中γ ≥ 1且⌊γ M」小于原始数据集的大小.通过均匀采样共选取⌊γ M」个样本用于训练模型, 原始数据集上剩余样本作为下游任务的测试数据, 对训练模型性能进行评估.实验数据集的具体信息如表1所示.

表1

Table1

表1(Table1)

表1 实验数据集信息 Table1 Details of experimental datasets 序号 名称 原始数据集样本数 训练数据集样本数 数值型特征数 分类型特征数 类别数 1 adult 32561 140 6 8 2 2 balance 625 60 4 0 3 3 bupa 345 60 6 0 2 4 contraceptive 1473 135 9 0 3 5 echocardiogram 74 45 6 0 2 6 glass-0-1-2-3vs4-5-6 214 90 9 0 2 7 hayes-roth 160 60 0 4 3 8 house-votes-84 435 160 0 16 2 9 ionosphere 351 248 33 0 2 10 iris 150 60 4 0 3 11 kr-vs-kp 3196 360 0 36 2 12 monk-2 432 60 6 0 2 13 mushroom 8124 220 0 22 2 14 penguins_size 100 67 4 2 3 15 pima 768 80 8 0 2 16 spambase 4597 570 57 0 2 17 splice 3190 900 60 0 3 18 ttt 958 90 0 9 2 19 winequality-red 1599 216 11 0 6 20 winequality-white 4898 291 11 0 7

表1 实验数据集信息 Table1 Details of experimental datasets

本文采用的调参方法为贝叶斯优化调参法.该方法通过构建超参数与模型性能之间的关系, 利用贝叶斯推断的思想选择下一组最有希望的超参数组合.维护一个概率模型以表示超参数空间中的模型性能, 并在每次迭代中选择最有希望的超参数进行实际评估.通过多次迭代, 贝叶斯调参能更智能地探索超参数空间, 更有效地找到性能最优的超参数组合, 从而在相同的计算资源下达到更优的模型性能.

在模型调参过程中需要对生成模型生成的数据进行评估, 以便选择更优参数.本文通过计算生成数据与原始数据之间的KL散度以评估生成数据的质量, KL散度越小, 两个分布之间的差异越小, 模型性能越优.但是, 由于数据原始分布较复杂, 无法显式得到其累积分布函数的表达形式, 直接计算KL散度较困难.为此, 本文利用统计学中“ 样本频率分布估计总体分布” 的思想, 通过样本频率分布的KL散度估计总体分布的KL散度.具体地, 首先将生成数据D_ge和训练数据D合并为一个大集合D_con, 再将D_con划分b个等宽区间, 分别计算D_ge和D落在每个区间中的频率作为其累积分布函数的估计, 最后利用该估计值计算原始数据分布与生成数据分布之间的KL散度, 用于贝叶斯调参过程中作为评估模型优劣的指标.

实验选用SMOTE^[34]、CTGAN^[35]、TVAE^[35]和DDPM^[20]作为对比方法.此外, 还利用原始训练数据作为对比方法, 以展示性能的提升.

1)原始训练数据.除了必要的数据预处理之外, 该基线方法直接使用原始训练数据训练下游模型, 与VD-DDPM训练的下游模型进行对比.

2)SMOTE.首先在特征空间中选择有限数量的训练样本和它们的邻居, 再在选定样本和选定邻居之间的线段上随机选择一个点作为新生成的样本点, 重复上述过程, 生成新的样本集.

3)CTGAN.是GAN在表格型数据上的推广, 在GAN的对抗学习基础上, 通过连续数据的归一化和离散数据的公平采样实现表格型数据生成.

4)TVAE.针对混合类型表格数据生成的神经网络生成模型, 基于变分自编码器改进而来, 通过调整预处理和损失函数以适应表格数据.

5)DDPM.经典的扩散模型之一, 分别通过两条加噪和去噪的马尔可夫链进行训练并生成数据.

实验采用PyTorch1.11框架, CPU为24核IntelXeonGold5318Y, 主频为2.10 GHz, 内存大小为256 GB, GPU由2块NVIDIATeslaA800组成, 显存大小为160 GB, CUDA版本为11.5.

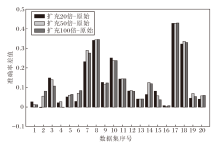
本节实验验证2.2.2节提出的邻域构建方法存在的有效性和局限性.在训练数据集样本量充足时, 通过对表格型数据标签弱相关特征加噪的方法构建邻域, 并从邻域中分别采样原始训练样本数量扩充20倍、50倍、100倍大小的邻域数据集, 特别地, 由于计算资源有限, 控制每个原始训练数据集的样本量不超过3 000, 这种限制不会对实验结论产生较大影响.再将这些邻域数据集分别训练下游分类任务的MLP(Multilayer Perceptron)模型, 输出结果利用准确率进行度量, 所得的准确率分别与原始训练数据集在下游MLP模型上的准确率作差并绘制柱状图, 得到的结果如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 邻域构建方法的有效性与局限性Fig.2 Effectiveness and limitation of vicinal construction method

由图2可观察到, 几乎对于全部的实验数据集而言, 利用扩充20倍、50倍、100倍的邻域数据集训练MLP, 准确率与原始训练数据集训练MLP的准确率之差大于0, 实验结果表明, 本文提出的邻域构建方法在一定程度上可提高训练数据在下游分类任务上的准确率.但是, 从图中也不难发现, 对于部分实验数据集而言, 当采样的倍数增大时, 准确率的差值增加不大, 甚至出现差值下降的情况, 实验结果表明, 本文提出的邻域构建方法对于原始训练数据的扰动较温和, 随着扩充倍数的增加, 训练数据集的变化单一、多样性不足, 模型性能可能会出现增加缓慢甚至下降的情况, 过拟合的风险仍然存在.

本节研究VD-DDPM生成数据的质量.在训练数据集样本数量有限时, 利用2.2.2节构建的邻域数据集训练扩散模型, 对标准高斯分布进行采样, 并逐步去噪逆转扩散模型前向过程, 从而生成若干新的样本.对比生成数据分布与原始训练数据分布的相似性, 判断扩散模型生成数据质量的优劣.

VD-DDPM在所有数据集上KL散度的近似值如表2所示.

表2

Table 2

表2(Table 2)

表2 数据生成质量的度量结果 Table 2 Measurement results of data generation quality 数据集 Score 数据集 Score adult 0.022 kr-vs-kp 0.007 balance 0.186 monk-2 0.020 bupa 0.047 mushroom 0.007 contraceptive 0.037 penguins_size 0.057 echocardiogram 0.046 pima 0.059 glass-0-1-2-3vs4-5-6 0.024 spambase 0.030 hayes-roth 0.026 splice 0.002 house-votes-84 0.005 ttt 0.001 ionosphere 0.042 winequality-red 0.079 Iris 0.115 winequality-white 0.107

表2 数据生成质量的度量结果 Table 2 Measurement results of data generation quality

实验中, 对不同类别分别进行生成质量的评估, 再将所有类别的评估值取平均, 记为VD-DDPM对于该数据生成质量的Score:

$Score=\frac{1}{\left| Y \right|}\overset{\left| Y \right.~|}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, K{{L}_{i}}({{x}_{ra{{w}_{i}}}}, {{x}_{ge{{n}_{i}}}})$,

其中KL_i(· , · )表示类别i中使用3.1节贝叶斯优化调参法估计的原始数据${{x}_{ra{{w}_{i}}}}$和生成数据${{x}_{ge{{n}_{i}}}}$之间KL散度的近似值.由于Score是作为KL散度的一个近似指标, 其值满足大于0, 且越接近0时表示生成数据的分布与原始训练数据的分布越相似, 生成质量越优.

由表2中的结果可看出, 在这些数据集上, VD-DDPM生成数据的Score值均小于0.2, 最大值为0.186, 最小值为0.001, 且在绝大多数实验数据集上的Score值小于0.05, 因此, VD-DDPM生成的数据与原始数据的分布相近.

为了进一步探究VD-DDPM的生成质量, 本文还给出部分数据集原始训练数据和VD-DDPM生成数据的箱线图和直方图对比.由于Iris、bupa数据集的特征均为连续型特征, 特征数量较少, 便于图形化展示, 并且两者分别具有较小和较大的Score值(分别为0.047和0.115), 具有一定的代表性, 因此选取这两个数据集作为示例, 使用箱线图展示原始训练数据和生成数据的数据分布, 具体如图3和图4所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 Iris数据集上原始数据与生成数据之间的箱线图Fig.3 Box plots of original data and generated data on Iris dataset

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 bupa数据集上原始数据与生成数据之间的箱线图Fig.4 Box plots of original data and generated data on bupa dataset

Iris数据集由3个类别组成, 从图3可观察到, 对于类别Iris-setosa, 原始训练数据和生成数据前3个特征的中位数较接近, 第4个特征的中位数略有差异, 4个特征的箱体大小较接近, 表明数据的集中程度相似.对于类别Iris-versicolor, 第1个特征的中位数和第3个特征的中位数相近, 但第2个特征与第4个特征的中位数存在差异, 4个特征的箱体大小较接近, 数据的集中程度相似.对于类别Iris-virginica, 4个特征的中位数均存在一定差异, 并且生成数据中第4个特征的箱体大小与原始训练数据存在较明显的差异.因此, Iris数据集的Score值略微偏大.

bupa数据集由2个类别组成, 从图4可看到, bupa数据集上类别1的第5个特征和类别2的第5个特征的中位数上略微存在差异, 除此之外, 生成数据其余特征的中位数及箱体大小与原始训练数据相差不大, 可认为VD-DDPM生成与原始训练数据分布相近的新数据.

由图3、图4和表2中2个数据集的Score值可得出结论, VD-DDPM生成的bupa数据和Iris数据与原始训练数据具有相似的数据分布.

为了图形化展示具有分类型特征数据集的数据生成结果, 实验选择特征数较少且Score值较小的hayes-roth数据集.具有分类型特征的数据集不适合用箱线图展示, 本文采用堆积直方图的方式展示.因为生成数据的样本量与原始训练数据存在差异, 所以直方图的值采用特征值频数占对应数据集样本总量百分比的方法给出, 对于同一特征的不同值采用不同颜色表示, 具体如图5所示.由图可观察到, 除类别1的第1个特征外, 原始训练数据与生成数据的分布几乎一致, 生成质量较优, 因此其Score值更接近于0.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 hayes-roth数据集上原始数据与生成数据之间的直方图Fig.5 Histogram of original data and generated data on hayes-roth dataset

综合表2、图3~图5的实验结果可得出结论:VD-DDPM能较好地捕获原始表格型训练数据的分布, 并且生成基本服从原始训练数据分布的数据.

本节通过下游分类任务, 展示VD-DDPM的有效性.具体地, 给定一个大小为N的数据集, 根据3.1节中有限数量样本选取方法, 将数据集划分为两个部分D和D_test.D为有限样本量的数据集, 作为VD-DDPM的输入用于训练, 最后通过采样, 输出一个生成数据集.

对于D_test, 有2种处理方式.第1种处理方式是直接作为测试集, 用于测试利用VD-DDPM生成的新数据集在下游任务中的表现.第2种处理方式是进一步将该数据集划分为2个部分, 一部分用于与生成数据混合“ 微调” 下游分类模型, 而另一部分作为测试数据评估VD-DDPM的性能, 将最后输出的分类模型用于测试数据, 预测分类的准确率作为评价指标.

本节采用SMOTE、CTGAN、TVAE、DDPM作为对比方法, 对有限样本量数据进行过采样, 生成与VD-DDPM生成数据量相同的新数据集用于下游模型的训练, 并与VD-DDPM进行对比.

实验选取的下游任务为分类任务, 采用的分类器为MLP, 对于所有方法, MLP均采用默认参数进行训练, VD-DDPM_s表示利用生成数据训练下游模型的结果, VD-DDPM_m表示利用混合数据训练下游模型的结果, 分类器性能度量采用准确率(Acc)、精确率(Pre)及F₁-Score(F₁).

各方法的Acc、Pre、F₁值对比如表3~表5所示, 表中黑体数字表示最优值.

表3

Table 3

表3(Table 3)

表3 下游预测任务中各方法的Acc值对比 Table 3 Acc comparison of different methods in downstream prediction tasks 数据集 原始训练数据 SMOTE CTGAN TVAE DDPM VD-DDPM_s VD-DDPM_m adult 0.775 0.758 0.743 0.781 0.527 0.756 0.824 balance 0.686 0.781 0.618 0.647 0.749 0.798 0.804 bupa 0.525 0.654 0.621 0.647 0.669 0.658 0.656 contraceptive 0.439 0.462 0.456 0.459 0.480 0.467 0.467 echocardiogram 0.697 0.721 0.710 0.748 0.714 0.703 0.729 glass-0-1-2-3vs4-5-6 0.901 0.922 0.935 0.930 0.892 0.932 0.929 hayes-roth 0.484 0.716 0.670 0.710 0.707 0.725 0.724 house-votes-84 0.832 0.742 0.902 0.939 0.915 0.951 0.947 ionosphere 0.749 0.897 0.830 0.918 0.886 0.908 0.900 iris 0.668 0.953 0.956 0.933 0.951 0.971 0.975 kr-vs-kp 0.658 0.949 0.797 0.844 0.931 0.946 0.949 monk-2 0.775 0.886 0.937 0.924 0.909 0.907 0.931 mushroom 0.711 0.976 0.918 0.933 0.983 0.985 0.994 penguins_size 0.839 0.950 0.979 0.985 0.973 0.979 0.985 pima 0.597 0.683 0.683 0.710 0.679 0.697 0.701 spambase 0.914 0.921 0.890 0.840 0.920 0.928 0.933 splice 0.448 0.929 0.854 0.879 0.916 0.927 0.925 ttt 0.457 0.714 0.589 0.686 0.647 0.770 0.798 winequality-red 0.358 0.450 0.349 0.444 0.427 0.452 0.458 winequality-white 0.242 0.342 0.289 0.342 0.240 0.339 0.355 平均值 0.638 0.770 0.736 0.765 0.756 0.790 0.799

表3 下游预测任务中各方法的Acc值对比 Table 3 Acc comparison of different methods in downstream prediction tasks

表4

Table 4

表4(Table 4)

表4 下游预测任务中各方法的Pre值对比 Table 4 Pre comparison of different methods in downstream prediction tasks 数据集 原始训练数据 SMOTE CTGAN TVAE DDPM VD-DDPM_s VD-DDPM_m adult 0.707 0.705 0.702 0.716 0.575 0.707 0.759 balance 0.578 0.691 0.598 0.644 0.674 0.667 0.670 bupa 0.578 0.654 0.622 0.639 0.662 0.652 0.650 contraceptive 0.451 0.459 0.459 0.451 0.483 0.468 0.467 echocardiogram 0.459 0.683 0.673 0.723 0.674 0.658 0.679 glass-0-1-2-3vs4-5-6 0.656 0.691 0.724 0.705 0.661 0.712 0.709 hayes-roth 0.415 0.752 0.722 0.730 0.746 0.767 0.758 house-votes-84 0.836 0.938 0.883 0.930 0.896 0.939 0.936 ionosphere 0.850 0.897 0.855 0.921 0.884 0.915 0.906 iris 0.527 0.954 0.957 0.936 0.953 0.972 0.976 kr-vs-kp 0.710 0.949 0.799 0.850 0.931 0.946 0.949 monk-2 0.783 0.889 0.940 0.928 0.911 0.910 0.932 mushroom 0.765 0.976 0.926 0.938 0.983 0.986 0.994 penguins_size 0.572 0.986 0.973 0.992 0.985 0.975 0.990 pima 0.634 0.671 0.676 0.697 0.663 0.684 0.688 spambase 0.908 0.914 0.886 0.838 0.913 0.922 0.927 splice 0.577 0.904 0.822 0.920 0.885 0.898 0.897 ttt 0.495 0.693 0.576 0.659 0.628 0.756 0.779 winequality-red 0.194 0.274 0.242 0.264 0.174 0.266 0.262 winequality-white 0.182 0.228 0.204 0.227 0.190 0.227 0.231 平均值 0.594 0.745 0.712 0.735 0.724 0.751 0.758

表4 下游预测任务中各方法的Pre值对比 Table 4 Pre comparison of different methods in downstream prediction tasks

表5

Table 4

表5(Table 4)

表5 下游预测任务中各方法的F1值对比 Table 5 F1 comparison of different methods in downstream prediction tasks 数据集 原始训练数据 SMOTE CTGAN TVAE DDPM VD-DDPM_s VD-DDPM_m adult 0.640 0.714 0.703 0.726 0.394 0.715 0.766 balance 0.532 0.669 0.525 0.561 0.641 0.665 0.667 bupa 0.442 0.649 0.608 0.633 0.660 0.650 0.647 contraceptive 0.423 0.452 0.449 0.445 0.471 0.460 0.459 echocardiogram 0.459 0.669 0.672 0.720 0.670 0.657 0.679 glass-0-1-2-3vs4-5-6 0.706 0.747 0.779 0.764 0.710 0.771 0.760 hayes-roth 0.406 0.744 0.719 0.736 0.741 0.751 0.748 house-votes-84 0.823 0.944 0.891 0.931 0.907 0.944 0.939 ionosphere 0.694 0.894 0.814 0.915 0.883 0.903 0.895 iris 0.562 0.953 0.956 0.934 0.951 0.971 0.975 kr-vs-kp 0.620 0.949 0.796 0.843 0.931 0.946 0.949 monk-2 0.775 0.885 0.937 0.924 0.909 0.907 0.931 mushroom 0.662 0.976 0.917 0.933 0.983 0.985 0.994 penguins_size 0.611 0.973 0.970 0.975 0.957 0.972 0.979 pima 0.572 0.667 0.668 0.695 0.660 0.682 0.686 spambase 0.910 0.917 0.883 0.837 0.916 0.924 0.929 splice 0.434 0.918 0.830 0.847 0.905 0.916 0.915 ttt 0.398 0.694 0.567 0.660 0.627 0.757 0.784 winequality-red 0.157 0.267 0.216 0.255 0.140 0.259 0.253 winequality-white 0.125 0.210 0.177 0.206 0.149 0.208 0.216 平均值 0.547 0.744 0.704 0.727 0.710 0.752 0.759

表5 下游预测任务中各方法的F1值对比 Table 5 F1 comparison of different methods in downstream prediction tasks

由表3~表5可得如下结论.

1)相比原始训练数据方法, VD-DDPM_s的Acc、Pre、F₁指标度量结果较优的数据集个数分别为19、19、20, 且相应指标的平均值分别提高0.152、0.157、0.205.结果表明, 在训练数据样本量有限时, VD-DDPM_s生成的数据可有效提高下游模型的性能.

2)相比SMOTE, VD-DDPM_s的Acc、Pre、F₁指标度量结果较优的数据集个数分别为15、12、13, 且相应指标的平均值分别提高0.02、0.006、0.008, 结果表明, 本文提出的生成式方法优于利用局部信息进行过采样的方法.

3)相比CTGAN, VD-DDPM_s的Acc、Pre、F₁指标度量结果较优的个数分别为16、17、17, 相应指标的平均值分别提高0.054、0.039、0.048.相比TVAE, VD-DDPM_s的Acc、Pre、F₁指标度量结果较优的数据集个数分别为13、12、14, 同时相应指标的平均值分别提高0.025、0.016、0.025.因此, 相比CTGAN和TVAE, VD-DDPM_s生成的数据更能覆盖原始表格型数据的真实分布.

4)相比DDPM, VD-DDPM_s的Acc、Pre、F₁指标度量结果较优的数据集个数分别为16、14、16, 相应指标的平均值分别提高0.099、0.037、0.059.在adult数据集上差距较明显, VD-DDPM_s的Acc、Pre、F₁指标分别比DDPM提高0.229、0.132、0.321.winequality-white、winequality-red数据集是2个较特殊的数据集, 不同类别的特征分布重叠现象严重, DDPM在2个数据集上表现很差, 但是VD-DDPM_s仍略有提高.

DDPM与VD-DDPM_s在实验数据集上生成数据在下游任务的总体表现如图6所示, 为了使实验结果更直观, 排除winequality-white数据集上的结果.图中, 横坐标表示DDPM生成数据在下游任务中的准确率, 纵坐标表示VD-DDPM_s生成数据在下游任务中的准确率, 一个点表示一个数据集的结果.

图6

Fig.6

	Figure Option ViewDownloadNew Window
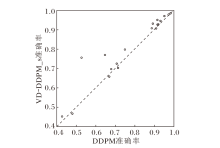	图6 VD-DDPM_s与DDPM在实验数据集上的准确率对比Fig.6 Accuracy comparison of VD-DDPM_s and DDPM on experimental datasets

由图6可清晰观察到, 在这些数据集上, VD-DDPM_s在下游任务中的准确率普遍高于DDPM, 在3个数据集上略微不足, 在2个数据集上效果相当.因此可说明, VD-DDPM_s可有效提高DDPM在训练样本量有限情况下的模型性能.

5)相比VD-DDPM_s, VD-DDPM_m的Acc、Pre、F₁指标度量结果中较优的数据集个数分别为14、12、12, 相应指标的平均值上分别提高0.009、0.007、0.007.因此, 在生成的数据中加入一些符合真实数据分布的数据, 在一定程度上可进一步提高下游预测模型的性能.由于本文仅采用生成数据和原始数据的简单混合以训练模型, 如果先利用生成数据训练好模型, 再利用原始数据微调模型, 可使下游模型的性能更佳.

此外, 为了确保实验结果具有统计意义, 本文采用Friedman检验分析实验结果差异的显著性, 显著性水平均设置为0.05.

首先, 根据表3的实验结果, 按照Acc将算法进行排序.再利用Friedman检验判断这些算法的性能是否相同, 作出假设“ 所有算法的性能均相同” , 变量

${{\tau }_{F}}=\frac{\left( n-1 \right)\tau _{\chi }^{2}}{n\left( k-1 \right)-\tau _{\chi }^{2}}$,

其中

$\tau _{\chi }^{2}=\frac{12n}{k\left( k+1 \right)}\left( \overset{k}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, r_{i}^{2}-\frac{k{{\left( k+1 \right)}^{2}}}{4} \right)$,

n表示数据集个数, k表示算法个数, r_i表示第i个算法的平均序值.

变量τ _F服从自由度为k-1和(k-1)(n-1)的F分布.查表得, 在显著性水平为0.05的条件下, 临界值F_α =2.179, 经计算,

τ _F=59.871> 2.179,

因此拒绝“ 所有算法的性能均相同” 的假设, 说明算法之间的性能是存在显著差异的.

综上所述, 无论是VD-DDPM_s还是VD-DDPM_m, 在大多数情况下均优于一些针对表格型数据的对比方法, 特别地, 相比DDPM, 提升效果较明显.因此, 在原始表格型训练数据有限的情况下, VD-DDPM_s和VD-DDPM_m都能有效提高下游任务中预测模型的性能.