现实生活中对项目进行测试时, 一般有多个测试尺度.通常来说, 尺度越粗, 测试代价越小, 同时分类能力越差, 尺度越细则相反.本文的目的是在保证可得到想要的分类效果的前提下, 尽可能选取较粗的尺度, 从而减少总测试代价.由于经典粗糙集中的概念及性质不适用于多尺度决策系统, 因此本节介绍适用于多尺度决策系统并且同时考虑属性因素和尺度因素的定义及性质, 为下文算法设计提供理论基础.

假设六元组MSDS=(U, C, L, V, f, d)表示多尺度决策系统, 其中, U为论域, C为属性全集, C中共有n个属性,

L=(L₁, L₂, …, L_n)

为所有属性的尺度个数组成的向量, $V=\{{{V}_{\left( a, {{l}_{a}} \right)}}\}$为值域,

${{V}_{\left( a, {{l}_{a}} \right)}}=\{{{x}_{\left( a, {{l}_{a}} \right)}}|x\in U\}$

为属性a在尺度l_a下的值域, $f=\{{{f}_{\left( a, {{l}_{a}} \right)}}\}$为信息函数,

${{f}_{\left( a, {{l}_{a}} \right)}}:U\to {{V}_{\left( a, {{l}_{a}} \right)}}$

为属性a在尺度l_a下的信息函数, 决策属性d∉C.各个属性的尺度个数不一定相等.

使用S表示C的尺度向量.例如:

S¹=(1, 1, …, 1)

表示所有属性都选择最细的尺度,

S^L=(L₁, L₂, …, L_n)

表示所有属性都选择最粗的尺度.同理, 对于∀ B⊆C, 假设B中有m个属性, 则可用

${{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \ldots , {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, ~j=1, 2, \ldots , m$,

表示B的尺度向量.属性集与其对应的尺度向量可组成有序对, 如(C, S)、(B, S_B).给定

${{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \ldots , {{l}_{{{i}_{m}}}}), S{{'}_{B}}=(l{{'}_{{{i}_{1}}}}, l{{'}_{{{i}_{2}}}}, \ldots , l{{'}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, 1\le l{{'}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}j=1, 2, \ldots , m$.

若

${{l}_{{{i}_{j}}}}\le l{{'}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

则S_B⪯S'_B, 称S_B细于S'_B; 若

${{l}_{{{i}_{j}}}}\le l{{'}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

并且存在k∈ {1, 2, …, m}, 使得${{l}_{{{i}_{k}}}}< l{{'}_{{{i}_{k}}}}$, 则S_B≺S'_B, 称S_B严格细于S'_B.

多尺度决策系统中同一属性的不同尺度之间存在联系, 这种联系使对象在同一属性的不同尺度下的属性值可互相转换.给定一个

MSDS=(U, C, L, V, f, d),

$\forall a\in C, 1\le {{l}_{a}}\le {{L}_{a}}-1$,

存在满射

$g_{a}^{{{l}_{a}}, {{l}_{a}}+1}\, \!:{{V}_{\left( a, {{l}_{a}} \right)}}\to {{V}_{\left( a, {{l}_{a}}+1 \right)}}$,

使得

${{x}_{\left( a, {{l}_{a}}+1 \right)}}=g_{a}^{{{l}_{a}}, {{l}_{a}}+1}~({{x}_{\left( a, {{l}_{a}} \right)}}), x\in U$,

其中$g_{a}^{{{l}_{a}}, {{l}_{a}}+1}$是将a的属性值从尺度l_a转换到尺度l_a+1的信息变换.并且, 对于$l_{a}^{1}$和$l_{a}^{2}$, $1\le l_{a}^{1}< l_{a}^{2}\le {{L}_{a}}$ , 同样存在满射

$g_{a}^{l_{a}^{1}, l_{a}^{2}}\, \!:{{V}_{\left( a, l_{a}^{1} \right)}}\to {{V}_{\left( a, l_{a}^{2} \right)}}$,

$g_{a}^{l_{a}^{1}, l_{a}^{2}}=g_{a}^{l_{a}^{1}, l_{a}^{1}+1}\circ g_{a}^{l_{a}^{1}+1, l_{a}^{1}+2}\circ \ldots \circ g_{a}^{l_{a}^{2}-1, l_{a}^{2}}$,

使得

${{x}_{\left( a, l_{a}^{2} \right)}}=g_{a}^{l_{a}^{1}, l_{a}^{2}}~({{x}_{\left( a, l_{a}^{1} \right)}}), x\in U.$ (1)

结合上述内容, 对象x关于属性子集和尺度向量的等价类定义如定义1.

定义1 给定一个

MSDS=(U, C, L, V, f, d),

$B\subseteq C, {{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \cdots {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

∀ x∈ U关于(B, S_B)的等价类定义为

${{[x]}_{\left( B, {{S}_{B}} \ \right)}}=\{y\in U|{{x}_{\left( a, {{l}_{a}} \right)}}={{y}_{\left( a, {{l}_{a}} \right)}}\forall (a, {{l}_{a}})\in (B, {{S}_{B}})\}$,

其中${{x}_{\left( a, {{l}_{a}} \right)}}={{y}_{\left( a, {{l}_{a}} \right)}}$表示x、y在属性a的l_a尺度下属性值相等.

由定义1不难得到等价类的自反性、对称性及传递性, 如性质1所示.

性质1 给定一个

MSDS=(U, C, L, V, f, d),

$B\subseteq C, {{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \cdots {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

则∀ x∈ U关于(B, S_B)的等价类满足

1)自反性.$\forall x\in U, x\in {{[x]}_{\left( B, {{S}_{B}} \ \right)}}$;

2)对称性.∀ x_i∈ U, x_j∈ U, 如果

${{x}_{j}}\in {{[{{x}_{i}}]}_{\left( B, {{S}_{B}} \ \right)}}$,

则${{x}_{i}}\in {{[{{x}_{j}}]}_{\left( B, {{S}_{B}} \ \right)}}$;

3)传递性.∀ x_i∈ U, x_j∈ U, x_k∈ U, 如果

${{x}_{i}}\in {{[{{x}_{j}}]}_{\left( B, {{S}_{B}} \ \right)}}, {{x}_{j}}\in {{[{{x}_{k}}]}_{\left( B, {{S}_{B}} \ \right)}}$,

则${{x}_{i}}\in {{[{{x}_{k}}]}_{\left( B, {{S}_{B}} \ \right)}}$.

结合定义1和性质1, 可得到等价关系以及广义决策值的概念, 如定义2~定义4所示.

定义2 给定一个

MSDS=(U, C, L, V, f, d),

$\forall a\in C, 1\le {{l}_{a}}\le {{L}_{a}}$_,

U关于(a, l_a)的等价关系为

${{R}_{\left( a, {{l}_{a}} \right)}}=\{(x, y)\in U\times U|{{x}_{\left( a, {{l}_{a}} \right)}}={{y}_{\left( a, {{l}_{a}} \right)}}\}$.

定义3 给定一个

MSDS=(U, C, L, V, f, d),

$B\subseteq C, {{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \cdots , {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

U关于(B, S_B)的等价关系为

${{R}_{\left( B, {{S}_{B}} \ \right)}}=\{(x, y)\in U\times U|{{x}_{\left( a, {{l}_{a}} \right)}}={{y}_{\left( a, {{l}_{a}} \right)}}$,

$\forall (a, {{l}_{a}})\in (B, {{S}_{B}})\}=\underset{\left( a, {{l}_{a}} \right)\in \left( B, {{S}_{B}} \ \right)}{\mathop{\cap }}\, {{R}_{\left( a, {{l}_{a}} \right)}}$.

等价关系可把论域划分成多个互不相交的集合, 并且这些集合的并集也是论域, 即

$U/{{R}_{\left( B, {{S}_{B}} \ \right)}}=\{{{[x]}_{\left( B, {{S}_{B}} \ \right)}}\text{ }\!\!|\!\!\text{ }x\in U\}$.

定义4 给定一个

MSDS=(U, C, L, V, f, d),

$B\subseteq C, {{S}_{B}}\text{=}({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \cdots , {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

则∀ x∈ U关于(B, S_B)的广义决策值为

${{\partial }_{\left( B, {{S}_{B}} \ \right)}}~(x)=\{d(y)|y\in {{[x]}_{\left( B, {{S}_{B}} \ \right)}}\}$,

其中d(y)为对象y的决策值.若对∀ x∈ U,

$|{{\partial }_{\left( C, {{S}^{1}} \right)}}(x)|=1$,

称该多尺度决策系统是协调的; 若∃x∈ U, 使得

$|{{\partial }_{\left( C, {{S}^{1}} \right)}}~(x)|\ge 2$,

称该多尺度决策系统是不协调的.

在下文的讨论过程中, 若定义和性质只适用于协调的多尺度决策系统或不协调的多尺度决策系统, 将会特别注明; 若都适用, 则统称为多尺度决策系统.进一步地, 在第2节的算法部分, 将针对协调的多尺度决策系统和不协调的多尺度决策系统, 给出基于测试代价敏感的属性和尺度同步选择的方法.

协调的多尺度决策系统和不协调的多尺度决策系统计算上下近似、正区域和边界区域的方法不同.两种多尺度决策系统中的上下近似的具体定义分别如定义5和定义6所示.

定义5 给定一个协调的

MSDS=(U, C, L, V, f, d),

对于∀ X⊆U, B⊆C,

${{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \ldots , {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

X关于(B, S_B)的上下近似分别为

$\overline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}~(X)=\{x\in U|{{[x]}_{\left( B, {{S}_{B}} \ \right)}}\cap X\ne \emptyset \}$,

$\underline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}(X)=\{x\in U|{{[x]}_{\left( B, {{S}_{B}} \ \right)}}\subseteq x\}$.

定义6 给定一个不协调的

MSDS=(U, C, L, V, f, d),

对于∀ X⊆U, B⊆C,

${{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \ldots , {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

X关于(B, S_B)的上下近似分别为

$\overline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}~(X)=\{x\in U|{{[x]}_{\left( B, {{S}_{B}} \ \right)}}\cap X\ne \emptyset , {{\partial }_{\left( B, {{S}_{B}} \ \right)}}(x)\cap {{\partial }_{\left( C, {{S}^{1}} \right)}}(x)\ne \emptyset \} $,

$\underline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}(X)=\{x\in U|{{[x]}_{\left( B, {{S}_{B}} \ \right)}}\subseteq X, {{\partial }_{\left( B, {{S}_{B}} \ \right)}}(x)\subseteq {{\partial }_{\left( C, {{S}^{1}} \right)}}(x)\}$.

决策属性{d}可将论域U划分成多个互不相交的集合, {d}关于(B, S_B)的上下近似如定义7所示.

定义7 给定一个

MSDS=(U, C, L, V, f, d),

$B\subseteq C, {{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \cdots , {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

$U/\{d\}=\{{{X}_{1}}, {{X}_{2}}, {{\ldots }_{, }}{{X}_{K}}\}$,

则{d}关于(B, S_B)的上下近似为

$\overline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}~(d)=\underset{i=1}{\overset{K}{\mathop \cup }}\, \overline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}~({{X}_{i}})$,

$\underline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}(d)=\underset{i=1}{\overset{K}{\mathop \cup }}\, \underline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}({{X}_{i}})$.

从表达式可很明显看出, {d}关于(B, S_B)的上下近似就是X_i关于(B, S_B)的上下近似的并集, i=1, 2, …, K.{d}关于(B, S_B)的下近似同时也是正区域, 表示为

$PO{{S}_{\left( B, {{S}_{B}} \ \right)}}~(d)=\underline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}~(d)=\underset{i=1}{\overset{K}{\mathop \cup }}\, \underline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}~({{X}_{i}})$.

{d}关于(B, S_B)的上近似与正区域(即下近似)的差为边界区域, 表示为

$B{{N}_{\left( B, {{S}_{B}} \ \right)}}~(d)=\overline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}~(d)-PO{{S}_{\left( B, {{S}_{B}} \ \right)}}~(d)=\overline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}(d)-\underline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}(d)$.

上下近似、正区域和边界区域之间存在如下性质2.

性质2 给定一个

MSDS=(U, C, L, V, f, d),

$B\subseteq C, {{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \cdots , {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

则

1)$PO{{S}_{\left(\emptyset , {{S}_{\emptyset }} \right)}}(d)= \emptyset $,

2)$\overline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}\left( d \right)=U$,

3)$PO{{S}_{\left( B, {{S}_{B}} \ \right)}}~(d)\cap B{{N}_{\left( B, {{S}_{B}} \ \right)}}(d)= \emptyset $,

4)$PO{{S}_{\left( B, {{S}_{B}} \ \right)}}~(d)\cup B{{N}_{\left( B, {{S}_{B}} \ \right)}}(d)=U$.

等价类、等价关系、上下近似、正区域和边界区域关于属性子集和尺度向量存在一些单调关系, 这些单调关系可减少后文算法的计算量, 起到加速算法的作用.

在介绍关于属性子集的单调性之前, 需要先了解一下符号$\sqsubseteq$.给定一个向量

S=(l₁, l₂, …, l_n),

若S'由S中的一个或多个部分组成, 称S'是S的子向量, 可表示为$S’ \sqsubseteq S$或$S\sqsupseteq S’ $^[13].例如:

S=(1, 2, 3, 4, 5), S'=(2, 5),

则S'为S的子向量, 记为$S'\sqsubseteq S$或$S\sqsupseteq S'$.

性质3 关于属性子集的单调性 给定一个

MSDS=(U, C, L, V, f, d),

${{B}_{1}}\subseteq {{B}_{2}}\subseteq C, {{S}_{{{B}_{2}}}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \cdots , {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m, {{S}_{{{B}_{1}}}}\sqsubseteq{{S}_{{{B}_{2}}}}$

则

1)$\forall x\in U, {{[x\text{ }\!\!~\!\!\text{ }]}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}~\supseteq {{[x]}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}$,

${{\partial }_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}~(x)\supseteq {{\partial }_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}~(x)$;

2)${{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}\supseteq {{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}$;

3)$\forall X\in U/\{d\}, \underline{{{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}}(X)\subseteq \underline{{{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}}(X)$,

$\overline{{{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}}\left( X \right)\supseteq \overline{{{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}}~(X)$;

4)$PO{{S}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}(d)\subseteq PO{{S}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}(d)$,

$B{{N}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}(d)\supseteq B{{N}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}(d)$.

证明 先证1).$\forall x'\in {{[x]}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}$, 根据定义1可知

$x{{'}_{\left( a, {{l}_{a}} \right)}}={{x}_{\left( a, {{l}_{a}} \right)}}, \forall (a, {{l}_{a}})\in ({{B}_{2}}, {{S}_{{{B}_{2}}}})$.

因为B₁⊆B₂, ${{S}_{{{B}_{1}}}}\sqsubseteq{{S}_{{{B}_{2}}}}$ , 所以

$x{{'}_{\left( a, {{l}_{a}} \right)}}={{x}_{\left( a, {{l}_{a}} \right)}}, \forall (a, {{l}_{a}})\in ({{B}_{1}}, {{S}_{{{B}_{1}}}})$.

故$x'\in {{[x]}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}$, 由x'的任意性可得

${{[x]}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}\supseteq {{[x]}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}$.

上述步骤证明

${{[x]}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}\supseteq {{[x]}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}$,

则根据定义4显然可知,

${{\partial }_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}~(x)\supseteq {{\partial }_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}(x)$.

再证2).

$\forall (x, y)\in {{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}$,

根据定义3可知

${{x}_{\left( a, {{l}_{a}} \right)}}={{y}_{\left( a, {{l}_{a}} \right)}}, \forall (a, {{l}_{a}})\in ({{B}_{2}}, {{S}_{{{B}_{2}}}})$.

因为B₁⊆B₂, ${{S}_{{{B}_{1}}}}\sqsubseteq{{S}_{{{B}_{2}}}}$ , 所以

${{x}_{\left( a, {{l}_{a}} \right)}}={{y}_{\left( a, {{l}_{a}} \right)}}, \forall (a, {{l}_{a}})\in ({{B}_{1}}, {{S}_{{{B}_{1}}}})$.

故

$\left( x, y \right)\in {{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}$,

由(x, y)的任意性可得

${{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}\supseteq {{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}$.

再证3).

$\forall x\in \underline{{{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}}(X)$,

根据定义5和定义6可得

${{[x]}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}\subseteq X, {{\partial }_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}(x)\subseteq {{\partial }_{\left( C, {{S}^{1}} \right)}}(x)$.

由1)可知

${{[x]}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}\subseteq {{[x\text{ }\!\!~\!\!\text{ }]}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}\subseteq X$,

${{\partial }_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}(x)\subseteq {{\partial }_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}(x)\subseteq {{\partial }_{\left( C, {{S}^{1}} \right)}}(x)$,

因此不论多尺度决策系统是否协调,

$x\in \underline{{{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}}\left( X \right)$.

由x的任意性可得

$\underline{{{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}}\left( X \right)\subseteq \underline{{{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}}\left( X \right)$.

类似可证

$\overline{{{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}}\left( X \right)\supseteq \overline{{{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}}\left( X \right)$.

最后证4).假设

$U/\{d\}=\{{{X}_{1}}, {{X}_{2}}, \ldots , {{X}_{K}}\}$,

由3)可知

$\underline{{{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}}({{X}_{i}})\subseteq \underline{{{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}}({{X}_{i}}), i=1, 2, \ldots , K$.

根据定义7可知

$PO{{S}_{\left( {{B}_{j}}, {{S}_{{{B}_{j}}}} \right)}}(d)=\underset{i=1}{\overset{K}{\mathop \cup }}\, \underline{{{R}_{\left( {{B}_{j}}, {{S}_{{{B}_{j}}}} \right)}}}~({{X}_{i}}), j=1, 2$,

因此显然

$PO{{S}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}(d)\subseteq PO{{S}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}(d)$.

同样, 由3)可知

$\overline{{{R}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}}~(X)\supseteq \overline{{{R}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}}~(X)$,

又由定义7可知

$B{{N}_{\left( {{B}_{j}}, {{S}_{{{B}_{j}}}} \right)}}(d)=\overline{{{R}_{\left( {{B}_{j}}, {{S}_{{{B}_{j}}}} \right)}}}~(d)-PO{{S}_{\left( {{B}_{j}}, {{S}_{{{B}_{j}}}} \right)}}(d), j=1, 2$,

所以

$B{{N}_{\left( {{B}_{1}}, {{S}_{{{B}_{1}}}} \right)}}(d)\supseteq B{{N}_{\left( {{B}_{2}}, {{S}_{{{B}_{2}}}} \right)}}(d)$.

性质3表示随着属性增多, 正区域越来越大的同时边界区域越来越小.关于尺度向量也有类似的单调性, 如性质4所示.

性质4 关于尺度向量的单调性 给定一个

MSDS=(U, C, L, V, f, d),

$B\subseteq C, S_{B}^{1}\preceq S_{B}^{M}\preceq S_{B}^{N}\preceq S_{B}^{L}$

1)$\forall x\in U, {{[x]}_{\left( B, S_{B}^{M} \right)}}\subseteq {{[x]}_{\left( B, S_{B}^{N} \right)}}$,

${{\partial }_{\left( B, S_{B}^{M} \right)}}(x)\subseteq {{\partial }_{\left( B, S_{B}^{N} \right)}}(x)$;

2)${{R}_{\left( B, S_{B}^{M} \right)}}\subseteq {{R}_{\left( B, S_{B}^{N} \right)}}$;

3)∀ X∈ U/{d}, $\underline{{{R}_{\left( B, S_{B}^{M} \right)}}}(X)\supseteq \underline{{{R}_{\left( B, S_{B}^{N} \right)}}}(X)$,

$\overline{{{R}_{\left( B, S_{B}^{M} \right)}}}(X)\subseteq \overline{{{R}_{\left( B, S_{B}^{N} \right)}}}(X)$;

4)$PO{{S}_{\left( B, S_{B}^{M} \right)}}(d)\supseteq PO{{S}_{\left( B, S_{B}^{N} \right)}}(d)$,

$B{{N}_{\left( B, S_{B}^{M} \right)}}(d)\subseteq B{{N}_{\left( B, S_{B}^{N} \right)}}(d)$.

证明 先证1).假设

$S_{B}^{M}=\left( l_{1}^{M}, l_{2}^{M}, \ldots , l_{m}^{M} \right), S_{B}^{N}=\left( l_{1}^{N}, l_{2}^{N}, \ldots , l_{m}^{N} \right)$.

由式(1)可知, 对于∀ x∈ U, 都存在尺度信息转换$g_{a}^{l_{a}^{M}, l_{a}^{N}}$, 使得

${{x}_{\left( a, l_{a}^{N} \right)}}=g_{a}^{l_{a}^{M}, l_{a}^{N}}\left( {{x}_{\left( a, l_{a}^{M} \right)}} \right)$.

对于

$\forall x'\in {{[x]}_{\left( B, S_{B}^{M} \right)}}, x{{'}_{\left( a, l_{a}^{M} \right)}}={{x}_{\left( a, l_{a}^{M} \right)}}$,

$\forall (a, l_{a}^{M})\in (B, S_{B}^{M})$,

因此

$x{{'}_{\left( a, l_{a}^{N} \right)}}=g_{a}^{l_{a}^{M}, l_{a}^{N}}~(x{{'}_{\left( a, l_{a}^{M} \right)}})=g_{a}^{l_{a}^{M}, l_{a}^{N}}({{x}_{\left( a, l_{a}^{M} \right)}})={{x}_{\left( a, l_{a}^{N} \right)}}$,

$\forall (a, l_{a}^{N}\in (B, S_{B}^{N})$.

故$x'\in {{[x]}_{\left( B, S_{B}^{N} \right)}}$, 由x'的任意性可得

${{[x]}_{\left( B, S_{B}^{M} \right)}}\subseteq {{[x]}_{\left( B, S_{B}^{N} \right)}}$.

上述步骤证明

${{[x]}_{\left( B, S_{B}^{M} \right)}}\subseteq {{[x]}_{\left( B, S_{B}^{N} \right)}}$,

根据定义4显然可知,

${{\partial }_{\left( B, S_{B}^{M} \right)}}(x)\subseteq {{\partial }_{\left( B, S_{B}^{N} \right)}}(x)$.

2)~4)的证明过程与性质3中证明过程类似, 为了节省篇幅, 不再给出证明过程.性质4表示随着尺度向量变细, 正区域越来越大, 边界区域越来越小.

性质3和性质4分别介绍多尺度决策系统关于属性子集以及尺度向量的单调性, 结合这两个性质可看出, 不论属性子集、尺度向量如何变化, (C, S¹)始终是使多尺度决策系统正区域最大、边界区域最小的有序对.

性质5 给定一个

MSDS=(U, C, L, V, f, d), B⊆C,

${{S}^{1}}=(1, 1, \ldots , 1), {{S}_{B}}=({{l}_{{{i}_{1}}}}, {{l}_{{{i}_{2}}}}, \cdots , {{l}_{{{i}_{m}}}})$,

$1\le {{l}_{{{i}_{j}}}}\le {{L}_{{{i}_{j}}}}, j=1, 2, \ldots , m$,

则有

1)∀ x∈ U, ${{[x]}_{\left( B, {{S}_{B}} \ \right)}}\supseteq {{[x]}_{\left( C, {{S}^{1}} \right)}}$, ${{\partial }_{\left( B, {{S}_{B}} \ \right)}}(x)\supseteq {{\partial }_{\left( C, {{S}^{1}} \right)}}(x)$;

2)${{R}_{\left( B, {{S}_{B}} \ \right)}}\supseteq {{R}_{\left( C, {{S}^{1}} \right)}}$;

3)∀ X∈ U/{d}, $\underline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}(X)\subseteq \underline{{{R}_{\left( C, {{S}^{1}} \right)}}}(X)$, $\overline{{{R}_{\left( B, {{S}_{B}} \ \right)}}}\left( X \right)\supseteq \overline{{{R}_{\left( C, {{S}^{1}} \right)}}}\left( X \right)$;

4)$PO{{S}_{\left( B, {{S}_{B}} \ \right)}}(d)\subseteq PO{{S}_{\left( C, {{S}^{1}} \right)}}(d)$, $B{{N}_{\left( B, {{S}_{B}} \ \right)}}(d)\supseteq B{{N}_{\left( C, {{S}^{1}} \right)}}(d)$.

证明 先证明

$PO{{S}_{\left( B, {{S}_{B}} \ \right)}}\left( d \right)\subseteq PO\text{ }\!\!~\!\!\text{ }{{S}_{\left( C, {{S}^{1}} \right)}}\left( d \right)$.

将S_B比S¹缺少的属性尺度位置补为1, 其余数值不变, 记为S'.显然可得S'⪰S¹, 结合性质4可知,

$PO{{S}_{(C, S')}}(d)\subseteq PO{{S}_{\left( C, {{S}^{1}} \right)}}(d)$.

又因为B⊆C, ${{S}_{B}} \sqsubseteq S'$ , 结合性质3可得

$PO{{S}_{\left( B, {{S}_{B}} \ \right)}}(d)\subseteq PO{{S}_{(C, S')}}(d)$.

所以

$PO{{S}_{\left( B, {{S}_{B}} \ \right)}}(d)\subseteq PO{{S}_{\left( C, {{S}^{1}} \right)}}(d)$.

其它性质证明过程类似, 为了节省篇幅, 不再给出详细的证明过程.

现有的关于多尺度决策系统中属性与尺度同步选择的算法大多未考虑测试代价, 但是在实际应用中, 测试代价经常会影响数据处理的效果, 并且目前还没有研究提出同时适用于协调的多尺度决策系统和不协调的多尺度决策系统的属性与尺度同步选择算法.因此, 本文基于测试代价, 设计启发式的属性与尺度同步选择算法, 同时适用于协调的多尺度决策系统和不协调的多尺度决策系统, 既能保持分类能力尽可能不变, 又能使总测试代价最小化.

在实际应用中, 度量越精细, 该属性的测试代价越大, 反之测试代价越小.因此, 为了使实验更贴近现实, 本文定义的测试代价函数在属性尺度为1时测试代价最大, 并且测试代价会随着尺度的增大而减小.具体测试代价函数如下:

$tc(a, {{l}_{a}})=\left\{ \begin{array}{* {35}{l}} tc\left( a, 1 \right), & {{l}_{a}}=1 \\ tc\left( a, 1 \right)\cdot \frac{\lambda }{{{l}_{a}}}, & 1< {{l}_{a}}\le {{L}_{a}} \\ \end{array} \right.$ (2)

其中:λ 为调节系数, 1≤ λ < 2; tc(a, 1)为属性a在尺度1下的测试代价.根据式(2)可得到(B, S_B)的总测试代价(Total Test Cost, TTC):

$TTC(B, {{S}_{B}})=\underset{\left( a, {{l}_{a}} \right)\in \left( B, {{S}_{B}} \ \right)}{\mathop \sum }\, tc(a, {{l}_{a}})$.(3)

结合第1节内容可知, 正区域会随着B中属性逐个增加而逐渐增大, 称在B中增加单个属性后正区域的增加部分为正区域的增量(Incremental Posi-tive Region, IPR), 表示为

$IP{{R}_{\left( B, {{S}_{B}} \ \right)}}~(a, {{l}_{a}})=PO{{S}_{\left( B\cup \left\{ a \right\}, {{S}_{B}}\ \vee {{l}_{a}} \right)}}\ (d)-PO{{S}_{\left( B, {{S}_{B}} \ \right)}}(d)$,

其中S_B∨ l_a表示在向量S_B中增加元素l_a.

基于式(2)和正区域增量定义属性-尺度重要度(Attribute-Scale Significance, ASS)函数:

$\begin{align} & AS{{S}_{\left( B, {{S}_{B}} \ \right)}}~(a, {{l}_{a}})= \\ & |IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a, {{l}_{a}})|{{[tc(a, {{l}_{a}})]}^{\delta }}= \\ & \frac{\left| IP{{R}_{\left( B, {{S}_{B}} \ \right)}}\left( a, {{l}_{a}} \right) \right|}{{{[tc(a, {{l}_{a}})]}^{\left| \delta \right|}}} \\ \end{align}$,

其中δ ≤ 0.

从式(4)中可看出, 属性-尺度重要度函数同时考虑属性的分类能力和测试代价.ASS随着IPR增大或测试代价减小而增大.δ 的取值影响测试代价对ASS的重要程度, δ 越小, 测试代价对ASS越重要, 用户倾向于选择测试代价小并且分类能力好的属性和尺度.注意到, δ =0时为未考虑测试代价的情况, 这时

$AS{{S}_{\left( B, {{S}_{B}} \ \right)}}~(a, {{l}_{a}})=|IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a, {{l}_{a}})|$.

下文会对比是否考虑测试代价的计算结果, 验证本文算法在考虑测试代价时的有效性.

结合上述定义及性质, 设计测试代价敏感的属性与尺度同步选择的启发式算法.该算法分为算法1和算法2, 算法2在算法1中被调用.具体算法步骤如下所示.

算法1 多尺度决策系统中测试代价敏感的属性与尺度同步选择算法

输入 一个MSDS=(U, C, L, V, f, d),

每个属性的测试代价函数, 权重δ

输出 全局最优的属性子集B, 尺度向量S_B

1.B=Ø ; //B为选择的属性子集

2.S_B=(); //S_B为选择的尺度向量

3.CA=C; //CA为未被选择的属性集

4.U'=U; //U'为还未被选择的对象集

5.$PO{{S}_{\left( B, {{S}_{B}} \ \right)}}(\{d\})=\emptyset $; //$PO{{S}_{\left( B, {{S}_{B}} \ \right)}}(\{d\})$为正区域

6.while (U'≠ Ø ) do

7. for (each a∈ CA) do

8. for (each x∈ U') do

9. sign_x=true; /* sign_x为全局变量, 在算法2中被调用* /

10. end for

11. for (l'_a=1; l'_a≤ L_a; l'_a++) do

12. SIGcomputing(U', B, S_B, a, l'_a); /* 调用算法2* /

13. end for

14. 选择尺度l_a使得

$AS{{S}_{\left( B, {{S}_{B}} \ \right)}}(a, {{l}_{a}})=\max (AS{{S}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}}))$;

15. end for

16. 选择属性a'使得

$AS{{S}_{\left( B, {{S}_{B}} \ \right)}}(a', {{l}_{a'}})=max(AS{{S}_{\left( B, {{S}_{B}} \ \right)}}(a, {{l}_{a}}))$;

17. if ($AS{{S}_{\left( B, {{S}_{B}} \ \right)}}(a', {{l}_{a'}})> 0$) then

18. B=B∪ {a'};

19. S_B=S_B∨ l_a';

20. $PO{{S}_{\left( B, {{S}_{B}} \ \right)}}(d)=PO{{S}_{\left( B, {{S}_{B}} \ \right)}}(d)\cup IP(a', {{l}_{a'}})$;

21. CA=CA-{a'};

22. $U'=U'-IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a', {{l}_{a'}})$;

23. else

24. exit while;

25. end if

26.end while

27.cmttc=TTC(B, S_B); //式(3)

28.return B, S_B

算法2 SIGcomputing

输入 正区域之外的对象集合U'

已选的属性子集B, 尺度向量S_B,

候选的属性a, 对应的尺度l'_a

输出 正区域的增量$IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}})$,

属性-尺度重要度$AS{{S}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}})$

1. IPR(B, SB)(a, l'_a)=Ø ;

2.for (each x∈ U') do

3. if (sign_x==true) then

4. if(多尺度决策系统是协调的) then

5. 计算${{[x]}_{\left( B\cup \left\{ a \right\}, {{S}_{B}}\vee l'{{\text{ }\!\!~\!\!\text{ }}_{a}} \right)}}$;

6. if(∃X∈ U/{d}, 使${{[x]}_{\left( B\cup \left\{ a \right\}, {{S}_{B}}\vee l'{{\text{ }\!\!~\!\!\text{ }}_{a}} \right)}}\subseteq X$ )

then

7. $IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}})=IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}})\cup \{x\}$;

8. else

9. sign_x=false;

10. end if

11. else if (多尺度决策系统是不协调的) then

12. 计算$\partial {{(x)}_{\left( B\cup \left\{ a \right\}, {{S}_{B}}\vee l{{'}_{a}} \right)}}$;

13. if $(\partial {{(x)}_{\left( B\cup \left\{ a \right\}, {{S}_{B}}\vee l{{'}_{a}} \right)}}\subseteq \partial {{(x)}_{\left( C, {{S}^{1}} \right)}})$ then

14. $IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}})=IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}})\cup \{x\}$;

15. else

16. sign_x=false;

17. end if

18. end if

19. end if

20.end for

21.根据式(2)计算tc(a, l'_a);

22.$AS{{S}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}})=|IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}})|{{[tc(a, l{{'}_{a}})]}^{\delta }}$;

23.return $IP{{R}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}}), AS{{S}_{\left( B, {{S}_{B}} \ \right)}}(a, l{{'}_{a}})$

下面分析本文算法的时间复杂度, 由于算法1调用算法2, 因此首先分析算法2的时间复杂度.算法2的关键步骤是计算x的等价类或广义决策值, 即第5行或第12行, 该步骤在最坏情况(每次计算x的等价类或广义决策值都要验证U中所有对象)下的时间复杂度为

O(|U||B∪ {a}|)=O(|U|(|B|+1)),

算法2的时间复杂度为O(|U'||U|(|B|+1)).

注意, 算法2进行两次加速处理.第1次加速是第3行至第19行, 运用性质4中等价类(广义决策值)关于尺度向量的单调性.若x在相对细的尺度向量下都不能被划分至正区域, 那么在粗尺度向量下更不会被划分至正区域, 所以可省略计算该对象的等价类或广义决策值的过程.第2次加速是第5行和第12行, 运用性质3中等价类(广义决策值)关于属性子集的单调性进行加速, 增加属性后x的等价类(广义决策值)一定包含于增加属性前的.要想得到增加属性后x的等价类(广义决策值), 只需要排查增加属性前x的等价类中包含的对象, 不需要再验证U中全部对象.因此算法2的实际时间复杂度要小于O(|U'||U|(|B|+1)).

假设属性子集B中一共选择k个属性, 即|B|=k, 则每选取一个有序对(a', l_a')平均可将$\frac{\left| U \right|}{k}$个对象划分到正区域.随着while循环的进行,

$|U'|=|U|\left( 1-\frac{i}{k} \right)=|U|\left( \frac{k-i}{k} \right), i=0, 1, \ldots , k$.

算法1中的关键步骤是第12行, 计算单个有序对(a, l'_a)的正区域增量和ASS, 即调用算法2.假设所有属性中的最大尺度数为E, 则算法1的时间复杂度为

$\begin{matrix} & O\left( E|C||U{{|}^{2}}+E\cdot 2(|C|-1)|U{{|}^{2}}\left( \frac{k-1}{k} \right) \right.+ \\ & E\cdot 3\left( \left| C \right|-2 \right){{\left| U \right|}^{2}}\left( \frac{k-2}{k} \right)+\cdots + \\ & E\cdot k(|C|-k+1)|U{{|}^{2}}\left. \frac{1}{k} \right)= \\ & O\left( \frac{E\left| U \right|{{\text{ }\!\!~\!\!\text{ }}^{2}}}{k}\overset{k-1}{\mathop{\underset{i=0}{\mathop \sum }\, }}\, (i+1)(k-i)(|C|-i) \right). \\ \end{matrix}$

算法1中第22行运用性质3中正区域关于属性子集的单调性进行加速, 若U中的x已被划分至正区域, 那么增加有序对(a, l'_a)后, 该对象x还是会被划分至正区域, 因此可将x从U'中删除, 不需要再重复计算x是否属于正区域.

综上所述, 由于算法1调用算法2, 算法2的时间复杂度实际上小于

O(|U'||U|(|B|+1)),

并且算法1也进行加速处理, 所以算法1的实际时间复杂度小于

$ O\left( \frac{E\left| U \right|{^{2}}}{k}\overset{k-1}{\mathop{\underset{i=0}{\mathop \sum }\, }}\, (i+1)(k-i)(|C|-i) \right)$.

在硬件配置环境为Intel(R) Core(TM) i5-7200U CPU @2.70 GHz和内存4 GB的电脑上进行实验.

本文一共选取11个UCI数据集和1个实际数据集, 具体信息如表1所示.将表1中的数据集转化成名词型的多尺度数据集, 之后对Hill、QSAR数据集进行特殊处理, 转变成不协调的名词型多尺度数据集.将单尺度数据转换成多尺度数据的方法借鉴文献[25], 通过合并相邻值生成不同的尺度.为了更容易观察算法所选尺度的差别, 生成的多尺度数据集的每个属性都有3个尺度.

表1

Table 1

表1(Table 1)

表1 实验数据集信息 Table 1 Details of experimental datasets 名称 领域 样本数 属性数 类别数 Musk Physics 476 166 2 Person Computer 48 321 15 Image Graphics 2310 19 7 Iono Physics 351 34 2 Wpbc Clinic 198 33 2 Wdbc Clinic 569 30 2 Wine Agriculture 178 13 3 Glass Manufacture 214 9 7 Abalone Biology 4177 8 3 QSAR Biology 1055 41 2 Hill Geography 606 101 2 Score Education 206 21 4

表1 实验数据集信息 Table 1 Details of experimental datasets

特别地, Score数据集为实际数据集, 收集自闽南师范大学某学院某专业2016级至2019级本科生的21门课程成绩.以21门课程为属性, 将样本按照这些课程的平均成绩从高到低排序, 之后分为4类.为了让该数据集转化成的多尺度数据更贴近实际, 将第一尺度设置为百分制成绩, 第二尺度通过合并相邻值设置为十级制成绩, 第三尺度通过相同处理方法设置为1~5的数值, 分别表示不及格、及格、中等、良好、优秀.

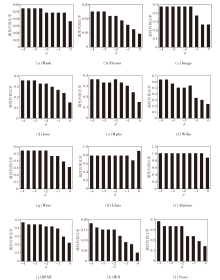
设置δ ∈ [-4, 0], 步长为0.5, 计算本文算法在不同δ 取值下的总测试代价(TTC)和属性约简比率, 其中

属性约简比率=算法所得属性子集中属性数属性全集中属性数,

具体结果如图1和图2所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 本文算法在12个数据集上的TTCFig.1 TTC of the proposed algorithm on 12 datasets

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 本文算法在12个数据集上的属性约简比率Fig.2 Attribute reduction ratios of the proposed algorithm on 12 datasets

从图1中可明显看出, δ < 0时所得TTC远小于δ =0时的TTC, 即本文算法在考虑测试代价时所得结果的总测试代价很大程度上小于不考虑测试代价时的结果, 同时, 观察图2可知, 属性约简比率相差也不大.

并且, 通过观察图1可发现, 最小TTC对应的δ 值受不同数据集影响, 但都集中在[-1.5, -0.5]范围内, 因此, 在后续的实验过程中δ 的取值范围将缩至[-1.5, -0.5], 达到减少计算时间的效果.

在对比实验中, 选择如下3种属性与尺度同步选择算法:文献[16]算法、文献[18]算法、文献[22]算法, 其中文献[22]算法考虑测试代价, 另外两种算法未考虑测试代价.

各算法在不协调的多尺度数据集(QSAR、Hill数据集)上计算所得的TTC、属性子集和其对应的尺度向量如表2所示, 表中黑体数字为最优值.选择KNN分类器(K=2)、随机森林分类器、SVM分类器, 各算法在3个分类器下的分类精度如表3所示.

表2

Table 2

表2(Table 2)

表2 各算法在2个不协调数据集上的指标值对比 Table 2 Index value comparison of different algorithms on 2 inconsistent datasets 数据集 算法 TTC 属性子集 尺度向量 QSAR 本文算法 308.75 {1, 2, 5, 7, 8, 13, 15, 16, 17, 22, 27, 35} (3, 1, 3, 3, 3, 3, 3, 2, 3, 3, 1, 3) 文献[22]算法 413.5 {1, 2, 5, 7, 8, 9, 14, 15, 22, 30, 34, 36, 37} (3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3) 文献[18]算法 632 {1, 5, 8, 9, 13, 14, 16, 18, 22, 27, 30, 34, 36, 37} (1, 3, 3, 3, 3, 3, 2, 1, 1, 1, 3, 3, 1, 3) 文献[16]算法 983.5 {1, 2, 9, 11, 12, 16, 18, 22, 27, 31, 33, 35, 36} (1, 1, 3, 1, 1, 1, 1, 1, 1, 1, 3, 3, 1) Hill 本文算法 171 {4, 10, 25, 30, 31, 32, 44, 53, 66} (3, 3, 3, 3, 3, 3, 3, 3, 3) 文献[22]算法 405.35 {4, 10, 25, 28, 29, 30, 31, 32, 33, 35, 44, 53, 66, 89} (3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3) 文献[18]算法 620.15 {26, 28, 29, 30, 31, 32, 33, 43, 66, 89, 100} (3, 2, 3, 1, 1, 3, 3, 3, 3, 3, 1) 文献[16]算法 637.7 {28, 29, 30, 31, 32, 33, 36, 51, 56, 66, 89} (3, 3, 1, 1, 3, 3, 3, 1, 3, 3, 3)

表2 各算法在2个不协调数据集上的指标值对比 Table 2 Index value comparison of different algorithms on 2 inconsistent datasets

表3

Table 3

表3(Table 3)

表3 各算法在2个不协调数据集上的分类精度对比 Table 3 Classification accuracy comparison of different algorithms on 2 inconsistent datasets % 数据集 算法 KNN分类器 随机森林分类器 SVM分类器 QSAR 本文算法 51.83± 5.14 52.03± 4.61 53.23± 4.75 文献[22]算法 51.47± 5.21 52.72± 5.17 53.36± 4.34 文献[18]算法 51.26± 5.13 51.14± 4.81 50.65± 4.26 文献[16]算法 51.17± 5.14 52.83± 4.89 50.66± 4.98 Hill 本文算法 48.11± 6.09 50.21± 6.34 65.73± 6.35 文献[22]算法 50.30± 5.80 49.87± 6.35 67.20± 5.11 文献[18]算法 49.03± 5.71 50.34± 6.09 68.36± 6.10 文献[16]算法 48.71± 5.95 48.40± 6.39 50.64± 6.71

表3 各算法在2个不协调数据集上的分类精度对比 Table 3 Classification accuracy comparison of different algorithms on 2 inconsistent datasets %

由表2可见, 本文算法的TTC最小, 并且由表3可见, 本文算法的分类精度也较优.这表示在不协调的多尺度数据集上, 本文算法可在保持分类能力的前提下实现总测试代价最小.

各算法在协调的多尺度数据集(Musk、 Person、Image、Iono、Wpbc、Wdbc、Wine、Glass、Abalone、Score数据集)上计算结果如表4所示, 表中黑体数字表示最优值.由表可明显看出, 本文算法的TTC大部分情况下是最小的, 只在Abalone、Score数据集上本文算法的TTC大于文献[22]算法.

表4

Table 4

表4(Table 4)

表4 各算法在10个协调数据集上的指标值对比 Table 4 Index value comparison of different algorithms on 10 consistent datasets 数据集 算法 TTC 属性子集 尺度向量 Musk 本文算法 28.8 {19, 27, 103, 108, 118, 126, 141, 152} (3, 3, 3, 3, 3, 3, 3, 3) 文献[22]算法 28.8 {19, 27, 103, 108, 118, 126, 141, 152} (3, 3, 3, 3, 3, 3, 3, 3) 文献[18]算法 275.733 {19, 33, 42, 88, 108, 158} (3, 3, 3, 3, 3, 3) 文献[16]算法 575.067 {16, 18, 63, 89, 101, 103, 125, 140, 166} (1, 3, 2, 3, 3, 3, 2, 3, 1) Person 本文算法 10 {148, 174, 285, 311} (1, 2, 1, 1) 文献[22]算法 12.75 {148, 174, 238, 285, 311} (2, 2, 2, 2, 2) 文献[18]算法 143.5 {1, 84, 188, 251} (3, 3, 3, 3) 文献[16]算法 362 {78, 85, 137, 138, 139, 238} (3, 1, 1, 2, 1, 3) Image 本文算法 174.133 {1, 2, 10, 18, 19} (3, 3, 3, 3, 2) 文献[22]算法 224.8 {1, 2, 10, 18, 19} (2, 2, 2, 2, 2) 文献[18]算法 286.933 {1, 2, 14, 15, 18} (3, 3, 3, 3, 3) 文献[16]算法 267.733 {1, 2, 10, 16, 18} (3, 2, 3, 2, 3) Iono 本文算法 211.125 {10, 13, 14, 15, 18, 23, 25, 29, 32} (2, 2, 3, 3, 3, 1, 2, 3, 3) 文献[22]算法 229 {10, 15, 18, 23, 29, 32, 33} (1, 1, 1, 1, 1, 1, 1) 文献[18]算法 709.5 {6, 8, 14, 15, 20, 25, 32, 33} (3, 3, 3, 3, 3, 3, 3, 3) 文献[16]算法 556.9 {5, 8, 10, 21, 28, 32, 33} (1, 3, 3, 2, 3, 2, 3) Wpbc 本文算法 121.933 {2, 8, 16, 17, 23, 28, 29, 30} (1, 3, 1, 2, 1, 2, 1, 3) 文献[22]算法 131 {2, 17, 23, 24, 28, 29, 33} (1, 1, 1, 1, 1, 1, 1) 文献[18]算法 351.2 {1, 3, 4, 6, 7, 13, 32} (3, 3, 3, 3, 3, 3, 2) 文献[16]算法 341.4 {1, 3, 19, 20, 23, 24} (3, 1, 3, 1, 1, 1) Wdbc 本文算法 363.5 {2, 3, 4, 9, 12, 18, 26, 27, 28} (3, 2, 1, 3, 1, 2, 1, 2, 2) 文献[22]算法 368 {3, 5, 9, 12, 21, 25, 26, 27} (1, 1, 1, 1, 1, 1, 1, 1) 文献[18]算法 659 {10, 15, 18, 22, 23, 25, 28, 29} (3, 2, 2, 3, 2, 2, 3, 3) 文献[16]算法 972.5 {3, 6, 9, 10, 14, 17, 19, 21, 22, 30} (2, 1, 1, 3, 2, 2, 1, 1, 2, 2) Wine 本文算法 166.95 {1, 3, 4, 9, 10} (1, 2, 1, 3, 2) 文献[22]算法 216.15 {1, 3, 4, 10, 12} (2, 2, 2, 2, 2) 文献[18]算法 242.55 {1, 4, 5, 10, 11, 12} (3, 3, 3, 3, 3, 3) 文献[16]算法 266.9 {1, 6, 10, 11, 12} (1, 3, 1, 3, 3) Glass 本文算法 278.75 {1, 2, 4, 5, 6, 7} (1, 2, 3, 3, 3, 3) 文献[22]算法 283 {1, 2, 4, 5, 6, 7, 9} (3, 3, 3, 3, 3, 3, 3) 文献[18]算法 281.5 {1, 2, 3, 4, 5, 7} (3, 3, 3, 3, 3, 3) 文献[16]算法 487.75 {1, 2, 3, 4, 5, 6, 7} (1, 2, 3, 1, 3, 1, 3) Abalone 本文算法 495 {1, 2, 3, 4, 5, 6, 7, 8} (2, 1, 2, 2, 3, 3, 3, 3) 文献[22]算法 92.5 {4} (3) 文献[18]算法 771.75 {1, 2, 3, 4, 5, 6, 7, 8} (2, 1, 1, 1, 1, 1, 1, 1) 文献[16]算法 771.75 {1, 2, 3, 4, 5, 6, 7, 8} (2, 1, 1, 1, 1, 1, 1, 1) Score 本文算法 195 {3, 14, 17, 18, 19} (3, 1, 1, 3, 3) 文献[22]算法 150 {14, 17, 19} (1, 1, 1) 文献[18]算法 375 {1, 4, 10, 11, 15, 17, 20} (3, 3, 3, 3, 3, 3, 3) 文献[16]算法 330 {3, 7, 17} (1, 1, 1)

表4 各算法在10个协调数据集上的指标值对比 Table 4 Index value comparison of different algorithms on 10 consistent datasets

各算法在3个分类器下的分类精度如表5所示.由表可见, 本文算法的分类精度和其它对比算法差别并不大, 但在Abalone数据集上的分类精度远高于文献[22]算法.因此, 本文算法在协调的多尺度决策系统中也可保持较好的分类能力, 并使总测试代价最小化.

表5

Table 5

表5(Table 5)

表5 各算法在10个协调数据集上的分类精度对比 Table 5 Classification accuracy comparison of different algorithms on 10 consistent datasets % 数据集 算法 KNN分类器 随机森林分类器 SVM分类器 Musk 本文算法 74.23± 6.17 77.78± 5.71 67.57± 6.07 文献[22]算法 74.23± 6.17 77.78± 5.71 67.57± 6.07 文献[18]算法 71.14± 6.81 76.32± 5.58 61.90± 6.66 文献[16]算法 72.92± 6.86 79.02± 5.54 58.60± 6.40 Person 本文算法 33.05± 22.88 43.20± 21.22 37.20± 21.30 文献[22]算法 40.10± 23.10 44.85± 24.13 30.80± 19.97 文献[18]算法 43.90± 24.54 53.10± 26.16 60.05± 24.60 文献[16]算法 26.80± 22.59 28.35± 20.01 31.95± 20.36 Image 本文算法 95.06± 1.38 97.14± 1.05 90.67± 1.53 文献[22]算法 95.00± 1.43 97.36± 0.98 90.83± 1.80 文献[18]算法 94.99± 1.34 96.97± 1.15 92.28± 1.40 文献[16]算法 94.40± 1.51 96.58± 1.27 89.80± 1.96 Iono 本文算法 84.66± 6.12 91.54± 4.64 79.42± 6.57 文献[22]算法 81.59± 6.82 88.64± 5.41 76.88± 6.78 文献[18]算法 84.72± 6.41 89.46± 5.20 82.32± 6.43 文献[16]算法 86.11± 5.36 89.95± 4.65 85.14± 6.01 Wpbc 本文算法 72.59± 10.75 70.23± 10.11 76.28± 9.51 文献[22]算法 72.46± 10.63 70.92± 9.06 76.25± 9.74 文献[18]算法 73.62± 9.25 77.59± 7.81 76.04± 9.38 文献[16]算法 74.98± 10.07 75.70± 9.73 75.61± 8.69 Wdbc 本文算法 93.62± 3.00 95.36± 2.72 95.77± 2.50 文献[22]算法 93.55± 3.34 95.92± 2.70 95.25± 2.87 文献[18]算法 89.40± 4.31 94.62± 2.90 94.88± 2.80 文献[16]算法 90.17± 3.90 92.63± 3.68 93.39± 3.01 Wine 本文算法 87.73± 8.51 90.68± 6.87 91.41± 6.53 文献[22]算法 90.23± 6.45 92.64± 5.79 93.65± 5.49 文献[18]算法 87.30± 8.38 90.48± 6.63 93.64± 4.94 文献[16]算法 87.23± 7.39 89.86± 6.55 88.64± 6.65 Glass 本文算法 70.08± 8.94 75.69± 8.17 62.86± 9.36 文献[22]算法 70.08± 8.94 75.69± 8.17 62.86± 9.36 文献[18]算法 72.19± 9.84 74.01± 8.58 61.94± 9.04 文献[16]算法 66.57± 9.28 72.35± 9.03 61.82± 9.80 Abalone 本文算法 51.93± 3.60 57.57± 2.29 54.31± 2.25 文献[22]算法 34.45± 2.52 34.39± 2.25 34.40± 2.30 文献[18]算法 52.13± 2.79 60.87± 2.27 59.72± 2.46 文献[16]算法 52.33± 2.81 60.80± 2.09 59.56± 2.28 Score 本文算法 38.16± 9.26 37.71± 11.52 35.83± 9.93 文献[22]算法 28.44± 8.50 32.90± 8.64 34.43± 10.41 文献[18]算法 34.15± 9.93 39.25± 11.43 34.61± 9.34 文献[16]算法 30.59± 9.93 37.36± 10.38 39.30± 9.86

表5 各算法在10个协调数据集上的分类精度对比 Table 5 Classification accuracy comparison of different algorithms on 10 consistent datasets %

观察表2~表5可得, 不论是协调的多尺度决策系统还是不协调的多尺度决策系统, 本文算法中属性所选尺度大多为最粗尺度, 在总测试代价最小化的同时也保持较优的分类能力.特别地, 相比同样考虑到测试代价的文献[22]算法, 本文算法中不同属性可选择不同尺度.相比不同属性可选择不同尺度的文献[18]算法和文献[16]算法, 本文算法考虑测试代价, 并且大幅减少总测试代价.这验证本文算法的优越性.在Score数据集上, 本文算法总测试代价仅次于文献[22]算法, 并且在3个分类器中的分类精度都高于文献[22]算法, 这验证本文算法的有效性和实用性.

现有的关于多尺度决策系统知识约简的研究大多未考虑代价因素的影响, 并且算法不能同时适用于协调的多尺度决策系统和不协调的多尺度决策系统.为了解决这一问题, 本文首先构造适用于多尺度决策系统, 并且同时考虑属性子集和尺度向量的粗糙集理论模型.再基于该理论模型, 提出测试代价敏感的属性与尺度同步选择算法, 同时适用于协调的多尺度决策系统和不协调的多尺度决策系统.最后通过实验验证本文算法可在使总测试代价最小化的同时保持较优的分类能力, 更适用于实际应用, 具有较好的有效性及实用性.相比只适用于协调的多尺度决策系统的理论及方法, 本文算法在测试代价敏感的环境下实现属性与尺度的同步选择, 同时还可用于不协调的多尺度决策系统.今后将探讨包含测试代价和其它代价因素, 并且适用于协调的多尺度决策系统和不协调的多尺度决策系统的属性与尺度同步选择算法, 期待算法解决更复杂的实际问题.

本文责任编委 张燕平

Recommended by Associate Editor ZHANG Yanping