联邦学习作为一种分布式的机器学习范式, 无需对私有数据进行传输或共享, 多个客户端通过向中央服务器提供本地计算的更新共同实现学习目标, 旨在实现数据隐私保护下的各方数据协同建模.2016年, Google最先提出一种经典的联邦学习算法— — FedAvg(Federated Averaging)^[1], 采用随机梯度下降(Stochastic Gradient Descent, SGD), 为所有客户端生成共享全局模型, 并通过增加客户端的计算、限制通信频率以降低通信成本.研究表明, 当客户端数据为Non-IID时, FedAvg得到的全局模型性能明显降低, 并且存在客户端漂移(Client Drift)现象^[22].

针对数据异构性带来的挑战和客户端漂移问题, Li 等^[22]提出FedProx, 在FedAvg目标函数的基础上引入一个正则项, 惩罚当前全局模型的较大变化, 减少权重差异, 提高模型对于异构数据的鲁棒性.Karimireddy等^[23]提出SCAFFOLD(Stochastic Controlled Averaging Algorithm), 使用控制变量减小方差以修正客户端训练的漂移.由于FedProx引入额外的正则化项, 导致模型的收敛速度降低.针对FedProx的缺点, Yao等^[24]提出FedCL(Federated Learning with Local Continual Training), 先评估参数重要性, 再根据重要程度针对性地对模型参数施加惩罚, 在减小权重差异的同时, 不断地将客户端本地的知识整合到全局模型中, 可有效解决权重差异导致的模型精度降低的问题.

然而, 以FedProx和SCAFFOLD为代表的算法通过限制客户端的更新缓解数据异构导致的客户端漂移问题, 同时也限制本地模型的学习能力.为了解决此问题, 张珉等^[25]提出基于结构增强的异质数据联邦学习模型正则优化算法(Regularization Optimi-zation Algorithm for Heterogeneous Data Federated Lear-ning Model Based on Structure Enhancement, FedS-ER), 通过数据增强和本地模型结构增强, 有效缓解客户端漂移现象.Shi等^[26]提出Fedl₁, 在联邦学习中引入l₁范数稀疏正则化项, 平衡本地权重和全局权重的差异, 控制各客户端的更新方向, 同时避免不必要的参数更新.

上述联邦学习算法一定程度上缓解异构数据的冲击, 提高全局模型的性能, 但仍局限于为所有客户端提供一个共享的全局模型, 无法满足个性化需求.更多关于联邦学习的研究进展可见文献[10].

全局联邦学习面临两个基本的挑战:1)在Non-IID数据上学习时, 得到的模型性能较差、收敛较慢, 单一共享的全局模型在客户端的本地数据上泛化误差较大; 2)对于智慧医疗、金融大数据和人工智能服务等特殊领域的解决方案缺乏个性化^[27].因此, 个性化联邦学习的研究具有可观的应用价值.

联邦优化的目标是在学习全局信息的同时为每个客户端学习适应其数据分布的本地模型^{[9, 10]}, 正则化联邦优化是应对Non-IID数据带来的挑战的一种常用技术, 通过在目标函数上加入正则化项, 加速模型收敛, 提高模型的泛化性能, 有效实现统计异构性下的客户端模型个性化.

pFedMe^[8]采用莫罗包络函数作为正则化损失函数, 将优化个性模型与学习全局模型解耦, 在更新全局模型的同时优化低复杂度的个性化模型.着眼于联邦学习的公平性和鲁棒性, Ditto^[7]对本地模型引入近端正则项, 使个性化模型接近最优全局模型, 以泛化为代价提高鲁棒性.

除了公平性和鲁棒性, Lin等^[28]提出lp-proj(Projection-Based L^p Regularized Personalized Federated Learning), 通过l_p正则化实现兼顾公平性、鲁棒性和通信效率的目的.为了从信息论的角度出发应对数据异构性和稀缺性的挑战, Zhang等^[29]提出Fed-CR(Personalized Federated Learning Based on Across-Client Common Representation with Conditional Mutual Information Regularization), 为客户端引入条件互信息正则化项, 将全局信息传递到客户端, 最小化本地和全局条件互信息之间的差异, 用于学习客户端之间的共享不变特征, 实现全局特征和局部特征分布的良好对齐, 有效防止过拟合.

l₁范数正则化在提供稀疏性的同时能保证提取到有效特征^[30], 通过为客户端引入l₁正则化项能在保证模型性能的同时减少训练过程中的参数更新.Liu等^[31]提出FedMac(Sparse Personalized Federated Learning Scheme via Maximizing Correlation), 在损失函数中引入l₁范数和个性化模型与全局模型之间的相关性, 实现基于相关性最大化的稀疏个性化联邦学习算法, 提高对异构数据的处理性能, 减少网络所需的通信和计算负荷.Huang等^[14]提出FedSLR(Federated Learning with Mixed Sparse and Low-Rank Representation), 使用l₁范数对个性化组件进行稀疏化, 减少客户端的参数量.

目前, 联邦学习与其它机器学习范式的交叉成为一种新兴趋势^[32], 其中多任务学习、元学习、迁移学习和强化学习常与联邦学习结合以实现个性化, 抵抗异构数据带来的冲击.

在多任务学习^[33]中, 同时解决多个相关的任务, 模型利用任务之间的共性和差异来共同学习, 提升原始任务的泛化能力.多任务学习是构建个性化联邦模型的自然选择^{[11, 34]}, 将基于正则化的方法与多任务学习结合可有效提高学习精度^[35].

结合多任务学习, Li等^[7]提出Ditto, 利用多任务学习的思想实现联邦学习个性化, 在本地目标函数上添加近端算子正则化项, 从全局模型中获取信息, 同时提高公平性和鲁棒性.在联邦多任务学习中, 任务分布在客户端之间, 由于不同的客户端的数据异构程度不一致、任务复杂性不同, 实现个性化时会产生不同任务的学习速度不匹配的现象, 降低整体的学习性能.针对此问题, Mortaheb等^[34]提出FedGradNorm(Personalized Federated Gradient-Nor-malized Multi-task Learning), 采用动态加权策略对梯度进行归一化, 平衡各客户端的学习速度, 提高训练速度, 获得更公平的学习性能.研究表明, 联邦多任务学习方法可通过制定适当的惩罚优化问题以学习个性化模型^{[35, 36, 37]}.

现阶段MAML(Model-Agnostic Meta-Learning Al-gorithm)^[38]与联邦学习的结合受到学者们的广泛关注.Fallah等^[6]将联邦学习与MAML结合, 提出FedAvg的个性化变体Per-FedAvg, 其初始模型在客户端经过少量几次本地训练即可得到个性化模型.Jiang等^[39]指出元学习与个性化联邦学习的目标一致.Vettoruzzo等^[40]提出CAFeMe(Context-Aware Fe-derated Learning Solution that Leverages Meta-lear-ning to Facilitate Personalization to Each Client), 为个性化联邦学习引入上下文信息和元学习技术, 有效改进模型性能和收敛速度.Wang等^[41]提出MOML和LocalMOML, 实现个性化联邦学习, 提高跨设备和跨组织联邦学习的通信效率.

此外, 基于迁移学习的个性化联邦学习^{[42, 43, 44]}及基于知识蒸馏的个性化联邦学习^{[45, 46, 47]}等范式交叉也得到广泛关注和研究.研究表明, 联邦学习与其它机器学习范式集成可实现高性能建模.更多关于个性化联邦学习的研究进展可参考文献[9]和文献[32].

不同于传统的联邦学习为所有客户端提供一个共享的全局模型, 本文提出一种稀疏个性化联邦学习算法, 引入l₁范数正则化项, 为模型引入稀疏个性化分量, 并采用多任务学习的思想, 允许客户端根据私有数据训练个性化模型.在此设置下, 本文通过解决一个双层优化问题同时学习共享的全局模型和特定于客户端的稀疏个性化模型.

综上所述, 本文考虑如下的双层优化问题:

$\min _{\boldsymbol{W} \in \mathbf{R}^{d}}\left(\frac{1}{M} \sum_{m=1}^{M} F_{m}(\boldsymbol{W})\right), $

其中

F_m(W)=minSm∈Rd( f_m(W+S_m)+β‖ S_m‖ ₁). (2)

W表示全局模型, 为多个客户端共享; S_m表示从客户端m的本地数据学到的个性化参数分量; m表示客户端编号, M表示总客户端数量; β表示控制稀疏强度的超参数; f_m(·)表示客户端m的损失函数.在客户端持有私有数据不进行交换或传输的前提下, 本文的目标是最小化损失函数, 得到最优的全局模型W^*, 并为各客户端生成高性能的个性化模型S₁, S₂, …, S_M.

作为对比, 本文讨论pFedMe^[8].pFedMe为客户端损失函数引入具有l₂范数的莫罗包络函数正则化项, 其数学建模为双层优化问题, 如式(1).pFedMe的主要思想为允许客户端追求个性化模型θ_m, 但θ_m与全局模型W保持有界距离.

pFedSRB与pFedMe相似, 均为基于正则化的双层优化问题, 而pFedSRB具有如下优势.1)pFedSRB为客户端个性化更新引入l₁范数稀疏正则化, 提升个性化模型的稀疏度, 减少客户端不必要的参数更新, 有效降低训练用时与空间开销.2)pFedSRB的内层优化阶段, 客户端本地模型初始化为全局信息与稀疏的个性化信息之和, 在不增加额外计算量的情况下保证客户端从全局模型中获取足够信息.3)pFedSRB的内层优化采用ADMM, 交替学习个性化模型与本地模型, 提升本地学习速度.

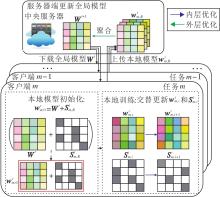
结合正则优化技术和多任务学习的思想, 本文提出pFedSRB, 整体流程图如图1所示.pFedSRB由1个中央服务器统筹M个客户端协同运算实现, 大致运算过程如下.

1)中央服务器向M个客户端广播当前的全局模型参数.

2)客户端下载全局模型参数后, 本地模型初始化为全局信息与个性化信息之和.

3)利用客户端本地数据进行训练, 采用ADMM, 以交替的方式分别更新本地模型和个性化模型, 多个任务并行运行.

4)客户端本地训练收敛后, 向服务器上传最新的本地模型参数.

5)服务器聚合各个客户端的本地模型参数, 更新全局模型.

重复上述过程, 直至学习到最优全局模型W^*.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 pFedSRB流程图Fig.1 Flow chart of pFedSRB

pFedSRB模型优化包含内层优化和外层优化, 分别用于更新个性化模型和全局模型.pFedSRB步骤如算法1所示.

算法1 pFedSRB

输入 全局通信轮数T, 本地更新轮数R,

客户端总数M, 客户端数据集D_m,

学习率η , 超参数β

输出 各客户端的个性化模型S₁, S₂, …, S_M,

全局模型W^*

初始化 全局模型参数W⁰,

客户端个性化模型Sm, 0t

服务器端运行

for t=0, 1, …, T-1 do

服务器向客户端广播全局模型参数W^t

for m=1, 2, …, M in parallel do:

wmt← 客户端本地训练(m, W^t)

end for

更新全局模型参数:W^t+1=1M∑m=1Mwm, Rt

end for

客户端本地训练(m, W^t):

初始化本地模型:wm, 0t=W^t+Sm, Rt

for i=0, 1, …, R-1 do:

更新wm, i+1t,Sm, i+1t

end for

returnwm, Rtto 服务器

3.3.1 内层优化

对于pFedSRB的内层优化目标:

F_m(W)=minSm∈Rd( f_m(W+S_m)+β‖ S_m‖ ₁),

其中全局信息W和个性化信息S_m存在耦合现象.为了解决这个问题, 采用ADMM^[18]作为内层优化算法, 根据ADMM的思想, 对原优化目标(2)进行变量分离, 将客户端的本地模型初始化为全局知识与稀疏个性化知识之和, 得到如下的约束优化问题:

$\min _{\boldsymbol{W} \in \mathbf{R}^{d}}\left(\frac{1}{M} \sum_{m=1}^{M} F_{m}(\boldsymbol{W})\right), $

其中

$\begin{array}{l} F_{m}(\boldsymbol{W})=\min _{\substack{w_{m} \in \mathbf{R}^{d} \\ S_{m} \in \mathbf{R}^{d}}}\left(f_{m}\left(\boldsymbol{w}_{m}\right)+\beta\left\|\boldsymbol{S}_{m}\right\|_{1}\right), \\ \text { s. t. } \boldsymbol{w}_{m}=\boldsymbol{W}+\boldsymbol{S}_{m}, \end{array}$(3)

w_m表示客户端m的本地模型.进一步考虑目标函数(3)的优化, 利用ADMM的拉格朗日乘子, 消除处理约束的困难, 以交替的方式联合学习本地模型w_m和个性化模型S_m.ADMM有如下优点:每步只更新一个变量而固定另外两个变量, 如此交替重复更新.具体而言, 在算法1中可先固定上一轮求得的全局模型参数W^t和本地模型wm, it, 作为ADMM中的已知参数, 对个性化模型Sm, i+1t进行优化.如此交替重复优化, 得到全局模型和个性化模型的最优解.

根据ADMM, 首先给出优化目标的增广拉格朗日函数:

$\begin{array}{l} L_{\rho}\left(\boldsymbol{w}_{m, i}^{t}, \boldsymbol{S}_{m, i}^{t}, \boldsymbol{y}_{m, i}\right)= \\ \quad f_{m}\left(\boldsymbol{w}_{m, i}^{t}\right)+\beta\left\|\boldsymbol{S}_{m, i}^{t}\right\|_{1}+\boldsymbol{y}_{m, i}\left(\boldsymbol{w}_{m, i}^{t}-\boldsymbol{S}_{m, i}^{t}-\boldsymbol{W}^{t}\right)+ \\ \quad \frac{\rho}{2}\left\|\boldsymbol{w}_{m, i}^{t}-\boldsymbol{S}_{m, i}^{t}-\boldsymbol{W}^{t}\right\|_{2}^{2}, \end{array}$ (4)

其中,wm, it表示第t轮通信客户端m的第i次迭代本地模型参数,Sm, it表示第t轮通信客户端m的第i次迭代个性化模型参数, W^t表示第t轮通信的全局模型参数.y_{m, i}表示ADMM中的对偶变量, 即拉格朗日乘子.式(4)是一个无约束的优化目标.

接下来, ADMM对各参数更新如下:

$\begin{array}{l} \boldsymbol{S}_{m, i+1}^{t}=\arg \min _{S_{m, i}^{\prime} \in \mathbf{R}^{d}} L_{\rho}\left(\boldsymbol{w}_{m, i}^{t}, \boldsymbol{S}_{m, i}^{t}, \boldsymbol{y}_{m, i}\right), \\ \boldsymbol{w}_{m, i+1}^{t}=\arg \min _{w_{m, i}^{\prime} \in \mathbf{R}^{d}} L_{\rho}\left(\boldsymbol{w}_{m, i}^{t}, \boldsymbol{S}_{m, i+1}^{t}, \boldsymbol{y}_{m, i}\right), \\ \boldsymbol{y}_{m, i+1}=\boldsymbol{y}_{m, i}+\rho\left(\boldsymbol{w}_{m, i+1}^{t}-\boldsymbol{S}_{m, i+1}^{t}-\boldsymbol{W}^{t}\right), \end{array}$

其中ρ >0表示ADMM的拉格朗日步长.

上述优化公式具有多项、复杂的特点, 这在实际运算中是难以处理的.因此, 进一步考虑ADMM的缩放形式.引入残差定义

r=wm, it-Sm, it-W^t,

将增广拉格朗日函数改写为如下形式:

$\begin{array}{l} L_{\rho}\left(\boldsymbol{w}_{m, i}^{t}, \boldsymbol{S}_{m, i}^{t}, \boldsymbol{r}_{m, i}, \boldsymbol{u}_{m, i}\right)= \\ \quad f_{m}\left(\boldsymbol{w}_{m, i}^{t}\right)+\beta\left\|\boldsymbol{S}_{m, i}^{t}\right\|_{1}+\frac{\rho}{2}\left\|\boldsymbol{r}_{m, i}+\boldsymbol{u}_{m, i}\right\|_{2}^{2}- \\ \quad \frac{\rho}{2}\left\|\boldsymbol{u}_{m, i}\right\|_{2}^{2}, \end{array}$

其中

u_{m, i}=ym, iρ

表示缩放后的对偶变量.利用缩放的增广拉格朗日函数, 变量更新通过如下公式迭代:

$\begin{aligned} \boldsymbol{S}_{m, i+1}^{t}= & \arg \min _{S_{m, i \in \mathbf{R}^{d}}}\left(\beta\left\|\boldsymbol{S}_{m, i}^{t}\right\|_{1}+\right. \\ & \left.\frac{\rho}{2}\left\|\boldsymbol{w}_{m, i}^{t}-\boldsymbol{S}_{m, i}^{t}-\boldsymbol{W}^{t}+\boldsymbol{u}_{m, i}\right\|_{2}^{2}\right), \\ \boldsymbol{w}_{m, i+1}^{t}= & \arg \min _{\boldsymbol{w}_{m, i \in}^{m} \mathbb{R}^{d}}\left(f_{m}\left(\boldsymbol{w}_{m, i}^{t}\right)+\right. \\ & \left.\frac{\rho}{2}\left\|\boldsymbol{w}_{m, i}^{t}-\boldsymbol{S}_{m, i+1}^{t}-\boldsymbol{W}^{t}+\boldsymbol{u}_{m, i}\right\|_{2}^{2}\right), \\ \boldsymbol{u}_{m, i+1}= & \boldsymbol{u}_{m, i}+\boldsymbol{w}_{m, i+1}^{t}-\boldsymbol{S}_{m, i+1}^{t}-\boldsymbol{W}^{t} . \end{aligned}$

3.3.2 外层优化

pFedSRB通过外层优化目标

$\min _{\boldsymbol{W} \in \mathbf{R}^{d}}\left(\frac{1}{M} \sum_{m=1}^{M} F_{m}(\boldsymbol{W})\right)$

更新全局模型.与FedAvg^[1]类似, 在每轮全局通信t中, 服务器向所有客户端广播最新的全局模型W^t, 客户端执行R轮本地更新后, 服务器收集各客户端的最新本地模型wm, Rt, 以执行模型聚合更新全局模型W^t+1.pFedMe^[8]使用额外的参数λ控制全局模型更新, 即

W^t+1=(1-λ)W^t+λM∑m=1Mwm, Rt.

当λ=1时, pFedMe全局模型更新与FedAvg类似, 通过加权平均聚合模型参数.pFedMe的实验表明, 当λ=1时, 能更好稳定全局模型和个性化模型.

受pFedMe的外层优化启发, 本文的外层优化全局模型的更新通过聚合客户端的本地模型以加权平均的方式实现, 即pFedSRB的外层优化通过

W^t+1=1M∑m=1Mwm, Rt

更新全局模型参数.

为了验证pFedSRB的性能和有效性, 在MNIS-T^[19]、Fashion-MNIST^[20]、Cifar-10^[21]、Cifar-100^[21]这4个联邦学习基准数据集上进行实验.

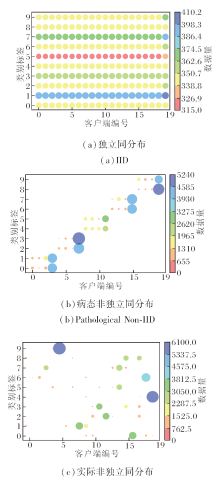
对于这4个公开数据集, 实验中采取3种数据拆分方式:独立同分布(Independent and Identically Distributed, IID)^[1]、病态非独立同分布(Pathological Non-IID)^[1]、实际非独立同分布(Practical Non-IID)^[15], 以模拟客户端数据独立同分布和非独立同分布的情形.

具体地, 在独立同分布数据设置下, 不同客户端之间数据均匀分布、并且服从同个分布.在病态非独立同分布数据设置下, 每个客户端拥有两类样本, 客户端数据之间没有相似性.特别地, Cifar-100数据集上的病态非独立同分布设置中, 每个客户端拥有10类样本(总类别数为100).在实际非独立同分布数据设置下, 对客户端进行分组, 同组中的客户端的数据分布具有相似性, 不同组之间数据分布不同, 每个客户端拥有所有类别的样本.实际非独立同分布的异构程度是受 Dirichlet分布Dir(α)控制的, α越小, 异构程度越高, 在本文实验中, α=0.1为默认的异构设置.

图2为MNIST数据集的数据分布情况可视化, 气泡的颜色和大小反映数据量.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 MNIST数据集上数据拆分可视化Fig.2 Visualization of data splitting on MNIST dataset

在本文实验中:对于MNIST、Fashion-MNIST数据集, 使用2层深度神经网络(Deep Neural Network, DNN)学习图像分类任务, 隐藏层大小为100; 对于Cifar-10、Cifar-100数据集, 使用4层卷积神经网络(Convolutional Neural Network, CNN)学习图像分类任务.数据集拆分为训练集和测试集的比例分别为75%和25%.为了平衡模型性能和稀疏程度, 设置超参数β=0.01.

为了验证pFedSRB的性能, 选择如下多个基线算法.

1)全局联邦学习算法:FedAvg^[1]、FedProx^[22]、FedNTD(Federated Not-True Distillation)^[48].

2)目前较优的个性化联邦学习算法:Per-FedAvg^[6]、Ditto^[7]、pFedMe^[8]、FedPAC^[16]、FedKD(Communication-Efficient Federated Learning Method Based on Knowledge Distillation)^[46]、FedALA (Fede-rated Learning with Adaptive Local Aggregation)^[49].

在MNIST、Fashion-MNIST、Cifar-10数据集上, 实验采用的批尺寸设置为16; 在Cifar-100数据集上, 批尺寸设置为4, 这是因为Cifar-100数据集的类别远多于其它3个数据集.各数据集的实际非独立同分布异构程度由α(α=0.1)控制, 客户端数量为20, 全局通信轮数T=1 000.

各算法在4个数据集上的分类准确率对比如表1所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可见, 在所有数据集的不同拆分下, pFed-SRB分类准确率均为最优, 其中, 在Cifar-10、Cifar-100数据集上, 相比全局联邦学习算法, pFedSRB性能显著提升.

表1

Table 1

表1(Table 1)

表1 各算法在4个数据集上的分类准确率对比 Table 1 Classification accuracy comparison of different algorithms on 4 datasets % 算法 MNIST Fashion-MNIST Cifar-10 Cifar-100 IID Pathological Non-IID Practical Non-IID IID Pathological Non-IID Practical Non-IID IID Pathological Non-IID Practical Non-IID IID Pathological Non-IID Practical Non-IID FedAvg 97.54 88.93 98.42 89.20 78.22 86.74 70.77 55.99 58.23 36.06 29.84 33.51 FedProx 97.49 89.03 98.43 89.30 79.51 86.63 72.35 56.15 58.60 36.23 29.82 33.21 FedNTD 97.52 89.90 94.07 89.57 77.02 90.07 73.30 60.45 58.72 37.86 31.60 34.83 Per-FedAvg 96.58 97.72 95.42 87.67 97.75 92.93 63.47 87.29 67.52 30.97 44.04 31.52 Ditto 97.43 99.14 99.19 89.36 98.21 96.96 71.69 88.67 89.03 35.83 48.85 39.02 pFedMe 97.62 99.42 98.82 89.57 98.33 97.22 66.09 89.92 89.35 35.90 48.48 45.46 FedKD 91.73 99.07 97.34 83.76 99.17 96.41 52.73 90.50 90.17 25.92 57.02 52.63 FedPAC 97.33 98.61 98.75 89.02 94.72 96.86 74.74 90.37 90.21 36.29 52.52 52.04 FedALA 97.21 99.56 98.69 89.21 98.36 96.69 73.42 91.68 90.08 33.66 58.13 50.38 pFedSRB 99.85 99.90 99.45 90.33 99.40 97.65 75.11 92.70 91.07 38.25 60.96 53.72

表1 各算法在4个数据集上的分类准确率对比 Table 1 Classification accuracy comparison of different algorithms on 4 datasets %

观察个性化联邦学习算法的分类准确率可发现, 当客户端的数据为IID时, 性能明显降低, 而pFedSRB的下降幅度较小.这是因为pFedSRB在客户端个性化更新中引入l₁范数稀疏正则化, 避免客户端的冗余参数更新, 最大限度提取有效特征, 保证模型的性能.

本文通过总参数量衡量模型的复杂度, 选择在Cifar-10数据集的实际非独立同分布(α=0.1)数据上训练1 000轮, 主干网络为CNN.不同个性化联邦学习算法的模型复杂度、通信时间和空间开销如表2所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可见, pFedSRB降低模型的复杂度以及训练所需的通信时间与内存开销, 是资源友好型的算法.

表2

Table 2

表2(Table 2)

表2 Cifar-10数据集上个性化联邦学习算法的模型复杂度与通信开销对比 Table 2 Comparison of model complexity and communication overhead of different personalized FL methods on Cifar-10 dataset 算法 平均每轮 通信时间/s 总参数量 /M 所需内存 /M Per-FedAvg 44.04 54.46 140.81 Ditto 53.84 107.18 274.91 pFedMe 63.63 72.92 211.21 FedKD 47.70 81.65 311.56 FedPAC 61.87 37.16 142.31 FedALA 33.59 37.00 141.21 pFedSRB 32.51 19.42 121.68

表2 Cifar-10数据集上个性化联邦学习算法的模型复杂度与通信开销对比 Table 2 Comparison of model complexity and communication overhead of different personalized FL methods on Cifar-10 dataset

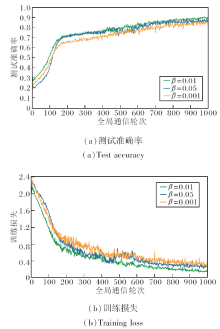
pFedSRB目标函数如式(2)所示, 其中, β为关键参数, 控制个性化模型的稀疏程度.为了探索β取值对算法性能的影响, 在Cifar-10数据集上进行实验, 对比β=0.01, 0.05, 0.001时pFedSRB的测试准确率和训练损失, 具体如图3所示.由图可见, 当β=0.01时, pFedSRB的测试准确率稳定上升, 训练损失稳定收敛, 因此, 本文默认β=0.01.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 Cifar-10数据集上β对pFedSRB性能的影响Fig.3 Effect of β on performance of pFedSRB on Cifar-10 dataset

结合联邦多任务学习的思想, 本文实验中所有客户端均参与训练, 参与训练的设备数对模型性能也存在一定影响.综合考虑全局模型(Global Model, GM)和个性化模型(Personalized Model, PM)的性能, 实验中客户端数量M=20.在MNIST数据集的实际非独立同分布(α=0.1)数据上, 不同客户端数量对应的pFedSRB的准确率如表3所示, 表中黑体数字表示最优值, 斜体数字表示次优值.从表可知, 当客户端数量M=20时, pFedSRB全局模型的性能接近最优准确率, 个性化模型取得最优准确率.

表3

Table 3

表3(Table 3)

表3 客户端数量不同时pFedSRB的准确率对比 Table 3 Accuracy comparison of pFedSRB with different numbers of clients % 算法 10 15 20 25 30 40 pFedSRB-GM 93.63 93.24 94.47 94.33 94.51 93.74 pFedSRB-PM 99.81 99.80 99.90 99.80 99.74 99.77

表3 客户端数量不同时pFedSRB的准确率对比 Table 3 Accuracy comparison of pFedSRB with different numbers of clients %

实验中MNIST、Fashion-MNIST、Cifar-10数据集上的默认批尺寸为16, Cifar-100数据集上默认批尺寸为4(Cifar-100数据集的总类别数为100).为了验证不同批尺寸对pFedSRB性能的影响, 在MNIST数据集的实际非独立同分布(α=0.1)数据上, 各算法的准确率对比如表4所示, 表中黑体数字表示最优值.由表可见, 当批尺寸 为16时, 多数算法取得最优准确率.

表4

Table 4

表4(Table 4)

表4 批尺寸不同时各算法的准确率对比 Table 4 Accuracy comparison of different methods of different batsh sizes % 算法 10 16 20 35 FedAvg 97.31 98.42 96.66 95.55 FedProx 96.58 98.43 94.55 92.92 FedNTD 94.11 94.07 92.31 91.10 Per-FedAvg 96.92 95.42 96.38 95.78 Ditto 98.94 99.19 98.85 98.84 pFedMe 98.64 98.82 97.44 96.99 FedKD 97.45 97.34 97.26 97.17 FedPAC 98.22 98.75 98.00 98.04 FedALA 98.73 98.69 98.60 98.44 pFedSRB 98.24 99.45 98.35 98.28

表4 批尺寸不同时各算法的准确率对比 Table 4 Accuracy comparison of different methods of different batsh sizes %

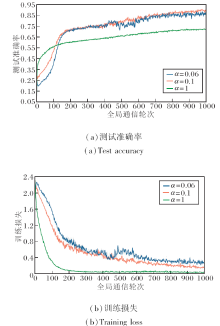
本文的数据划分方式分别为独立同分布、病态非独立同分布、实际非独立同分布, 其中, 实际非独立同分布的数据异构程度由Dirichlet分布Dir(α)控制, α越小, 异构程度越高, 实验中α = 0.1为默认的异构设置.为了验证不同的数据异构程度对算法性能的影响, 设置3种异构程度, 分别为α=0.06, 0.1, 1, Cifar-10数据集上3种异构程度下数据分布情况如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
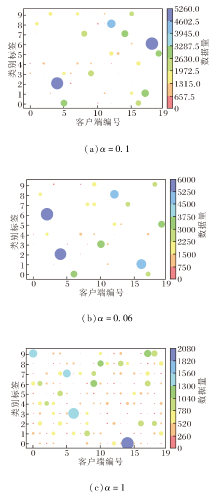	图4 Cifar-10数据集上不同异构程度的数据分布可视化Fig.4 Visualization of data distribution with different degrees of heterogeneity on Cifar-10 dataset

Cifar-10数据集上不同数据异构程度的pFedSRB性能如图5所示.由图可见, 当α = 1时, 数据异构程度最低, 测试准确率达到一定程度后上升缓慢.当α = 0.1时, pFedSRB性能上升且收敛最稳定.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 Cifar-10数据集上数据异构程度对pFedSRB性能的影响Fig.5 Effect of data heterogeneity on performance of pFedSRB on Cifar-10 dataset