基于异构网络语言形式背景的知识发现及规则提取

引用本文

沙立伟, 杨政, 刘红平, 邹丽. 基于异构网络语言形式背景的知识发现及规则提取. 模式识别与人工智能, 2024,37(5): 469-478
SHA Liwei, YANG Zheng, LIU Hongping, ZOU Li. Knowledge Discovery and Rule Extraction Based on Heterogeneous Network Linguistic Formal Context. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2024,37(5): 469-478. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202405008
Permissions

《模式识别与人工智能》编辑部

基于异构网络语言形式背景的知识发现及规则提取

沙立伟¹, 杨政¹, 刘红平², 邹丽¹

1.山东建筑大学计算机科学与技术学院济南 250101

2.山东建筑大学理学院济南 250101

通讯作者:

邹丽,博士,教授,主要研究方向为智能信息处理、非经典逻辑、不确定性推理.E-mail:zoulicn@163.com.

作者简介:

沙立伟,硕士研究生,主要研究方向为智能信息处理、非经典逻辑、不确定性推理.E-mail:19819791939@163.com.

杨政,硕士研究生,主要研究方向为智能信息处理、非经典逻辑、不确定性推理.E-mail:yzharder@163.com.

刘红平,博士,副教授,主要研究方向为模糊拓扑、Domain理论、智能信息处理等.E-mail:liuhongping@sdjzu.edu.cn.

收稿日期: 2024-04-07 接受日期: 2024-05-31

资助项目: 国家自然科学基金项目(No.62176142,62177031)、山东省自然科学基金项目(No.ZR2021MF099,ZR2022MF334)资助

摘要

在不确定性环境下,如何处理具有复杂关系的数据是研究热点之一.网络形式背景将复杂网络分析和形式概念分析结合,为复杂关系数据的知识发现提供一种有效的数学工具.文中首先从网络结构的异构性出发,提出异构网络语言形式背景.异构网络包含专家给出的主观网络,又包含通过对象的特征挖掘的客观网络.然后,考虑网络的连通性,得到全局和局部异构网络语言概念,并给出异构网络下的全局连通及局部连通知识发现算法.最后,基于异构网络语言形式背景构建关联规则提取模型,通过实例验证知识发现及规则提取的合理性和有效性.

关键词: 形式概念分析; 异构网络; 模糊聚类; 知识发现; 规则提取

中图分类号:TP18

Knowledge Discovery and Rule Extraction Based on Heterogeneous Network Linguistic Formal Context

SHA Liwei¹, YANG Zheng¹, LIU Hongping², ZOU Li¹

1. School of Computer Science and Technology, Shandong Jianzhu University, Jinan 250101

2. School of Science, Shandong Jianzhu University, Jinan 250101

Corresponding author:
ZOU Li, Ph.D., professor. Her research interests include intelligent information processing, non-classical logic and uncertainty reasoning.

About Author:
SHA Liwei, Master student. His research interests include intelligent information processing, non-classical logic and uncertainty reasoning.
YANG Zheng, Master student. His research interests include intelligent information processing, non-classical logic and uncertainty reasoning.
LIU Hongping, Ph.D., associate profe-ssor. Her research interests include fuzzy topology, Domain theory and intelligent information processing.

Fund:National Natural Science Foundation of China(No.62176142,62177031), Natural Science Foundation of Shandong Province(No.ZR2021MF099,ZR2022MF334)

Abstract

One of the research hotspots is how to handle data with complex relationships under the uncertainty environment. The network formal context combines complex network analysis and formal concept analysis to provide an effective mathematical tool for knowledge discovery of complex relational data. In this paper, the heterogeneous network linguistic formal context is firstly proposed based on the heterogeneity of network structure. The heterogeneous network contains a subjective network given by experts and an objective network mined by the features of objects. Then, global and local heterogeneous network language concepts are obtained by considering the connectivity of the network, and the algorithms for global and local connectivity knowledge discovery in heterogeneous networks are provided. Finally, an association rule extraction model is constructed based on the heterogeneous network linguistic formal context, and the rationality and effectiveness of knowledge discovery and rule extraction are verified by examples.

Key words: Formal Concept Analysis; Heterogeneous Network; Fuzzy Clustering; Knowledge Disco-very; Rule Extraction

文章图片

形式概念分析(Formal Concept Analysis, FCA)^[1]是一种强大的数学工具, 用于数据处理和规则提取.作为基于形式背景的一种重要的数据处理和可视化方法, FCA通过对象与属性的关联获取潜在的概念知识, 目前已在知识发现、数据挖掘、机器学习、特征选择等领域^{[2, 3, 4, 5, 6, 7]}得到广泛应用.Wu等^[8]将粒计算思想融入形式概念分析, 研究概念格的粒度结构在知识约简中的应用.Wang等^[9]受粗糙集理论启发, 从近似算子角度研究形式背景, 并构建概念格.Zhi等^[10]基于形式概念分析定义新的三支概念, 提出一种快速冲突分析信息融合方法.

在经典的形式背景中, 通常使用0或1表示对象和属性之间是否存在关系, 而在实际生活中, 人们更习惯使用语言值表达信息.Zadeh^{[11, 12]}提出模糊集和语言变量的概念, 可有效描述使用语言值表达的信息.近年来, 学者们研究和扩展模糊集和语言变量理论.Herrera等^[13]提出语言术语集, 描述离散语言变量.Xu^[14]研究基于概率语言信息的聚合算子.Zou等^[15]提出语言概念形式背景, 用于处理现实生活中使用语言值描述的数据.Pang等^[16]利用语言真值格蕴含代数构建多专家语言形式背景, 提出一种有效的多属性群决策意见聚合方法.

模糊聚类是一种基于模糊集理论的聚类方法, 与传统的硬聚类方法不同, 它允许对象同时属于多个类别, 并给出每个对象属于每个聚类类别的概率.模糊C均值聚类(Fuzzy C-means, FCM)^{[17, 18, 19]}作为常用的模糊聚类方法之一, 因为开销低和鲁棒性而广泛应用于图像分割、故障诊断等^{[20, 21]}领域.研究发现, 模糊聚类可帮助建模复杂网络中的模糊关系, 通过将节点聚类为模糊群集, 可更好地描述网络中的模糊关联.

复杂网络分析理论可更好地处理对象节点间复杂的模糊关联信息.复杂网络分析是一种研究复杂系统中节点之间相互关系和结构特征的方法, 通过帮助揭示网络中的隐藏结构、关键节点和子群体, 分析网络的内部机制和特点.近年来, 学者们拓展与研究复杂网络分析理论.Zhao等^[22]将复杂动态网络完全视为由两个相互耦合的子系统组成的动态复合系统, 提出一种跟踪控制方案.Fan等^{[23, 24]}结合复杂网络分析与形式概念分析, 提出网络形式背景, 并研究知识发现与更新、规则提取等问题.在结构上看, 复杂网络可分为同构网络和异构网络.相比同构网络, 异构网络在现实生活中更常见.

综合异构网络与形式概念分析, 本文提出异构网络语言形式背景, 使用语言值更好地描述偏好关系, 并且异构网络包含对象之间由专家给出的主观关系, 又包含通过对象的特征挖掘的客观关系, 其中客观关系利用FCM将对象聚类为模糊群集, 反映网络中的模糊关联.在此基础上, 分析网络的连通性, 定义全局和局部异构网络语言概念, 并讨论和证明异构网络语言概念的相关性质.由于在不同的认知环境下, 判断物体间是否存在关系的标准不同, 又基于异构网络语言形式背景, 提出两种知识发现算法, 进而提取关联规则.最后, 通过实例验证算法及规则的合理性和有效性.本文的理论和方法可应用于数据挖掘及推荐系统等领域.

1 预备知识

定义1^[25] 设

S={s_t|t=-τ, …, -1, 0, 1, …, τ}

表示由奇数个语言项组成的有限语言项集, 其中τ表示正整数, 若S符合

1)有序性:s_i≥s_j⇔i≥j,

2)负算子:Neg(s_-_i)=s_i, 特别的, Neg(s₀)=s₀,

3)最大算子:s_i≥s_j⇔max(s_i, s_j)=s_i,

4)最小算子:s_i≤s_j⇔min(s_i, s_j)=s_i,

则称集合S为下标对称的语言术语集.

定义2^[1] 称三元组(U, A, I)为一个形式背景, 其中U={x₁, x₂, …, x_n}表示非空有限的对象集, A={a₁, a₂, …, a_m}表示非空有限的属性集, I⊆U×A表示U与A之间的二元关系.对于∀x∈U, a∈A, 如果(x, a)∈I, 则称对象x拥有属性a, 记为xIa.

定义3^[25] 称三元组(U, $L_{S_{α}}$ , I)为一个语言概念形式背景, U={x₁, x₂, …, x_n}表示非空有限的对象集,

$\begin{aligned} L_{S_{\alpha}}= & \left\{l_{-t}^{1}, \cdots, l_{0}^{1}, \cdots, l_{t}^{1}, l_{-t}^{2}, \cdots, l_{0}^{2}, \cdots, l_{t}^{2}, \cdots, \right. \\ & \left.l_{-t}^{n}, \cdots, l_{0}^{n}, \cdots, l_{t}^{n}\right\}, \end{aligned}$

表示非空有限的语言概念集, I⊆U× $L_{S_{α}}$ 表示U与 $L_{S_{α}}$ 之间的二元关系.对于x∈U和 $l_{s_{a}}^{i}$ ∈ $L_{S_{α}}$ , 如果(x, $l_{s_{a}}^{i}$ )∈I, 则称对象x拥有语言概念 $l_{s_{a}}^{i}$ , 记为xI $l_{s_{a}}^{i}$ .

定义4^[25] 设F=(U, $L_{S_{α}}$ , I)为一个语言概念形式一个语言概念形式背景, 对于∀X⊆U, $B_{S_{α}}$ ⊆ $L_{S_{α}}$ , 定义诱导算子“ '” 如下:

$\begin{array}{l} X^{\prime}=\left\{l_{s_{a}}^{i} \in L_{S_{\alpha}} \mid x I l_{s_{a}}^{i}, \forall x \in X\right\}, \\ B_{S_{\alpha}}^{\prime}=\left\{x \in U \mid x I l_{s_{a}}^{i}, \forall l_{s_{a}}^{i} \in B_{S_{\alpha}}\right\}, \end{array}$

X'表示X中所有对象共同拥有的语言概念集, B $'_{S_{α}}$ 表示具有语言概念集 $B_{S_{α}}$ 的对象集合.

若X'= $B_{S_{α}}$ 且B $'_{S_{α}}$ =X, 则称(X, $B_{S_{α}}$ )为语言概念形式背景F中的一个语言概念知识, X称为语言概念知识(X, $B_{S_{α}}$ )的外延, $B_{S_{α}}$ 称为语言概念知识(X, $B_{S_{α}}$ )的内涵.L(U, $L_{S_{α}}$ , I)表示语言概念形式背景中的所有语言概念知识.

对于

(X¹, $B_{S_{α}}^{1}$ )∈L(U, $L_{S_{α}}$ , I), (X², $B_{S_{α}}^{2}$ )∈L(U, $L_{S_{α}}$ , I),

定义(X¹, $B_{S_{α}}^{1}$ )与(X², $B_{S_{α}}^{2}$ )之间的偏序关系:

(X¹, $B_{S_{α}}^{1}$ )≤(X², $B_{S_{α}}^{2}$ )⇔X¹⊆X²⇔ $B_{S_{α}}^{1}$ ⊆ $B_{S_{α}}^{2}$ .

L(U, $L_{S_{α}}$ , I)在偏序关系下生成的完备格称为概念格, 它们之间的上确界和下确界分别为

(X₁, $B_{S_{α}}^{1}$ )∨ (X₂, $B_{S_{α}}^{2}$ )=((X₁∪X₂)″, $B_{S_{α}}^{1}$ ∩ $B_{S_{α}}^{2}$ ),

(X₁, $B_{S_{α}}^{1}$ )∧ (X₂, $B_{S_{α}}^{2}$ )=(X₁∩ X₂, ( $B_{S_{α}}^{1}$ ∪ $B_{S_{α}}^{2}$ )″).

定义5^[23] 四元组(U, M, A, I)为一个网络形式背景, U={x₁, x₂, …, x_n}表示一个有限非空对象集, M={m₁, m₂, …, m_p}表示一个网络邻接矩阵集, m_i(1, 2, …, p)为n×n的网络邻接矩阵, A={a₁, a₂, …, a_m}表示一个非空有限属性集,

I={I_s|i=1, 2, …, p+1},

其中, I₁, I₂, …, I_p表示笛卡尔积U×U上的二元关系, (x_i, x_j)∈I_k表示对象i、 j是k阶邻接的, I_p₊₁表示笛卡尔积U×A上的二元关系, (x_i, a_q)∈I_p₊₁表示对象x_i具有属性a_q.

2 基于异构网络语言形式背景的知识发现

2.1 异构网络语言形式背景

异构网络由多种类型的节点组成, 还包含不同节点间的复杂关系.本节结合异构网络理论与形式概念分析理论, 介绍异构网络语言形式背景.使用语言值描述偏好关系, 并且融合FCM^{[26, 27]}挖掘对象间的相似关系及专家事先给出的对象间关系, 重新计算网络邻接矩阵.

FCM使用隶属度表示每个样本属于各个聚类的程度, 根据隶属度的大小将样本集上的每个样本模糊分配到不同的聚类中.通过算法迭代后可得到聚类中心矩阵

C= $(c_{i})_{1 \times q}$ , i=1, 2, …, q

和隶属度矩阵

U= $(μ_{ik})_{k \times q}$ , i=1, 2, …, q, k=1, 2, …, n.

定义6 设(U, $L_{S_{α}}$ , I)为语言概念形式背景, 对于∀x_i∈U, x_j∈U, 定义对象x_i、x_j在第q类中的相似度:

Si $m_{ij}^{q}$ =1- $d_{ij}^{q}$ , (1)

其中, q表示FCM中给定的类别数,

$d_{ij}^{q}$ = $\sqrt[]{(μ_{iq} - μ_{jq})^{2}}$

表示对象x_i、x_j在第q类中的欧氏距离.

性质1 对于∀x_i∈U, x_j∈U, 对象x_i、x_j在第q类中满足

1)Si $m_{ij}^{q}$ =Si $m_{ji}^{q}$ ,

2)当i=j时, Si $m_{ij}^{q}$ =1,

3) $d_{ij}^{q}$ ≤ $d_{ik}^{q}$ ⇔Si $m_{ij}^{q}$ ≥Si $m_{ik}^{q}$ ,

4)Si $m_{ij}^{q}$ ∈[0, 1].

证明 1)、2)由定义6显然得证.

下证3).根据定义6可知两个对象在同类中的距离越大, 则这两个对象在这类中的相似度越低; 反之, 两个对象在同类中的距离越小, 则这两个对象在这类中的相似度越高.

最后证4).由于FCM计算的模糊隶属矩阵元素μ_iq、 μ_jq取值范围为[0, 1], 因此 $d_{ij}^{q}$ 取值范围为[0, 1], 由式(1)所得, 对象相似度Si $m_{ij}^{q}$ 取值范围也为[0, 1].

例1 表1为一个语言概念形式背景(U, $L_{S_{α}}$ , I), 其中, U={x₁, x₂, x₃, x₄, x₅, x₆}表示6个对象, L={l¹, l², l³, l⁴}分别表示对象具有的4个属性, S_α={s_-1, s₀, s₁}表示语言术语集,

$L_{s_{α}}$ ={ $l_{s_{- 1}}^{1}$ , $l_{s_{0}}^{1}$ , $l_{s_{1}}^{1}$ , $l_{s_{- 1}}^{2}$ , $l_{s_{0}}^{2}$ , $l_{s_{1}}^{2}$ , $l_{s_{- 1}}^{3}$ , $l_{s_{0}}^{3} l_{s_{1}}^{3}$ , $l_{s_{- 1}}^{4}$ , $l_{s_{0}}^{4}$ , $l_{s_{1}}^{4}$ }

表示对应的语言概念集.

表1 语言概念形式背景(U,

L_{S_{α}}

, I) Table 1 Linguistic concept formal context(U,

L_{S_{α}}

, I)

	$l_{s_{- 1}}^{1}$	$l_{s_{0}}^{1}$	$l_{s_{1}}^{1}$	$l_{s_{0}}^{2}$	$l_{s_{1}}^{2}$	$l_{s_{- 1}}^{3}$	$l_{s_{0}}^{3}$	$l_{s_{1}}^{3}$	$l_{s_{- 1}}^{4}$	$l_{s_{0}}^{4}$	$l_{s_{1}}^{4}$
x₁	0	0	1	1	0	0	1	0	0	1	0
x₂	0	0	1	0	1	0	1	0	0	0	1
x₃	1	0	0	1	0	1	0	0	0	0	1
x₄	0	0	1	0	1	0	1	0	0	1	0
x₅	0	0	1	0	1	0	1	0	0	1	0
x₆	0	1	1	0	1	0	0	1	1	0	0

表1 语言概念形式背景(U,

L_{S_{α}}

, I) Table 1 Linguistic concept formal context(U,

L_{S_{α}}

, I)

基于表1语言概念形式背景中的数据, 取类别数q=3, 根据FCM计算模糊隶属矩阵, 如表2所示.

表2 隶属度矩阵 Table 2 Affiliation matrix

根据式(1)分别计算对象x₁、x₂在c₁类的相似度:

$ \begin{array}{c} \operatorname{Sim}_{11}^{c_{1}}=1-d_{11}^{c_{1}}=1-\sqrt{\left(\mu_{1 c_{1}}-\mu_{1 c_{1}}\right)^{2}}= \\ 1-\sqrt{(0.2-0.2)^{2}}=1 . \end{array}$

定义7 设四元组(U, $L_{S_{α}}$ , WM_s, I)为一个异构网络语言形式背景, U={x₁, x₂, …, x_n}表示一个有限非空对象集,

$ \begin{aligned} L_{S_{\alpha}}= & \left\{l_{-t}^{1}, \cdots, l_{0}^{1}, \cdots, l_{t}^{1}, l_{-t}^{2}, \cdots, l_{0}^{2}, \cdots, l_{t}^{2}, \cdots, \right. \\ & \left.l_{-t}^{n}, \cdots, l_{0}^{n}, \cdots, l_{t}^{n}\right\} \end{aligned}$

表示非空有限的语言概念集, I∈U× $L_{S_{α}}$ 表示对象与属性间的二元关系,

WM_s={SM₁, SM₂, …, SM_k, OM}

表示k+1个不同的邻接矩阵,

SM_m= $(S D_{ij}^{m})_{n \times n}$ , 1≤m≤k

表示具有n个顶点的第m个主观网络邻接矩阵,

$ S D_{i j}^{m}=\left\{\begin{array}{ll} 1, & i=j \text { 或对象 } i 、 j \text { 之间存在关系 } \\ 0, & \text { 其它 } \end{array}\right.$

OM= $(O D_{ij})_{n \times n}$ 表示具有n个顶点的客观网络邻接矩阵,

$ O D_{i j}=\frac{1}{q}\left(\sum_{n=1}^{q} \operatorname{Sim}_{i j}^{n}\right), $

q表示FCM中给定的类别数.

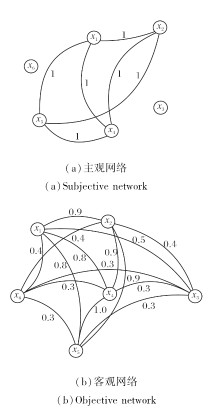
图1分别表示一个主观网络和一个客观网络.

	Figure Option View Download New Window
	图1 对象异构网络Fig.1 Heterogeneous networks of objects

定义8 设四元组(U, $L_{S_{α}}$ , WM_s, I)为异构网络语言形式背景, X⊆U, λ∈[0, 1],

WM_s={SM₁, SM₂, …, SM_k, OM},

如果

∀x_i∈X, x_j∈X, ∀m∈[1, k] , OD_ij≥λ

且

S $D_{ij}^{m}$ =1,

则称x_i、x_j连通, 如果X中任意子网络是连通的, 则称X是在λ下连通的.若X∪Y在λ下连通, 则X与Y在λ下连通.

定义9 设四元组(U, $L_{S_{α}}$ , WM_s, I)为异构网络语言形式背景, λ∈[0, 1], 对于∀X⊆U, ∀ $B_{S_{α}}$ ⊆ $L_{S_{α}}$ , 如果X'= $B_{S_{α}}$ , B $'_{S_{α}}$ =X且X是在λ下连通的, 则称(X, $B_{S_{α}}$ )是λ下的全局异构网络语言概念(OOLL_λ-concept).OverL_λ(U, $L_{S_{α}}$ , WM_s, I)表示异构网络语言形式背景中的所有OOLL_λ-concept.

定义10 设四元组(U, $L_{S_{α}}$ , WM_s, I)为异构网络语言形式背景, λ∈[0, 1], 对于∀X⊆U, ∀ $B_{S_{α}}$ ⊆ $L_{S_{α}}$ , 如果X'= $B_{S_{α}}$ , X是在λ下连通的, 且∀x∈B'-X与X在λ下是不连通的, 则称(X, $B_{S_{α}}$ )是λ下的局部异构网络语言概念(POLL_λ-concept).PartL_λ(U, $L_{S_{α}}$ , WM_s, I) 表示异构网络语言形式背景中的所有POLL_λ-concepts.

注本文把OOLL_λ-concept与POLL_λ-concept统称为异构网络语言概念.

例2 (续例1) 根据定义10, 专家确定对象x₁、x₂、x₄、x₅具有关系, 因此得到主观网络邻接矩阵SM; 同时通过对6个对象的属性进行模糊聚类, 得到客观网络邻接矩阵OM.进而构建异构网络语言形式背景(U, $L_{S_{α}}$ , WM_s, I), 如表3和表4所示.

表3 对象间存在的关系 Table 3 Relationship between objects

表4 对象与属性间的关系 Table 4 Relationship between objects and attributes

	$l_{s_{- 1}}^{1}$	$l_{s_{1}}^{1}$	$l_{s_{0}}^{2}$	$l_{s_{1}}^{2}$	$l_{s_{- 1}}^{3}$	$l_{s_{0}}^{3}$	$l_{s_{1}}^{3}$	$l_{s_{- 1}}^{4}$	$l_{s_{0}}^{4}$	$l_{s_{1}}^{4}$
x₁	0	1	1	0	0	1	0	0	1	0
x₂	0	1	0	1	0	1	0	0	0	1
x₃	1	0	1	0	1	0	0	0	0	1
x₄	0	1	0	1	0	1	0	0	1	0
x₅	0	1	0	1	0	1	0	0	1	0
x₆	0	1	0	1	0	0	1	1	0	0

表4 对象与属性间的关系 Table 4 Relationship between objects and attributes

性质2 设四元组(U, $L_{S_{α}}$ , WM_s, I)为异构网络语言形式背景, 对于L(U, $L_{S_{α}}$ , I)、OverL_λ(U, $L_{S_{α}}$ , WM_s, I)和Part(U, $L_{S_{α}}$ , WM_s, I), 如下性质成立:

1)OverL_λ(U, $L_{S_{α}}$ , WM_s, I)⊆L(U, $L_{S_{α}}$ , I),

2)OverL_λ(U, $L_{S_{α}}$ , WM_s, I)⊆PartL_λ(U, $L_{S_{α}}$ , WM_s, I),

3)L(U, $L_{S_{α}}$ , I)与PartL_λ(U, $L_{S_{α}}$ , WM_s, I)无直接联系,

4)若μ≥λ, 则

OverL_μ(U, $L_{S_{α}}$ , WM_s, I)⊆OverL_λ(U, $L_{S_{α}}$ , WM_s, I),

5)若μ≥λ, 则

PartL_μ(U, $L_{S_{α}}$ , WM_s, I)⊆PartL_λ(U, $L_{S_{α}}$ , WM_s, I).

证明根据定义5和定义9, 1)显然得证.根据定义9和定义10, 2)显然得证.

下证3)根据定义5和定义10可知, POLL_λ-concept和语言概念知识的外延都需满足X'= $B_{S_{α}}$ ; 对于内涵来说, 语言概念知识的外延需要满足B $'_{S_{α}}$ =X, POLL_λ-concept反而较宽松, 只需满足∀x∈B $'_{S_{α}}$ -X与X在λ下不连通.但是POLL_λ-concept还需满足X是在λ下连通的, 因此从判断条件上看, 无法进一步讨论它们之间的关系.

再证4).根据定义8和定义9可知, OOLL_λ-con-cepts满足X'= $B_{S_{α}}$ , B $'_{S_{α}}$ =X且X是在λ下连通的.当λ值越小, 满足连通的对象越多, 因此OOLL_λ-concepts越多.

最后, 根据4), 5)同理可证.

2.2 知识发现

由于在不同的认知和环境下, 判断对象与对象之间是否具有关系的准则是不同的, 所以通过规定对象间的相似度阈值可得到相似度较高的模糊集群.在本节中, 基于异构网络语言形式背景, 根据网络的全局连通及局部连通, 提出两种知识发现算法.

全局连通性描述整个网络中所有节点之间的连接情况.一个网络是全局连通的, 意味着任意两个节点之间都存在路径相连, 无论路径的长度或是否经过其它节点.具体步骤如算法1所示.

算法1 全局网络语言概念挖掘

输入 (U, $L_{S_{α}}$ , WM_s, I), 相似度阈值λ

输出OverL_λ(U, $L_{S_{α}}$ , WM_s, I)

1.for X⊆2^U do

2. if X在λ下连通 then

3. X=X″, $B_{S_{α}}$ =X'

4. else

5. 计算X的最大连通子集X₁, 令X=X₁, 跳转2

6. end if

7. if $B_{S_{α}}$ =Ø then

8. return (X, $B_{S_{α}}$ )=Ø

9. else if X″在λ下连通 then

10. 令X=X″, $B_{S_{α}}$ =X'

11. return (X, $B_{S_{α}}$ )

12. else

13. return (X, $B_{S_{α}}$ )=Ø

14. end if

15.end for

局部连通性是指网络中某个节点与其相邻节点之间的连接情况.在一个网络中, 某个节点是否与其相邻节点直接相连或通过其它节点间接相连, 这种连通性称为局部连通性.具体步骤如算法2所示.

算法2 局部网络语言概念挖掘

输入 (U, $L_{S_{α}}$ , WM_s, I)λ

输出PartL_λ(U, $L_{S_{α}}$ , WM_s, I)

1. for X⊆2^U do

2. if X在λ下连通then

3. if x∈X″-X与X在λ下不连通 then

4. $B_{S_{α}}$ =X'

5. else

6. X=X∪{x}, $B_{S_{α}}$ =X'

7. end if

8. if $B_{S_{α}}$ =Ø then

9. return (X, $B_{S_{α}}$ )=Ø

10. else

11. return (X, $B_{S_{α}}$ )

12. end if

13. else

14. 计算X的最大连通子集X₁, 令 X=X₁, 跳转2

15. end if

16.end for

3 基于异构网络语言形式背景的关联规则提取

关联规则^[28]是数据挖掘中一种用于发现数据集中项之间关联的技术.为了进一步挖掘在对象具有关系的情况下产生的属性之间的关联性, 本节提出基于异构网络语言形式背景的关联规则提取算法.

定义11 设四元组(U, $L_{S_{α}}$ , WM_s, I)为异构网络语言形式背景,

(X, $B_{S_{α}}$ )∈OverL_λ(U, $L_{S_{α}}$ , WM_s, I),

X≠Ø , 任意S⊆ $B_{S_{α}}$ 且S≠Ø , 则称S为基于异构网络语言形式背景的数据项集.

定义12 设S为基于异构网络语言形式背景的数据项集, 则S的支持度定义为

Support(S)= $\frac{| S' |}{|U|}$ . (2)

定义13 设S为基于异构网络语言形式背景的数据项集, 进行关联规则提取的S必须满足给定的最小阈值, 这一阈值可定义为最小支持度, 支持度大于最小支持度的数据项集称为频繁项集.

定义14 设S为基于异构网络语言形式背景的频繁项集, 则基于异构网络语言形式背景的关联规则可表示为A⇒ B, 其中

A⊆S, B=S-A,

A为关联规则的前件, B为关联规则的后件.

定义15 对于基于异构网络语言形式背景的关联规则A⇒ B, 其中

A⊆S, B=S-A.

规则R的置信度定义为

Confidence(R)= $\frac{Support (A ⋃ B)}{Support (A)}$ . (3)

定义16 设A⇒ B为基于异构网络语言形式背景的关联规则, 为了筛选置信度较高的关联规则, 给定一个阈值, 保留的关联规则置信度要满足给定的最小阈值, 这一阈值可定义为最小置信度.

定义17 设四元组(U, $L_{S_{α}}$ , WM_s, I)为异构网络语言形式背景, 对于任意置信度θ的关联规则X⇒ Y, 如果规则库中存在置信度为δ 的关联规则A⇒ B, 且θ≤δ , X⊆A, B⊆Y, 则称规则X⇒ Y为冗余关联规则.

基于定义11~定义17, 概念的内涵能发掘可进行关联规则提取的数据项集, 而概念的外延可辅助计算数据项集的支持度及关联规则的置信度.因此, 可构建一种基于异构网络语言形式背景的关联规则提取模型, 主要步骤如算法3所示.

算法3 基于异构网络语言形式背景的关联规则

提取模型

输入 (U, $L_{S_{α}}$ , WM_s, I)

输出关联规则

step 1 基于算法1提取异构网络语言形式背景的OverL_λ(U, $L_{S_{α}}$ , WM_s, I), 根据概念的外延可确定概念的类别.

step 2 计算所有类别的概念中的数据项集, 基于式(2)计算所有数据项集的支持度.

step 3 基于给定的最小支持度筛选频繁项集.

step 4 根据频繁项集及定义14计算每个类别所有的关联规则.

step 5 基于式(3)计算所有关联规则的置信度, 并根据定义17删除冗余关联规则.

step 6 基于给定的最小置信度筛选可靠的关联规则.

在社交网络分析中, 全局连通性可帮助揭示整个社交网络的结构和影响力传播路径.了解社交网络的全局连通性有助于理解信息传播、疾病传播等现象, 因此, 本文在后文实验中只进行全局异构网络语言概念的关联规则研究, 获取强连通的更准确有效的规则.

例3 (续例2) 关联规则提取的具体过程如下.基于算法1, 提取OverL₀_.₄(U, $L_{S_{α}}$ , WM_s, I)如下:

$\begin{array}{l} \left(x_{1} x_{2} x_{4} x_{5}, l_{s_{1}}^{1} l_{s_{0}}^{3}\right), \left(x_{1} x_{4} x_{5}, l_{s_{1}}^{1} l_{s_{0}}^{3} l_{s_{0}}^{4}\right), \left(x_{2} x_{4} x_{5}, l_{s_{1}}^{1} l_{s_{1}}^{2} l_{s_{0}}^{3}\right), \\ \left(x_{4} x_{5}, l_{s_{1}}^{1} l_{s_{1}}^{2} l_{s_{0}}^{3} l_{s_{0}}^{4}\right), \left(x_{1}, l_{s_{1}}^{1} l_{s_{0}}^{2} l_{s_{0}}^{3} l_{s_{0}}^{4}\right), \left(x_{2}, l_{s_{1}}^{1} l_{s_{1}}^{2} l_{s_{0}}^{3} l_{s_{1}}^{4}\right), \\ \left(x_{3}, l_{s_{-1}}^{1} l_{s_{0}}^{2} l_{s_{-1}}^{3} l_{s_{1}}^{4}\right), \left(x_{6}, l_{s_{1}}^{1} l_{s_{1}}^{2} l_{s_{1}}^{3} l_{s_{-1}}^{4}\right) . \end{array}$

设置最小支持度为0.5, 基于式(2)计算项集支持度, 如表5所示.

表5 频繁数据项集支持度 Table 5 Frequent data item set support

频繁项集	支持度	频繁项集	支持度
$l_{s_{1}}^{1}$	0.83	$l_{s_{1}}^{2}$	0.5
$l_{s_{1}}^{1} l_{s_{0}}^{3}$	0.67	$l_{s_{1}}^{2} l_{s_{0}}^{3}$	0.5
$l_{s_{0}}^{3}$	0.67	$l_{s_{1}}^{1} l_{s_{1}}^{2}$	0.5
$l_{s_{1}}^{1} l_{s_{1}}^{2} l_{s_{0}}^{3}$	0.5	$l_{s_{1}}^{1} l_{s_{0}}^{3} l_{s_{0}}^{4}$	0.5

表5 频繁数据项集支持度 Table 5 Frequent data item set support

设置最小置信度为1.0, 根据定义14和式(3)计算得到的无冗余关联规则及规则置信度, 如表6所示.

表6 关联规则表 Table 6 Association rule table

关联规则	置信度
r₁∶ $l_{s_{0}}^{3}$ ⇒ $l_{s_{1}}^{1}$	1.0
r₂∶ $l_{s_{1}}^{2}$ ⇒ $l_{s_{1}}^{1} l_{s_{0}}^{3}$	1.0
r₃∶ $l_{s_{0}}^{4}$ ⇒ $l_{s_{1}}^{1} l_{s_{0}}^{3}$	1.0

表6 关联规则表 Table 6 Association rule table

4 实验及结果分析

4.1 实验数据集

本文使用公开的kaggle数据集上德国Ebay网站二手车相关数据集.二手车原始数据集包括车辆的使用情况、交易地区、成交价格等, 数据集常用于进行成交价格预测等相关研究.在原有数据集上剔除一些冗余及不相关属性后, 每个样本都含有一个关系属性(Name)、4个特征属性(Year、Kilometers_Driven、Power、New_Price), 具体信息如表7所示.

表7 二手车数据集特征属性 Table 7 Feature attributes of used car dataset

选取数据集上3种品牌的汽车的交易情况, 共138条数据, 5个属性列, 本文在此数据集上展开研究.

4.2 实验环境及预处理

实验在Windows(64位)系统上使用PyCharm工具、Python3.9.由于表7中的Year、Kilometers_Driven、Power、New_Price都是连续型的变量, 为了构造(U, $L_{S_{α}}$ , WM_s, I), 需要引入模糊控制中的模糊化方法, 转化为语言值.选取语言术语集

S={s_-1=小, s₀=中, s₁=大},

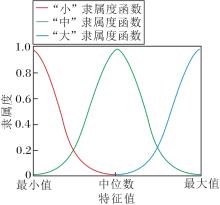
描述特征属性的情况.例如:首次上牌时间(Year)情况“ 早” 是指上牌时间久远, 已行驶里程“ 大” 是指行驶距离大等描述.语言术语集中的语言术语分别对应3个模糊集.为3个模糊集合选取适当的隶属度函数, 具体如图2所示.

	Figure Option View Download New Window
	图2 隶属度函数图像Fig.2 Image of affiliation function

分别计算每个元素相对3个隶属函数的隶属度, 隶属度最大的即为样本在对应属性的语言变量.模糊化后所得异构网络语言形式背景(U, $L_{S_{α}}$ , WM_s, I)如表8所示.

U={x₁, x₂, …, x₁₃₈}

表8 异构网络语言形式背景(U,

L_{S_{α}}

, WM_s, I) Table 8 Heterogeneous network linguistic formal context(U,

L_{S_{α}}

, WM_s, I)

	x₁	x₂	…	x₁₃₈	x₁	x₂	…	x₁₃₈	$l_{s_{- 1}}^{1}$	$l_{s_{0}}^{1}$	$l_{s_{1}}^{1}$	$l_{s_{- 1}}^{2}$	$l_{s_{0}}^{2}$	$l_{s_{1}}^{2}$	…	$l_{s_{- 1}}^{4}$	$l_{s_{0}}^{4}$	$l_{s_{1}}^{4}$
x₁	1	1	…	0	1	0.9	…	0.4	1	0	0	0	0	1	…	1	0	0
x₂	1	1	…	0	0.9	1	…	0.4	1	0	0	0	0	1	…	1	0	0
x₃	1	1	…	0	0.9	1	…	0.4	1	0	0	0	0	1	…	1	0	0
︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙	︙
x₁₃₇	0	0	…	1	0.4	0.4	…	1	0	0	1	1	0	0	…	1	0	0
x₁₃₈	0	0	…	1	0.4	0.4	…	1	0	0	1	1	0	0	…	1	0	0

表8 异构网络语言形式背景(U,

L_{S_{α}}

, WM_s, I) Table 8 Heterogeneous network linguistic formal context(U,

L_{S_{α}}

, WM_s, I)

表示138个销售样本,

$L_{S_{α}}$ ={ $l_{s_{- 1}}^{1}$ , $l_{s_{0}}^{1}$ , $l_{s_{1}}^{1}$ , $l_{s_{- 1}}^{2}$ , $l_{s_{0}}^{2}$ , $l_{s_{1}}^{2}$ , $l_{s_{- 1}}^{3}$ , $l_{s_{0}}^{3}$ , $l_{s_{1}}^{3}$ , $l_{s_{- 1}}^{4}$ , $l_{s_{0}}^{4}$ , $l_{s_{1}}^{4}$ }

表示具有4个属性且每个属性具有3个语言项的语言概念集, 其中, l¹表示Year, l²表示Kilometers_Driven, l³表示Power, l⁴表示New_Price, I⊆U× $L_{s_{α}}$ 表示对象与语言概念二元关系,

WM_s={SM, OM}

表示2个邻接矩阵, SM= $(S D_{ij})_{138 \times 138}$ 表示具有138个顶点的主观网络邻接矩阵,

SD_ij= $\{\begin{array}{l} 1, & i = j 或对象 i 、 j 属于相同品牌 \\ 0, & 其它 \end{array}$

OM= $(O D_{ij})_{138 \times 138}$ 表示具有138个顶点的客观网络邻接矩阵, 通过定义8, 类比例1可得到.

4.3 实验结果

针对表8调用算法1中OverL_λ(U, $L_{S_{α}}$ , WM_s, I)的知识发现, 在不同的相似度阈值λ下, 提取的3种汽车品牌相关的概念以及总概念数(SUM)都会随λ增大而减少, 具体如图3所示.这是因为样本对象是具有差异的, 随着对相似度做出限制, 满足条件的对象会越来越少, 导致产生的概念减少, 而保留的概念自然具有较高的普遍性和频繁性, 挖掘的关联规则具有更高的代表性.

	Figure Option View Download New Window
	图3 三种车型概念数随λ的变化情况Fig.3 Concept numbers for 3 vehicle types changing with λ

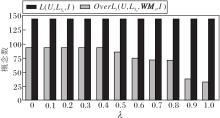经典语言形式概念L(U, $L_{S_{α}}$ , I)与OverL_λ(U, $L_{S_{α}}$ , WM_s, I)的对比如图4所示, 经典语言形式概念忽略对象有关分类的属性, 会造成一定的信息损失.

	Figure Option View Download New Window
	图4 L(U, $L_{S_{α}}$ , I)与OverL_λ(U, $L_{S_{α}}$ , WM_s, I)概念数对比Fig.4 Comparison of concept numbers between L(U, $L_{S_{α}}$ , I) and OverL_λ(U, $L_{S_{α}}$ , WM_s, I)

在相似度阈值λ=0.6时, 设置最小支持度为0.1, 最小置信度为0.6.按照算法3, 根据BMW品牌汽车相关的概念计算所得无冗余关联规则8条, 如表9所示.根据Honda品牌汽车相关的概念计算所得无冗余关联规则7条, 如表10所示.根据Renault品牌汽车相关的概念计算所得无冗余关联规则5条, 如表11所示.

表9 BMW汽车关联规则 Table 9 Association rules of BMW car

关联规则	置信度	关联规则	置信度
r₁∶ $l_{s_{1}}^{4}$ ⇒ $l_{s_{1}}^{3}$	1.0	r₅∶ $l_{s_{0}}^{2} l_{s_{1}}^{3}$ ⇒ $l_{s_{1}}^{4}$	0.8
r₂∶ $l_{s_{0}}^{4}$ ⇒ $l_{s_{1}}^{3}$	1.0	r₆∶ $l_{s_{- 1}}^{1}$ ⇒ $l_{s_{1}}^{3}$	0.7
r₃∶ $l_{s_{1}}^{1} l_{s_{1}}^{3}$ ⇒ $l_{s_{1}}^{4}$	0.8	r₇∶ $l_{s_{1}}^{3}$ ⇒ $l_{s_{1}}^{4}$	0.7
r₄∶ $l_{s_{- 1}}^{2}$ ⇒ $l_{s_{1}}^{1}$	0.8	r₈∶ $l_{s_{1}}^{1}$ ⇒ $l_{s_{- 1}}^{2}$	0.7

表9 BMW汽车关联规则 Table 9 Association rules of BMW car

表10 Honda汽车关联规则 Table 10 Association rules of Honda car

关联规则	置信度	关联规则	置信度
r₁∶ $l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₅∶ $l_{s_{0}}^{3}$ ⇒ $l_{s_{- 1}}^{2} l_{s_{- 1}}^{4}$	0.7
r₂∶ $l_{s_{- 1}}^{2}$ ⇒ $l_{s_{- 1}}^{4}$	0.8	r₆∶ $l_{s_{- 1}}^{4}$ ⇒ $l_{s_{- 1}}^{2}$	0.6
r₃∶ $l_{s_{0}}^{2} l_{s_{- 1}}^{4}$ ⇒ $l_{s_{- 1}}^{3}$	0.8	r₇∶ $l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{2} l_{s_{- 1}}^{4}$	0.6
r₄∶ $l_{s_{- 1}}^{4}$ ⇒ $l_{s_{- 1}}^{3}$	0.7

表10 Honda汽车关联规则 Table 10 Association rules of Honda car

表11 Renault汽车关联规则 Table 11 Association rules of Renault car

关联规则	置信度	关联规则	置信度
r₁∶ $l_{s_{0}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₄∶ $l_{s_{- 1}}^{4}$ ⇒ $l_{s_{1}}^{1}$	0.7
r₂∶ $l_{s_{1}}^{1} l_{s_{0}}^{2}$ ⇒ $l_{s_{- 1}}^{4}$	0.9	r₅∶ $l_{s_{0}}^{3}$ ⇒ $l_{s_{1}}^{1} l_{s_{- 1}}^{4}$	0.6
r₃∶ $l_{s_{1}}^{1}$ ⇒ $l_{s_{- 1}}^{4}$	0.8

表11 Renault汽车关联规则 Table 11 Association rules of Renault car

选取2个提取的Renault品牌汽车相关的关联规则作文字表述如下.

r₁:若汽车发动机动力“ 一般” , 则新车价格“ 低” .

r₂:若汽车首次上牌时间“ 早” , 已行驶里程“ 中等” , 则新车价格“ 低” .

汽车的新车价格受多种因素影响, 其中发动机动力作为衡量汽车配置的重要指标之一, 因此通常价格较高的汽车发动机动力较大.而汽车的首次上牌时间体现汽车的使用时间, 使用时间越长的汽车通常已行驶里程较大.

为了进一步说明基于异构网络语言形式背景的关联规则提取模型的有效性, 将所得的无冗余的关联规则(表9~表11)与经典语言形式概念L(U, $L_{S_{α}}$ , I)提取的关联规则(如表12)进行对比.

表12 L(U,

L_{S_{α}}

, I)关联规则 Table 12 Association rules of L(U,

L_{S_{α}}

, I)

关联规则	置信度	关联规则	置信度
r₁∶ $l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₁₂∶ $l_{s_{0}}^{2} l_{s_{1}}^{4}$ ⇒ $l_{s_{1}}^{3}$	1.0
r₂∶ $l_{s_{1}}^{0} l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₁₃∶ $l_{s_{0}}^{4}$ ⇒ $l_{s_{1}}^{3}$	1.0
r₃∶ $l_{s_{1}}^{1} l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	︙	︙
r₄∶ $l_{s_{- 1}}^{2} l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₄₇∶ $l_{s_{0}}^{3}$ ⇒ $l_{s_{1}}^{1} l_{s_{- 1}}^{4}$	0.6
r₅∶ $l_{s_{1}}^{1} l_{s_{- 1}}^{2} l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₄₈∶ $l_{s_{0}}^{3} l_{s_{- 1}}^{4}$ ⇒ $l_{s_{1}}^{1}$	0.6
r₆∶ $l_{s_{0}}^{2} l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₄₉∶ $l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{2}$	0.6
r₇∶ $l_{s_{0}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₅₀∶ $l_{s_{- 1}}^{3}$ ⇒ $l_{s_{- 1}}^{2} l_{s_{- 1}}^{4}$	0.6
r₈∶ $l_{s_{1}}^{1} l_{s_{0}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₅₁∶ $l_{s_{- 1}}^{3} l_{s_{- 1}}^{4}$ ⇒ $l_{s_{- 1}}^{2}$	0.6
r₉∶ $l_{s_{- 1}}^{2} l_{s_{0}}^{3}$ ⇒ $l_{s_{- 1}}^{4}$	1.0	r₅₂∶ $l_{s_{- 1}}^{2}$ ⇒ $l_{s_{1}}^{1} l_{s_{- 1}}^{4}$	0.6
r₁₀∶ $l_{s_{1}}^{4}$ ⇒ ${l_{s}^{3}}_{1}$	1.0	r₅₃∶ $l_{s_{- 1}}^{4}$ ⇒ $l_{s_{- 1}}^{2}$	0.6
r₁₁∶ $l_{s_{1}}^{1} l_{s_{1}}^{4}$ ⇒ $l_{s_{1}}^{3}$	1.0

表12 L(U,

L_{S_{α}}

, I)关联规则 Table 12 Association rules of L(U,

L_{S_{α}}

, I)

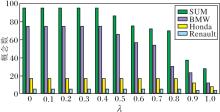
在相同的数据集上, 按照经典语言形式概念L(U, $L_{S_{α}}$ , I)的关联规则提取模型, 得到53条关联规则.取置信度为1.0的13条关联规则分析发现, 仅有r₁、r₇、r₁₀、r₁₃是非冗余的, 而基于异构网络语言形式背景的关联规则提取模型所得规则, 其置信度为1.0的4条关联规则不仅涵盖经典语言形式概念L(U, $L_{S_{α}}$ , I)的4条非冗余关联规则, 且不会出现较大规模冗余规则的情况.另外, 经典语言形式概念L(U, $L_{S_{α}}$ , I)的4条关联规则不具有针对性, 不能产生针对不同品牌的关联规则.而基于异构网络语言形式背景的关联规则提取模型可综合对象各方面关系为不同类别的对象提取相关的关联规则.

经实验分析可知, 异构网络语言形式背景下的关联规则提取具有可行性及可信性, 具有的优势如下.1)语言值描述的规则更具有可解释性, 可通俗理解.2)可针对不同种类的对象挖掘每类对象特有的关联规则, 并且避免出现大规模的规则冗余状况.

5 结束语

本文提出一种异构网络语言形式背景, 通过对象相似度建立网络邻接矩阵, 挖掘潜在对象间的客观关系.对应的异构网络语言概念更具有代表性, 一定程度上剔除部分冗余概念.简化后的概念格不仅考虑对象与属性之间的关系, 而且考虑对象之间的联系, 提取的关联规则关联性和代表性更强, 又因为形式背景结合语言概念, 关联规则的可解释性更强.在实验阶段, 采用模糊控制中的数据模糊化方法, 实现客观的语言评价, 以概念格的方式实现模糊推理, 但一个完整的模糊系统需要对输出进行去模糊化, 实现这样一个理想的模糊控制是今后重要研究方向之一.

本文责任编委苗夺谦

Recommended by Associate Editor MIAO Duoqian

参考文献

文献选项

[1]	WILLE R. Restructuring Lattice Theory: An Approach Based on Hie-rarchies of Concepts // Proc of the 7th International Conference on Formal Concept Analysis. Berlin, Germany: Springer, 2009: 314-339. [本文引用:2]
[2]	MEDINA J, NAVAREÑO P, RAMÍREZ-POUSSA E. *Knowledge Im-plications in Multi-adjoint Concept Lattices // CORNEJO M E, KÓCZY L T, MEDINA-MORENO J, et al. , eds. Computational Intelligence and Mathematics for Tackling Complex Problems 2. Berlin, Germany: Springer*, 2022: 155-161. [本文引用:1]
[3]	HAO F, YANG Y X, MIN G Y, et al. Incremental Construction of Three-Way Concept Lattice for Knowledge Discovery in Social Networks. Information Sciences, 2021, 578: 257-280. [本文引用:1]
[4]	BAYHAN S. Textural Dependency and Concept Lattices. Internatio-nal Journal of Approximate Reasoning, 2021, 136: 36-65. [本文引用:1]
[5]	LI J H, HUANG C C, QI J J, et al. Three-Way Cognitive Concept Learning via Multi-granularity. Information Sciences, 2017, 378: 244-263. [本文引用:1]
[6]	YAN E L, YU C G, LU L M, et al. Incremental Concept Cognitive Learning Based on Three-Way Partial Order Structure. Knowledge-Based Systems, 2021, 220. DOI: 10.1016/j.knosys.2021.106898. [本文引用:1]
[7]	HU Q, QIN K Y, YANG H, et al. A Novel Approach to Attribute Reduction and Rule Acquisition of Formal Decision Context. App-lied Intelligence, 2023, 53(11): 13834-13851. [本文引用:1]
[8]	WU W Z, LEUNG Y, MI J S. Granular Computing and Knowledge Reduction in Formal Contexts. IEEE Transactions on Knowledge and Data Engineering, 2008, 21(10): 1461-1474. [本文引用:1]
[9]	WANG S N, WEI L, LI Q. Construct New Lattices Based on Rough Set Theory // Proc of the 2nd International Conference on Information Science and Engineering. Washington, USA: IEEE, 2010: 5013-5016. [本文引用:1]
[10]	ZHI H L, QI Z H, LI Y N. An Efficient Conflict Analysis Method Based on Splitting and Merging of Formal Contexts. Information Sciences, 2024, 661. DOI: 10.1016/j.ins.2024.120154. [本文引用:1]
[11]	ZADEH L A. Fuzzy Sets. Information and Control, 1965, 8(3): 338-353. [本文引用:1]
[12]	ZADEH L A. The Concept of a Linguistic Variable and Its Applica-tion to Approximate Reasoning-III. Information Sciences, 1975, 9(1): 43-80. [本文引用:1]
[13]	HERRERA F, HERRERA-VIEDMA E, VERDEGAY J L. A Mo-del of Consensus in Group Decision Making under Linguistic Asse-ssments. Fuzzy Sets and Systems, 1996, 78(1): 73-87. [本文引用:1]
[14]	XU Z S. On Generalized Induced Linguistic Aggregation Operators. International Journal of General Systems, 2006, 35(1): 17-28. [本文引用:1]
[15]	ZOU L, PANG K, SONG X Y, et al. A Knowledge Reduction App-roach for Linguistic Concept Formal Context. Information Sciences, 2020, 524: 165-183. [本文引用:1]
[16]	PANG K, MARTÍNEZ L, LI N, et al.* A Concept Lattice-Based Expert Opinion Aggregation Method for Multi-attribute Group Decision-Making with Linguistic Information. Expert Systems with App-lications*, 2024, 237. DOI: 10.1016/j.eswa.2023.121485. [本文引用:1]
[17]	YU G L, CUI Z W, YUAN Q F. Image Segmentation Method Based on Improved PSO Optimized FCM Algorithm and Its Application. Journal of Computers, 2023, 34(2). DOI: 10.53106/199115992023043402001. [本文引用:1]
[18]	YANG Y, WEN Z C. Image Segmentation Based on Super-Pixel with Neighborhood Constrained and Multi-level FCM Clustering. Journal of Computational Methods in Sciences and Engineering, 2022, 22(4): 1117-1130. [本文引用:1]
[19]	PANG Y, SHI M L, ZHANG L Y, et al. PR-FCM: A Polynomial Regression-Based Fuzzy C-means Algorithm for Attribute-Associa-ted Data. Information Sciences, 2022, 585: 209-231. [本文引用:1]
[20]	沈浩, 王士同. 按风格划分数据的模糊聚类算法. 模式识别与人工智能, 2019, 32(3): 204-213. (SHEN H, WANG S T. A Fuzzy Style Clustering Algorithm on Stylistic Data. Pattern Recognition and Artificial Intelligence, 2019, 32(3): 204-213. ) [本文引用:1]
[21]	祁宏宇, 吴小俊, 王士同, 等. 一种协同的FCPM模糊聚类算法. 模式识别与人工智能, 2010, 23(1): 120-126. (QI H Y, WU X J, WANG S T, et al. Collaborative FCPM Fuzzy Clustering Algorithm. Pattern Recognition and Artificial Intelligence, 2010, 23(1): 120-126. ) [本文引用:1]
[22]	ZHAO J X, WANG Y H, GAO P T, et al. Asymptotical Tracking Control for the Complex Network Based on the Dynamic Topology. ISA Transactions, 2024, 148: 105-113. [本文引用:1]
[23]	FAN M, LUO S, LI J H. Network Rule Extraction under the Network Formal Context Based on Three-Way Decision. Applied Inte-lligence, 2023, 53: 5126-5145. [本文引用:2]
[24]	范敏, 郭瑞欣, 李金海. 网络决策形式背景下基于因果力的邻域推荐算法. 模式识别与人工智能, 2022, 35(11): 977-988. (FAN M, GUO R X, LI J H. Neighborhood Recommendation Al-gorithm Based on Causality Force under Network Formal Decision Con-text. Pattern Recognition and Artificial Intelligence, 2022, 35(11): 977-988. ) [本文引用:1]
[25]	庞阔, 陈思琪, 宋笑迎, 等. 基于粒计算的语言概念决策形式背景分析. 山东大学学报(工学版), 2018, 48(6): 74-81. (PANG K, CHEN S Q, SONG X Y, et al. Linguistic Concept Formal Decision Context Analysis Based on Granular Computing. Journal of Shand ong University(Engineering Science), 2018, 48(6): 74-81. ) [本文引用:3]
[26]	VERMA K R, TIWARI R, THAKUR S P. Partition Coefficient and Partition Entropy in Fuzzy C Means Clustering. Journal of Scien-tific Research and Reports, 2023, 29(12): 1-6. [本文引用:1]
[27]	YU H Y, JIANG L R, FAN J L, et al. A Feature-Weighted Su-ppressed Possibilistic Fuzzy C-means Clustering Algorithm and Its Application on Color Image Segmentation. Expert Systems with App-lications, 2024. DOI: 10.1016/j.eswa.2023.122270. [本文引用:1]
[28]	AGRAWAL R, IMIELIŃSKI T, SWAMI A. Mining Association Rules Between Sets of Items in Large Databases. ACM SIGMOD Record, 1993, 22(2): 207-216. [本文引用:1]

2009

0.0

... 形式概念分析(Formal Concept Analysis, FCA)^[1]是一种强大的数学工具,用于数据处理和规则提取 ...

... 定义2^[1] 称三元组(U,A,I)为一个形式背景,其中U={x₁,x₂,…,x_n}表示非空有限的对象集,A={a₁,a₂,…,a_m}表示非空有限的属性集,I⊆U#cod#x000D7 ...

2022

0.0

... 作为基于形式背景的一种重要的数据处理和可视化方法,FCA通过对象与属性的关联获取潜在的概念知识,目前已在知识发现、数据挖掘、机器学习、特征选择等领域^{[2,3,4,5,6,7]}得到广泛应用 ...

2021

0.0

2021

0.0

2017

0.0

2021

0.0

2023

0.0

2008

0.0

... Wu等^[8]将粒计算思想融入形式概念分析,研究概念格的粒度结构在知识约简中的应用 ...

2010

0.0

... Wang等^[9]受粗糙集理论启发,从近似算子角度研究形式背景,并构建概念格 ...

2024

0.0

... Zhi等^[10]基于形式概念分析定义新的三支概念,提出一种快速冲突分析信息融合方法 ...

1965

0.0

... Zadeh^[11,12]提出模糊集和语言变量的概念,可有效描述使用语言值表达的信息 ...

1975

0.0

... Zadeh^[11,12]提出模糊集和语言变量的概念,可有效描述使用语言值表达的信息 ...

1996

0.0

... Herrera等^[13]提出语言术语集,描述离散语言变量 ...

2006

0.0

... Xu^[14]研究基于概率语言信息的聚合算子 ...

2020

0.0

... Zou等^[15]提出语言概念形式背景,用于处理现实生活中使用语言值描述的数据 ...

2024

0.0

... Pang等^[16]利用语言真值格蕴含代数构建多专家语言形式背景,提出一种有效的多属性群决策意见聚合方法 ...

2023

0.0