设

U={x₁, x₂, …, x_n}

为非空有限对象集, 也称为论域, P(U)表示U的幂集, ~X表示集合X关于U的补集, 即

~X=U-X={x∈ U|x∉X}.

定义1^[36] 称(U, AT)为一个信息系统, 其中

U={x₁, x₂, …, x_n}

为论域,

AT={a₁, a₂, …, a_m}

为非空有限属性集, 对于∀ a∈ AT, 有a∶ U→ V_a, 即a(x)∈ V_a, x∈ U, 其中

V_a={a(x)|x∈ U}

为属性a的值域.对于A⊆AT, U上的不可分辨关系如下:

R_A={(x, y)∈ U× U|a(x)=a(y), ∀ a∈ A}.

R_A可将U中对象分成互不相交的等价类, 构成U的一个划分

U/R_A={[x]_A|x∈ U},

其中

[x]_A={y∈ U|(x, y)∈ R_A}, ∀ x∈ U.

对于X∈ P(U), X关于属性子集A的下近似$\underline{{{R}_{A}}}(X)$与上近似$\overline{{{R}_{A}}}(X)$分别定义如下:

$\underline{{{R}_{A}}}(X)=\{x\in U|{{[x]}_{A}}\subseteq X\}$,

$\overline{{{R}_{A}}}(X)=\{x\in U [ x{{]}_{A}}\cap X\ne \emptyset \}$.

定义2 称二元组(W, ≤ )为一个全序集, 其中W≠ Ø 称为标记集, ≤ 为W上的二元关系, 且对于∀ a∈ W, b∈ W, c∈ W, 满足

1)自反性.a≤ a.

2)传递性.若a≤ b, b≤ c, 则a≤ c.

3)≤ 是线性序.a≤ b或b≤ a.

定义3 对于任意2个全序集(W₁, ≤ ₁)和(W₂, ≤ ₂), 若映射

g∶ (W₁, ≤ ₁)→ (W₂, ≤ ₂),

对于∀ a∈ W₁, b∈ W₁, 有a≤ ₁b蕴含g(a)≤ ₂g(b), 则称映射g是保序的.

定义4^[16] 设S=(U, AT)为一个信息系统, 若某个属性的值域为全序集, 即属性值按升序或降序排列, 则称该属性为一个准则.若每个a∈ AT都是一个准则, 则称S为一个序信息系统.对于A⊆AT, U上的优势关系为:

$R_{A}^{\uparrow }=\{(y, x)\in U\times U|a(y)\ge a(x), \forall a\in A\}$.

本文在所有属性值域上用同一个符号≥ 表示优序关系, 且a(y)≥ a(x)当且仅当a(x)≤ a(y).则对象x关于A的优势类为:

$[x]_{A}^{\uparrow }=\{y\in U|a(y)\ge a(x), \forall a\in A\}=\{y\in U|(y, x)\in R_{A}^{\uparrow }\}$,

x∈ U.

对于∀ X∈ P(U), 集合X关于$R_{A}^{\uparrow }$的下近似$\underline{R_{A}^{\uparrow }}(X)$与上近似$\overline{R_{A}^{\uparrow }}(X)$分别定义如下:

$\underline{R_{A}^{\uparrow }}(X)=\{x\in U|[x]_{A}^{\uparrow }\subseteq X\}$,

$\overline{R_A^{\uparrow}}(X)=\left\{x \in U \mid[x]_A^{\dagger} \cap X \neq \emptyset\right\}$.

定义5^[16] 称(U, AT∪ {d})为一个序决策系统, 若(U, AT)为一个序信息系统, 且决策属性d∉AT也是一个准则, 由d导出如下的优势关系:

$R_{d}^{\uparrow }=\{(y, x)\in U\times U|d(y)\ge d(x)\}$.

对象x在d下的决策优势类为:

$[x]_{d}^{\uparrow }=\{y\in U|d(y)\ge d(x)\}=\{y\in U|(y, x)\in R_{d}^{\uparrow }\}$,

x∈ U.

定义6^{[21, 22]} 称

S=(U, AT∪ {d})

为一个广义多尺度决策系统, 其中

U={x₁, x₂, …, x_n}

为论域,

AT={a₁, a₂, …, a_m}

为条件属性集, 且每个属性都有多个尺度标记, d∉AT为决策属性.若a_j有I_j个等级尺度标记, 则S可表示为

$S=(U, \{a_{j}^{k}|k=1, 2, \ldots , {{I}_{j}}_{, }j=1, 2, \ldots , m\}\cup \{d\})$,

其中, $a_{j}^{k}\, \!:U\to V_{j}^{k}$, $V_{j}^{k}$为a_j在第k个尺度标记下的值域, 且对于j∈ {1, 2, …, m}, 1≤ k≤ I_j-1, 存在一个满射$g_{j}^{k, k+1}$∶ $V_{j}^{k}\to V_{j}^{k+1}$, 使得

$a_{j}^{(k+1)}=g_{j}^{(k, k+1)}\circ a_{j}^{k}$,

即

$a_{j}^{k+1}(x)=g_{j}^{k, k+1}(a_{j}^{k}(x)), x\in U$,

称$g_{j}^{k, k+1}$为信息粒度变换.

定义7^[22] 设

$S=(U, \{a_{j}^{k}|k=1, 2, \ldots , {{I}_{j}}_{, }j=1, 2, \ldots , m\}\cup \{d\})$

为一个广义多尺度决策系统, 若条件属性a_j∈ AT取第l_j个尺度标记, 1≤ l_j≤ I_j, j∈ {1, 2, …, m}, 则称

K=(l₁, l₂, …, l_m)

为S的一个尺度组合.S的所有尺度组合构成的集合如下:

$\mathcal{L}=\left\{\left(l_{1}, l_{2}, \cdots, l_{m}\right) \mid 1 \leqslant l_{j} \leqslant I_{j}, j=1, 2, \cdots, m\right\}$.

每个尺度组合

$K=\left(l_{1}, l_{2}, \cdots, l_{m}\right) \in \mathcal{L}$

对应一个单尺度决策系统S^K,

$S^{K}= \left(U, A T^{K} \cup\{d\}\right)=\left(U, \left\{a_{1}^{l_{1}}, a_{2}^{L_{2}}, \cdots, a_{m}^{l_{m}}\right\} \cup\{d\}\right)$.

设

$K_{1}=\left(l_{1}^{1}, l_{2}^{1}, \cdots, l_{m}^{1}\right) \in \mathcal{L}$,

$K_{2}=\left(l_{1}^{2}, l_{2}^{2}, \cdots, l_{m}^{2}\right) \in \mathcal{L}$

为2个尺度组合.若对于∀ j∈ {1, 2, …, m}, 有 lj1≤ lj2, 则称K₁比K₂细, 或K₂比K₁粗, 记为K₁⪯K₂.若K₁⪯K₂, 且存在j∈ {1, 2, …, m}使得 lj1< lj2, 则称K₁严格细于K₂, 或K₂严格粗于K₁, 记为K₁≺K₂.显然, $ (\mathcal{L}, \leq)$为一个偏序集.进一步, 定义

$K_{1} \wedge K_{2}=\left(l_{1}^{1} \wedge l_{1}^{2}, l_{2}^{1} \wedge l_{2}^{2}, \cdots, l_{m}^{1} \wedge l_{m}^{2}\right)$,

$K_{1} \vee K_{2}=\left(l_{1}^{1} \vee l_{1}^{2}, l_{2}^{1} \vee l_{2}^{2}, \cdots, l_{m}^{1} \vee l_{m}^{2}\right)$,

其中,

$l_{j}^{1} \wedge l_{j}^{2}=\min \left\{l_{j}^{1}, l_{j}^{2}\right\}$,

$l_{j}^{1} \vee l_{j}^{2}=\max \left\{l_{j}^{1}, l_{j}^{2}\right\}$,

j∈ {1, 2, …, m}.则易证, $(\mathcal{L}, \leq, \wedge, \vee)$为一个有界格, 也是完备格, 最小元为

K₀=(1, 1, …, 1),

最大元为

K_I=(I₁, I₂, …, I_m),

并且

K₁⪯K₂⇔ K₁∧ K₂=K₁⇔ K₁∨ K₂=K₂.

定义8^[27] 设U为论域, 若集函数

$ m:(U) \rightarrow \mathcal{P}[0, 1] $

满足

1)m(Ø )=0,

2)$\underset{X\in \text{P}\left( U \right)}{\mathop \sum }\, ~m(X)=1$,

则称m为U上的一个mass函数.若m(X)> 0, 称$ X\in \mathcal{P}(U) $为m的焦元.记

$ \mathscr{M}=\{X \in \mathcal{P}(U) \mid m(X)> 0\} $,

称序对$(\mathscr{M}, m)$为U上的一个信任结构.

定义9^[27] 设$(\mathscr{M}, m)$为U上的信任结构.若

$\operatorname{Bel}(X)=\sum_{Y \subseteq X} m(Y), X \in \mathcal{P}(U)$,

则称集函数

$\text { Bel }: \mathcal{P}(U) \rightarrow[0, 1]$

为U上的信任函数.若

$P l(X)=\sum_{Y \cap X \neq \emptyset} m(Y), X \in \mathcal{P}(U)$,

则称集函数

$P l: \mathcal{P}(U) \rightarrow[0, 1]$

为U上的似然函数.易得

$P l: \mathcal{P}(U) \longrightarrow[0, 1]$,

即在同个$(\mathscr{M}, m)$中信任函数和似然函数是对偶的, 且

Bel(X)≤ Pl(X).

定理1^[30] 设(U, AT)为一个信息系统, A⊆AT, 对于$\forall X\in \mathcal{P}(U)$, 记

$Be{{l}_{A}}(X)=P\left( \underline{{{R}_{A}}}(X) \right), P{{l}_{A}}(X)=P\left( \overline{{{R}_{A}}}(X) \right)$,

其中

P(X)=|X|/|U|,

|X|为集合X的基数, 则

$\operatorname{Bel}_{A}: \mathcal{P}(U) \longrightarrow[0, 1]$

为U上的信任函数,

$P l_{A}: \mathcal{P}(U) \rightarrow[0, 1]$

为U上的似然函数, 对应如下的mass函数:

mA(X)=P(X), X∈U/RA0, X∉U/RA

定义10^[37] 称(U, AT)为一个模糊信息系统, 其中

U={x₁, x₂, …, x_n}

为论域,

AT={a₁, a₂, …, a_m}

为非空有限属性集, 对于∀ a∈ AT, 有

a∶ U→ [0, 1],

即a(x)∈ [0, 1], x∈ U.称(U, AT∪ {d})为一个模糊决策系统.若(U, AT)为一个模糊信息系统, d∉AT为决策属性,

d∶ U→ [0, 1],

d(x)∈ [0, 1]为对象x在d上的取值.

定义11 设S=(U, AT)为一个模糊信息系统, 若∀ a∈ AT都是一个准则, 则称S为一个序模糊信息系统.此时, 对于A⊆AT, A在U上导出优势关系:$R_{A}^{\uparrow }=\{(y, x)\in U\times U|a(y)\ge a(x), \forall a\in A\}$, 即在任意属性a∈ A下, 对象y的取值大于或等于对象x的取值.

对象x在A下的优势类为:

$[x]_{A}^{\uparrow }=\{y\in U|a(y)\ge a(x), \forall a\in A\}=\{y\in U|(y, x)\in R_{A}^{\uparrow }\}$,

x∈ U.

记优势关系$R_{A}^{\uparrow }$在U上导出的优势类全体:

$U/R_{A}^{\uparrow }=\{[x]_{A}^{\uparrow }|x\in U\}$.

对于$\forall X \in \mathcal{P}(U)$, 集合X关于$R_{A}^{\uparrow }$的下近似$\underline{R_{A}^{\uparrow }}(X)$与上近似$\overline{R_{A}^{\uparrow }}(X)$分别定义如下:

$\underline{R_{A}^{\uparrow }}(X)=\{x\in U|[x]_{A}^{\uparrow }\subseteq X\}$,

$\overline{R_{A}^{\uparrow}}(X)=\left\{x \in U \mid[x]_{A}^{\uparrow} \cap X \neq \emptyset\right\} $.

定义12 称(U, AT∪ {d})为一个序模糊决策系统, 若(U, AT)为一个序模糊信息系统, 决策属性d∉AT也是一个准则, 由d导出优势关系:

$R_{d}^{\uparrow }=\{(y, x)\in U\times U|d(y)\ge d(x)\}$,

即在决策属性d下, $(y, x)\in R_{d}^{\uparrow }$表示对象y的取值大于或等于对象x的取值.

对象x在d下的决策优势类为:

${[x]_{d}^{\uparrow}=}\{y \in U \mid d(y) \geqslant d(x)\}=\left\{y \in U \mid(y, x) \in R_{d}^{\uparrow}\right\}$,

x∈ U.

记优势关系$R_{d}^{\uparrow }$在U上导出的优势类全体为:

$U / R_{d}^{\uparrow}=\left\{[x]_{d}^{\uparrow} \mid x \in U\right\} $.

定义13 称

$(U, A T)=\left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I_{j}, j=1, 2, \cdots, m\right\}\right) $

为一个广义多尺度模糊信息系统, 若(U, AT)为一个广义多尺度信息系统, 且对于∀ j∈ {1, 2, …, m}与1≤ k≤ I_j, ajk都是模糊属性, 即$a_{j}^{k}: U \longrightarrow V_{j}^{k}$, $V_{j}^{k}$为属性a_j在第k个尺度下的值域, 且$a_{j}^{k}(x) \in[0, 1]$.称

S=(U, AT∪ {d})

为一个广义多尺度模糊决策系统, 若

$ (U, A T)=\left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I_{j}, j=1, 2, \cdots, m\right\}\right)$

为一个广义多尺度模糊信息系统, 决策d∉AT为一个模糊属性, 即d(x)∈ [0, 1], ∀ x∈ U.若属性a_j∈ AT取第l_j个尺度标记, 1≤ l_j≤ I_j, j∈ {1, 2, …, m}, 则称

K=(l₁, l₂, …, l_m)

为S的一个尺度组合.S的所有尺度组合构成的集合:

$ \mathcal{L}=\left\{\left(l_{1}, l_{2}, \cdots, l_{m}\right) \mid 1 \leqslant l_{j} \leqslant I_{j}, j=1, 2, \cdots, m\right\}$.

每个尺度组合

$ K=\left(l_{1}, l_{2}, \cdots, l_{m}\right) \in \mathcal{L}$

对应一个单尺度模糊决策系统S^K,

$ S^{K}= \left(U, A T^{K} \cup\{d\}\right)= \left(U, \left\{a_{1}^{l_{1}}, a_{2}^{l_{2}}, \cdots, a_{m}^{l_{m}}\right\} \cup\{d\}\right)$.

L上粗细关系的定义与定义7相同, 这里不再赘述.

定义14 设

S=(U, AT∪ {d})

为一个广义多尺度模糊决策系统, 若对于

$ K_{0}=(1, 1, \cdots, 1) \in \mathcal{L}$,

$ S^{K_{0}}=\left(U, A T^{K_{0}} \cup\{d\}\right)$

为一个序模糊决策系统, 且对于每个条件属性a_j(j∈ {1, 2, …, m})和每个尺度k∈ {1, 2, …, I_j-1}, 信息粒度变换$g_{j}^{k, k+1}$都是保序的, 则称S为一个广义多尺度序模糊决策系统.

易知在S中, 若

$S^{K_{0}}=\left(U, A T^{K_{0}} \cup\{d\}\right)$

为序模糊决策系统, 且条件属性的粒度变换是保序的, 则对于∀ K∈ L, 对应的模糊决策系统

S^K=(U, AT^K∪ {d})

也是一个序模糊决策系统.

定义15 设

$(U, A T)=\left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I_{j}, j=1, 2, \cdots, m\right\}\right)$

为一个广义多尺度序模糊信息系统, K∈ L, A⊆AT, 由A^K(A^K为尺度组合K在对应属性集A上的限制生成的属性子集)导出优势关系:

$R_{A^{K}}^{\uparrow}=\left\{(y, x) \in U \times U \mid a_{j}^{l_{j}}(y) \geqslant a_{j}^{l_{j}}(x), \forall a_{j}^{l_{j}} \in A^{K}\right\} $,

对象x关于优势关系$R_{{{A}^{K}}}^{\uparrow}$的优势类为:

${[x]_{A^{K}}^{\uparrow}=} \left\{y \in U \mid a_{j}^{l_{j}}(y) \geqslant a_{j}^{l_{j}}(x), \forall a_{j}^{l_{j}} \in A^{K}\right\}= \\ \left\{y \in U \mid(y, x) \in R_{A^{K}}^{\uparrow}\right\} $,

x∈ U.

记优势关系$R_{{{A}^{K}}}^{\uparrow }$在U上导出的优势类全体:

$U / R_{A^{K}}^{\uparrow}=\left\{[x]_{A^{K}}^{\uparrow} \mid x \in U\right\}$.

对于$\forall X \in \mathcal{P}(U)$, 集合X关于$R_{{{A}^{K}}}^{\uparrow }$的下近似$\underline{R_{{{A}^{K}}}^{\uparrow }}(X)$与上近似$\overline{R_{{{A}^{K}}}^{\uparrow }}(X)$分别定义如下:

$\underline{R_{A^{K}}^{\uparrow}}(X)=\left\{x \in U \mid[x]_{A^{K}}^{\uparrow} \subseteq X\right\} $,

$\overline{R_{A^{K}}^{\uparrow}}(X)=\left\{x \in U \mid[x]_{A^{K}}^{\uparrow} \cap X \neq \emptyset\right\}$.

定义16 设

$S=(U, A T \cup\{d\})=\left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I_{j}, j=1, 2, \cdots, m\right\} \cup\{d\}\right) $

为一个广义多尺度序模糊决策系统, 对于∀ x∈ U, y∈ U, 由d导出优势关系:

$R_{d}^{\uparrow}=\{(y, x) \in U \times U \mid d(y) \geqslant d(x)\} $.

对象x在d下的决策优势类:

${[x]_{d}^{\uparrow}=} \{(y, x) \in U \times U \mid d(y) \geqslant d(x)\}= \left\{y \in U \mid(y, x) \in R_{d}^{\uparrow}\right\}$,

x∈ U.

记优势关系$R_{d}^{\uparrow }$在U上导出的优势类的全体为:

$U/R_{d}^{\uparrow }=\{[x]_{d}^{\uparrow }|x\in U\}$.

对于∀ x∈ U, $ K \in \mathcal{L}$ , A⊆AT, $[x]_{d}^{\uparrow }$关于条件属性集A^K的下近似$\underline{R_{{{A}^{K}}}^{\uparrow }}~([x]_{d}^{\uparrow })$与上近似$\overline{R_{{{A}^{K}}}^{\uparrow }}([x]_{d}^{\uparrow })$定义如下:

$\underline{R_{A^{K}}^{\uparrow}}\left([x]_{d}^{\uparrow}\right)=\left\{y \in U \mid[y]_{A^{K}}^{\uparrow} \subseteq[x]_{d}^{\uparrow}\right\}$,

$\overline{R_{A^{K}}^{\uparrow}}\left([x]_{d}^{\uparrow}\right)=\left\{y \in U \mid[y]_{A^{K}}^{\uparrow} \cap[x]_{d}^{\uparrow} \neq \emptyset\right\}$.

命题1 设

$S= (U, A T \cup\{d\})=\left(U, \left\{a_{j}^{k} \mid k=1, 2, \cdots, I_{j}, j=1, 2, \cdots, m\right\} \cup\{d\}\right)$

为一个广义多尺度序模糊决策系统, A⊆AT, $K_{1} \in \mathcal{L}$, $K_{2} \in \mathcal{L}$, 若K₁⪯K₂, 则对于∀ x∈ U, $ X \in \mathcal{P}(U)$, 有

1)$[x]_{{{A}^{{{K}_{1}}}}}^{\uparrow }\subseteq [x]_{{{A}^{{{K}_{2}}}}}^{\uparrow }$,

2)$\underline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}\left( X \right)\subseteq \underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)$.

3)$\overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)\subseteq \overline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}\left( X \right)$.

证明 先证1).对于∀ x∈ U, 由于

$\left[ x \right]_{{{A}^{{{K}_{1}}}}}^{\uparrow }=\{y\in U|a_{j}^{{{K}_{1}}}(y)\ge a_{j}^{{{K}_{1}}}(x), \forall a_{j}^{{{K}_{1}}}\in {{A}^{{{K}_{1}}}}\}$,

$\left[ x \right]_{{{A}^{{{K}_{2}}}}}^{\uparrow }\text{=}\{y\in U|a_{j}^{{{K}_{2}}}(y)\ge a_{j}^{{{K}_{2}}}(x), \forall a_{j}^{{{K}_{2}}}\in {{A}^{{{K}_{2}}}}\}$,

其中$a_{j}^{{{K}_{1}}}$表示属性${{a}_{j}}$在尺度组合K₁取对应尺度得到的属性, 因此, 由K₁⪯K₂及信息粒度变换, 得

$\left\{y \in U \mid a_{j}^{K_{1}}(y) \geqslant a_{j}^{K_{1}}(x), \forall a_{j}^{K_{1}} \in A^{K_{1}}\right\} \subseteq \left\{y \in U \mid a_{j}^{K_{2}}(y) \geqslant a_{j}^{K_{2}}(x), \forall a_{j}^{K_{2}} \in A^{K_{2}}\right\}$,

从而

$[x]_{{{A}^{{{K}_{1}}}}}^{\uparrow }\subseteq [x]_{{{A}^{{{K}_{2}}}}}^{\uparrow }$.

再证2).对于∀ x∈ U, 由结论1) 得

$x\in \underline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}\left( X \right)\Leftrightarrow [x\text{ }\!\!~\!\!\text{ }]_{{{A}^{{{K}_{2}}}}}^{\uparrow }\subseteq X\Rightarrow [x]_{{{A}^{{{K}_{1}}}}}^{\uparrow }\subseteq X\Rightarrow x\in \underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)$,

因此

$\underline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}\left( X \right)\subseteq \underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)$

得证.

最后证3).对于∀ x∈ U, 由结论1) 得

$ x\in \overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)\Leftrightarrow \left[ x \right]_{{{A}^{{{K}_{1}}}}}^{\uparrow }\cap X\ne \emptyset \Rightarrow {[x]_{A^{K_{2}}}^{\uparrow} \cap X \neq \emptyset \Leftrightarrow x \in \overline{R_{A^{K_{2}}}^{\uparrow}}(X)} $,

因此

$\overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)\subseteq \overline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}\left( X \right)$

得证.

证毕.

命题2 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , {{I}_{j}}_{, }j=1, 2, \ldots , m\}\cup \{d\})$

为一个广义多尺度序模糊决策系统, A⊆AT, $ K\in \mathcal{L}$ , $X\in \mathcal{P}(U)$, $Y\in \mathcal{P}(U)$ , 则

1)$\underline{R_{{{A}^{K}}}^{\uparrow }}~(X)\subseteq X\subseteq \overline{R_{{{A}^{K}}}^{\uparrow }}(X)$.

2)$\underline{R_{{{A}^{K}}}^{\uparrow }}\left( \tilde{\ }X \right)=\tilde{\ }\overline{R_{{{A}^{K}}}^{\uparrow }}\left( X \right)$,

$\overline{R_{{{A}^{K}}}^{\uparrow }}\left( \tilde{\ }X \right)=\tilde{\ }\underline{R_{{{A}^{K}}}^{\uparrow }}\left( X \right)$.

3)$\underline{R_{{{A}^{K}}}^{\uparrow }}\left(\emptyset \right)=\overline{R_{{{A}^{K}}}^{\uparrow }}\left(\emptyset \right)= \emptyset $,

$\underline{R_{{{A}^{K}}}^{\uparrow }}\left( U \right)=\overline{R_{{{A}^{K}}}^{\uparrow }}\left( U \right)=U$.

4)$\underline{R_{{{A}^{K}}}^{\uparrow }}\left( X\cap Y \right)=\underline{R_{{{A}^{K}}}^{\uparrow }}\left( X \right)\cap \underline{R_{{{A}^{K}}}^{\uparrow }}\left( Y \right)$,

$\overline{R_{{{A}^{K}}}^{\uparrow }}\left( X\cup Y \right)=\overline{R_{{{A}^{K}}}^{\uparrow }}\left( X \right)\cup \overline{R_{{{A}^{K}}}^{\uparrow }}\left( Y \right)$.

5)$\underline{R_{{{A}^{K}}}^{\uparrow }}\left( X\cup Y \right)\supseteq \underline{R_{{{A}^{K}}}^{\uparrow }}\left( X \right)\cup \underline{R_{{{A}^{K}}}^{\uparrow }}\left( Y \right)$,

$\overline{R_{{{A}^{K}}}^{\uparrow }}\left( X\cap Y \right)\subseteq \overline{R_{{{A}^{K}}}^{\uparrow }}\left( X \right)\cap \overline{R_{{{A}^{K}}}^{\uparrow }}\left( Y \right)$.

6)若X⊆Y, 则

$\underline{R_{{{A}^{K}}}^{\uparrow }}\left( X \right)\subseteq \underline{R_{{{A}^{K}}}^{\uparrow }}\left( Y \right)$,

$\overline{R_{{{A}^{K}}}^{\uparrow }}\left( X \right)\subseteq \overline{R_{{{A}^{K}}}^{\uparrow }}\left( Y \right)$.

证明 类似文献[34], 可直接证明.

命题3 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , I_{j}, j=1, 2, \ldots , m\}\cup \{d\})$

为一个广义多尺度序模糊决策系统, A⊆AT, $ K_{1}\in \mathcal{L}$ , $ K_{2}\in \mathcal{L}$, 若K₁⪯K₂, 则对于∀ x∈ U,

1)$\underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}([x]_{d}^{\uparrow })\subseteq [x]_{d}^{\uparrow }\subseteq \overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}([x]_{d}^{\uparrow })$.

2)$\underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}([x]_{d}^{\uparrow })=\tilde{\ }\overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}(\tilde{\ }[x]_{d}^{\uparrow })$.

3)$\underline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}([x]_{d}^{\uparrow })\subseteq \underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}([x]_{d}^{\uparrow })$,

$\overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}([x]_{d}^{\uparrow })\subseteq \overline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}([x]_{d}^{\uparrow })$.

证明 类似文献[34]与命题2, 可直接证明.

定义17 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , {{I}_{j}}_{, }j=1, 2, \ldots , m\}\cup \{d\})$

为一个广义多尺度序模糊决策系统,

${{K}_{0}}=(1, 1, \ldots , 1)\in \mathcal{L}$.

若$R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }\subseteq R_{d}^{\uparrow }$, 则称S是协调的; 否则, 称S是不协调的.

定理2 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , I_{j}, j=1, 2, \ldots , m\}\cup \{d\})$

为一个协调广义多尺度序模糊决策系统, A⊆AT, $K \in \mathcal{L}$, 对于$\forall X\in \mathcal{P}(U)$, 记

$Bel_{{{A}^{K}}}^{\uparrow }(X)=P\left( \underline{R_{{{A}^{K}}}^{\uparrow }}(X) \right)$,

$Pl_{{{A}^{K}}}^{\uparrow }(X)=P\left( \overline{R_{{{A}^{K}}}^{\uparrow }}(X) \right)$,

则

$Bel_{{{A}^{K}}}^{\uparrow }\, \!:(U)\to [0, 1]$

为U上的信任函数,

$Pl_{{{A}^{K}}}^{\uparrow }\, \!:(U)\to [0, 1]$

为U上的似然函数, 对应的mass函数为:

$m_{{{A}^{K}}}^{\uparrow }(X)=\left\{ \begin{array}{* {35}{l}} \frac{\left| h_{{{A}^{K}}}^{\uparrow }\left( X \right) \right|}{\left| U \right|}, & X\in U/R_{{{A}^{K}}}^{\uparrow }, \\ 0, & X\notin U/R_{{{A}^{K}}}^{\uparrow } \\ \end{array} \right.$

其中

$h_{{{A}^{K}}}^{\uparrow }~(X)=\{x\in U|[x]_{{{A}^{K}}}^{\uparrow }=X\}$.

定理3 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , I_{j}, j=1, 2, \ldots , m\}\cup \{d\})$

为一个协调广义多尺度序模糊决策系统, A⊆AT, $K_{1}\in \mathcal{L}$, $K_{2}\in \mathcal{L}$, $X\in \mathcal{P}(U)$, 若K₁⪯K₂, 则

$Bel_{{{A}^{{{K}_{2}}}}}^{\uparrow }(X)\le Bel_{{{A}^{{{K}_{1}}}}}^{\uparrow }(X)\le \frac{\left| X \right|}{\left| U \right|}\le Pl_{{{A}^{{{K}_{1}}}}}^{\uparrow }(X)\le Pl_{{{A}^{{{K}_{2}}}}}^{\uparrow }(X)$.

证明 由命题1知

$\underline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}\left( X \right)\subseteq \underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)$,

从而

$Bel_{{{A}^{{{K}_{2}}}}}^{\uparrow }(X)=P\left( \underline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}(X) \right)\le P\left( \underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}(X) \right)=Bel_{{{A}^{{{K}_{1}}}}}^{\uparrow }(X)$.

又因为

$\overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)\subseteq \overline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}\left( X \right)$,

于是

$Pl_{{{A}^{{{K}_{1}}}}}^{\uparrow }\left( X \right)=P\left( \overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}(X) \right)\le P\left( \overline{R_{{{A}^{{{K}_{2}}}}}^{\uparrow }}(X) \right)Pl_{{{A}^{{{K}_{2}}}}}^{\uparrow }(X)$.

因为

$\underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)\subseteq X\subseteq \overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}\left( X \right)$,

所以有

$P\left( \underline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}(X) \right)\le P(X)\le P\left( \overline{R_{{{A}^{{{K}_{1}}}}}^{\uparrow }}(X) \right)$.

证毕.

例1表1为一个包含10个对象和4个条件属性的广义多尺度序模糊决策系统

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , I_{j}, j=1, 2, 3, 4\}\cup \{d\})$,

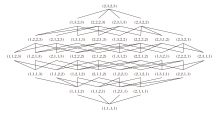
其中, 条件属性a₁和a₃有2个尺度, 条件属性a₂和a₄有3个尺度.每个条件属性在各个尺度标记下的值域均为[0, 1], 全序关系取自然序, 如0.6< 0.8.因此, 系统S共有36个不同的尺度组合, 全体尺度组合形成的格结构如图1所示.

表1

Table 1

表1(Table 1)

表1 广义多尺度序模糊决策系统 Table 1 Generalized multi-scale ordered fuzzy decision system a11 a12 a21 a22 a23 a31 a32 a41 a42 a43 d x1 0.8 1.0 0.5 0.4 0.5 0.6 0.6 0.7 1.0 0.9 0.7 x2 0.2 0.2 0.2 0.2 0.1 0.3 0.2 0.4 0.4 0.5 0.2 x3 0.3 0.2 0.3 0.2 0.1 0.3 0.2 0.4 0.4 0.5 0.4 x4 0.4 0.4 0.5 0.4 0.5 0.3 0.2 0.5 0.4 0.5 0.4 x5 0.8 1.0 0.9 1.0 0.9 1.0 1.0 0.8 1.0 0.9 0.9 x6 0.4 0.4 0.5 0.4 0.5 0.5 0.4 0.5 0.4 0.5 0.7 x7 0.1 0.0 0.1 0.0 0.1 0.2 0.2 0.3 0.2 0.1 0.2 x8 0.8 1.0 0.9 1.0 0.9 0.9 1.0 0.8 1.0 0.9 0.8 x9 0.8 1.0 0.9 1.0 0.9 1.0 1.0 0.8 1.0 0.9 0.9 x10 0.2 0.2 0.2 0.2 0.1 0.3 0.2 0.5 0.4 0.5 0.4

表1 广义多尺度序模糊决策系统 Table 1 Generalized multi-scale ordered fuzzy decision system

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 尺度组合的格结构Fig.1 Lattice structure of scale combinations

不同尺度间的序信息粒度变换如下.当j=1, 2, 3, 4时, 有

$g_{j}^{1, 2}(a_{j}^{1}(x))=\left\{ \begin{array}{* {35}{l}} 0.0, & a_{j}^{1}\left( x \right)\in \left[ 0.0, 0.2 \right) \\ 0.2, & a_{j}^{1}\left( x \right)\in \left[ 0.2, 0.4 \right) \\ 0.4, & a_{j}^{1}\left( x \right)\in \left[ 0, 4, 0.6 \right) \\ 0.6, & a_{j}^{1}\left( x \right)\in \left[ 0.6, 0.7 \right) \\ 1.0, & a_{j}^{1}\left( x \right)\in \left[ 0.7, 1.0 \right] \\ \end{array} \right.$

当j=2, 4时, 有

$g_{j}^{2, 3}\left( a_{j}^{2}\left( x \right) \right)=\left\{ \begin{array}{* {35}{l}} 0.1, & a_{j}^{2}\left( x \right)\in \left[ 0.0, 0.4 \right) \\ 0.5, & a_{j}^{2}\left( x \right)\in \left[ 0.4, 0.8 \right) \\ 0.9, & a_{j}^{2}\left( x \right)\in \left[ 0.8, 1.0 \right] \\ \end{array} \right.$

对于尺度组合K₀=(1, 1, 1, 1), 经计算可得关于决策属性d的优势类:

$[{{x}_{1}}]{{\uparrow }_{d}}=[{{x}_{6}}]_{d}^{\uparrow }=\{{{x}_{1}}, {{x}_{5}}, {{x}_{6}}, {{x}_{8}}, {{x}_{9}}\}$,

$[{{x}_{2}}]_{d}^{\uparrow }=[{{x}_{7}}]_{d}^{\uparrow }=\{{{x}_{1}}, {{x}_{2}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{6}}, {{x}_{7}}, {{x}_{8}}, {{x}_{9}}, {{x}_{10}}\}$,

$[{{x}_{3}}]_{d}^{\uparrow }=[{{x}_{4}}]_{d}^{\uparrow }=[{{x}_{10}}]_{d}^{\uparrow }=\{{{x}_{1}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{6}}, {{x}_{8}}, {{x}_{9}}, {{x}_{10}}\}$,

$[{{x}_{5}}]_{d}^{\uparrow }=[{{x}_{9}}]_{d}^{\uparrow }=\{{{x}_{5}}, {{x}_{9}}\}$,

$[{{x}_{8}}]_{d}^{\uparrow }=\{{{x}_{5}}, {{x}_{8}}, {{x}_{9}}\}$,

则

$\begin{aligned}U / R_{d}^{\uparrow}= & \left\{U, \left\{x_{5}, x_{9}\right\}, \left\{x_{5}, x_{8}, x_{9}\right\}, \right. \\ & \left\{x_{1}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}, x_{10}\right\}, \\ & \left.\left\{x_{1}, x_{5}, x_{6}, x_{8}, x_{9}\right\}\right\} .\end{aligned}$

在尺度组合K₀=(1, 1, 1, 1)下, 关于条件属性$A{{T}^{{{K}_{0}}}}$的优势类为:

$[{{x}_{1}}]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }=\{{{x}_{1}}, {{x}_{5}}, {{x}_{8}}, {{x}_{9}}\}$,

$[{{x}_{2}}]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }=\{{{x}_{1}}, {{x}_{2}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{6}}, {{x}_{8}}, {{x}_{9}}, {{x}_{10}}\}$,

$[{{x}_{3}}]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }=\{{{x}_{1}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{6}}, {{x}_{8}}, {{x}_{9}}\}$,

$[{{x}_{4}}]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }=\{{{x}_{1}}, {{x}_{4}}, {{x}_{5}}, {{x}_{6}}, {{x}_{8}}, {{x}_{9}}\}$,

$\left[ {{x}_{5}} \right]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }\text{=}\left[ {{x}_{9}} \right]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }=\{{{x}_{5}}, {{x}_{9}}\}$,

$[{{x}_{6}}]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }=\{{{x}_{1}}, {{x}_{5}}, {{x}_{6}}, {{x}_{8}}, {{x}_{9}}\}$,

$[{{x}_{7}}]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }=U$,

$[{{x}_{8}}]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }=\{{{x}_{5}}, {{x}_{8}}, {{x}_{9}}\}$,

$[{{x}_{10}}]_{A{{T}^{{{K}_{0}}}}}^{\uparrow }=\{{{x}_{1}}, {{x}_{4}}, {{x}_{5}}, {{x}_{6}}, {{x}_{8}}, {{x}_{9}}, {{x}_{10}}\}$,

则

$\begin{array}{l} U / R_{A T^{K_{0}}}^{\uparrow}= \\ \left\{U, \left\{x_{5}, x_{9}\right\}, \left\{x_{5}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}\right\}\right. \text {, } \\ \left\{x_{1}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}, x_{10}\right\}, \left\{x_{1}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}\right\} \text {, } \\ \left\{x_{1}, x_{5}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{5}, x_{6}, x_{8}, x_{9}\right\} \text {, } \\ \left.\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}, x_{10}\right\}\right\} . \\ \end{array}$

由于$R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }\subseteq R_{d}^{\uparrow }$, 故S是协调的.

定义18 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , I_{j}, j=1, 2, \ldots , m\}\cup \{d\})$

为一个协调广义多尺度序模糊决策系统,

${{K}_{0}}=(1, 1, \ldots , 1), K\in \mathcal{L}$,

则

1)若

$R_{A{{T}^{K}}}^{\uparrow }\subseteq R_{d}^{\uparrow }$,

则称S^K是协调的, 否则, 称S^K是不协调的; 若S^K是协调的, 且对于满足K≺K₁的$\forall K_{1}\in \mathcal{L}$, ${{S}^{{{K}_{1}}}}$是不协调的, 则称K是S的一个最优尺度组合.

2)若对于∀ x∈ U, 都有

$\underline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)=\underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)$,

则称S^K是下近似协调的, 否则, 称S^K不是下近似协调的; 若S^K是下近似协调的, 且对于满足K≺K₁的$\forall K_{1}\in \mathcal{L}$, 存在y∈ U, 使得

$\underline{R_{A{{T}^{{{K}_{1}}}}}^{\uparrow }}\left( \left[ y \right]_{d}^{\uparrow } \right)\ne \underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ y \right]_{d}^{\uparrow } \right)$,

即${{S}^{{{K}_{1}}}}$不是下近似协调的, 则称K是S的一个下近似最优尺度组合.

3)若对于∀ x∈ U, 都有

$\overline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)=\overline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)$,

则称S^K是上近似协调的, 否则, 称S^K不是上近似协调的; 若S^K是上近似协调的, 且对于满足K≺K₁的$\forall K_{1}\in \mathcal{L}$, 存在y∈ U, 使得

$\overline{R_{A{{T}^{{{K}_{1}}}}}^{\uparrow }}\left( \left[ y \right]_{d}^{\uparrow } \right)\ne \overline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ y \right]_{d}^{\uparrow } \right)$,

即 SK1不是上近似协调的, 则称K是S的一个上近似最优尺度组合.

4)若对于∀ x∈ U, 都有

$Bel_{A{{T}^{K}}}^{\uparrow }\left( \left[ x \right]_{d}^{\uparrow } \right)=Be\text{ }\!\!~\!\!\text{ }l_{A{{T}^{{{K}_{0}}}}}^{\uparrow }\left( \left[ x \right]_{d}^{\uparrow } \right)$,

则称S^K是信任协调的, 否则, 称S^K不是信任协调的; 若S^K是信任协调的, 且对于满足K≺K₁的$\forall K_{1}\in \mathcal{L}$, 存在y∈ U, 使得

$Bel_{A{{T}^{{{K}_{1}}}}}^{\uparrow }\left( \left[ y \right]_{d}^{\uparrow } \right)\ne Be\text{ }\!\!~\!\!\text{ }l_{A{{T}^{{{K}_{0}}}}}^{\uparrow }\left( \left[ y \right]_{d}^{\uparrow } \right)$,

即${{S}^{{{K}_{1}}}}$不是信任协调的, 则称K是S的一个信任最优尺度组合.

5)若对于∀ x∈ U, 都有

$Pl_{A{{T}^{K}}}^{\uparrow }\left( \left[ x \right]_{d}^{\uparrow } \right)=P\text{ }\!\!~\!\!\text{ }l_{A{{T}^{{{K}_{0}}}}}^{\uparrow }\left( \left[ x \right]_{d}^{\uparrow } \right)$,

则称S^K是似然协调的, 否则, 称S^K不是似然协调的; 若S^K是似然协调的, 且对于满足K≺K₁的∀ K₁∈ L, 存在y∈ U, 使得

$Pl_{A{{T}^{{{K}_{1}}}}}^{\uparrow }\left( \left[ y \right]_{d}^{\uparrow } \right)\ne P\text{ }\!\!~\!\!\text{ }l_{A{{T}^{{{K}_{0}}}}}^{\uparrow }\left( \left[ y \right]_{d}^{\uparrow } \right)$,

即${{S}^{{{K}_{1}}}}$不是似然协调的, 则称K是S的一个似然最优尺度组合.

定理4 设

$S=(U,AT\cup \{d\})=(\text{U},\{a_{j}^{k}|k=1,2,\ldots ,I_{j},j=1,2,\ldots ,m\}\cup \{d\})$

为一个协调广义多尺度序模糊决策系统,

${{K}_{0}}=(1, 1, \ldots , 1), K\in \mathcal{L}$,

则

1)S^K是下近似协调的当且仅当S^K是信任协调的.

2)K是S的一个下近似最优尺度组合当且仅当K是S的一个信任最优尺度组合.

3)S^K是上近似协调的当且仅当S^K是似然协调的.

4)K是S的一个上近似最优尺度组合当且仅当K是S的一个似然最优尺度组合.

证明 先证1).

必要性(⇒ ).若S^K是下近似协调的, 则对∀ x∈ U, 有

$\underline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)=\underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)$,

从而

$P\left( \underline{R_{A{{T}^{K}}}^{\uparrow }}(\left[ x \right]_{d}^{\uparrow }) \right)=P\left( \underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}(\left[ x \right]_{d}^{\uparrow }) \right)$,

于是

$Bel_{A{{T}^{K}}}^{\uparrow }(\left[ x \right]_{d}^{\uparrow })=Bel_{A{{T}^{{{K}_{0}}}}}^{\uparrow }(\left[ x \right]_{d}^{\uparrow })$,

因此, S^K是信任协调的.

充分性(⇐).若S^K是信任协调的, 则对∀ x∈ U, 有

$Bel_{A{{T}^{K}}}^{\uparrow }(\left[ x \right]_{d}^{\uparrow })=Bel_{A{{T}^{{{K}_{0}}}}}^{\uparrow }(\left[ x \right]_{d}^{\uparrow })$,

即

$\frac{\left| \underline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right) \right|}{\left| U \right|}=\frac{\left| \underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right) \right|}{\left| U \right|}$,

又因为

$\underline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)\subseteq \underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)$,

于是可得

$\underline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)=\underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)$,

因此, S^K是下近似协调的.

再证2).由结论1)可得.

再证3).

必要性(⇒ ).设S^K是上近似协调的, 则对∀ x∈ U, 有

$\overline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)=\overline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)$,

从而

$P\left( \overline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right) \right)=P\left( \overline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right) \right)$,

于是

$Pl_{A{{T}^{K}}}^{\uparrow }\left( \left[ x \right]_{d}^{\uparrow } \right)=P\text{ }\!\!~\!\!\text{ }l_{A{{T}^{{{K}_{0}}}}}^{\uparrow }\left( \left[ x \right]_{d}^{\uparrow } \right)$,

因此, S^K是似然协调的.

充分性(⇐).若S^K是似然协调的, 则对∀ x∈ U, 有

$Pl_{A{{T}^{K}}}^{\uparrow }\left( \left[ x \right]_{d}^{\uparrow } \right)=P\text{ }\!\!~\!\!\text{ }l_{A{{T}^{{{K}_{0}}}}}^{\uparrow }\left( \left[ x \right]_{d}^{\uparrow } \right)$,

即

$\frac{\left| \overline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right) \right|}{\left| U \right|}=\frac{\left| \overline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right) \right|}{\left| U \right|}$,

又因为

$\overline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)\subseteq \overline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)$,

从而

$\overline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)=\overline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)$,

因此, S^K是上近似协调的.

最后证4).由结论3)可得.

证毕.

定理5 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}\text{ }\!\!|\!\!\text{ }k=1, 2, \ldots , {{I}_{j}}_{, }j=1, 2, \ldots , m\}\cup \{d\})$

为一个协调广义多尺度序模糊决策系统, $ K\in \mathcal{L}$, 则S^K是协调的当且仅当S^K是信任协调的.

证明 必要性(⇒ ).设S^K是协调的, 则对∀ x∈ U, 有

$\left[ x \right]_{A{{T}^{K}}}^{\uparrow }\subseteq \left[ x \right]_{d}^{\uparrow }$.

显然

$\underline{R_{A{{T}^{K}}}^{\uparrow }}\left( \left[ x \right]_{d}^{\uparrow } \right)\subseteq \left[ x \right]_{d}^{\uparrow }$

成立.对于$\forall y\in \left[ x \right]_{d}^{\uparrow }$, 由$\left[ x \right]_{d}^{\uparrow }$的定义可知, 有

$\left[ y \right]_{d}^{\uparrow }\subseteq \left[ x \right]_{d}^{\uparrow }$.

由于S^K是协调的, 即

$\left[ y \right]_{A{{T}^{K}}}^{\uparrow }\subseteq \left[ y \right]_{d}^{\uparrow }$,

从而

$\left[ y \right]_{A{{T}^{K}}}^{\uparrow }\subseteq \left[ x \right]_{d}^{\uparrow }$,

即

$y\in \underline{R_{A{{T}^{K}}}^{\uparrow }}(\left[ x \right]_{d}^{\uparrow })$,

故有

$\left[ x \right]_{d}^{\uparrow }\subseteq \underline{R_{A{{T}^{K}}}^{\uparrow }}(\left[ x \right]_{d}^{\uparrow })$,

故证得

$\left[ x \right]_{d}^{\uparrow }=\underline{R_{A{{T}^{K}}}^{\uparrow }}(\left[ x \right]_{d}^{\uparrow })$.

又因为

K₀=(1, 1, 1, 1)

为最细的尺度组合, 因此

[x]ATK0↑⊆[x]ATK↑,

即${{S}^{{{K}_{0}}}}$也是协调的, 从而有

RATK0↑¯([x]d↑)=[x]d↑

成立, 于是

RATK↑¯([x]d↑)=RATK0↑¯([x]d↑),

由定理4知

BelATK↑([x]d↑)=BelATK0↑([x]d↑),

故S^K是信任协调的.

充分性(⇐).反证法.假设S^K是不协调的, 即

RATK↑⊈Rd↑,

则存在y∈ U, 使得

[y]ATK↑⊈[y]d↑.

因为S是协调的, 因此

[y]ATK0↑⊆[y]d↑,

由下近似定义知

y∈RATK0↑¯([y]d↑).

又因为S^K是信任协调的, 由定理4知, 对于∀ x∈ U, 有

RATK↑¯([x]d↑)=RATK0↑¯([x]d↑),

所以有

y∈RATK↑¯([y]d↑),

即

[y]ATK↑⊆[y]d↑,

矛盾.故S^K是协调的. 证毕.

定理6 设

$S=(U,AT\cup \{d\})=(U,\{a_{j}^{k}|k=1,2,\ldots ,I_{j},j=1,2,\ldots ,m\}\cup \{d\})$

为一个协调广义多尺度序模糊决策系统,

${{K}_{0}}=(1, 1, \ldots , 1), K\in \mathcal{L}$,

若S^K是下近似协调的, 则S^K是上近似协调的.

证明 由下近似协调定义和上近似协调定义可证.

定义19 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , {{I}_{j}}_{, }j=1, 2, \ldots , m\}\cup \{d\})$

为一个协调广义多尺度序模糊决策系统, 对于$K\in \mathcal{L}$, S的信任和$B{{M}^{K}}(U/R_{d}^{\uparrow })$与似然和$P{{N}^{K}}(U/R_{d}^{\uparrow })$分别定义如下:

$B{{M}^{K}}(U/R_{d}^{\uparrow })=\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{A{{T}^{K}}}^{\uparrow }(D)$,
$P{{N}^{K}}(U/R_{d}^{\uparrow })=\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Pl_{A{{T}^{K}}}^{\uparrow }(D)$,

其中

U/Rd↑={[x]d↑|x∈U}

为优势关系 Rd↑在U上导出的优势类的全体.

定理7 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , {{I}_{j}}_{, }j=1, 2, \ldots , m\}\cup \{d\})$

为一个协调广义多尺度序模糊决策系统,

${{K}_{0}}=(1, 1, \ldots , 1), K\in \mathcal{L} $,

则

1)S^K是信任协调的当且仅当

$B{{M}^{K}}(U/R_{d}^{\uparrow })=B{{M}^{{{K}_{0}}}}(U/R_{d}^{\uparrow })$.

2)K为S的一个信任最优尺度组合当且仅当

$B{{M}^{K}}(U/R_{d}^{\uparrow })=B{{M}^{{{K}_{0}}}}(U/R_{d}^{\uparrow })$,

且对于满足K≺K₁的$ \forall K_{1}\in \mathcal{L} $, 有

$B{{M}^{{{K}_{1}}}}(U/R_{d}^{\uparrow })< B{{M}^{{{K}_{0}}}}(U/R_{d}^{\uparrow })$.

3)S^K是似然协调的当且仅当

$P{{N}^{K}}(U/R_{d}^{\uparrow })=P{{N}^{{{K}_{0}}}}(U/R_{d}^{\uparrow })$.

4)K为S的一个似然最优尺度组合当且仅当

$P{{N}^{K}}(U/R_{d}^{\uparrow })=P{{N}^{{{K}_{0}}}}(U/R_{d}^{\uparrow })$,

且对于满足K≺K₁的$\forall K_{1}\in \mathcal{L}$, 有

$P{{N}^{{{K}_{1}}}}(U/R_{d}^{\uparrow })> P{{N}^{{{K}_{0}}}}(U/R_{d}^{\uparrow })$.

证明 先证1).由定理5可证.

再证2).由结论1)和定理3可得.

3)、4)的证明与1)、2)类似, 此处略.

例2(续例1) 计算表1中由定义18定义的5种最优尺度组合.由例1知, S是协调的.

1)求S的最优尺度组合.

对于尺度组合K₁=(2, 1, 1, 1), 经计算有

$\begin{array}{l}U / R_{A T^{K_{1}}}^{\uparrow}= \\ \left\{U, \left\{x_{5}, x_{9}\right\}, \left\{x_{5}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}\right\}\right. \text {, } \\ \left\{x_{1}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}, x_{10}\right\}, \left\{x_{1}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}\right\} \text {, } \\ \left\{x_{1}, x_{5}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{5}, x_{6}, x_{8}, x_{9}\right\} \text {, } \\ \left.\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}, x_{10}\right\}\right\}, \\ \end{array} $

易知 RATK1↑⊆Rd↑.

对于尺度组合K₂=(2, 1, 1, 2), 经计算有

$\begin{array}{l} U / R_{A T^{K_{2}}}^{\uparrow}= \\ \left\{U, \left\{x_{5}, x_{9}\right\}, \left\{x_{5}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}\right\}, \right. \\ \left\{x_{1}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{5}, x_{8}, x_{9}\right\}, \\ \left.\left\{x_{1}, x_{5}, x_{6}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}, x_{10}\right\}\right\}, \end{array} $

因此 RATK2↑⊈Rd↑.

对于尺度组合K₃=(2, 1, 2, 1), 经计算有

$\begin{array}{l}U / R_{A T^{K_{3}}}^{\uparrow}= \\\left\{U, \left\{x_{5}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}\right\}, \right. \\ \left\{x_{1}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{5}, x_{8}, x_{9}\right\}, \\ \left.\left\{x_{1}, x_{5}, x_{6}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}, x_{10}\right\}\right\}, \end{array}$

因此 RATK3↑⊈Rd↑.

对于尺度组合K₄=(2, 2, 1, 1), 经计算有

$\begin{array}{l} U / R_{A T^{K_{4}}}^{\uparrow}= \\ \left\{U, \left\{x_{5}, x_{9}\right\}, \left\{x_{5}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{5}, x_{8}, x_{9}\right\}\right. \text {, } \\ \left\{x_{1}, x_{5}, x_{6}, x_{8}, x_{9}\right\}, \left\{x_{1}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}\right\} \text {, } \\ \left.\left\{x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}, x_{8}, x_{9}, x_{10}\right\}\right\}, \\ \end{array}$

因此 RATK4↑⊈Rd↑.

所以K₁=(2, 1, 1, 1)为S的一个最优尺度组合.

2)求S的下近似最优尺度组合.

对于尺度组合K₀=(1, 1, 1, 1), 经计算有

$\underline{R_{A T^{x_{0}}}^{\uparrow}}\left(\left[x_{1}\right]_{d}^{\uparrow}\right)=\underline{R_{A T^{x_{0}}}^{\uparrow}}\left(\left[x_{6}\right]_{d}^{\uparrow}\right)=\left\{x_{1}, x_{5}, x_{6}, x_{8}, x_{9}\right\}$,

$R_{A T^{K_{0}}}^{\uparrow}\left(\left[x_{2}\right]_{d}^{\uparrow}\right)=R_{A T^{K_{0}}}^{\uparrow}\left(\left[x_{7}\right]_{d}^{\dagger}\right)=U$,

$\underline{R_{A T^{K_{0}}}^{\uparrow}}\left(\left[x_{3}\right]_{d}^{\uparrow}\right)=\underline{R_{A T^{K_{0}}}^{\uparrow}}\left(\left[x_{4}\right]_{d}^{\uparrow}\right)=\underline{R_{A T^{K_{0}}}^{\uparrow}}\left(\left[x_{10}\right]_{d}^{\uparrow}\right)=\{{{x}_{1}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{6}}, {{x}_{8}}, {{x}_{9}}, {{x}_{10}}\}$,

$\underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\left( \left[ {{x}_{5}} \right]_{d}^{\uparrow } \right)=\underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}\text{ }\!\!~\!\!\text{ }\left( \left[ {{x}_{9}} \right]_{d}^{\uparrow } \right)=\{{{x}_{5}}, {{x}_{9}}\}$,

$\underline{R_{A{{T}^{{{K}_{0}}}}}^{\uparrow }}([{{x}_{8}}]_{d}^{\uparrow })=\{{{x}_{5}}, {{x}_{8}}, {{x}_{9}}\}$.

对于∀ x∈ U, 当K₁=(2, 1, 1, 1), 经计算可知

RATK1↑¯([x]d↑)=RATK0↑¯([x]d↑)

成立, 所以 SK1是下近似协调的.当K₂=(2, 1, 1, 2), 经计算可知

RATK2↑¯([x10]d↑)≠RATK0↑¯([x10]d↑).

当K₃=(2, 1, 2, 1), 经计算可知

RATK3↑¯([x5]d↑)≠RATK0↑¯([x5]d↑)

且

RATK3↑¯([x10]d↑)≠RATK0↑¯([x10]d↑).

当K₄=(2, 2, 1, 1), 经计算可知

RATK4↑¯([x3]d↑)≠RATK0↑¯([x3]d↑).

所以称K₁=(2, 1, 1, 1)是S的一个下近似最优尺度组合.

3)求S的上近似最优尺度组合.

对于∀ x∈ U, 当K₀=(1, 1, 1, 1), 经计算有

RATK0↑¯([x]d↑)=U.

当K₁=(2, 1, 1, 1), 有

RATK1↑¯([x]d↑)=RATK0↑¯([x]d↑).

当K₂=(2, 1, 1, 2), 有

RATK2↑¯([x]d↑)=RATK0↑¯([x]d↑).

同理可得, 对于K₃₆=(2, 3, 2, 3), 有

RATK36↑¯([x]d↑)=RATK0↑¯([x]d↑),

所以K₃₆=(2, 3, 2, 3)是S的上近似最优尺度组合.由于

RATK2↑¯([x]d↑)=RATK0↑¯([x]d↑),

但

RATK2↑¯([x10]d↑)≠RATK0↑¯([x10]d↑),

故 SK2是上近似协调的, 但不是下近似协调的, 即为定理6的反例.

4)求S的信任最优尺度组合.

当K₀=(1, 1, 1, 1), 经计算有

BMK0(U/Rd↑)=145.

当K₁=(2, 1, 1, 1), 经计算有

BMK1(U/Rd↑)=145.

当K₂=(2, 1, 1, 2), 经计算有

BMK2(U/Rd↑)=2710< 145.

当K₃=(2, 1, 2, 1), 经计算有

BMK3(U/Rd↑)=135< 145.

当K₄=(2, 2, 1, 1), 经计算有

BMK4(U/Rd↑)=2710< 145.

所以称K₁=(2, 1, 1, 1)是S的一个信任最优尺度组合.

5)求S的似然最优尺度组合.

由于S的上近似最优尺度组合为

K₃₆=(2, 3, 2, 3),

只需验证K₃₆即可.

PNK0(U/Rd↑)=1+1+1+1+1=5,
PNK36(URd↑)=1+1+1+1+1=5,

有

PNK36(U/Rd↑)=PNK0(U/Rd↑).

所以K₃₆=(2, 3, 2, 3)是S的似然最优尺度组合.

算法1 一个信任最优尺度组合的逐步搜索算法

输入 一个协调广义多尺度序模糊决策系统

S=(U, AT∪ {d}),

K₀=(1, 1, …, 1),

K_I=(I₁, I₂, …, I_m)

输出S的一个信任最优尺度组合K

初始化K← K_I;

计算各对象的决策优势类$U/R_{d}^{\uparrow }=\{{{D}_{1}}, {{D}_{2}}, \ldots , {{D}_{r}}\}$;

计算尺度组合K下各对象的优势类

$U/R_{A{{T}^{K}}}^{\uparrow }=\{\left[ x \right]_{A{{T}^{K}}}^{\uparrow }|x\in U\}$;

计算最细尺度组合K₀下的信任和B MK0(U/ Rd↑);

for i=1∶ m do

k_i← I_i;

计算尺度组合K下各对象的优势类

U/RATK↑={[x]ATK↑|x∈U};

计算尺度组合K下的信任和$B{{M}^{K}}(U/R_{d}^{\uparrow })$;

while $B{{M}^{K}}(U/R_{d}^{\uparrow })\ne B{{M}^{{{K}_{0}}}}(U/R_{d}^{\uparrow })$ and

k_i≠ 1 do

k_i← k_i-1;

计算尺度组合K下各对象的优势类

U/RATK↑={[x]ATK↑|x∈U};

计算尺度组合K下的信任和$B{{M}^{K}}(U/R_{d}^{\uparrow })$;

end while

end for

return K

算法1是计算一个信任最优尺度组合的逐步搜索算法, 其中计算$U/R_{d}^{\uparrow }$, $U/R_{A{{T}^{K}}}^{\uparrow }$, $B{{M}^{{{K}_{0}}}}(U/R_{d}^{\uparrow })$的时间复杂度为O( |U|2).for语句筛选出一个最优尺度组合, 在最坏的情况下其时间复杂度为

$O\left( 2|U{{|}^{2}}\left( m+\text{ }\!\!~\!\!\text{ }\overset{m}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, {{I}_{i}} \right) \right)$.

所以算法1的时间复杂度为

$O\left( |U{{|}^{2}}\left( m+\text{ }\!\!~\!\!\text{ }\overset{m}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, {{I}_{i}} \right) \right)$.

定义20^[31] 设

S=(U, AT∪ {d})

为一个序决策系统, A⊆AT.

1)若对于$\forall D\in U/R_{d}^{\uparrow }$, 有

BelA↑(D)=BelAT↑(D),

则称A是S的一个信任协调集; 进一步, 若A的真子集都不是S的信任协调集, 则称A是S的一个信任约简.

2)若对于 ∀D∈U/Rd↑, 有

PlA↑(D)=PlAT↑(D),

则称A是S的一个似然协调集; 进一步, 若A的真子集都不是S的似然协调集, 则称A是S的一个似然约简.

定义21 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , {{I}_{j}}_{, }j=1, 2, \ldots , m\}\cup \{d\})$

为一个协调广义多尺度序模糊决策系统, K∈ L, 且K为S的一个最优尺度组合, A⊆AT.

1)若对于 ∀D∈U/Rd↑, 有

BelAK↑(D)=BelATK↑(D),

则称A是S在K下的一个信任协调集; 进一步, 若A的真子集都不是S在K下的信任协调集, 则称A是S在K下的一个信任约简.

2)若对于 ∀D∈U/Rd↑, 有

PlAK↑(D)=PlATK↑(D),

则称A是S在K下的一个似然协调集; 进一步, 若A的真子集都不是S在K下的似然协调集, 则称A是S在K下的一个似然约简.

定义22 设

$S=(U, AT\cup \{d\})=(U, \{a_{j}^{k}|k=1, 2, \ldots , I_{j}, j=1, 2, \ldots , m\}\cup \{d\})$

为一个协调的广义多尺度序模糊决策系统, $K \in \mathcal{L}$, 且K是S的一个最优尺度组合, A⊆AT.

1)若$a_{j}^{{{l}_{j}}}\in {{A}^{K}}$, $a_{j}^{{{l}_{j}}}$在A^K中关于d的内重要度定义为

$si{{g}_{inner}}(a_{j}^{{{l}_{j}}}, {{A}^{K}}, d)=\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{{{A}^{K}}}^{\uparrow }(D)-\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{{{A}^{K}}-\left\{ a_{j}^{{{l}_{j}}} \right\}}^{\uparrow }(D)$.

2)若$a_{j}^{{{l}_{j}}}\in {{A}^{K}}$, ajlj在A^K中关于d的外重要度定义为

$si{{g}_{outer}}(a_{j}^{{{l}_{j}}}, {{A}^{K}}, d)=\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{{{A}^{K}}\cup \left\{ a_{j}^{{{l}_{j}}} \right\}}^{\uparrow }(D)-\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{{{A}^{K}}}^{\uparrow }(D)$.

信任核 COREBelK是信任约简的交集, 包含A^K中所有的必要属性, 可以验证

$COR{{E}_{Be{{l}^{K}}}}=\{a_{j}^{{{l}_{j}}}\in {{A}^{K}}|si{{g}_{inner}}(a_{j}^{{{l}_{j}}}, {{A}^{K}}, d)> 0\}$.

通过增加一些属性, 可扩充为一个信任约简B^K, 直到满足

$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{{{B}^{K}}}^{\uparrow }(D)=B{{M}^{{{K}_{0}}}}(U/R_{d}^{\uparrow })$.

例3(续例2) 已知K₁=(2, 1, 1, 1)为S的一个信任最优尺度组合, 且

BMK1(U/Rd↑)=5+10+8+2+310=145.

1)设

A1K1={a21, a31, a41},

有

$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{A_{1}^{{{K}_{1}}}}^{\uparrow }(D)=\frac{5+10+8+2+3}{10}=\frac{14}{5}$,

故

$si{{g}_{inner}}(a_{1}^{2}, A_{1}^{{{K}_{1}}}, d)=B{{M}^{{{K}_{1}}}}(U/R_{d}^{\uparrow })-\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{A_{1}^{{{K}_{1}}}}^{\uparrow }(D)=-\frac{14}{5}=\frac{14}{5}$.

2)设

A2K1={a12, a31, a41},

有

$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{A_{2}^{{{K}_{1}}}}^{\uparrow }(D)=\frac{5+10+7+2+3}{10}=\frac{27}{10}$,

故

$si{{g}_{inner}}(a_{2}^{1}, A_{2}^{{{K}_{1}}}, d)=B{{M}^{{{K}_{1}}}}(U/R_{d}^{\uparrow })-\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{A_{2}^{{{K}_{1}}}}^{\uparrow }(D)=-\frac{14}{5}=\frac{27}{10}> \frac{1}{10}$.

3)设

A3K1={a12, a21, a41},

有

$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{A_{3}^{{{K}_{1}}}}^{\uparrow }(D)=\frac{4+10+8+3}{10}=\frac{5}{2}$,

故

$si{{g}_{inner}}(a_{3}^{1}, A_{3}^{{{K}_{1}}}, d)=B{{M}^{{{K}_{1}}}}(U/R_{d}^{\uparrow })-\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{A_{3}^{{{K}_{1}}}}^{\uparrow }(D)=\frac{14}{5}-\frac{5}{2}=\frac{3}{10}> 0$.

4)设

A4K1={a12, a21, a31},

有

$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{A_{4}^{{{K}_{1}}}}^{\uparrow }(D)=\frac{5+10+7+2+3}{10}=\frac{27}{10}$,

故

$si{{g}_{inner}}(a_{4}^{1}, A_{4}^{{{K}_{1}}}, d)=B{{M}^{{{K}_{1}}}}(U/R_{d}^{\uparrow })-\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{A_{4}^{{{K}_{1}}}}^{\uparrow }(D)=-\frac{14}{5}=\frac{27}{10}> \frac{1}{10}$.

由上可得S在K₁下的信任核为 {a21, a31, a41}.

设 B1K1={a21, a31}, 有

$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{B_{1}^{{{K}_{1}}}}^{\uparrow }(D)\ne B{{M}^{{{K}_{1}}}}(U/R_{d}^{\uparrow })$.

设 B2K1={a21, a41}, 有

$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{B_{2}^{{{K}_{1}}}}^{\uparrow }(D)\ne B{{M}^{{{K}_{2}}}}(U/R_{d}^{\uparrow })$.

设 B3K1={ a31, a41}, 有

$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{B_{3}^{{{K}_{1}}}}^{\uparrow }(D)\ne B{{M}^{{{K}_{3}}}}(U/R_{d}^{\uparrow })$.

设 B4K1={ a21, a31, a41}, 有

$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{B_{4}^{{{K}_{1}}}}^{\uparrow }(D)=B{{M}^{{{K}_{4}}}}(U/R_{d}^{\uparrow })$.

所以

B4K1={a21, a31, a41}

为一个信任约简.

算法2 基于信任和的属性约简搜索算法

输入 一个协调广义多尺度序模糊决策系统

S=(U, AT∪ {d}),

一个信任最优尺度组合K

输出 约简B

初始化B← Ø ;

计算最优尺度组合K下的信任和$B{{M}^{K}}(U/R_{d}^{\uparrow })$;

$B{{M}_{1}}\leftarrow B{{M}^{K}}(U/R_{d}^{\uparrow })$;

for each a∈ AT^K do

计算a的内重要度sig_inner(a, AT^K, d);

if sig_inner(a, AT^K, d)> 0 then

B← B∪ {a};

end if

end for

计算在B下的信任和$\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{B}^{\uparrow }(D)$;

while $\underset{D\in U/R_{d}^{\uparrow }}{\mathop \sum }\, Bel_{B}^{\uparrow }(D)\ne B{{M}_{1}}$ do

for ∀ b∈ AT^K-B do

计算b的外重要度sig_outer(b, B, d);

end for

找出外重要度最大的属性

$b=\underset{b}{\mathop{\text{arg}}}\, \underset{b\in A{{T}^{K}}-B}{\mathop{\text{max}}}\, \{si{{g}_{outer}}(b, B, d)\}$;

B← B∪ {b};

end while

for ∀ c∈ B do

计算c的内重要度sig_inner(c, B, d);

if sig_inner(c, B, d)=0 then

B← B-{c};

end if

end for

return B

算法2是搜索一个基于信任和的属性约简算法, 计算信任和、内外重要度的时间复杂度均为 O(|U|2).第1组for语句求出条件属性AT^K的所有核属性, 时间复杂度为

O(m(|U|2+1)).

while语句找出条件属性AT^K的协调集, 时间复杂度为

O((m-1)(m|U|2+m-1)).

第2组for语句删除协调集中的冗余属性, 时间复杂度为

O(m(|U|2+1)).

所以算法2 的时间复杂度为

$O({{m}^{2}}(|U{{|}^{2}}+1))$.

为了验证本文算法的可行性与有效性, 从UCI数据库中选取8个数据集进行实验分析, 数据集的详细信息如表2所示.

表2

Table 2

表2(Table 2)

表2 实验数据集信息 Table 2 Description of experimental datasets 名称 简称 样本数 特征数 类数 Iranian Churn IC 3150 13 2 Darwin DN 174 451 2 NHANES Age Prediction Subset HAPS 6287 7 2 Rice (Cammeo and Osmancik) RCO 3810 7 2 Spambase SE 4601 57 2 Vertebral Column(2C) VCC 310 6 2 Wine Quality(Red) WQR 1599 11 6 Wine Quality(White) WQW 4898 11 7

表2 实验数据集信息 Table 2 Description of experimental datasets

实验采用的硬件配置为13th Gen Intel(R) Core(TM) i5-13500H@2.60 GHz和16 GB内存的PC, 操作系统为 Windows 11, 软件为PyCharm Community Edition 2023.2.5.

由于协调广义多尺度序模糊决策系统不能从UCI数据库上直接获得, 需对数据进行预处理, 具体步骤如下.

1)数据标准化.采用min-max法将原始数据集标准化, 对于任意条件属性a∈ AT, 对象x的条件属性值标准化后为a'(x), 即

a'(x)=a(x)-aminamax-amin,

其中a_max、a_min分别为条件属性a的值域中的最大值与最小值.

对于决策属性d, 对象x的决策属性值标准化后得

d'(x)=d(x)-dmindmax-dmin,

其中d_max、d_min分别为决策属性d的值域中的最大值与最小值.

2)相关性分析.采用皮尔逊相关性分析法判断条件属性a∈ AT与决策属性d的相关性, 其相关系数

$\hat{r}=\frac{\mathop{\sum }_{x}\left( a\left( x \right)-\bar{a} \right)\left( d\left( x \right)-\bar{d} \right)}{\sqrt{\mathop{\sum }_{x}{{(a\left( x \right)-\bar{a}\ )}^{2}}}\ \ \sqrt{\mathop{\sum }_{x}{{(d\left( x \right)-\bar{d}\ )}^{2}}}\ }$,

其中, a-表示所有对象在a上条件属性值的平均值, d-表示所有对象在d上决策属性值的平均值.易知, $\hat{r}\in [-1, 1]$为满足

$[x]_{a}^{\uparrow }\subseteq [x]_{d}^{\uparrow }$,

系统的条件属性与决策属性需具有正相关性, 故把对象条件属性值重新赋值, 即

${{a}^{* }}(x)=\left\{ \begin{array}{* {35}{l}} 1-a'\left( x \right), & \hat{r}\in \left[ -1, 0 \right) \\ a'\left( x \right), & \hat{r}\in \left[ 0, 1 \right] \\ \end{array} \right.$

3)删除异常值.设决策属性d的优势类矩阵

$M_{D}^{\uparrow }={{[{{p}_{ij}}]}_{n\times n}}$,

其中

${{p}_{ij}}=\left\{ \begin{array}{* {35}{l}} 1, & d\left( {{x}_{j}} \right)\ge d\left( {{x}_{i}} \right) \\ 0, & d\left( {{x}_{j}} \right)< d\left( {{x}_{i}} \right) \\ \end{array} \right.$

设条件属性a∈ AT的优势类矩阵

$M_{a}^{\uparrow }={{[{{t}_{ij}}]}_{n\times n}}$,

其中

${{t}_{ij}}=\left\{ \begin{array}{* {35}{l}} 1, & a\left( {{x}_{j}} \right)\ge a\left( {{x}_{i}} \right) \\ 0, & a\left( {{x}_{j}} \right)< a\left( {{x}_{i}} \right) \\ \end{array} \right.$

则AT的优势类矩阵

$M_{AT}^{\uparrow }=\underset{a\in AT}{\mathop{\wedge }}\, M_{a}^{\uparrow }={{[{{q}_{ij}}]}_{n\times n}}$,

其中

${{q}_{ij}}=\underset{a\in AT}{\mathop{\wedge }}\, {{t}_{ij}}$.

那么, 给定i∈ {1, 2, …, n}, [p_ij]_{1× n}反映x_i关于d的优势类, [q_ij]_{1× n}反映x_i关于AT的优势类.令

M=MD↑-MAT↑=[oij]n×n.

若 [oij]1×n的所有分量都为0或1, 则说明

[xi]AT↑⊆[xi]d↑.

若 [oij]1×n至少存在一个分量o_ij'=-1, 则说明x_i关于d优于x_j', 但x_j'关于AT优于x_i, 即

[xi]AT↑⊈[xi]d↑.

为了保证系统的协调性, 在数据集中删去x_i, 同时也需要删除 MD↑与 MAT↑的第i行和第i列.预处理后数据集删除对象个数如表3所示.

表3

Table 3

表3(Table 3)

表3 预处理后数据集删除对象个数 Table 3 Number of deleted objects in preprocessed datasets 数据集 IC DN HAPS RCO SE VCC WQR WQW 对象个数 307 0 0 645 34 40 259 961

表3 预处理后数据集删除对象个数 Table 3 Number of deleted objects in preprocessed datasets

4)生成多尺度.对于任意条件属性a_j∈ AT, 其尺度标记构造方法如下.

(1)将对象x∈ U在a_j的第1个尺度标记下的属性值记为 aj* (x), 即

aj1(x)=aj* (x),

此时

Vj1={aj* (x)|x∈U}.

若$\left| V_{j}^{1} \right|\le 3$, 则完成构造; 否则跳转(2).

(2)将全体对象在a_j的第1个尺度标记下的属性值从小到大排序后, 将其分成十等份.然后从每份中取出最大的属性值, 构成集合 Vj2, Vj2为a_j在第2个尺度标记下的属性值域.为了方便叙述, 记

Vj2={vj, w2|w=1, 2, …, Wj2}, Wj2≤10,

其中对于 ∀w∈{1, 2, …, Wj2-1}, 有

vj, w2< vj, w+12.

对于x∈ U和 w∈{1, 2, …, Wj2-1}, 有

aj2(x)=gj1, 2(aj1(x))=vj, w+12,

$a_{j}^{1}(x)\in (v_{j, w}^{2}, v_{j, w+1}^{2}]$.

若$\left| V_{j}^{2} \right|\le 3$, 则完成构造; 否则, 令k=3, 跳转(3).

(3)若 Wjk-1为偶数, 则

Vjk={vj, wk|w=1, 2, …, Wjk},

其中

Wjk=Wjk-12, vj, wk=vj, 2wk-1.

若 Wjk-1为奇数, 则

Vjk={vj, wk|w=1, 2, …, Wjk},

其中

Wjk=Wjk-1-12+1.

当 w∈{1, 2, …, Wjk-1}时,

vj, wk=vj, 2wk-1;

当 w=Wjk时,

vj, w3=vj, Wjk-12.

若$\left| V_{j}^{k} \right|\le 3$, 则完成构造; 否则, 令k=k+1, 跳转(3).

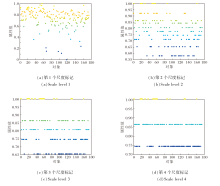
通过上述步骤, 完成协调广义多尺度序模糊决策系统的构造, 其中每个属性的尺度标记不超过4.下面以DN数据集上属性mean_gmrt1为例, 给出属性mean_gmrt1在不同尺度标记下每个对象的属性值的分布情况, 具体如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 在4个尺度标记下的属性值分布图Fig.2 Distribution of attribute values under 4 scale levels

为了验证本文算法的有效性, 首先设置随机种子为56, 将所有对象随机排列.再采用K-近邻(K Nearest Neighbor, KNN)和朴素贝叶斯(Naive Bayes, NB)分类器, 通过十折交叉验证法进行分类性能评估.

本文仅对算法1和算法2得到的信任最优尺度组合(简记为Bel-Op)、信任最优尺度下的约简(简记为Bel-Re)与最细尺度组合(简记为Fin)在分类器上的分类精度进行对比, 具体如表4和表5所示, 表中黑体数字表示最优值.

表4

Table 4

表4(Table 4)

表4 在KNN分类器(K=3)上的分类精度对比 Table 4 Comparison of classification accuracy on KNN classifier(K=3) % 数据集 组合 1折 2折 3折 4折 5折 6折 7折 8折 9折 10折 平均精度 Fin 99.30 98.95 99.65 99.30 100.00 99.30 100.00 98.59 99.30 100.00 99.44± 0.45 IC Bel-Op 99.30 99.65 99.65 100.00 100.00 99.30 99.65 98.24 99.65 100.00 99.54± 0.50 Bel-Re 99.65 99.65 100.00 99.65 100.00 100.00 100.00 98.59 100.00 100.00 99.75± 0.42 Fin 50.00 66.67 61.11 77.78 82.35 82.35 100.00 94.12 47.06 94.12 75.56± 17.71 DN Bel-Op 44.44 61.11 55.56 66.67 94.12 64.71 100.00 76.47 58.82 94.12 71.60± 17.84 Bel-Re 83.33 83.33 66.67 66.67 70.59 76.47 88.24 82.35 76.47 88.24 78.24± 7.75 Fin 96.05 93.86 96.93 95.61 95.18 94.74 95.61 96.93 93.39 94.27 95.26± 1.15 HAPS Bel-Op 96.49 99.12 96.49 98.25 95.18 98.25 95.18 97.81 97.36 93.83 96.79± 1.59 Bel-Re 100.00 100.00 100.00 100.00 100.00 100.00 100.00 100.00 100.00 100.00 100.00± 0.00 Fin 98.42 98.11 95.90 98.74 98.74 98.73 98.73 97.15 97.47 96.84 97.88± 0.95 RCO Bel-Op 98.74 98.11 97.16 99.05 98.42 98.73 98.42 97.78 97.15 96.20 97.98± 0.85 Bel-Re 98.42 98.11 97.16 98.42 99.05 98.73 98.42 97.47 97.47 96.52 97.98± 0.75 Fin 91.47 91.03 90.81 92.56 91.68 92.56 93.22 91.89 91.89 91.23 91.83± 0.72 SE Bel-Op 91.03 91.47 92.12 90.59 91.03 92.34 91.90 94.74 93.64 92.54 92.14± 1.21 Bel-Re 91.68 92.34 92.34 90.81 91.25 93.22 91.25 94.08 93.42 92.98 92.34± 1.03 Fin 85.19 88.89 100.00 96.30 88.89 85.19 92.59 77.78 92.59 100.00 90.74± 6.68 VCC Bel-Op 92.59 96.30 100.00 96.30 92.59 81.48 88.89 85.19 96.30 96.30 92.59± 5.49 Bel-Re 85.19 96.30 100.00 96.30 92.59 85.19 88.89 85.19 96.30 100.00 92.59± 5.74 Fin 53.73 62.69 64.18 56.72 59.70 55.22 60.45 58.96 59.70 56.72 58.81± 3.09 WQR Bel-Op 53.73 62.69 64.18 56.72 59.70 55.22 60.45 58.96 59.70 56.72 58.81± 3.09 Bel-Re 53.73 62.69 64.18 56.72 59.70 55.22 60.45 58.96 59.70 56.72 58.81± 3.09 Fin 64.21 57.36 60.15 57.11 61.17 55.58 59.90 60.31 60.05 59.29 59.51± 2.29 WQW Bel-Op 64.21 57.36 60.15 57.11 61.17 55.58 59.90 60.31 60.05 59.29 59.51± 2.29 Bel-Re 64.21 57.36 60.15 57.11 61.17 55.58 59.90 60.31 60.05 59.29 59.51± 2.29

表4 在KNN分类器(K=3)上的分类精度对比 Table 4 Comparison of classification accuracy on KNN classifier(K=3) %

表5

Table 5

表5(Table 5)

表5 在NB分类器上的分类精度对比 Table 5 Comparison of classification accuracy on NB classifier % 数据集 组合 1折 2折 3折 4折 5折 6折 7折 8折 9折 10折 平均精度 Fin 90.18 81.40 82.81 76.06 75.70 81.34 88.38 80.99 78.52 83.45 81.88± 4.46 IC Bel-Op 94.04 88.42 91.23 85.92 87.32 91.55 92.61 85.21 87.32 90.14 89.38± 2.82 Bel-Re 99.30 98.95 98.60 97.89 98.94 98.94 99.30 97.89 99.30 99.65 98.87± 0.56 Fin 94.44 66.67 88.89 83.33 70.59 82.35 88.24 76.47 82.35 88.24 82.16± 8.23 DN Bel-Op 94.44 94.44 94.44 88.89 70.59 76.47 88.24 88.24 94.12 82.35 87.22± 7.90 Bel-Re 72.22 83.33 83.33 66.67 70.59 88.24 82.35 94.12 94.12 76.47 81.14± 9.06 Fin 96.49 95.61 97.37 96.93 96.05 96.93 95.18 96.49 96.04 93.83 96.09± 0.98 HAPS Bel-Op 96.05 83.33 82.02 85.96 85.96 85.53 84.21 83.77 85.02 83.70 85.56± 3.70 Bel-Re 99.56 99.12 99.12 99.56 97.37 99.56 99.12 99.12 98.68 98.68 98.99± 0.62 Fin 94.95 95.27 96.85 96.85 97.48 96.52 97.78 97.47 98.10 93.99 96.52± 1.29 RCO Bel-Op 94.32 92.11 94.95 94.95 96.85 93.99 94.94 95.89 97.15 92.41 94.76± 1.57 Bel-Re 95.27 94.32 96.53 96.85 96.21 95.25 97.15 96.84 98.10 93.99 96.05± 1.24 Fin 79.43 82.49 82.93 80.31 80.96 82.49 87.09 82.02 79.61 83.77 82.11± 2.16 SE Bel-Op 82.28 80.74 82.49 82.49 81.40 82.28 82.06 81.58 80.92 83.11 81.94± 0.72 Bel-Re 80.74 78.77 82.28 81.62 81.40 81.40 81.40 80.26 78.95 80.70 80.75± 1.08 Fin 88.89 88.89 96.30 81.48 77.78 74.07 85.19 88.89 85.19 81.48 84.81± 6.07 VCC Bel-Op 85.19 88.89 96.30 81.48 77.78 77.78 85.19 88.89 88.89 85.19 85.56± 5.35 Bel-Re 85.19 88.89 100.00 88.89 77.78 77.78 85.19 85.19 88.89 88.89 86.67± 6.02 Fin 55.97 52.24 50.75 57.46 61.94 59.70 64.18 56.72 46.27 55.97 56.12± 5.05 WQR Bel-Op 55.97 52.24 50.75 57.46 61.94 59.70 64.18 56.72 46.27 55.97 56.12± 5.05 Bel-Re 55.97 52.24 50.75 57.46 61.94 59.70 64.18 56.72 46.27 55.97 56.12± 5.05 Fin 52.28 47.21 52.28 48.22 54.06 46.45 53.55 44.78 46.82 50.89 49.66± 3.16 WQW Bel-Op 52.28 47.21 52.28 48.22 54.06 46.45 53.55 44.78 46.82 50.89 49.66± 3.16 Bel-Re 52.28 47.21 52.28 48.22 54.06 46.45 53.55 44.78 46.82 50.89 49.66± 3.16

表5 在NB分类器上的分类精度对比 Table 5 Comparison of classification accuracy on NB classifier %

由表4可见, 在5个数据集上信任最优尺度组合下的分类精度均高于最细尺度组合下的分类精度, 而在2个数据集上信任最优尺度组合下的分类精度与最细尺度组合下的分类精度相等.类似地, 在表5中也可得到类似结果.在信任最优尺度组合下搜索属性约简时, 大部分数据集在约简下的分类精度均高于或等于在最优尺度组合下的分类精度.这说明本文提出的约简是适用于后续规则提取的.综上所述, 本文算法是有效的.

多尺度数据分析是多粒度粗糙集数据分析的一个重要研究方向.本文讨论协调广义多尺度序模糊决策系统的最优尺度组合与属性约简问题, 处理的数据类型为条件属性和决策属性都是模糊属性并且属性值域具有优序关系, 从细尺度属性值域到粗尺度属性值域存在保序的粒度变换.由于最优尺度组合选择是广义多尺度数据知识获取的一个关键步骤, 因此, 本文定义协调广义多尺度序模糊决策系统的5种最优尺度组合的概念, 验证信任最优尺度组合与下近似最优尺度组合是等价的、似然最优尺度组合与上近似最优尺度组合是等价的, 给出计算一个信任最优尺度组合的逐步搜索算法和基于信任和的属性约简搜索算法, 在UCI数据集上的实验验证本文算法的可行性和有效性.在后续的研究中, 一方面在算法上可将最优尺度组合与属性约简的过程同步进行, 另一方面可应用到动态更新的系统中, 在增加对象或属性时进行最优尺度选择和属性约简.

本文责任编委 苗夺谦

Recommended by Associate Editor MIAO Duoqian