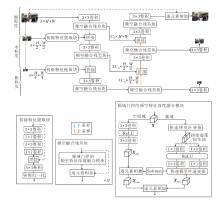
本文提出深度融合频域和空间域特征的多粒度动态场景图像去模糊网络, 整体结构如图1所示.主干网络采用编码器-解码器架构.对于运动场景, 提取单一粒度的特征不能较好处理不同尺度的模糊现象.因此, 本文网络采用从粗到细的方案, 分为粗粒度、中粒度和细粒度这3个粒度级别进行去模糊任务的分层处理.${{X}_{crs}}\in {{\text{R}}^{4{{\text{C}}_{fn}}\times \frac{\text{H}}{4}\times \frac{\text{W}}{4}}}$表示粗粒度阶段特征图, ${{X}_{med}}\in {{\text{R}}^{2{{\text{C}}_{fn}}\times \frac{\text{H}}{2}\times \frac{\text{W}}{2}}}$表示中粒度阶段特征图, ${{X}_{fn}}\in {{\text{R}}^{{{\text{C}}_{fn}}\times H\times W}}$表示细粒度阶段特征图, C_fn表示细粒度阶段特征图的通道数.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 本文网络结构Fig.1 Architecture of the proposed network

在每个粒度阶段, 首先, 需要将输入图像转换为特征, 细粒度阶段通过单独的3× 3卷积完成, 而中粒度及粗粒度阶段则是由初级特征提取块(Primary Feature Extraction Block, PFEB)实现.然后, 编码器融合当前粒度和更细粒度的特征, 获得更抽象和高级的表示.解码器利用跳跃连接, 在当前粒度编码特征的基础上补充更粗粒度的解码特征, 恢复清晰图像的相关特征.最后, 由单层的3× 3卷积压缩解码特征图, 重建清晰图像.

PFEB从经过原始输入图像下采样后的图像I∈ R^{3× H× W}中提取初级特征X_p∈ R^{C× H× W}.为了保证效率, 首先, 通过堆叠2个3× 3卷积和1× 1卷积进行浅层的特征提取, 同时扩张通道数, 得到的中间特征通道数X_m∈ R^{(C-3)× H× W}.然后, 将中间特征与输入图像拼接, 使通道数变为C× H× W, 保证特征通道数在后续处理中的一致性.最后, 使用3× 3卷积细化连接后的特征, 并利用实例归一化调整特征值的取值范围.PFEB将不同粒度的输入图像与上一粒度的特征图对齐, 减少图像和特征之间的语义差异, 保证在去模糊任务中多粒度特征的有效传递.

每个粒度阶段的编码器和解码器均由一个频空融合残差块(Frequency-Spatial Fusion Residual Block, FSF-ResBlock)构成.FSF-ResBlock由FGFM及跳跃连接堆叠N层组成.对于输入特征图X∈ R^{C× H× W}, 第i个FGFM的输出为:

$X_{\text{FSFR}}^{i}=\left\{ \begin{array}{* {35}{l}} X+FGFM\left( X \right), & i=1 \\ X\text{ }\!\!~\!\!\text{ }_{\text{FSFR}}^{i-1}+FGFM\left( X\text{ }\!\!~\!\!\text{ }_{\text{FSFR}}^{i-1} \right), & i=2, 3, \ldots , N \\ \end{array} \right.$

其中+表示逐元素相加操作.最终得到输出:

${{X}_{FSFR}}=X_{FSFR}^{N}\in {{R}^{C}}^{\times H\times W}$.

FSF-ResBlock利用FGFM融合频域和空间域之间的特征, 确保特征表示的全面性, 同时通过跳跃连接机制增强特征传递的稳定性, 使去模糊效果更优.

采用多粒度的网络结构, 能减少单粒度特征提取而导致的信息丢失, 利用感受野更大、语义性更强的粗粒度信息和中粒度信息, 助力细粒度特征的学习,

从而生成全面的多粒度特征, 实现更精细的去模糊效果.

傅里叶变换是一种常用的频域变换工具, 可将时间域上的信号转换到频率域进行处理.对于图像而言, 使用实数形式的二维离散傅里叶变换相当于将信息从空间域变换到频域, 该过程的数学形式如下:

$F(a, b)=\overset{H-1}{\mathop{\underset{x=0}{\mathop \sum }\, }}\, \overset{W-1}{\mathop{\underset{y=0}{\mathop \sum }\, }}\, f(x, y)\left[ \cos \left( 2\pi \left( \frac{ax}{H}+\frac{by}{W} \right) \right)-\sin \left( 2\pi \left( \frac{ax}{H}+\frac{by}{W} \right) \right)i \right]$, (1)

其中, H、W表示图像的高和宽, (x, y)表示空间坐标, f(x, y)表示对应位置的像素值, (a, b)表示频域坐标, i表示虚数单位.傅里叶变换后的结果F(a, b)值为复数, 可表示相应频率分量的幅度和相位.

频域特征图中的某一点并不对应于二维图像中该位置的像素, 而是整幅图像的所有像素对于该频率的响应.因此, 傅里叶变换能从整体上分析图像特性, 具有全局性的感受野.从频域角度出发处理图像, 可揭示不同频率的分布和特征, 而不仅仅局限于像素级的信息.

为了解决CNN感受野受限的问题, 本文基于傅里叶变换, 补充频域特征, 扩大感受野范围, 提出频域门控的频空特征深度融合模块(FGFM), 帮助网络整合全局频域特征和局部空间域特征, 生成高质量的特征表示.FGFM主要涉及两个分支, 对于输入特征图同步提取空间域和频域的模糊特征, 两个分支分别关注局部信息和全局信息.频域分支的结果反向作用于空间域, 以增强空间域分支对全局的感知能力和特征融合效果.

空间域分支应用2个3× 3卷积, 在当前粒度级别对输入特征图进行进一步的特征提取, 中间增加ReLU激活函数, 用于提高特征的表达能力.卷积核的大小固定, 通道数保持不变, 保持较低的参数量及计算量.对于输入的多通道特征图X∈ R^{C× H× W}, 输出的空间域特征:

X_spat=Conv_{3× 3}(ReLU(Conv_{3× 3}(X)))∈ R^{C× H× W}.

不同运动目标之间的运动模式各不相同, 导致局部范围内的模糊方向和程度表现出多样性.利用局部感知的卷积获取短距离特征, 满足对于不同运动目标进行小范围处理的需求, 能对细节结构进行精细复原.然而, 传统的卷积操作受限于其局部感受野, 仅能考虑相邻像素的信息, 这限制其对远距离像素之间依赖关系的建模能力.因此, 引入频域分支, 从全局特征提取的角度弥补空间域分支的不足.

首先利用傅里叶变换将特征图转换到频域, 然后通过2次1× 1逐点卷积学习平滑变化结构的低频分量与快速变化细节的高频分量之间的关联, 中间辅以ReLU函数进行激活, 实现特定阈值频率成分的选择, 最后通过逆变换将频域特征转换到原始的空间域, 实现对特征的频率域处理和空间域重建的结合.对于相同的输入特征图X∈ R^{C× H× W}, 输出的频域特征:

${{X}_{freq}}=iFFT(Con{{v}_{1}}_{\times 1}(ReLU(Con{{v}_{1}}_{\times 1}(FFT(X)))))\in {{R}^{C\times }}{{^{H}}^{\times W}}$

其中, FFT(· )表示实数信号的二维离散快速傅里叶变换, iFFT(· )表示其逆变换.

目前引入频域的去模糊算法^{[17, 18]}通常直接将两域特征进行相加处理, 这种简单的融合方式导致两个分支完全独立, 忽略不同域信息之间潜在的相关性.与上述方法不同, 本文从探索频域和空间域特征相关性的角度出发, 提出频域门控, 利用全局频域信息控制空间域的学习.频域分支在特征提取时, 分离一个并行的门控分支, 用于约束空间域特征, 改善空间域的信息流.门控分支的结构基于原本的频域分支, 在获得经过频域处理的所有位置像素的状态后, 使用Softmax函数判定是否允许相关特征向网络深层流动, 让学到的空间域特征具有全局意识.获取门控结果的过程如下:

X_gate=Softmax(iFFT(Conv_{1× 1}(ReLU(Conv_{1× 1}(FFT(X))))))∈ R^{C× H× W}.

门控结果作用于空间分支, 进行逐元素相乘, 并与频域特征结合, 可得到FGFM的最终输出:

$Y={{X}_{gate}}\otimes {{X}_{spat}}+{{X}_{freq}}\in {{R}^{C}}^{\times H\times W}$,

其中$\otimes$表示逐元素相乘操作.

局部的空间内容与全局的频率内容叠加混合, 这种后期融合方式实现特征提取上的补充效果.该融合方式利用频域门控对空间域特征进行限制, 考虑两域特征之间的相关性, 减少在互补特征中存在的潜在冗余, 实现特征的深度融合.在频域上计算门控单元, 允许网络以全局视野查询每个像素点的重要性, 将基于卷积的空间域门控推广到全局, 网络能根据全局频域信息动态调整空间域特征的学习过程.总之, FGFM有机结合不同域的特征, 善用空间域的精准细化和频域的整体内容感知, 允许网络在考虑全局上下文的同时关注特征图的精细属性, 有效扩大感受野范围, 提升对全局特征和局部特征的融合能力, 改善网络性能, 生成高质量的复原结果.

考虑到实际拍摄的模糊图像分辨率往往远高于模型训练时使用的补丁大小, 因此, 在对高分辨率的模糊图像进行测试时, 不仅成倍增加显存的负担, 还会由于整幅图像和裁剪的补丁图像之间尺寸不一致, 导致训练和测试时频域特征图不匹配^[26], 从而对去模糊任务性能产生负面影响.具体地, 将式(1)的正弦函数及余弦函数的加权和, 通过欧拉公式转换为如下形式:

$\cos \left( 2\pi \left( \frac{ax}{W}+\frac{by}{H} \right) \right)-\sin \left( 2\pi \left( \frac{ax}{W}+\frac{by}{H} \right) \right)\text{i}=\exp \left( -\text{i}2\pi \left( \frac{ax}{W}+\frac{by}{H} \right) \right)$.

在将特征图f(x, y)映射为频谱图F(a, b)时, 水平频率a或垂直频率b每增加1个单位, 增加的频率绝对值为2π /W或2π /H, 即频谱图相邻点的频率分辨率差异由输入特征图尺寸H、W决定.因此, 将从固定大小裁剪补丁上训练学到的频域分支模型权重在测试阶段直接应用于高分辨率图像并不合适.

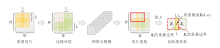
为了解决这个问题, 本文采用频域分辨率自适应的测试策略, 对于测试时输入的高分辨率图像进行预处理及后处理, 具体流程如图2所示.在预处理阶段, 首先对图像进行重叠切片.以GoPro测试集为例, 图像分辨率均为1280× 720, 以256× 256的滑动窗口按照从左到右、从上到下的移动方向在特征图上滑动, 其中滑动步长设置为224, 实现32像素的重叠区域, 并按照以往的切片策略^[23]对边缘部分进行补偿.最终可得到24幅尺寸为256× 256的带有重叠区域的图像块, 实现频率分辨率的统一, 网络不再受到原始输入图像尺寸的影响, 同时降低边界处的不连续性, 减少边界伪影的产生.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 频域分辨率自适应的测试策略流程图Fig.2 Flowchart of frequency domain resolution adaptive testing strategy

在后处理阶段, 需要对经过网络去模糊的图像切片进行重构.受到地理信息系统中反距离加权的启发, 对于重叠部分, 认为重叠点距离另一重叠切片的重叠边界越近, 表示距离本切片的重叠边界越远, 也就是处于本切片越中心的位置, 因此, 能访问的相邻像素越多, 信息越准确, 对该点的影响力也越大, 切片结果的权重也越大.基于这种观点, 对于重叠区域的像素进行加权赋值时, 使距离另一切片重叠边界更远的像素对重构结果具有更大的权重, 产生更显著的影响.以图2中水平方向的一个重叠区域为例, 原始特征图中位于(h, w)处的重叠像素为:

$X(h, w)=\overset{{{n}_{o}}}{\mathop{\underset{i=1}{\mathop \sum }\, }}\, \left( 1-\frac{{{l}_{i}}}{{{l}_{o}}} \right){{N}_{h}}_{, w}({{X}_{i}})$,

其中, n_o表示切片后该像素的重叠次数, l_i表示第i切片的重叠像素与另一重叠切片边界的距离, l_o表示重叠区域的长度, N_{h, w}表示网络对于重叠像素的输出, X_i表示第i张切片.

相比切片不考虑重叠部分^[23]或对重叠部分重构时取平均值^[24]等其它测试策略, 频域分辨率自适应的测试策略使网络的鲁棒性进一步提高, 可有效利用重叠区域的信息, 提高处理边界和过渡区域的准确性和稳健性, 并有助于保持图像整体的一致性和连续性.

本文网络在训练过程中的损失函数由主要的像素损失及两个辅助损失组成, 共同监督网络学习模糊与清晰图像之间的映射关系, 实现高质量的去模糊效果.

对于图像去模糊, 像素损失是为了评估清晰图像与复原图像间的像素级差异, 本文采用Char-bonnier损失, 添加正则项, 可比L1损失更稳定, 其表达式如下:

${{L}_{char}}=\sqrt{\|{{I}_{S}}-{{I}_{R}}{{\|}^{2}}+{{\varepsilon }^{2}}}$.

其中, I_S表示清晰图像, I_R表示复原的去模糊图像, 常数ε =0.001.

为了提高复原图像的细节表现, 使复原图像在视觉感知上的效果更优, 还使用边缘损失指导网络生成的复原图像向清晰图像的结构逐渐逼近, 其表达式如下:

${{L}_{edge}}=\sqrt{E\left( {{I}_{S}} \right)-E\left( {{I}_{R}} \right){{\|}^{2}}+{{\varepsilon }^{2}}}$,

其中E(· )表示拉普拉斯算子, 常数ε =0.001.

由于在频域上学习相关特征, 因此频域中清晰图像与复原图像间的距离也可作为中间约束以监督图像的重建, 其表达式如下:

L_fft=‖ F(I_S)-F(I_R)‖ ,

其中F(· )表示快速傅里叶变换.

因此, 总的损失:

L=L_char+λ ₁L_edge+λ ₂L_fft,

其中λ ₁、λ ₂表示超参数.

在像素域、梯度域和频域的联合监督下, 本文网络在学习精细映射的同时, 加强结构的表达, 弱化几何及光度上的失真现象, 提高复原图像的质量.

目前图像去模糊领域常用的数据集有:GoPro^[8]、HIDE^[27]、RealBlur^[28]数据集.GoPro数据集作为图像运动去模糊的基准数据集, 训练集和测试集分别包含2 103个和1 111个模糊和清晰图像对.HIDE数据集场景更局限于行人和街道, 包含2025个测试图像对.RealBlur数据集包含2个子集:RealBlur-J和RealBlur-R, 2个子集内容相同, 但RealBlur-R亮度相对更低, 测试集均由980对图像组成.

本文网络在合成数据集GoPro上进行训练和测试, 为了验证其泛化能力, 使用GoPro数据集上训练的网络在合成数据集HIDE和真实数据集RealBlur上进行测试.

本文所有实验基于PyTorch深度学习框架完成, 在NVIDIA RTX 3090 GPU上进行训练与测试.在训练过程中, 模糊图像和对应的真实清晰图像利用双线性插值获得不同粒度的输入和真值, 用于计算多粒度损失.在网络细粒度阶段, 特征图的通道数C_fn=32, FSF-ResBlock中FGFM及跳跃连接的堆叠层数N=8.设定损失函数中的超参数λ ₁=0.05, 这是根据以往文献多次网格搜索得到的较优参数^{[11, 29]}.设定λ ₂=0.01, 根据经验该值在平衡损失项时表现良好^{[17, 30]}.设定实验的批量大小为16, 使用Adam(Adaptive Moment Estimation)优化器进行优化, β ₁=0.9, β ₂=0.999, 初始学习率为2× 10^-4, 先使用预热策略再使用余弦退火策略调整学习率, 可稳定网络加速收敛, 最终衰减到1× 10^-6.输入图像随机裁剪为256× 256, 并使用随机翻转和旋转进行数据增强.

为了评估本文网络的去模糊性能, 与近年来基于深度学习的多个去模糊网络在合成和真实数据集上进行对比:文献[8]网络、SRN^[9]、DeblurGAN-v2^[10]、MPRNet^[11]、MIMO-UNet+^[12]、Restormer^[13]、SFNet^[16]、MRDNet+^[18]、DBGAN(+)^[31]、MSSNet(Multi-scale-stage Network)^[32]、CODE(Comprehensive and Delicate Image Restoration)^[33]、DDANet(Dual-Do-main Attention Network)^[34]、文献[35]网络、文献[36]网络.所有作为对比的去模糊结果都是采用作者论文的原始数据或开源代码在本文实验环境运行获得.

本文使用图像去模糊领域的常用评价指标— — 峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)和结构相似性(Structural Similarity Index Measure, SSIM), 全面、客观地评定恢复图像的清晰度.除了定量分析之外, 还展示部分可获得的网络去模糊效果作为主观对比.

各网络在合成数据集GoPro和HIDE上的指标值结果如表1所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可见, 本文网络在GoPro数据集上表现出卓越的性能, PSNR及SSIM指标均高于其它网络.相比CNN方法, 本文网络在处理复杂运动模糊场景时表现更优, 归因于频域分支在捕捉长距离依赖方面的优势.相比Transformer方法, 本文网络中的卷积分支更高效利用图像中的局部信息, 实现更优的去模糊效果.在保持图像细节和边缘方面, 本文网络得益于频域门控实现的空间域特征和频域特征有机结合, 在性能方面更占优势.将在GoPro数据集上训练的网络权重泛化到HIDE数据集进行测试时, 结果显示本文网络仍保持最优性能.这表明本文网络对于其它合成数据集具有良好的泛化性, 为实际应用中的各种场景提供广泛的适用性.

表1

Table 1

表1(Table 1)

表1 各网络在合成数据集上的实验结果对比 Table 1 Experiment result comparison of different networks on synthetic datasets 网络 GoPro HIDE PSNR/dB SSIM PSNR/dB SSIM 文献[8]网络 30.40 0.902 27.87 0.827 SRN 30.26 0.934 28.36 0.915 DeblurGAN-v2 29.55 0.934 26.61 0.875 DBGAN(+) 31.10 0.942 28.94 0.915 MPRNet 32.66 0.959 30.96 0.939 MIMO-UNet+ 32.45 0.957 29.99 0.930 Restormer 32.92 0.961 31.22 0.942 MSSNet 33.01 0.961 - - CODE 31.94 0.954 29.68 0.927 DDANet 33.07 0.962 30.64 0.937 SFNet 33.27 0.963 31.10 0.942 MRDNet+ 32.47 0.959 30.54 0.939 文献[35]网络 32.55 0.960 30.42 0.934 文献[36]网络 33.35 0.963 31.02 0.940 本文网络 33.38 0.965 31.47 0.946

表1 各网络在合成数据集上的实验结果对比 Table 1 Experiment result comparison of different networks on synthetic datasets

各网络在合成数据集GoPro和HIDE上的视觉效果分别如图3和图4所示, 为了充分对比去模糊效果, 对图像中的局部区域进行放大以展示细节.对比网络在对图3中车牌号码进行恢复时无法恢复清晰的边缘结构, 留下较多的伪影, 而本文网络重建的数字清晰锐利.本文网络在恢复图3中地砖这种具有复杂细节的物体时, 纹理及光影都更精确.对于图4的大面积模糊, 本文网络正确恢复清晰的人脸五官及手指形状, 并且衣服图案与眼镜等细节都得到完整复原, 其它网络在恢复时不仅未完全消除模糊, 还引入错误的形变.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 各网络在合成数据集GoPro上的视觉效果对比Fig.3 Visual result comparison of different networks on synthetic dataset GoPro

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 各网络在合成数据集HIDE上的视觉效果对比Fig.4 Visual result comparison of different networks on synthetic dataset HIDE

结合图3和图4可说明:基于深度学习的方法虽然能去除一定程度的模糊, 但对模糊严重区域处理受限; Transformer方法的远程建模能力能更好地应对大面积的模糊区域, 但边缘还不够锐利; 基于频率的方法弥补这些缺陷, 但在纹理上不够逼真.相比之下, 本文网络在纹理细节及边缘轮廓上的重建效果都更精细.

为了验证本文网络在真实场景中的去模糊效果, 在真实数据集RealBlur上与其它网络进行对比, 在RealBlur-J、RealBlur-R测试集上的具体指标值结果如表2所示.表中黑体数字表示最优值, 斜体数字表示次优值.由表可见, 本文网络在RealBlur-J数据集上的PSNR值达到最优, SSIM值达到次优, 在Real-Blur-R数据集上仅次于Restormer和MRDNet+, 反映本文网络在真实场景下良好的通用性和去模糊能力.在真实环境下拍摄的RealBlur数据集对去模糊算法的鲁棒性提出更高要求, 本文网络通过FGFM准确学习图像中的关键结构和运动模式, 实现在真实场景下的良好表现.

表2

Table 2

表2(Table 2)

表2 各网络在真实数据集RealBlur上的实验结果对比 Table 2 Experiment result comparison of different networks on real dataset RealBlur 网络 RealBlur-J RealBlur-R PSNR/dB SSIM PSNR/dB SSIM 文献[8]网络 27.87 0.827 32.51 0.841 SRN 28.56 0.867 35.66 0.947 DeblurGAN-v2 28.71 0.866 35.26 0.944 DBGAN(+) 24.93 0.745 33.78 0.909 MPRNet 28.70 0.873 35.99 0.952 MIMO-UNet+ 27.63 0.837 35.54 0.947 Restormer 28.96 0.879 36.19 0.957 MSSNet 28.79 0.879 35.93 0.953 CODE 28.14 0.851 35.68 0.943 DDANet - - 35.81 0.951 SFNet 28.64 0.869 35.80 0.947 MRDNet+ 28.68 0.871 35.81 0.956 文献[35]网络 27.89 0.898 - - 本文网络 29.07 0.886 36.04 0.954

表2 各网络在真实数据集RealBlur上的实验结果对比 Table 2 Experiment result comparison of different networks on real dataset RealBlur

各网络在真实数据集RealBlur-J、RealBlur-R上的视觉效果分别如图5和图6所示.由图可见, 对比网络难以完全去除模糊, 对于图5中线条的恢复产生振铃伪影, 对图6的文字部分难以抑制几何失真, 而本文网络复原完整的图案形状及清晰的文字, 取得最优的视觉效果.虽然在定量比较中, 本文网络在RealBlur-R数据集上的性能略低于Restormer, 但从视觉感知的角度进行对比, 本文网络生成的去模糊图像仍展现出较高质量.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 各网络在真实数据集RealBlur-J上的视觉效果对比Fig.5 Visual result comparison of different networks on real dataset RealBlur-J

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 各网络在真实数据集RealBlur-R上的视觉效果对比Fig.6 Visual result comparison of different networks on real dataset RealBlur-R

本文还在GoPro数据集上对比各网络的网络参数、模型复杂度和运行时间, 结果如表3所示.在256× 256的图像块上计算每秒浮点运算次数(Floating Point Operations per Second, FLOPs), 运行时间在1280× 720的图像上评估, 黑体数字表示最优值.由表可见, 本文网络具有相对较低的参数量, 而模型复杂度和运行时间均处于第三优.本文网络产生优越性能, 可实现性能与计算效率及成本之间的较好权衡, 具有较强的竞争力.

表3

Table 3

表3(Table 3)

表3 各网络在GoPro数据集上的复杂性对比 Table 3 Complexity comparison of different networks on GoPro dataset 网络 参数/M FLOPs/G 时间/s 文献[8]网络 11.7 336 0.952 SRN 6.8 101 1.266 DebluGAN-v2 60.9 42 0.351 MPRNet 20.1 761 1.464 Restormer 26.1 141 1.160 CODE 12.2 45 1.373 SFNet 13.3 125 0.527 MRDNet+ 9.9 117 0.970 文献[36]网络 50.2 982 1.372 本文网络 12.4 92 0.585

表3 各网络在GoPro数据集上的复杂性对比 Table 3 Complexity comparison of different networks on GoPro dataset

为了验证本文网络的有效性, 进行全面的消融实验, 探究各组成部分对去模糊任务的提升作用, 所有结果均在GoPro数据集上获得.

不同组件消融实验结果如表4所示, 表中黑体数字表示最优值, 本文网络对应表中的序号7.对于频域门控的频空特征深度融合模块(FGFM), 分别探究空间域特征、频域特征及门控机制这三条支路对去模糊性能的影响.对比序号1和序号3发现, 仅利用频域特征效果差于仅利用空间域特征, 这表明对于去模糊任务, 空间信息的重要性超过频域信息, 符合不同区域具有不同程度模糊的任务特性.对比序号3、序号4和序号5发现, 在空间域特征的基础上增加频域特征可显著提升性能, 这说明频域特征与空间域特征之间存在一定的相关性和较强的互补性.将序号7与序号4、序号5进行对比发现, PSNR值和SSIM值进一步提升, 这表明结合频域、空间域之间的关联, 考虑相关性以减少互补中的冗余, 进行特征的深度融合, 能有效提高去模糊效果, 从而可利用图像的局部空间信息和全局频域信息助力去模糊任务.对于频域分辨率自适应的测试策略, 由表可见, 相比序号2和序号3, 在参数量无改变的前提下指标值升高, 说明强化训练和测试时空间域中全局特征分布的一致性有利于获得更优的性能.对比序号6和序号7发现, 去除本文策略后的性能大幅度下降, 说明频域特征图分辨率不匹配对去模糊任务的不利影响, 同时说明频域分辨率自适应的测试策略的有效性.

表4

Table 4

表4(Table 4)

表4 本文网络不同组件的消融实验结果 Table 4 Results of ablation experiment on different components of the proposed algorithm 序号 FGFM 频域分辨率自适应的 测试策略 PSNR/dB SSIM 参数/M 空间域特征 频域特征 门控机制 1 ✓ ✓ 29.97 0.932 3.4 2 ✓ 31.36 0.947 6.9 3 ✓ ✓ 31.88 0.952 6.9 4 ✓ ✓ ✓ 32.11 0.954 9.6 5 ✓ ✓ ✓ 33.13 0.963 9.6 6 ✓ ✓ ✓ 31.36 0.947 12.4 7 ✓ ✓ ✓ ✓ 33.38 0.965 12.4

表4 本文网络不同组件的消融实验结果 Table 4 Results of ablation experiment on different components of the proposed algorithm

多粒度结构的消融实验结果如表5所示, 表中黑体数字表示最优值.由表可见, 仅使用细粒度信息时, 虽然复杂度和运行时间较低, 但去模糊效果较差, 局限的感受野使得在处理较大范围模糊时效果欠佳.添加中粒度信息或粗粒度信息能明显增强去模糊效果, 分别针对中等范围模糊和大范围模糊进行复原.结合所有粒度信息后, 结果达到最优, 表明多粒度网络结构能充分利用不同粒度的语义、边缘和模糊模式等特征, 显著提升去模糊性能, 因此多粒度结构是有效的.

表5

Table 5

表5(Table 5)

表5 多粒度结构的消融实验结果 Table 5 Results of ablation experiment on multi-granularity structures 细粒度 中粒度 粗粒度 PSNR/dB SSIM 参数/M 运行 时间/s ✓ 30.96 0.944 0.6 0.297 ✓ ✓ 32.93 0.961 2.9 0.476 ✓ ✓ 32.94 0.961 10.1 0.422 ✓ ✓ ✓ 33.38 0.965 12.4 0.585

表5 多粒度结构的消融实验结果 Table 5 Results of ablation experiment on multi-granularity structures

本文对损失函数进行额外的消融实验, 结果如表6所示.由表可见, 当3种损失同时存在时, 性能最佳.在像素域损失的基础上添加梯度域损失略微提升性能, 而频域损失的加入带来显著的质量提高, 表明对应超参数下损失函数的有效性.

表6

Table 6

表6(Table 6)

表6 损失函数的消融实验 Table 6 Ablation experiment on loss function 损失函数 PSNR/dB SSIM Lchar 33.17 0.963 Lchar+λ 1Ledge 33.18 0.964 Lchar+λ 1Ledge+λ 2Lfft 33.38 0.965

表6 损失函数的消融实验 Table 6 Ablation experiment on loss function

本文将频域分辨率自适应的测试策略替换为常用的测试策略以验证其优越性, 具体结果如表7所示.在表中:序号1表示将整幅特征图作为输入进行测试, 代表方法有MIMO-UNet^[12]; 序号2表示膨胀预测, 是语义分割任务中的常用方法, 核心思想是对边缘填充后进行预测, 且仅保留中心部分以增强效果; 序号3表示将图像划分为不重叠的切片, 代表方法有SDWNet^[23]; 序号4表示将图像按一定的重叠大小进行滑动切片, 对于重叠部分取切片测试结果的均值; 黑体数字表示最优值.由表可见, 本文网络在两个指标上的性能均最优, 仅运行时间略高, 但也实现性能与效率之间的较好权衡.将序号5与序号4进行对比, 表明对于重叠部分的重构, 相比取平均值, 反距离加权更适合图像去模糊任务.

表7

Table 7

表7(Table 7)

表7 不同测试策略的性能对比 Table 7 Performance comparison of different testing strategies 序号 测试策略 PSNR/dB SSIM 运行 时间/s 1 整幅测试 31.36 0.947 0.373 2 膨胀预测 32.98 0.963 1.485 3 不重叠分块 32.99 0.962 0.366 4 重叠分块-平均重构 33.31 0.964 0.583 5 本文网络 33.38 0.965 0.585

表7 不同测试策略的性能对比 Table 7 Performance comparison of different testing strategies

不同测试策略的视觉效果如图7所示, 除整幅测试和本文网络之外, 其它网络在地面的光影部分都有一定方块状的拼接痕迹, 而整幅测试对于花盆边缘具有振铃效应.相比而言, 本文网络对于切片边界的过渡效果更自然, 可恢复物体的锐利边缘.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同测试策略在GoPro数据集上的视觉效果对比Fig.7 Visual result comparison of different testing strategies on GoPro dataset