魏玲,博士,教授,主要研究方向为形式概念分析、粗糙集、三支决策、粒计算.E-mail:wl@nwu.edu.cn.
作者简介:

王啸,硕士研究生,主要研究方向为形式概念分析、三支决策.E-mail:w19513389739@163.com.

张琴,博士研究生,主要研究方向为形式概念分析、三支概念分析.E-mail:xzzonly1@163.com.

祁斌,硕士研究生,主要研究方向为形式概念分析、三支概念分析.E-mail:1519262721@qq.com.
三元概念分析作为形式概念分析理论的扩展,是一种分析三维数据的理论.获取三元概念是三元概念分析理论的重要问题之一,文中提出基于待选集的三元概念构造方法.首先,定义正则三元背景和净化三元背景,研究这两种三元背景的性质,证明三元背景诱导的形式背景的所有形式概念的外延集包含三元背景所有三元概念的外延集.然后,定义外延待选集,给出利用外延待选集构造三元概念的方法,加快获取三元概念的速度.进一步,证明依据该构造方法获取三元概念的可行性和完备性,同时将该构造方法推广到三元背景诱导的另两种形式背景上.最后,给出基于待选集的三元概念构造算法,并通过实验验证文中算法性能较优.
WEI Ling, Ph.D., professor. Her research interests include formal concept analysis, rough set, three-way decision and granular computing.
About Author:
WANG Xiao, Master student. His research interests include formal concept analysis and three-way decision.
ZHANG Qin, Ph.D. candidate. Her research interests include formal concept analysis and three-way concept analysis.
QI Bin, Master student. His research interests include formal concept analysis and three-way concept analysis.
As an extension of formal concept analysis, triadic concept analysis is a theory for analyzing three-dimensional data. The acquisition of triadic concepts is one of the key issues in triadic concept analysis. A triadic concept construction method based on candidate set is proposed. Firstly, the regular triadic context and the purified triadic context are defined, and properties of these two triadic contexts are studied. Secondly, it is proven that the extent set of all formal concepts of the formal context induced by the triadic context contains the extent set of all triadic concepts of triadic context. Then, by defining an extent candidate set, a method for constructing triadic concepts using the extent candidate set is presented to speed up the acquisition of triadic concepts. Moreover, the feasibility and completeness of obtaining triadic concepts based on this construction method are proven, and this method is extended to two other types of formal contexts induced by the triadic context. Finally, an algorithm for constructing triadic concepts based on the candidate set is presented, and experimental results demonstrate superior performance of the proposed algorithm.
Wille等[1, 2]提出形式概念分析(Formal Concept Analysis, FCA), 包括形式背景、形式概念等基本概念.形式背景由对象集、属性集及两者间的二元关系组成, 形式概念由外延和内涵组成.形式概念分析作为一种数据分析和知识发现的有效工具, 已被广泛应用于机器学习[3]、推荐系统[4]、知识发现[5, 6]等诸多领域.
随着时代的发展, 数据量不断增长, 越来越多的三维数据也日益涌现, 形式概念分析已无法满足对三维数据分析的需求.Wille等[7, 8]将形式概念分析中的形式背景扩展到三元背景, 提出三元概念分析(Triadic Concept Analysis, TCA)理论.类似于形式概念分析, 三元概念分析定义三元背景、三元概念等.相比形式背景, 三元背景增加条件集, 二元关系变化为三元关系.相比形式概念, 三元概念增加方式, 由外延、内涵和方式组成.魏玲等[9]详细介绍2014年以前的三元概念分析的研究现状及发展趋势.目前, 三元概念分析的主要研究包括:概念三元格的建立[7, 8, 10, 11]、三元背景的简化及约简[12, 13]、三元蕴含及关联规则挖掘[14, 15, 16, 17]、三元概念约简[18]、三元概念的布尔表示[19, 20]、三元背景的模糊化[21]、三元概念分析的应用[22, 23, 24]等.
三元概念是三元概念分析理论中的重要基础, 如何获取三元概念是将三元概念分析理论应用到实际生活中面临的首要问题, 也是当今三元概念分析体系中的关键点和突破点.在三元概念构造方面, Lehmann等[8]提出三元概念枚举法, 从对象幂集、属性幂集和条件幂集中选定两个集合, 再从这两个幂集的任意子集出发构造三元概念, 该方法直接从三元概念的定义出发, 操作简单但计算量较大.由于三元概念与形式概念联系紧密, 一些学者尝试从形式概念出发构造三元概念.王霞等[25]提出三元概念的增量式构造法, 从单个条件的三元背景的三元概念出发, 通过增加方式判断是否为原三元背景的三元概念, 其本质上是根据三元背景的条件集将三元背景拆分成多个形式背景, 再从多个形式背景的所有形式概念出发构造三元概念.
三元背景由对象集、属性集和条件集组成, 实际上可通过诱导将任意两个集合的笛卡尔积和第三个集合一起组成形式背景, 其包涵的信息和三元背景相同, 且三元背景诱导的形式背景的形式概念外延集包涵三元背景的三元概念外延集, 这种关联可在构造三元概念时, 缩小三元概念外延的可能范围, 加快获取三元概念的速度.因此, 本文从三元背景诱导的形式背景出发, 利用其形式概念构造三元概念, 提出基于待选集的三元概念构造方法.首先, 定义正则三元背景和净化三元背景, 研究这两种三元背景的性质, 证明三元背景诱导的形式背景的所有形式概念的外延集包含三元背景所有三元概念的外延集.然后, 定义外延待选集, 给出利用外延待选集构造三元概念的方法, 加快获取三元概念的速度.进一步, 证明依据该构造方法获取三元概念的可行性和完备性, 同时将该构造方法推广到三元背景诱导的另两种形式背景上.最后, 给出基于待选集的三元概念构造算法, 并通过实验验证本文算法性能较优.
定义1[1] 称(G, M, I)为形式背景, 其中
G={x1, x2, ···, xp}
为对象集, 每个xi(i≤ p)称为一个对象,
M={a1, a2, ···, aq}
为属性集, 每个aj(j≤ q)称为一个属性, I为G和M之间的二元关系, I⊆G× M.若(x, a)∈ I, 则表示对象x具有属性a, 记为xIa.
在形式背景(G, M, I)中, 对于任意对象子集X⊆G和属性子集B⊆M, Wille[1]定义一对导出算子如下:
${{X}^{* }}=\left\{ a\in M\left| \forall x\in X \right., xIa \right\}$
${{B}^{* }}=\left\{ x\in G\left| \forall a\in B \right., xIa \right\}$
其中, X* 表示X中所有对象共同具有的属性集合, B* 表示共同具有B中所有属性的对象集合.若二元组(X, B)满足X* =B且X=B* , 则称(X, B)为形式概念, 简称概念, 其中X称为概念的外延, B称为概念的内涵, 使用L(G, M, I)表示形式背景(G, M, I)的全体概念.
性质1[2] 设(G, M, I)为形式背景, ∀ X⊆G, X1⊆G, X2⊆G且∀ B⊆M, B1⊆M, B2⊆M, 如下性质成立:
1)X1⊆X2⇒
2)X⊆X* * , B⊆B* * ;
3)X* =X* * * , B=B* * * ;
4)X⊆B* ⇔ B⊆X* ;
5)(X1∪ X2)* =
6)(X1∩ X2)* ⊇
定义2[8] 称(K1, K2, K3, Y)为一个三元背景, 其中:
K1={g1, g2, ···, gp}
为对象集, 每个gi(i≤ p)称为一个对象;
K2={m1, m2, ···, mq}
为属性集, 每个mj(j≤ q)称为一个属性;
K3={b1, b2, ···, br}
为条件集, 每个bk(k≤ r)称为一个条件; Y为K1、K2和K3之间的三元关系,
Y⊆K1× K2× K3.
若(g, m, b)∈ Y, 则表示对象g在条件b下具有属性m.
定义3[16] 设K=(K1, K2, K3, Y)为三元背景, 称
$\begin{array}{l} K^{(1)}=\left(K_{1}, K_{2} \times K_{3}, Y^{(1)}\right), \\ K^{(2)}=\left(K_{2}, K_{1} \times K_{3}, Y^{(2)}\right), \\ K^{(3)}=\left(K_{3}, K_{1} \times K_{2}, Y^{(3)}\right) \end{array}$
为K诱导的三个形式背景.K诱导的形式背景K(i)(i∈ {1, 2, 3})上的* 算子记为* Y(i).
定义4[8] 设K=(K1, K2, K3, Y)为三元背景, {i, j, k}={1, 2, 3}且j< k.对于∀ X⊆Ki, Z⊆Kj× Kk.定义(i)-诱导算子如下:
${{X}^{\left( i \right)}}=\left\{ ({{a}_{j}}, {{a}_{k}})\in {{K}_{j}}\times {{K}_{k}}\left| \left( {{a}_{i}}, {{a}_{j}}, {{a}_{k}} \right)\in Y \right., \forall {{a}_{i}}\in X \right\}$,
${{Z}^{\left( i \right)}}=\left\{ {{a}_{i}}\in {{K}_{i}}\left| \left( {{a}_{i}}, {{a}_{j}}, {{a}_{k}} \right)\in Y \right., \forall ({{a}_{j}}, {{a}_{k}})\in Z \right\}$.
实际上, (i)-诱导算子相当于形式背景
${{K}^{\left( 1 \right)}}=\left( {{K}_{1}}, {{K}_{2}}\times {{K}_{3}}, {{Y}^{\left( 1 \right)}} \right)$,
${{K}^{\left( 2 \right)}}=\left( {{K}_{2}}, {{K}_{1}}\times {{K}_{3}}, {{Y}^{\left( 2 \right)}} \right)$,
${{K}^{\left( 3 \right)}}=\left( {{K}_{3}}, {{K}_{1}}\times {{K}_{2}}, {{Y}^{\left( 3 \right)}} \right)$
上的* 算子.
定义5[8] 设K=(K1, K2, K3, Y)为三元背景, {i, j, k}={1, 2, 3}.对于∀ Xi⊆Ki, Xj⊆Kj且Xk⊆Kk, 定义(i, j, Xk)-诱导算子如下:
${{X}_{i}}^{\left( i, j, {{X}_{k}} \right)}=\left\{ {{a}_{j}}\in {{K}_{j}}\left| \left( {{a}_{i}}, {{a}_{j}}, {{a}_{k}} \right)\in Y, \forall \left( {{a}_{i}}, {{a}_{k}} \right)\in {{X}_{i}}\times {{X}_{k}} \right. \right\}$,
${{X}_{j}}^{\left( i, j, {{X}_{k}} \right)}=\left\{ {{a}_{i}}\in {{K}_{i}}\left| \left( {{a}_{i}}, {{a}_{j}}, {{a}_{k}} \right)\in Y, \forall \left( {{a}_{j}}, {{a}_{k}} \right)\in {{X}_{j}}\times {{X}_{k}} \right. \right\}$.
定义6[8] 设K=(K1, K2, K3, Y)为三元背景, Ai⊆Ki, i=1, 2, 3.若满足
Ai=(Aj× Ak)(i),
其中{i, j, k}={1, 2, 3}且j< k, 则称(A1, A2, A3)为三元背景K的三元概念, 并称A1为外延, A2为内涵, A3为方式.记K中所有三元概念构成的集合为T(K).
引理1[8] 设K=(K1, K2, K3, Y)为三元背景, Xi⊆Ki, Xk⊆Kk, {i, j, k}={1, 2, 3}.记
${{A}_{j}}={{X}_{i}}^{\left( i, j, {{X}_{k}} \right)}$,
${{A}_{i}}={{A}_{j}}^{\left( i, j, {{X}_{k}} \right)}$,
${{A}_{k}}={{({{A}_{i}}\times {{A}_{j}})}^{\left( k \right)}}, \left( i< j \right) $
则(A1, A2, A3)为三元概念.
为了简化三元概念的书写, 本文将一般集合写成其元素的序列.例如, 对象集{2, 4}简写为24, 属性集{c, d}简写为cd, 条件集{A, B, C}简写为ABC.
例1 表1是一个三元背景K=(K1, K2, K3, Y), 其中, 对象集K1={1, 2, 3, 4}, 属性集K2={a, b, c, d, e}, 条件集K3={A, B, C}.
| 表1 三元背景K=(K1, K2, K3, Y) Table 1 Triadic context K=(K1, K2, K3, Y) |
由定义6可求得该三元背景的所有三元概念如下:
$\begin{array}{l} (124, a, A), (1, a, A B C), (1, a e, A B), \\ (1, a b e, A), (24, a c d, A), (24, c d, A B C), \\ (24, b c d, C), (13, b, A), (13, a e, B), \\ (3, b, A B), (3, e, B C), (3, a b e, B), \\ (3, c d e, C), (234, c d, C), \left(K_{1}, K_{2}, \varnothing\right), \\ \left(K_{1}, \varnothing, K_{3}\right), \left(\varnothing, K_{2}, K_{3}\right) . \end{array}$
为了更高效地获取三元概念, 借鉴形式背景中净化背景和正则背景的思想, 本节定义正则三元背景和净化三元背景, 并阐明其性质.
定义7 设K=(K1, K2, K3, Y)为三元背景, 其诱导的3个形式背景分别为
${{K}^{\left( 1 \right)}}=\left( {{K}_{1}}, {{K}_{2}}\times {{K}_{3}}, {{Y}^{\left( 1 \right)}} \right)$,
${{K}^{\left( 2 \right)}}=\left( {{K}_{2}}, {{K}_{1}}\times {{K}_{3}}, {{Y}^{\left( 2 \right)}} \right)$,
${{K}^{\left( 3 \right)}}=\left( {{K}_{3}}, {{K}_{1}}\times {{K}_{2}}, {{Y}^{\left( 3 \right)}} \right)$.
若对于∀ x∈ Ki, 都有${{x}^{* {{Y}^{\left( i \right)}}}}\ne {{K}_{j}}\times {{K}_{k}}$, 其中{i, j, k}={1, 2, 3}且j< k, 则称K=(K1, K2, K3, Y)为正则三元背景.
定义8 设K=(K1, K2, K3, Y)为三元背景, 其诱导的3个形式背景分别为
${{K}^{\left( 1 \right)}}=\left( {{K}_{1}}, {{K}_{2}}\times {{K}_{3}}, {{Y}^{\left( 1 \right)}} \right)$,
${{K}^{\left( 2 \right)}}=\left( {{K}_{2}}, {{K}_{1}}\times {{K}_{3}}, {{Y}^{\left( 2 \right)}} \right)$,
${{K}^{\left( 3 \right)}}=\left( {{K}_{3}}, {{K}_{1}}\times {{K}_{2}}, {{Y}^{\left( 3 \right)}} \right)$.
对于∀ x∈ Ki, y∈ Ki, i∈ {1, 2, 3}, 若${{x}^{* {{Y}^{\left( i \right)}}}}={{y}^{* {{Y}^{\left( i \right)}}}}$, 都有x=y, 则称K=(K1, K2, K3, Y)为净化三元背景.
例2 (续例1) 例1中的三元背景K=(K1, K2, K3, Y)诱导的3个形式背景K(1)、K(2)、K(3)分别如表2~表4所示.
| 表2 K诱导的形式背景K(1)=(K1, K2× K3, Y(1)) Table 2 Formal context K(1)=(K1, K2× K3, Y(1)) induced by K |
| 表3 K诱导的形式背景K(2)=(K2, K1× K3, Y(2)) Table 3 Formal context K(2)=(K2, K1× K3, Y(2)) induced by K |
| 表4 K诱导的形式背景K(3)=(K3, K1× K2, Y(3)) Table 4 Formal context K(3)=(K3, K1× K2, Y(3)) induced by K |
由表2~表4可看出, 形式背景K(1)、K(2)、K(3)均无满行, 故由定义7知该三元背景为正则三元背景.形式背景K(1)、K(2)存在相同行, 因此根据定义8知该三元背景不是净化三元背景.
下面给出正则三元背景和净化三元背景的一些性质.
性质2 设K=(K1, K2, K3, Y)为正则三元背景, 则
(K1, K2, Ø )∈ T(K), (K1, Ø , K3)∈ T(K), (Ø , K2, K3)∈ T(K).
证明 由定义7知, K诱导的3个形式背景均无满行存在, 因此有
${{\left( {{K}_{1}}\times {{K}_{2}} \right)}^{\left( 3 \right)}}=\varnothing $,
${{\left( {{K}_{1}}\times {{K}_{3}} \right)}^{\left( 2 \right)}}=\varnothing $,
${{\left( {{K}_{2}}\times {{K}_{3}} \right)}^{\left( 1 \right)}}=\varnothing $
又由定义6知, (K1, K2, Ø )、(K1, Ø , K3)、(Ø , K2, K3)一定为三元概念.
性质3 设K=(K1, K2, K3, Y)为非正则三元背景, (A1, A2, A3)∈ T(K), 则如下性质成立:
1)对于∀ x∈ K1, 若
2)对于∀ y∈ K2, 若y
3)对于∀ z∈ K3, 若
证明 先证1).对于∀ x∈ K1, 有
即对于∀ x和∀ (y, z)∈ K2× K3, 有(x, y, z)∈ Y.因此对于∀ A2⊆K2, A3⊆K3, 都有x∈ (A2× A3)(1), 故三元概念的外延都含有x, 即x∈ A1.
2)、3)同理可证.
性质3表明, 对于非正则三元背景会存在某些元素出现在每个三元概念中, 并且这些计算都是重复的.因此, 在获取非正则三元背景的三元概念时可先删除这部分元素, 得到正则三元背景.获取正则三元背景的三元概念后, 再添加被删除的元素到三元概念的外延(内涵或方式)中, 从而得到原三元背景的三元概念.这种删除处理降低获取三元概念所需的时间, 且不会对三元概念的准确性造成影响.
性质4 设K=(K1, K2, K3, Y)为非净化三元背景, 则如下性质成立:
1)对于∀ x1∈ K1, x2∈ K1, 若
2)对于∀ y1∈ K2, y2∈ K2, 若
3)对于∀ z1∈ K3, z2∈ K3, 若
证明 先证1).对于∀ A2⊆K2, A3⊆K3, y1∈ A2, z1∈ A3, 若(x1, y1, z1)∈ Y, 由于
因此有(x2, y1, z1)∈ Y, 故有
{x1, x2}⊆(A2× A3)(1),
因此对象x1、x2会同时出现在三元概念的外延中.
2)、3)同理可证.
根据性质4可知, 在非净化三元背景中, 部分元素是等价的.因此, 获取非净化三元背景的三元概念时可先删除x1(y1或z1), 得到净化三元背景.获取其三元概念之后, 再添加被删除的x1(y1或z1)到含有x2(y2或z2)的三元概念的外延(内涵或方式)中, 从而得到原三元背景的三元概念.
例3 (续例2) 由例2知三元背景K不是净化的, 因此对其进行净化处理, 删除冗余的对象4和属性d, 得到净化三元背景K', 如表5所示.
| 表5 净化三元背景K'=(K'1, K'2, K'3, Y') Table 5 Clarified triadic context K'=(K'1, K'2, K'3, Y') |
本节利用三元背景诱导的形式背景的形式概念构造三元概念, 并引入待选集的定义, 给出基于待选集的三元概念构造方法.
定义9 设K=(K1, K2, K3, Y)为三元背景,
K(1)=(K1, K2× K3, Y(1))
为K诱导的形式背景, (X, B)∈ L(K(1)),
$EC\left( X \right)=\left\{ \underset{E\in A}{\mathop{\bigcap }}\, E\left| A\subseteq B_{{{K}_{3}}}^{X} \right., A\ne \varnothing \right\}$
为X的外延待选集.
由于(X, B)为K(1)上的形式概念, 故也可记
$B_{{{K}_{3}}}^{X}=\left\{ {{\left( X\times k \right)}^{\left( 2 \right)}}, k\in {{K}_{3}} \right\}$,
类似地, 也可记X的外延待选集
$EC\left( X \right)=\left\{ \underset{i\subseteq I}{\mathop{\bigcap }}\, {{\left( X\times i \right)}^{\left( 2 \right)}}, I\subseteq {{K}_{3}}, I\ne \varnothing \right\}$.
设K为三元背景, 记T(K)中所有三元概念外延的集合为
$E\left( K \right)=\left\{ \left. {{A}_{1}} \right|\left( {{A}_{1}}, \right.\left. {{A}_{2}}, {{A}_{3}} \right)\in T\left( K \right) \right\}$,
T(K)中所有三元概念内涵的集合为
$I\left( K \right)=\left\{ \left. {{A}_{2}} \right| \right.\left( {{A}_{1}}, {{A}_{2}}, {{A}_{3}} \right)$$\left. \in T\left( K \right) \right\}$,
T(K)中所有三元概念方式的集合为
$M\left( K \right)=\left\{ \left. {{A}_{3}} \right|\left( {{A}_{1}}, {{A}_{2}}, {{A}_{3}} \right) \right.\left. \in T\left( K \right) \right\}$.
K(i)为K诱导的形式背景, 其中i=1, 2, 3.记K(i)的所有形式概念外延的集合为
$E\left( {{K}^{\left( i \right)}} \right)=\left\{ \left. X \right|\left( X, B \right)\in L\left( {{K}^{\left( i \right)}} \right) \right\}$.
例4 (续例3) 例3中的净化三元背景
K'=(K'1, K'2, K'3, Y),
其诱导的形式背景K'(1)如表6所示.
| 表6 K'诱导的形式背景K'(1)=(K'1, K'2× K'3, Y'(1)) Table 6 Formal context K'(1)=(K'1, K'2× K'3, Y'(1)) induced by K' |
K'(1)的形式概念如下:
$\begin{array}{l} (12, (A, a)), (23, (C, c)), \\ (1, (A, a)(A, b)(A, e)(B, a)(B, e)(C, a)), \\ (3, (A, b)(B, a)(B, b)(B, e)(C, c)(C, e)), \\ (13, (A, b)(B, a)(B, e)), \\ (2, (A, a)(A, c)(B, c)(C, b)(C, c)), \\ \left(K_{1}^{\prime}, \varnothing\right), \left(\varnothing, K_{2}^{\prime} \times K_{3}^{\prime}\right) . \end{array}$
由定义9知外延2对应的外延待选集为{ac, c, bc}, 外延3对应的外延待选集为{Ø , b, abe, ce, e}.
定理1 设K=(K1, K2, K3, Y)为三元背景,
K(1)=(K1, K2× K3, Y(1))
为K诱导的形式背景, 则有
E(K)⊆E(K(1)).
证明 取(A1, A2, A3)∈ T(K), 则有
A1=(A2× A3)(1),
其在形式背景K(1)上等价于
A1=(A2× A3)* ,
故由性质1知,
A2× A3⊆
首先, 若
A2× A3=
则显然有
(A1, (A2× A3))∈ L(K(1)).
其次, 若
A2× A3⊂
则存在
Q∈ K2× K3\A2× A3,
使得
故若
A1=((A2× A3)∪ Q)* ,
则
(A1, (A2× A3)∪ Q)
为形式概念.
下证
A1=((A2× A3)∪ Q)* .
假设
A1≠ ((A2× A3)∪ Q)* ,
即
A1≠ (A2× A3)* ∩ Q* ,
又因为
A1=(A2× A3)* ,
故有Q* ⊂A1.又由
知Q⊆
Q⊆
而A1⊆Q* 与Q* ⊂A1矛盾, 因此假设不成立, 故一定有
A1=((A2× A3)∪ Q)* .
综上所述, A1一定为形式背景K(1)的某个形式概念的外延, 即E(K)⊆E(K(1)).
定理1表明三元背景K诱导的形式背景K(1)的所有形式概念的外延集包含三元背景K的所有三元概念的外延集, 从而提供利用形式背景K(1)的形式概念构造三元概念的基础.
定理2 设K=(K1, K2, K3, Y)为三元背景,
K(1) =(K1, K2× K3, Y(1))
为K诱导的形式背景, (X, B)∈ L(K(1)).若
(A× (X× A)(3))(1)=X,
则
(X, A, (X× A)(3))∈ T(K),
其中A∈ EC(X).
证明 因为
(A× (X× A)(3))(1)=X,
故只需证
(X× (X× A)(3))(2)=A.
令Z=(X× A)(3), 即证(X× Z)(2)=A.假设存在
u∈ (X× Z)(2)\A,
即u∈ (X× Z)(2)且u∉A.又因为A∈ EC(X), 故存在I⊆K3, 使得
A=
因此有
u∉
即u∉(X× I)(2).若I⊆Z, 则有
(X× Z)(2)⊆(X× I)(2),
又因为u∉(X× I)(2), 故u∉(X× Z)(2), 与
u∈ (X× Z)(2)
矛盾.因此不存在
u∈ (X× Z)(2)\A,
也即
(X× Z)(2)=A.
下证I⊆Z.假设Z⊂I, 即存在k∈ I\Z, 又因为
A=
有A∈ (X× k)(2), 故对于∀ x∈ X, a∈ A, 有(x, a, k)∈ Y, 因此有
(X× A)(3)=Z∪ {k},
与
(X× A)(3)=Z
矛盾, 故I⊆Z.
综上所述, (X, A, (X× A)(3))为三元概念.
定理2给出基于外延待选集的三元概念构造方法, 即利用形式背景K(1)的形式概念外延和其外延待选集相结合构造三元概念, 同时说明该构造方法的可行性.
定理3 设K=(K1, K2, K3, Y)为三元背景,
$\begin{array}{l} \left(A_{1}, A_{2}, A_{3}\right) \in T(K) \\ K^{(1)}=\left(K_{1}, K_{2} \times K_{3}, Y^{(1)}\right) \end{array}$
为K诱导的形式背景, 则存在(X, B)∈ L(K(1))使得
(X, A, (X× A)(3))=(A1, A2, A3),
其中A∈ EC(X).
证明 由定理1知, 对于三元概念(A1, A2, A3)一定存在一个形式概念(X, B)与其外延相等, 取X=A1.因为(A1, A2, A3)∈ T(K), 有
(A1× A3)(2)=A2.
在三元背景K诱导的形式背景K(2)上取
A1× A3∈ K1× K3,
有
${{\left( {{A}_{1}}\times {{A}_{3}} \right)}^{* }}=\bigcap\limits_{i\subseteq {{A}_{3}}}{{{\left( {{A}_{1}}\times i \right)}^{\left( 2 \right)}}}={{\bigcap\limits_{i\subseteq {{A}_{3}}}{\left( X\times i \right)}}^{\left( 2 \right)}}\in EC\left( X \right)$
又因为
A2=(A1× A3)(2),
故A2∈ EC(X), 因此一定存在A∈ EC(X), 使得A=A2.
综上所述, 一定存在(X, B)∈ L(K(1))使得
(X, A, (X× A)(3))=(A1, A2, A3).
定理3表明, 任何一个三元概念都可通过某个形式概念依据定理2的构造方法得到, 即证明该构造方法的完备性.
定理2和定理3两者结合就可确保基于外延待选集的三元概念构造方法能获取三元概念, 且能获取所有的三元概念.
基于外延待选集的三元概念构造方法是将三元背景K诱导为形式背景K(1), 从K(1)的形式概念出发构造三元概念.由于K1、K2和K3在三元背景上地位的平等性, 故将上述方法推广到三元背景诱导的另外两个形式背景K(2)和K(3)上.
首先在形式背景K(2)上定义内涵待选集, 并在形式背景K(2)上给出基于内涵待选集的三元概念构造方法.由于K1和K2地位的平等性, 后文定理4、定理5和定理6的证明与定理1、定理2和定理3的证明类似, 故省略.
类似地, 在三元背景诱导的形式背景K(3)上也可给出方式待选集的定义和基于方式待选集的三元概念构造方法.由于K1和K3地位的平等性, 故后文定理7、定理8和定理9也不再进行证明.
定义10 设K=(K1, K2, K3, Y)为三元背景,
K(2)=(K2, K1× K3, Y(2))
为K诱导的形式背景, (X, B)∈ L(K(2)),
$IC\left( X \right)=\left\{ \underset{I\in C}{\mathop{\bigcap }}\, I\left| C\subseteq B_{{{K}_{1}}}^{X} \right., C\ne \varnothing \right\}$
为X的内涵待选集.
定理4 设K=(K1, K2, K3, Y)为三元背景,
K(2)= (K2, K1× K3, Y(2))
为K诱导的形式背景, 则有
I(K)⊆E(K(2)).
定理5 设K=(K1, K2, K3, Y)为三元背景,
K(2)=(K2, K1× K3, Y(2))
为K诱导的形式背景, (X, B)∈ L(K(2)).若
((X× A)(1)× A)(2)=X,
则
((X× A)(1), X, A)∈ T(K),
其中A∈ IC(X).
定理6 设K=(K1, K2, K3, Y)为三元背景,
$\begin{array}{l} \left(A_{1}, A_{2}, A_{3}\right) \in T(K) \\ K^{(2)}=\left(K_{2}, K_{1} \times K_{3}, Y^{(2)}\right) \end{array}$
为K诱导的形式背景, 则存在(X, B)∈ L(K(2))使得
((X× A)(1), X, A)=(A1, A2, A3),
其中A∈ IC(X).
定理4表明, 形式背景K(2)的形式概念的外延集包含K的三元概念的内涵集.定理5给出基于内涵待选集的三元概念构造方法.定理6在此基础上确保基于内涵待选集的三元概念构造方法的完备性.
定义11 设K=(K1, K2, K3, Y)为三元背景,
K(3)=(K3, K1× K2, Y(3))
为K诱导的形式背景, (X, B)∈ L(K(3)),
$MC\left( X \right)=\left\{ \underset{M\in O}{\mathop{\bigcap }}\, M\left| O\subseteq B_{{{K}_{2}}}^{X} \right., O\ne \varnothing \right\}$
为X的方式待选集.
定理7 设K=(K1, K2, K3, Y)为三元背景,
K(3)=(K3, K1× K2, Y(3))
为K诱导的形式背景, 则有
M(K)⊆E(K(3)).
定理8 设K=(K1, K2, K3, Y)为三元背景,
K(3)=(K3, K1× K2, Y(3))
为K诱导的形式背景, (X, B)∈ L(K(3)).若
(A× (A× X)(2))(3)=X,
则
(A, (A× X)(2), X)∈ T(K),
其中A∈ MC(X).
定理9 设K=(K1, K2, K3, Y)为三元背景,
$\begin{array}{l} \left(A_{1}, A_{2}, A_{3}\right) \in T(K) \\ K^{(3)}=\left(K_{3}, K_{1} \times K_{2}, Y^{(3)}\right) \end{array}$
为K诱导的形式背景, 则存在(X, B)∈ L(K(3))使得
(A, (A× X)(2), X)=(A1, A2, A3),
其中A∈ MC(X).
定理7表明, 形式背景K(3)的形式概念的外延集包含K的三元概念的方式集.定理8给出基于方式待选集的三元概念方法.定理9在此基础上确保基于方式待选集的构造方法的完备性.
基于外延待选集的三元概念构造方法是利用三元背景K诱导的形式背景K(1)的形式概念和其外延待选集来构造三元概念, 其速度主要取决于形式概念和外延待选集的数量.
上述三种三元概念构造方法的原理相同, 主要区别在于通过诱导得到的每个形式背景的形式概念和待选集的数量不同, 这些差异直接影响构造三元概念的速度.因此针对不同的三元背景, 可选择最合适的三元概念构造方法, 加快获取三元概念的速度.
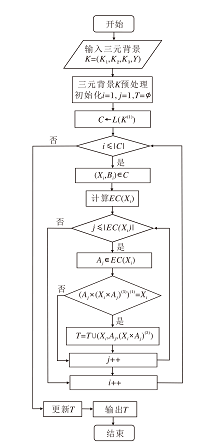
设K=(K1, K2, K3, Y)为三元背景, 以基于外延待选集的三元概念构造算法为例, 具体算法步骤如算法1所示, 算法流程图如图1所示.
算法1 基于外延待选集的三元概念构造算法
输入 三元背景K=(K1, K2, K3, Y)
输出 三元概念集T
三元背景K预处理
T=Ø , C← L(K(1))
for each (X, B)∈ C do
计算EC(X)
for each A∈ EC(X) do
if (A× (X× A)(3))(1)=X then
T=T∪ (X, A, (X× A)(3))
end
end
end
更新 T
return T
第2节中介绍两类特殊的三元背景, 分别是正则三元背景和净化三元背景.对于一个三元背景而言, 正则且净化三元背景是最简化的, 因为在这种三元背景中没有冗余的对象、属性和条件.因此, 在获取三元概念时, 首先, 对原三元背景进行预处理, 删除冗余的对象、属性和条件, 得到正则且净化三元背景.然后, 利用算法获取该三元背景的三元概念.最后, 更新三元概念, 将已被删除的对象、属性和条件添加到对应的三元概念的外延、内涵和方式中, 进一步加快构造三元概念的速度.
记C3为形式背景K(1)的形式概念的集合, 则基于外延待选集的三元概念构造算法的时间复杂度为$O\left( \left| {{C}_{3}} \right|\times {{2}^{\left| {{K}_{3}} \right|}} \right)$.类似地, 令C1、C2分别为形式背景K(2)和K(3)的形式概念的集合, 则基于内涵待选集的三元概念构造算法的时间复杂度为$O\left( \left| {{C}_{1}} \right|\times {{2}^{\left| {{K}_{1}} \right|}} \right)$, 基于方式待选集的三元概念构造算法的时间复杂度为$O\left( \left| {{C}_{2}} \right|\times {{2}^{\left| {{K}_{2}} \right|}} \right)$.因此3种算法对应的最小的时间复杂度为$O\left( \left| {{C}_{i}} \right|\times {{2}^{\left| {{K}_{i}} \right|}} \right)$, 其中
$\left|K_{i}\right|=\min \left\{\left|K_{1}\right|, \left|K_{2}\right|, \left|K_{3}\right|\right\} $.
故在选择构造方法时, 可根据不同的三元背景, 选择时间复杂度最小的三元概念构造方法.
关于三元概念的构造方法, Lehmann等[8]提出的枚举法, 是从对象幂集、属性幂集和条件幂集中选定两个幂集的任意子集, 逐个检查它们是否构成三元概念.以对象幂集和条件幂集为例, 枚举法的时间复杂度为O(
例5(续例4) 计算例1中三元背景
K=(K1, K2, K3, Y)
的所有三元概念, 详细步骤如下.
1)三元背景预处理.根据例2, 首先对三元背景K=(K1, K2, K3, Y)进行预处理, 删除冗余的对象(属性或条件), 得到正则且净化三元背景
K'=(K'1, K'2, K'3, Y').
由性质2知(K'1, K'2, Ø )、(K'1, Ø , K'3)、(Ø , K'2, K'3)一定为K'的三元概念, 因此在构造过程中不考虑外延、内涵为空的形式概念.
2)计算K'诱导的形式背景K'(1)的形式概念(除外延、内涵为空的形式概念).根据例4, K'(1)的形式概念如下:
$\begin{array}{l} (12, (A, a)), (23, (C, c)), \\ (1, (A, a)(A, b)(A, e)(B, a)(B, e)(C, a)), \\ (3, (A, b)(B, a)(B, b)(B, e)(C, c)(C, e)), \\ (13, (A, b)(B, a)(B, e)), \\ (2, (A, a)(A, c)(B, c)(C, b)(C, c)) . \end{array}$
3)计算每个形式概念外延对应的外延待选集(除空集以外的外延待选集).
(1)外延12的外延待选集:{a}.
(2)外延23的外延待选集:{c}.
(3)外延1的外延待选集:{abe, ae, a}.
(4)外延3的外延待选集:{b, abe, ce, e}.
(5)外延13的外延待选集:{b, ae}.
(6)外延2的外延待选集:{ac, c, bc}.
4)利用形式概念外延和其外延待选集生成相应的三元概念.
(1)外延12, 外延待选集:{a}.
(a× (12× a)(3))(1)=12,
故(12, a, A)为三元概念.
(2)外延23, 外延待选集:{c}.
(c× (23× c)(3))(1)=23,
故(23, c, C)为三元概念.
(3)外延1, 外延待选集:{abe, ae, a}.
(a× (1× a)(3))(1)=1,
故(1, a, ABC)为三元概念.
(abe× (1× abe)(3))(1)=1,
故(1, abe, A)为三元概念.
(ae× (1× ae)(3))(1)=1,
故(1, ae, AB)为三元概念.
(4)外延3, 外延待选集:{b, abe, ce, e}.
(b× (3× b)(3))(1)=3,
故(3, b, AB)为三元概念.
(abe× (3× abe)(3))(1)=3,
故(3, abe, B)为三元概念.
(ce× (3× ce)(3))(1)=3,
故(3, ce, C)为三元概念.
(e× (3× e)(3))(1)=3,
故(3, e, BC)为三元概念.
(5)外延13, 外延待选集:{b, ae}.
(b× (13× b)(3))(1)=13,
故(13, b, A)为三元概念.
(ae× (13× ae)(3))(1)=13,
故(13, ae, B)为三元概念.
(6)外延2, 外延待选集:{ac, c, bc}.
(ac× (2× ac)(3))(1)=2,
故(2, ac, A)为三元概念.
(c× (2× c)(3))(1)=2,
故(2, c, ABC)为三元概念.
(bc× (2× bc)(3))(1)=2,
故(2, bc, C)为三元概念.
5)正则且净化三元背景K'=(K'1, K'2, K'3, Y')的所有三元概念的集合如下:
$\begin{aligned} T= & \left\{\left(K_{1}^{\prime}, K_{2}^{\prime}, \varnothing\right), \left(K_{1}^{\prime}, \varnothing, K_{3}^{\prime}\right), \left(\varnothing, K_{2}^{\prime}, K_{3}^{\prime}\right), \right. \\ & (12, a, A), (23, c, C), (1, a, A B C) \\ & (1, a b e, A), (1, a e, A B), (3, b, A B) \\ & (3, a b e, B), (3, c e, C), (3, e, B C) \\ & (13, b, A), (13, a e, B), (2, a c, A) \\ & (2, c, A B C), (2, b c, C)\} \end{aligned}$
6)更新三元概念.添加被删除的对象、属性到上述三元概念中, 成为原三元背景的三元概念.
原三元背景删除的对象为4, 删除的属性为d.将其添加到T中对应的三元概念中, 则原三元背景K=(K1, K2, K3, Y)的所有三元概念如下:
(K1, K2, Ø ), (K1, Ø , K3), (Ø , K2, K3),
(124, a, A), (234, cd, C), (1, a, ABC),
(1, abe, A), (1, ae, AB), (3, b, AB),
(3, abe, B), (3, cde, C), (3, e, BC),
(13, b, A), (13, ae, B), (24, acd, A),
(24, cd, ABC), (24, bcd, C).
综上所述, 利用算法1所得三元背景
K=(K1, K2, K3, Y)
的三元概念共有17个, 与例1中的三元概念一致.
本文实验是在Intel(R) Core(TM) i5-8300H CPU, 24 GB内存的硬件环境下进行的, 使用Java实现基于待选集的三元概念构造算法.
三元背景由对象个数、属性个数、条件个数和三元背景密度控制, 实验使用的三元背景均为随机生成.为了减少随机生成的三元背景造成的算法运行时间误差, 后文每组实验的数据均为在相同实验条件下, 随机生成10个三元背景, 算法运行时间为10个三元背景的运行时间平均值.
文献[26]给出形式背景密度的定义, 现推广到三元背景上, 三元背景密度的定义如下.
定义12 三元背景密度ρ (1)是指三元背景中1值个数占0值和1值总数的百分比:
ρ (1)=
其中, N(1)表示三元背景中1值的个数, K1表示对象集, K2表示属性集, K3表示条件集, $\left| {{K}_{1}} \right|\times \left| {{K}_{2}} \right|\times \left| {{K}_{3}} \right|$表示3个集合个数乘积.
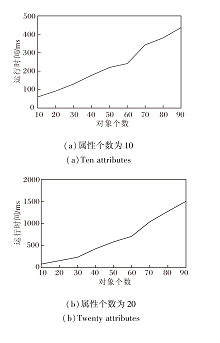
首先分析对象个数对算法运行时间的影响.设置属性个数为10, 20, 条件个数为5, 三元背景密度为0.3, 当对象个数从10增至90时, 运行时间如图2所示.
由图2可看出, 随着对象个数的增加, 运行时间也在增加, 在对象个数达到60之后, 运行时间的增加更明显.原因是此时对象对待选集数量的影响变大, 使三元概念数量的增幅变大, 导致算法的运行时间增幅变大.当属性个数从10增至20, 算法运行时间的倍数由最初的1~2倍, 慢慢增至4倍.
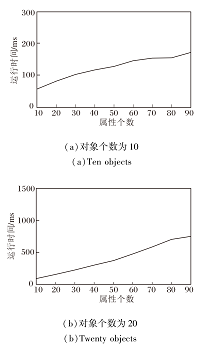
下面分析属性个数对算法运行时间的影响.设置对象个数为10, 20, 条件个数为5, 三元背景密度为0.3, 当属性个数从10增至90时, 运行时间如图3所示.
由图3可看出, 随着属性个数的增加, 算法的运行时间不断增加, 但慢慢趋于平缓.主要原因是对象个数和条件个数固定, 属性个数的增加不会导致待选集数量的明显增加, 使三元概念数量的增加也相对平缓, 因此算法运行时间的增加趋于平缓.当对象个数从10增至20, 算法运行时间的倍数由最初的2倍, 慢慢增至4倍.
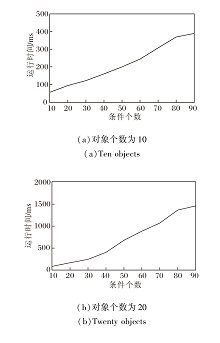
再分析条件个数对算法运行时间的影响, 设置对象个数为10, 20, 属性个数为5, 三元背景密度为0.3, 当条件个数从10增至90, 运行时间如图4所示.
由图4可看出, 随着条件个数的增加, 算法的运行时间不断增加, 最初的时间增加较明显, 但在条件个数到达80之后趋于平缓.原因是此时条件个数增加对待选集数量的影响降低, 使三元概念数量的增加趋于平缓, 因此算法运行时间的增加趋于平缓.当对象个数从10增至20, 运行时间的倍数由最初的1~2倍, 慢慢增至4倍.
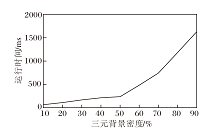
最后分析三元背景密度对算法运行时间的影响.设置对象个数为10, 属性个数为10, 条件个数为10, 三元背景密度从10%增至90%时, 运行时间如图5所示.由图可看出, 在三元背景密度小于50%时, 其对算法运行时间的影响较小, 但三元背景密度超过50%后, 算法运行时间大幅增加.主要原因是, 在低密度阶段三元背景中的三元关系较少, 使待选集的增量较少, 因此运行时间增幅较小, 但随着三元背景密度的增加, 待选集的增量也逐渐变多, 从而使运行时间大幅增加.
为了进一步验证本文算法的性能, 在不同的三元背景上与文献[8]算法、文献[25]算法进行对比实验.
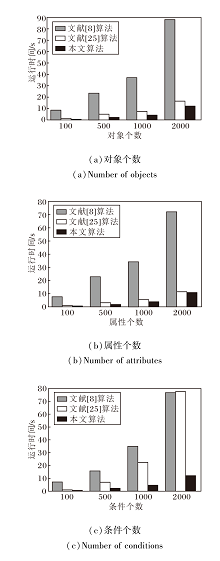
首先考察对象个数对3种算法运行时间的影响.设置三元背景对象个数分别为100, 500, 1 000, 2 000, 属性个数为10, 条件个数为10, 三元背景密度为0.3.具体运行时间如图6(a)所示.
再考察属性个数对3种算法运行时间的影响.设置三元背景对象个数为10, 属性个数分别为100, 500, 1 000, 2 000, 条件个数为10, 三元背景密度为0.3.具体运行时间如图6(b)所示.
最后考察条件个数对3种算法运行时间的影响.设置三元背景对象个数为10, 属性个数为10, 条件个数分别为100, 500, 1 000, 2 000, 三元背景密度为0.3.具体运行时间如图6(c)所示.
由图6可见, 本文算法都保持最短的运行时间, 这充分说明本文算法获取三元概念的有效性.
从图6可看出, 本文算法运行时间明显低于文献[8]算法, 原因在于文献[8]算法要考虑两个幂集, 而本文算法只考虑一个幂集, 因此运行时间较短.
从图6还可看出, 在(a)、(b)中本文算法稍快于文献[25]算法, 但在(c)中文献[25]算法的运行时间大约是本文算法的3~5倍, 并且随着条件个数的增加, 文献[25]算法与本文算法运行时间的差距越来越大.主要原因在于文献[25]算法需要计算每个单条件下的三元概念, 并重复遍历, 而本文算法是考虑条件集的整体, 因此当条件个数不断增加时, 本文算法依然保持较低的运行时间.
综合分析, 本文算法的性能最佳.
为了更快速地获取三元概念, 本文提出基于待选集的三元概念构造方法.首先, 定义净化三元背景和正则三元背景, 删减冗余信息, 简化三元背景.然后, 提出基于待选集的三元概念构造方法, 定义待选集, 加快获取三元概念的速度, 并证明其完备性.最后, 给出基于待选集的三元概念构造算法, 并通过实验验证本文算法性能较优.
三元概念的获取仍有许多值得研究的问题.例如, 现实中的数据往往是动态变化的, 这种情况下三元概念的更新不可避免, 今后可考虑三元概念动态更新问题.此外还可考虑三元背景上的规则获取问题, 这些研究都将有助于丰富三元概念分析理论.
本文责任编委 张燕平
Recommended by Associate Editor ZHANG Yanping
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|