何玉林,博士,研究员,主要研究方向为大数据系统计算技术、多样本统计分析方法、机器学习算法及应用.E-mail:yulinhe@gml.ac.cn.
作者简介:

赖俊龙,硕士研究生,主要研究方向为社交网络链路预测算法、随机权重网络优化及应用.E-mail:junlong_lai1@163.com.

崔来中,博士,教授,主要研究方向为互联网体系结构、边缘计算、大数据、人工智能驱动的新型网络优化设计.E-mail: cuilz@szu.edu.cn.

黄哲学,博士,教授,主要研究方向为数据挖掘、机器学习、大数据系统计算技术.E-mail:zx.huang@szu.edu.cn.

尹剑飞,博士,副教授,主要研究方向为大数据、机器学习、统计和数值优化.E-mail: yjf@szu.edu.cn.
社交网络链路预测旨在根据已知的网络信息预测未来的链接关系,在推荐系统和合著网络中具有重要作用.然而,现有链路预测算法往往忽视社交网络的多元演化特点,训练时间复杂度较高,限制其执行效率.针对上述问题,文中提出基于多演化特征的社交网络链路预测算法(Multi-evolutionary Features Based Link Prediction Algorithm for Social Network, MEF-LP).首先,设计一种简单高效的时间极限学习机模型,利用门控网络和极限学习机自编码器传递与聚合社交网络快照序列的时间信息.然后,构建多个深度极限学习机,对时间特征进行多角度映射,挖掘社交网络不同的演化特征,并最终融合成综合演化特征.最后,使用基于极限学习机的分类器完成链路预测.在6个真实社交网络上的实验表明,MEF-LP能合理学习社交网络的多演化特征,并获得较优的预测性能.
HE Yulin, Ph.D., professor. His research interests include big data system computing technologies, statistical analysis methods for multi-sample, and machine learning algorithms and their applications.
About Author:
LAI Junlong, Master student. His research interests include link prediction algorithms for social networks, optimizations and applications of random weight networks.
CUI Laizhong, Ph.D., professor. His research interests include internet architecture, edge computing, big data and AI-driven new network design and optimization.
HUANG Zhexue, Ph.D., professor. His research interests include data mining, machine learning and big data system computing technologies.
YIN Jianfei, Ph.D., associate professor. His research interests include big data, machine learning, and statistics and numerical optimizations.
Social network link prediction aims to predict future link relationships based on known network information, in which there are important applications for recommender systems and co-authorship networks. However, existing link prediction algorithms often ignore multi-evolutionary features of social networks and have high training time complexity, limiting their execution efficiency and application performance. To address these problems, a multi-evolutionary features based link prediction algorithm for social network(MEF-LP) is proposed. Firstly, a simple and efficient time extreme learning machine model is designed to transfer and aggregate the temporal information of social network snapshot sequences, using gated networks and extreme learning machine self-encoders. Secondly, multiple multilayer extreme learning machines are constructed to map temporal features from multiple perspectives, mining different evolutionary features of social networks and ultimately integrating them into comprehensive evolutionary features. Finally, the extreme learning machine-based classifiers are utilized to complete the link prediction. Experiments on six real social networks show that MEF-LP can reasonably learn the multi-evolution features of social networks and achieve better prediction performance.
现实世界中的各种社会实体之间的关系形成社交网络, 其中, 社会实体可以是人、组织或国家, 实体之间的关系可以是不同类型的关系, 如友谊、合作、邮件往来等.近年来, 社交网络中的链路预测引起学者们的广泛关注.链路预测是一种根据已知的网络结构信息预测未来网络链接关系的技术, 在日常生活中具有广泛应用, 如朋友推荐[1]、合著关系预测[2, 3]、社区发现[4]等.准确的链路预测对提升这些实际应用的性能和质量至关重要.
社交网络在现实生活中具备如下特点:1)社交网络是动态变化的, 随着时间的推移, 人际关系、合作关系等的不断变化会导致网络结构持续动态演变; 2)社交网络呈现多元演化的特点, 多种潜在因素(如工作日与节假日)的不同活动模式以及节点间不同的社交行为, 使网络呈现多元演化的状态; 3)社交网络的变化是高度非线性的, 这种频繁互动可迅速改变网络结构.鉴于上述特点, 设计有效的社交网络链路预测算法时, 必须充分考虑社交网络的动态性、多样性和非线性, 以提高算法的预测准确性和适应性.
现有的链路预测算法可根据其关键技术分为三类:基于相似性指数的链路预测算法、基于矩阵分解的链路预测算法及基于深度学习的链路预测算法.基于相似性指数的链路预测算法通常通过衡量节点间的相似性以推断它们之间是否存在链接.常用的相似性指数包括AA指数[5]和Katz指数[6]等.基于矩阵分解的链路预测算法通常将社交网络的邻接矩阵分解为多个低维矩阵的乘积, 将网络中的节点和边映射至低维向量空间, 并利用这些学到的潜在表示预测未来链接.基于深度学习的链路预测算法可细分为与任务无关的图嵌入方法和针对链路预测任务的方法.该类方法通过建立深度学习模型以提取网络结构中的深层次抽象特征, 再将学到的特征用于链路预测等下游任务.
尽管现有链路预测算法已取得不错的预测效果, 但深入分析后发现它们仍存在一些固有的缺陷, 需要进一步完善与改进.1)现有算法通常仅考虑单一的网络演化特征, 忽略社交网络在现实中是受多种因素影响的, 表现出多元演化的特性.这种局限性可能会影响预测的准确性.2)大部分算法只关注预测未来可能出现的新链接, 忽略预测未来可能断开的现有链接.对网络整体结构的预测有助于更深入地理解社交网络的演化过程.3)在训练过程中, 现有算法本身的高时间复杂度在一定程度上限制其在实际应用中的效率和实用性.
为了克服当前链路预测算法的不足, 本文提出基于多演化特征的社交网络链路预测算法(Multi-evolutionary Features Based Link Prediction Algorithm for Social Network, MEF-LP).为了建模社交网络的时间信息, 设计时间极限学习机模型(Time Extreme Learning Machine, T-ELM), 并使用随机映射将时间特征映射到不同的特征空间中, 从而学习社交网络的多元演化.基于融合后的综合演化特征构建极限学习机(Extreme Learning Machine, ELM)分类器, 完成社交网络链路预测任务.在6个真实社交网络数据集上的对比实验验证MEF-LP在链路预测问题上的优越性.
相似性指数是链路预测中常用的链路存在可能性评价指标.Newman[7]提出CN(Common Neighbour)指数, 认为两个节点之间的共同邻居越多, 它们之间的相似度就越高.这种方法属于局部相似性指数, 因为它只考虑节点的直接邻居.AA指数[5]和RA指数(Resource Allocation Index)[8]是CN的变体, 在计算相似度时对邻居节点的连接度进行加权, 通常被视为局部相似性指数的一种扩展或改进.Katz相似性指数[6]为不同阶的邻居节点赋予不同的权重, 用于考虑节点间更广泛的连接模式.Jeh等[9]提出Sim-Rank, 认为如果两个节点的邻居节点越相似, 那么这两个节点本身的相似性就越高.Katz指数和SimRank属于全局相似性指数, 计算复杂度较高.为了平衡预测准确性和计算效率, 引入准局部相似性指数, 如LP(Local Path)指数[10].
近年来, 链路预测领域出现一种新的趋势:以多种相似性指数或节点中心性作为输入特征, 再以分类算法作为预测器进行链路预测.Kumari等[11]使用6种不同的相似性指数构建特征向量, 并对比5种分类算法在链路预测任务上的表现.Kumar等[12]提出NC-LGBM, 以6种节点中心性作为特征, 通过LGBM(Light Gradient Boosting Machine)分类器进行链路预测.Liu等[13]集合15种相似度指数, 利用堆叠法结合逻辑回归与LGBM, 提出LLSLP(Logistic-Regression Light GBM Stacking Link Prediction).Chau- bey等[14]以多种相似性指数作为拓扑特征, 使用随机森林和XGBoost(Extreme Gradient Boosting)进行社交网络链路预测.
在链路预测中, 非负矩阵分解(Nonnegative Ma- trix Factorization, NMF)是一种常用的矩阵分解方法, 对要分解的矩阵有非负约束.DEEPEYE[15]和GrNMF(Graph Regularized NMF Algorithm)[16]使用NMF学习网络快照的嵌入, 并进行线性组合, 提取时间特征.Mahmoodi等[17]提出LPANMF(Link Pre-diction by Adversarial NMF), 采用对抗性非负矩阵分解, 并添加基于CN相似性的图形正则化项, 交替优化目标函数.Nasiri等[18]提出RGNMFAN(Robust Gra- ph Regularization NMF for Attributed Networks), 通过随机游走得到相似性矩阵, 采用图正则化技术结合相似性矩阵、网络结构和节点属性, 从而得到目标函数.Chen等[19]利用CN指数计算网络结构的相似性, 并使用NMF将其映射至多层低维潜在空间, 融合稀疏性约束以完成链路预测任务.Ma等[20]将链路预测任务建模为多标签学习任务, 提出MLjFE(Joint Multi-label Learning and Feature Extraction).
除了NMF以外, 还存在一些无非负约束的矩阵分解方法.Yu等[21]提出TMF(Temporal Matrix Facto-rization Model), 将网络结构分解为常数矩阵和时间矩阵, 并将时间矩阵建模为多项式函数.Yu等[22]提出LIST(Link Prediction Model with Spatial and Tem- poral Consistency), 将动态网络建模为时间函数, 并在每个快照上结合标签传播.
针对链路预测任务, Chen等[23]提出E-LSTM-D(Encoder-LSTM-Decoder), 将解码器和编码器设计为多层全连接层, 在它们之间叠加LSTM(Long Short-Term Memory), 用于学习时间依赖关系.Jiao等[24]提出TVAE(Temporal Network Embedding Method Based on the Variational Autoencoder Framework), 使用变分自编码器(Variational Autoencoder, VAE)进行网络结构特征学习, 并结合自注意机制和RNN(Recurrent Neural Networks)保持时间依赖性.Chen等[25]将GCN(Graph Convolution Network)嵌入LSTM单元中, 提出GC-LSTM.Tan等[26]引入时域和频域感知的信息, 基于图对比学习提出TF-GCL(Tem-porality- and Frequency-Aware Graph Contrastive Lear-ning for Temporal Networks).Mei等[27]提出GCN_MA, 结合GCN、RNN和多头注意力机制, 准确全面地完成链接预测任务.Qin等[28]综合GNN(Graph Neural Network)和改进的RNN, 提出基于GAN(Generative Adversarial Network)的IDEA(Inductive Dynamic Embedding Aggregation), 用于解决加权图的链路预测问题.Yin等[29]提出SRG(Super Reso-lution Graph), 从图像超分辨率(Super-Resolution, SR)的角度出发, 引入LR(Low-Resolution)图像和HR(High-Resolution)图像的概念, 通过条件归一化流实现LR图像和HR图像之间的转换.
与任务无关的图嵌入方法应用于链路预测时, 往往将学到的节点表示用于计算节点对的相似性, 从而判断节点对之间是否存在链接.Zhou等[30]基于三元闭包过程和网络演化过程中的平滑性, 设计DynamicTriad.Sankar等[31]利用自注意力机制对动态图的结构维度和时间维度建模, 构建DySAT(Dy- namic Self-Attention Network).
社交网络可定义为一个由一系列网络快照构成的集合G={G1, G2, ···, Gτ }, 其中Gt=(V, Et)表示第t个时间步的网络快照, t∈ {1, 2, ···, τ }.不失一般性, 本文工作只考虑所有网络快照共享同一个节点集V, 并且每个网络快照是无向无权图的情况.第t个时间步的网络快照Gt包含一组节点集V和一组边集Et, 使用邻接矩阵At∈
否则
社交网络链路预测问题定义为:给定先前观察到的l个网络快照{A1, A2, ···, Al}, 预测第l+1个时间步的网络快照Al+1, 网络快照Al+1的预测值为:
${{\widetilde{\mathbf{A}}}_{l+1}}=f({{\mathbf{A}}_{1}}, {{\mathbf{A}}_{2}}, \cdots , {{\mathbf{A}}_{l}})$
其中 f(· )表示社交网络链路预测方法.
ELM是一种特殊的单隐藏层前馈网络(Single-Hidden Layer Feedforward Network, SLFN), 已有的研究成果表明ELM在多种实际应用中具有较优的泛化性和较快的训练速度[32].ELM由输入层、单隐藏层和输出层构成, 随机选取输入权重和隐藏层偏置, 无需调整, 训练中唯一要确定的参数是输出权重, 可通过求解隐含层输出矩阵的伪逆得到[33].
假定有一个包含N个样本的训练集(xi, ti), 其中i∈ {1, 2, ···, N}, 样本特征
xi=
样本标签
ti=
具有L个隐藏层神经元和激活函数σ (· )的标准SLFN的数学表示形式:
$\begin{array}{l} h\left(\boldsymbol{x}_{i}\right)=\sigma\left(\boldsymbol{w} \boldsymbol{x}_{i}+\boldsymbol{b}\right), \\ h\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}} \boldsymbol{\beta}=\boldsymbol{t}_{i}^{\mathrm{T}}, i \in\{1, 2, \cdots, N\}, \end{array}$ (1)
其中,
w=
表示输入权重,
b=
表示隐藏层偏置, β ∈ RL× m表示隐藏层和输出层之间的输出权重.式(1)可写为矩阵形式:
$\mathbf{H\beta }=\mathbf{T}$, (2)
其中, H∈ RN× L, T∈ RN× m.
在ELM中, 随机初始化设定输入权重和隐藏层偏置, 一旦设定就不再改变.因此, 训练SLFN的过程实际上就是求解式(2)的解, 根据文献[34], 该线性系统的最小二乘解为:
$\mathbf{\hat{\beta }}={{\mathbf{H}}^{\mathbf{\dagger }}}\mathbf{T}$
其中H† 表示隐藏层输出矩阵H的Moore-Penrose广义逆.为了使模型具有更好的泛化性能, 可添加L2正则化项, 此时式(2)的求解可转化为如下优化问题:
$\min \left(\frac{1}{2}\|\boldsymbol{\beta}\|_{\mathrm{F}}^{2}+\frac{C}{2}\|\boldsymbol{H} \boldsymbol{\beta}-\boldsymbol{T}\|_{\mathrm{F}}^{2}\right) $,
其中C表示正则化系数.通过求解该优化问题, 得到其解为
$\hat{\boldsymbol{\beta}}=\left(\frac{\boldsymbol{I}}{C}+\boldsymbol{H}^{\mathrm{T}} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{T}$, (3)
其中I表示单位矩阵.
自动编码器(Autoencoder, AE)是一种无监督神经网络, 通过对输入进行编码, 再进行解码以重构原始输入.ELM-AE是一种创新的神经网络自编码方法, 继承ELM快速训练的优点, 并能迅速重构输入数据.与ELM不同, ELM-AE的输出即为其输入, 对随机初始化的输入权重和隐藏层偏置正交化:
wTw=I, bTb=I.
可通过式 (3) 计算得到ELM-AE的输出权重.求得权重β 后, 通过
H1=σ (H0β T)
有意义地表示输入特征, 即将输入特征映射到新的特征空间, 其中, H0表示输入特征, H1表示变换后的特征.
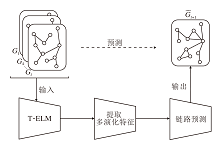
针对社交网络多元演化的特点和现有模型训练复杂度较高的问题, 本节提出基于多演化特征的社交网络链路预测算法(MEF-LP), 总体架构如图1所示.
MEF-LP主要分成3部分.1)时间极限学习机模型(T-ELM).将社交网络快照序列的时间信息进行传递与聚合, 学习网络的时间特征.2)多演化特征的提取.通过多个具有不同权重和偏置的深度极限学习机(Multilayer ELM, ML-ELM)学习不同的演化特征, 融合这些特征, 形成综合的特征表示.3)链路预测.使用ELM分类器完成社交网络未来链路的预测.
传统的链路预测算法通常集中于分析静态网络结构, 但现实世界的社交网络是持续随时间演变的.静态链路预测算法虽然简化问题, 却因未能捕捉到网络的动态特性往往导致预测准确性不足.在链路预测中, RNN是学习网络动态性常用技术之一, 通过记忆先前时间步的信息, 并应用于当前时间步, 可有效处理时序数据.
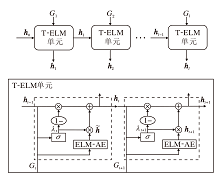
然而, 基于RNN的社交网络链路预测算法存在计算复杂性较高的挑战.为了解决这一问题, 本文设计T-ELM, 结构如图2所示.T-ELM由多个T-ELM单元组成, 每个T-ELM单元负责处理先前时间步的社交网络快照信息和当前时间步的社交网络快照信息.具体地, 第t个T-ELM单元把第t-1个T-ELM单元的输出ht-1和第t个时间步的网络快照Gt作为输入, 并输出新的特征ht.因此, 对长度为l的社交网络快照序列而言, 需要l个T-ELM单元, 这些单元依次连接, 分别处理时间步为1, 2, ···, l的社交网络快照.
为了清晰描述T-ELM单元的结构, 不失一般性, 本文以第t个T-ELM单元作为示例, 详细描述其计算流程.给定训练数据集Z∈ RN× l× |V|× |V|, 其中, N表示样本个数, 每个样本是一个社交网络快照序列{G1, G2, ···, Gl}, l表示序列长度, $|V|\times |V|$表示社交网络快照对应的邻接矩阵维度.为了以向量的形式处理每个网络快照, 将训练数据集上的邻接矩阵转化为一维向量, 即通过
X=Flatten(Z)
计算得到转化后的训练数据集X∈ RN× l× D, 其中$D=\text{ }|V{{|}^{2}}$.在训练中, Gt以xt的形式输入第t个T-ELM单元, 其中xt∈ RN× D.通过ELM-AE学习它的低维特征表示${{\mathbf{\tilde{h}}}_{t}}$, 该计算过程可表示为
${{\mathbf{\tilde{h}}}_{t}}=\sigma ({{\mathbf{x}}_{t}}\cdot \mathbf{\beta }_{t}^{T})$,
其中, ${{\mathbf{\tilde{h}}}_{t}}\in {{\mathbf{R}}^{N\times L}}$表示第t个时间步社交网络快照的信息, β t∈ RL× D表示权重参数, 通过式(3)完成该参数训练过程.此外, 先前时间步的信息ht-1∈ RN× L也输入第t个T-ELM单元, 将其与xt进行拼接, 通过非线性变换得到更新门λ t∈ RN× L, 该过程表示如下:
λ t=σ ([ht-1, xt]· Wt), (4)
其中, Wt表示服从0~1均匀分布的随机矩阵.更新门λ t用于控制先前时间步的信息ht-1和当前信息${{\mathbf{\tilde{h}}}_{t}}$对输出特征ht的影响程度, 它的元素取值范围为0~1, 表示门控信号.为了聚合先前时间步的信息和当前信息, 使用更新门对它们加权求和, 得到第t个T-ELM单元的输出特征:
${{\mathbf{h}}_{t}}=(1-{{\mathbf{\lambda }}_{t}})* {{\mathbf{h}}_{t-1}}+{{\mathbf{\lambda }}_{t}}* {{\mathbf{\tilde{h}}}_{t}}$,
其中* 表示逐元素乘法.门控信号越接近0, 表示ht-1对输出特征ht的影响越大; 越接近1, 表示${{\mathbf{\tilde{h}}}_{t}}$对输出特征ht的影响越大.
第t个T-ELM单元的输出特征ht在学习当前社交网络快照信息的同时, 也保留历史社交网络快照的信息.后续ht输入第t+1个T-ELM单元, 从而完成社交网络时间信息的传递.特别地, 初始状态的h0为零矩阵.整个T-ELM由多个T-ELM单元堆叠而成, 每个T-ELM单元以ELM的训练方式进行训练.因此, T-ELM的训练过程是按时间步顺序逐层进行的, 不需要复杂的迭代优化, 训练的时间复杂度较低.
现实世界中, 社交网络的演化是由多种因素驱动的, 展现多样化的特点.例如:某一社会事件的发生可能引发人们对特定话题的关注, 从而推动相关讨论的蔓延; 一个人在某一时期对音乐特别感兴趣, 与喜好相同的人建立联系.他的兴趣也可能在未来转向其它领域, 导致社交网络的结构随之发生变化.这些现象表明, 仅考虑单一演化特征不足以反映现实中社交网络的复杂性, 因此, 对社交网络的多元演化进行建模是准确预测未来链接的关键.
受ELM的随机映射思想[35, 36]启发, 可通过不同的权重和偏置将数据映射至不同的特征空间中.此外, 随着模型深度的增加, 原始数据的低层次特征可被逐层映射至新的特征空间, 形成高阶的特征表示.基于这一理念, 本文采用k个具有不同权重和偏置的ML-ELM学习社交网络的多元演化特征.相比其它深度网络, ML-ELM的优势在于它不需要迭代优化, 而是通过堆叠ELM-AE构建深层网络, 这不仅简化训练过程, 还提高模型的泛化能力.
多演化特征的提取过程如图3上半部分所示, 输入为社交网络的时间特征hl, 输出为经过k个不同演化特征融合后的综合特征$\mathbf{\tilde{H}}$.本文描述第j个ML-ELM学习第j个演化特征的过程, 剩余的k-1个演化特征的学习过程与此类似.在T-ELM中, 可得到长度为l的社交网络快照序列的时间特征hl∈ RN× L, 其中, N表示样本个数, L表示每个样本的特征维度.给定社交网络时间特征hl, 将其输入第j个ML-ELM,
将时间特征映射至新的特征空间, 第1层网络输出的特征:
其中
其中,
假定k个不同的ML-ELM输出的社交网络演化特征分别表示为
在完成不同演化特征的维度对齐后, 记
$\widetilde{\boldsymbol{H}}=\operatorname{Average}\left(\sum_{j} \boldsymbol{H}_{j}^{c_{j}}\right) \in \mathbf{R}^{N \times L_{c}}$,
其中Average(· )表示均值操作.
为了平衡计算复杂度和特征表达的需求, 本文选取3个ML-ELM, 即令k=3.每个ML-ELM都采用两层结构.在这3个ML-ELM中, 第1层网络分别采用不同的隐藏层神经元个数
分别表示对社交网络时间特征的压缩映射、等维映射和稀疏映射.
在成功提取社交网络快照序列的特征之后, 接下来的任务是构建一个能进行链路预测的分类器.本文使用ELM构建分类器, 具体链路预测的提取过程如图3下半部分所示, ELM分类器将学到的综合演化特征$\mathbf{\tilde{H}}$作为输入, 然后根据真实标签进行网络参数的训练, 最后利用训练好的模型预测未来链路, 并输出预测结果${{\widetilde{\mathbf{A}}}_{l+1}}$.
训练数据集上的真实标签Y∈ RN× |V|× |V|, 其中N表示样本个数.每个样本对应一个未来社交网络快照Gl+1, 而$|V|\times |V|$表示Gl+1对应的邻接矩阵维度.为了便于以向量的形式进行计算, 将Y中的邻接矩阵转化为一维向量, 转化后的训练标签为:
Agnd=Flatten(Y)∈ RN× D,
其中$D=\text{ }|V{{|}^{2}}$.为了训练ELM分类器中的参数β ∈
$\mathcal{L}=\frac{1}{2}\left\| \mathbf{\beta } \right\|_{F}^{2}+\frac{C}{2}\left\| \mathbf{\tilde{H}\beta }-{{\mathbf{A}}_{gnd}} \right\|_{F}^{2}$,
其中C表示正则化系数.计算$\mathcal{L}$的梯度$\nabla \mathcal{L}$, 则
$\frac{\partial \mathcal{L}}{\partial \mathbf{\beta }}=\mathbf{\beta }+C{{\mathbf{\tilde{H}}}^{\top }}\mathbf{\tilde{H}\beta }-C{{\mathbf{\tilde{H}}}^{\top }}{{\mathbf{A}}_{\mathbf{gnd}}}$.
由于(I+CHTH)是可逆的, 其中I表示单位矩阵, 可解得如下$\nabla \mathcal{L}=0$的结果:
$\mathbf{\hat{\beta }}={{(\frac{\mathbf{I}}{C}+{{\mathbf{\tilde{H}}}^{T}}\mathbf{\tilde{H}})}^{-1}}{{\mathbf{\tilde{H}}}^{T}}{{\mathbf{A}}_{\mathbf{gnd}}}$.(5)
因为Hessian矩阵
$\nabla {{\mathcal{L}}^{2}}=\left( \mathbf{I}+\mathbf{C}{{\mathbf{H}}^{\top }}\mathbf{H} \right)$
为正定矩阵, 所以$\mathbf{\hat{\beta }}$为目标函数$\mathcal{L}$的严格最优解.
在完成ELM分类器的训练后, 使用训练后的模型预测第l+1个时间步社交网络快照, 第l+1个时间步社交网络快照对应的邻接矩阵为:
$\widetilde{\boldsymbol{A}}_{l+1}=\widetilde{\boldsymbol{H}} \hat{\boldsymbol{\beta}} \in \mathbf{R}^{N \times D}$.(6)
MEF-LP的整体训练过程如算法1所示.
算法1 MEF-LP的训练流程
输入 训练样本Z, 训练标签Y, 时间步长l
输出 训练好的 f* (· )
FOR t=1, 2, ···, l DO
IF t=0 THEN
emb[t]=ae_elm(A0)
ELSE
temp_emb=ae_elm(At)
通过式(4)计算更新门λ t
emb[t]=(1-λ t)emb[t-1]+λ t· temp_emb
END IF
END FOR
multi_ features[1]=ml_elm_compressed(emb[-1])
multi_ features[2]=ml_elm_sparse(emb[-1])
multi_ features[3]=ml_elm_equal(emb[-1])
通过式(5)训练ELM分类器
通过式(6)进行链路预测
MEF-LP的时间复杂度主要包含T-ELM、多演化特征模块、链路预测模块3部分.在T-ELM中, 主要是对式(4)的计算, 相应的计算复杂度为
O(N(L+D)L),
其中, N表示样本个数, L表示T-ELM输出的特征维度, D表示输入数据的特征维度, 具体数值为节点数的平方.在多演化特征模块中, 计算复杂度由多个ML-ELM组成, 每个ML-ELM的计算复杂度为
O(NLL1+NL1L2+···+NLc-1Lc),
其中Li, i∈ {1, 2, ···, c}表示ML-ELM特征变换过程中的特征维度.在链路预测模块中, 主要是对式(6)的计算, 时间复杂度为O(NLcD).由于网络节点数总大于其它参数, 因此, MEF-LP的整体时间复杂度为
O(D)=O(
当前的链路预测算法的时间复杂度通常为关于节点数的平方或更高, 如SRG[29]的时间复杂度为节点数的立方级别.尽管MEF-LP未能将时间复杂度降至平方级别以下, 但在训练过程中, MEF-LP只需一次训练即可实现对未来链路的高质量预测, 而现有算法通常需要多次迭代训练才能达到较优的预测性能.后续实验也验证现有算法的训练时长显著多于MEF-LP.
本节在6个公开的社交网络数据集上验证MEF-LP的性能, 将数据集按照6:2:2的比例随机划分成训练集、验证集和测试集.数据集基本信息如表1所示.
| 表1 实验数据集的基本信息 Table 1 Basic information of experimental datasets |
数据集的详细描述如下.
1)Haggle(contact)数据集(http://konect.cc/networks/contact).人与人之间的接触网络, 两个节点的链接表示两个人之间有过接触.
2)fb-forum数据集(https://networkrepository.com/fb-forum.php).用户在类似facebook的论坛中的互动活动.
3)Enron(ia-enron-employees)数据集(https://networkrepository.com/ia-enron-employees.php).美国能源公司Enron的电子邮件数据集, 时间跨度为1999年至2002年.
4)Radoslaw(ia-radoslaw-email)数据集(https://networkrepository.com/ia-radoslaw-email.php).中型制造公司员工之间的内部电子邮件通信网络.
5)Malawi(contact-patterns-in-a-village-in-rural-malawi)数据集(http://www.sociopatterns.org/datasets/contact-patterns-in-a-village-in-rural-malawi).关于马拉维村庄中社区之间联系的数据集, 这些联系包括社交关系、资源共享等.
6)InVS13(copresence-InVS13)数据集(https://networkrepository.com/copresence-InVS13.php).In-VS13研究项目中的COPRESENCE数据集, 主要涉及人们在现实生活中的互动情况.
所有实验均在Ubuntu服务器(CPU:Intel(R) Xeon(R) Gold 5118 CPU @2.30 GHz, GPU:NVIDIA GeForce RTX 2080 Ti)上进行.
本文引入如下3种评估指标以衡量链路预测算法的性能:均方根误差(Root Mean Squared Error, RMSE)、AUC(Area Under the Curve)和错配率(Mis- match Rate, MR)[37].
RMSE用于衡量预测值与真实值之间的差异程度, 能有效评估链路预测算法的预测精度, 数值越小表示算法的预测效果越优.具体计算公式如下:
$\text{RMSE}=\sqrt{\frac{1}{{{\left| V \right|}^{2}}}\left\| \mathbf{A}-\text{ }\widetilde{\mathbf{A}} \right\|_{F}^{2}}$,
其中,
AUC为一种综合性的预测性能评估指标, 同时考虑链路预测正确和预测错误的情况, 取值范围在0~1之间, 数值越大表示模型性能越优.具体计算公式如下:
AUC=
其中, n表示比较的次数, n'表示选取的存在链接的节点对比选取的不存在链接的节点对得分更高的次数, n″表示二者得分相同的次数.
在无权网络的链路预测问题中, MR考虑错误预测的链接数, 定义为预测错误的链接数(Nf)与节点个数的平方的比率.具体计算公式如下:
MR=
本节探讨参数选择对MEF-LP预测性能和收敛性的影响.MEF-LP的关键参数包括:T-ELM中的隐藏层神经元个数L0和正则化系数C0、多演化特征中第j个ML-ELM的第c层网络隐藏层神经元个数
本节在Radoslaw数据集上描述MEF-LP的参数选择过程.在实验中, 链路预测中的正则化系数范围设为{1, 5, ···, 300}, 其它正则化系数范围设为{1, 100, ···, 1 000}, 所有隐藏层神经元个数范围设为{5, 10, ···, 500}.上述取值范围是根据经验而定, 无固定标准, 过多过少分别存在欠拟合和过拟合问题.
T-ELM中隐藏层神经元个数L0和正则化系数C0在训练集和验证集上AUC曲线如图4(a)所示.由图可见, 在训练集上, 随着L0的增加, AUC指标先增加后减小.这种现象主要是因为当L0大于一定程度时, 模型的复杂度和计算难度都会迅速增加, 从而导致对训练数据的过度拟合.C0对AUC指标的影响呈现波动性.在验证集上, C0越大, 模型性能越优.最终本文选定L0=100和C0=900.
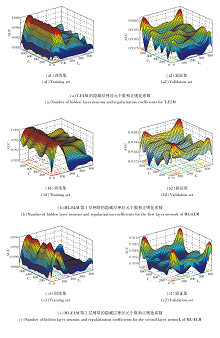 | 图4 Radoslaw数据集上MEF-LP中参数对AUC值的影响Fig.4 Effect of parameters on AUC values in MEF-LP on Radoslaw dataset |
在多演化特征中, ML-ELM第1层网络的隐藏层神经元个数L1和正则化系数C1在训练集和验证集上AUC曲线如图4(b)所示.
由图4(b)可看出, 当L1和C1的组合为(50, 960), (100, 30), (440, 1 000)时, MEP-LP在训练集和验证集的性能较优, 因此, 选定如下:
$\begin{array}{l} L_{1}^{1}=50, C_{1}^{1}=960 ; L_{1}^{2}=100, C_{1}^{2}=30 ; L_{1}^{3}=440, C_{1}^{3}=1000 . \end{array}$
在多演化特征中, ML-ELM第2层网络的隐藏层神经元个数L2和正则化系数C2在训练集和验证集上AUC曲线如图4(c)所示.
由图4(c)可看出, 当神经元个数L2=95和正则化系数C2=950时, MEF-LP在训练集和验证集上性能较优.
ELM分类器中正则化系数C在训练集和验证集上的AUC曲线如图5所示.
由图5可看出, 在训练集和验证集上, 随着C的增加, AUC先增加再趋于稳定.基于这一趋势, 选定C=100.实验表明MEF-LP训练过程的收敛性.
类似地, 其它数据集上的参数选择也依据AUC指标进行优化, 所有数据集上对应的MEF-LP参数汇总于表2中.
| 表2 MEF-LP参数汇总 Table 2 Summary statistics of MEF-LP parameters |
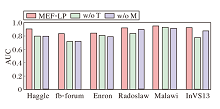
为了验证MEF-LP的合理性, 本文构建如下两个变体以研究核心组件的有效性.1)w/o T.在MEF-LP中删除T-ELM组件, 研究T-ELM是否有效学习社交网络的动态性.2)w/o M.在MEF-LP中删除多演化特征组件, 研究社交网络中的多元演化对预测性能的影响.
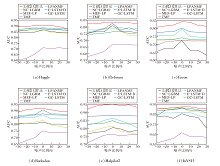
3种算法在6个数据集上的消融实验结果如图6所示.由图可观察到, 相比MEF-LP, w/o T的表现较差.特别地, 这种差异在fb-forum、InVS13数据集上表现得更明显.这一结果强调社交网络的动态性, 同时证明T-ELM可较好学到社交网络的时间特征.类似地, 删除多演化特征组件的变体w/o M, 在Haggle、fb-forum数据集上的AUC指标也出现明显下降, 这一发现进一步证实考虑社交网络的多元演化对于提升模型预测准确性的重要性.上述算法在RMSE和MR评估指标上也呈现出相似的趋势, 即核心组件的移除导致性能下降.上述结果一致表明, 本文设计的核心组件, 无论是T-ELM还是多演化特征模块, 都对提高社交网络链路预测的准确性起到积极作用.
本节选择如下6种新近提出的链路预测算法作为对比算法, 记录10次实验的平均结果和标准差.
1)文献[11]算法.使用CN[7]、Jaccard[38]、PA(Preferential Attachment)[39]、AA[5]这4种局部相似性指数和Katz[6]、SimmRank[9]这2种全局相似性指数作为特征向量, 使用SVM(Support Vector Machine)分类器进行链路预测.
2)NC-LGBM[12].它以LID(Local Interaction Den- sity)[40]、LTR(Linear Threshold Rank)[41]、Between- ness[42]、Katz[6]、Hubs and Authorities[43]和PageRank[44]共6种中心性作为节点特征, 并使用LGBM分类器进行链路预测.
3)LPANMF[17].在非负矩阵分解模型中添加一个攻击者矩阵, 并将基于CN指标的图正则化项添至目标函数中, 通过交替优化进行训练.
4)TMF[21].将动态网络的邻接矩阵表示为时间函数, 并分解每个矩阵, 通过建立一个最小二乘优化
问题求解参数.
5)E-LSTM-D[23].采用编码器-解码器架构和堆叠的LSTM预测未来网络链接, 其中编码器和解码器都采用全连接网络.
6)GC-LSTM[25].将GCN嵌入LSTM中, 从而改进LSTM的结构, 旨在学习节点的局部结构特征和动态网络的时间特征.
各算法在6个数据集上的RMSE、AUC和MR指标的对比结果如表3~表5所示, 表中黑体数字表示最佳值.
| 表3 各算法在6个数据集上RMSE值对比 Table 3 RMSE value comparison of different algorithms on 6 datasets |
| 表4 各算法在6个数据集上AUC值对比 Table 4 AUC value comparison of different algorithms on 6 datasets |
| 表5 各算法在6个数据集上MR值对比 Table 5 MR value comparison of different algorithms on 6 datasets |
由表3~表5可知, 文献[11]算法和NC-LGBM在AUC指标上的整体表现不如E-LSTM-D和GC-LSTM, 原因在于它们忽略社交网络的动态特性, 仅依赖网络的结构特征进行预测.TMF虽然考虑时间信息, 但其设计并非专门针对链路预测任务, 因此在AUC和MR指标上表现较差.LPANMF在RMSE指标上表现一般, 这与其在邻接矩阵中加入攻击者矩阵, 从而影响低秩矩阵的训练有关.基于深度学习的E-LSTM-D和GC-LSTM考虑社交网络的时间信息, 在RMSE和AUC指标上表现较优, 这证实深度学习方法在链路预测问题上的优势.然而, 它们在与MEF-LP的对比中仍显不足, 原因在于它们未充分利用社交网络的多元演化特征.
此外, 大部分算法在MR指标上表现不佳, 这意味着它们在预测社交网络中的大量链接时出现错误.在6个数据集上, MEF-LP在RMSE、AUC和MR指标上均最优, 这一结果表明MEF-LP在链路预测应用中的有效性和优越性.
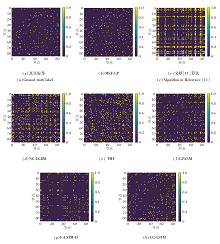
为了直观观察预测结果, 在Malawi数据集上随机选取一条测试样本, 将不同算法的预测结果以热力图的形式展示, 具体如图7所示, 图中, 元素0表示不存在链接, 元素1表示存在链接.
从图7(a) 的热力图中可发现, 真实社交网络是稀疏的, 只存在少量链接.文献[11]算法、NC-LGBM、TMF的预测结果过于稠密, 与实际的稀疏网络结构有较大偏差.其它方法则表现出较优的预测结果, 但相比真实网络, LMNMF、GC-LSTM的预测结果更稠密, 而E-LSTM-D的结果较稀疏.如(b)所示, 相比其它方法, MEF-LP的预测结果质量更高, 与真实网络的稀疏模式更吻合.
为了评估各算法在计算性能上的差异, 选取训练时间和AUC值作为评估指标, 具体结果如图8所示.
 | 图8 各算法在6个数据集上的计算性能对比Fig.8 Computational performance comparison of different algorithms on 6 datasets |
由图8可见, 文献[11]算法和NC-LGBM的训练时间与数据集的大小紧密相关, 例如, 在fb-forum、InVS13数据集上, 这两种算法的训练时间明显更长, 这是因为随着社交网络规模的增大, 一些相似性指标和节点中心性计算所需的时间也大幅增加.
LPANMF由于仅基于单个社交网络快照进行训练, 因此所需的训练时间较少, 而TMF、E-LSTM-D、GC-LSTM都是基于梯度下降迭代优化的, 训练时间远超其它算法.尽管TMF由于参数较少而具有较优的计算性能, 但其AUC指标并不理想.相比而言, 基于深度学习的E-LSTM-D和GC-LSTM在AUC指标上表现较优, 但也带来计算开销的显著增加.
从训练时间上看, MEF-LP所需的时间明显低于其它算法, 这表明MEF-LP在社交网络链路预测问题上的高效率.同时, 从AUC指标上看, MEF-LP表现优于其它算法.这些结果综合表明, 相比其它链路预测算法, MEF-LP不仅计算成本更低, 而且预测精度更高, 显示出其在实际应用场景中的明显优势.
在社交网络链接数据的收集过程中, 不可避免地存在噪声, 可能错误标记本不存在的链接或漏掉已存在的链接.为了评估MEF-LP在这种现实条件下的表现, 引入噪声扰动实验以测试鲁棒性.在社交网络快照数据中, 模拟现实世界中可能遇到的噪声问题, 在数据中加入不同程度随机噪声.在具体实验中, 按10%、20%、30%的比例随机增加或删除社交网络快照中的链接, 并使用AUC指标进行评估.
具体AUC曲线如图9所示, 图中横坐标表示加入或删除链接的比例.由图可看出, 随着噪声比例的增加, 所有算法的预测精度均随之下降, 但MEF-LP的AUC值始终最高, 这表明MEF-LP在面对不同噪声水平时, 展现出更强的鲁棒性.特别地, 在社交网络链接被随机删除30%的极端情况下, MEF-LP性能仍最优.考虑到现实世界中社交网络的稀疏性, MEF-LP在处理更稀疏的社交网络时, 具有更高的应用价值和准确性.
本文提出基于多演化特征的社交网络链路预测算法(MEF-LP), 准确高效地预测未来链接.MEF-LP综合社交网络的动态性和多元演化特点, 设计一种低时间复杂度的网络架构.首先, 使用极限学习机自编码器学习快照特征, 通过门控网络控制时间信息传递与特征聚合, 提出T-ELM.然后, 利用随机映射在不同的深度极限学习机中学习并融合不同演化特征.最后, 通过极限学习机分类器预测未来链路.实验表明, MEF-LP的预测准确率较高, 且训练时间较短、鲁棒性较高.未来工作主要集中在如下两方面.
1)提升社交网络的潜藏信息, 如结构特征和节点属性的利用效率, 进一步提高链路预测算法的准确率.
2)结合网络分割策略探索算法在分布式环境下的并行化实现技术, 用于处理大型网络的链路预测问题.
本文责任编委 陈恩红
Recommended by Associate Editor CHEN Enhong
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|