丁卫平,博士,教授,主要研究方向为数据挖掘、机器学习、粒计算、演化计算、大数据分析等.E-mail:dwp9988@163.com.
作者简介:

王静,硕士研究生,主要研究方向为深度学习、模糊理论.E-mail:wikj_1225@163.com.

尹涛,博士研究生,主要研究方向为粒计算、粗糙集、超图神经网络.E-mail:haszyt@163.com.

鞠恒荣,博士,副教授,主要研究方向为粒计算、粗糙集、机器学习、知识发现.E-mail:juhengrong@ntu.edu.cn.

黄嘉爽,博士,副教授,主要研究方向为脑网络分析、深度学习.E-mail:hjshdym@163.com.
深度神经网络可通过训练从大脑图像中预测年龄,作为识别衰老相关疾病的生物标志物.传统的脑龄预测方法往往依赖于单一模态的图像数据,而多模态数据可提供更全面的信息,提高预测精度.然而,现有的多模态融合方法往往不能充分利用不同模态之间的相关性和互补性.为了克服上述问题,文中提出基于多模态模糊特征融合的脑龄协同预测算法(CMFF),设计模糊融合模块和多模态协同卷积模块,可有效利用多模态信息之间的相关信息和互补信息.首先,利用卷积神经网络从多模态脑图中提取特征张量,径向拼接后整合到一个全局特征张量中.然后,利用模糊融合模块学习被模糊化的特征,再将特征应用到多模态协同卷积模块,通过特定的卷积层增强模态间的互补信息.最后,基于性别信息和经过模糊协同处理的特征执行年龄预测回归任务,得到准确的预测年龄.在SRPBS多重障碍MRI数据集上的实验表明,CMFF性能较优.
DING Weiping, Ph.D., professor. His research interests include data mining, machine learning, granular computing, evolutionary computing and big data analytics.
About Author:
WANG Jing, Master student. Her research interests include deep learning and fuzzy theory.
YIN Tao, Ph.D. candidate. His research interests include granular computing, rough sets and hypergraph neural networks.
JU Hengrong, Ph.D., associate professor. His research interests include granular computing, rough sets, machine learning and know-ledge discovery.
HUANG Jiashuang, Ph.D., associate pro- fessor. His research interests include brain net- work analysis and deep learning.
Deep neural networks can be trained to predict age from brain image and the predicted brain age serves as a biomarker for identifying diseases associated with aging. Traditional brain age prediction methods tend to rely on unimodal image data, whereas multimodal data can provide more comprehensive information and improve prediction accuracy. However, existing multimodal fusion methods often fail to fully exploit the correlations and complementarities between different modalities. To overcome these challenges, a collaborative brain age prediction algorithm based on multimodal fuzzy feature fusion(CMFF) is proposed. Fuzzy fusion module and multimodal collaborative convolution module are designed to effectively utilize the correlation and complementary information between the multimodal information. Firstly, feature tensors are extracted from multimodal brain images by a convolutional neural network, and are integrated into a global feature tensor via radial joins. Then, the fuzzy fusion module is employed to learn the fuzzified features, and these features are applied to the multimodal collaborative convolutional module to enhance the complementary information of these features through modality-specific convolutional layers. Finally, the age prediction regression task is performed based on the gender information and the fuzzy collaborative processed features to obtain an accurate predicted age. Experimental results on SRPBS multi-disorder MRI dataset demonstrate the superior performance of CMFF.
随着全球平均寿命的延长和人口老龄化趋势的加剧, 人们越来越关注衰老与神经退行性疾病之间的联系.衰老不仅是身体各系统功能逐渐衰退的过程, 也是大脑结构和功能逐渐变化的重要时期.神经退行性疾病[1, 2], 如阿尔兹海默病和帕金森病, 主要影响老年人群, 严重威胁他们的生活质量和健康.在这一背景下, 评估大脑健康状态, 及早发现和预防潜在神经退行性疾病变得尤为重要.
在脑龄预测任务中, 结构性磁共振成像(Struc-tural Magnetic Resonance Imaging, sMRI)、功能性磁共振成像(Functional Magnetic Resonance Imaging, fMRI)、弥散张量成像和核磁共振血管成像等神经影像模态数据被广泛应用.在预测大脑年龄时, 研究者们主要依赖单一模态数据和多模态数据这两类数据来源.
单一模态神经影像数据在脑龄预测的精度方面具有重要作用[3].T1加权(T1-weighted, T1w) MRI能提供高分辨率的大脑结构图像, 显示灰质、白质和脑脊液等组织结构的详细信息, 被广泛应用于探索大脑结构与认知功能、情绪调节、神经疾病诊断等研究领域.近期研究表明, 应用卷积神经网络(Convo- lutional Neural Network, CNN)与T1w MRI能预测受试者的年龄[4, 5, 6]; 基于Transformer模型与T1w MRI数据集可探索脑部结构信息, 执行脑龄预测任务[7, 8].
此外, fMRI单模态数据也被广泛应用于预测年龄任务[9, 10], 低频振幅(Amplitude of Low-Frequency Fluctuations, ALFF)、低频振幅比率(Fractional ALFF, fALFF)与局部一致性(Regional Homogeneity, ReHo)都是fMRI数据分析中的常用模态, 用于研究大脑的功能状态和连接性.Zhai等[11]应用fALFF构建功能网络模型, 相对准确地预测患者的脑龄.Guan等[12]发现ReHo在发育的大脑中会随着年龄的增长而降低, 这种变化可与脑龄预测关联.因此, fALFF、ReHo与T1w等不同模态的磁共振成像数据在脑龄预测任务中具有重要作用, 是未来监测疾病发展和治疗效果的重要生物标志物.
尽管单一模态的神经影像学数据在脑龄预测方面已取得一定成功, 但仍存在一些局限性.例如:sMRI数据提供关于大脑灰质和白质结构的详细信息, 但缺少功能活动的相关信息; fMRI反映大脑在不同任务和静息状态下的功能活动, 但缺少大脑结构的相关信息.单一模态数据往往只能提供特定方面的信息, 无法全局反映大脑的多方面特征, 泛化能力也受限, 这在很大程度上限制其在临床实践和科研中的应用.
为了解决这一问题, 研究者们开始探索整合不同模态信息的途径, 全局融合大脑结构和功能状态信息, 提高多模态特征的关联性, 进一步提升脑龄预测的准确性[13].研究发现, 不同模态的数据具有一定的相关性和互补性.例如:ALFF和fALFF模态的数据存在一定的相关性; sMRI和fMRI模态的数据呈现出一定的互补性.选择恰当的方式融合这些不同模态的信息可提高脑龄预测方法的准确率.然而, 现有的多模态数据融合方法通常采用简单拼接或加权融合的方式, 无法充分捕捉不同模态特征之间的相互作用.尽管多模态数据具有互补性, 现有方法却往往无法充分挖掘和利用这种互补性.例如:简单拼接可能导致信息冗余, 增加方法的复杂度, 不一定能提升预测性能; 简单的加权融合无法有效处理权重确定、特征空间差异、信息冗余和非线性关系等问题, 在脑龄预测任务中表现有限.
为了应对当前面临的挑战, 本文提出基于多模态模糊特征融合的脑龄协同预测算法(Collaborative Brain Age Prediction Algorithm Based on Multimodal Fuzzy Feature Fusion, CMFF).首先构建CNN, 初步提取各模态的特征, 再利用径向拼接的方式组合各模态特征, 形成一个全局特征张量, 全面捕捉数据的内在特性.然后, 根据输入特征维度计算空间相关性子集个数, 并基于子集个数初始化模糊测度矩阵大小, 计算模糊测度值, 进行归一化处理, 构造模糊测度矩阵.将模糊融合后的特征输入一个自定义的协同卷积层, 进一步增强算法的表征能力和模态间互补信息.最后, 将性别信息和经过模糊协同处理后的特征输入年龄预测模块执行回归任务, 得到预测年龄.实验表明CMFF能准确捕捉多模态数据之间的相关性和互补性, 提高预测性能.
脑龄预测是神经影像学和计算机科学交叉的研究方向, 分析脑部结构和功能的变化, 预测受试者的大脑年龄.随着先进的神经影像技术(如sMRI和fMRI), 以及机器学习和深度学习等方法的发展, 这一领域得到迅猛发展.脑龄预测任务的数据来源主要分为单一模态和多模态数据.
已有多种基于单一模态数据进行脑龄预测的方法取得显著成功[14, 15, 16, 17, 18, 19, 20].Cole等[16]使用CNN和高斯回归方法对T1w数据进行脑龄预测建模, 成功提取单一模态有效信息并准确预测健康个体的实际年龄.Peng等[17]提出SFCN(Simple Fully Convolutional Network), 融合数据增强、预训练、模型正则化、模型集成和预测偏差校正等多种技术, 应用T1w数据进行脑龄预测.He等[8]提出Global-Local Transformer, 通过注意力机制融合局部图像块的细粒度信息与全局上下文信息, 预测大脑年龄.Poloni等[20]使用单一模态数据, 进行阿尔茨海默病的诊断.然而, 这些都是基于单一模态医学图像数据进行脑龄预测研究, 未考虑多模态特征融合, 可能会导致部分特征关联信息的缺失, 限制方法的预测性能.
因此, 当前研究逐渐转向关注多模态融合过程中的相关性和互补性, 尝试结合不同模态的特征进行脑龄预测[21, 22, 23].Mouches等[6]通过两个独立的子模型分别对T1w MRI和TOF MRA(Time-of-Flight Mag-netic Resonance Angiography)进行年龄预测, 再通过一个线性回归模块对得到的两个预测年龄进行回归预测, 但未考虑不同模态特征融合时的相关性和互补性.在进一步的工作中, Mouches等[24]分别使用独立的多层感知器和CNN对T1w MRI和TOF MRA进行大脑年龄预测, 再通过线性组合模块融合得到的四个预测年龄.这种直接融合或组合多个模态预测结果的方式缺乏对模态之间关系的深入挖掘和融合, 同时缺乏对不同模态相关性信息和互补性信息的考虑.因此, 今后的研究需要更深入地挖掘模态之间的相关性和互补性, 并探索如何有效融合多模态的特征信息, 以进一步优化脑龄预测算法.
多模态特征融合方法可分为四类:特征级融合、决策级融合、混合级融合和模型级融合.
特征级融合又称早期融合, 是指在特征级上的融合, 即将不同形态的特征融合成统一的特征表示.一般通过简单拼接、加权求和、CNN或自注意机制实现[25, 26].Zhao等[27]构建一个双流密集网络, 从T2-sMRI(T2-weighted sMRI)和dMRI(Diffusion MRI)中学习模态特征, 再通过自注意力机制融合这些特征.Rallabandi等[28]通过二维傅里叶和离散小波变换将sMRI与PET(Positron Emission Tomography)图像融合, 在健康状况和痴呆分期的自动分类方面取得较令人满意的结果.然而, 这种融合方法可能会引入冗余信息和噪声, 降低方法的泛化性和准确性.
决策级融合又称后期融合, 是指在方法输出或决策层面的融合, 即结合不同模态的输出或决策[29].Asgharzadeh-Bonab等[30]提出决策级融合和特征级融合两种方案, 利用深度学习方法、正交Ripplet II变换技术和二维离散正交Stockwell变换技术, 将从MRI中提取的深度特征及其变换进行融合, 提高早期阿尔茨海默病诊断的准确性.然而, 这种方法通常假设各模态的决策相互独立, 容易忽略不同模态特征之间的相互性和互补性.
混合级融合是早期融合方法和晚期融合方法的结合, 在特征层和决策层同时融合[31].Song等[32]采用对齐和掩膜编码技术融合脑MRI和FDG-PET(18-Fluorodeoxyglucose Positron Emission Tomography)中的灰质组织区域.Zhou等[33]提出用于多模态核磁共振图像特征融合的Hi-Net(Hybrid-Fusion Net- work), 学习模态特定表示和多模态混合融合策略, 实现缺失模态的有效融合.然而, Hi-Net是两种方案的折中, 未能解决实质问题.
模型级融合是指使用同一模型同时处理来自多个模型的输入[34, 35].该方法通常设计一个多分支神经网络模型以处理不同模态的输入, 并在适当的层次上进行特征融合.Nie等[36]结合多层网络与传统的长短期记忆(Long Short-Term Memory, LSTM)网络, 实现文本、音频、视频特征的有效融合, 再输入全连接层中, 得到预测结果.然而, 这种融合方法通常需要设计复杂的神经网络结构, 花费大量的计算资源和训练时间.
基于模糊理论的深度学习方法在特征提取与表征学习、决策融合、不确定性建模、多模态数据融合等方面都展现出广泛的应用潜力.Dey等[37]提出基于模糊Choquet积分的分类器集成技术, 结合CNN和迁移学习, 成功分类胸部X射线图像.Bhowal等[38]结合信息论和联盟博弈理论, 提出一种评估模糊度量的方法, 并利用三组不同的模糊度量计算Choquet积分, 在COVIDx数据集上取得不错性能.Xue等[39]提出基于Choquet积分的多模态融合风险预测方法, 有效融合三种模态数据的信息, 得到可靠的预测结果.Palanisami等[40]在多种不同模态上进行实验, 利用高斯滤波器、Sugeno直觉模糊图像等技术, 成功生成具有良好视觉质量、对比度增强、无伪影的融合图像.Tirupal等[41]基于加权快速离散曲波变换、优化的Type-2模糊熵、混合元启发式算法等, 开发多模态医学图像融合模型.在这些研究中, Choquet积分被用于整合和分析多种数据或信息源, 可提高相关算法的性能.
尽管Choquet积分在其它领域, 如特征选择、分类器集成、信息融合等方面, 展现出强大的应用潜力, 模糊理论也在医学影像融合上颇有建树, 但在脑龄预测领域尚未得到充分应用.鉴于模糊理论在多模态信息融合方面具有一定优势, 或许可通过其整合多模态医学图像数据中的特征信息, 全面捕捉大脑结构和功能的复杂变化, 提高脑龄预测的精度.
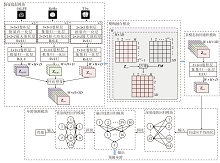
本文提出基于多模态模糊特征融合的脑龄协同预测算法(CMFF), 结构如图1所示.
CMFF主要包括四个模块:特征提取模块、模糊融合模块(Fuzzy Fusion Module, FFM)、多模态协同卷积模块(Multimodal Collaborative Convolutional Mo- dule, MCCM)、年龄预测模块.CMFF流程如算法1所示.
算法1 CMFF
输入 各模态脑部磁共振成像I, 性别G
输出 预测年龄y
step 1 构造用于各个模态的特征提取卷积层f1.
step 2 提取各模态特征Z=f1(I).
step 3 利用CNN提取的各模态特征进行径向拼接,
Zcat=
step 4 根据输入特征维度计算空间相关性子集的个数, 并初始化模糊测度矩阵FM的大小.
step 5 遍历空间相关性子集, 根据空间相关性子集中的特征权重计算模糊测度值, 并进行归一化处理, 构造模糊测度矩阵FM'.
step 6
for h in length(H) do
Z, Zindex=sorted(Zcat[h][:][:])
/* 按升序排序并记录对应的索引值* /
Z=cat((Z, zeros(length(H), 1)))
Zd=Z[:, :-1] -Z[:, 1:]
/* 根据排序后的索引计算差值* /
Z'=sum(2Zd)-ones(1)
/* 根据排序索引计算差值的累积和* /
ZCHI= FM'☉Z'
Z[h][:][:]=ZCHI/* 赋值回溯* /
Done
ZCHI=Z
step 7 采用协同卷积融合技术融合多模态模糊医学图像数据特征
Zcol=f2(ZCHI).
step 8 对模糊协同融合的多模态特征进行自适应最大池化操作
Zpool=f3(Zcol).
step 9 对多模态融合特征Zpool进行深度线性回归.
step 10 将性别G输入性别线性回归模块.
step 11 拼接经过回归的Zpool和G后, 输入融合特征线性回归模块, 得到预测年龄y.
在特征提取模块中, 借鉴SFCN[17]的特征提取策略, 对各模态图像进行卷积、批归一化、池化和激活等操作, 初步提取各模态的特征.最后将各模态特征数据径向拼接成融合模块的初始特征.
特征提取模块包含3条相同的通路, 分别用于提取fALFF、ReHo和T1w三个模态的特征, 通道数设置为32, 64, 128, 256, 256, 64.通路中前五个模块相同, 包含一个3× 3× 3的卷积层、一个批量归一化层、一个步长为2的2× 2× 2的最大池化层和一个ReLU(Rectified Linear Unit)激活函数层.第六个模块包含一个1× 1× 1的卷积层、一个批量归一化层和一个ReLU激活函数层.最后, 通过径向拼接, 整合成一个全局特征张量.
定理1[42] 给定一个论域U, 则U引申到单位区间[0, 1]的一个映射μ A:U→ [0, 1]称为U上的一个模糊集, 或U的一个模糊子集.μ A(· )称为模糊集A的隶属函数.对于∀ x∈ U, μ A(x)称为元素x对模糊集A的隶属度.
定理2[43]X为一个非空集合, P(X)为X的幂集, A⊆X, B⊆X为P(X)中的元素.若函数g:P(X)→ [0, 1]满足如下3个特性, 则称为模糊测度:
1)g(Ø )=0, g(X)=1;
2)若A⊆B⊆X, 则g(A)≤ g(B);
3)假设{Ai}为X子集的递增序列, 则
$g\left(\bigcup_{i=1}^{\infty} A_{i}\right)=\lim _{i \rightarrow \infty} g\left(A_{i}\right) $ .
为了解决现有的多模态融合方法往往不能充分利用不同模态之间相关性的问题, 本文提出基于模糊Choquet积分的模糊融合模块, 用于融合fALFF、ReHo、T1w三个模态的特征信息.该模块利用Cho- quet积分的非线性属性, 深入挖掘不同模态空间维度上的交互信息, 提升脑龄预测的准确度.关于模糊测度μ 的函数f的模糊Choquet积分[44]如下所示:
${{\text{C}}_{\mu (f)}}=\sum\limits_{i=1}^{n}{[(f({{x}_{i}})-f({{x}_{i-1}}))\cdot \mu ({{A}_{i}})]}$,
其中, x1, x2, ···, xn表示f(x)在集合X上的升序排列, Ai={xi, xi+1, ···, xn}表示f在xi之后值的集合, f(x0)=0, μ (Ai)表示模糊测度μ 在集合Ai上的值.
在多模态特征融合中, 设有不同模态的数据特征向量X=(x1, x2, ···, xn), 特征值xi表示第i个模态的特征值.本文应用Choquet积分进行多模态融合的步骤如下.
1)构造模糊测度矩阵.基于不同模态空间维度特征之间的相关性, 构建模糊测度矩阵, 衡量特征子集间的重要性.
2)特征值排序.对x1, x2, ···, xn进行递增排序, 得到x(1), x(2), ···, x(n).
3)计算积分.应用Choquet积分公式, 将排序后的特征值按模糊测度值加权融合, 得到最终模糊融合特征.
假设输入特征数为Nin, 则相关性子集的数量
V=
再初始化模糊测度矩阵FM.各模态维度特征相关性组合的模糊测度如表1所示.
| 表1 模糊测度矩阵 Table 1 Fuzzy measure matrix |
通过定义2和表1可发现, 模糊积分通过赋予每个模态维度特征相关性和不同维度特征相关性组合的权重, 衡量多模态空间维度特征子集相关性.
对于单一模态i(i=1, 2, ···, n), 初始化模糊测度:
μ ({Mi})=χ i,
其中 χ i表示模态fALFF的初始测度值.
对于任意非空子集A⊆{M1, M2, ···, Mn}, 模糊测度可通过如下递归方式实现:
$\mu (A)=\underset{B\subset A}{\mathop{\max }}\, (\mu (B))+{{\chi }_{A}}$,
其中, B表示A的子集, χ A表示A对应的模糊测度值.
为了保证模糊测度的值在[0, 1]内, 需要对每个模糊测度值进行归一化处理, 即
μ =min(μ , 1).
通过上述步骤构建最终的模糊测度矩阵FM'.
在模糊融合部分, 首先采用嵌套循环的方式遍历待融合特征张量Z的各个维度, 即高度H、宽度W、深度D.再对每个维度内的局部特征张量进行升序排序, 并记录对应的索引值, 将排序后的特征张量与一个全0张量拼接, 用于计算局部特征张量相邻元素之间的差值.然后, 根据排序后的索引计算差值的累和, 并映射到对应的索引位置, 得到累和向量Z'.最后, 将模糊测度矩阵FM'与累和向量Z'进行矩阵乘法计算, 得到局部特征向量的Choquet积分结果, 并将结果赋值回溯到原融合特征张量在Z中的对应位置.在遍历结束后, 所有局部特征向量完成模糊积分处理的操作, 整个融合特征张量Z也随之转化为模糊融合特征张量ZCHI.
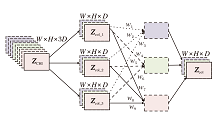
在深度学习中, 卷积操作是提取图像特征的关键步骤.传统的卷积操作往往只对空间维度(H, W)进行卷积, 但在处理多模态数据时, 不仅要提取空间特征, 还需要加强不同模态之间的特征交互.因此, 本文设计多模态协同卷积模块(MCCM), 用于对模糊融合后的特征数据进行径向交互性增强处理, 得到多模态模糊协同融合特征.MCCM结构如图2所示.
MCCM主要由特定参数配置的3D卷积层、批归一化层和ELU激活函数组成.每个组成部分都有其独特的作用, 并协同工作以实现多模态特征的有效融合.首先, 3D卷积层是模块的核心部分.设置核尺寸为(1, 1, 3), 确保卷积操作仅在深度维度上进行, 避免空间信息的损失.同时, 设定步长为1, 不进行填充, 保证卷积特征图的空间大小不变和原始特征边界的完整性.此外, 使用空洞卷积, 在W、H方向上不进行空洞插入, 在D方向上每两个特征元素之间插入一个空洞, 增大卷积核在深度维度上的感受野, 进一步增强3个模态特征之间的互补性.然后, 应用批归一化层对卷积层的输出进行归一化处理, 有助于加速训练过程, 提高算法收敛速度.最后, 应用ELU激活函数, 引入非线性特性, 学习并表达更复杂的多模态特征关系.
设输入数据为ZCHI, 维度为(W, H, D), 其中W、H、D分别表示宽度、高度和深度.MCCM的数学表达式为
Y=ELU(BN(Conv3D(ZCHI))),
其中, Conv3D(· )表示3D卷积操作, BN(· )表示批归一化操作, ELU(· )表示ELU激活操作.
年龄预测模块由如下3个线性回归模块组成, 每个模块内部均包含若干线性层及相应的激活函数层, 实现对不同来源特征的有效回归, 得到准确的预测值.
1)深度线性回归模块(Deep Linear Regression Module, DLRM).包含线性层和ELU激活函数层, 用于处理模糊协同与自适应最大池化处理后的64维特征, 提取与年龄预测密切相关的32维特征表示.
2)性别线性回归模块(Gender Linear Regre- ssion Module, GLRM).包含两层线性层和ELU激活函数层, 用于将原始的2维性别信息转化为更具预测价值的8维特征, 中间设置16维的隐藏层.
3)融合线性回归模块(Fusion Linear Regression Module, FLRM).包含两层线性层和RELU激活函数层, 用于处理DLRM输出的32维特征与GLRM输出的8维特征, 拼接得到40维融合特征, 映射至16维隐藏层, 完成融合与抽象, 再映射至单维度预测值, 得到最终的年龄预测结果.
均方误差损失(Mean Squared Error, MSE)和平均误差损失(Mean Absolute Error, MAE)是脑龄预测任务中常用的两种标准损失函数.考虑到MAE值大于1时, MSE会对较大误差给予更大的惩罚, 且现有方法得到的MAE值通常大于1[45, 46, 47], 所以本文应用MSE作为主损失函数.此外, 本文使用随机梯度下降优化算法, 结合Adam(Adaptive Moment Es- timation)自适应优化器调整损失函数参数.本文的优化排序对比损失函数加权融合MSE损失函数、斯皮尔曼损失函数[45]、年龄差损失函数和对比损失函数.相关公式定义如下:
${{L}_{MSE}}=\frac{1}{N}\sum\limits_{i}{{{({{{\hat{y}}}_{i}}-{{y}_{i}})}^{2}}}$
${{L}_{spear}}=\sum\limits_{i=0}^{N}{{{\left( Rank({{{\hat{y}}}_{i}})-Rank({{y}_{i}}) \right)}^{2}}}$
${{L}_{diff}}=\frac{1}{N}\sum\limits_{(i, j)}{(({{{\hat{y}}}_{i}}-{{{\hat{y}}}_{j}})-({{y}_{i}}-{{y}_{j}})}{{)}^{2}}$
其中:Rank(· )表示分数阶运算符, 即为相同的每个值分配分数阶, 该分数阶等于它们按值升序排列的位置的平均值; ${{\hat{y}}_{i}}$表示模型的预测年龄, yi表示受试者的实际年龄; N表示受试者样本数.
本文应用对比损失函数衡量预测年龄和真实年龄的对比度一致性, 有助于学到多模态的相似度较高的特征, 具体计算公式如下:
$L_{\mathrm{con}}=-\frac{1}{N} \sum_{i=1}^{N} \log \left(\frac{\exp \left(\frac{S}{\tau}\right)}{\sum_{j=1}^{B} \exp \left(\frac{S}{\tau}\right)}\right) $ (1)
其中,
S=
yn和${{\hat{y}}_{n}}$分别表示实际年龄和预测年龄归一化后的向量, ε 表示数值稳定性参数, τ 表示调节参数.
因此, 模型总损失函数如下:
L=LMSE+λ (Lspear+Ldiff)+ω Lcon,
其中, λ 、ω 表示损失权重参数.
CMFF结合深度学习和模糊理论.空间复杂度涉及模型在训练和推理过程中所需的内存, 包括模型参数、激活值及临时变量等.时间复杂度涉及模型在训练和推理过程中所需的计算时间, 包括卷积操作、全连接层操作和模糊积分计算等.
在空间复杂度方面, 首先需要考虑模型参数, 包括卷积层参数和模糊测度参数.卷积层参数的空间复杂度为:
S1(n)=O(CinCoutK3),
其中, Cin表示卷积层的输入通道数, Cout表示卷积层的输出通道数, K表示卷积核大小.
模糊测度参数的空间复杂度为:
S2(n)=O(VNout),
其中, V表示模糊测度的参数数量, Nout表示输出通道数.
其次, 需要考虑激活值和临时变量, 每层输出的空间复杂度为:
S3(n)=O(BCWHD),
其中, B表示批次大小, C表示每个卷积层的通道数, W、H、D分别表示输入图像的宽度、高度和深度.
因此, 模型的总体空间复杂度为:
$\begin{array}{l} S(n)= O\left(\sum_{i=1}^{6}\left(C_{\text {in }}^{i} C_{\text {out }}^{i} K^{3}\right)+V N_{\text {out }}+\sum_{j=1}^{6}\left(B C_{j} W_{j} H_{j} D_{j}\right)\right) \end{array}$.
在时间复杂度方面, 首先需要考虑卷积操作, 每层的卷积操作的时间复杂度为:
T1(n)=O(CinCoutK3WHD).
还需要考虑全连接操作, 每层全连接层的时间复杂度为:
T2(n)=O(NinNout),
其中, Nin表示输入通道数, Nout表示输出通道数.
最后, 还需要考虑模糊积分计算, 计算Choquet积分的时间复杂度为:
T3(n)=O(VNout).
因此, 模型的总体时间复杂度为:
$\begin{array}{l} T(n)= O\left(\sum_{i=1}^{6}\left(C_{\text {in }}^{i} C_{\text {out }}^{i} K^{3} W H D\right)+\sum_{j=1}^{6}\left(N_{\text {in }}^{j} N_{\text {out }}^{j}\right)+V N_{\text {out }}\right) \end{array}$.
本文使用的实验数据集源于DecNef项目数据存储库.该项目由日本医疗研究开发机构(The Japan Agency for Medical Research and Development, AME-D)组织.SRPBS多重障碍MRI数据集[48]包含来自11个站点的1 410名参与者的3T MRI成像数据, 包括脑成像数据集、参与者人口统计信息、MRI协议、质量控制结果等信息.其中, 健康参与者790名, 非健康参与者620名.所有数据均以NIFTI格式提供, 并在参与者同意下无限制发布, 详细信息如表2所示.
| 表2 SRPBS参与者数据集特征 Table 2 Characteristics of SRPBS participant dataset |
本文使用DPARSF 7.0工具箱预处理数据集.在处理过程中进行格式转换、切片计时、头部运动校正和空间归一化.切片计时设定为2 s, 数量设定为32, 应用头部运动校正去除数据中头动频繁带来的噪声, 将运动超过2.5 mm或2.5° 的数据排除, 并将图像中的所有像素值归一化为[0, 1].经过上述处理之后, 获得1 138名参与者的脑部fALFF图像、ReHo图像和T1w图像, 参与者的年龄在18~80岁之间, 其中男性623名, 女性515名, 健康参与者636名, 非健康参与者502名.
本文采用的实验平台为PC(Intel(R) Core(TM) i9-10940X@3.30 GHz), 显卡为NVIDIA GeForce RTX-4090, 内存大小为64 GB, 开发工具为JetBrains Py-Charm 2023专业版, 开发语言为Python.
实验超参数设置如下.批处理数为16, 总训练次数为150, 早停为20.学习率和权重衰减均为5e-4.式(1)中损失调节参数τ 为0.8, 式(2)中数值稳定性参数ε 为1e-8.此外, 损失函数的权重参数经过多次训练调试, 分别设置为0.2、0.8.
本文应用MAE和Pearson相关系数(Pearson Correlation Coefficient, PCC)作为评估脑龄预测准确性的指标.设置测试集为原数据集的10%, 在训练和验证阶段, 使用4折交叉验证评估算法性能.具体地, 将训练集和验证集分成四个子集, 在每个子集上进行训练和验证, 然后取平均结果作为最终性能指标.
本文使用MAE衡量脑龄预测算法的性能, 计算方式为预测值与实际值之间的绝对误差的平均值.MAE越小表示预测误差越小.计算公式如下:
$\text{MAE}=\frac{1}{N}\sum{_{i=1}^{N}}|{{y}_{i}}-{{\hat{y}}_{i}}|$,
其中, N表示受试者数量, yi表示受试者实际年龄,
PCC衡量脑龄预测算法输出值与实际值之间的线性相关性.PCC的取值范围为[-1, 1].PCC趋近于1, 表示两者呈正相关; 趋近于-1, 表示两者呈负相关; 接近0, 表示两者之间无线性关系.具体计算公式如下:
$P C C=\frac{\sum_{i=1}^{N}\left(y_{i}-\bar{y}\right)\left(\hat{y}_{i}-\overline{\hat{y}}\right)}{\sqrt{\sum_{i=1}^{N}\left(y_{i}-\bar{y}\right)^{2} \sum_{i=1}^{N}\left(\hat{y}_{i}-\overline{\hat{y}}\right)^{2}}}$,
其中,
为了验证CMFF的有效性, 本文在包含1 138名受试者的SRPBS数据集上进行实验.当前脑龄预测领域存在许多常用算法, 本文选择Global-Local Transformer[8]、SFCN[17]、TSAN[45]作为对比算法.
考虑到SFCN、TSAN及Global-Local Transformer原先都是针对单一模态预测设计的, 在本文实验中, 将其修改用于多模态特征融合预测脑龄, 融合操作见2.1节, 先使用算法提取各模态的特征信息, 径向拼接后进行年龄回归预测.
单一模态特征和多模态特征下各算法的MAE和PCC的结果如表3所示, 表中黑体数字表示最优值.
| 表3 各算法的指标值对比 Table 3 Metric value comparison of different algorithms |
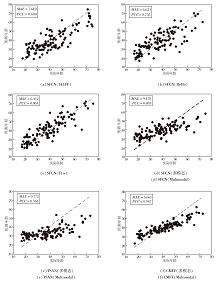
由表3可见, 在单一模态特征下, TSAN的性能略差于SFCN.在fALFF模态特征下, TSAN预测误差较大, 相关性较弱.在多模态特征下, SFCN具有较高的PCC值, 但MAE值也较高.这表明, 虽然SFCN实现更优的相关性, 但其预测误差较大.TSAN在多模态特征方面表现较差, 表明其在处理多模态特征方面存在一定挑战.Global-Local Transformer也是性能较差.CMFF的MAE值和PCC值都最优, 体现其可有效进行多模态特征融合, 在保持最小误差的同时, 还具有较高的相关性.
基于单一模态和多模态的预测结果绘制各算法脑龄预测的散点图, 如图3所示.由图可见, CMFF的散点分布图表现出较高的聚集度和稳定性, 数据点之间的分布相对均匀, 由此表明CMFF的脑龄预测结果相对稳定, 可有效提升脑龄预测的精度.综合分析和对比散点图, 根据散点的分布情况和指标值可发现, SFCN和TSAN在多模态数据下的散点分布图数据点分散度较高, 不一致性较大, 预测不够准确.
为了深入验证本文提出的多模态协同卷积模块(MCCM)与模糊融合模块(FFM)的有效性, 设计如下一系列算法进行消融实验:1)basic1.通过拼接方式实现多模态特征融合, 直接连接不同模态的特征向量.2)basic2.采用求和方式进行特征融合, 将多个模态特征向量对应元素相加.3)basic3.在特征提取阶段实现多模态数据深度融合, 将融合后的向量直接用于年龄回归预测.4)basic4.采用决策级融合, 各个模态分别预测再在决策阶段整合多个模态的预测结果.5)basic1+FFM.在basic1的基础上增加FFM.6)basic1+MCCM.在basic1的基础上增加MCCM.7)basic1+FFM+MCCM.融合FFM和MCCM, 综合多模块技术, 进一步提升预测性能.
具体消融实验结果如表4所示, 表中黑体数字表示最优值.由表可见, 在basic1基础上分别加入FFM和MCCM, 进一步探索这些模块对CMFF性能的影响.FFM的引入显著降低MAE值, 表明其通过模糊逻辑可有效融合多模态特征中的相关性信息, 提升预测精度.而MCCM的加入不仅降低MAE值, 还提高PCC值, 这表明MCCM在提取和融合高度相关及互补的多模态特征方面的卓越能力.最终, 当FFM与MCCM协同工作时, 性能达到最优.这一结果不仅展示FFM在降低预测误差方面的显著效果, 也凸显MCCM在增强特征相关性和互补性上的关键作用.两者结合不仅分别发挥各自在特征融合上的优势, 而且通过协同工作进一步增强CMFF整体性能, 实现对多模态数据的深度挖掘和年龄的精确预测.
| 表4 消融实验结果 Table 4 Ablation experiment results |
为了深入探讨优化排序对比损失函数中正则化参数λ 和ω (ω =1-λ )对CMFF的影响, 进行相关实验, 结果如表5所示, 表中黑体数字表示最优值.
| 表5 正则化参数λ 对CMFF的影响 Table 5 Effect of regularization parameter λ on CMFF |
由表5可发现, 不同的λ 和ω 组合对CMFF的MAE和PCC指标有显著影响.当λ =0.2和ω =1-λ =0.8时, MAE值为5.661, PCC值为0.947, 这表明CMFF在损失函数的各个组件之间找到平衡, 可提高预测准确性和相关性.而当λ 继续增加时, MAE呈现升高的趋势, PCC呈现下降的趋势, 这表明过高的λ 可能会对CMFF产生负面影响, 导致准确率和相关性下降.当λ =0.8和ω =1-λ =0.2时, MAE和PCC指标都有所改善, 但与最佳性能相比仍有差距.总之, 通过适当的平衡可显著提高算法的预测准确性和相关性.
文献[15]的脑龄预测算法能实现MAE低于3的优异表现, 但CMFF却未能达到这一水平, 主要有如下两个原因.1)本文使用数据集是SRPBS多重障碍MRI数据集, 具有多中心和多类疾病的特点.2)文献[15]中提到的部分研究仅在包含健康受试者的数据集上进行实验, 这种数据集因其同质性高和噪声水平低而相对简单.例如:Peng等[17]使用UK Biobank收集的14 503名健康参与者的T1w数据, MAE值为2.14; Ning等[18]使用的数据集包含来自UK Biobank的16 998名欧洲血统的研究对象, 所有受试者均无脑和神经系统相关疾病, 包括认知障碍、神经系统疾病等, MAE值为2.7.结合文本实验可知, 算法在相对简单、噪声较小的数据集上取得优异表现, 并不直接等同于在更复杂、更具挑战性的数据集上也能保持同样精度.
此外, 本文还进行一些双模态融合的实验, 在SRPBS数据集上效果尚可, 但在一个较小的数据集上性能提升得不够明显.综合分析后认为可能有如下原因:1)数据集规模较小, 算法无法充分学习不同模态特征之间的关联性.2)不同模态的数据在空间上差异较大, 无法在较小的数据集上学到这种复杂的融合策略.3)较小的数据集存在数据质量问题, 如噪声较多、数据分布不均等.
本文基于医学图像数据和深度学习模型, 结合模糊理论、多模态特征融合等, 提出基于多模态模糊特征融合的脑龄协同预测算法(CMFF), 在脑龄预测任务中取得较优性能.此外, 训练和验证时还使用优化排序对比损失函数, 能更准确地拟合实际脑龄与预测脑龄之间的关系.
今后将考虑在脑龄预测算法中继续应用其它基于模糊理论的方法, 特别是一些新的积分形式, 如基于t-模的Choquet积分、基于重叠函数的Choquet积分、优化后的Sugeno积分等, 评估其在脑龄预测中的潜在优势.此外, 将继续研究更高级的特征融合技术, 如基于深度学习的自适应特征融合等, 针对不同模态的数据进行特定的噪声消除和增强处理, 在更多更大的多模态数据集上进行实验, 提升算法的适用性和稳健性.
本文责任编委 黄华
Recommended by Associate Editor HUANG Hua
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
|
| [47] |
|
| [48] |
|