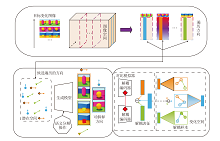
从解耦表征学习用于图像生成的角度出发, 本文提出解耦表征学习视角下认知图像属性特征的图像生成方法(CF-DRL), 结构如图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 CF-DRL结构图Fig.1 Structure of CF-DRL

CF-DRL由如下3部分组成.

1)潜在空间的特征解耦.在潜在空间中提供关于目标变化图像的候选遍历方向.

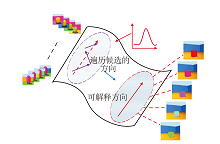
2)无监督语义分解.在给定生成模型的潜在空间中探索候选遍历的方向, 发现目标变化图像的可解释方向.可解释方向的发现过程如图2所示.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 可解释方向的发现过程Fig.2 Process of discovering interpretable directions

3)解耦表征学习.根据可解释方向, 结合对比学习, 构建基于解耦编码器E的对比模拟器(C-S), 提取解耦表征.通过C-S建立变化空间, 获得解耦样本, 实现解耦表征学习.

在图像生成领域, 许多方法逐级生成图像, 但在生成过程中未增添控制, 容易发生特征纠缠, 无法获知上一级学到的特征, 导致模型控制生成图像特定特征的能力有限.通过预训练生成模型StyleGAN的学习, 可将潜在编码映射到更高维的空间, 表现出较好的解耦特性, 较好地模拟真实数据的潜在表征.

此外, 增加对模型可解释性的关注, 使训练过程更可控, 减少训练难度.因此, 为了发现生成图像某些方面的表征, 并使表征间的影响尽可能小, 本文结合预训练生成模型StyleGAN, 对模型训练进行进一步的提升, 实现潜在空间的特征解耦, 得到关于目标变化图像的候选遍历的方向.CF-DRL的训练结构如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 CF-DRL的训练结构Fig.3 Training structure of CF-DRL

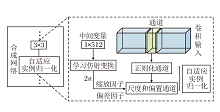
本文关注生成器网络, 利用渐进层的优良结构特性控制图像的不同视觉特征.层间分辨率越低, 影响的特征越粗糙.训练结构由如下两部分组成^[9].

1)映射网络.将潜在变量z生成中间变量w, 其中w用于控制生成图像的风格.可找到目标变化图像特征下隐藏的深层次关系, 并将这些特征解耦, 得到隐藏特征, 建立生成图像的潜在空间.引入该映射网络的目的是将输入向量编码为中间向量, 并传送至生成网络中得到控制向量.该向量的不同元素对应不同的视觉特征.

2)合成网络.用于生成图像, 其中由w得到的仿射变换A控制生成图像的风格, 噪声用于丰富生成图像的细节.合成网络由9个阶段组成, 从4× 4变化到1 024× 1 024, 每个阶段受2个控制向量的影响.一个控制向量在上采样后对其影响一次, 另一个控制向量在卷积操作之后对其影响一次.影响的方式采用自适应实例归一化(Adaptive Instance Norma-lization, AdaIN)^[9]:

$\text{AdaIN}({{x}_{i}}; y)={{y}_{s, i}}\left[ \frac{{{x}_{i}}-\mu ({{x}_{i}})}{\sigma ({{x}_{i}})} \right]+{{y}_{b, i}}$,

其中, x_i表示映射特征, y表示样式风格, y_{s, i}表示缩放因子, y_{b, i}表示偏差因子.

w变换为多个控制向量传给生成器, 并通过可学习的仿射变换获得y_{s, i}和y_{b, i}.其与标准化后的卷积输出加权求和, 实现一次w影响原始输出x_i的过程.w影响图像的全局信息, 可实现样式控制.另一方面, 保留生成图像的关键信息由上采样层和卷积层决定, 具有一定的解耦特性.AdaIN的实现过程如图4所示.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 AdaIN的实现过程Fig.4 Implementation process of AdaIN

根据文献[13], 给定一个训练完备的生成模型StyleGAN, 生成器存在确定的函数关系G:S→ I.其中, S∈ R^d表示d维潜在空间, I表示图像空间.每个目标变化图像包含确定的语义信息.存在语义得分函数F_L:I→ M, M∈ R^k表示存在k种语义的图像语义空间.在潜在空间和图像语义空间中有语义得分

m=F_L(G(s)),

其中s表示采样的潜在编码.

潜在空间中的2个潜在编码s₁、s₂使用线性插值时会发生相应的图像变化, 意味着图像中对应的语义也在变化^[13].给定n∈ R^d且n≠ 0, 集合

{z∈ R^d:n^Tz=0}

定义R^d中的超平面, n称为法向量.所有满足

n^Tz> 0

的向量z∈ R^d都位于超平面的同一侧.通过s₁、s₂之间的线性插值, 在潜在空间中形成一个方向, 由此定义一个超平面.因此, 对于任意2维语义, 潜在空间中存在一个超平面作为分离边界.当潜在编码在超平面的同侧变化时, 语义信息保持不变, 否则表示另一种语义.由此形成不同语义信息的方向(在超平面的同侧变化), 单一语义信息上的方向即为可解释方向.在超平面中存在单位法向量n∈ R^d, 样本s到该超平面的矢量距离:

d(n, s)=n^Ts,

当s在边界附近移动并穿越超平面时, 距离和语义均会相应变化, 进而语义属性发生变化.因此, 期望两者线性相关, 则

F(G(s))=γ d(n, s),

其中, F(· )表示特定语义得分函数, γ > 0衡量语义随距离变化而变化的“ 速率” .

给定n∈ R^d, 其中n^Tn=1(定义超平面), 多元随机变量z∈ N(0, I_d), 对于∀ α ≥ 1且d≥ 4, 有

$\begin{array}{l} P\left(\left|\boldsymbol{n}^{\mathrm{T}} z\right|\right.\left.\leqslant 2 \alpha \sqrt{\frac{d}{d-2}}\right) \geqslant \\ \quad(1-3 \exp (-c d))\left(1-\frac{2}{\alpha} \exp \left(\frac{-\alpha^{2}}{2}\right)\right) \end{array}$

其中, P(· )表示概率, c表示固定正常数.从N(0, I_d)中采样的随机样本位于足够靠近给定超平面的位置^[13].因此, 相应的语义信息通过法向量定义的子空间建模.对于多个语义的情形, 有

m=F_L(G(s))=Λ N^Ts,

其中

m= [m1, m2, ···, mλ]T

表示语义得分,

Λ =diag(ζ ₁, ζ ₂, ···, ζ _λ )

表示线性系数矩阵,

N=[n₁, n₂, ···, n_λ ]

表示分离边界(方向).随机样本z的分布为N(0, I_d), 语义得分m的均值μ _m和协方差矩阵Σ _m如下:

μ _m=E(Λ N^Ts)=0,

Σ _m=E(Λ N^Tss^TNΛ ^T)=Λ N^TNΛ ,

其中, m服从正态分布, 有m~N(0, Σ _m).当且仅当Σ _m为对角矩阵时, 法向量

N=[n₁, n₂, ···, n_λ ]

正交, 进而有不同语义间是高度解耦的特质, 否则图像变化的语义信息相互关联. nTan_b衡量语义a、b之间的关联.

在潜在空间中进行单一属性操作时, 潜在空间中变化属性的潜在编码s有

${{s}_{E}}=s+\delta n$,

$F(G({{s}_{E}}))=F(G(s))+\gamma \delta $.

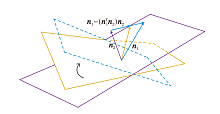
当δ > 0时, 生成图像在相应语义上的特性更优.在条件操作中, 由于部分语义特征相互耦合, 对多个图像变化特征而言, 一个特征的变化会影响另一个特征的变化形式.为了达到解耦效果, 利用N^TN为对角矩阵进行条件操作.如图5所示, 2个超平面的法向量分别为n₁、n₂, 其投影的方向为

n₁-( nT1n₂)n₂.

通过使用投影进行向量的正交化, 沿着投影的方向可变化单一的属性特征.投影方向上的特征不易与其它属性特征纠缠, 具有一定解耦特性.因此, 该方向即为可解释方向.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 潜在空间中的投影操作Fig.5 Projection operation in latent space

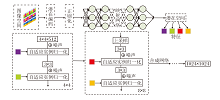
在获得目标变化图像的可解释方向后, 模拟生成图像的各种变化是必要的.根据文献[10], 构建基于解耦编码器E的对比模拟器(C-S), 由2个共享权重的解耦编码器E构成, 解耦编码器E的结构如表1所示.通过C-S的对比学习机制建立变化空间, C-S将解耦表征之间的差值作为图像变化表示输出.在变化空间中, 根据获取的图像变化相似度和非相似度提取图像变化的解耦样本, 实现解耦表征学习.

表1

Table 1

表1(Table 1)

表1 解耦编码器E的结构 Table 1 Structure of disentangled encoder E 层名称 配置 步长 激活函数 卷积层 7× 7× 3× 64 1 ReLU 卷积层 4× 4× 64× 128 2 ReLU 卷积层 4× 4× 128× 256 2 ReLU 卷积层 4× 4× 256× 256 2 ReLU 卷积层 4× 4× 256× 256 2 ReLU 全连接层 4096× 256 - ReLU 全连接层 256× 256 - ReLU 全连接层 256× J - -

表1 解耦编码器E的结构 Table 1 Structure of disentangled encoder E

C-S将图像对编码为解耦样本v∈ V:

$v(z, d, \varepsilon )=\left| E(G(z+D(d, \varepsilon )))-E(G(z)) \right|$,

其中, V∈ R+J表示变化空间, D(d, ε )表示在方向d上位移ε 大小.

根据无监督语义分解在潜在空间中发现的可解释方向, C-S将目标变化图像的潜在编码遍历到变化空间中.变化空间中的解耦样本对应于沿可解释方向的图像变化.通过将遍历同一可解释方向的解耦样本聚集为一类, 遍历不同可解释方向的解耦样本推离, C-S从目标变化图像中提取解耦表征.在变化空间中, 同类图像变化在一个明显的可解释方向上响应.因此, 通过解耦表征分离维度的响应, CF-DRL实现解耦表征提取和图像生成.

本文在Shapes3D、MPI3D、Cars3D、MNIST、Anime这5个解耦数据集上进行实验.Shapes3D数据集包含6个地面真值因子(物体颜色、地板颜色、墙壁颜色及物体的尺寸、形状和方向)生成的3D形状图像.MPI3D数据集包含真实世界图像的3维物体图像, 这些图像捕获具有7个地面真值因子的3D打印对象(背景颜色、相机高度、水平轴、垂直轴及物体的颜色、形状和大小).Cars3D数据集包含183个3D汽车模型, 具有4个相机仰角和24个旋转角度的变化.MNIST数据集由手写数字的图像和相应的标签组成, 图像一共分为10类, 分别对应从0~9的阿拉伯数字.Anime数据集包含64× 64的卡通风格头像.

本文使用如下指标评估方法的解耦性能.

1)综合性指标.DCI(Disentanglement, Comple-teness and Informativeness)^[21]评估潜在表征的模块性、紧凑性和确定性.

解耦度D衡量每个潜在维度最多捕获一个属性的程度:

$\text{D}=1+\sum\limits_{k=0}^{K-1}{{{P}_{ik}}{{\log }_{K}}{{P}_{ik}}}$,

其中,

$P_{i j}=R_{i j}\left(\sum_{k=0}^{K-1} R_{i k}\right)^{-1}$

表示潜在维度对预测生成因子的重要性, R_ij表示潜在维度在预测时的权重.

完整性C衡量每个属性被一个潜在维度控制的程度:

$\text{C}=1-{{H}_{D}}({{\tilde{P}}_{\cdot j}})$,

其中

${{H}_{D}}({{\tilde{P}}_{\cdot j}})=-\sum\limits_{d=0}^{D-1}{{{{\tilde{P}}}_{dj}}{{\log }_{D}}{{{\tilde{P}}}_{ij}}}$

表示分布${{\tilde{P}}_{\cdot j}}$的熵.

信息性I衡量潜在表征属性的分类精度:

$\text{I}=E({{z}_{j}}, {{\hat{z}}_{j}})$,

其中, z_j表示生成因子的真实值, ${{\hat{z}}_{j}}$表示预测值, E(· )表示误差函数.

DCI表示潜在变量解耦得分的加权和:

$D C I=\sum_{i}\left(\frac{\sum_{j} R_{i j}}{\sum_{i, j} R_{i j}}\left(1+\sum_{k=0}^{K-1} P_{i k} \log _{K} P_{i k}\right)\right) $.

2)紧凑性指标.MIG(Mutual Information Gap)^[22]使用生成因子与潜在变量的互信息I(v_i, z_j)作为信息量概念, 衡量潜在变化因子在潜在编码相应维度的实现程度, 定义

$M I G=\frac{I\left(v_{i}, z_{a}\right)-I\left(v_{i}, z_{b}\right)}{\sum_{j=1}^{d} I\left(v_{i}, z_{j}\right)} $,

其中, I(v_i, z_a)表示潜在变量各维度与生成因子的互信息的最优值, I(v_i, z_b)表示次优值.

3)模块化指标.β -VAE Score^[5]和FactorVAE Score^[23]衡量潜在变化因子解耦的程度.

(1)β -VAE Score.首先获取N个数据对{ x1l, x2l}, 再计算数据对潜在编码的绝对值差异

$Z_{\text {diff }}^{l}(i)=\left|z_{1}^{l}(i)-z_{2}^{l}(i)\right|$,

最后通过线性回归器和平均差值

$z_{\text {diff }}^{\mu}=\frac{1}{N} \sum_{i=1}^{N} z_{\text {diff }}^{l}(i) $

预测固定的生成因子, 预测准确率即为β -VAE Score得分.

(2)FactorVAE Score.首先生成因子k固定但其它因子随机变化的数据

{x⁽¹⁾, x⁽²⁾, ···, x^(L)}.

再通过数据潜在表征的经验标准差s对数据的每个维度归一化, 获得新表征

{ z·(L)/s, z·(L-1)/s, ···, z·(1)/s}.

然后取每个维度的经验方差

Varl z·(l)/s,

令

d^* =arg mindVarl zd(l)/s_d.

最后得到多投票分类器的训练点, 分类器的精度即为FactorVAE Score得分.

本文所有实验均在NVIDIA Tesla A100 GPU上进行, 并基于PyTorch框架实现.在训练过程中, 使用Adam(Adaptive Moment Estimation)优化器, 批量大小为32, 学习率为1.0× 10^-4, 方向数为64, 生成器的索引值范围为1~5, 编码器的输出大小为64× 64.根据模型的可行性和经验设置, 在各数据集上设置不同迭代次数, 在Shapes3D、MPI3D、Cars3D数据集上训练的迭代次数分别为20 000、30 000和40 000.

为了公平起见, 对比方法的实验均在相同的条件和设置下进行, 遵循官方源码并通过仔细调节参数实现.参数调节基于对应文献中给出的参数值, 或根据参数范围使用网格搜索进行, 以获得最佳结果.

为了验证CF-DRL的有效性, 在Shapes3D、MPI3D、Cars3D数据集上进行实验.对比方法如下:DisCo-GAN^[10]、DisCo-VAE^[10]、SAE(Structural Autoencoder)^[24]、Vec-β -TCVAE^[25]、vec-VCT^[25]、DAVA(Disentangling Adversarial Variational Autoencoder)^[26]、VCT(Visual Concept Tokenization)^[27]、文献[28]方法、FDAE(Factorized Diffusion Autoencoder)^[29]、CF(Closed-Form)^[30]、DS(Deep-Spectral)^[30]、DisDiff-VQ^[31]和文献[32]方法.

各方法在3个数据集上的指标值结果如表2和表3所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表2和表3可知, CF-DRL在DCI、MIG指标上的总体得分最优.在Shapes3D数据集上的解耦效果最显著.相比FDAE, CF-DRL在DCI指标上提高0.02.相比DisDiff-VQ, CF-DRL在MIG指标上提高0.02.在MPI3D数据集上, CF-DRL在β -VAE Score和FactorVAE Score指标上的得分均是最佳值.相比vec-VCT, CF-DRL在β -VAE Score指标上提高0.05.相比FDAE, CF-DRL在FactorVAE Score指标上提高0.03.在Shapes3D、Cars3D数据集上, 由于FDAE引入内容掩码分解网络, 在表征的信息量获取和视觉概念的解耦方面表现较优, 获得相应最佳解耦得分.

表2

Table 2

表2(Table 2)

表2 各方法在3个数据集上的DCI和MIG指标值对比 Table 2 Comparison of DCI and MIG metric values for different methods on 3 datasets 方法 Shapes3D MPI3D Cars3D DCI MIG DCI MIG DCI MIG SAE 0.75± 0.18 0.38± 0.10 0.41± 0.05 0.15± 0.03 0.35± 0.14 0.15± 0.02 vec-VCT 0.81± 0.15 0.48± 0.18 0.30± 0.06 0.17± 0.04 0.19± 0.02 0.13± 0.02 DAVA 0.78± 0.03 0.62± 0.05 0.27± 0.03 0.11± 0.05 0.23± 0.04 0.15± 0.01 DisCo-VAE 0.84± 0.03 0.33± 0.16 0.29± 0.02 0.07± 0.03 0.21± 0.04 0.10± 0.03 VCT 0.88± 0.01 0.53± 0.03 0.48± 0.01 0.23± 0.05 0.38± 0.08 0.12± 0.05 文献[28]方法 0.11± 0.01 0.01± 0.00 0.51± 0.02 0.06± 0.00 0.31± 0.02 0.02± 0.03 FDAE 0.92± 0.04 0.47± 0.08 0.64± 0.03 0.20± 0.02 0.42± 0.04 0.14± 0.02 CF 0.53± 0.08 0.31± 0.12 0.32± 0.01 0.18± 0.08 0.24± 0.05 0.08± 0.02 DS 0.51± 0.08 0.36± 0.09 0.25± 0.04 0.09± 0.04 0.22± 0.04 0.12± 0.04 DisDiff-VQ 0.72± 0.01 0.63± 0.05 0.33± 0.05 0.11± 0.05 0.23± 0.01 0.15± 0.01 Vec-β -TCVAE 0.31± 0.03 0.28± 0.16 0.11± 0.02 0.12± 0.03 0.21± 0.04 0.10± 0.03 文献[32]方法 0.60± 0.01 0.53± 0.03 0.35± 0.01 0.31± 0.05 0.26± 0.08 0.10± 0.05 DisCo-GAN 0.71± 0.05 0.51± 0.07 0.29± 0.02 0.22± 0.03 0.27± 0.04 0.18± 0.04 CF-DRL 0.94± 0.03 0.65± 0.02 0.60± 0.05 0.27± 0.04 0.40± 0.06 0.24± 0.01

表2 各方法在3个数据集上的DCI和MIG指标值对比 Table 2 Comparison of DCI and MIG metric values for different methods on 3 datasets

表3

Table 3

表3(Table 3)

表3 各方法在3个数据集上的β -VAE Score和FactorVAE Score指标值对比 Table 3 Comparison of β -VAE Score and FactorVAE Score metric values for different methods on 3 datasets 方法 Shapes3D MPI3D Cars3D β -VAE Score FactorVAE Score β -VAE Score FactorVAE Score β -VAE Score FactorVAE Score SAE 0.84± 0.10 0.89± 0.08 0.72± 0.03 0.68± 003 0.84± 0.05 0.91± 0.05 vec-VCT 0.85± 0.04 0.91± 0.13 0.83± 0.07 0.65± 0.02 0.91± 0.06 0.86± 0.05 DAVA 0.86± 0.02 0.82± 0.03 0.60± 0.06 0.48± 0.05 0.87± 0.04 0.94± 0.01 DisCo-VAE 0.94± 0.03 0.95± 0.04 0.41± 0.03 0.39± 0.08 0.93± 0.04 0.76± 0.11 VCT 0.92± 0.01 0.96± 0.04 0.82± 0.07 0.69± 0.04 0.94± 0.03 0.97± 0.03 文献[28]方法 0.89± 0.06 0.43± 0.02 0.60± 0.06 0.86± 0.02 0.87± 0.07 0.96± 0.03 FDAE 0.94± 0.02 0.99± 0.02 0.41± 0.03 0.90± 0.03 0.97± 0.02 0.92± 0.03 CF 0.92± 0.06 0.95± 0.02 0.67± 0.03 0.52± 0.06 0.93± 0.04 0.87± 0.04 DS 0.94± 0.02 0.93± 0.07 0.65± 0.04 0.50± 0.04 0.88± 0.03 0.87± 0.05 DisDiff-VQ 0.92± 0.02 0.90± 0.03 0.60± 0.06 0.61± 0.07 0.87± 0.04 0.97± 0.01 Vec-β -TCVAE 0.94± 0.03 0.80± 0.04 0.41± 0.03 0.40± 0.08 0.94± 0.04 0.76± 0.11 文献[32]方法 0.89± 0.01 0.75± 0.07 0.48± 0.01 0.23± 0.05 0.96± 0.08 0.87± 0.05 DisCo-GAN 0.97± 0.02 0.88± 0.03 0.53± 0.02 0.37± 0.03 0.95± 0.04 0.86± 0.07 CF-DRL 0.96± 0.04 0.94± 0.02 0.88± 0.03 0.93± 0.01 0.92± 0.05 0.98± 0.02

表3 各方法在3个数据集上的β -VAE Score和FactorVAE Score指标值对比 Table 3 Comparison of β -VAE Score and FactorVAE Score metric values for different methods on 3 datasets

为了验证CF-DRL的泛化性, 分别在5个解耦数据集上进行可视化, 结果如图6所示, 每个数据集的可视化结果由上至下依次分为3类, 每类展示3组解耦表征学习结果.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 CF-DRL解耦目标变化图像的可视化结果Fig.6 Visualization results of CF-DRL disentangling target variation images

由图6可知, CF-DRL在相应数据集上均获得较理想的结果, 生成的图像不存在多个属性特征纠缠的问题.CF-DRL发现潜在变化因子, 并解耦目标变化图像, 生成基于单因子变化的图像.CF-DRL在Sha-pes3D数据集上分别发现墙壁颜色因子、物体颜色因子和地板颜色因子.对于抽象体, CF-DRL在MPI-3D数据集上分别发现背景颜色、抽象体的旋转角度因子和颜色因子.在Cars3D数据集上, CF-DRL分别发现汽车颜色因子、汽车方位因子和汽车样式因子.对于手写数字, CF-DRL在MNIST数据集上分别发现数字厚度因子、数字角度因子和数字类型因子, 倾向于更宽且平滑的连续变换学习, 获得更丰富的因子.

具体以数字3和数字9为例, 通过投影向量的正交化, 在水平方向和垂直方向上分别发现数字类型因子和数字厚度因子, 结果如图7所示.CF-DRL在Anime数据集上解耦人物图像的头发颜色因子、眼镜因子和自然度因子, 获得更丰富的图像生成样式, 为特定任务提供参考样本.

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 投影向量正交的示例Fig.7 Example of orthogonality of projection vectors

在解耦表征学习的过程中还发现视觉特征无信息的情况, 即后验的KL发散与高斯先验无较大差异.沿一个无信息特征的方向进行遍历不会导致视觉图像的变化.在Shapes3D数据集上展示视觉特征无信息的示例, 如图8所示.

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 Shapes3D数据集上视觉特征无信息的示例Fig.8 Example of visual features without information on Shapes3D dataset

总之, CF-DRL可发现更多的潜在变化因子, 并且发现的方向容易解释, 其还学习更干净、独立的表达方式, 生成具有单因子解耦特性的图像, 具有一定的泛化性.

为了定量分析CF-DRL在视觉特征上生成图像的可解释度, 利用10组64批量大小的可视化结果, 并按照5幅图像为一个解耦组进行实验统计, 计算不同数据集上发现的视觉特征的可解释度.视觉特征的可解释度越高, 方法在目标视觉特征上的图像生成效果越优.平均可解释度为同一数据集下发现的视觉特征可解释度的算术平均, 衡量方法在总体图像生成上的可解释性情况.

各数据集上具体可解释度结果如表4所示.由表可知, CF-DRL在Cars3D数据集上的平均可解释度最高, 为93.7%, 表明其在Cars3D数据集上发现的视觉特征的图像生成效果较优, 而在Anime数据集上的平均解释度仅为86.3%.在Shapes3D数据集上, CF-DRL发现的物体、地板和墙壁的颜色的视觉特征的可解释度均大于90%, 结合图像生成的效果发现, CF-DRL在这3个视觉特征上的生成图像较丰富.在Cars3D数据集上, 本文进行3类视觉特征的可解释度分析(汽车颜色、汽车方位和汽车样式), 其视觉特征少于其它数据集上的.这是因为其它视觉特征存在纠缠的问题, 并非表明其它视觉特征无信息.因此, CF-DRL具有发现并解耦潜在变化因子的能力, 在视觉特征和潜在变化因子之间存在一一映射关系, 能有效防止纠缠结果的发生.

表4

Table 4

表4(Table 4)

表4 各数据集上发现的视觉特征的可解释度 Table 4 Interpretability of visual features discovered in different datasets % 数据集 视觉特征 可解释度 平均可解释度 Cars3D 汽车颜色 汽车方位 汽车样式 94 95 92 93.7 MNIST 数字厚度 数字角度 数字类型 数字宽度 96 91 92 94 93.3 MPI3D 背景颜色 旋转角度 物体颜色 物体形状 物体尺寸 95 96 92 83 88 90.8 Shapes3D 物体颜色 地板颜色 墙壁颜色 物体尺寸 物体形状 物体方向 97 93 95 83 85 80 88.8 Anime 头发颜色 眼镜 自然度 人物位置 人物肤色 人物白度 93 86 90 83 85 84 86.3

表4 各数据集上发现的视觉特征的可解释度 Table 4 Interpretability of visual features discovered in different datasets %

在图像生成过程中涉及不同的潜在空间, 最普遍的潜在空间Z通常是正态分布的.目标变化图像的潜在编码z∈ Z通过一系列全连接层被变换到中间潜在空间W中, W能更好地反映目标图像变化的解耦特性.W为风格网络的输出, 输入是随机潜在空间Z.每个w∈ W被进一步变换为多个控制变量s, 并传给生成器.为了便于评估, 将这些控制变量s对应的空间称为风格空间S, 维度为样式的空间通道数.在一些其它研究中还设计W⁺, 用于风格转换和反转.

本节分别对不同潜在空间Z、W、W⁺和S进行实验, 验证不同潜在空间中CF-DRL的有效性.实验在Shapes3D数据集上进行, 结果如表5所示.由表可知, CF-DRL在S上的解耦性能最优.潜在空间组织得越优, CF-DRL的解耦效果就越优.虽然W和S的信息性均较高且可比较, 但S在解耦度和完整性方面的得分更优.表明对应潜在空间的每个维度更可能控制单个属性特征, 由此验证潜在空间在CF-DRL中的有效性.

表5

Table 5

表5(Table 5)

表5 不同潜在空间中的方法解耦性能对比 Table 5 Disentangled performance comparison in different latent spaces 潜在空间 解耦度 完整性 信息性 MIG Z 0.30 0.25 0.65 0.28 W 0.49 0.52 0.90 0.56 W+ 0.54 0.62 0.87 0.59 S 0.68 0.82 0.94 0.64

表5 不同潜在空间中的方法解耦性能对比 Table 5 Disentangled performance comparison in different latent spaces

为了更完备地验证CF-DRL的有效性, 分别从训练过程和噪声条件这2个维度进行实验.

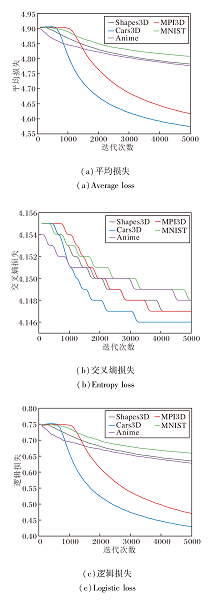
从训练过程出发, 在5个解耦数据集上进行实验.在训练过程中以100次迭代为一个节点, 记录训练损失情况, 并在每完成1 000次迭代时验证其对目标变化图像的解耦表征学习效果.由于空间限制, 本文以5 000次迭代训练为基准, 具体损失情况如图9所示.

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 CF-DRL在5个数据集上的损失变化曲线Fig.9 Loss variation curves of CF-DRL on 5 datasets

由图9可知, 在第1 000次和第5 000次迭代的损失差值对比中, CF-DRL在不同数据集上迭代节点的损失差值变化较大, 一定程度上影响解耦表征学习效果.特别地, CF-DRL在MPI3D数据集上的变化较显著.

本文展示在Shapes3D、MPI3D、Cars3D数据集上每1 000个节点处的解耦结果, 具体如图10所示.

图10

Fig.10

	Figure Option ViewDownloadNew Window
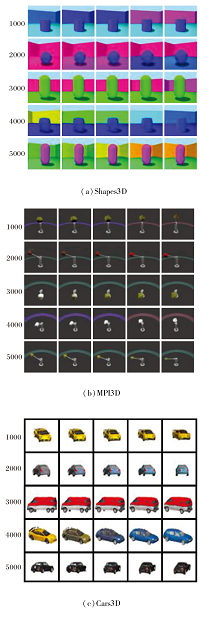	图10 CF-DRL在3个数据集上每1 000个节点处的解耦结果Fig.10 Disentangled results of CF-DRL at every 1 000 nodes on 3 datasets

综上可知, 在一定范围内随着训练迭代次数的增加, CF-DRL解耦表征学习效果越来越优.在图像生成上, CF-DRL在潜在变化因子中的图像表征趋于完整.在变化图像多样性上, CF-DRL发现更多可解释的潜在变化因子, 生成的图像丰富, 具备较优的解耦特性.

从噪声条件出发, 在不同程度混合高斯噪声的负样本中进行实验.在Shapes3D数据集上定量分析CF-DRL的解耦性能在不同噪声强度下的变化, 结果如表6所示.

表6

Table 6

表6(Table 6)

表6 不同噪声强度下CF-DRL的解耦性能 Table 6 Disentangled performance of CF-DRL under different noise intensities 噪声/% 负样本数 DCI MIG β -VAE Score FactorVAE Score 15 8 0.33 0.37 0.75 0.78 30 16 0.34 0.40 0.77 0.81 45 32 0.37 0.43 0.80 0.83 60 64 0.53 0.50 0.92 0.85 75 128 0.52 0.48 0.91 0.82 90 256 0.51 0.49 0.90 0.83

表6 不同噪声强度下CF-DRL的解耦性能 Table 6 Disentangled performance of CF-DRL under different noise intensities

由表6可知, 随着混合高斯噪声的增加, CF-DRL的解耦得分逐渐提高, 表明随着负样本数K(不同程度混合高斯噪声条件)的增加, CF-DRL忽略目标数据中与任务无关的生成信息和噪声, 增强对噪声的容忍性.当K≥ 64后, 解耦得分趋于平缓且维持在一个较优的水平, 整体波动幅度在0.01~0.02之间, 表明CF-DRL对噪声具有更强的鲁棒性.总之, CF-DRL能排除产生干扰的噪声信息, 解耦出与目标变化图像相关的因子, 提高样本的学习效率, 具有一定的泛化性.

为了验证关键实验组件在CF-DRL中的有效性, 从批量大小、方向数、方向类型(正交或投影)和变化空间这4个方面设计消融实验.实验在MPI3D数据集上进行, 结果如表7所示, 表中黑体数字表示最优值.

表7

Table 7

表7(Table 7)

表7 CF-DRL组件的消融实验结果 Table 7 Ablation experiment results of CF-DRL components 组件 对象 解耦度 完整性 信息性 MIG β -VAE Score FactorVAE Score 批量大小 8 16 32 64 0.20 0.26 0.48 0.45 0.33 0.35 0.42 0.46 0.30 0.37 0.45 0.41 0.29 0.38 0.57 0.52 0.84 0.92 0.96 0.93 0.81 0.87 0.90 0.89 方向数 32 64 128 0.55 0.62 0.60 0.61 0.67 0.63 0.49 0.54 0.52 0.43 0.51 0.54 0.90 0.94 0.93 0.87 0.88 0.85 方向类型 投影 正交 0.28 0.25 0.30 0.27 0.33 0.30 0.42 0.40 0.87 0.82 0.81 0.83 变化空间 使用 未使用 0.47 0.39 0.45 0.40 0.48 0.42 0.52 0.45 0.93 0.90 0.90 0.88

表7 CF-DRL组件的消融实验结果 Table 7 Ablation experiment results of CF-DRL components

根据经验, 在训练过程中设置批量大小为8、16、32、64, 评估方法的解耦性能.由表7可知, 批量过小或过大都影响方法的解耦性能, 选择合适的批量大小尤为重要.当批量大小为32时, CF-DRL的解耦性能最优.

对于潜在空间中的方向数, 根据实验需求, 在训练过程中设置为32、64、128, 研究方向数对方法解耦性能的影响.由表7可知, 过多或过少的方向数都将影响方法的解耦性能.当方向数为64时, CF-DRL的解耦性能最优.

为了探究CF-DRL选择不同方向类型达到的解耦效果, 分别在正交和投影的方式下进行实验.由表7可知, 当方向类型为投影时, 方法的解耦效果较优.这说明在解耦表征学习时若使用正交方式, 应当引入更多的归纳偏差和监督.

由表7可知, 变化空间影响CF-DRL的解耦性能.相比未使用变化空间模块进行解耦表征学习, 通过变化空间进行解耦和图像生成, 解耦效果更优.在变化空间的基础上目标变化图像的编码表征被更好地解耦, 通过变化空间中的对比学习, 更好地实现解耦表征.