基于核极限学习机的多标签数据流半监督在线分类方法

引用本文

王雨晨, 邱士远, 李培培, 胡学钢. 基于核极限学习机的多标签数据流半监督在线分类方法. 模式识别与人工智能, 2024,37(8): 741-754
WANG Yuchen, QIU Shiyuan, LI Peipei, HU Xuegang. Semi-supervised Online Classification Method for Multi-label Data Stream Based on Kernel Extreme Learning Machine. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2024,37(8): 741-754. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202408007
Permissions

《模式识别与人工智能》编辑部

基于核极限学习机的多标签数据流半监督在线分类方法

王雨晨^1,², 邱士远^1,², 李培培^1,^2,³, 胡学钢^1,^2,⁴

1.合肥工业大学计算机与信息学院合肥 230601

2.合肥工业大学大数据知识工程教育部重点实验室合肥 230009

3.合肥综合性国家科学中心大健康研究院健康大数据与群体医学研究所合肥 230032

4.合肥工业大学安徽省工业安全与应急技术重点实验室合肥 230009

通讯作者:

李培培,博士,教授,主要研究方向为数据挖掘.E-mail:peipeili@hfut.edu.cn.

作者简介:

王雨晨,硕士研究生,主要研究方向为半监督多标签数据流分类.E-mail:2023110549@mail.hfut.edu.cn.

邱士远,硕士,主要研究方向为半监督多标签数据流分类.E-mail:2020171138@mail.hfut.edu.cn.

胡学钢,博士,教授,主要研究方向为数据挖掘、知识工程.E-mail:jsjxhuxg@hfut.edu.cn.

收稿日期: 2024-06-15 接受日期: 2024-08-30

资助项目: 国家自然科学基金项目(No.62376085,62076085,62120106008)、合肥综合性国家科学中心大健康研究院健康大数据与群体医学研究所专项资金项目(No.JKS20230030)资助

摘要

实际应用中涌现的大量流数据具有高速到达、海量、动态变化等特点,同时,这些数据流常含有多个标签且只有少量数据被标记,从而带来多标签数据环境下的概念漂移与标签缺失问题.为此,文中提出基于核极限学习机的多标签数据流半监督在线分类方法.首先,针对多标签数据流的标签缺失问题,根据滑动窗口将数据流划分为 k块,对每块数据构造特征相似性矩阵和标签相似性矩阵,并加入核极限学习机的训练中.同时为了适应流数据的特点,设计增量式更新机制,构建半监督在线核极限学习机.然后,为了适应数据流中的概念漂移问题,采用基于时间戳丢弃更新的机制,预先设定数据规模,当数据到达指定规模后,丢弃最旧的无标签数据,将新的数据加入更新.最后,在10个多标签数据集上的实验表明,文中方法对标签缺失和概念漂移问题具有较强的适应能力,并能保持较优的分类效果.

关键词: 数据流分类; 半监督分类; 多标签分类; 核极限学习机; 概念漂移

中图分类号:TP181

Semi-supervised Online Classification Method for Multi-label Data Stream Based on Kernel Extreme Learning Machine

WANG Yuchen^1,², QIU Shiyuan^1,², LI Peipei^1,^2,³, HU Xuegang^1,^2,⁴

1. School of Computer Science and Information Engineering, He-fei University of Technology, Hefei 230601

2. Key Laboratory of Knowledge Engineering with Big Data of Ministry of Education of China, Hefei University of Technology, Hefei 230009

3. Institute of Health Big Data and Population Medicine, Institute of Health and Medicine, Hefei Comprehensive National Science Center, Hefei 230032

4. Anhui Province Key Laboratory of Industry Safety and Emergency Technology, Hefei University of Technology, Hefei 230009

Corresponding author:
LI Peipei, Ph.D., professor. Her research interests include data mining.

About Author:
WANG Yuchen, Master student. His research interests include semi-supervised multi-label data stream classification.
QIU Shiyuan, Master. Her research inte-rests include semi-supervised multi-label data stream classification.
HU Xuegang, Ph.D., professor. His research interests include data mining and know-ledge engineering.

Fund:Supported by National Natural Science Foundation of China(No.62376085,62076085,62120106008), Research Funds of Center for Big Data and Population Health of Institute of Health and Medicine of Hefei Comprehensive National Science Center(No.JKS2023003)

Abstract

In practical applications, a large amount of streaming data emerges, and it is characterized of high arrival speed, massive volume and dynamic variation. Moreover, the data streams often contain multiple labels but only a small amount of data in the streams is labeled, causing the problems of concept drift and label missing in the multi-label data. To solve these problems, a semi- supervised online classification method for multi-label data stream based on kernel extreme learning machine is proposed in this paper. Firstly, the data stream is divided into k blocks according to the sliding window to tackle the label missing problem in multi-label data stream. A feature similarity matrix and a label similarity matrix are constructed for each piece of data and they are added to the training of kernel extreme learning machine model. An incremental update mechanism is designed to construct a semi-supervised online kernel extreme learning machine to adapt to the characteristics of streaming data. Secondly, to address the issue of the concept drift problem in data stream, the timestamp mechanism is adopted for discarding update. The data size is preset in advance. When the data reaches the specified size, the oldest unlabeled data is discarded and new data is added for updating. Finally, experiments on 10 multi-label datasets demonstrate that the proposed method possesses strong adaptability to the problems of label missing and concept drift, while maintaining good classification performance.

Key words: Data Stream Classification; Semi-supervised Classification; Multi-label Classification; Kernel Extreme Learning Machine; Concept Drift

文章图片

现实的硬件设备和软件应用每天都以数据流的形式产生大量数据^[1], 如监控系统、天气预报、电子商务、金融交易等.由于数据信息复杂多变, 单个标签或类别无法完整描述多样化的数据.因此, 多标签数据流分类^[2]的研究得到更多的关注.

目前, 静态数据的多标签学习取得许多成果^{[3, 4]}.半监督多标签学习具有更多的挑战性.半监督多标签学习分为直推式多标签学习和归纳式多标签学习.代表性的直推式多标签学习是基于图的半监督方法, 在标记数据和未标记数据之间构建相似图, 再通过标签传播^{[5, 6]}或流形正则化^[7]预测未标记实例的标签.归纳式多标签学习能预测新实例的标签.例如:多标签分类的协同训练^[8]通过构建多个数据视图, 在特定视图分类器之间传递未标记数据的成对排名预测.但现有方法采用批处理方式, 不适用于多标签数据流.

不同于传统静态数据的多标签分类, 多标签数据流表现出如下特点.1)数据含多个标签, 标签往往是缺失的, 实际应用中给海量数据打标签的时间、人力等成本代价较高.所以, 利用有标签数据和无标签数据的分布特征和潜在的结构信息构建分类模型, 适用于半监督多标签数据流环境^[9].2)实际数据流呈现高速到达、海量等特点, 并且随着新数据的不断到来, 数据分布可能发生变化, 即存在概念漂移问题^[10].所以数据流分类方法需要对发生变化的数据流具有高灵敏度, 可自适应调整模型.

对于数据流的数据不断到来的问题, Huang等^[11]提出OS-ELM(Online Sequential Extreme Lear-ning Machine), 能应对数据流的标签分类问题, 而且相比深度学习方法, OS-ELM具有更快的学习速度和更优的泛化性, 能更好地适应数据流的特点.之后, 学者们提出ELM(Extreme Learning Machine)的许多变体^{[12, 13]}.Xu等^[14]提出DELM(Dynamic ELM for Data Stream Classification).Park等^[15]提出OR-ELM(Online Recurrent ELM).为了结合核函数和I-ELM(Incremental ELM), Zhou等^[16]提出RKRIELM(Regularization I-ELM with Random Reduced Kernel), 提高ELM的稳定性.Wang等^[17]结合核函数与OSELM(Online Sequential ELM), 提出OS-ELMK(Online Sequential ELM with Kernels).Yang等^[18]提出ILR-ELM(Incremental Laplacian Regularization ELM).然而, 上述方法都是针对单标签分类任务设计的, 忽略多标签数据分类和标签缺失的情况.

现有的多标签数据流分类方法主要分为3类:问题转化的方法^[19]、算法自适应的方法^[20]、基于集成学习的方法^[21].上述方法大多建立在标签全部标记的假设条件上, 难以适应标签缺失问题.因此, 研究者们提出半监督数据流分类算法, 主要分为基于图的方法^[22]、基于树的方法^[23]、基于聚类的方法^[24].这些方法虽然考虑标签缺失的问题, 却只针对单标记数据流的分类任务.

基于上述情况, 本文提出基于核极限学习机的多标签数据流半监督在线分类方法, 同时考虑多标签数据流下的标签缺失和概念漂移问题.首先, 改进核极限学习机(Kernel Extreme Learning Machine, KELM), 提出适应多标签数据流的半监督分类方法.结合特征相关性、标签相关性与KELM, 提出半监督分类模型, 并设计增量式更新机制, 推导在线学习分类模型.然后, 考虑概念漂移问题, 采用基于时间戳丢弃更新的机制, 更新在线分类模型, 有效适应多标签数据流环境下的概念漂移.最后, 在10个多标签数据集上的实验表明, 本文方法对标签缺失和概念漂移问题具有较强的适应能力, 并能保持较优的分类效果.

1 基于核极限学习机的多标签数据流半监督在线分类方法

1.1 问题定义

本节给出半监督多标签数据流分类问题的定义.首先给定多标签流数据

Θ =(x_i, y_i $)_{i = 1}^{\infty}$ ,

其中, x_i∈ R^d, 表示流数据中的第i个实例, R^d表示d维样本空间,

y_i∈ {-1, 1}^m∈ $\aleph$,

$\aleph$={1, 2, …, m}表示流数据的标签集.如果实例x_i具有第j个标签, 那么y₍_i_,_j₎=1, 否则y₍_i_,_j₎=-1, 当第i个实例x_i的第j个标签丢失时, 则y₍_i_,_j₎=0.

流数据的标记数据

Θ _l=(x_i, y_i $)_{i = 1}^{n_{l}}$ ,

未标记数据

Θ _u={x_i $}_{i = 1}^{n_{u}}$ ,

其中, n_l表示标记数据的数量, n_u表示未标记数据的数量.

为了更好地模拟数据流分类的情况, 假设多标签流数据Θ 被等分为多个数据块

Θ ={θ ₀, …, θ _k, …, θ _n},

时刻k的数据块可表示为

θ _k={(x_i, y_i) $}_{i = 1}^{N}$ ,

N表示每个数据块的实例数量.数据块θ _k中有标签数据和无标签数据分别表示为

θ _kl={(x_i, y_i) $}_{i = 1}^{l}$ , θ _ku={x_i $}_{i = 1}^{u}$ , u+l=N.

半监督多标签数据流分类的任务描述为

D={(x_i, y_i)|1≤ i≤ m},

即从已有数据集学习一个函数h∶ χ → 2^$\aleph$, 对于新实例x⊆χ , 分类器预测h(x)⊆$\aleph$作为该样本的标签集合.

同时假设多标签流数据Θ 具有标签缺失问题, 且每块数据标记率不同.

1.2 方法框架

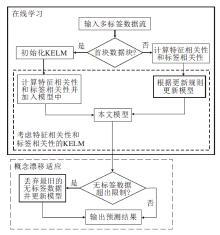
本文提出基于核极限学习机的多标签数据流半监督在线分类方法, 具体流程如图1所示.本文方法可分为如下3部分.

	Figure Option View Download New Window
	图1 本文方法流程图Fig.1 Flowchart of the proposed method

1)在线学习.对于首块数据块, 先构建核极限学习机, 学习有标签数据并预测缺失的标签, 随着新数据的不断到来, 更新模型.

2)考虑数据间的特征相关性和标签相关性的KELM.修改目标函数, 提高预测准确性.

3)概念漂移适应.当无标签数据超出阈值时, 丢弃最旧的无标签数据并更新模型, 从而适应概念漂移.

1.3 半监督极限学习机

本文使用的ELM是一种单隐层前馈神经网络^[25], 其目标是最小化训练样本X的函数输出Hβ 和真实标签Y之间的训练误差, 即

$\min_{β}$ |Hβ -Y|²,

其中, H表示ELM隐含层的输出, β 表示需要求解的输出权重, 闭式解为

β =H^†Y.

考虑多标签数据存在标签缺失情况, 在ELM的优化函数中引入流形正则化项和核函数, 得到半监督的核极限学习机.由此得到算法的初始化阶段, 具体细节如下.

将首块数据块作为流数据的初始状态, 表示为

θ ₀={(x_i, y_i) $}_{i = 1}^{N}$ ,

有标签数据集和无标签数据集分别表示为

θ ₀_l={x_i, y_i $}_{i = 1}^{l}$ , θ ₀_u={x_i $}_{i = 1}^{u}$ .

在ELM的目标函数中引入流形正则化项, 可表示为

arg $\min_{β}$ l(β )= $\frac{1}{2}$ {|β |²+|CHβ -T|²+tr(λ (Hβ )^TL_l₊_uHβ )},

其中, L_l₊_u表示由有标签数据θ ₀_l和无标签数据θ ₀_u构建的图拉普拉斯矩阵.将目标函数关于β 的梯度设为0, 可得

β ₀=(I₀+ ${H^{T}}_{0}$ C₀H₀+λ ${H^{T}}_{0}$ L₀H₀)^-1 ${H^{T}}_{0}$ C₀T₀.

其中:I₀表示第一个数据块θ ₀的单位矩阵;

C₀=diag(J₁, J₂, …, 0, 0),

表示一个前l个对角项等于J_i, 其余为0的对角矩阵, J_i=J₀/ $N_{y_{i}}$ , 表示关于标签y_i训练错误的惩罚系数, $N_{y_{i}}$ 表示属于标签y_i的实例x_i的数量; L₀表示由有标签数据集θ ₀_l和无标签数据集θ ₀_u构建的图拉普拉斯矩阵, 表示数据间的相似性, 由L=A-S计算得到, A表示一个对角矩阵, 对角元素$A_{i i}=\sum_{j=1}^{m} S_{i j}$, S=[s_ij]表示相似矩阵, s_ij表示两个实例x_i、x_j之间的成对相似性; λ 表示拉普拉斯因子, 即权衡参数; T₀∈ R⁽^l⁺^u^)×^m, 表示扩充标签空间, 前l行等于Y₀_l, 其余行等于0.

数据块中的实例数量通常少于隐藏层节点数量, 即H的列数多于行数, 并且行满秩时, θ ₀的输出权重矩阵^[12]如下所示:

β ₀= ${H^{T}}_{0}$ (I₀+ ${H^{T}}_{0}$ C₀H₀+λ ${H^{T}}_{0}$ L₀H₀)^-1C₀T₀.

1.3.1 基于特征相关性和标签相关性的核极限学习机

对于数据流中存在的标签缺失问题, 本文对数据块构建特征相关性矩阵和标签相关性矩阵, 并加入核极限学习机的训练之中.

引入流形正则化项的核极限学习机的目标函数可表示为

arg $\min_{β}$ l(β )= $\frac{1}{2}$ {|β |²+|CHβ -T|²+ tr(λ (Hβ )T^Lx_Hβ )+tr(λ (Hβ )T^Ly_Hβ )},

其中, L_x表示有标签数据和无标签数据的特征相关性矩阵, L_y表示标签相关性矩阵, 由此可得

β =H^T(I+H^TCH+λ H^TL_xH+γ H^TL_yH)^-1CT.

将首块数据块作为数据流的初始状态, 可表示为

θ ₀={(x_i, y_i) $}_{i = 1}^{N}$ ,

有标签数据集和无标签数据集分别表示为

θ ₀_l={x_i, y_i $}_{i = 1}^{l}$ , θ ₀_u={x_i $}_{i = 1}^{u}$ .

对于第一块数据, 分类模型的目标函数为:

$\begin{array}{l}\boldsymbol{\beta}_{0} =\boldsymbol{H}_{0}^{\mathrm{T}}\left(\boldsymbol{I}_{0}+\boldsymbol{H}_{0}^{\mathrm{T}} \boldsymbol{C}_{0} \boldsymbol{H}_{0}+\lambda \boldsymbol{H}_{0}^{\mathrm{T}} \boldsymbol{L}_{x 0} \boldsymbol{H}_{0}+\gamma \boldsymbol{H}^{\mathrm{T}} \boldsymbol{L}_{20} \boldsymbol{H}\right)^{-1} \boldsymbol{C}_{0} \boldsymbol{T}_{0} .\end{array}$

其中:L_x₀为由有标签数据集θ ₀_l和无标签数据集θ ₀_u的特征空间构建的图拉普拉斯矩阵, 表示数据间的特征相关性; L_y₀为θ ₀_l和θ ₀_u的标签空间构建的图拉普拉斯矩阵, 表示数据间的标签相关性; λ 、γ 为拉普拉斯因子(权衡参数); T₀为无标签数据的标签空间.由于流数据存在标签缺失, 且不同数据块的缺失程度不同, 故数据块θ ₀的输出函数为:

$\begin{array}{l}f^{0}(\boldsymbol{x})=\boldsymbol{H}_{0} \boldsymbol{\beta}_{0}=\boldsymbol{H}_{0} \boldsymbol{H}_{0}^{\mathrm{T}} \cdot \\\left(\boldsymbol{I}_{0}+\boldsymbol{H}_{0}^{\mathrm{T}} \boldsymbol{C}_{0} \boldsymbol{H}_{0}+\lambda \boldsymbol{H}_{0}^{\mathrm{T}} \boldsymbol{L}_{x 0} \boldsymbol{H}_{0}+\gamma \boldsymbol{H}_{0}^{\mathrm{T}} \boldsymbol{L}_{y 0} \boldsymbol{H}_{0}\right)^{-1} \boldsymbol{C}_{0} \boldsymbol{T}_{0}\end{array}$

再引入核函数K(u, v), 核函数表示为

${K^{T}}_{0}$ =H₀ ${H^{T}}_{0}$ .

分类模型采用核函数替代隐含层映射, 可得到多向量输出, 具体输出函数如下:

f⁰(x)= ${K^{T}}_{0}$ (I₀+C₀ ${K^{T}}_{0}$ +λ L_x₀ ${K^{T}}_{0}$ +γ L_y₀ ${K^{T}}_{0}$ )^-1C₀T₀.

令

Ω ₀=I₀+C₀ ${K^{T}}_{0}$ +λ L_x₀ ${K^{T}}_{0}$ +γ L_y₀ ${K^{T}}_{0}$ ,

简化上式, 可得首块数据块的分类函数:

f⁰(x)= ${K^{T}}_{0}$ (Ω ₀)^-1C₀T₀.

上述过程为本文方法的初始化阶段.为了方便之后的公式推导, 用Φ ₀代替Ω ₀, 可得

f⁰(x)= ${K^{T}}_{0} Φ_{0}^{- 1}$ C₀T₀.

1.3.2 在线学习的半监督分类方法

考虑到数据流场景, 本文方法采用在线学习, 利用已有模型, 预测新到来的数据块.

随着新数据块θ _k(k≥ 1)的到来, 本文方法采用在线学习模式.对于第2块到来的数据块

$\boldsymbol{\theta}_{1}=\left\{\left(\boldsymbol{x}_{i}, \boldsymbol{y}_{i}\right)\right\}_{i=N+1}^{N+N}$,

数据块中有标签数据集和无标签数据集分别表示为

$\boldsymbol{\theta}_{1 l}=\left\{\boldsymbol{x}_{i}, \boldsymbol{y}_{i}\right\}_{i=1}^{l}, \boldsymbol{\theta}_{1 u}=\left\{\boldsymbol{x}_{i}\right\}_{i=1}^{u} .$

根据流数据的特性, 将新来的数据块作为测试集.首先使用初始数据块θ ₀的输出函数f⁰(x)测试新的数据块θ ₁, 结果如下:

Y $_{1}^{test}$ =K(θ ₁, θ ₀)^T $Φ_{0}^{- 1}$ C₀T₀,

其中核函数

K(θ ₁, θ ₀)=H₁ ${H^{T}}_{0}$ .

对于单独的数据块θ ₁, 输出函数为:

f¹(x)=H₁β ₁=H₁ ${H^{T}}_{1}$ · (I₁+ ${H^{T}}_{1}$ C₁H₁+λ ${H^{T}}_{1}$ L_x₁H₁+γ ${H^{T}}_{1}$ L_y₀H₁)^-1C₁T₁.

在流数据环境下, 构建分类器时需要考虑历史数据包含的信息, 因此将新的数据块θ ₁添加至初始数据块θ ₀中用于训练.对于数据块θ ₀和数据块θ ₁隐含层的输出矩阵和标签空间矩阵, 采用简单累积的方式进行更新, $L_{x θ_{0} ⋃ θ_{1}}$ 和 $L_{y θ_{0} ⋃ θ_{1}}$ 分别表示数据块θ ₀和θ ₁之间的特征相关性和标签相关性的更新, 由于流数据之间的稀疏相关性, 可忽略块与块之间的结构关系, 则

$L_{x θ_{0} ⋃ θ_{1}}$ = $[\begin{array}{l} L_{x 0} & 0 \\ 0 & L_{x 1} \end{array}]$ , $L_{y θ_{0} ⋃ θ_{1}}$ = $[\begin{array}{l} L_{y 0} & 0 \\ 0 & L_{y 1} \end{array}]$ ,

可得

$\begin{aligned} f^{1}(\boldsymbol{x}) & =\left[\begin{array}{l} \boldsymbol{K}_{0} \\ \boldsymbol{K}_{1} \end{array}\right]^{\mathrm{T}}\left(\left[\begin{array}{cc} \boldsymbol{I}_{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{I}_{1} \end{array}\right]+\left[\begin{array}{cc} \boldsymbol{C}_{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{C}_{1} \end{array}\right]\left[\begin{array}{l} \boldsymbol{H}_{0} \\ \boldsymbol{H}_{1} \end{array}\right]\left[\begin{array}{l} \boldsymbol{H}_{0} \\ \boldsymbol{H}_{1} \end{array}\right]^{\mathrm{T}}+\lambda\left[\begin{array}{cc} \boldsymbol{L}_{x 0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{L}_{x 1} \end{array}\right]\left[\begin{array}{l} \boldsymbol{H}_{0} \\ \boldsymbol{H}_{1} \end{array}\right]\left[\begin{array}{l} \boldsymbol{H}_{0} \\ \boldsymbol{H}_{1} \end{array}\right]^{\mathrm{T}}\right. \\ & \left.+\gamma\left[\begin{array}{cc} \boldsymbol{L}_{y 0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{L}_{y 1} \end{array}\right]\left[\begin{array}{l} \boldsymbol{H}_{0} \\ \boldsymbol{H}_{1} \end{array}\right]\left[\begin{array}{l} \boldsymbol{H}_{0} \\ \boldsymbol{H}_{1} \end{array}\right]^{\mathrm{T}}\right)^{-1} \cdot\left[\begin{array}{cc} \boldsymbol{C}_{0} & \mathbf{0} \\ \mathbf{0} & \boldsymbol{C}_{1} \end{array}\right]\left[\begin{array}{l} \boldsymbol{T}_{0} \\ \boldsymbol{T}_{1} \end{array}\right] \end{aligned}$,

其中, 数据块θ ₁的核函数 ${K^{T}}_{1}$ =H₁ ${H^{T}}_{1}$ , C₁表示数据块θ ₁的相关对角线矩阵, 则上式可表示为

$\begin{array}{l} f^{1}(\boldsymbol{x})=\left[\begin{array}{l} \boldsymbol{K}_{0} \\ \boldsymbol{K}_{1} \end{array}\right]^{\mathrm{T}}\left(\left[\begin{array}{c} \boldsymbol{I}_{0}+\boldsymbol{C}_{0} \boldsymbol{H}_{0} \boldsymbol{H}_{0}^{\mathrm{T}}+\lambda \boldsymbol{L}_{x 0} \boldsymbol{H}_{0} \boldsymbol{H}_{0}^{\mathrm{T}}+\gamma \boldsymbol{L}_{y 0} \boldsymbol{H}_{0} \boldsymbol{H}_{0}^{\mathrm{T}} \\ \boldsymbol{C}_{1} \boldsymbol{H}_{1} \boldsymbol{H}_{0}^{\mathrm{T}}+\lambda \boldsymbol{L}_{x 1} \boldsymbol{H}_{1} \boldsymbol{H}_{0}^{\mathrm{T}}+\gamma \boldsymbol{L}_{y 1} \boldsymbol{H}_{1} \boldsymbol{H}_{0}^{\mathrm{T}} \end{array}\right.\right. \\ \left.\left.\begin{array}{c} \boldsymbol{C}_{0} \boldsymbol{H}_{0} \boldsymbol{H}_{1}^{\mathrm{T}}+\lambda \boldsymbol{L}_{x 0} \boldsymbol{H}_{0} \boldsymbol{H}_{1}^{\mathrm{T}}+\gamma \boldsymbol{L}_{y 0} \boldsymbol{H}_{0} \boldsymbol{H}_{1}^{\mathrm{T}} \\ \boldsymbol{I}_{1}+\boldsymbol{C}_{1} \boldsymbol{H}_{1} \boldsymbol{H}_{1}^{\mathrm{T}}+\lambda \boldsymbol{L}_{x 1} \boldsymbol{H}_{1} \boldsymbol{H}_{1}^{\mathrm{T}}+\gamma \boldsymbol{L}_{\boldsymbol{y} 1} \boldsymbol{H}_{1} \boldsymbol{H}_{1}^{\mathrm{T}} \end{array}\right]\right)^{-1}\left[\begin{array}{l} \boldsymbol{C}_{0} \boldsymbol{T}_{0} \\ \boldsymbol{C}_{1} \boldsymbol{T}_{1} \end{array}\right] . \end{array}$.(2)

令

$\begin{array}{l}\boldsymbol{\Omega}_{0}=\boldsymbol{I}_{0}+\boldsymbol{C}_{0} \boldsymbol{H}_{0} \boldsymbol{H}_{0}^{\mathrm{T}}+\lambda \boldsymbol{L}_{x 0} \boldsymbol{H}_{0} \boldsymbol{H}_{0}^{\mathrm{T}}+\gamma \boldsymbol{L}_{y 0} \boldsymbol{H}_{0} \boldsymbol{H}_{0}^{\mathrm{T}}, \boldsymbol{\Omega}_{1}=\boldsymbol{I}_{1}+\boldsymbol{C}_{1} \boldsymbol{H}_{1} \boldsymbol{H}_{1}^{\mathrm{T}}+\lambda \boldsymbol{L}_{x 1} \boldsymbol{H}_{1} \boldsymbol{H}_{1}^{\mathrm{T}}+\gamma \boldsymbol{L}_{y 1} \boldsymbol{H}_{1} \boldsymbol{H}_{1}^{\mathrm{T}} . \\\boldsymbol{R}_{01}=\boldsymbol{C}_{0} \boldsymbol{H}_{0} \boldsymbol{H}_{1}^{\mathrm{T}}+\lambda \boldsymbol{L}_{x 0} \boldsymbol{H}_{0} \boldsymbol{H}_{1}^{\mathrm{T}}+\gamma \boldsymbol{L}_{\wedge 0} \boldsymbol{H}_{0} \boldsymbol{H}_{1}^{\mathrm{T}}, \boldsymbol{R}_{10}=\boldsymbol{C}_{1} \boldsymbol{H}_{1} \boldsymbol{H}_{0}^{\mathrm{T}}+\lambda \boldsymbol{L}_{x 1} \boldsymbol{H}_{1} \boldsymbol{H}_{0}^{\mathrm{T}}+\gamma \boldsymbol{L}_{y 1} \boldsymbol{H}_{1} \boldsymbol{H}_{0}^{\mathrm{T}} .\end{array}$

于是得到

$f^{1}(\boldsymbol{x})=\left[\begin{array}{l}\boldsymbol{K}_{0} \\\boldsymbol{K}_{1}\end{array}\right]^{\mathrm{T}}\left(\left[\begin{array}{ll}\boldsymbol{\Omega}_{0} & \boldsymbol{R}_{01} \\\boldsymbol{R}_{10} & \boldsymbol{\Omega}_{1}\end{array}\right]\right)^{-1}\left[\begin{array}{l}\boldsymbol{C}_{0} \boldsymbol{T}_{0} \\\boldsymbol{C}_{1} \boldsymbol{T}_{1}\end{array}\right]$

用Φ ₁代替 $[\begin{array}{l} Ω_{0} & R_{01} \\ R_{10} & Ω_{1} \end{array}]$ , 对于 $Φ_{1}^{- 1}$ , 采用矩阵取逆方式, 计算得

$Φ_{1}^{- 1}$ = ${[\begin{array}{l} Ω_{0} & R_{01} \\ R_{10} & Ω_{1} \end{array}]}^{- 1}$ = $[\begin{array}{l} Ω_{0}^{- 1} + D_{1} Δ_{1} {D^{T}}_{1} & - D_{1} Δ_{1} \\ - Δ_{1} {D^{T}}_{1} & Δ_{1} \end{array}]$ ,

其中

Δ ₁=(Ω ₁-R¹⁰ $Ω_{0}^{- 1}$ R⁰¹)^-1, D₁= $Ω_{0}^{- 1}$ R⁰¹, ${D^{T}}_{1}$ =R¹⁰ $Ω_{0}^{- 1}$ .

将式(1)代入式(2), 可将f¹(x)重写为

$\begin{aligned}f^{1}(\boldsymbol{x})= & {\left[\begin{array}{l}\boldsymbol{K}_{0} \\\boldsymbol{K}_{1}\end{array}\right]^{\mathrm{T}}\left[\begin{array}{cc}\boldsymbol{\Omega}_{0}^{-1}+\boldsymbol{D}_{1} \boldsymbol{\Delta}_{1} \boldsymbol{D}_{1}^{\mathrm{T}} & -\boldsymbol{D}_{1} \boldsymbol{\Delta}_{1} \\-\boldsymbol{\Delta}_{1} \boldsymbol{D}_{1}^{\mathrm{T}} & \boldsymbol{\Delta}_{1}\end{array}\right]\left[\begin{array}{l}\boldsymbol{C}_{0} \boldsymbol{T}_{0} \\\boldsymbol{C}_{1} \boldsymbol{T}_{1}\end{array}\right]=} \\& \boldsymbol{K}_{0}^{\mathrm{T}} \boldsymbol{\Omega}_{0}^{-1} \boldsymbol{C}_{0} \boldsymbol{T}_{0}+\boldsymbol{K}_{0}^{\mathrm{T}} \boldsymbol{D}_{1} \boldsymbol{\Delta}_{1} \boldsymbol{D}_{1}^{\mathrm{T}} \boldsymbol{C}_{0} \boldsymbol{T}_{0}-\boldsymbol{K}_{1}^{\mathrm{T}} \boldsymbol{\Delta}_{1} \boldsymbol{D}_{1}^{\mathrm{T}} \boldsymbol{C}_{0} \boldsymbol{T}_{0}-\boldsymbol{K}_{0}^{\mathrm{T}} \boldsymbol{D}_{1} \boldsymbol{\Delta}_{1} \boldsymbol{C}_{1} \boldsymbol{T}_{1}+\boldsymbol{K}_{1}^{\mathrm{T}} \boldsymbol{\Delta}_{1} \boldsymbol{C}_{1} \boldsymbol{T}_{1}= \\& f^{0}(\boldsymbol{x})+\left(\boldsymbol{K}_{0}^{\mathrm{T}} \boldsymbol{D}_{1}-\boldsymbol{K}_{1}^{\mathrm{T}}\right) \boldsymbol{\Delta}_{1}\left(\boldsymbol{D}_{1}^{\mathrm{T}} \boldsymbol{C}_{0} \boldsymbol{T}_{0}-\boldsymbol{C}_{1} \boldsymbol{T}_{1}\right) .\end{aligned}$

由此得到 f¹(x)根据 f⁰(x)递推得到的函数形式.当新的数据块到达时, 模型更新推导如下.

当k+1时刻的数据块

θ _k₊₁=(x_i, y_i $)_{i = (k + 1) N + 1}^{(k + 1) N + N}$ , k≥ 1

到来时, 首先用前k个时刻的数据块训练的模型进行预测, 对于数据块θ _k₊₁, 预测输出为:

Y $_{k + 1}^{test}$ =K(θ _k₊₁, θ ₀~θ _k)^T $Φ_{k}^{- 1}$ [C₀T₀ … C_kT_k]^T,

其中, 核函数

K(θ _k₊₁, θ ₀~θ _k)^T=H_k₊₁( ${H^{T}}_{0}$ , ${H^{T}}_{1}$ , …, ${H^{T}}_{k}$ ),

θ ₀~θ _k表示从数据块θ ₀到数据块θ _k的累积, Φ _k表示前k个时刻的数据块训练的分类模型的核心矩阵.

然后将k+1时刻的块数据加入训练, 参考上面的推导过程, 可推导出输出函数:

f^k⁺¹(x)= ${[\begin{array}{l} K_{0} \\ K_{1} \\ ︙ \\ K_{k + 1} \end{array}]}^{T} {[\begin{array}{l} R^{0 (k + 1)} \\ Φ_{K} & ︙ \\ R^{k (k + 1)} \\ R^{(k + 1) 0} & \dots & R^{(k + 1) k} & Ω_{k + 1} \end{array}]}^{- 1} [\begin{array}{l} C_{0} T_{0} \\ C_{1} T_{1} \\ ︙ \\ C_{k + 1} T_{k + 1} \end{array}]$ .

令

$\begin{array}{l}\boldsymbol{\Omega}_{k+1}=\boldsymbol{I}_{k+1}+\left(\boldsymbol{C}_{k+1}+\lambda \boldsymbol{L}_{x k+1}+\gamma \boldsymbol{L}_{y k+1}\right) \boldsymbol{H}_{k+1} \boldsymbol{H}_{k+1}^{\mathrm{T}}, \\\boldsymbol{R}_{k+1}^{0-n}=\left[\begin{array}{llll}\boldsymbol{R}^{0(k+1)} & \boldsymbol{R}^{1(k+1)} & \cdots & \boldsymbol{R}^{k(k+1)}\end{array}\right]^{\mathrm{T}}, \\\boldsymbol{R}_{k+1}^{n-0}=\left[\begin{array}{llll}\boldsymbol{R}^{(k+1) 0} & \boldsymbol{R}^{(k+1) 1} & \cdots & \boldsymbol{R}^{(k+1) k}\end{array}\right], \end{array}$

将输出函数f^k⁺¹(x)展开计算, 可得到最终形式:

$\begin{array}{l}f^{k+1}(\boldsymbol{x})=f^{k}(\boldsymbol{x})+ \\\quad\left(\widetilde{\boldsymbol{K}}_{k} \boldsymbol{D}_{k+1}-\boldsymbol{K}_{k+1}\right) \boldsymbol{\Delta}_{k+1}\left(\boldsymbol{D}_{k+1}^{\mathrm{T}} \boldsymbol{C}_{k} \widetilde{\boldsymbol{T}}_{k}-\boldsymbol{C}_{k+1} \boldsymbol{T}_{k+1}\right), \end{array}$(3)

其中,

${\tilde{K}}_{k}$ =[K₀K₁ … K_k]^T,

D_k₊₁= $Φ_{k}^{- 1} R_{k + 1}^{0 - n}$ , ${D^{T}}_{k + 1}$ = $R_{k + 1}^{n - 0} Φ_{k}^{- 1}$ ,

Δ _k₊₁=Ω _k₊₁- $R_{k + 1}^{n - 0} Φ_{k}^{- 1} R_{k + 1}^{0 - n}$ ,

${\tilde{T}}_{k}$ =[T₀T₁ … T_k]^T.

1.4 概念漂移适应与模型更新

对于数据流中数据分布变化问题, 本文采用滑动窗口机制以适应概念漂移.当已到达的数据中的无标签数据数量超过一定限制时, 抛弃旧的无标签数据, 保留新数据.

首先使用B_U记录每块数据块中无标签数据的数量, 并预先定义B_U的大小为S_U, 如果|B_U|> S_U, 则删除B_U中最旧的实例.

基于上述说明推导出一种自适应规模且迭代更新的在线半监督分类模型:

f $_{update}^{k + 1}$ (x)= ${[\begin{array}{l} K_{0 - B_{0}} \\ K_{1 - B_{1}} \\ ︙ \\ K_{k + 1} \end{array}]}^{T} {[\begin{array}{l} R^{0 - B_{0} (k + 1)} \\ Φ_{k - B} & ︙ \\ R^{k (k + 1)} \\ R^{(k + 1) 0 - B_{0}} & \dots & R^{(k + 1) k} & Ω_{k + 1} \end{array}]}^{- 1} [\begin{array}{l} C_{0 - B_{0}} T_{0 - B_{0}} \\ C_{1 - B_{1}} T_{1 - B_{1}} \\ ︙ \\ C_{k + 1} T_{k + 1} \end{array}]$ ,

其中, B表示B_U中最旧的无标签实例, B₀表示数据块θ ₀中的无标签数据, B₁表示数据块θ ₁中的无标签数据.上述方法既考虑历史数据对于模型构建的贡献, 又避免分类模型消耗过大的问题, 能适应数据流中的概念漂移问题.

1.5 方法步骤及时间复杂度分析

本文提出基于核极限学习机的多标签数据流半监督在线分类方法, 具体伪代码如下所示.

算法基于核极限学习机的多标签数据流半监督在线分类方法

输入数据流Θ , 核函数K(u, v), 权衡参数J₀,

拉普拉斯参数λ , γ , 无标签数据量限制S_U

输出对前k个数据块的预测输出,

第k+1块数据块的输出函数f^k⁺¹(x)

初始化 k← 0

模型参数核映射K₀、Ω ₀, 图拉普拉斯矩阵L₀,

参数矩阵C₀,

输出函数f⁰(x)

for k=1, 2, …, do

函数f^k^-1(x)预测第k块数据块的缺失标签并保

留结果

计算第k+1块数据块的L_K、C_K、核映射K₀、Ω ₀以

及 $R_{K}^{n - 0}$ 、 $R_{K}^{0 - n}$ 、D_K、Δ _K

计算输出函数f^k(x)和无标签数据量B_U

if B_U> S_U do

以数据块为单位抛弃最旧(最先处理)的无标

签数据并更新模型

end if

end for

return对前k个数据块的预测输出, 第k+1数据块的输出函数f^k⁺¹(x)

本文方法的时间复杂度主要有两个部分:初始化阶段和在线更新阶段.初始化阶段时间复杂度为Ο (kaNd), 其中, N表示单个数据块大小(实例数量), d表示数据集的特征维度.ELM时间复杂度为k, 处理一个实例的成本为a.在在线更新阶段, 本文采取以单个数据块的规模更新模型, 时间复杂度为Ο (kaNd).对于概念漂移只有适应并无检测, 不会有时间消耗.所以, 本文方法最终时间复杂度为Ο (kaNd).

2 实验及结果分析

2.1 实验数据集及评价指标

本文选择在10个多标签数据集上评估方法性能, 数据集信息汇总如表1所示.考虑到数据流中每个时刻的数据标记率不一样, 实验采用先设置数据的标记率再分块的方法.

表1 实验数据集信息 Table 1 Information of experimental datasets

实验中采用滑动窗口的方法设计数据块大小为100.对于所有基于ELM的方法, 选择RBF(Radial Basis Function)作为核函数, 权衡参数J₀=10^-3, 拉普拉斯参数λ =γ =0.1.

所有实验都在I9-10900和32 GB内存的系统上运行.各方法在不同数据集上运行10次, 取10次实验结果的平均值.

为了更好地评估方法性能, 采用如下6个广泛采用的评价指标:Average-Precision(Ave-Pre)、Mirco-F1(MicF1)、AUC(Area Under Curve)、Hamming Loss(HL)、Ranking Loss(RL)、One-Error(OE).Ave-Pre、MicF1、AUC指标值越大, 表示分类性能越优, HL、RL、OE指标则相反, 指标值越小, 表示分类性能越优.

对于本文方法, 实验选择RBF作为核函数, 将拉普拉斯参数λ 和γ 范围调整在{0.05, 0.1, …, 1}内, 权衡参数J₀, 范围调整在{10^-5, 10^-4, …, 10⁵}内.为了公平地与其它方法进行对比, 实验只保留最后一块数据块的预测结果, 即针对最新数据块的分类结果.

2.2 消融实验

设定标记率从10%增长到100%, 本文方法在6个数据集上的HL指标变化如图2所示.

	Figure Option View Download New Window
	图2 本文方法在不同标记率的数据集上的HL指标对比Fig.2 Comparison of HL metric values of the proposed method on datasets with different labeled rates

由图2可见, 本文方法对于标签缺失的数据流分类具有有效性.

在10个数据集上, 面对概念漂移问题, 本文方法是否更新后的指标值对比如表2所示, 表中黑体数字表示最优值.

由表2可看出, 不考虑概念漂移适应方法, 本文方法在大部分数据集上的分类效果均有一定损失, 也有一些分类效果反而更优.本文考虑的概念漂移适应方法是被动方法, 不能主动检测数据中的概念漂移情况, 可能不适用于所有数据集, 由此带来一些分类误差.但是, 从大部分数据集上的结果来看, 本文的概念漂移适应方法仍然有效.

表2 本文方法是否更新对指标值的影响 Table 2 Effect of updates or non-updates of the proposed method on metric values

2.3 对比实验

对比方法选取如下两个在线多标签分类方法和一个批处理的半监督分类方法.

1)OnSeML(Online Semi-supervised Multi-label Learning Algorithm)^[26].允许在半监督环境中进行实时多标签预测, 并且对进化的标签分布具有鲁棒性, 适用于多标签数据流分类中的标签缺失问题.

2)OS-ELM^[11].基于核极限学习机的在线分类器, 在非平稳时间序列预测中具有良好性能, 但主要针对单标签数据流分类.

3)SSO-KELM(Semi-supervised Online Kernel Extreme Learning Machine Algorithm for Multi-label Data Stream)^[27].半监督极限学习机结合流形正则化, 利用标记数据与未标记数据的隐含信息, 在标记数据稀缺时提高分类精度.

由于现实中数据标记率较低, 现只对比标记率为10%和20%的情况.在10个数据集上各方法的平均指标值对比结果如表3~表12所示, 表中黑体数字表示最优值.由表可得出如下结论.

表3 各方法在Business数据集上的指标值对比 Table 3 Metric value comparison of different methods on Business dataset

表4 各方法在Computer数据集上的指标值对比 Table 4 Metric value comparison of different methods on Computer dataset

表5 各方法在Entertainment数据集上的指标值对比 Table 5 Metric value comparison of different methods on Entertainment dataset

表6 各方法在Health数据集上的指标值对比 Table 6 Metric value comparison of different methods on Health dataset

表7 各方法在Recreation数据集上的指标值对比 Table 7 Metric value comparison of different methods on Recreation dataset

表8 各方法在Reference数据集上的指标值对比 Table 8 Metric value comparison of different methods on Reference dataset

表9 各方法在Science数据集上的指标值对比 Table 9 Metric value comparison of different methods on Science dataset

表10 各方法在Social数据集上的指标值对比 Table 10 Metric value comparison of different methods on Social dataset

表11 各方法在Society数据集上的指标值对比 Table 11 Metric value comparison of different methods on Society dataset

表12 各方法在Yeast数据集上的指标值对比 Table 12 Metric value comparison of different methods on Yeast dataset

1)本文方法在大部分指标上取得的结果均优于对比方法.即使只有10%和20%的标记率, 本文方法也能得到较优的分类效果.这表明本文方法在处理标签缺失的多标签流数据时产生一定的分类效果.

2)OnSeML考虑标签相关性但未考虑特征相关性, 因此, 在标签缺失的流数据分类问题上取得一定效果, 但在处理数据时忽略数据之间的部分隐含信息, 从而影响算法的分类性能.

3)OS-ELM在所有评价指标上的表现都相对较差.虽然OS-ELM已证实是一个高效的数据流分类方法, 但未考虑数据流中的标签缺失问题, 无法对无标签数据做出正确预测, 且OS-ELM也未考虑数据中的特征相关性和标签相关性, 未利用数据间的隐藏信息, 因此分类效果较差.由此也从侧面表明本文方法的必要性和有效性.

4)SSO-KELM可利用大部分数据作为训练实例, 在分类时考虑数据的实例相关性, 因此在一些数据集上取得较优性能, 但SSO-KELM忽略多标签数据中的标签相关性.本文方法不仅考虑数据的特征相关性, 同时考虑标签相关性, 因此利用少量的数据进行训练后, 仍可取得较优结果.此外, SSO-KELM是批处理的方法, 不适用于数据流分类, 而本文方法是在线学习方法, 适合数据流场景.

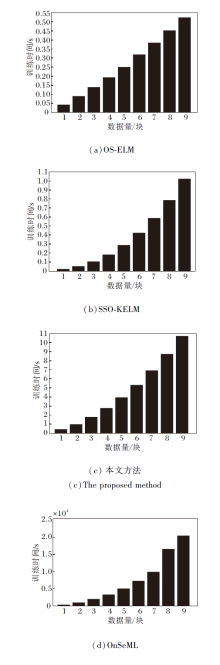
下文对比各方法的训练时间.实验设置如下:Business数据集作为实验数据集, 标签率设置为10%, 以50个实例作为一个数据块.各方法的训练时间对比如图3所示.由于数据流分类要求高精度和短时间, 本文方法需要更多的时间.主要原因是本文方法考虑数据特征相关性和标签相关性, 构建相关性矩阵较耗时.当流数据划分成多块数据块时, 在每块数据块上的训练时间相对较短.故本文方法仍是一种快速算法, 能适应数据流环境.

	Figure Option View Download New Window
	图3 各方法的训练时间对比Fig.3 Training time comparison of different methods

由上述分析所知, 在半监督多标签数据流学习中, 相比其它分类方法, 本文方法性能具有一定提升.

2.4 与CNN和LSTM的对比

深度学习中的CNN(Convolutional Neural Net-work)和LSTM(Long-Short Term Memory Network)在面对标签分类问题时, 采取批量式处理, 并且也是单标签分类.本文将CNN和LSTM作为对比方法, 使用批量式处理和问题转化的思想, 将数据流问题作为批量处理问题, 将多标签分类当成多个单标签分类, 在10%、20%的标记率下, 分别在8个数据集上进行对比实验, 指标值结果如表13~表20所示, 表中黑体数字表示最优值.

表13 本文方法与CNN、LSTM在Computer数据集上的指标值对比 Table 13 Metric value comparison of the proposed method, CNN and LSTM on Computer dataset

表14 本文方法与CNN、LSTM在Entertainment数据集上的指标值对比 Table 14 Metric value comparison of the proposed method, CNN and LSTM on Entertainment dataset

表15 本文方法与CNN、LSTM在Health数据集上的指标值对比 Table 15 Metric value comparison of the proposed method, CNN and LSTM on Health dataset

表16 本文方法与CNN、LSTM在Recreation数据集上的指标值对比 Table 16 Metric value comparison of the proposed method, CNN and LSTM on Recreation dataset

表17 本文方法与CNN、LSTM在Reference数据集上的指标值对比 Table 17 Metric value comparison of the proposed method, CNN and LSTM on Reference dataset

表18 本文方法与CNN、LSTM在Science数据集上的指标值对比 Table 18 Metric value comparison of the proposed method, CNN and LSTM on Science dataset

表19 本文方法与CNN、LSTM在Social数据集上的指标值对比 Table 19 Metric value comparison of the proposed method, CNN and LSTM on Social dataset

表20 本文方法与CNN、LSTM在Entertainment数据集上的指标值对比 Table 20 Metric value comparison of the proposed method, CNN and LSTM on Entertainment dataset

由表13~表20可知, 在所有数据集上, 本文方法在Ave-Pre和AUC指标上的表现均优于CNN和LSTM, 而在MicF1指标上则相反.这是因为CNN和LSTM对正标签(即标签为1)的预测不佳, 绝大多数预测为负标签(即标签为-1), 这一点可从Ave-Pre指标值低而MicF1指标值高看出(MicF1指标对应负标签, 故对比方法产生的此指标值较高).另外在HL、OE指标上, 本文方法和对比方法差别不大.所以, 在多标签分类问题上, 本文方法优于CNN和LSTM.

3 结束语

本文提出基于核极限学习机的多标签数据流半监督在线分类方法, 解决多标签数据流场景下的标签缺失和概念漂移问题.首先, 改进核极限学习机, 提出多标签数据流半监督分类方法, 将特征相关性和标签相关性与核极限学习机结合, 得到新的半监督分类模型.然后, 推导在线学习的分类模型, 又考虑到概念漂移问题, 对在线模型进行更新, 从而避免因数据分布改变导致模型精度下降的问题.实验表明, 相比经典的半监督分类方法和多标签数据流分类方法, 本文方法在标签缺失的多标签数据流分类问题上性能更优, 特别是在同样的数据集上, 本文方法的训练时间要远短于其它对比方法.

今后将尝试对本文方法进行改进以应对突变式和重复式概念漂移问题, 另外尝试探索更高效且能降低耗时的方法, 此外也会将数据维度爆炸问题和特征提取方法作为研究方向.在数据流场景下, 如何实现多标签分类算法的鲁棒性和快速高效也是未来需要考虑的问题.

本文责任编委杨明

Recommended by Associate Editor YANG Ming

参考文献

文献选项

[1]	UD DIN S, SHAO J M, KUMAR J, et al. Online Reliable Semi-supervised Learning on Evolving Data Streams. Information Sciences, 2020, 525: 153-171. [本文引用:1]
[2]	WU H X, HAN M, CHEN Z Q, et al. A Weighted Ensemble Cla-ssification Algorithm Based on Nearest Neighbors for Multi-label Data Stream. ACM Transactions on Knowledge Discovery from Data, 2023, 17(5). DOI: 10.1145/357096. [本文引用:1]
[3]	HOSSEINI M J, GHOLIPOUR A, BEIGY H. An Ensemble of Cluster-Based Classifiers for Semi-supervised Classification of Non-stationary Data Streams. Knowledge and Information Systems, 2016, 46: 567-597. [本文引用:1]
[4]	ADAMS J N, PITSCH C, BROCKHOFF T, et al. An Experimental Evaluation of Process Concept Drift Detection. Proceedings of the VLDB Endowment, 2023, 16(8): 1856-1869. [本文引用:1]
[5]	GULCAN E B, ECEVIT I S, CAN F. Binary Transformation Method for Multi-label Stream Classification // Proc of the 31st ACM International Conference on Information and Knowledge Management. New York, USA: ACM, 2022: 3968-3972. [本文引用:1]
[6]	LI J N, ZHANG Y C, CHEN S W, et al. Enhancing Multi-label Classification via Dynamic Label-Order Learning. Proceedings of the AAAI Conference on Artificial Intelligence, 2024, 38(17): 18527-18535. [本文引用:1]
[7]	SUN Y G, SHAO H, WANG S S. Efficient Ensemble Classification for Multi-label Data Streams with Concept Drift. Information, 2019, 10(5). DOI: 10.3390/info10050158. [本文引用:1]
[8]	TANHA J, SAMADI N, ABDI Y, et al. CPSSDS: Conformal Prediction for Semi-supervised Classification on Data Streams. Information Sciences, 2022, 584: 212-234. [本文引用:1]
[9]	WANG Y, LI T. Improving Semi-supervised Co-forest Algorithm in Evolving Data Streams. Applied Intelligence, 2018, 48: 3248-3262. [本文引用:1]
[10]	CAI J H, HAO J, YANG H F, et al. A Review on Semi-supervised Clustering. Information Sciences, 2023, 632: 164-200. [本文引用:1]
[11]	HUANG G B, LIANG N Y, RONG H J, et al. On-Line Sequential Extreme Learning Machine[C/OL]. [2024-05-17]. https://www.researchgate.net/publication/220939946. [本文引用:2]
[12]	HUANG G, SONG S J, GUPTA J N D, et al. Semi-supervised and Unsupervised Extreme Learning Machines. IEEE Transactions on Cybernetics, 2014, 44(12): 2405-2417. [本文引用:2]
[13]	LIANG N Y, HUANG G B, SARATCHANDRAN P, et al. A Fast and Accurate Online Sequential Learning Algorithm for Feedforward Networks. IEEE Transactions on Neural Networks, 2006, 17(6): 1411-1423. [本文引用:1]
[14]	XU S L, WANG J H. Dynamic Extreme Learning Machine for Data Stream Classification. Neurocomputing, 2017, 238: 433-449. [本文引用:1]
[15]	PARK J M, KIM J H. Online Recurrent Extreme Learning Machine and Its Application to Time-Series Prediction // Proc of the International Joint Conference on Neural Networks. Washington, USA: IEEE, 2017: 1983-1990. [本文引用:1]
[16]	ZHOU Z Y, CHEN J, ZHU Z F. Regularization Incremental Extreme Learning Machine with Rand om Reduced Kernel for Regre-ssion. Neurocomputing, 2018, 321: 72-81. [本文引用:1]
[17]	WANG X Y, HAN M. Online Sequential Extreme Learning Machine with Kernels for Nonstationary Time Series Prediction. Neurocomputing, 2014, 145: 90-97. [本文引用:1]
[18]	YANG L X, YANG S Y, LI S J, et al. Incremental Laplacian Regularization Extreme Learning Machine for Online Learning. Applied Soft Computing, 2017, 59: 546-555. [本文引用:1]
[19]	TSOUMAKAS G, KATAKIS I, VLAHAVAS I. Mining Multi-label Data // MAIMON O, ROKACH L, eds. Data Mining and Know-ledge Discovery Hand book. Berlin, Germany: Springer, 2010: 667-685. [本文引用:1]
[20]	ZHANG M L, ZHOU Z H. A Review on Multi-label Learning Algorithms. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(8): 1819-1837. [本文引用:1]
[21]	KONG X N, NG M K, ZHOU Z H. Transductive Multilabel Lear-ning via Label Set Propagation. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(3): 704-719. [本文引用:1]
[22]	WANG B, TU Z W, TSOTSOS J K. Dynamic Label Propagation for Semi-supervised Multi-class Multi-label Classification // Proc of the IEEE International Conference on Computer Vision. Washington, USA: IEEE, 2013: 425-432. [本文引用:1]
[23]	CHEN G, SONG Y Q, WANG F, et al. Semi-supervised Multi-label Learning by Solving a Sylvester Equation // Proc of the SIAM International Conference on Data Mining. Philadelphia, USA: SIAM, 2008: 410-419. [本文引用:1]
[24]	XING Y Y, YU G X, DOMENICONI C, et al. Multi-label Co-training // Proc of the 27th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2018: 2882-2888. [本文引用:1]
[25]	HUANG G B, CHEN L, SIEW C K. Universal Approximation Using Incremental Constructive Feedforward Networks with Rand om Hi-dden Nodes. IEEE Transactions on Neural Networks, 2006, 17(4): 879-892. [本文引用:1]
[26]	LI P Y, WANG H L, BÖHM C, et al. Online Semi-supervised Multi-label Classification with Label Compression and Local Smooth Regression // Proc of the 29th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2020: 1359-1365. [本文引用:1]
[27]	QIU S Y, LI P P, HU X G. Semi-supervised Online Kernel Extreme Learning Machine for Multi-label Data Stream Classification // Proc of the International Joint Conference on Neural Networks. Washington, USA: IEEE, 2022. DOI: 10.1109/IJCNN55064.2022.9892701. [本文引用:1]

2020

0.0

... 现实的硬件设备和软件应用每天都以数据流的形式产生大量数据^[1],如监控系统、天气预报、电子商务、金融交易等 ...

2023

0.0

... 因此,多标签数据流分类^[2]的研究得到更多的关注 ...

2016

0.0

... 目前,静态数据的多标签学习取得许多成果^[3,4] ...

2023

0.0

... 目前,静态数据的多标签学习取得许多成果^[3,4] ...

2022

0.0

... 代表性的直推式多标签学习是基于图的半监督方法,在标记数据和未标记数据之间构建相似图,再通过标签传播^[5,6]或流形正则化^[7]预测未标记实例的标签 ...

2024

0.0

2019

0.0

2022

0.0

... 例如:多标签分类的协同训练^[8]通过构建多个数据视图,在特定视图分类器之间传递未标记数据的成对排名预测 ...

2018

0.0

... 所以,利用有标签数据和无标签数据的分布特征和潜在的结构信息构建分类模型,适用于半监督多标签数据流环境^[9] ...

2023

0.0

... 2)实际数据流呈现高速到达、海量等特点,并且随着新数据的不断到来,数据分布可能发生变化,即存在概念漂移问题^[10] ...

0.0

... 对于数据流的数据不断到来的问题,Huang等^[11]提出OS-ELM(Online Sequential Extreme Lear-ning Machine),能应对数据流的标签分类问题,而且相比深度学习方法,OS-ELM具有更快的学习速度和更优的泛化性,能更好地适应数据流的特点 ...

... 2)OS-ELM^[11] ...

2014

0.0

... 之后,学者们提出ELM(Extreme Learning Machine)的许多变体^[12,13] ...

... ₀的输出权重矩阵^[12]如下所示: ...

2006

0.0

... 之后,学者们提出ELM(Extreme Learning Machine)的许多变体^[12,13] ...

2017

0.0

... Xu等^[14]提出DELM(Dynamic ELM for Data Stream Classification) ...

2017

0.0

... Park等^[15]提出OR-ELM(Online Recurrent ELM) ...

2018

0.0

... 为了结合核函数和I-ELM(Incremental ELM),Zhou等^[16]提出RKRIELM(Regularization I-ELM with Random Reduced Kernel),提高ELM的稳定性 ...

2014

0.0

... Wang等^[17]结合核函数与OSELM(Online Sequential ELM),提出OS-ELMK(Online Sequential ELM with Kernels) ...

2017

0.0

... Yang等^[18]提出ILR-ELM(Incremental Laplacian Regularization ELM) ...

2010

0.0

... 现有的多标签数据流分类方法主要分为3类:问题转化的方法^[19]、算法自适应的方法^[20]、基于集成学习的方法^[21] ...

2014

0.0

... 现有的多标签数据流分类方法主要分为3类:问题转化的方法^[19]、算法自适应的方法^[20]、基于集成学习的方法^[21] ...

2013

0.0

... 现有的多标签数据流分类方法主要分为3类:问题转化的方法^[19]、算法自适应的方法^[20]、基于集成学习的方法^[21] ...

2013

0.0

... 因此,研究者们提出半监督数据流分类算法,主要分为基于图的方法^[22]、基于树的方法^[23]、基于聚类的方法^[24] ...

2008

0.0

... 因此,研究者们提出半监督数据流分类算法,主要分为基于图的方法^[22]、基于树的方法^[23]、基于聚类的方法^[24] ...

2018

0.0

... 因此,研究者们提出半监督数据流分类算法,主要分为基于图的方法^[22]、基于树的方法^[23]、基于聚类的方法^[24] ...

2006

0.0

... 3 半监督极限学习机本文使用的ELM是一种单隐层前馈神经网络^[25],其目标是最小化训练样本X的函数输出H#cod#x003b2 ...

2020

0.0

... 1)OnSeML(Online Semi-supervised Multi-label Learning Algorithm)^[26] ...

2022

0.0

... 3)SSO-KELM(Semi-supervised Online Kernel Extreme Learning Machine Algorithm for Multi-label Data Stream)^[27] ...