联邦学习是一种分布式机器学习方法, 其中多个客户端在服务器的协调下协作训练一个模型^[4].在联邦学习中, 原始数据集保留在客户端的本地设备上, 客户端仅需将本地更新的模型参数(如梯度或模型权重)上传到服务器.联邦学习过程通常可分解为多个训练轮次.在每轮中, 服务器首先将初始模型或更新后的全局模型发送给客户端, 然后每个客户端使用自己的数据在本地训练模型, 最后将训练后的模型更新上传到服务器进行聚合, 形成新的全局模型.如此反复进行, 直到模型收敛, 训练过程结束.假设所有域的集合

D={D₁, D₂, …, D_m},

用于训练的样本集

$\widetilde{D}=\left\{\widetilde{D}_{1}, \widetilde{D}_{2}, \cdots, \widetilde{D}_{i} \cdots, \widetilde{D}_{m}\right\}, $

其中m为训练域(或客户端)数量.令(x, y)表示来自同一个域的样本对, L表示为损失函数, 用于衡量模型预测f(x, θ )(由模型参数θ )与标签y之间的距离.给定一个域D_i∈ D, 对应样本集

$\widetilde{D}_{i}=\left\{x_{j}^{i}, y_{j}^{i}\right\}_{j=1}^{N_{i}} .$

定义期望损失

εDi(θ )= E(x, y)∈Di[(f(x; θ ), y],

则经验损失

$\widetilde{\varepsilon}_{\widetilde{D}_{i}}(\theta)=\frac{1}{N_{i}} \sum_{j=1}^{N_{i}} L\left(\left(x_{j}^{i} ; \theta\right), y_{j}^{i}\right) .$

联邦域泛化的理想目标是最小化整个数据集D上的总损失.实际上, 通常知道采样域 D˙和每个域 D˙i中相应的采样数据对 {xji, yji}j=1Ni.因此, 可不再优化未知的期望损失, 而是优化如下经验损失函数:

$\begin{aligned} \min _{\theta} \varepsilon_{D} \approx & \sum_{i=1}^{m} \alpha_{i} \widetilde{\varepsilon}_{\widetilde{D}_{i}}(\theta)= \\ & \sum_{i=1}^{m} \alpha_{i} \sum_{j=1}^{N_{i}} L\left(f\left(\left(x_{j}^{i} ; \theta\right), y_{j}^{i}\right)\right), \\ \text { s.t. } \alpha_{i}= & \frac{N_{i}}{\sum_{i^{\prime}=1}^{m} N_{i^{\prime}}} . \end{aligned}$ (1)

注意到, 联邦域泛化和跨设备(Cross-Device)联邦学习之间有如下两个不同点.首先, 联邦域泛化遵循跨机构(Cross-Silo)联邦学习, 客户端(或域)的数量m较少, 而在跨设备联邦学习中, 客户端数量较多, 且通常在全局聚合之前对客户端拥有的本地数据进行采样.其次, 尽管跨设备联邦学习中每个客户端的本地数据是异质的, 但它们都来自同个总体分布.

相比之下, 在联邦域泛化中, 每个客户端对应一个域, 数据不仅是异质的, 并且来自不同的域.这使得联邦域泛化比传统的联邦学习更具有挑战性.因此, 在联邦域泛化场景中, 式(1)中的全局优化目标容易与本地优化目标发生冲突, 而本地训练过程往往会过拟合每个客户端(或域)的本地数据分布.上述两种情况都会降低全局模型的泛化性能.

如果有两个相邻的数据x∈ X和x'∈ X, 即

|x△ x'|=1.

M为一个随机算法, range(M)表示算法M的所有可能输出, 并且S为range(M)的任意子集, 那么M符合如下条件:

Pr[M(x)∈ S]≤ e^ε Pr[M(x')∈ S]+δ .

差分隐私方法通常通过向查询结果添加模糊噪声以实现, 其本质是通过向数据中加入可量化的随机扰动保护敏感信息.常用的噪声添加机制有高斯机制和拉普拉斯机制.在高斯机制中, 添加噪声后的查询结果如下:

M(d)≜f(d)+N(0, Sf2σ ).

其中:N(0, Sf2σ ²)表示高斯噪声机制, 均值为0、标准差为S_f σ ; S_f表示敏感度.在差分隐私的相关定义中, 更小的隐私预算意味着数据更安全, 但可用性更低.当隐私预算用尽时, 数据将无法再被访问.

添加噪声的大小与查询算法M对数据的敏感度以及隐私安全的程度有关.全局敏感度为:

S_G( f )= maxd, d'f(d)-f(d')k.

在具体应用中, 需要根据数据特征选择合适的噪声干扰机制, 并根据隐私安全要求和全局敏感度合理添加噪声.

知识蒸馏(Knowledge Distillation)旨在将教师模型的知识传递给学生模型, 是一种可用于解决迁移学习和遗忘问题的方法.蒸馏网络的优化模型可表示为

$\begin{aligned} \min _{\theta_{s}} F_{\mathrm{kd}}\left(D, \theta_{s}, \theta_{t}, \iota^{\prime}\right)= & L_{\mathrm{kd}}+L_{\mathrm{EC}}= \\ & E C(\tilde{y}, \check{y})+E C(y, O), \end{aligned}$

其中, $\tilde{y}$表示教师模型预测输出的软标签, $\check{y}$表示学生模型预测输出的软标签, O表示学生模型的输出, y表示训练样本的真实输出.损失函数F_kd(· )由蒸馏损失L_kd和交叉熵损失L_EC组成.蒸馏损失是指学生模型预测与教师模型预测之间的差异; 交叉熵损失是指学生模型预测与硬标签之间的差异.

同时, 蒸馏损失可转换为软标签$\tilde{y}$、$\check{y}$之间的交叉熵损失.软标签通常作为类别的概率分布, 在神经网络输出阶段, 使用温度参数ι '对Softmax输出进行处理.假设学生模型的Softmax输出为

$O=\left(O_{1}, O_{2}, \cdots, O_{r}\right), \tilde{y}=\left(\tilde{y}_{1}, \tilde{y}_{2}, \cdots, \tilde{y}_{r}\right), $

则有

$\tilde{y}_{i}=\frac{\left(O_{i}\right)^{\frac{1}{l^{\prime}}}}{\sum_{i=1}^{r}\left(O_{i}\right)^{\frac{1}{\iota^{\prime}}}} .$

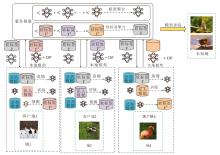
为了提升模型的域泛化能力, 保证训练数据的隐私安全, 本文提出面向多域数据场景的安全高效联邦学习方案(SEFL-MDS), 总体架构如图1所示.方案主要由单一的服务器与多个客户端组成.假设服务器是诚实且好奇的, 即诚实遵守联邦学习聚合协议, 但对客户端的敏感信息好奇, 通过发起各种攻击窃取用户隐私信息.该服务器在现实场景中可能是第三方机构或企业, 主要目标是借助客户端数据完善模型, 提升其产品(如图像分类、目标检测)性能.参与训练的客户端可以是各种移动终端设备, 本文中假设客户端为诚实节点, 主要完成模型的训练与更新, 并输出带有差分隐私的本地模型和域泛化差异.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 SEFL-MDS总体架构Fig.1 Overall architecture of SEFL-MDS

在SEFL-MDS的训练过程中, 首先初始化一个全局模型.SEFL-MDS完成一轮联邦域泛化训练过程的具体实现过程如下所示.

1)本地客户端接收服务器下发的全局模型, 首先计算当前全局模型的期望损失与上一轮本地模型的期望损失之间的差值, 得到域泛化差异.

2)本地客户端利用前一轮的本地模型、全局软标签和公共数据集对当前全局模型进行知识蒸馏, 并利用自身的域数据对蒸馏后的全局模型进行微调, 得到本地更新的梯度.

3)根据高斯差分隐私策略, 对本地更新的梯度重新缩放并添加高斯噪声, 利用梯度得到新的隐私保护本地模型, 并对域泛化差异进行高斯差分隐私处理.更新后的本地模型对公共数据集进行预测并更新本地软标签.

4)将隐私保护的本地模型、隐私保护的域泛化差异以及本地软标签发送给服务器端.

5)服务器在接收到客户端模型参数后, 根据动态泛化权重算法进行聚合, 得到新的全局模型.同时聚合本地软标签, 得到新的全局软标签.

重复上述1)~5), 可实现对跨域数据的学习, 并推广到未知域, 增强模型的泛化能力.

SEFL-MDS一轮联邦域泛化训练过程具体步骤如算法1所示.

算法1 SEFL-MDS一轮联邦域泛化训练过程

输入 客户端数量m, 域数据$\widetilde{D}=\left\{\widetilde{D}_{1}, \widetilde{D}_{2}, \cdots, \widetilde{D}_{m}\right\}$,

公共数据集D^pub, 全局模型θ ^r,

全局软标签Y^r, 前一轮本地模型 θir-1,

当前训练轮数r+1

输出θ ^r+1, Y^r+1

初始化 学习率μ , 全局敏感度S

step 1 计算$G_{\widetilde {D}_{i}}\left(\theta^{r}\right) $;

step 2 LocalUpdate $\left(\widetilde{D}_{i}, D^{\mathrm{pub}}, \theta^{r}, \theta^{r-1}, Y^{r}, \mu\right)$;

step 3 $\hat{g}_{i}^{r+1}, G_{\widetilde{D}_{i}}^{* }\left(\theta^{r}\right)$←

$D P\left(g_{i}^{r+1}, S, G_{\widetilde{D}_{i}}\left(\theta^{r}\right), N_{\mathrm{GS}}\left(\delta^{2} S^{2}\right)\right)$;

step 4 上传 θir+1、$G_{\widetilde {D}_{i}}^{* }\left(\theta^{r}\right) $和Y_i^r+1至服务器端;

step 5 服务器计算 αir+1, 并聚合得到θ ^r+1, Y^r+1, 随后广播给所有客户端.

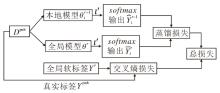
本文设计基于联邦知识蒸馏的本地训练算法, 处理不同域数据导致的灾难性遗忘问题, 具体流程如图2所示.为了防止先前的数据被遗忘, 将学到的知识存储在模型 θir-1中.在后续学习中, θir-1为教师模型, 将学到的知识传递给学生模型θ ^r, 通过此方式确保模型不会遗忘之前学到的知识, 并加速模型对不同域数据的学习.

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于联邦知识蒸馏的本地训练算法流程图Fig.2 Flow chart of local training based on federated knowledge distillation

基于联邦知识蒸馏的本地训练算法具体实现过程如下所示.

1)初始化.本地模型为本地客户端从服务器下载到的全局模型θ ^r.首先计算全局模型与本地模型的域泛化差异:

$G_{\widetilde{D}_{i}}\left(\theta^{r}\right)=\widetilde{\varepsilon}_{\widetilde{D}_{i}}\left(\theta^{r}\right)-\widetilde{\varepsilon}_{\widetilde{D}_{i}}\left(\theta^{r-1}\right), i=1, 2, \cdots, m . $

并将D^pub中数据的真实标签Y^pub替换成全局软标签Y^r, 得到(X^pub, Y^r).

2)本地模型更新.首先, 公共数据D^pub基于模型 θir-1生成软标签 Y︿ir-1.然后, 全局模型 θir基于D^pub生成蒸馏后的Softmax输出 Y¯ir.模型训练的总损失函数为蒸馏损失与交叉熵损失总和, 则优化目标为:

$\begin{aligned} \min _{\theta^{r}} & F_{\mathrm{kd}}\left(D^{\mathrm{pub}}, \theta^{r-1}, \theta^{r}, \iota^{\prime}\right)= \\ & L_{\mathrm{kd}}\left(D^{\mathrm{pub}}, \theta^{r-1}, \theta^{r}, \iota^{\prime}\right)+L_{\mathrm{EC}}\left(D^{\mathrm{pub}}, \theta^{r}\right)= \\ & E C\left(\widehat{Y}_{i}^{r-1}, \bar{Y}_{i}^{r}\right)+E C\left(Y^{r}, Y^{\mathrm{pub}}\right), \end{aligned} $

其中, Y^pub表示数据D^pub对应的真实标签, L_kd(· )表示蒸馏损失, L_EC(· )表示交叉熵损失, EC(· )表示交叉熵计算.最后, 利用域数据$\widetilde{D}_{i}$对蒸馏后的模型W^r+1进行微调, 更新得到本地模型 θir+1.利用本地模型 θir+1对D^pub进行预测, 更新本地软标签Y_i^r+1.

基于联邦知识蒸馏的本地训练算法步骤如算法2所示.

算法2 基于联邦知识蒸馏的本地训练算法

输入 域数据$\widetilde{D}_{i}$, 公共数据D^pub, 全局模型θ ^r,

上一轮全局模型θ ^r-1, 全局软标签Y^r,

学习率μ

输出 本地模型参数 θir+1, 本地软标签Y_i^r+1,

域泛化差异$ G_{\widetilde{D}_{i}}\left(\theta^{r}\right)$

step 1 $G_{\widetilde{D}_{i}}\left(\theta^{r}\right)=\widetilde{\varepsilon}_{\widetilde{D}_{i}}\left(\theta^{r}\right)-\widetilde{\varepsilon}_{\widetilde{D}_{i}}\left(\theta^{r-1}\right), $,

i=1, 2, …, m;

step 2 (X^pub, Y^r)← (X^pub, Y^pub);

/* 将D^pub中真实标签Y^pub替换成全局软标签Y^r* /

step 3

for 本地迭代次数从1到E do

g^r+1=Ñ F_kd(D^pub, θ ^r-1, θ ^r);

W^r+1=θ ^r-μ g^r+1;

gir+1=Ñ F_l($\widetilde{D}_{i}$, W^r+1);

/* F_l表示在$\widetilde{D}$上的损失函数* /

end for

step 4 $\hat{g}_{i}^{r+1}, G_{\widetilde{D}_{i}}^{* }\left(\theta^{r}\right)$←

$D P\left(g_{i}^{r+1}, S, G_{\widetilde{D} i}\left(\theta^{r}\right), N_{\mathrm{GS}}\left(\delta^{2} S^{2}\right)\right)$;

/* 向$\hat{g}_{i}^{r+1}$, $ G_{\widetilde{D}_{i}}^{* }\left(\theta^{r}\right)$添加高斯噪声* /

step 5 $\theta_{i}^{r+1}=W^{r+1}-\mu \hat{g}_{i}^{r+1}$;

step 6 Y_i^r+1← f(Dpub; θir+1);

/* 利用 θir+1对D^pub进行预测* /

step 7 return θir+1, Y_i^r+1, $ G_{\widetilde{D}_{i}}^{* }\left(\theta^{r}\right)$.

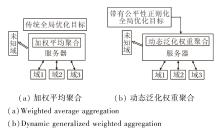
为了使联邦学习在不同域数据场景中仍具有较强的学习能力, 本文不再使用传统的加权平均聚合算法聚合本地模型, 而是采用一种动态泛化权重聚合算法更新全局模型, 整体架构如图3所示.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 2种聚合方式的整体架构Fig.3 Overall architecture of 2 aggregation methods

在联邦学习训练过程中, 每个域的平坦度可通过全局模型和本地模型之间的泛化差异反映, 泛化差异如下:

$G_{\widetilde{D}_{i}}(\theta)=G_{\widetilde{D_{i}}}\left(\sum_{i} \alpha_{i} \theta_{i}\right)=\widetilde{\varepsilon}_{\widetilde{D}_{i}}\left(\sum_{i} \alpha_{i} \theta_{i}\right)-\widetilde{\varepsilon}_{\widetilde{D}_{i}}\left(\theta_{i}\right), $

其中, θ _i表示在域 D˙i上的本地模型,

θ = ∑iα _iθ _i.

文献[27]引入一个联邦域泛化全局优化目标, 充分考虑各本地客户端之间泛化差异, 保证最优全局模型在所有域上具有平坦性.全局优化目标为:

$\begin{array}{l} \min _{\theta_{1}, \theta_{2}, \cdots, \theta_{m}} \widetilde{\varepsilon}_{\widetilde{D}}(\theta)= \\ \sum_{i=1}^{m} \alpha_{i} \widetilde{\varepsilon}_{\widetilde{D}_{i}}(\theta)+\varphi \operatorname{Var}\left(\left\{G_{\widetilde{D}_{i}}(\theta)\right\}_{i=1}^{m}\right), \\ \text { s.t. } \sum_{i=1}^{m} \alpha_{i}=1, \theta=\sum_{i} \alpha_{i} \theta_{i}, \forall i, \alpha_{i} \geqslant 0 . \end{array}$ (2)

可把客户端(或域)的泛化权重表示为

α =(α ₁, α ₂, …, α _m),

并通过φ ∈ [0, ¥ ]平衡全局损失和域泛化差异之间的公平.其中, 当φ =0时, 即为FedAvg; 当φ → ¥ 时, 每个域的泛化差异相等.

在式(2)中, α 和θ _i不能在联邦学习中同时优化.同时观察到α _i与相应的域泛化差异$G_{\widetilde{D}_{i}}(\theta)$之间存在关联, 改变权重α 会影响泛化差异.因此, 将优化操作分为如下两个阶段.在本地训练阶段, 通过梯度下降优化模型参数θ _i.在聚合阶段, 通过动态泛化调整算法优化权重α _i.通过调整泛化权重最小化各个域的泛化差异, 获得一个具有较强域泛化能力的全局模型.形式上, 给定一个特定的域k, 全局模型参数θ 和局部模型参数θ _i之间的关系为:

θ =θ _k+Δ θ ,

其中

Δ θ =(1-α _k)θ _k+ ∑i≠kα _iθ _i,

可看作是对θ _k的扰动.对于损失$\widetilde{\varepsilon}_{\widetilde{D}_{k}}(\theta)$, 如果增加权重α _k, 则相应减少 {αi}i≠k的占比, Δ θ 的扰动程度会下降.在这种情况下, θ 会更趋近于本地模型θ _k, 并减少基于域数据$\widetilde{D}_{k}$的损失$\widetilde{\varepsilon}_{\widetilde{D}_{k}}(\theta)$.在下一轮训练中, 聚合后的全局模型θ 作为所有客户端的初始本地模型, 使θ _k更接近Δ θ , 进而逐渐减少域泛化差异.相反, 如果减少α _k, 情况正好相反.同时, $\widetilde{\varepsilon}_{\widetilde{D}_{k}}(\theta)$可看作一个常数, 和聚合权重α _k相关.

当服务器接收到客户端上传的数据后, 通过动态泛化调整算法计算权重α ^r+1的具体实现过程如下.

1)初始化.服务器接收所有客户端上传的域泛化差异${\{G_{\widetilde{D}_{i}}(\theta^{r})\}}_{i=1}^{m}$、本地软标签 {Y_ir+1}i=1m和本地模型 {θir+1}i=1m.

2)泛化权重更新.基于前一轮泛化权重 αir和域泛化差异${\{G_{\widetilde{D}_{i}}(\theta^{r})\}}_{i=1}^{m}$更新泛化权重:

αi(r+1)*= (GD˙i(θr)-δ)πrmaxj(GD˙j(θr)-δ)+ αir, (3)

αir+1= αi(r+1)* ∑i=1mαi(r+1)*, (4)

其中

$\begin{array}{l} \delta=\frac{1}{m} \sum_{i=1}^{m} G_{\widetilde{D}_{i}}\left(\theta^{r}\right), \\ \pi^{r+1}=\left(1-\frac{r+1}{R}\right) \pi, \end{array}$

π ∈ (0, 1)表示一个超参数, 用于控制更新步长.为了使训练过程稳定, 采用线性衰减策略.同时, 当

αi(r+1)*> 0

时, 对其进行裁剪, 并令

∑i=1mαi(r+1)*=1.

3)全局模型更新.基于泛化权重 αir+1对本地模型 {θir+1}i=1m进行聚合, 即

θ ^r+1= ∑i=1mαir+1θir+1.

4)全局软标签更新.聚合本地软标签 {Y_ir+1}i=1m, 得到全局软标签:

Y^r+1= 1m∑i=1mYir+1.

在第r+1轮结束时, 全局模型θ ^r+1和全局软标签Y^r+1作为初始化参数广播给每个客户端, 并用于下一轮训练.特别说明的是, 当客户端i的聚合权重为0时, 通过式(3)和式(4)可得

GD˙i(θ ^r)-δ =0 ⇔ GD˙i(θ ^r)=δ ,

同时平均域泛化差异

$\delta=\frac{1}{m} \sum_{i=1}^{m} G_{\widetilde{D}_{i}}\left(\theta^{r}\right) .$

当满足$G_{\widetilde{D}_{i}}\left(\theta^{r}\right)=\delta$时, 表示各域的泛化差异相等, 全局模型已通过其它客户端(或域)的数据充分学习, 并且展现出较强的域泛化能力.

具体动态泛化权重聚合算法步骤如算法3所示.

算法3 动态泛化权重聚合算法

输入 全局模型θ =θ ⁰,

m个客户端(或域)$ \widetilde{D}=\left\{\widetilde{D}_{1}, \widetilde{D}_{2}, \cdots, \cdots, \widetilde{D}_{m}\right\}$,

初始泛化权重α ⁰= 1m, 全局训练次数R

输出 全局模型θ ^r+1, 全局软标签Y^r+1

初始化 当前迭代次数为r+1

服务器端 θi0=θ ⁰, 初始化本地模型

for 全局训练轮数r+1∈ (1, R) do

客户端i:

基于θ ^r计算$ G_{\widetilde{D}_{i}}\left(\theta^{r}\right)$

$\left(\theta_{i}^{r+1}, Y_{i}^{r+1}\right)=\operatorname{LocalUpdate}\left(\widetilde{D}_{i}, D^{\mathrm{pub}}, \theta^{r}, \theta^{r-1}, Y^{r}, \mu\right)$

/* 本地训练* /

服务器端:

基于$\{G_{\widetilde{D}_{i}}(\theta^{r})\}_{i=1}^{m}$和α ^r更新泛化权重α ^r+1

αi(r+1)*= (GD˙i(θr-δ))πrmaxj(GD˙j(θr-δ))+ αir

αir+1= αi(r+1)* ∑i=1mαi(r+1)*

聚合本地模型:θ ^r+1= ∑i=1mαir+1θir+1

聚合本地软标签:Y^r+1= 1m∑i=1mY_i^r+1

对所有客户端广播θ ^r+1, Y^r+1

end for

为了解决联邦学习中每个客户端的隐私安全问题, 当服务器聚合本地模型提供的参数更新信息时, 采用差分隐私方法避免隐私泄露.相比传统的隐私保护机制, 这种方法具有可量化的隐私预算和用户级敏感行为隐藏的特点.根据数据特性和全局敏感度S_g, 可在每轮收集本地模型参数更新信息.例如:如果参与训练轮次的客户端数量为k, 则每个用户获得的平均噪声为 1kN(0, δ ²S²).在这个过程中, 规范化和缩放每个用户提供的更新, 并根据用户数量分配隐私预算值.

在联邦学习过程中, 对每次迭代的更新 gir+1进行缩放:

$\hat{g}_{i}^{r+1}=\frac{g_{i}^{r+1}}{\max \left(1, \frac{\left\|g_{i}^{r+1}\right\|_{1}}{S}\right)} .$

并对缩放后的本地更新 gir+1通过添加噪声的方式进行随机扰动, 同时对域泛化差异添加噪声, 即

$\begin{array}{l} \hat{g}_{i}^{r+1}=\hat{g}_{i}^{r+1}+N_{G S}\left(\delta^{2} S^{2}\right), \\ G_{\widetilde{D}_{i}}^{* }\left(\theta^{r}\right)=G_{\widetilde{D}_{i}}\left(\theta^{r}\right)+N_{\mathrm{GS}}\left(\delta^{2} S^{2}\right) . \end{array}$

具体高斯差分隐私机制步骤如算法4所示.

算法4 高斯差分隐私机制

输入 本地更新的梯度 gir+1, 域泛化差异 GD˙i(θ ^r),

全局敏感度S

输出 gir+1, $ G_{\widetilde{D}_{i}}\left(\theta^{r}\right)$

初始化 全局敏感度S, 高斯噪声N_GS(δ ²S²)

step 1 $\hat{g}_{i}^{r+1}=\frac{g_{i}^{r+1}}{\max \left(1, \frac{\left\|g_{i}^{r+1}\right\|_{1}}{S}\right)}$;

step 2 $\hat{g}_{i}^{r+1}=\hat{g}_{i}^{r+1}+N_{\mathrm{GS}}\left(\delta^{2} S^{2}\right)$;

step 3 $G_{\widetilde{D}_{i}}^{* }\left(\theta^{r}\right)=G_{\widetilde{D}_{i}}\left(\theta^{r}\right)+N_{\mathrm{GS}}\left(\delta^{2} S^{2}\right)$;

step 4 return $\hat{g}_{i}^{r+1}, G_{\widetilde{D}_{i}}^{* }\left(\theta^{r}\right)$.

在SEFL-MDS中, 主要利用高斯差分隐私机制抵御各种隐私攻击, 提高模型的健壮性.因此, 对SEFL-MDS的健壮性分析转换为对高斯差分隐私机制的安全性分析.

定理1 假设隐私预算ε 为任意值, 当常数b的上限约束为

$b^{2}> 2 \operatorname{In}\left(\frac{1.25}{\delta}\right)$,

那么具有

σ ≥ bΔ2fε

的高斯机制满足(ε , δ )-差分隐私, 其中

Δ ₂f=max‖ f(d)-f(d')‖ ,

f (· )为查询函数.

证明 由高斯差分隐私定义

$\operatorname{Pr}[M(d) \in S] \leqslant \exp \left(\frac{x^{2}}{2 \sigma^{2}}\right) \operatorname{Pr}\left[M\left(d^{\prime}\right) \in S\right]+\delta$

可得

Pr[M(d)]Pr[M(d')]= exp(-x22σ2)exp(-(x+Δf)22σ2),

由于概率恒为正值, 则有

$\begin{array}{l} \left|\ln \left(\frac{\exp \left(-\frac{x^{2}}{2 \sigma^{2}}\right)}{\exp \left(-\frac{(x+\Delta f)^{2}}{2 \sigma^{2}}\right)}\right)\right|= \\ \left|\operatorname{In}\left(\exp \left(-\frac{1}{2 \sigma^{2}}\left[x^{2}-(x+\Delta f)^{2}\right]\right)\right)\right|= \\ \left|-\frac{1}{2 \sigma^{2}}\left[x^{2}-(x+\Delta f)^{2}\right]\right|= \\ \left|\frac{1}{2 \sigma^{2}}\left(2 x \Delta f+(\Delta f)^{2}\right)\right|< \varepsilon \end{array}$

当

x< σ2εΔf- Δf2

时, ε 为上界限.为了确保隐私损失以至少1-δ 的概率被限制在ε 内, 需满足

$\operatorname{Pr}\left[|x| \geqslant \frac{\delta^{2} \varepsilon}{\Delta f}-\frac{\Delta f}{2}\right]< \sigma$

假定ε ≤ 1≤ Δ f, 那么下界限

$\operatorname{Pr}[x> t] \leqslant \frac{\sigma}{\sqrt{2 \pi t}} \exp \left(-\frac{t^{2}}{2 \sigma^{2}}\right)$

并且还需满足

$\begin{array}{l} \frac{\sigma}{\sqrt{2 \pi t}} \exp \left(-\frac{t^{2}}{2 \sigma^{2}}\right)< \frac{\sigma}{2} \Leftrightarrow \\ \operatorname{In}\left(\frac{t}{\sigma}\right)+t^{2}> \operatorname{In}\left(\frac{2}{\sqrt{2 \pi \delta}}\right) \end{array}$

令

t= δ2εΔf- Δf2,

得

$\begin{array}{c} \operatorname{In}\left(\frac{\frac{\sigma^{2} \varepsilon}{\Delta f}-\frac{\Delta f}{2}}{\sigma}\right)+\frac{\left(\frac{\sigma^{2} \varepsilon}{\Delta f}-\frac{\Delta f}{2}\right)^{2}}{2 \sigma^{2}}> \\ \operatorname{In}\left(\frac{2}{\sqrt{2 \pi \delta}}\right)=\operatorname{In}\left(\sqrt{\frac{2}{\pi}} \frac{1}{\sigma}\right) \end{array}$

令

σ = bΔfε,

并对b进行界定, 从第一个非负项开始, 则有

$\begin{aligned} \frac{1}{\sigma}\left(\frac{\sigma^{2} \varepsilon}{\Delta f}-\frac{\Delta f}{2}\right)= & \frac{1}{\sigma}\left[\left(\frac{b^{2}(\Delta f)^{2}}{\varepsilon^{2}}\right) \frac{\varepsilon}{\Delta f}-\frac{\Delta f}{2}\right]= \\ & \frac{1}{\sigma}\left[b^{2}\left(\frac{\Delta f}{\varepsilon}\right)-\frac{\Delta f}{2}\right]= \\ & b-\frac{\varepsilon}{2 b} \end{aligned}$.

又因为ε < 1, 当b> 1.5时, b²-b+ ε24b对b的导数为正, 因此得到

b-b+ ε24b> c- 89,

同时需要满足

b²- 89> 2In 2π 1σ.

综上得到

$\begin{array}{c} b^{2}> 2 \operatorname{In}\left(\sqrt{\frac{2}{\pi}}+2 \operatorname{In}\left(\frac{1}{\sigma}\right)\right)+\operatorname{In}\left(e^{\frac{8}{9}}\right)= \\ \operatorname{In}\left(\frac{2}{\pi}\right)+\operatorname{In}\left(e^{\frac{8}{9}}\right)+2 \operatorname{In}\left(\frac{1}{\sigma}\right) \end{array}$

由于

2ε· 89< 1.55,

因此只要

$b^{2}> 2 \operatorname{In}\left(\frac{1.25}{\sigma}\right)$,

就满足该条件. 证毕

首先证明, 对于目标域k, 在$\widetilde{\varepsilon}_{\widetilde{D}}(\theta)$上的最优解引起的泛化差异的上界是由源域中的泛化差异决定的(见定理2).根据定理2, 未知域k上的域泛化差异受域平坦性 GD˙i(θ )和域差异$d_{H \Delta H}\left(\widetilde{D}_{i}, k\right)$约束.传统域泛化方法通过隐式对齐多个域优化域差异$d_{H \Delta H}\left(\widetilde{D}_{i}, k\right)$, 缩小这个界限.然而, 由于联邦域泛化中每次只能访问一个域, 因此无法直接使用上述优化方法.在这种情况下, 联邦域泛化可通过调整聚合权重α 进一步收紧这个界限.

定理2 假设θ 表示经过r轮联邦学习后的全局模型, θi*表示各个源域的局部最优解, θk*表示未知域的局部最优解.利用

$\begin{aligned} \arg \min _{\alpha} & \sum_{i=1}^{m} \alpha_{i} d_{H \Delta H}\left(\widetilde{D}_{i}, k\right) \approx \\ & \arg \min _{\alpha} \operatorname{Var}\left(\left\{G_{D_{i}}(\theta)\right\}_{i=1}^{m}\right), \end{aligned}$ (5)

中的泛化权重α .对于∀ ρ ∈ (0, 1), 则未知域k的域泛化差异可用

$\begin{aligned} \varepsilon_{k}(\theta)-\varepsilon_{k}(\theta_{i}^{*}) \leqslant & \sum_{i=1}^{m} \alpha_{i}(G_{\widetilde{D}_{i}}(\theta)+d_{H \Delta H}(\widetilde{D}_{i}, k)+. \\ & .\frac{\sqrt{\log _{2}(\frac{d}{\rho})}+\sqrt{\log _{2}(\frac{m d}{\rho})}}{\sqrt{2 N_{i}}})+\lambda, \end{aligned}$

进行界定, 其概率至少为1-ρ .

然而, 精确估计α 需要明确域差异$d_{H \Delta H}\left(\widetilde{D}_{i}, k\right)$和各个域上的偏导数$\frac{\partial \widetilde{\varepsilon}_{\widetilde{D}_{i}}(\theta)}{\partial \alpha_{i}}$.然而, 在实际场景中, 域k的信息是未知的, 因此无法找到最优α .

为了解决这一挑战, 本文提出一种替代方法近似计算α .根据文献[37], 全局模型可视为客户端i的稳健风险(Robust Risk)最小化问题的解, 表示为

$\widetilde{\varepsilon}_{\widetilde{D}_{i}}(\theta)=\max _{\|\Delta \theta\| \leqslant \tau} \widetilde{\varepsilon}_{\widetilde{D}_{i}}\left(\theta_{i}+\Delta \theta\right) .$

由于获得最优估计需要所有域的平坦性相似, 因此可通过最小化域平坦性的方差以优化α , 并可通过解决式(5)的域平坦性方差最小化问题以近似获得.

由于式(5)的目标是实现零方差, 将为所有域近似达到一个常数平坦性C, 即对∀ i, 有

$G_{\widetilde{D}_{i}}(\theta)=C, $

在这种情况下, 则

$\sum_{i=1}^{m} \alpha_{i} G_{\widetilde{D}_{i}}(\theta)=\sum_{i=1}^{m} c_{i} G_{\widetilde{D}_{i}}(\theta)$

成立.此外, 考虑到式(5)中α 是最优的, 对于∀ c, 则有

$\min \sum_{i=1}^{m} \alpha_{i} d_{H \Delta H}\left(\widetilde{D}_{i}, k\right) \leqslant \min \sum_{i=1}^{m} c_{i} d_{H \Delta H}\left(\widetilde{D}_{i}, k\right) .$

结合上述结果, 可得出结论:定理2中用α 表示的约束比用常数C={c₁, c₂, …, c_m}替代α (如FedAvg)表示的约束更严密.这表明, 使用全局目标与动态泛化权重聚合算法的结合能在未知域上实现更好的泛化性能.

SEFL-MDS的时间复杂度主要由通信、计算和同步等因素决定.在通信方面, 模型参数维度为θ , 每次通信的复杂度为O(θ ), 则总的通信复杂度为O(Rθ ), 其中R为全局训练轮数.客户端的计算复杂度与本地训练相关, 由于每个客户端执行E次本地训练, 样本数为n, 每次梯度更新复杂度为f(θ , n), 则每个客户端的计算复杂度为O(Ef(θ , n)).由于添加高斯噪声和计算域泛化差异只涉及简单的加减运算, 可忽略不计.则总的计算复杂度为

O(mEf(θ , n)).

此外, 同步延迟取决于最慢客户端的计算和通信时间.综上所述, SEFL-MDS的总时间复杂度为

O(R(mEf(θ , n))+θ ).

因此, 为了优化时间复杂度, 可通过减少通信频率、模型压缩和异步联邦学习等策略降低通信和同步开销.

本文主要是在域自适应图像数据集PACS和Office-Home上对EDPDGFL进行性能评估实验.PACS数据集包含photo、art、cartoon、sketch这4个领域中的9 991幅图像, 每个领域有7类.Office-Home数据集包含real world、art、clipart、product这4个领域中的15 588幅图像, 每个领域有65类, 且每个类别平均70幅图像.

本文同时进行离域(Leave-One-Domain-Out)验证评估:依次选择一个领域作为未知域, 剩下的所有领域作为训练域.各源域内的训练集和验证集的划分保持与文献[38]中的划分方式相同, 整个未知域用于测试.对于本地训练, 采用公共数据集ImageNet预训练ResNet18, 并利用域自适应图像数据集进行微调.

主要基于联邦学习架构进行仿真实验, 客户端采用小批量随机梯度下降的训练方法, 设置批量大小为16, 学习率为0.001, 泛化权重的步长为0.05, 全局迭代次数为100.

使用Python 3.97编程语言, 实验环境配置为RTX 4090、64 GB内存、Window 11操作系统.

为了验证SEFL-MDS的有效性, 选取FedAvg^[4]作为基线方案.在域泛化方面, 对比基于正则化的DG方法RSC(Representation Self-Challenging)^[39]和基于傅里叶变换的数据增强方法ELCFS(Episodic Learning in Continuous Frequency Space)^[22].对于数据异构性, 对比5种联邦学习方案:SCAFFOLD(Stochastic Controlled Averaging Algorithm)^[5]、FedProx^[6]、StableFDG^[26]、MCGDM^[28]、FedSAM^[40], 以及两种重新加权方法:ARFL^[25]和FedNova^[24].

在PACS、Office-Home数据集上进行离域验证, 评估SEFL-MDS在未知领域中的学习效果.以准确度作为评估指标.同时还对这两个数据集中各域的数据进行采样, 评估联邦知识蒸馏的准确度和训练时间.

SEFL-MDS在PACS、Office-Home数据集上各域训练过程的准确度如图4所示.由图可见, SEFL-MDS表现出良优的收敛性.在PACS数据集上, SEFL-MDS对photo域的泛化能力最优, 准确度达到95.56%, 在Office-Home数据集上, SEFL-MDS对real world域具有较优的泛化能力, 但是由于在该域中有65个类别, 每类的图像较少, 因此准确度只有75.44%, 在其它3个域上的准确度也能达到50%以上.在PACS、Office-Home数据集上进行离域验证的结果可表明, SEFL-MDS具有较强的域泛化能力.

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 SEFL-MDS在2个数据集上各域的准确度对比Fig.4 Accuracy comparison of SEFL-MDS on different domains of 2 datasets

下面基于PACS、Office-Home数据集上每个域的数据, 对比不同方法的准确度, 如表1所示.

表1

Table 1

表1(Table 1)

表1 不同方案在2个数据集上的准确度对比 Table 1 Accuracy comparison of different schemes on 2 datasets % 方案 PACS Office-Home photo art cartoon sketch product art clipart real world SEFL-MDS 95.56 79 77.98 80.91 73.93 58.83 52.43 75.44 FedAvg 92.64 77.13 77.87 79.02 72.52 57.49 52.24 73.37 RSC 92.62 77.96 77.80 79.65 73.24 57.42 50.32 73.38 ELCFS 93.29 78.54 77.56 79.99 73.22 57.74 51.65 73.28 FedProx 93.15 77.72 77.73 80.12 73.32 58.23 51.57 73.16 Scaffold 92.54 78.03 77.21 80.64 72.14 58.43 52.75 73.23 ARFL 92.12 76.23 75.74 80.47 73.82 56.91 52.15 73.13 FedNova 93.02 78.94 76.36 79.24 73.72 58.72 49.92 73.21 StableFDG 93.48 78.24 77.90 77.73 72.33 57.50 52.34 73.22 MCGDM 93.52 78.91 78.02 80.87 73.91 58.72 52.35 73.42

表1 不同方案在2个数据集上的准确度对比 Table 1 Accuracy comparison of different schemes on 2 datasets %

由表1可见, SEFL-MDS在photo域和real world域上的准确度分别为95.56%和75.44%, 比其它方案的准确度至少提高2%, 在其它域上, SEFL-MDS的准确度与其它方法相差不大, 这证明SEFL-MDS对未知域具有较强的学习能力.

值得注意的是, 尽管SEFL-MDS在训练过程中为了实现隐私保护而注入高斯噪声, 仍表现出较高的准确度.

对PACS、Office-Home数据集上各域的数据进行采样, 并基于采样数据对比有无进行联邦知识蒸馏, 准确度结果如图5所示.

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 知识蒸馏对各域性能的影响Fig.5 Effect of knowledge distillation on the performance of different domains

由图5可见, 当模型在训练过程中未进行知识蒸馏时, 由于采样数据来源为不同的源域, 且每域的数据分布不一样, 导致模型的准确度显著下降.同时由于联邦学习的分布式特性, 模型参数并不是连续更新的, 而是通过周期性的聚合更新, 这样会导致每次局部模型更新后可能会丢失一些之前全局模型学到的信息.因此, 在联邦域泛化训练过程中引入知识蒸馏技术, 能有效避免模型发生灾难性遗忘, 显著提高模型性能.

不同本地训练方法每轮训练耗时对比如表2所示.

表2

Table 2

表2(Table 2)

表2 不同本地训练方法每轮训练时间对比 Table 2 Comparison of training time per epoch for different local training methods s FedAvg 动态泛化权重聚合算法 高斯差分隐私机制 知识蒸馏 PACS Office-Home √ - - - 20.4 34.8 √ √ - - 20.6 35.0 √ √ √ - 21.2 35.3 √ √ √ √ 15.2 25.4

表2 不同本地训练方法每轮训练时间对比 Table 2 Comparison of training time per epoch for different local training methods s

由表2可得, 当本地训练方法为FedAvg时, 在PACS、Office-Home数据集上的训练时间为分别为20.4 s和34.8 s.这是由于Office-Home数据集上图像和类别多于PACS数据集上, 导致训练时间增加.当引入动态泛化权重聚合算法和高斯差分隐私机制时, 增加额外的计算开销和通信开销, 导致每轮训练时间也随之增加.然而, 当引入知识蒸馏后, 在PACS、Office-Home数据集上的通信时间分别为15.2 s和25.4 s, 每轮训练时间分别减少28.4%和28.1%.由于知识蒸馏将大型教师模型的知识传递给较小的学生模型, 减少模型规模和训练复杂度, 从而缩短训练时间.同时, 在联邦学习中, 知识蒸馏还能降低通信成本, 加快本地训练速度, 并通过更快的模型收敛提高整体训练效率.

为了深入探究隐私预算对性能的影响, 在PACS数据集的photo域和Office-Home数据集的real world域上进行实验.选择从1至10作为隐私预算范围, 并根据敏感度和个体隐私需求, 设置不同的隐私预算, 具体准确度如图6所示.由图可得出, 当隐私预算不断增大时, 对准确度的影响逐渐减少.尽管添加高斯噪声会在一定程度上降低准确度, 却保证模型训练的安全性, 并防御推理攻击等恶意攻击.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同隐私预算对SEFL-MDS性能的影响Fig.6 Effect of privacy budgets on the performance of SEFL-MDS