广义多尺度多重集值决策系统的最优尺度约简

Loading [MathJax]/jax/output/HTML-CSS/jax.js

引用本文

刘梦欣, 谢祯晃, 吴伟志, 朱康. 广义多尺度多重集值决策系统的最优尺度约简. 模式识别与人工智能, 2025,38(1): 2-21
LIU Mengxin, XIE Zhenhuang, WU Weizhi, ZHU Kang. Optimal Scale Reducts for Generalized Multi-scale Multiset-Valued Decision Systems. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2025,38(1): 2-21. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202501001
Permissions

《模式识别与人工智能》编辑部

广义多尺度多重集值决策系统的最优尺度约简

刘梦欣¹, 谢祯晃¹, 吴伟志¹, 朱康¹

1.浙江海洋大学信息工程学院舟山 316022

通讯作者：

吴伟志,博士,教授,主要研究方向为粗糙集、粒计算、数据挖掘、人工智能.E-mail: wuwz@zjou.edu.cn.

作者简介:

刘梦欣,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:liumengxin2023@163.com.

谢祯晃,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:xiezh1120@163.com.

朱康,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:zhukang0318@163.com.

修回日期: 2025-01-04 接受日期: 2025-01-31

资助项目: 国家自然科学基金项目(No.12371466,62076221)资助

摘要

多尺度数据的知识表示与知识获取是现阶段多粒度计算研究的一个重要方向.在分析多尺度数据时,一个关键问题是最优尺度组合的选择,其目的是选择合适的子系统用于最终决策.因此文中针对多尺度多重集值数据的知识获取问题展开研究.首先,基于海林格距离,在广义多尺度多重集值决策系统中构造不同尺度组合下对象集上的相似关系,给出广义多尺度多重集值决策系统的信息粒表示.然后,在协调广义多尺度多重集值决策系统中,定义最优尺度约简与熵最优尺度约简的概念,证明最优尺度约简与熵最优尺度约简的等价性.在不协调广义多尺度多重集值决策系统中,引入广义决策函数,给出广义决策最优尺度约简的定义.进一步地,基于条件熵和广义决策函数,分别给出熵最优尺度约简搜索算法和广义决策最优尺度约简搜索算法.最后,提出构造广义多尺度多重集值决策系统的方法,并通过实验验证文中最优尺度约简算法的有效性和合理性.

关键词: 属性约简; 条件熵; 广义多尺度决策系统; 多重集; 最优尺度约简

中图分类号:TP18

Optimal Scale Reducts for Generalized Multi-scale Multiset-Valued Decision Systems

LIU Mengxin¹, XIE Zhenhuang¹, WU Weizhi¹, ZHU Kang¹

1. School of Information Engineering, Zhejiang Ocean University, Zhoushan 316022

Corresponding author：
WU Weizhi,Ph.D., professor. His research interests include rough sets, granular computing, data mining and artificial intelligence.

About Author:
LIU Mengxin, Master student. Her research interests include rough sets and granular computing.
XIE Zhenhuang, Master student. His research interests include rough sets and granular computing.
ZHU Kang, Master student. His research interests include rough sets and granular computing.

Fund:National Natural Science Foundation of China(No.12371466,62076221)

Abstract

The knowledge representation and the knowledge acquisition of multi-scale data are crucial research directions in multi-granularity computing. While analyzing multi-scale data, a key issue is the selection of the optimal scale combination, with the aim of choosing a suitable subsystem for the final decision. To solve the problem of knowledge acquisition from multi-scale multiset-valued data, at first, similarity relations determined by the set of objects under different scale combinations are constructed based on Hellinger distance in generalized multi-scale multiset-valued decision systems, and the information granule representation is provided. Second, the concepts of optimal scale reducts and entropy optimal scale reducts are defined in consistent generalized multi-scale multiset-valued decision systems, and the equivalence between the optimal scale reducts and the entropy optimal scale reducts is proven. In inconsistent generalized multi-scale multiset-valued decision systems, the definition of generalized decision optimal scale reducts is proposed by introducing generalized decision functions. Furthermore, by employing conditional entropies and generalized decision functions, search algorithms of entropy optimal scale reducts and generalized decision optimal scale reducts are designed. Finally, a method of constructing generalized multi-scale multiset-valued decision systems is proposed, and the experiments demonstrate the validity and rationality of the proposed algorithms.

Key words: Attribute Reduction; Conditional Entropy; Generalized Multi-scale Decision System; Multiset; Optimal Scale Reduct

文章图片

粒计算(Granular Computing, GrC)^{[1, 2, 3]}是数据分析和信息处理的新型计算范式, 以粒(Granule)为基本计算单位, 从不同视角和层次观察、分析与解决问题, 是研究复杂问题求解、海量数据挖掘和不确定性信息处理等问题的有效工具之一.迄今为止, 学者们已提出多种粒计算模型, 如基于模糊集的数据分析、粗糙集数据分析、形式概念分析和商空间理论等, 其中粗糙集数据分析对粒计算的研究与发展具有重要推动作用.

粗糙集是由Pawlak^[4]提出的分析不完全、不精确数据的一个重要数学工具.粗糙集数据分析的数据表述主要以信息系统或决策系统的形式呈现, 利用属性子集定义在对象集上的等价关系, 将论域粒化为若干等价类(信息粒), 以粒代替样本, 并通过独特的属性约简方法挖掘蕴含在数据集上的决策知识.由于等价关系这一要求过于严格, 一些学者针对不同类型的数据集, 将等价关系推广为各种二元关系^{[5, 6, 7]}, 得到不同类型的信息粒, 同时利用证据理论、熵及三支决策等方法进行知识约简, 获得蕴含在数据集上的决策知识^{[8, 9, 10]}.

在经典粗糙集数据分析中, 数据集呈现的是单尺度系统, 即一个对象在一个属性下取值唯一, 但在实际应用中, 人们可能需要在不同尺度或粒度下描述问题和做出决策, 单尺度系统已不能满足实际需求.为此, Wu等^[11]提出一个对象在同一个属性下依据不同尺度取不同值的多尺度粗糙集数据分析模型, 简称Wu-Leung模型.Wu-Leung模型的建模思想是:根据决策目标对每个属性选择合适的尺度, 构造一个单尺度子系统, 再在保持给定目标约束条件下进行属性约简, 获得蕴含在数据集上的决策知识, 并对所获知识进行不确定性分析.因此, 筛选最优尺度(保持目标约束不变的最粗尺度)^[12]并在最优尺度下进行属性约简是多尺度数据分析的一个关键问题, 很多学者针对一些特定多尺度数据集的决策知识获取进行研究^{[13, 14, 15, 16, 17, 18, 19]}.由于Wu-Leung模型中每个属性都具有相同数量的尺度, Li等^[20]推广该模型, 提出广义多尺度决策系统, 并通过定义尺度组合的概念, 给出广义多尺度决策系统的最优尺度组合选择和知识获取方法.由于在数据集上先计算最优尺度组合再计算约简需分为两步进行, 为了在搜索最优尺度组合的同时得到约简, Cheng等^[21]定义最优尺度约简的概念, 给出广义多尺度决策系统的知识获取方法.廖淑娇等^[22]基于测试代价给出多尺度决策系统中属性约简与尺度选择同步搜索的算法, 可节省搜索时间、提高计算效率.近年来, 各类广义多尺度决策系统的最优尺度组合与属性约简的问题受到学者的关注, 并取得一些重要研究进展^{[23, 24, 25, 26, 27]}.

作为度量不确定性的测度, 熵在研究系统的不确定性问题中发挥显著作用.熵这一概念最早是热力学中表示物质状态的参量, 熵越大表示物质体系越混乱.后来Shannon^[28] 将熵引入信息论中, 用于度量知识的不确定性.在粗糙集数据分析中, 熵最早被用于刻画信息系统中知识的粗糙性^[29], 随后被用于各种类型数据的属性约简, 在知识获取方面取得较优效果^{[30, 31, 32]}.近年来, 熵在研究多尺度数据的最优尺度选择方面也发挥重要作用.基于条件熵和测试成本, Wu等^[33]提出考虑成本的多尺度三支多属性决策模型.Wang等^[34]基于多尺度模糊熵, 考虑属性的冗余性、相关性和互补性, 对多尺度决策系统进行特征选择.Xie等^[17]基于条件熵给出多尺度区间集决策系统中最优尺度选择和属性约简的方法.

多重集^[35]是指元素可以重复出现的集合, 并且元素的顺序对多重集不构成影响, 是管理决策与数据分析的常用工具之一.例如:有多位专家参与某个议题或投票表决的评审投票结果就是一个多重集.多重集在网络安全^[36]、特征融合^[37]、模式识别^[38]等方面都有重要应用.当信息系统的属性值为多重集时, 称该系统为多重集值信息系统, 相应的决策系统称为多重集值决策系统.在粗糙集数据分析方面, Zhao等^[39]结合三支决策与决策粗糙集模型, 将损失函数推广到多重集, 提出多重集决策理论粗糙集模型.Huang等^[40]应用不确定性度量方法分析多重集值信息系统的信息结构.Song等^[41]构造多重集值信息系统中的相容关系, 并研究多重集值信息系统的离群值检测问题.

然而, 上述研究的多重集值系统都是单尺度的.王蕾晰等^[42]提出多尺度多重集值信息系统的概念, 并给出基于知识粗糙熵的最优尺度选择和属性约简的算法.然而该算法处理的数据是Wu-Leung模型下的多尺度多重集值信息系统, 并且分两步提取数据集特征:先计算最优尺度, 再在最优尺度的基础上进行属性约简.

迄今为止, 未见关于广义多尺度多重集值决策系统的最优尺度组合和属性约简的研究.本文利用信息熵研究广义多尺度多重集值决策系统的最优尺度约简问题, 并给出最优尺度约简的搜索算法.采用文献[21]定义的尺度组合思路, 这样在选择最优尺度组合的同时就可得到属性约简(即最优尺度约简).

1 预备知识

在本文中, |· |表示集合的基数.本节介绍多重集、多重集值系统和信息熵的相关概念.

定义1^[35] 对于一个集合M, Z={z₁, z₂, …, z_o}为一个非空有限集合, 若Z中的元素z_i(z_i∈ Z)在M中重复出现e_i次, 即

$M=\overbrace{z_{1}, \cdots, z_{1}}^{e_{1}}, \cdots, \overbrace{z_{o}, \cdots, z_{o}}^{e_{o}},$

则称M为Z上的一个多重集.记集合Z上所有多重集构成的集合为M(Z).

若给定一个函数C_M:Z→ N, N为自然数集合, 使得

C_M(z_i)=e_i, z_i∈ Z, e_i∈ N,

则多重集M还可表示为

$M=\left\{\left.\frac{C_{M}(z)}{z} \right\rvert\, z \in Z\right\},$

多重集M的基数定义为

$|M|=\sum_{i=1}^{o} C_{M}\left(z_{i}\right) .$

定义2^[40] 对于Z={z₁, z₂, …, z_o}上的两个多重集M₁∈ M(Z), M₂∈ M(Z), M₁和M₂之间的海林格距离定义为

$H D\left(M_{1}, M_{2}\right)=\sqrt{1-\sum_{i=1}^{o} \sqrt{p_{i} q_{i}}},$

其中

p_i= $\frac{C_{M_{1}} (z_{i})}{|M_{1}|}$ , q_i= $\frac{C_{M_{2}} (z_{i})}{|M_{2}|}$ , i=1, 2, …, o.

由定义2可知, 一个多重集又可表示为

M={ $\frac{z_{1}, z_{2}, \dots, z_{o}}{p_{1}, p_{2}, \dots, p_{o}}$ },

其中

p_i= $\frac{C_{M} (z_{i})}{|M|}$ , i=1, 2, …, o.

例1 有2名选手参加一场晋级赛, 由4位专家进行评价并给出成绩“ 晋级(p)” 或“ 淘汰(f)” , 那么4位专家给2名选手的成绩M₁与M₂就是2个多重集.此时Z={p, f}, M₁∈ M(Z), M₂∈ M(Z), 若其中一名选手得到2张“ 晋级” 票和2张“ 淘汰” 票, 另一名选手得到3张“ 晋级” 票和1张“ 淘汰” 票, 则由定义1,

M₁={p, p, f, f}, M₂={p, p, p, f}.

还可表示为

$M_{1}=\left\{\frac{2}{p}, \frac{2}{f}\right\}, M_{2}=\left\{\frac{3}{p}, \frac{1}{f}\right\} .$

进一步, 由定义2, M₁和M₂又可表示为

M₁= $\{\frac{p, f}{\frac{1}{2}, \frac{1}{2}}\}$ , M₂= $\{\frac{p, f}{\frac{3}{4}, \frac{1}{4}}\}$ ,

且M₁与M₂之间的海林格距离为

$\begin{aligned}H D\left(M_{1}, M_{2}\right)= & \sqrt{1-\sum_{i=1}^{2} \sqrt{p_{i} q_{i}}}= \\& \sqrt{1-\left(\sqrt{\frac{1}{2} \cdot \frac{3}{4}}+\sqrt{\frac{1}{2} \cdot \frac{1}{4}}\right)}= \\& \sqrt{\frac{\sqrt{8}-\sqrt{3}-1}{\sqrt{8}}} \approx 0.1846 .\end{aligned}$

定义3^[3] 称二元组(U, C)为一个信息系统, 其中U={x₁, x₂, …, x_n}为论域, C={c₁, c₂, …, c_m}为非空有限属性集, 对于∀ c_j∈ C, 有

c_j:U→ V_j, j=1, 2, …, m,

其中V_j为c_j的值域.

称二元组(U, C∪ {d})为一个决策系统, 其中(U, C)为一个信息系统, 称C为条件属性集, d∉C为决策属性, d:U→ V_d, V_d为d的值域.若系统中存在缺省值*, 则称此决策系统为不完备决策系统.

定义4^[39] 称二元组(U, C∪ {d})为一个多重集值决策系统, 其中U={x₁, x₂, …, x_n}为论域, C={c₁, c₂, …, c_m}为条件属性集, 且每个对象的条件属性取值都为多重集, 即对于∀ c_j∈ C,

c_j:U→ M(V_j),

其中, V_j为条件属性c_j的值域, d∉C为决策属性.

定义5^{[20, 21]} 称二元组(U, C∪ {d})为一个广义多尺度决策系统, 其中U={x₁, x₂, …, x_n}为论域, C={c₁, c₂, …, c_m}为条件属性集, 且每个条件属性都有I_j个尺度, d∉C为决策属性, 一个广义多尺度决策系统可表示为

(U, C∪ {d})=

(U,{ $c_{j}^{l}$ |=|1, 2, …,m,l=1, 2, …,Ij}∪ {d}),

其中

$c_{j}^{l}$ :U→ $V_{j}^{l}$ , j=1, 2, …, m, l=1, 2, …, I_j,

d:U→ Vd_,

V_d为d的值域, $V_{j}^{l}$ 为c_j在第l个尺度下的值域, 对于∀ l∈ {2, 3, …, I_j}, 存在一个满射

$g_{j}^{l, l - 1}$ : $V_{j}^{l}$ → $V_{j}^{l - 1}$ ,

使得

$c_{j}^{l-1}=g_{j}^{l, l-1} \circ c_{j}^{l},$

即

$c_{j}^{l - 1}$ (x)= $g_{j}^{l, l - 1}$ ( $c_{j}^{l}$ (x)), x∈ U,

称 $g_{j}^{l, l - 1}$ 为信息粒度变换.

定义6^[21] 设

S=(U, C∪ {d})=

(U,{ $c_{j}^{l}$ |=|1, 2, …,m,l=1, 2, …,Ij_}∪ {d})

为一个广义多尺度决策系统, 对于∀ c_j∈ C, 将属性c_j所选尺度标记l_j限制在{0, 1, …, I_j}上, 当l_j=0时, 表示属性c_j被删除; 当l_j≠ 0时, 表示属性c_j选择第l_j个尺度, 此时称所选指标集构成S的一个尺度组合L=(l₁, l₂, …, l_m), 其中l_j∈ {0, 1, …, I_j}.

显然, 一个尺度组合L对应一个单尺度决策系统

$S^{L}=\left(U, \left\{c_{j}^{l_{j}} \mid j=1, 2, \cdots, m\right\} \cup\{d\}\right) .$

定义7^[42] 称二元组(U, C)为一个多尺度多重集值信息系统, 其中U={x₁, x₂, …, x_n}为论域, C={c₁, c₂, …, c_m}为非空有限属性集, 每个属性都有I个尺度且属性值都是多重集, 一个多尺度多重集值信息系统可表示为

(U, { $c_{j}^{l}$ |j=1, 2, …, m, l=1, 2, …, I}),

其中

$c_{j}^{l}$ :U→ M( $V_{j}^{l}$ ), j=1, 2, …, m, l=1, 2, …, I,

$V_{j}^{l}$ 为c_j在第l个尺度下的值域, 对于∀ l∈ {2, 3, …, I}, 存在一个满射

$g_{j}^{l, l - 1}$ : $V_{j}^{l}$ → $V_{j}^{l - 1}$ ,

使得

$c_{j}^{l-1}=g_{j}^{l, l-1} \circ c_{j}^{l},$

即

$c_{j}^{l - 1}$ (x)= $g_{j}^{l, l - 1}$ ( $c_{j}^{l}$ (x)), x∈ U,

称 $g_{j}^{l, l - 1}$ 为信息粒度变换.

定义8^[42] 设

(U, C)=(U, { $c_{j}^{l}$ |j=1, 2, …, m, l=1, 2, …, I})

为一个多尺度多重集值信息系统, 则对于

∀ x∈ U, y∈ U, c_j∈ C, l∈ {1, 2, …, I},

x与y在 $c_{j}^{l}$ 下的相似度为:

SIM( $c_{j}^{l}$ (x), $c_{j}^{l}$ (y))=1-HD( $c_{j}^{l}$ (x), $c_{j}^{l}$ (y)),

其中HD( $c_{j}^{l}$ (x), $c_{j}^{l}$ (y))表示x、y在 $c_{j}^{l}$ 下的海林格距离.

命题1^[42] 设

(U, C)=(U, { $c_{j}^{l}$ |j=1, 2, …, m, l=1, 2, …, I})

为一个多尺度多重集值信息系统, 则对于

∀ x∈ U, y∈ U, c_j∈ C, l∈ {1, 2, …, I},

有

SIM( $c_{j}^{l}$ (x), $c_{j}^{l}$ (y))≤ SIM( $c_{j}^{l - 1}$ (x), $c_{j}^{l - 1}$ (y)).

设U为一个非空有限集合, 幂集记作P(U), 对于

C={C₁, C₂, …, C_e}⊆P(U),

若Ø∉C且 $\bigcup_{i=1}^{e} C_{i}=U$ , 则称C为U的一个覆盖.

进一步, 若

C_i∩ C_j=Ø,

i≠ j, i∈ {1, 2, …,e}, j∈ {1, 2, …,e},

则称C为U的一个划分.

定义9^[29] 设(U, C)为一个信息系统, P⊆C, Q⊆C, 若

X={X₁, X₂, …, X_t}, Y={Y₁, Y₂, …, Y_s}

为P和Q导出的U的两个划分, 则P的信息熵为:

$H(P)=-\sum_{i=1}^{t} p\left(X_{i}\right) \log _{2} p\left(X_{i}\right),$

其中

$p\left(X_{i}\right)=\frac{\left|X_{i}\right|}{|U|}, i=1, 2, \cdots, t .$

Q关于P的条件熵为:

$H(Q \mid P)=-\sum_{i=1}^{t} \sum_{j=1}^{s} p\left(X_{i}\right) p\left(Y_{j} \mid X_{i}\right) \log _{2} p\left(Y_{j} \mid X_{i}\right),$

其中

p(Y_j|X_i)= $\frac{| Y_{j} ⋂ X_{i} |}{|X_{i}|}$ ,

i=1, 2, …,t, j=1, 2, …,s.

Q与P的联合熵为:

$H(Q \cup P)=-\sum_{i=1}^{t} \sum_{j=1}^{s} p\left(Y_{j} \cap X_{i}\right) \log _{2} p\left(Y_{j} \cap X_{i}\right),$

其中

p(Y_j∩ X_i)= $\frac{| Y_{j} ⋂ X_{i} |}{| U |}$ ,

i=1, 2, …,t, j=1, 2, …,s.

定义9中所述的条件熵是建立在等价关系上的, 并非适用于相似关系, 为此, Dai等^[32]提出相似关系下的条件熵.

对于一个不完备决策系统(U, C∪ {d}), B⊆C为一个条件属性子集, R_B为论域U中由B导出的相似关系, 即

R_B={(x, y)∈ U× U|c(x)=c(y)∨

c(x)=*∨ c(y)=* ,∀ c∈ B},

则R_B导出U上的一个覆盖:

U/R_B={[x]_B|x∈ U},

其中

[x]_B={y∈ U|(x, y)∈ R_B}

为x关于R_B的相似类.对于决策属性d, 不失一般性, 假定V_d={1, 2, …, r}, R_d为论域U关于d的等价关系:

R_d={(x, y)∈ U× U|d(x)=d(y)},

U/R_d为由R_d生成的U上的一个划分, 将U粒化为r个等价类:

U/R_d={[x]_d|x∈ U}={D₁, D₂, …, D_r}.

对于x∈ U, 若∃j∈ {1, 2, …, r}, 使得x∈ D_j, 则称D_j为x的决策类, 即

D_j={x∈ U|d(x)=j}=[x]_d.

定义10^[32] 设(U, C∪ {d})为一个不完备决策系统,

U/R_d={D₁, D₂, …, D_r},

B⊆C为一个条件属性子集, 则d关于B的条件熵为:

$\begin{array}{l}H(d \mid B)= \\-\sum_{i=1}^{n} \sum_{j=1}^{r}\left(\frac{\left|\left[x_{i}\right]_{B} \cap D_{j}\right|}{n}\right) \log _{2}\left(\frac{\left|\left[x_{i}\right]_{B} \cap D_{j}\right|}{\left|\left[x_{i}\right]_{B}\right|}\right) .\end{array}$

2 广义多尺度多重集值决策系统

定义11 称二元组(U, C)为一个广义多尺度多重集值信息系统, 其中U={x₁, x₂, …, x_n}为论域, C={c₁, c₂, …, c_m}为非空有限属性集, 对于∀ c_j∈ C有I_j个尺度(I_j不必完全相同), 且每个对象的属性值均为多重集, 则一个广义多尺度多重集值信息系统可表示为

(U, { $c_{j}^{l}$ |j=1, 2, …, m, l=1, 2, …, I_j}),

其中

$c_{j}^{l}$ :U→ M( $V_{j}^{l}$ ), j=1, 2, …, m, l=1, 2, …, I_j,

$V_{j}^{l}$ 为c_j在第l个尺度下的值域, 对于

∀ l=2, 3, …, I_j, j=1, 2, …, m,

存在两个满射, 一个是

$g_{j}^{l, l - 1}$ : $V_{j}^{l}$ → $V_{j}^{l - 1}$ ,

使得

w=g^l^,^l^-1(v), v∈ $V_{j}^{l}$ ,

另一个是

$φ_{j}^{l, l - 1}$ :M( $V_{j}^{l}$ )→ M( $V_{j}^{l - 1}$ ),

使得

$c_{j}^{l-1}=\varphi_{j}^{l, l-1} \circ c_{j}^{l},$

即对于∀ x∈ U, 记

$c_{j}^{l}$ (x)=M₁, $c_{j}^{l - 1}$ (x)=M₂,

有

$\begin{aligned} c_{j}^{l-1}(x)= & \varphi_{j}^{l, l-1}\left(c_{j}^{l}(x)\right)=\varphi_{j}^{l, l-1}\left(M_{1}\right)= \\ & \varphi_{j}^{l, l-1}\left(\left\{\left.\frac{C_{M_{1}}(v)}{v} \right\rvert\, v \in V_{j}^{l}\right\}\right)= \\ & \left\{\left.\frac{C_{M_{1}}\left(g_{j}^{l, l-1}(v)\right)}{g_{j}^{l, l-1}(v)} \right\rvert\, v \in V_{j}^{l}\right\}= \\ & \left\{\left.\frac{C_{M_{2}}(w)}{w} \right\rvert\, w \in V_{j}^{l-1}\right\}, \end{aligned}$

称 $g_{j}^{l, l - 1}$ 为信息粒度变换, $φ_{j}^{l, l - 1}$ 为信息值域变换.

定义12 称二元组

$\begin{array}{l} (U, C \cup\{d\})= \\ \quad\left(U, \left\{c_{j}^{l} \mid j=1, 2, \cdots, m, l=1, 2, \cdots, I_{j}\right\} \cup\{d\}\right) \end{array}$

为一个广义多尺度多重集值决策系统, 其中

(U, C)=(U, { $c_{j}^{l} |j = 1, 2, \dots, m, l = 1, 2, \dots, I_{j}$ })

为一个广义多尺度多重集值信息系统, d∉C, d:U→ V_d为决策属性.

定义13 设

$\begin{aligned} S= & (U, C \cup\{d\})= \\ & \left(U, \left\{c_{j}^{l} \mid j=1, 2, \cdots, m, l=1, 2, \cdots, I_{j}\right\} \cup\{d\}\right) \end{aligned}$

为一个广义多尺度多重集值决策系统, 对于∀ c_j∈ C, 将属性c_j所选尺度标记l_j限制在{0, 1, …, I_j}上, 当l_j=0时, 表示属性c_j被删除; 当l_j≠ 0时, 表示属性c_j选择第l_j个尺度, 此时称所选指标集构成S的一个尺度组合L, 即

L=(l₁, l₂, …, l_m), l_j∈ {0, 1, …, I_j},

j∈ {1, 2, …,m}.

记广义多尺度多重集值决策系统S的全部尺度组合为L, 即

L={(l₁, l₂, …, l_m) $|l_{j} \in {0, 1, \dots, I_{j}}$ , j∈ {1, 2, …, m}}.

显然, 每个尺度组合

L=(l₁, l₂, …, l_m)∈ L

对应一个单尺度多重集值决策系统

S^L=(U, C^L∪ {d}),

其中

C^L={ $c_{j}^{l_{j}}$ |j=1, 2, …, m, l_j≠ 0},

为条件属性集C在尺度组合L上的限制.

例如:若

C={c₁, c₂, c₃, c₄}, L=(1, 0, 2, 2)∈ L,

则

C^L={ $c_{1}^{1}$ , $c_{3}^{2}$ , $c_{4}^{2}$ }.

定义14 对于一个广义多尺度多重集值决策系统(U, C∪ {d}), 记

L=( $l_{1}^{1}$ , $l_{2}^{1}$ , …, $l_{m}^{1}$ )∈ L, K=( $l_{1}^{2}$ , $l_{2}^{2}$ , …, $l_{m}^{2}$ )∈ L,

如果

∀ j∈ {1, 2, …, m}, $l_{j}^{1}$ ≤ $l_{j}^{2}$ ,

那么称尺度组合K强于L或称L弱于K, 记作K≽L.进一步, 若∃j∈ {1, 2, …, m}, 使得 $l_{j}^{1}$ < $l_{j}^{2}$ , 则称尺度组合K严格强于L或称L严格弱于K, 记作K≻L.

另外, 如果定义

L∧ K={ $l_{1}^{1}$ ∧ $l_{1}^{2}$ , $l_{2}^{1}$ ∧ $l_{2}^{2}$ , …, $l_{m}^{1}$ ∧ $l_{m}^{2}$ },

L∨ K={ $l_{1}^{1}$ ∨ $l_{1}^{2}$ , $l_{2}^{1}$ ∨ $l_{2}^{2}$ , …, $l_{m}^{1}$ ∨ $l_{m}^{2}$ },

其中

$l_{j}^{1}$ ∧ $l_{j}^{2}$ =min{ $l_{j}^{1}$ , $l_{j}^{2}$ }, $l_{j}^{1}$ ∨ $l_{j}^{2}$ =max{ $l_{j}^{1}$ , $l_{j}^{2}$ },

j∈ {1, 2, …,m},

那么(L, ≽, ∧ , ∨ )为一个完备格, 其中最小元为(0, 0, …, 0), 最大元为(I₁, I₂, …, I_m).

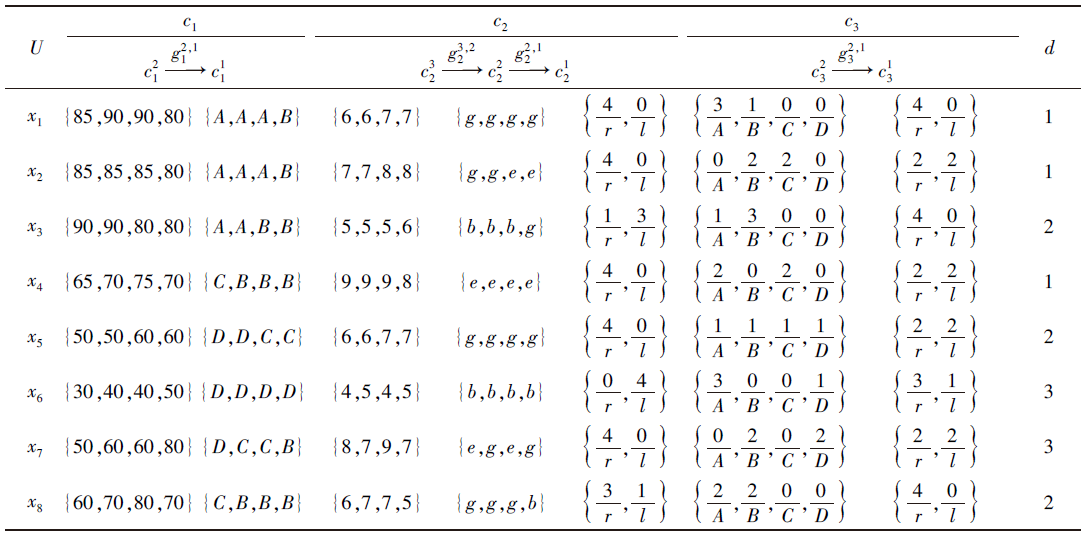
例2表1为一个广义多尺度多重集值决策系统S=(U, C∪ {d}), U={x₁, x₂, …, x₈}表示8名参赛选手的论文, C={c₁, c₂, c₃}, c₁表示论文的创新性, c₂表示论文的语言描写, c₃表示论文的严谨性, d表示论文最终的成绩等级, V_d={1, 2, 3}, 1表示一等奖, 2表示二等奖, 3表示三等奖.

表1 一个广义多尺度多重集值决策系统 Table 1 A generalized multi-scale multiset-valued decision system

属性值域的信息粒度变换如下:

$g_{1}^{2, 1}$ (u)= $\{\begin{array}{l} A, & 85 \leq u \\ B, & 70 \leq u 85 \\ C, & 55 \leq u 70 \\ D, & u 55 \end{array}$

$g_{2}^{2, 1}$ (v)= $\{\begin{array}{l} r, & v \in {e, g} \\ l, & v \in {b} \end{array}$

$g_{2}^{3, 2}(z)=\left\{\begin{array}{ll} e, & 8 \leqslant z \leqslant 10 \\ g, & 6 \leqslant z< 8 \\ b, & 1 \leqslant z< 6 \end{array}\right.$

$g_{3}^{2, 1}$ (h)= $\{\begin{array}{l} r, & h \in {A, B} \\ l, & h \in {C, D} \end{array}$

图1(a)给出属性c₃下, 第2个尺度与第1个尺度之间的信息粒度变换.(b)给出对象x₆在属性c₃下, 第2个尺度与第1个尺度之间的信息值域变换.

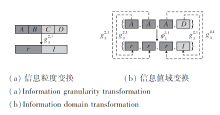	Figure Option View Download New Window
	图1 信息粒度变换与信息值域变换的转换图Fig.1 Schematic diagram of information granularity transformation and information domain transformation

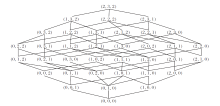
属性c₁有2个尺度, 属性c₂有3个尺度, 属性c₃有2个尺度, 系统S共有36个尺度组合, 最强尺度组合为(2, 3, 2).由定义14, S的所有尺度组合的格结构如图2所示.

	Figure Option View Download New Window
	图2 尺度组合的格结构Fig.2 Lattice structure of scale combinations

定义15 对于一个广义多尺度多重集值决策系统(U, C∪ {d}),

L=(l₁, l₂, …, l_m)∈ L,

若∃j∈ {1, 2, …, m}, 使得l_j≠ 0, 给定一个阈值α∈ (0, 1], 则定义由C^L导出的相似关系:

$\begin{aligned} R_{C^{L}}^{\alpha}= & \left\{(x, y) \in U \times U \mid \forall c_{j}^{l_{j}} \in C^{L}, \right. \\ & \left.\operatorname{SIM}\left(c_{j}^{l_{j}}(x), c_{j}^{l_{j}}(y)\right) \geqslant \alpha\right\} . \end{aligned}$

$R_{C^{L}}^{α}$ 将U粒化为若干相似类:

U/ $R_{C^{L}}^{α}$ ={ ${[x]}_{C^{L}}^{α}$ |x∈ U},

其中

${[x]}_{C^{L}}^{α}$ ={y∈ U| (x, y)∈ $R_{C^{L}}^{α}$ },

且相似类的全体U/ $R_{C^{L}}^{α}$ 构成U的一个覆盖, 即

$\cup_{x}^{\in} {[x]}_{C^{L}}^{α}$ =U, Ø∉U/ $R_{C^{L}}^{α}$ .

特别地, 对于∀ c_j∈ C, l∈ {1, 2, …, I_j}, c_j在第l个尺度下导出的相似关系:

$R_{c_{j}^{l}}^{α}$ ={(x, y)∈ U× U|SIM( $c_{j}^{l}$ (x), $c_{j}^{l}$ (y))≥ α},

显然

$R_{C^{L}}^{α}$ = $\cap_{c_{j}^{l}}^{\in} R_{c_{j}^{l}}^{α}$ .

命题2 设(U, C∪ {d})为一个广义多尺度多重集值决策系统, α∈ (0, 1], 对于

∀ c_j∈ C, j∈ {1, 2, …, m}, l∈ {2, 3, …, I_j},

有

$R_{c_{j}^{l}}^{α}$ ⊆ $R_{c_{j}^{l - 1}}^{α}$ .

证明对于∀ (x, y)∈ $R_{c_{j}^{l}}^{α}$ , 由定义15得

SIM( $c_{j}^{l}$ (x), $c_{j}^{l}$ (y))≥ α,

由命题1可得

SIM( $c_{j}^{l}$ (x), $c_{j}^{l}$ (y))≤ SIM( $c_{j}^{l - 1}$ (x), $c_{j}^{l - 1}$ (y)),

从而

SIM( $c_{j}^{l - 1}$ (x), $c_{j}^{l - 1}$ (y))≥ α,

因此, (x, y)∈ $R_{c_{j}^{l - 1}}^{α}$ , 于是

$R_{c_{j}^{l}}^{α}$ ⊆ $R_{c_{j}^{l - 1}}^{α}$ . 证毕.

性质1 设(U, C∪ {d})为一个广义多尺度多重集值决策系统, 对于α∈ (0, 1], L∈ L, K∈ L, 若K≽L, 则 $R_{C^{K}}^{α}$ ⊆ $R_{C^{L}}^{α}$ .

证明设

L=( $l_{1}^{1}$ , $l_{2}^{1}$ , …, $l_{m}^{1}$ ), K=( $l_{1}^{2}$ , $l_{2}^{2}$ , …, $l_{m}^{2}$ ),

则由K≽L及定义14可得, 对于∀ j∈ {1, 2, …, m}有 $l_{j}^{1}$ ≤ $l_{j}^{2}$ , 记

J={j| $l_{j}^{1}$ ≠ 0, j=1, 2, …, m}.

若j∈ J, 由命题2可得

$R_{c_{j}^{l_{j}^{2}}}^{α}$ ⊆ $R_{c_{j}^{l_{j}^{1}}}^{α}$ .

由于

$R_{C^{L}}^{α}$ = $\cap_{c_{j}^{l_{j}^{1}}}^{\in} R_{c_{j}^{l_{j}^{1}}}^{α}$ , $R_{C^{K}}^{α}$ = $\cap_{c_{j}^{l_{j}^{2}}}^{\in} R_{c_{j}^{l_{j}^{2}}}^{α}$ ,

因此

$R_{C^{K}}^{α}$ ⊆ $\cap_{j}^{\in} R_{c_{j}^{l_{j}^{2}}}^{α}$ ⊆ $\cap_{j}^{\in} R_{c_{j}^{l_{j}^{1}}}^{α}$ = $R_{C^{L}}^{α}$ . 证毕.

例3 (续例2) 给定4个尺度组合

L₀=(2, 3, 2)∈ L, L₁=(1, 2, 0)∈ L,

L2₌(1, 1, 0)∈ L, L3₌(0, 2, 0)∈ L,

α=0.6, 经计算可得

$R_{C^{L_{0}}}^{0.6}$ ={(x₁, x₁), (x₂, x₂), (x₃, x₃), (x₄, x₄),

(x₅, x₅), (x₆, x₆), (x₇, x₇), (x₈, x₈)},

$R_{C^{L_{1}}}^{0.6}$ ={(x₁, x₁), (x₂, x₂), (x₃, x₃), (x₄, x₄),

(x5_,x5₎, (x6_,x6₎, (x7_,x7₎, (x8_,x8₎},

= $R_{C^{L_{2}}}^{0.6}$ (x1,_x1)_,(x1,_x2)_,(x2,_x1)_,(x2,_x2)_,

(x3, x₃),₍x4, x₄),₍x4, x₈),₍x5, x₅),

(x5,x7₎, (_x6, x6₎, (_x7, x5₎, (_x7, x7₎,

(x7, x8)_,(x₈, x4)_,(x₈, x7)_,(x₈, x8)_},

={(x1 $R_{C^{L_{3}}}^{0.6}$ x1),₍x1_,x5),₍x1_,x8),₍x2_,x2),

(_x2, x7), (_x3,_x3), (_x3,_x6), (_x3,_x8),

(x₄, x4),(x₅, x₁), (x₅, x₅), (x₅, x₈),

₍x6_,x3), (x6_,x6₎, (x7_,x2₎, (x7_,x7₎,

(_x8,_x1), (x8,_x3)_,(x8,_x5)_,(x8,_x8)_}.

3 广义多尺度多重集值决策系统的最优尺度约简

本节基于条件熵和广义决策函数研究广义多尺度多重集值决策系统中的α -熵最优尺度约简和α -广义决策最优尺度约简.

定义16 对于一个广义多尺度多重集值信息系统(U, C), 设α∈ (0, 1], L∈ L, 则C^L的信息熵为:

H_α(C^L)=- $\sum_{i}^{=}$ ( $\frac{|[x_{i}]_{C^{L}}^{α}|}{n}$ log₂( $\frac{|[x_{i}]_{C^{L}}^{α}|}{n}$ )).

定义17 对于一个广义多尺度多重集值决策系统(U, C∪ {d}), 设α∈ (0, 1], L∈ L,

U/R_d={D₁, D₂, …, D_r},

则d关于C^L的条件熵为:

定义18 对于一个广义多尺度多重集值决策系统(U, C∪ {d}), 设α∈ (0, 1], L∈ L,

U/R_d={D₁, D₂, …, D_r},

则d关于C^L的联合熵为:

$\begin{array}{l} H_{\alpha}\left(d \cup C^{L}\right)= \\ -\sum_{i=1}^{n} \sum_{j=1}^{r}\left(\frac{\left|\left[x_{i}\right]_{C^{L}}^{\alpha} \cap D_{j}\right|}{n} \log _{2}\left(\frac{\left|\left[x_{i}\right]_{C^{L}}^{\alpha} \cap D_{j}\right|}{n}\right)\right) . \end{array}$

定理1 对于一个广义多尺度多重集值决策系统(U, C∪ {d}), 若α∈ (0, 1], L∈ L,

U/R_d={D₁, D₂, …, D_r},

则

$H_{\alpha}\left(d \mid C^{L}\right)=H_{\alpha}\left(d \cup C^{L}\right)-H_{\alpha}\left(C^{L}\right) .$

证明由

U/R_d={D₁, D₂, …, D_r}

是U的一个划分可得

$\begin{array}{l} H_{\alpha}\left(d \mid C^{L}\right)= \\ -\sum_{i=1}^{n} \sum_{j=1}^{r}\left(\frac{\left|\left[x_{i}\right]_{C^{L}}^{\alpha} \cap D_{j}\right|}{n} \log _{2}\left(\frac{\left|\left[x_{i}\right]_{C^{L}}^{\alpha} \cap D_{j}\right|}{\left|\left[x_{i}\right]_{C^{L}}^{\alpha}\right|}\right)\right)= \\ -\sum_{i=1}^{n} \sum_{j=1}^{r}\left(\frac { | [ x _ { i } ] _ { C ^ { L } } ^ { \alpha } \cap D _ { j } | } { n } \left(\log _{2}\left(\frac{\left|\left[x_{i}\right]_{C^{L}}^{\alpha} \cap D_{j}\right|}{n}\right)-\right.\right. \\ \left.\left.\quad \log _{2}\left(\frac{\left|\left[x_{i}\right]_{C^{L}}^{\alpha}\right|}{n}\right)\right)\right)= \\ H_{\alpha}\left(d \cup C^{L}\right)+\sum_{i=1}^{n}\left(\frac{\left|\left[x_{i}\right]_{C^{L}}^{\alpha}\right|}{n} \log _{2}\left(\frac{\left|\left[x_{i}\right]_{C^{L}}^{\alpha}\right|}{n}\right)\right)= \\ H_{\alpha}\left(d \cup C^{L}\right)-H_{\alpha}\left(C^{L}\right) .证毕 \end{array}$

性质2 对于一个广义多尺度多重集值决策系统(U, C∪ {d}), U=(x₁, x₂, …, x_n), 设α∈ (0, 1], L∈ L, K∈ L, 若K≽L, 则

H_α(d|C^K)≤ H_α(d|C^L).

证明对于∀ x∈ U, D∈ U/R_d, 令

p=| ${[x]}_{C^{L}}^{α}$ ∩ D|, q=| ${[x]}_{C^{L}}^{α}$ ∩ D^C|,

其中D^C表示D的补集, 则

p+q=| ${[x]}_{C^{L}}^{α}$ |.

一方面, 当p> 0且q≥ 0时, 函数-plog₂( $\frac{p}{p + q}$ )为单调递增^[32], 另一方面, 由性质1知

${[x]}_{C^{K}}^{α}$ ⊆ ${[x]}_{C^{L}}^{α}$ ,

可得

| ${[x]}_{C^{K}}^{α}$ ∩ D|≤ | ${[x]}_{C^{L}}^{α}$ ∩ D|,

所以

$\begin{aligned} 0 \leqslant & -\left|[x]_{C^{K}}^{\alpha} \cap D\right| \log _{2}\left(\frac{\left|[x]_{C^{K}}^{\alpha} \cap D\right|}{\left|[x]_{C^{K}}^{\alpha}\right|}\right) \leqslant \\ & -\left|[x]_{C^{L}}^{\alpha} \cap D\right| \log _{2}\left(\frac{\left|[x]_{C^{L}}^{\alpha} \cap D\right|}{\left|[x]_{C^{L}}^{\alpha}\right|}\right), \end{aligned}$

故

$\begin{aligned} 0 \leqslant & -\frac{\left|[x]_{C^{K}}^{\alpha} \cap D\right|}{n} \log _{2}\left(\frac{\left|[x]_{C^{K}}^{\alpha} \cap D\right|}{\left|[x]_{C^{K}}^{\alpha}\right|}\right) \leqslant \\ & -\frac{\left|[x]_{C^{L}}^{\alpha} \cap D\right|}{n} \log _{2}\left(\frac{\left|[x]_{C^{L}}^{\alpha} \cap D\right|}{\mid[x)]_{C^{L}}^{\alpha} \mid}\right), \end{aligned}$

因此

H_α(d|C^K)≤ H_α(d|C^L). 证毕

定理2 对于一个广义多尺度多重集值决策系统(U, C∪ {d}), U=(x₁, x₂, …, x_n), 若α∈ (0, 1], L∈ L, 则如下结论等价:

1) $R_{C^{L}}^{α}$ ⊆R_d,

2)H_α(d∪ C^L)=H_α(C^L),

3)H_α(d|C^L)=0.

证明 1)⇒ 2).对于∀ x∈ U, 若 $R_{C^{L}}^{α}$ ⊆R_d, 则∃j'∈ {1, 2, …, r}, 满足

${[x]}_{C^{L}}^{α}$ ∩ D_j= $\{\begin{array}{l} {[x]}_{C^{L}}^{α}, & j = j' \\ Ø, & j \neq j' \end{array}$

于是

$\begin{array}{c} \sum_{j=1}^{r}\left(\frac{\left|[x]_{C^{L}}^{\alpha} \cap D_{j}\right|}{n} \log _{2}\left(\frac{\left|[x]_{C^{L}}^{\alpha} \cap D_{j}\right|}{n}\right)\right)= \\ \frac{\left|[x]_{C^{L}}^{\alpha}\right|}{n} \log _{2}\left(\frac{\left|[x]_{C^{L}}^{\alpha}\right|}{n}\right) \end{array}$

因此

H_α(d∪ C^L)=H_α(C^L).

2)⇒ 3).由定理1可得.

3)⇒ 1).对于∀ x∈ U, D∈ U/R_d, 由性质2的证明过程可知, 若

H_α(d|C^L)=0,

则有

$\frac{| {[x]}_{C^{L}}^{α} ⋂ D |}{n}$ log₂( $\frac{| {[x]}_{C^{L}}^{α} ⋂ D |}{|{[x]}_{C^{L}}^{α}|}$ )=0,

即

| ${[x]}_{C^{L}}^{α}$ ∩ D|| ${[x]}_{C^{L}}^{α}$ ∩ D^C|=0.

因此, 对于∀ x∈ U, ∃D'∈ U/R_d使得

${[x]}_{C^{L}}^{α}$ ⊆[x]_d=D',

故

$R_{C^{L}}^{α}$ ⊆R_d. 证毕

定义19 对于一个广义多尺度多重集值决策系统S=(U, C∪ {d}), 设α∈ (0, 1],

L₀=(I₁, I₂, …, I_m)∈ L,

若

$R_{C^{L_{0}}}^{α}$ ⊆R_d,

则称S是α -协调的, 否则称S不是α -协调的.

定义20 对于一个广义多尺度多重集值决策系统S=(U, C∪ {d}), 设α∈ (0, 1], L∈ L, 若

$R_{C^{L}}^{α}$ ⊆R_d,

则称S^L关于S是α -协调的.进一步, 若对于满足L≻K的∀ K∈ L, 有

$R_{C^{K}}^{α}$ ⊈R_d,

则称L是S的一个α -最优尺度组合, 称C在L上的限制C^L是S的一个α -最优尺度约简.

定义21 对于一个广义多尺度多重集值决策系统S=(U, C∪ {d}), 设α∈ (0, 1],

L₀=(I₁, I₂, …, I_m)∈ L, L∈ L,

若

H_α(d|C^L)=H_α(d| $C^{L_{0}}$ ),

则称S^L关于S是α -熵协调的.进一步, 若对于满足L≻K的∀ K∈ L, 有

H_α(d|C^K)≠ H_α(d| $C^{L_{0}}$ ),

则称L是S的一个α -熵最优尺度组合, 称C在L上的限制C^L是S的一个α -熵最优尺度约简.

定理3 设S=(U, C∪ {d})是一个α -协调的广义多尺度多重集值决策系统, 若α∈ (0, 1],

L₀=(I₁, I₂, …, I_m)∈ L, L∈ L,

则

1)S^L关于S是α -协调的当且仅当S^L关于S是α -熵协调的,

2)L是S的一个α -最优尺度组合当且仅当L是S的一个α -熵最优尺度组合,

3)C^L是S的一个α -最优尺度约简当且仅当C^L是S的一个α -熵最优尺度约简.

证明先证1).必要性.若S^L关于S是α -协调的, 则

$R_{C^{L}}^{α}$ ⊆R_d,

又因为S是α -协调的, 即

$R_{C^{L_{0}}}^{α}$ ⊆R_d,

从而由定理2可得

H_α(d|C^L)=H_α(d| $C^{L_{0}}$ )=0,

因此, S^L关于S是α -熵协调的.

充分性.若S^L关于S是α -熵协调的, 即

H_α(d|C^L)=H_α(d| $C^{L_{0}}$ ),

又因为S是α -协调的, 即

$R_{C^{L_{0}}}^{α}$ ⊆R_d,

从而由定理2可得

H_α(d|C^L)=H_α(d| $C^{L_{0}}$ )=0.

若S^L关于S不是α -协调的, 即

$R_{C^{L}}^{α}$ ⊈R_d,

则∃x∈ U, j∈ {1, 2, …, r}使得

d(x)=j,

但

${[x]}_{C^{L}}^{α}$ ⊈D_j,

即

${[x]}_{C^{L}}^{α}$ ∩ D_j≠ ${[x]}_{C^{L}}^{α}$ ,

所以

$\log _{2}\left(\frac{\left|[x]_{C^{L}}^{\alpha} \cap D_{j}\right|}{\left|[x]_{C^{L}}^{\alpha}\right|}\right)< 0,$

故

$\begin{array}{l} H_{\alpha}\left(d \mid C^{L}\right) \geqslant \\ \quad-\frac{\left|[x]_{C^{L}}^{\alpha} \cap D_{j}\right|}{n} \log _{2}\left(\frac{\left|[x]_{C^{L}}^{\alpha} \cap D_{j}\right|}{\left|[x]_{C^{L}}^{\alpha}\right|}\right)> 0, \end{array}$

这与H_α(d|C^L)=0矛盾.

再证2).由1)可得.

最后证3).由1), 定义20和定义21可得. 证毕

例4 (续例3) 由表1可知

R_d={(x₁, x₁), (x₁, x₂), (x₁, x₄), (x₂, x₁),

(x₂, x₂), (x₂, x₄), (x₃, x₃), (x₃, x₅),

(x₃, x₈), (x₄, x₁), (x₄, x₂), (x₄, x₄),

(x₅, x₃), (x₅, x₅), (x₅, x₈), (x₆, x₆),

(x₆, x₇), (x₇, x₆), (x₇, x₇), (x₈, x₃),

(x₈, x₅), (x₈, x₈)},

再由例3可得

$R_{C^{L_{2}}}^{0.6}$ ⊈R_d, $R_{C^{L_{3}}}^{0.6}$ ⊈R_d, $R_{C^{L_{1}}}^{0.6}$ ⊆R_d,

由于L中严格弱于L₁的尺度组合只有L₂与L₃, 因此, L₁=(1, 2, 0)是S的一个α -最优尺度组合,

$C^{L_{1}}$ ={ $c_{1}^{1}$ , $c_{2}^{2}$ }

是S的一个α -最优尺度约简.又因为

$\begin{array}{l} H_{\alpha}\left(d \mid C^{L_{1}}\right)=H_{\alpha}\left(d \mid C^{L_{0}}\right), \\ H_{\alpha}\left(d \mid C^{L_{2}}\right) \neq H_{\alpha}\left(d \mid C^{L_{0}}\right), \\ H_{\alpha}\left(d \mid C^{L_{3}}\right) \neq H_{\alpha}\left(d \mid C^{L_{0}}\right), \end{array}$

所以L₁也是S的一个α -熵最优尺度组合, 故C在L₁上的限制 $C^{L_{1}}$ ={ $c_{1}^{1}$ , $c_{2}^{2}$ }是S的一个α -熵最优尺度约简.

定义22 对于一个广义多尺度多重集值决策系统S=(U, C∪ {d}), 设α∈ (0, 1], L∈ L, 记

$\partial_{C^{L}}^{α}$ (x)={d(y) |y∈ ${[x]}_{C^{L}}^{α}$ }, x∈ U,

称 $\partial_{C^{L}}^{α}$ (x)为x关于C^L在S中的α -广义决策值.

定义23 对于一个广义多尺度多重集值决策系统S=(U, C∪ {d}), 设α∈ (0, 1],

L₀=(I₁, I₂, …, I_m)∈ L, L∈ L,

若对于∀ x∈ U, 有

$\partial_{C^{L}}$ (x)= $\partial_{C^{L_{0}}}$ (x),

则称S^L关于S是α -广义决策协调的.进一步, 若对于满足L≻K的∀ K∈ L, S^K关于S不是α -广义决策协调的, 即∃x∈ U使得

$\partial_{C^{K}}$ (x)≠ $\partial_{C^{L_{0}}}$ (x),

则称L为S的一个α -广义决策最优尺度组合, 称C在L上的限制C^L为S的一个α -广义决策最优尺度约简.

定理4 设S=(U, C∪ {d})是一个α -协调广义多尺度多重集值决策系统, 对于α∈ (0, 1],

L₀=(I₁, I₂, …, I_m)∈ L, L∈ L,

则S^L关于S是α -协调的当且仅当S^L关于S是α -广义决策协调的.

证明由于S是α -协调的, 由定义19知

$R_{C^{L_{0}}}^{α}$ ⊆R_d,

即对于∀ x∈ U, 有

${[x]}_{C^{L_{0}}}^{α}$ ⊆[x]_d,

于是, 对于∀ y∈ ${[x]}_{C^{L_{0}}}^{α}$ , 有

d(y)=d(x),

从而

$\partial_{C^{L_{0}}}$ (x)={d(x)}.

必要性.对于∀ x∈ U, 若S^L关于S是α -协调的, 则由定义20知

$R_{C^{L}}^{α}$ ⊆R_d,

即

${[x]}_{C^{L}}^{α}$ ⊆[x]_d,

所以对于∀ y∈ ${[x]}_{C^{L}}^{α}$ , 有

d(y)=d(x),

即

$\partial_{C^{L}}$ (x)={d(x)}= $\partial_{C^{L_{0}}}$ (x),

因此, S^L关于S是α -广义决策协调的.

充分性.对于∀ x∈ U, 若S^L关于S是α -广义决策协调的, 即

$\partial_{C^{L}}$ (x)= $\partial_{C^{L_{0}}}$ (x)={d(x)}.

由广义决策值的定义知

$\partial_{C^{L}}^{α}$ (x)={d(y) | y∈ ${[x]}_{C^{L}}^{α}$ }={d(x)},

所以

${[x]}_{C^{L}}^{α}$ ⊆[x]_d,

即

$R_{C^{L}}^{α}$ ⊆R_d.

因此, S^L关于S是α -协调的. 证毕

由定理4知, 若系统S是α -协调的, L∈ L, 则S^L关于S是α -广义决策协调的可退化为S^L关于S是α -协调的.

定理5 设S=(U, C∪ {d})是一个α -不协调广义多尺度多重集值决策系统, 对于α∈ (0, 1],

L₀=(I₁, I₂, …, I_m)∈ L, L∈ L,

若S^L关于S是α -熵协调的, 则S^L关于S是α -广义决策协调的.

证明因为S^L关于S是α -熵协调的, 所以有

H_α(d|C^L)=H_α(d| $C^{L_{0}}$ ).

对于∀ x∈ U, D∈ U/R_d, 由性质2的证明过程可知

$\begin{array}{l} -\frac{\left|[x]_{C^{L_{0}}}^{\alpha} \cap D\right|}{n} \log _{2}\left(\frac{\left|[x]_{C^{L_{0}}}^{\alpha} \cap D\right|}{\left|[x]_{C^{L_{0}}}^{\alpha}\right|}\right) \leqslant \\ \quad-\frac{\left|[x]_{C^{L}}^{\alpha} \cap D\right|}{n} \log _{2}\left(\frac{\left|[x]_{C^{L}}^{\alpha} \cap D\right|}{\left|[x]_{C^{L}}^{\alpha}\right|}\right), \end{array}$

再结合

H_α(d|C^L)=H_α(d| $C^{L_{0}}$ ),

可得

$\begin{array}{l} -\frac{\left|[x]_{C^{L_{0}}}^{\alpha} \cap D\right|}{n} \log _{2}\left(\frac{\left|[x]_{C^{L_{0}}}^{\alpha} \cap D\right|}{\left|[x]_{C^{L_{0}}}^{\alpha}\right|}\right)= \\ \quad-\frac{\left|[x]_{C^{L}}^{\alpha} \cap D\right|}{n} \log _{2}\left(\frac{\left|[x]_{C^{L}}^{\alpha} \cap D\right|}{\left|[x]_{C^{L}}^{\alpha}\right|}\right), \end{array}$

于是

${[x]}_{C^{L_{0}}}^{α}$ ∩ D= ${[x]}_{C^{L}}^{α}$ ∩ D,

从而

${[x]}_{C^{L_{0}}}^{α}$ = ${[x]}_{C^{L}}^{α}$ ,

故对于∀ x∈ U, 有

$\partial_{C^{L}}$ (x)= $\partial_{C^{L_{0}}}$ (x),

因此, S^L关于S是α -广义决策协调的. 证毕

定理5的逆命题一般不成立, 见例5.

例5 设S=(U, C∪ {d})为一个α -不协调广义多尺度多重集值决策系统, 其中条件属性部分与表1相同, 决策属性部分如下:

d(x₁)=d(x₃)=d(x₄)=d(x₇)=1,

d(x2₎=d(x8₎=2,

d(x5)₌d(x6)₌3.

给定尺度组合:

L₀=(2, 3, 2)∈ L, L₁=(1, 2, 0)∈ L,

L4₌(2, 2, 0)∈ L, L5₌(2, 1, 0)∈ L.

阈值α=0.2, 经计算, 有

U/R_d={{x₁, x₃, x₄, x₇}, {x₂, x₈}, {x₅, x₆}}=

{D1_,D2_,D3_},

$R_{C^{L_{0}}}^{0.2}$ ={(x1,_x1)_,(x1,_x2)_,(x1,_x3)_,(x2,_x1)_,

(x2, x₂),₍x3, x₁),₍x3, x₃),₍x3, x₈),

(x4,x4₎, (_x5, x5₎, (_x5, x7₎, (_x5, x8₎,

(x6, x6)_,(x₇, x5)_,(x₇, x7)_,(x₇, x8)_,

₍x8, x3),₍x8_,x5),₍x8_,x7),₍x8_,x8)}_,

$R_{C^{L_{1}}}^{0.2}$ ={(x₁, x₁), (x₁, x₂), (x₁, x₃), (x₁, x₈),

(x₂, x₁), (x₂, x₂), (x₂, x₃), (x₂, x₄),

(x₂, x₈), (x₃, x₁), (x₃, x₂), (x₃, x₃),

(x₃, x₇), (x₃, x₈), (x₄, x₂), (x₄, x₄),

(x₄, x₇), (x₅, x₅), (x₅, x₇), (x₅, x₈),

(x₆, x₆), (x₇, x₃), (x₇, x₄), (x₇, x₅),

(x₇, x₇), (x₇, x₈), (x₈, x₁), (x₈, x₂),

(x₈, x₃), (x₈, x₅), (x₈, x₇), (x₈, x₈)},

$R_{C^{L_{4}}}^{0.2}$ ={(x₁, x₁), (x₁, x₂), (x₁, x₃), (x₂, x₁),

(x₂, x₂), (x₂, x₃), (x₃, x₁), (x₃, x₂),

(x₃, x₃), (x₃, x₇), (x₃, x₈), (x₄, x₄),

(x₅, x₅), (x₅, x₇), (x₅, x₈), (x₆, x₆),

(x₇, x₃), (x₇, x₅), (x₇, x₇), (x₇, x₈),

(x₈, x₃), (x₈, x₅), (x₈, x₇), (x₈, x₈)},

$R_{C^{L_{5}}}^{0.2}$ ={(x₁, x₁), (x₁, x₂), (x₁, x₃), (x₂, x₁),

(x₂, x₂), (x₂, x₃), (x₃, x₁), (x₃, x₂),

(x₃, x₃), (x₃, x₇), (x₃, x₈), (x₄, x₄),

(x₄, x₈), (x₅, x₅), (x₅, x₇), (x₅, x₈),

(x₆, x₆), (x₇, x₃), (x₇, x₅), (x₇, x₇),

(x₇, x₈), (x₈, x₃), (x₈, x₄), (x₈, x₅),

(x₈, x₇), (x₈, x₈)}.

根据上述结果可得, 对于∀ x∈ U,

$\partial_{C^{L_{4}}}$ (x)= $\partial_{C^{L_{0}}}$ (x),

所以 $S^{L_{4}}$ 关于S是α -广义决策协调的, 但是由于

$\begin{array}{l} H_{0.2}\left(d \mid C^{L_{0}}\right)= \\ -\sum_{i=1}^{8} \sum_{j=1}^{3}\left(\frac{\left|\left[x_{i}\right]_{C^{L_{0}}}^{0.2} \cap D_{j}\right|}{n} \log _{2}\left(\frac{\left|\left[x_{i}\right]_{C^{L_{0}}}^{0.2} \cap D_{j}\right|}{\left|\left[x_{i}\right]_{C_{0}^{L_{0}}}^{0.2}\right|}\right)\right)= \\ \frac{3}{2} \log _{2} 3+\frac{1}{2} \log _{2} 2 \approx 0.3010, \\ H_{0.2}\left(d \mid C^{L_{4}}\right)= \\ -\sum_{i=1}^{8} \sum_{j=1}^{3}\left(\frac{\left|\left[x_{i}\right]_{C^{L_{4}}}^{0.2} \cap D_{j}\right|}{n} \log _{2}\left(\frac{\left|\left[x_{i}\right]_{C^{L_{4}}}^{0.2} \cap D_{j}\right|}{\left|\left[x_{i}\right]_{C^{L_{4}}}^{0.2}\right|}\right)\right)= \\ \frac{3}{4} \log _{2} 3+\frac{5}{8} \log _{2} 5 \approx 0.6990, \end{array}$

因此

H₀_.₂(d| $C^{L_{4}}$ )≠ H₀_.₂(d| $C^{L_{0}}$ ),

从而 $S^{L_{4}}$ 关于S不是α -熵协调的.又因为

$\partial_{C^{L_{0}}}$ (x₄)={1}≠ {1, 2}= $\partial_{C^{L_{1}}}$ (x₄)= $\partial_{C^{L_{5}}}$ (x₄),

所以L₄是S的一个α -广义决策最优尺度组合, 进而C在L⁴上的限制

$C^{L_{4}}$ ={ $c_{1}^{2}$ , $c_{2}^{2}$ }

是S的一个α -广义决策最优尺度约简.

称所有条件属性在全部尺度下导出的相似关系构成的集合为相似关系集, 记为P, 即

P={ $R_{c_{j}^{l}}^{α}$ |j=1, 2, …, m, l=1, 2, …, I_j}.

下面分别给出计算相似关系集和决策属性导出的等价关系、搜索一个α -熵最优尺度约简和搜索一个α -广义决策最优尺度约简的算法.

算法1 计算相似关系集和决策属性导出的等价

关系

输入一个广义多尺度多重集值决策系统

S=(U, C∪ {d}), α∈ (0, 1]

输出相似关系集P,

决策属性导出的等价关系R_d

初始化 P← Ø;

for c_j∈ C do

for l∈ {1, 2, …, I_j} do

计算 $c_{j}^{l}$ 导出的相似关系 $R_{c_{j}^{l}}^{α}$ ;

P← P∪ { $R_{c_{j}^{l}}^{α}$ };

end for

计算d导出的等价关系R_d;

return P, R_d

算法2 一个α -熵最优尺度约简的搜索算法

输入一个广义多尺度多重集值决策系统

S=(U, C∪ {d}), α∈ (0, 1],

L₀=(I₁, I₂, …, I_m)

输出一个α -熵最优尺度约简C^L

初始化L← (l₁, l₂, …, l_m);

(l₁, l₂, …, l_m)← L₀;

计算条件熵H_α(d|C^L);

记temp=H_α(d|C^L);

for i=1:m do

l_i← 0;

计算条件熵H_α(d|C^L);

while H_α(d|C^L)≠ temp and l_i≠ I_i do

l_i=l_i+1;

计算条件熵H_α(d|C^L);

end while

end for

计算C在L上的限制C^L;

return C^L

算法3 一个α -广义决策最优尺度约简的搜索

算法

输入一个广义多尺度多重集值决策系统

S=(U, C∪ {d}), α∈ (0, 1],

L₀=(I₁, I₂, …, I_m)

输出一个α -广义决策最优尺度约简C^L

初始化L← (l₁, l₂, …, l_m);

(l₁, l₂, …, l_m)← L₀;

计算广义决策 $\partial_{C^{L}}^{α}$ ={ $\partial_{C^{L}}^{α}$ (x₁), $\partial_{C^{L}}^{α}$ (x₂), …, $\partial_{C^{L}}^{α}$ (x_n)};

记Q= $\partial_{C^{L}}^{α}$ ;

for i=1:m do

l_i← 0;

计算广义决策 $\partial_{C^{L}}^{α}$ ;

while $\partial_{C^{L}}^{α}$ ≠ Q and l_i≠ I_i do

l_i=l_i+1;

计算广义决策 $\partial_{C^{L}}^{α}$ ;

end while

end for

计算C在L上的限制C^L;

return C^L

在算法1中, for语句用于计算相似关系集, 过程的时间复杂度为O( $\sum_{j}^{=}$ I_jn²), 其中, n为对象集的基数, m为条件属性个数, I_j为属性c_j的尺度个数.计算d导出的等价关系的时间复杂度为O(n²), 所以算法1总体时间复杂度为

O((1+ $\sum_{j}^{=}$ I_j)n²).

在算法2和算法3中, 最坏情况下所有属性都是不能删除的, 且属性c_j的最优尺度为I_j, 因此算法2和算法3的时间复杂度都为

O(m+ $\sum_{j}^{=}$ I_j).

4 实验及结果分析

本文实验采用的硬件配置为13th Gen Intel(R) Core(TM) i5-13500H@2.60 GHz和16 GB内存的PC, 操作系统为Windows 11, 软件为PyCharm Commu-nity Edition 2023.2.5.

实验内容主要分为2部分.第1部分讨论α -熵最优尺度约简、α -广义决策最优尺度约简与k近邻法(K Nearest Neighbor, KNN)结合后的分类性能.鉴于目前尚未涉及广义多尺度多重集值决策系统的研究, 因此在算法评估时, 仅对比本文的算法2与算法3.第2部分分析相似度阈值α和缺失率阈值β变化对算法性能的影响.

由于UCI数据库上现存的数据集都是单尺度数据且属性值不为多重集, 因此需要构造广义多尺度多重集值决策系统.结合文献[20]的构造广义多尺度决策系统的方法, 通过如下5步将数值型数据集S=(U, C∪ {d})构造为广义多尺度多重集值决策系统.

1)调整数据集缺失率.定义S的缺失率:

$L R=1-\sum_{j=1}^{|C|}\left(\frac{\left|U_{j}\right|}{|C||U|}\right),$

其中

U_j={x∈ U|c_j(x)≠ *},

为属性c_j下属性值完备的对象集合.令阈值β∈ (0, 1], 分3种情况讨论.

(1)若数据集是完备的, 则随机将对象的条件属性值赋值为缺省值*, 直至LR=β .

(2)若数据集是不完备的且LR< β, 则随机将对象的条件属性值赋值为缺省值*, 直至LR=β .

(3)若数据集是不完备的且LR≥ β, 则数据集保持不变.

2)连续型数据离散化.对于∀ x∈ U, c_j∈ C, 记σ _j和m_j分别为V_j中元素的标准差和最小值.针对x在c_j下的属性值, 做如下离散化:

c'_j(x)= $\{\begin{array}{l} [\frac{c_{j} (x) - m_{j}}{σ_{j}}], & c_{j} (x) \neq * \\ *, & c_{j} (x) = * \end{array}$

其中[k]表示不大于k的最大整数.生成离散化后的属性值域:

V_j={c'_j(x) | x∈ U}={*, k₁, k₂, …, k_t},

其中

k₁< k₂< …< k_t.

对于∀ x∈ U, 若

c'_j(x)∈ V_j, c'_j(x)≠ *,

记

c'_j(x)=k,

则

c_j(x)∈ [m_j+kσ _j, m_j+(k+1)σ _j).

3)构造多尺度属性值域.分两种情况讨论.

(1)若

|V_j-{*}|≤ 3,

则属性c_j有1个尺度, 即I_j=1.令2)中构造的属性值域V_j为属性c_j在第I_j个尺度下的属性值域, 即

$V_{j}^{I_{j}}$ =V_j.

(2)若

|V_j-{*}|> 3,

则属性c_j有|V_j-{*}|-2个尺度, 即

I_j=|V_j-{*}|-2.

令2)中构造的属性值域V_j为属性c_j在第I_j个尺度下的属性值域, 即

$V_{j}^{I_{j}}$ =V_j.

对于l∈ {1, 2, …, I_j-1}, 合并属性值 $k_{t + l - I_{j}}$ , $k_{t + l + 1 - I_{j}}$ , …, k_t为 $k_{t + l - I_{j}}^{\geq}$ , 则属性c_j在第l个尺度下的属性值域如下所示:

$V_{j}^{l}$ = $V_{j}^{I_{j}}$ ∪ { $k_{t + l - I_{j}}^{\geq}$ }-{ $k_{t + l - I_{j}}$ , $k_{t + l + 1 - I_{j}}$ , …, k_t}.

4)构造最强尺度组合下的多重集值决策系统.对于∀ c_j∈ C, x∈ U, 将x在c_j下的属性值构造为多重集.

(1)若

c'_j(x)=k_s,

则

$c_{j}^{I_{j}}$ (x)={ $\frac{0}{k_{1}}$ , $\frac{0}{k_{2}}$ , …, $\frac{0}{k_{s - 1}}$ , $\frac{1}{k_{s}}$ , $\frac{0}{k_{s + 1}}$ , …, $\frac{0}{k_{t}}$ },

其中s∈ {1, 2, …, t}.

(2)若

c'_j(x)=*,

则

$c_{j}^{I_{j}}$ (x)={ $\frac{| m_{j, 1} (x) |}{k_{1}}$ , $\frac{| m_{j, 2} (x) |}{k_{2}}$ , …, $\frac{| m_{j, t} (x) |}{k_{t}}$ },

其中

m_j_,_p(x)={y∈ U|d(y)=d(x), c'_j(y)=k_p},

p∈ {1, 2, …,t}.

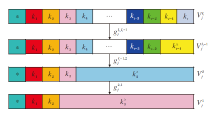
5)构造广义多尺度多重集值决策系统.对于∀ c_j∈ C, l∈ {2, 3, …, I_j}, 根据定义11及2)和3), 得到信息粒度变换:

$g_{j}^{l, l - 1}$ (v)= $\{\begin{array}{l} k_{1}, & v = k_{1} \\ k_{2}, & v = k_{2} \\ \dots, & \dots \\ k_{t + l - I_{j} - 2}, & v = k_{t + l - I_{j} - 2} \\ k_{t + l - I_{j} - 1}^{\geq}, & v \in {k_{t + l - I_{j} - 1}, k_{t + l - I_{j}}^{\geq}} \end{array}$

如图3所示, 属性c_j在第I_j个尺度下的值域

$V_{j}^{I_{j}}$ =V_j={*, k₁, k₂, …, k_t},

	Figure Option View Download New Window
	图3 多尺度属性值域的构造Fig.3 Construction of multi-scale attribute domains

信息粒度变换 $g_{j}^{I_{j}, I_{j} - 1}$ 将属性值k_t与k_t_-1合并为 $k_{t - 1}^{\geq}$ , $V_{j}^{I_{j}}$ 中其它属性值保持不变, 得到第I_j-1个尺度下的值域:

$V_{j}^{I_{j} - 1}$ ={*, k₁, k₂, …, $k_{t - 1}^{\geq}$ }.

以此类推, 直至信息粒度变换 $g_{j}^{2, 1}$ 将属性值k₃与 $k_{4}^{\geq}$ 合并为 $k_{3}^{\geq}$ , 而k₁和k₂保持不变, 最终得到第1个尺度下的值域:

$V_{j}^{1}$ ={*, k₁, k₂, $k_{3}^{\geq}$ }.

进一步, 对于∀ x∈ U, c_j∈ C和l∈ {2, 3, …, I_j}, 根据信息值域变换, 将x在c_j的第l-1个尺度下的属性值构造为多重集.至此, 完成广义多尺度多重集值决策系统的构造.

为了保证实验的可重复性和结果的一致性, 在上述1)中设置缺失值时, 设置随机种子为50.随机种子是一个用于启动随机数生成器的数值, 确保使用相同种子时生成相同的随机数序列, 这样能保证实验生成的缺省值的分布是一致的, 也保证可重复实验的结果一致性.

实验选取的10个数据集的具体信息如表2所示.通过1)~5), β=0.2, 将10个数据集分别转换为10个不同的广义多尺度多重集值决策系统, 每个广义多尺度多重集值决策系统在各属性下的尺度个数如表3所示.

表2 实验数据集 Table 2 Experimental datasets

表3 构造的广义多尺度多重集值决策系统的尺度个数 Table 3 Scale numbers in constructed generalized multi-scale multiset-valued decision systems

通过十折交叉验证法, 将原始数据拆为10份, 在每次计算中, 取其中9份作为训练集, 1份作为测试集, 在训练集上求得系统的最优尺度约简, 并在最优尺度约简下, 利用KNN分类器, 预测测试集上对象的决策属性值.对于KNN分类器, k=5, 且KNN中的距离公式为定义2中的海林格距离.对于构造的广义多尺度多重集值决策系统(U, C∪ {d}), 记L₀为决策系统的最强尺度组合, L_H为一个α -熵最优尺度组合, L_GD为一个α -广义决策最优尺度组合, 则 $C^{L_{0}}$ 为C在L₀下的限制, $C^{L_{H}}$ 为一个α -熵最优尺度约简, $C^{L_{GD}}$ 为一个α -广义决策最优尺度约简.

首先, 设置阈值α=0.9, β=0.2, 对比此时构造的广义多尺度多重集值决策系统在 $C^{L_{0}}$ 、 $C^{L_{H}}$ 和 $C^{L_{GD}}$ 下的分类精度, 具体如表4所示.

表4 条件属性集在不同尺度组合下的分类精度 Table 4 Classification accuracies of conditional attribute sets with different scale combinations %

由表4可得, 在α -熵最优尺度约简和α -广义决策最优尺度约简下的分类精度均高于或等于属性集C在最强尺度组合L₀下限制的分类精度.这说明通过搜索α -熵最优尺度约简和α -广义决策最优尺度约简可简化信息, 降低信息获取成本的同时保持模型的泛化能力.

进一步, 设置缺失率阈值β=0.2, 对比在不同相似度阈值α下α -熵最优尺度约简和α -广义决策最优尺度约简的分类精度, α∈ {0.1, 0.2, …, 0.9}, 结果如图4所示.由图可观察到, α取不同值时, 大多数数据集上两种最优尺度约简的分类精度是相同的.然而, 在少数情况下, 两种最优尺度约简下的分类精度是不同的.例如:在图4(a)中, 当α=0.3时, α -熵最优尺度约简的分类精度低于α -广义决策最优尺度约简; 在(b)中, 当α=0.2时, α -熵最优尺度约简的分类精度高于α -广义决策最优尺度约简.因此, 在实际应用中, 可根据实际需求选择α -熵最优尺度约简或α -广义决策最优尺度约简进行后续的规则提取.

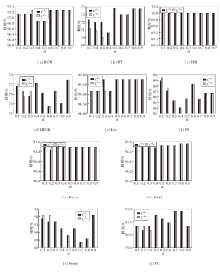	Figure Option View Download New Window
	图4 α不同时两种最优尺度约简的精度变化Fig.4 Classification accuracies of two kinds of optimal scale reducts with different values of α

最后, 当相似度阈值α和缺失率阈值β同时变化时, 观测α -熵最优尺度约简和α -广义决策最优尺度约简的分类精度的变化情况, α∈ {0.1, 0.2, …, 0.9}, β∈ {0.05, 0.10, 0.15, 0.20, 0.25}, 结果如图5和图6所示.由图可得, 在大部分数据集上, 当β增加时, 分类精度随之提升, 这一现象表明在不完备的多尺度决策系统中, 使用多重集表示缺失值, 能有效提高最优尺度约简下的分类精度.

	Figure Option View Download New Window
	图5 α、 β变化时一个α -熵最优尺度约简的精度图Fig.5 Accuracies of an α-entropy optimal scale reduct with varying α and β

	Figure Option View Download New Window
	图6 α、 β变化时一个α -广义决策最优尺度约简的精度图Fig.6 Accuracies of an α-generalized decision optimal scale reduct with varying α and β

上述结果证实多重集表示方法在处理缺失数据方面的优越性, 为系统在应对不完备信息时提供更佳的性能保障.然而, α 变动时, 最优尺度约简的分类精度无显著变化规律.

5 结束语

本文讨论广义多尺度多重集值决策系统的最优尺度约简问题.讨论数据集上条件属性值均为多重集, 基于海林格距离定义广义多尺度多重集值决策系统的相似关系.针对α -协调决策系统, 利用条件熵给出α -协调和α -熵协调的概念, 并进一步定义α -最优尺度组合、α -熵最优尺度组合、α -最优尺度约简和α -熵最优尺度约简等概念, 证明α -最优尺度约简和α -熵最优尺度约简之间的等价性.针对α -不协调广义多尺度多重集值决策系统, 引入广义决策函数, 提出α -广义决策协调和α -广义决策最优尺度约简的概念, 讨论α -熵协调与α -广义决策协调之间的关系.最后给出α -熵最优尺度约简搜索算法和α -广义决策最优尺度约简搜索算法, 并通过实验验证α -熵最优尺度约简和α -广义决策最优尺度约简的分类性能.本文只讨论基于条件熵和广义决策函数的广义多尺度多重集值决策系统的最优尺度约简问题, 在后续研究中, 可进一步关注其它类型最优尺度组合、决策知识获取以及相关不确定性分析等问题.

本文责任编委张燕平

Recommended by Associate Editor ZHANG Yanping

参考文献

文献选项

[1]	PEDRYCZ W. Granular Computing for Data Analytics: A Manifesto of Human-Centric Computing. IEEE/CAA Journal of Automatica Sinica, 2018, 5(6): 1025-1034. [本文引用:1]
[2]	LIN T Y. Granular Computing: Structures, Representations, and Applications // Proc of the 9th International Conference on Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing. Berlin, Germany: Springer, 2003: 16-24. [本文引用:1]
[3]	ZADEH L A. Toward a Theory of Fuzzy Information Granulation and Its Centrality in Human Reasoning and Fuzzy Logic. Fuzzy Sets and Systems, 1997, 90(2): 111-127. [本文引用:2]
[4]	PAWLAK Z. Rough Sets: Theoretical Aspects of Reasoning about Data. Boston, USA: Kluwer Academic Publishers, 1991. [本文引用:1]
[5]	WANG W J, ZHAN J M, ZHANG C, et al. A Regret-Theory-Based Three-Way Decision Method with a Priori Probability Tolerance Dominance Relation in Fuzzy Incomplete Information Systems. Information Fusion, 2023, 89: 382-396. [本文引用:1]
[6]	XU W H, PAN Y Z, CHEN X W, et al. A Novel Dynamic Fusion Approach Using Information Entropy for Interval-Valued Ordered Datasets. IEEE Transactions on Big Data, 2023, 9(3): 845-859. [本文引用:1]
[7]	ZHANG X Y, HOU J L. A Novel Rough Set Method Based on Adjustable-Perspective Dominance Relations in Intuitionistic Fuzzy Ordered Decision Tables. International Journal of Approximate Reasoning, 2023, 154: 218-241. [本文引用:1]
[8]	CHEN B W, ZHANG X Y, YANG J L. Feature Selections Based on Three Improved Condition Entropies and One New Similarity Degree in Interval-Valued Decision Systems. Engineering Applications of Artificial Intelligence, 2023, 126. DOI: DOI:10.1016/j.engappai.2023.107165. [本文引用:1]
[9]	LUO L H, YANG J L, ZHANG X Y, et al. Tri-level Attribute Reduction Based on Neighborhood Rough Sets. Applied Intelligence, 2024, 54: 3786-3807. [本文引用:1]
[10]	YE J, ZHAN J M, DING W P, et al. A Novel Three-Way Decision Approach in Decision Information Systems. Information Sciences, 2022, 584: 1-30. [本文引用:1]
[11]	WU W Z, LEUNG Y. Theory and Applications of Granular Labelled Partitions in Multi-scale Decision Tables. Information Sciences, 2011, 181(18): 3878-3897. [本文引用:1]
[12]	WU W Z, LEUNG Y. Optimal Scale Selection for Multi-scale Decision Tables. International Journal of Approximate Reasoning, 2013, 54(8): 1107-1129. [本文引用:1]
[13]	胡军, 陈艳, 张清华, 等. 广义多尺度集值决策系统最优尺度选择. 计算机研究与发展, 2022, 59(9): 2027-2038. (HU J, CHEN Y, ZHANG Q H, et al. Optimal Scale Selection for Generalized Multi-scale Set-Valued Decision Systems. Journal of Computer Research and Development, 2022, 59(9): 2027-2038. ) [本文引用:1]
[14]	LI R K, YANG J L, ZHANG X Y. Optimal Scale Selection Based on Three-Way Decisions with Decision-Theoretic Rough Sets in Multi-scale Set-Valued Decision Tables. International Journal of Machine Learning and Cybernetics, 2023, 14: 3719-3736. [本文引用:1]
[15]	WANG W J, HUANG B, WANG T X. Optimal Scale Selection Based on Multi-scale Single-Valued Neutrosophic Decision-Theoretic Rough Set with Cost-Sensitivity. International Journal of Approximate Reasoning, 2023, 155: 132-144. [本文引用:1]
[16]	XIAO Y B, ZHAN J M, ZHANG C, et al. A Preference Group Consensus Method with Three-Way Decisions and Regret Theory under Multi-scale Information Systems. Information Sciences, 2024, 660. DOI: DOI:10.1016/j.ins.2024.120126. [本文引用:1]
[17]	XIE Z H, WU W Z, WANG L X, et al. Entropy Based Optimal Scale Selection and Attribute Reduction in Multi-scale Interval-Set Decision Tables. International Journal of Machine Learning and Cybernetics, 2024, 15: 3005-3026. [本文引用:2]
[18]	ZHAN J M, DENG J, XU Z S, et al. A Three-Way Decision Methodology with Regret Theory via Triangular Fuzzy Numbers in Incomplete Multi-scale Decision Information Systems. IEEE Tran-sactions on Fuzzy Systems, 2023, 31(8): 2773-2787. [本文引用:1]
[19]	张庐婧, 林国平, 林艺东, 等. 多尺度邻域决策信息系统的特征子集选择. 模式识别与人工智能, 2023, 36(1): 49-59. (ZHANG L J, LIN G P, LIN Y D, et al. Feature Subset Selection for Multi-scale Neighborhood Decision Information System. Pattern Recognition and Artificial Intelligence, 2023, 36(1): 49-59. ) [本文引用:1]
[20]	LI F, HU B Q. A New Approach of Optimal Scale Selection to Multi-scale Decision Tables. Information Sciences, 2017, 381: 193-208. [本文引用:3]
[21]	CHENG Y L, ZHANG Q H, WANG G Y, et al. Optimal Scale Selection and Attribute Reduction in Multi-scale Decision Tables Based on Three-Way Decision. Information Sciences, 2020, 541: 36-59. [本文引用:4]
[22]	廖淑娇, 吴迪, 卢亚倩, 等. 多尺度决策系统中测试代价敏感的属性与尺度同步选择. 模式识别与人工智能, 2024, 37(4): 368-382. (LIAO S J, WU D, LU Y Q, et al. Test Cost Sensitive Simultaneous Selection of Attributes and Scales in Multi-scale Decision Sys-tems. Pattern Recognition and Artificial Intelligence, 2024, 37(4): 368-382. ) [本文引用:1]
[23]	朱康, 吴伟志, 刘梦欣. 协调广义多尺度序模糊决策系统的最优尺度组合与属性约简. 模式识别与人工智能, 2024, 37(6): 538-556. (ZHU K, WU W Z, LIU M X. Optimal Scale Combinations and Attribute Reduction for Consistent Generalized Multi-scale Ordered Fuzzy Decision Systems. Pattern Recognition and Artificial Intelligence, 2024, 37(6): 538-556. ) [本文引用:1]
[24]	WANG F, LI J H, YU C C. Optimal Scale Selection Approach for Classification Based on Generalized Multi-scale Formal Context. Applied Soft Computing, 2024, 152. DOI: DOI:10.1016/j.asoc.2024.111277. [本文引用:1]
[25]	ZHANG L J, LIN G P, WEI L, et al. Feature Subset Selection for Multi-scale Neighborhood Decision Information System via Mutual Information. Artificial Intelligence Review, 2024, 57. DOI: DOI:10.1007/s10462-023-10626-w. [本文引用:1]
[26]	ZHANG Q H, CHENG Y L, ZHAO F, et al. Optimal Scale Combination Selection Integrating Three-Way Decision with Hasse Diagram. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(8): 3675-3689. [本文引用:1]
[27]	ZHANG X Y, HUANG Y Y. Optimal Scale Selection and Know-ledge Discovery in Generalized Multi-scale Decision Tables. International Journal of Approximate Reasoning, 2023, 161. DOI: DOI:10.1016/j.ijar.2023.108983. [本文引用:1]
[28]	SHANNON C E. A Mathematical Theory of Communication. The Bell System Technical Journal, 1948, 27(3): 379-423. [本文引用:1]
[29]	苗夺谦, 王珏. 粗糙集理论中知识粗糙性与信息熵关系的讨论. 模式识别与人工智能, 1998, 11(1): 34-40. (MIAO D Q, WANG J. On the Relationships between Information Entropy and Roughness of Knowledge in Rough Set Theory. Pattern Recognition and Artificial Intelligence, 1998, 11(1): 34-40. ) [本文引用:2]
[30]	LIANG J Y, SHI Z Z. The Information Entropy, Rough Entropy and Knowledge Granulation in Rough Set Theory. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2004, 12(1): 37-46. [本文引用:1]
[31]	LIANG J Y, SHI Z Z, LI D Y, et al. Information Entropy, Rough Entropy and Knowledge Granulation in Incomplete Information Systems. International Journal of General Systems, 2006, 35(6): 641-654 . [本文引用:1]
[32]	DAI J H, DAI W T, XU Q. An Uncertainty Measure for Incomplete Decision Tables and Its Applications. IEEE Transactions on Cybernetics, 2013, 43(4): 1277-1289. [本文引用:4]
[33]	WU J M, LIU D Y, HUANG Z H, et al. Multi-scale Decision Systems with Test Cost and Applications to Three-Way Multi-attribute Decision-Making. Applied Intelligence, 2024, 54(4): 3591-3605. [本文引用:1]
[34]	WANG Z H, CHEN H M, YUAN Z, et al. Multiscale Fuzzy Entropy-Based Feature Selection. IEEE Transactions on Fuzzy Systems, 2023, 31(9): 3248-3262. [本文引用:1]
[35]	MIYAMOTO S. Multisets and Fuzzy Multisets // LIU Z Q, MIYAMOTO S, eds. Soft Computing and Human-Centered Machines. Berlin, Germany: Springer, 2000: 9-33. [本文引用:2]
[36]	王维琼, 谢琼, 许豪杰, 等. 两方有理数多重集的保密计算. 电子与信息学报, 2023, 45(5): 1722-1730. (WANG W Q, XIE Q, XU H J, et al. Secure Computation of Two-Party Multisets with Rational Numbers. Journal of Electronics and Information Technology, 2023, 45(5): 1722-1730. ) [本文引用:1]
[37]	赵前进, 平昕瑞, 苏树智, 等. 标签敏感的多重集正交相关特征融合方法. 电子与信息学报, 2022, 44(10): 3458-3464. (ZHAO Q J, PING X R, SU S Z, et al. Feature Fusion Method Based on Label-Sensitive Multi-set Orthogonal Correlation. Journal of Electronics and Information Technology, 2022, 44(10): 3458-3464. ) [本文引用:1]
[38]	DU D H, FENG Q J, CHEN W F, et al. Mix-Supervised Multiset Learning for Cancer Prognosis Analysis with High-Censoring Survi-val Data. Expert Systems with Applications, 2024, 239. DOI: DOI:10.1016/j.eswa.2023.122430. [本文引用:1]
[39]	ZHAO X R, HU B Q. Three-Way Decisions with Decision-Theore-tic Rough Sets in Multiset-Valued Information Tables. Information Sciences, 2020, 507: 684-699. [本文引用:2]
[40]	HUANG D, LIN H, LI Z W. Information Structures in a Multiset-Valued Information System with Application to Uncertainty Mea-surement. Journal of Intelligent and Fuzzy Systems, 2022, 43(6): 7447-7469. [本文引用:2]
[41]	SONG Y, LIN H, LI Z W. Outlier Detection in a Multiset-Valued Information System Based on Rough Set Theory and Granular Computing. Information Sciences, 2024, 657. DOI: DOI:10.1016/j.ins.2023.119950. [本文引用:1]
[42]	王蕾晰, 吴伟志, 谢祯晃. 基于熵的多尺度多重集值信息系统的最优尺度选择与属性约简. 模式识别与人工智能, 2023, 36(6): 495-510. (WANG L X, WU W Z, XIE Z H. Optimal Scale Selection and Attribute Reduction of Multi-scale Multiset-Valued Information Systems Based on Entropy. Pattern Recognition and Artificial Intelligence, 2023, 36(6): 495-510. ) [本文引用:4]

2018

0.0

... 粒计算(Granular Computing, GrC)^[1,2,3]是数据分析和信息处理的新型计算范式,以粒(Granule)为基本计算单位,从不同视角和层次观察、分析与解决问题,是研究复杂问题求解、海量数据挖掘和不确定性信息处理等问题的有效工具之一 ...

2003

0.0

1997

0.0

... 定义3^[3] 称二元组(U,C)为一个信息系统,其中U={x₁,x₂,…,x_n}为论域,C={c₁,c₂,…,c_m}为非空有限属性集,对于#cod#x02200 ...

1991

0.0

... 粗糙集是由Pawlak^[4]提出的分析不完全、不精确数据的一个重要数学工具 ...

2023

0.0

... 由于等价关系这一要求过于严格,一些学者针对不同类型的数据集,将等价关系推广为各种二元关系^[5,6,7],得到不同类型的信息粒,同时利用证据理论、熵及三支决策等方法进行知识约简,获得蕴含在数据集上的决策知识^[8,9,10] ...

2023

0.0

2023

0.0

2023

0.0

2024

0.0

2022

0.0

2011

0.0

... 为此,Wu等^[11]提出一个对象在同一个属性下依据不同尺度取不同值的多尺度粗糙集数据分析模型,简称Wu-Leung模型 ...

2013

0.0

... 因此,筛选最优尺度(保持目标约束不变的最粗尺度)^[12]并在最优尺度下进行属性约简是多尺度数据分析的一个关键问题,很多学者针对一些特定多尺度数据集的决策知识获取进行研究^{[13,14,15,16,17,18,19]} ...

2022

0.0

2023

0.0

2023

0.0

2024

0.0

2024

0.0

... Xie等^[17]基于条件熵给出多尺度区间集决策系统中最优尺度选择和属性约简的方法 ...

2023

0.0

2023

0.0

2017

0.0

... 由于Wu-Leung模型中每个属性都具有相同数量的尺度,Li等^[20]推广该模型,提出广义多尺度决策系统,并通过定义尺度组合的概念,给出广义多尺度决策系统的最优尺度组合选择和知识获取方法 ...

... 定义5^[20,21] 称二元组(U,C#cod#x0222a ...

... 结合文献[20]的构造广义多尺度决策系统的方法,通过如下5步将数值型数据集S=(U,C#cod#x0222a ...

2020

0.0

... 由于在数据集上先计算最优尺度组合再计算约简需分为两步进行,为了在搜索最优尺度组合的同时得到约简,Cheng等^[21]定义最优尺度约简的概念,给出广义多尺度决策系统的知识获取方法 ...

... 采用文献[21]定义的尺度组合思路,这样在选择最优尺度组合的同时就可得到属性约简(即最优尺度约简) ...

... 定义5^[20,21] 称二元组(U,C#cod#x0222a ...

... 定义6^[21] 设 ...

2024

0.0

... 廖淑娇等^[22]基于测试代价给出多尺度决策系统中属性约简与尺度选择同步搜索的算法,可节省搜索时间、提高计算效率 ...

2024

0.0

... 近年来,各类广义多尺度决策系统的最优尺度组合与属性约简的问题受到学者的关注,并取得一些重要研究进展^{[23,24,25,26,27]} ...

2024

0.0

... 近年来,各类广义多尺度决策系统的最优尺度组合与属性约简的问题受到学者的关注,并取得一些重要研究进展^{[23,24,25,26,27]} ...

2024

0.0

... 近年来,各类广义多尺度决策系统的最优尺度组合与属性约简的问题受到学者的关注,并取得一些重要研究进展^{[23,24,25,26,27]} ...

2022

0.0

... 近年来,各类广义多尺度决策系统的最优尺度组合与属性约简的问题受到学者的关注,并取得一些重要研究进展^{[23,24,25,26,27]} ...

2023

0.0

... 近年来,各类广义多尺度决策系统的最优尺度组合与属性约简的问题受到学者的关注,并取得一些重要研究进展^{[23,24,25,26,27]} ...

1948

0.0

... 后来Shannon^[28] 将熵引入信息论中,用于度量知识的不确定性 ...

1998

0.0

... 在粗糙集数据分析中,熵最早被用于刻画信息系统中知识的粗糙性^[29],随后被用于各种类型数据的属性约简,在知识获取方面取得较优效果^[30,31,32] ...

... 定义9^[29] 设(U,C)为一个信息系统,P⊆C,Q⊆C,若 ...

2004

0.0

... 在粗糙集数据分析中,熵最早被用于刻画信息系统中知识的粗糙性^[29],随后被用于各种类型数据的属性约简,在知识获取方面取得较优效果^[30,31,32] ...

2006

0.0

... 在粗糙集数据分析中,熵最早被用于刻画信息系统中知识的粗糙性^[29],随后被用于各种类型数据的属性约简,在知识获取方面取得较优效果^[30,31,32] ...

2013

0.0

... 在粗糙集数据分析中,熵最早被用于刻画信息系统中知识的粗糙性^[29],随后被用于各种类型数据的属性约简,在知识获取方面取得较优效果^[30,31,32] ...

... 定义9中所述的条件熵是建立在等价关系上的,并非适用于相似关系,为此,Dai等^[32]提出相似关系下的条件熵 ...

... 定义10^[32] 设(U,C#cod#x0222a ...

... 0时,函数-plog₂(pp+q)为单调递增^[32],另一方面,由性质1知 ...

2024

0.0

... 基于条件熵和测试成本,Wu等^[33]提出考虑成本的多尺度三支多属性决策模型 ...

2023

0.0

... Wang等^[34]基于多尺度模糊熵,考虑属性的冗余性、相关性和互补性,对多尺度决策系统进行特征选择 ...

2000

0.0

... 多重集^[35]是指元素可以重复出现的集合,并且元素的顺序对多重集不构成影响,是管理决策与数据分析的常用工具之一 ...

... 定义1^[35] 对于一个集合M,Z={z₁,z₂,…,z_o}为一个非空有限集合,若Z中的元素z_i(z_i#cod#x02208 ...

2023

0.0

... 多重集在网络安全^[36]、特征融合^[37]、模式识别^[38]等方面都有重要应用 ...

2022

0.0

... 多重集在网络安全^[36]、特征融合^[37]、模式识别^[38]等方面都有重要应用 ...

2024

0.0

... 多重集在网络安全^[36]、特征融合^[37]、模式识别^[38]等方面都有重要应用 ...

2020

0.0

... 在粗糙集数据分析方面,Zhao等^[39]结合三支决策与决策粗糙集模型,将损失函数推广到多重集,提出多重集决策理论粗糙集模型 ...

... 定义4^[39] 称二元组(U,C#cod#x0222a ...

2022

0.0

... Huang等^[40]应用不确定性度量方法分析多重集值信息系统的信息结构 ...

... 定义2^[40] 对于Z={z₁,z₂,…,z_o}上的两个多重集M₁#cod#x02208 ...

2024

0.0

... Song等^[41]构造多重集值信息系统中的相容关系,并研究多重集值信息系统的离群值检测问题 ...

2023

0.0

... 王蕾晰等^[42]提出多尺度多重集值信息系统的概念,并给出基于知识粗糙熵的最优尺度选择和属性约简的算法 ...

... 定义7^[42] 称二元组(U,C)为一个多尺度多重集值信息系统,其中U={x₁,x₂,…,x_n}为论域,C={c₁,c₂,…,c_m}为非空有限属性集,每个属性都有I个尺度且属性值都是多重集,一个多尺度多重集值信息系统可表示为 ...

... 定义8^[42] 设 ...

... 命题1^[42] 设 ...