引用本文
黄峰, 刘鸿伟, 沈英, 裘兆炳, 陈丽琼. 基于多尺度空间自适应注意力网络的轻量级图像超分辨率方法. 模式识别与人工智能, 2025,38(1): 36-50
HUANG Feng, LIU Hongwei, SHEN Ying, QIU Zhaobing, CHEN Liqiong. Lightweight Image Super-Resolution Reconstruction Method Based on Multi-scale Spatial Adaptive Attention Network. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2025,38(1): 36-50.  
Doi: 10.16451/j.cnki.issn1003-6059.202501003
Permissions
Copyright©2025, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于多尺度空间自适应注意力网络的轻量级图像超分辨率方法
黄峰1, 刘鸿伟1, 沈英1, 裘兆炳1, 陈丽琼1
1.福州大学 机械工程及自动化学院 福州 350108
通讯作者：

陈丽琼,博士,副教授,主要研究方向为深度学习、图像处理等.E-mail:liqiongchen@fzu.edu.cn.

作者简介:

黄 峰,博士,研究员,主要研究方向为光电成像等.E-mail:huangf@fzu.edu.cn.

刘鸿伟,硕士研究生,主要研究方向为深度学习、图像处理等.E-mail:lhw13600728242@163.com.

沈 英,博士,教授,主要研究方向为光机电一体化等.E-mail:yshen@fzu.edu.cn.

裘兆炳,博士,副教授,主要研究方向为深度学习、信号处理等.E-mail:qiuzhaobing@fzu.edu.cn.

修回日期: 2024-11-05 接受日期: 2025-01-25
资助项目: 国家自然科学基金青年基金项目(No.62405060)、福建省自然科学基金项目(No.2022J05113,2024J01245)、福建省中青年教师教育科研项目(No.JAT210035)资助
摘要

针对现有图像超分辨率重建方法存在模型复杂度过高和参数量过大等问题,文中提出基于多尺度空间自适应注意力网络(Multi-scale Spatial Adaptive Attention Network, MSAAN)的轻量级图像超分辨率重建方法.首先,设计全局特征调制模块(Global Feature Modulation Module, GFM),学习全局纹理特征.同时,设计轻量级的多尺度特征聚合模块(Multi-scale Feature Aggregation Module, MFA),自适应聚合局部至全局的高频空间特征.然后,融合GFM和MFA,提出多尺度空间自适应注意力模块(Multi-scale Spatial Adaptive Attention Module, MSAA).最后,通过特征交互门控前馈模块(Feature Interactive Gated Feed-Forward Module, FIGFF)增强局部信息提取能力,同时减少通道冗余.大量实验表明,MSAAN能捕捉更全面、更精细的特征,在保证轻量化的同时显著提升图像的重建效果.

关键词: 卷积神经网络; Transformer; 轻量级图像超分辨率重建; 多尺度空间自适应注意力
中图分类号:TP391
Lightweight Image Super-Resolution Reconstruction Method Based on Multi-scale Spatial Adaptive Attention Network
HUANG Feng1, LIU Hongwei1, SHEN Ying1, QIU Zhaobing1, CHEN Liqiong1
1. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350108
Corresponding author：
CHEN Liqiong, Ph.D., associate professor. Her research interests include deep learning and image processing.

About Author:
HUANG Feng, Ph.D., professor. His research interests include optoelectronic imaging.
LIU Hongwei, Master student. His resear-ch interests include deep learning and image processing.
SHEN Ying, Ph.D., professor. Her research interests include optical mechatronics.
QIU Zhaobing, Ph.D., associate profe-ssor. His research interests include deep lear-ning and signal processing.

Fund:Young Scientist Fund of National Natural Science Foundation of China(No.62405060), Natural Science Founda-tion of Fujian Province(No.2022J05113,2024J01245), the Edu-cational Research Program for Young and Middle-Aged Teachers of Fujian Province(No.JAT210035)
Abstract

To address the challenges of high model complexity and excessive parameter counts in existing image super-resolution(SR) reconstruction methods, a lightweight image SR reconstruction method based on multi-scale spatial adaptive attention network(MSAAN) is proposed. First, a global feature modulation module(GFM) is designed to learn global texture features. Additionally, a lightweight multi-scale feature aggregation module(MFA) is introduced to adaptively aggregate high-frequency spatial features from local to global scales. Second, the multi-scale spatial adaptive attention module(MSAA) is proposed by integrating GFM and MFA. Finally, a feature interactive gated feed-forward module(FIGFF) is incorporated to enhance the local feature extraction capability while reducing the channel redundancy. Extensive experiments demonstrate that MSAAN effectively captures more comprehensive and refined features, significantly improving reconstruction quality while maintaining a lightweight structure.

Key words: Convolution Neural Network; Transformer; Lightweight Image Super-Resolution Recons-truction; Multi-scale Spatial Adaptive Attention

图像超分辨率(Super-Resolution, SR)是计算机视觉领域中的重要任务之一, 旨在从低分辨率(Low-Resolution, LR)图像中恢复高分辨率(High-Resolution, HR)图像[1, 2], 被广泛应用于交通监控、医疗诊断和遥感成像等领域.目前, 由于硬件或传感器的限制, 许多图像在获取过程中受到分辨率的限制, 导致图像分辨率较低、细节信息不够清晰.因此, 如何利用SR技术提高图像的分辨率成为计算机视觉领域的研究热点之一.

随着深度学习的发展, 基于卷积神经网络(Convolutional Neural Networks, CNN)的SR模型取得较优的重建性能[1, 2, 3].然而, 堆叠大量卷积层或残差块的方式虽然提升图像重建的性能, 但也显著增加计算成本.因此, 近年来学者们提出轻量化的超分辨率重建方法.Ahn等[4]提出CARN(Cascading Residual Network), 结合组卷积和残差块级联结构, 有效捕捉复杂的图像细节, 实现轻量、高效的图像超分辨率重建.Hui等提出IDN(Information Distillation Net-work)[5]和IMDN(Information Multi-distillation Net-work)[6], 通过信息蒸馏块提取特征, 在压缩参数的同时提升性能.基于IMDN, Liu等[7]提出RFDN(Re-sidual Feature Distillation Network), 引入FDC(Feature Distillation Connections), 在减少网络复杂度的同时进一步提升网络性能.Li等[8]提出LAPAR(Linearly-Assembled Pixel-Adaptive Regression Network), 直接将LR图像到HR图像映射学习转化为基于多个预定义滤波器基字典的线性系数回归任务.Kong等[9]提出RLFN(Residual Local Feature Network), 简化RFDB(Residual Feature Distillation Block)中的特征聚合过程, 以较少的参数实现较快的推理速度和较优性能.Sun等[10]提出Shuffle-Mixer, 引入大卷积核的概念, 通过增加感受野以聚合空间信息, 同时减少参数量和浮点运算数(Floating Point Operations, FLOPs).上述基于CNN的轻量化超分辨率重建方法虽然取得不错的重建性能, 但由于缺少对图像远距离依赖关系的特征建模, 细节恢复能力有限.

ViT(Vision Transformer)在低级视觉任务中表现出优于CNN的性能, 其捕捉非局部特征交互的能力在实现高质量图像重建中起到关键作用[11, 12, 13].因此, 越来越多的学者将注意力转到基于Transformer的图像超分辨率重建方法.Lu等[14]提出ESRT(Efficient Super-Resolution Transformer), 在降低计算成本的同时保留图像中的高频信息.Gao等[15]提出LBNet(Lightweight Bimodal Network), 利用递归机制, 在不增加参数的情况下加深Transformer的深度, 捕捉长距离依赖关系, 从而促进细节和纹理的重建.Sun等[16]提出SAFMN(Spatially-Adaptive Feature Modulation Network), 设计SAFM(Spatially-Adaptive Feature Modulation), 动态选择具有代表性的特征, 以较低的计算成本实现类似ViT的效果.

由于图像内部存在自相似性, 重建图像某一区域时不仅需要有效提取该区域自身的特征, 而且在不同的图像区域也需要提取相似的特征分布, 这些相似的图像块可以相互作为参考, 从而利用参考区域恢复特定区域的纹理细节.因此, 通过捕获像素之间的短距离和长距离依赖关系, 可利用更多的像素信息实现图像的高质量重建[17, 18, 19].

上述ESRT、LBNet和SAFMN等方法在轻量化超分辨率图像重建领域取得显著进展, 但由于对高频信息的局部感知和长距离建模能力的有限, 重建性能不尽理想.因此, 如何在有限的计算资源下高效整合短距离和长距离的建模能力, 对于实现精确的重建至关重要.

为此, 本文提出基于多尺度空间自适应注意力网络(Multi-scale Spatial Adaptive Attention Network, MSAAN)的轻量级图像超分辨方法, 实现对短距离局部细节和长距离依赖关系的高效建模, 同时降低网络复杂度.MSAAN主要由多个堆叠的空间特征混合器(Spatial Feature Mixers, SFM)组成.本文针对传统多尺度特征聚合与注意力机制在高频细节捕获和远距离依赖建模上的局限性, 进一步设计具有自适应特性和高效建模能力的多尺度空间自适应注意力模块(Multi-scale Spatial Adaptive Attention Mo-dule, MSAA), 作为SFM的核心模块.MSAA由两部分组成:全局特征调制模块(Global Feature Modula-tion Module, GFM)和多尺度特征聚合模块(Multi-scale Feature Aggregation Module, MFA).在GFM中, 采用差异特征提取的方式, 学习图像的全局纹理特征, 为后续特征聚合提供良好的特征基础, 同时可降低计算成本.在MFA中, 将输入特征进行通道分割, 进一步降低计算复杂度, 利用不同大小的感受野自适应聚合局部至全局的高频空间特征, 通过深度卷积在不同尺度的分支上进行特征提取, 有效降低网络的参数量.最后, 设计局部增强模块(Local Enhancement Block, LEB)和特征交互门控前馈模块(Feature Interactive Gated Feed-Forward Module, FI- GFF).LEB通过强化局部几何细节捕获能力, 解决卷积操作对局部特征敏感性不足的问题, 而FIGFF通过通道分割与门控机制, 优化前馈网络的非线性建模能力, 同时减少通道的计算冗余.

1 基于多尺度空间自适应注意力网络的轻量级图像超分辨率方法
1.1 整体框架

本文提出基于多尺度空间自适应注意力网络的轻量级图像超分辨率方法, 整体结构如图1所示.

图1 MSAAN总体架构Fig.1 Overall architecture of MSAAN

MSAAN主要由三部分组成:浅层特征提取模块(Shallow Feature Extraction Module, SFEM)、深层特征提取模块(Deep Feature Extraction Module, DFE-M)和图像重建模块(Image Reconstruction Module, IRM).

1.1.1 浅层特征提取模块

输入LR图像ILR∈ R3× H× W, 其中H表示LR图像高度, W表示LR图像宽度.首先经过浅层特征提取模块(SFEM).SFEM由一个3× 3卷积组成, 将输入的LR图像转换到特征空间, 并提取浅层特征:

F0=HSFEM(ILR)∈ RC× H× W,

其中HSFEM(· )表示SFEM.

1.1.2 深层特征提取模块

在深层特征提取模块(DFEM)中, 多个堆叠的空间特征混合器(SFM)被用于从浅层特征F0中提取更精细的深层特征, 用于HR图像重建.最终提取的深层特征图如下所示:

Fn=HDFEM(F0),

其中HDFEM(· )表示DFEM.

逐组提取中间特征F1, F2, …, Fn:

Fi= HSFMi(Fi-1), i=1, 2, …, n,

其中, HSFMi(· )表示第i个SFM, n表示SFM的数量.

为了恢复HR目标图像, 在DFEM中引入全局残差连接, 用于学习高频细节.因此, 最终的深层特征输出:

FDF=Fn+F0.

1.1.3 图像重建模块

获得的深层特征FDF被送入图像重建模块(IRM), 以完成图像的超分辨率重建.IRM设计为一个轻量级的上采样层, 用于快速重建.上采样层由一个3× 3卷积和一个Pixel Shuffle操作[20]组成.过程可描述如下:

ISR=HUpsample(FDF)+bilinear(ILR),

其中, HUpsample(· )表示上采样模块, bilinear(· )表示双线性插值上采样模块操作.

将LR图像ILR经双线性插值后的结果与最终的SR结果相加, 可提升网络性能, 加速网络的收敛速度.

1.2 空间特征混合器

空间特征混合器(SFM)由局部增强模块(LEB)、多尺度空间自适应注意力模块(MSAA)和特征交互门控前馈模块(FIGFF)组成, 能混合全局空间特征和局部空间特征, 为SR任务提供丰富的空间特征.

对于输入特征X∈ RC× H× W, SFM的输出特征:

YSFM=HFIGFF(LN(Z2))+Z2,

其中,

Z2=HMSAA(LN(Z1))+Z1,

Z1=HLEB(X),

表示SFM计算过程中产生的中间特征, LN(· )表示层归一化(Layer Normalization, LN)[21], HLEB(· )表示LEB, HMSAA(· )表示MSAA, HFIGFF(· )表示FIGFF.

1.2.1 局部增强模块

为了使网络结构更简洁高效, 一些轻量级的图像超分辨率重建方法[16, 22, 23]在设计特征提取模块时, 从MetaFormer[24]结构中去除相对位置嵌入操作.然而, 在Swin Transformer[25]中, 相对位置嵌入操作主要用于解决自注意力机制中的排列不变性问题, 对网络的局部细节特征建模能力具有提升作用.

基于这一思想, 为了进一步增强MSAA的局部表达能力, 并且不让网络的计算变得复杂, 本文提出局部增强模块(LEB), 作为网络的相对位置嵌入, 有助于提升网络对局部细节特征建模的能力.LEB由带有残差连接的深度卷积组成, 输出特征为:

YLEB=HDWConv3× 3(X)+X,

其中HDWConv3× 3(· )表示3× 3深度卷积.

1.2.2 多尺度空间自适应注意力模块

为了增强输入图像的特征表示能力, 并使方法有效关注和利用不同尺度的信息, 设计多尺度空间自适应注意力模块(MSAA), 结构如图1所示.MSAA由两个级联的组件组成, 输出特征为:

YMSAA=HMFA(HGFM(X)),

其中, HGFM(· )表示全局特征调制模块(GFM), HMFA(· )表示多尺度特征聚合模块(MFA).

为了提高空间特征的多样性, 引入GFM, 调制连续空间特征.GFM主要由1× 1卷积、全局平均池化(Global Average Pooling, GAP)[26]和GeLU激活函数[27]组成.首先, GFM通过1× 1卷积提取局部特征, 并通过GAP捕捉全局远程依赖关系.再通过减法计算局部特征与全局特征的差异, 结合线性缩放操作, 对不重要的交互成分进行重加权, 调制并增强全局特征.

然后, 将原始特征与调制后的特征融合, 实现全局信息与局部信息的互补, 增强非局部映射的灵活性并增加特征多样性.

最后, 在模块末尾使用GeLU激活函数, 对融合后的特征进行非线性映射, 进一步提升网络学习复杂特征表示的能力.GFM的输出特征为:

M1=HGeLU(X1+γ☉(X1-GAP(X1))),

其中,

X1=HConv1× 1(X),

表示GFM提取的初始特征, HConv1× 1(· )表示1× 1卷积, γ∈ RC× 1表示初始值为0的缩放因子, GAP(· )表示全局平均池化操作, HGeLU(· )表示GeLU激活函数.

基于差异特征提取的思想[28], GFM通过动态排除非必要的特征交互, 使网络能更专注于平衡复杂交互并提取准确、多样的全局特征信息.

为了学习具备全尺度信息的注意力图, 提出多尺度特征聚合模块(MFA).采用金字塔池化[29]方式设计MFA, 在多尺度特征金字塔中, 高层特征图具有较低的分辨率、较大的感受野和较强的语义表示能力, 主要关注非局部信息, 但缺乏空间几何细节; 低层特征图具有较高的分辨率、较小的感受野和较强的几何细节表示能力, 更关注局部细节, 但语义表示能力较弱.通过聚合来自多尺度特征金字塔的高层特征和低层特征, 特征的语义信息和空间信息得到有效互补, 从而提升方法对重建细节和远距离依赖关系的建模能力.

首先, 为了降低方法的计算复杂度, 采用通道分割操作, 将GFM输出的M1特征划分为四组:

HSplit(M1)=[X0, X1, X2, X3],

其中HSplit(· )表示通道分割操作.

通过自适应最大池化操作, 方法能检测显著特征, 从而更好地学习局部信息与非局部信息之间的相互关系, 提升重构效果.因此, 采用不同下采样因子的自适应最大池化操作, 处理上述四组特征, 提取多尺度的显著特征.在每个不同层次的池化操作之后, 应用深度卷积从不同尺度层次中提取特征, 单独增强每层对应尺度的局部信息, 从而不会因直接聚合导致低层几何细节的丢失.这一步骤显式加强低层特征对局部细节的捕捉能力.

最后, 为了进行后续的特征聚合, 使用最近邻插值, 将特征图上采样至指定层次的原始分辨率, 得到待聚合特征:

ˆXi=H↑s(HDWConn3×3(H↓s2(Xi))),i=0,1,2,3,

其中, H↓s2i(· )表示通过自适应最大池化操作将输入特征下采样至尺寸为 s2i, HDWConv3× 3(· )表示3× 3深度卷积, H↑s(· )表示通过最近邻插值将特定层次的特征上采样至原始分辨率s, 实现快速处理.

然后, 拼接来自不同层次的特征(包含空间局部细节特征和全局结构特征), 有机结合包含局部细节的低层特征和全局语义信息的高层特征, 确保低层细节不会被高层特征稀释.这些特征通过1× 1卷积进行聚合, 从而在空间维度和通道维度上实现细节信息和语义信息的协同.具体聚合特征如下:

ˆX=HConv1 ×1(HConcat ([ˆX0,ˆX1,ˆX2,ˆX3])),

其中, HConcat(· )表示沿通道维度的拼接操作, HConv1× 1(· )表示1× 1卷积.

在获得聚合特征 ︿X之后, 通过GeLU非线性映射计算注意力图, 专注于多尺度特征的全局信息与局部信息.同时, 对原始输入特征应用1× 1卷积和GeLU激活函数, 计算注意力图, 保留原始细节的全局依赖性, 使方法在这条支路上学习对特征的远距离建模能力.再将这两幅注意力图相乘, 自适应调整各个通道的注意力权重, 强化重要特征的表达, 同时抑制无关特征的干扰.

最后, 使用1× 1卷积提取最终优化的特征表示:

Y=HConv1×1(HGeLU(ˆX)⊙HGeLU(HConv1×1(M1))),

其中, HConv1× 1表示1× 1卷积, HGeLU(· )表示GeLU激活函数, ☉表示元素级乘法.

这一过程融合图像特征的多尺度信息、局部细节及远距离依赖, 提升对图像重建的细节刻画能力.

1.2.3 特征交互门控前馈模块

为了设计一个轻量级的前馈网络, 采用带有空间移位操作的卷积(Shift-Conv)[30]和特征门控(Feature Gate, FG)机制设计特征交互门控前馈模块(FIGFF).

Shift-Conv通过无参数、无需额外计算量的“ 移位” 操作与逐点卷积结合, 能在较大感受野下有效提取局部细节特征, 计算复杂度与1× 1卷积相同.在Transformer[31]中使用MLP(Multilayer Perceptron)往往忽略对空间信息的建模, 并且通道中的冗余信息阻碍特征表达能力, 可通过FG机制克服上述限制.FG机制由深度卷积和逐元素乘法组成.

如图1所示, FIGFF设计为两个Shift-Conv层, 中间通过GeLU激活函数和FG机制连接.首先, 通过一层Shift-Conv和GeLU激活函数编码输入特征, 得到特征

Z=HGeLU(HShift-Conv(X))

之后, 输入FG机制中, 其中, HGeLU(· )表示GeLU激活函数, HShift-Conv(· )表示1× 1 Shift-Conv操作.在FG机制中, 输入特征沿通道维度划分为两组:

HSplit(Z)=[ˆZ1,ˆZ2],

其中, ︿Z1、 ︿Z2表示FIGFF的中间特征, HSplit(· )表示通道分割操作.每组分别通过乘法分支和卷积分支.在卷积分支中, 利用深度卷积进一步提取优化的特征, 同时保持计算效率.在乘法分支中, 将卷积得到的特征与初始特征相乘, 促进不同细粒度特征之间的信息交互, 得到特征

ˆZ=ˆZ1⊙HDWCCnv3×3(ˆZ2),

其中HDWConv3× 3(· )表示3× 3深度卷积.最后, 通过一个Shift-Conv层, 求得最终输出:

YFIGFF=HShift-Conv (ˆZ)

FIGFF通过特征交互确保局部特征中的重要信息在网络中得到显著关注, 提高网络的局部特征提取能力, 为网络补充重要信息, 并减少通道冗余.

2 实验及结果分析
2.1 实验设置

本文采用Flickr2K[3]、DIV2K[32]数据集作为训练数据集, 分别包含800幅和2 650幅训练图像.本文对参考的HR图像应用标准的双三次退化处理生成LR图像.在网络测试过程中, 采用Set5[33]、Set14[34]、B100[35]、Urban100[36]、Manga109[37]基准数据集.实验采用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)和结构相似性(Structural Similarity, SSIM)评估图像重建的质量, 还采用参数量和FLO- Ps评价方法性能.

所有重建的SR图像均从RGB色彩空间转换为YCbCr色彩空间, 在Y通道上计算PSNR和SSIM值.

为了全面评估MSAAN, 训练两种不同复杂度的网络版本:轻量级版本MSAAN-light(SFM数量设为12, 通道数设为40)和标准版本MSAAN(SFM数量设为24, 通道数设为60).在训练过程中, 通过随机水平翻转和旋转进行数据增强.对于MSAAN-light, 从LR图像中随机裁剪64个64× 64的图像块作为基本训练输入.对于MSAAN, 从LR图像中随机裁剪48个48× 48图像块作为基本训练输入.两种模型均采用Adam(Adaptive Moment Estimation)[38]优化器进行训练, 超参数设为 β1=0.9和β2=0.99.对于MSAAN-light, 初始学习率设为1× 10-3, 最小学习率设为1× 10-5.对于MSAAN, 初始学习率设为3× 10-4, 最小学习率设为1× 10-6.两种方法均使用余弦退火(Cosine Annealing)策略[39]进行学习率更新, 迭代次数设为5× 105, 每5 000次保存一次模型, 并基于PSNR和SSIM指标确定是否为当前最优方法.

与SAFMN[16]类似, 本文使用L1像素损失[40]与基于FFT(Fast Fourier Transform)频率损失[10]的组合优化模型参数, 权重参数经验性设为 λ1=1.0,λ2=0.05.

所有实验均在PyTorch框架下, 通过NVIDIA GeForce RTX 3090 GPU进行.

2.2 消融实验

为了更好地理解和评估MSAAN中各模块的性能, 在Set5、Urban100数据集上进行消融实验.为了进行公平对比, 所有实验均基于MSAAN-light, 放大倍数为4, 在相同的设置下进行训练.

首先分析SFM数量对MSAAN-light性能影响.定义SFM数量为8, 10, 12, 14, 16, 相应指标值如表1所示, 表中黑体数字表示最优值.由表可见, 随着SFM数量的小幅增加, MSAAN-light性能变化表现出非线性趋势, 从12层开始, MSAAN的性能仅有微小变化, 这是由于在轻量化网络设计中, 网络层数存在局部平衡点, 在网络深度接近时, 减少层数会导致训练得到的方法能力不足, 增加网络层数时若仅小幅增加, 会导致特征冗余, 阻碍方法学习, 因此性能遇到瓶颈.

表1 SFM数量对MSAAN-light性能的影响 Table 1 Effect of the number of SFM on MSAAN-light performance

在SAFMN[16]和MSAAN-light中分析LEB对方法性能的影响, 具体指标值如表2所示, 表中黑体数字表示最优值.

表2 LEB对方法性能的影响 Table 2 Effect of LEB on method performance

由表2可见, 引入LEB之后, MSAAN-light在Set5、Urban100数据集上的PSNR值分别提升0.04 dB和0.06 dB, 而对SAFMN添加LEB之后, PSNR值同样也得到0.06 dB和0.04 dB的提升, 由此验证LEB在增强网络局部鲁棒建模能力上的有效性.由于LEB的作用类似于ViT中的位置编码, 这有助于MSAA更好地学习局部细节特征的映射关系[11, 25], 增强对局部几何细节的建模能力.此外, LEB设计为残差深度卷积, 仅增加约0.5 K的参数量.

为了验证MSAA的有效性, 分别移除GFM、MFA、整个MSAA, 观察MSAAN-light的性能变化, 具体指标值如表3可知, 表中黑体数字表示最优值.由表可见, 同时使用GFM和MFA构成MSAA时, MS-AAN-light性能最佳.实验结果表明, 引入MSAA之后, GFM通过全局特征调制和增强, 可有效提升纹理结构的连续性并增加空间特征的多样性[28], 为MFA提供更好的特征基础, 而MFA能提取丰富的尺度感知特征, 并聚合不同尺度上的信息, 实现多尺度特征的精细化和融合[41].二者组合可提高重建结果的细节保留能力和视觉质量.

表3 MSAA对MSAAN-light性能的影响 Table 3 Effect of MSAA on MSAAN-light performance

为了直观展示MSAA的工作机制, 图2包含移除MSAA、包含MSAA(移除GFM)、包含MSAA(移除MFA)以及MSAAN-light的输出特征图.由图可见, 无论是移除整个MSAA, 还是其内部组件GFM或MFA, 随着网络的加深, 学习信息都会出现显著丢失, 由此表明MSAA在学习高频信息和低频信息中的重要性.此外, 移除整个MSAA后, 捕捉的高频信息和低频信息非常有限.根据其组成部分的消融实验结果, GFM的输出特征主要集中于重建连续的纹理结构, 而MFA通过多尺度机制捕捉长距离信息, 重点关注并融合局部细粒度细节.因此, GFM获取的全局纹理结构信息引导MFA中多尺度机制的学习, 并调制MFA提取的局部信息, 最终实现MFA学习特征的聚合.两者之间的协同作用使MSAA能获得更精细的特征表示.这些结论表明, MSAA更关注高频细节, 重建更清晰的结构, 从而促进图像的超分辨率重建.

图2 MSAA移除前后特征图可视化Fig.2 Visualization of feature maps before and after MSAA removal

在Transformer[31]中使用MLP[11]作为前馈网络, 增强方法的非线性建模能力和局部特征表示能力.实验对比是否使用MLP和FIGFF对MSAAN-light性能的影响, 如表4所示, 表中黑体数字表示最优值.由表可见, 使用FIGFF时模型性能最佳, 可显著提升方法的局部特征提取能力.

表4 FIGFF对MSAAN-light性能的影响 Table 4 Effect of FIGFF on MSAAN-light performance

为了验证特征门控(FG)机制在FIGFF中的作用, 移除该部分, 结果如表5所示, 表中黑体数字表示最优值.

表5 FG机制对MSAAN-light性能的影响 Table 5 Effect of FG mechanism on MSAAN-light performance

由表5可观察到, 删除FG机制后, MSAAN-light的参数量和FLOPs均有所增加, 且性能有所下降.这一现象归因于FG机制的设计, 它不仅减少通道冗余, 使FIGFF更加轻量化, 促进不同位置特征的交互和融合, 还能有效控制信息流动并选择性地提取关键特征, 增强特征表达能力和表示的丰富性[42].

2.3 对比实验

2.3.1 定量对比

为了评估MSAAN和MSAAN-light的重建性能, 选择如下轻量化超分辨率方法进行对比.

与MSAAN-light对比的方法如下:Bicubic、RF-DN[7]、LAPAR-B[8]、ShuffleMixer[10]、LBNet-T[15]、SAFMN[16]、PAN(Pixel Attention Network)[26].

与MSAAN对比的方法如下:ESRT[14]、LB-Net[15]、LatticeNet[43]、HPUN(Hybrid Pixel-Unshuffled Network)[44]、DiVANet(Directional Variance Attention Network)[45]、FMEN(Fast and Memory-Efficient Network)[46]、NGswin(N-Gram Swin Transformer)[47].

在Set5、Set14、B100、Urban100、Manga109数据集上, 定义放大倍数为2, 3, 4, 各方法的指标值如表6~表11所示, 表中黑体数字表示最优值, 斜体数字表示次优值.

表6 放大倍数为2时MSAAN-light与对比方法的指标值 Table 6 Metric values of MSAAN-light and contrastive methods at a magnification factor of 2
表7 放大倍数为3时MSAAN-light与对比方法的指标值 Table 7 Metric values of MSAAN-light and contrastive methods at a magnification factor of 3
表8 放大倍数为4时MSAAN-light与对比方法的指标值 Table 8 Metric values of MSAAN-light and contrastive methods at a magnification factor of 4
表9 放大倍数为2时MSAAN与对比方法的指标值 Table 9 Metric values of MSAAN and contrastive methods at a magnification factor of 2
表10 放大倍数为3时MSAAN与对比方法的指标值 Table 10 Metric values of MSAAN and contrastive methods at a magnification factor of 3
表11 放大倍数为4时MSAAN与对比方法的指标值 Table 11 Metric values of MSAAN and contrastive methods at a magnification factor of 4

得益于轻量化且高效的结构, MSAAN-light和MSAAN在参数量较少时, 在多个基准数据集和三种放大倍数下取得较优的性能表现, 并在部分数据集上达到最优值.

以Manga109数据集为例, 由表7可看出:相比RFDN, MSAAN-light的PSNR值提升0.13 dB; 相比PAN, MSAAN-light的PSNR值提升0.19 dB; 相比ShuffleMixer, MSAAN-light的PSNR值提升0.11 dB.同时, MSAAN-light的参数量分别减少68%、33%和58%.同样地, 从表10可看出:相比ESRT, MSAAN的PSNR值提升0.28 dB; 相比DiVANet, MSAAN的PSNR值提升0.29 dB; 相比NGswin, MSAAN的PSNR值提升0.34 dB.同时, MSAAN的参数量分别减少8%、26%、30%.

各方法在Manga109数据集上放大倍数为2时的FLOPs、PSNR、参数量对比如图3所示, 图中黑点大小表示参数量.

图3 放大倍数为2时各方法在Manga109数据集上指标值对比Fig.3 Comparison of metric values for different methods at a magnification factor of 2 on Manga109 dataset

由图3可看出, MSAAN在重建性能和模型复杂度之间取得良好平衡.

上述结果表明, MSAAN通过轻量化结构设计减少计算冗余, 并引入MSAA, 提供全面的语义信息和像素理解能力, 提升网络在超分辨率任务中捕捉有用信息(如全局上下文信息和局部细节信息)的能力.

为了进一步验证MSAAN的有效性, 选择如下对比方法:SAFMN[16]、FM-Net(Fluid Micelle Net-work)[48]、HTI-Net(Heat-Transfer-Inspired Network)[49]、CCN(Curvature Consistent Network)[50].放大倍数为2, 3, 4时, 在Set5、Set14、B100、Urban100数据集上各方法与MSAAN-light的指标值如表12~表14所示, 表中黑体数字表示最优值, 斜体数字表示次优值.

表12 放大倍数为2时各方法的指标值对比 Table 12 Metric value comparison of different methods at a magnification factor of 2
表13 放大倍数为3时各方法的指标值对比 Table 13 Metric value comparison of different methods at a magnification factor of 3
表14 放大倍数为4时各方法的指标值对比 Table 14 Metric value comparison of different methods at a magnification factor of 4

由表12~表14可见, MSAAN-light均实现最佳性能.MSAAN-light加强局部细节捕获和全局建模能力, 可提高网络对综合像素语义信息的理解, 增强图像重建的有效性.

2.3.2 定性对比

为了直观反映MSAAN的重建效果, 将MSAAN-light与Bicubic、RFDN[7]、LAPAR-B[8]、LBNet-T[15]、SAFMN[16]、PAN[26]进行可视化对比, 结果如图4所示.

图4 放大倍数为4时MSAAN-light与对比方法的可视化结果Fig.4 Visualization results of MSAAN-light and contrastive methods at a magnification factor of 4

由图4可见, 对于Img_024图像的条纹, 大多数方法生成的纹理细节和边缘信息模糊、不准确, 而MSAAN-light能重建更精确且纹理分布一致的线条.在具有重复图案和边缘信息的Img_004图像中, MSAAN-light的优势更明显.

MSAAN与Bicubic、ESRT[14]、LBNet[15]、HP-UN[44]、DiVANet[45]、NGswin[47]的可视化对比结果如图5所示.

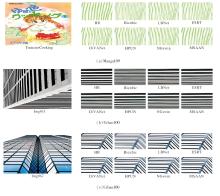图5 放大倍数为4时MSAAN与对比方法的可视化结果Fig.5 Visualization results of MSAAN and contrastive methods at a magnification factor of 4

由图5可看出, 对于图像YumeiroCooking和Img_011, 相比其它方法, MSAAN能更准确地重建垂直条纹和平行线.

综上所述, MSAAN-light和MSAAN在大多数场景中都实现最佳的视觉效果, 特别是在包含丰富结构信息和文字的图像中, 重建图像的效果明显更优.由此证实MSAA结合局部和非局部建模能力, 可增强网络对纹理结构和局部高频细节的关注, 重建高质量图像.

2.4 局部归因图

为了深入分析MSAAN如何聚焦于图像的特定部分以提升重建细节, 对不同的方法进行局部归因图(Local Attribution Map, LAM)[17]的可视化对比.LAM突出对SR结果具有最大影响的像素, 如果LAM涉及更多的像素范围, 可认为SR方法利用来自更多像素的信息用于重建.此外, 采用扩散指数(Diffusion Index, DI)[17]作为量化指标, 衡量局部归因图涉及像素的范围, 具体公式如下:

DI=(1-G)×100,

其中 G为Gini系数.如果只有少数像素对结果有贡献, Gini系数相对较高.如果LAM结果相对均匀, 表示SR方法注意到很多地方, Gini系数相对较低.

MSAAN-light、RFDN[7]、SAFMN[16]、PAN[26]的LAM和DI结果如图6所示, 图中红色表示方法利用的像素.由图可知, 相比其它方法, MSAAN-light在重建图像的红框所示区域时利用的像素信息更多, DI值更高, 这表明MSAA能利用GFM和MFA捕捉更多的上下文信息, 用于重建低分辨率输入图像.

图6 MSAAN-light和对比方法的局部归因图Fig.6 LAM of MSAAN-light and contrastive methods

3 结束语

针对现有超分辨率方法在图像重建性能和模型参数量之间的矛盾, 本文提出基于多尺度空间自适应注意力网络(MSAAN)的轻量级图像超分辨率方法.以多尺度空间自适应注意力模块(MSAA)作为核心模块, 对提取的全局信息进行调制, 自适应聚合多尺度局部特征, 获得精细的特征表示.MSAA主要由全局特征调制模块(GFM)和多尺度特征聚合模块(MFA)组成.GFM采用差异特征提取方式, 引导方法建立连续的全局纹理结构, 为后续特征聚合提供良好的特征基础.MFA利用不同大小的感受野, 自适应聚合局部至全局的高频空间特征.设计局部增强模块(LEB), 提升方法对局部复杂纹理和几何细节的捕获能力.设计特征交互门控前馈模块(FIGFF), 增强前馈网络的非线性建模能力, 同时减少通道计算冗余.大量实验表明, MSAAN在图像重建性能和模型复杂度之间实现良好平衡.今后可考虑通过模拟真实场景的退化模式, 在更多样化的数据集上进行训练, 进一步提升方法的泛化性等性能.

本文责任编委 徐 勇

Recommended by Associate Editor XU Yong

参考文献
[1] DONG C, LOY C C, HE K M, et al. Image Super-Resolution Using Deep Convolutional Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2), 295-307. [本文引用:2]
[2] KIM J, LEE J K, LEE K M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 1646-1654. [本文引用:2]
[3] LIM B, SON S, KIM H, et al. Enhanced Deep Residual Networks for Single Image Super-Resolution // Proc of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Washington, USA: IEEE, 2017: 1132-1140. [本文引用:2]
[4] AHN N, KANG B, SOHN K A. Fast, Accurate, and Lightweight Super-Resolution with Cascading Residual Network // Proc of the European Conference on Computer Vision. Berlin, Germany: Sprin-ger, 2018: 256-272. [本文引用:1]
[5] HUI Z, WANG X M, GAO X B. Fast and Accurate Single Image Super-Resolution via Information Distillation Network // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 723-731. [本文引用:1]
[6] HUI Z, GAO X B, YANG Y C, et al. Lightweight Image Super-Resolution with Information Multi-distillation Network // Proc of the 27th ACM International Conference on Multimedia. New York, USA: ACM, 2019: 2024-2032. [本文引用:1]
[7] LIU J, TANG J, WU G S. Residual Feature Distillation Network for Lightweight Image Super-Resolution // Proc of the European Confe-rence on Computer Vision. Berlin, Germany: Springer, 2021: 41-55. [本文引用:4]
[8] LI W B, ZHOU K, QI L, et al. LAPAR: Linearly-Assembled Pixel-Adaptive Regression Network for Single Image Super-Resolution and Beyond // Proc of the 34th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2020: 20343-20355. [本文引用:3]
[9] KONG F Y, LI M X, LIU S W, et al. Residual Local Feature Network for Efficient Super-Resolution // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Washington, USA: IEEE, 2022: 765-775. [本文引用:1]
[10] SUN L, PAN J S, TANG J H. ShuffleMixer: An Efficient ConvNet for Image Super-Resolution // Proc of the 36th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2022: 17314-17326. [本文引用:3]
[11] DOSOVITSKIY A, BEYER L, KOLESNIKOV A, et al. An Image Is Worth 16×16 Words: Transformers for Image Recognition at Scale[C/OL]. [2024-10-25]. https://arxiv.org/pdf/2010.11929. [本文引用:3]
[12] CHEN H T, WANG Y H, GUO T Y, et al. Pre-trained Image Processing Transformer // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 12294-12305. [本文引用:1]
[13] LIANG J Y, CAO J Z, SUN G L, et al. SwinIR: Image Restoration Using Swin Transformer // Proc of the IEEE/CVF International Conference on Computer Vision Workshops. Washington, USA: IEEE, 2021: 1833-1844. [本文引用:1]
[14] LU Z S, LIU H, LI J C, et al. Efficient Transformer for Single Image Super-Resolution[C/OL]. [2024-10-25]. https://arxiv.org/pdf/2108.11084v1. [本文引用:3]
[15] GAO G W, WANG Z X, LI J C, et al. Lightweight Bimodal Network for Single-Image Super-Resolution via Symmetric CNN and Recursive Transformer // Proc of the 31st International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2022: 913-919. [本文引用:5]
[16] SUN L, DONG J X, TANG J H, et al. Spatially-Adaptive Feature Modulation for Efficient Image Super-Resolution[C/OL]. [2024-10-25]. https://arxiv.org/pdf/2302.13800. [本文引用:8]
[17] GU J J, DONG C. Interpreting Super-Resolution Networks with Local Attribution Maps // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 9195-9204. [本文引用:3]
[18] LU T, WANG J M, JIANG J J, et al. Global-Local Fusion Net-work for Face Super-Resolution. Neurocomputing, 2020, 387: 309-320. [本文引用:1]
[19] WANG L, SHEN J, TANG E, et al. Multi-scale Attention Network for Image Super-Resolution. Journal of Visual Communication and Image Representation, 2021, 80. DOI: DOI:10.1016/j.jvcir.2021.103300. [本文引用:1]
[20] SHI W Z, CABALLERO J, HUSZÁR F, et al. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2016: 1874-1883. [本文引用:1]
[21] BA J L, KIROS J R, HINTON G E. Layer Normalization[C/OL]. [2024-10-25]. https://arxiv.org/pdf/1607.06450. [本文引用:1]
[22] WANG Y, LI Y S, WANG G, et al. Multi-scale Attention Network for Single Image Super-Resolution[C/OL]. [2024-10-25]. https://arxiv.org/pdf/2209.14145. [本文引用:1]
[23] FAN Q H, HUANG H B, CHEN M R, et al. RMT: Retentive Networks Meet Vision Transformers // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2024: 5641-5651. [本文引用:1]
[24] YU W H, LUO M, ZHOU P, et al. MetaFormer Is Actually What You Need for Vision // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 10809-10819. [本文引用:1]
[25] LIU Z, LIN Y T, CAO Y, et al. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2021: 9992-10002. [本文引用:2]
[26] ZHAO H Y, KONG X T, HE J W, et al. Efficient Image Super-Resolution Using Pixel Attention // Proc of the European Confe-rence on Computer Vision. Berlin, Germany: Springer, 2020: 56-72. [本文引用:4]
[27] HENDRYCKS D, GIMPEL K. Gaussian Error Linear Units(GELUs)[C/OL]. [2024-10-25]. https://arxiv.org/pdf/1606.08415. [本文引用:1]
[28] LI S Y, WANG Z D, LIU Z C, et al. Efficient Multi-order Gated Aggregation Network[C/OL]. [2024-10-25]. https://arxiv.org/pdf/2211.03295. [本文引用:2]
[29] ZHAO H S, SHI J P, QI X J, et al. Pyramid Scene Parsing Network // Proc of the IEEE Conference on Computer Vision and Pa-ttern Recognition. Washington, USA: IEEE, 2017: 2881-2890. [本文引用:1]
[30] WU B C, WAN A, YUE X Y, et al. Shift: A Zero FLOP, Zero Parameter Alternative to Spatial Convolutions // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 9127-9135. [本文引用:1]
[31] VASWANI A, SHAZEER N, PARMAR N, et al. Attention Is All You Need // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 6000-6010. [本文引用:2]
[32] TIMOFTE R, AGUSTSSON E, VAN GOOL L, et al. NTIRE 2017 Challenge on Single Image Super-Resolution: Methods and Results // Proc of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Washington, USA: IEEE, 2017: 1110-1121. [本文引用:1]
[33] BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-Com-plexity Single-Image Super-Resolution Based on Nonnegative Neigh-bor Embedding[C/OL]. [2024-10-25]. https://bmva-archive.org.uk/bmvc/2012/BMVC/paper135/abstract135.pdf. [本文引用:1]
[34] ZEYDE R, ELAD M, PROTTER M. On Single Image Scale-Up Using Sparse-Representations // Proc of the 7th International Con-ference on Curves and Surfaces. Berlin, Germany: Springer, 2012: 711-730. [本文引用:1]
[35] ARBELÁEZ P, MAIRE M, FOWLKES C, et al. Contour Detection and Hierarchical Image Segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898-916. [本文引用:1]
[36] HUANG J B, SINGH A, AHUJA N. Single Image Super-Resolution from Transformed Self-Exemplars // Proc of the IEEE Confe-rence on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2015: 5197-5206. [本文引用:1]
[37] MATSUI Y, ITO K, ARAMAKI Y, et al. Sketch-Based Manga Retrieval Using Manga10Dataset. Multimedia Tools and Applications, 2016, 76: 21811-21838. [本文引用:1]
[38] KINGMA D P, BA J L. Adam: A Method for Stochastic Optimization[C/OL]. [2024-10-25]. https://arxiv.org/pdf/1412.6980. [本文引用:1]
[39] LOSHCHILOV I, HUTTER F. SGDR: Stochastic Gradient Descent with Warm Restarts[C/OL]. [2024-10-25]. https://arxiv.org/pdf/1608.03983. [本文引用:1]
[40] ZHANG Y L, LI K P, LI K, et al. Image Super-Resolution Using Very Deep Residual Channel Attention Networks // Proc of the European Conference on Computer Vision. Berlin, Germany: Sprin-ger, 2018: 294-310. [本文引用:1]
[41] LAI W S, HUANG J B, AHUJA N, et al. Fast and Accurate Image Super-Resolution with Deep Laplacian Pyramid Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(11): 2599-2613. [本文引用:1]
[42] CHEN Z, ZHANG Y L, GU J J, et al. Dual Aggregation Transformer for Image Super-Resolution // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2023: 12278-12287. [本文引用:1]
[43] LUO X T, XIE Y, ZHANG Y L, et al. LatticeNet: Towards Lightweight Image Super-Resolution with Lattice Block // Proc of the European Conference on Computer Vision. Berlin, Germany: Springer, 2020: 272-289. [本文引用:1]
[44] SUN B, ZHANG Y L, JIANG S Y, et al. Hybrid Pixel-Unshuffled Network for Lightweight Image Super-Resolution. Proceedings of the AAAI Conference on Artificial Intelligence, 2023, 37(2): 2375-2383. [本文引用:2]
[45] BEHJATI P, RODRIGUEZ P, FERNÁNDEZ C, et al. Single Image Super-Resolution Based on Directional Variance Attention Network. Pattern Recognition, 2023, 133. DOI: DOI:10.1016/j.patcog.2022.108997. [本文引用:2]
[46] DU Z C, LIU D, LIU J, et al. Fast and Memory-Efficient Network towards Efficient Image Super-Resolution // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Washington, USA: IEEE, 2022: 852-861. [本文引用:1]
[47] CHOI H, LEE J, YANG J. N-gram in Swin Transformers for Efficient Lightweight Image Super-Resolution // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2023: 2071-2081. [本文引用:2]
[48] ZHANG M J, WU Q Q, ZHANG J, et al. Fluid Micelle Network for Image Super-Resolution Reconstruction. IEEE Transactions on Cybernetics, 2023, 53(1): 578-591. [本文引用:1]
[49] ZHANG M J, WU Q Q, GUO J, et al. Heat Transfer-Inspired Network for Image Super-Resolution Reconstruction. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(2): 1810-1820. [本文引用:1]
[50] ZHANG M J, XIN J W, ZHANG J, et al. Curvature Consistent Network for Microscope Chip Image Super-Resolution. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(12): 10538-10551. [本文引用:1]