引用本文
白盛兴, 张玉红, 周鹏, 吴信东. 基于无负采样和权重去相关对比网络的图无关聚类. 模式识别与人工智能, 2025,38(10): 861-875
BAI Shengxing, ZHANG Yuhong, ZHOU Peng, WU Xindong. Negative-Free and Weight-Decorrelated Contrastive Network for Graph-Agnostic Clustering. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2025,38(10): 861-875.  
Doi: 10.16451/j.cnki.issn1003-6059.202510001
Permissions
Copyright©2025, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于无负采样和权重去相关对比网络的图无关聚类
白盛兴1,2, 张玉红1,2, 周鹏3, 吴信东1,2
1.合肥工业大学 大数据知识工程教育部重点实验室 合肥 230009
2.合肥工业大学 计算机与信息学院 合肥 230009
3.安徽大学 计算机科学与技术学院 合肥 230601
通讯作者：

吴信东,博士,教授,主要研究方向为数据挖掘、大数据分析、基于知识的系统.E-mail：xwu@hfut.edu.cn.

作者简介:

白盛兴,博士研究生,主要研究方向为数据挖掘.E-mail：sxbai@mail.hfut.edu.cn.

张玉红,博士,副教授,主要研究方向为数据挖掘、机器学习.E-mail：zhangyh@hfut.edu.cn.

周 鹏,博士,副教授,主要研究方向为数据挖掘、机器学习.E-mail：doodzhou@ahu.edu.cn.

收稿日期: 2025-10-13 接受日期: 2025-10-31
资助项目: 国家自然科学基金项目（No.62120106008）、安徽省科技攻关项目（No.202423k09020015）、大数据知识工程教育部重点实验室开放课题项目（No.BigKEOpen2025-05）资助
摘要

现有的对比深度图聚类方法严重依赖输入图的同配性假设,在异配图中容易引发负采样假阴性与特征冗余的问题,导致聚类性能下降.为此,文中提出基于无负采样与权重去相关对比网络的图无关聚类方法（Negative-Free and Weight-Decorrelated Contrastive Network for Graph-Agnostic Clustering, NFWD）.首先,利用节点属性相似性构建特征图作为补充视图,通过拉普拉斯平滑滤波与共享参数的多层感知机（Multilayer Perceptron, MLP）分别获得特征图和原始图的节点表示,缓解同配性假设的原始图依赖.然后,针对异配图类冲突导致的负采样假阴性问题,基于自适应融合的节点表示获取聚类信息,构建簇中心节点表示,设计有效解决此问题的节点级与簇级双重特征对比的无负采样策略.最后,对MLP的权重矩阵施加正交约束,主动抑制冗余特征产生.在6个基准图数据集上的实验表明NFWD在图无关场景中的高效性与鲁棒性.

关键词: 图无关聚类; 节点相似性; 权重去相关; 对比学习
中图分类号:TP 391
Negative-Free and Weight-Decorrelated Contrastive Network for Graph-Agnostic Clustering
BAI Shengxing1,2, ZHANG Yuhong1,2, ZHOU Peng3, WU Xindong1,2
1. Key Laboratory of Knowledge Engineering with Big Data of Ministry of Education, Hefei University of Technology, Hefei 230009
2. School of Computer Science and Information Engineering, He-fei University of Technology, Hefei 230009
3. School of Computer Science and Technology, Anhui University, Hefei 230601
Corresponding author：
WU Xindong, Ph.D., professor. His research interests include data mining, big data analysis, and knowledge-based systems.

About Author:
BAI Shengxing, Ph.D.candidate. His research interests include data mining.
ZHOU Peng, Ph.D., associate professor. His research interests include data mining and machine learning.
ZHANG Yuhong, Ph.D., associate professor. Her research interests include data mi-ning and machine learning.

Fund:National Natural Science Foundation of China（No.62120106008）, Anhui Provincial Science and Technology Fortification Plan（No.202423k09020015）, Open Project of the Key Laboratory of Knowledge Engineering with Big Data of the Ministry of Education（No.BigKEOpen2025-05）
Abstract

Existing contrastive deep graph clustering methods heavily rely on the homophily assumption of the input graph, and thereby result in false negatives in negative sampling and feature redundancy in heterophilous graphs. These problems degrade clustering performance. To solve these problems, a graph-agnostic clustering framework, negative-free and weight-decorrelated contrastive network（NFWD）, is proposed. First, a feature graph is constructed as a supplementary view by node attribute similarity. Node representations from the feature graph and the original graph are obtained via Laplacian smoothing filters and a shared-parameter multilayer perceptron, respectively. Consequently, the reliance of the original graph on the homophily assumption is significantly reduced. Second, to tackle the false negative problem caused by class conflicts in heterophilous graphs, cluster information is derived from adaptively fused node representations for the construction of cluster-central node representations. Then, a negative-free strategy combining node-level and cluster-level feature contrast is proposed to effectively mitigate this problem. Finally, an orthogonal constraint is applied to the weight matrix of MLP to actively suppress redundant features. Experiments on six benchmark graph datasets demonstrate the effectiveness and robustness of NFWD in graph-agnostic scenarios.

Key words: Key Words Graph-Agnostic Clustering; Node Similarity; Weight Decorrelation; Contrastive Learning

图作为一种复杂的数据结构, 能有效建模现实世界中对象间的关联关系.图由节点集合、边集合及节点属性构成[1], 被广泛应用于计算机视觉[2]、自然语言处理[3]和复杂网络分析[4]等领域.图聚类作为网络分析的核心任务, 旨在以无监督方式将节点划分为具有紧密连接和相似属性的簇结构, 从而揭示系统的潜在功能特性[5, 6].近年来, 随着图神经网络的发展, 深度图聚类方法通过融合拓扑结构与节点属性信息, 在推荐系统[7]、目标检测[8]和社区网络分析[9]等场景中展现出显著优势.

深度图聚类方法根据学习机制可大致分为三类：生成方法、对抗方法、对比方法.生成方法通过重构图结构信息以构建监督信号, 利用图自动编码器[10]或变分图自动编码器[11]学习节点表示后, 结合传统聚类算法得到聚类结果.对抗方法采用生成对抗网络[12], 通过生成器与判别器的博弈优化特征空间.对比方法构造正负样本对, 在潜在空间中最大化类内相似性与类间差异性, 通过自监督对比损失可有效避免人工预训练干扰, 在特征判别性和聚类一致性方面展现出显著优势, 现已成为当前深度图聚类的主流范式.

现有对比深度图聚类方法通常基于原始图实施数据增强, 并采用各种负采样策略构建正负样本对, 旨在通过增强节点表示的判别能力, 提升方法的聚类性能.Hassani等[13]提出Contrastive Multi-view Re-presentation Learning on Graphs, 通过图扩散生成增强视图, 随机采样节点作为负样本, 进行跨视图对比学习.Yang等[14]提出CCGC（Cluster-Guided Contras-tive Deep Graph Clustering Network）, 使用非参数共享的孪生编码器生成跨视图节点表示, 并基于高置信度聚类伪标签, 将不同视图的同类样本作为正样本, 不同视图不同类的样本中心作为负样本, 然而此类方法忽略特征冗余问题, 会间接削弱节点表示的判别能力.为了缓解特征冗余问题, 已有方法使用特征去相关以提升特征独立性.Gong等[15]提出AGC-DRR（Attributed Graph Clustering with Dual Redun- dancy Reduction）, 强制跨视图节点表示的相关矩阵逼近单位矩阵, 增强特征独立性并抑制潜在空间中的冗余特征.

上述研究工作在不同应用场景下均取得不错效果, 但仍存在三重局限.1）现有方法依赖输入图的同配性假设, 生成的视图难以捕获节点间真实的相似性关系, 尤其在图拓扑与节点属性不一致的异配图场景（如社交网络中兴趣相似但无连接的节点）中, 难以避免节点相似性误判.2）样本级对比严重依赖负采样以防止表示坍缩, 而在异配图中因跨类边密集, 类冲突进一步加剧负采样错误, 导致假阴性问题, 显著制约方法的可扩展性与鲁棒性, 难以避免高计算开销.3）现有方法采用后处理方式直接约束已学习的节点表示, 未能直接处理特征冗余的根源问题, 即编码器的权重矩阵相关性过高导致特征冗余问题, 因此难以保证处理特征冗余问题的有效性.

针对上述问题, 本文提出基于无负采样与权重去相关对比网络的图无关聚类方法（Negative-Free and Weight-Decorrelated Contrastive Network for Graph-Agnostic Clustering, NFWD）, 采用三阶段优化框架实现节点表示与聚类分配的协同优化.首先, 设计节点相似性保持的编码模块, 通过k近邻（k-Nearest Neighbor, KNN）构建属性驱动的特征图, 作为与原始拓扑图无关的补充视图, 通过拉普拉斯平滑滤波与共享参数的多层感知机（Multilayer Perceptron, MLP）分别获得特征图和原始图的节点表示, 缓解同配性假设的原始图依赖, 提升跨图泛化能力.然后, 针对异配图类冲突导致负采样假阴性问题, 基于自适应融合的节点表示获取聚类伪标签, 构建簇中心节点表示, 设计节点级与簇级特征对比学习机制.采用实例特征不变性约束跨视图特征一致性, 并利用簇中心特征对齐策略实现簇分布语义对齐, 以节点级与簇级双重特征对比完全替代负采样过程.最后, 引入权重去相关模块, 对MLP权重矩阵进行正交化约束, 最大化权重向量间的正交性, 主动抑制冗余特征产生.

1 相关工作
1.1 对比深度图聚类

深度图聚类旨在基于节点属性与拓扑结构信息, 以无监督方式将图数据节点划分为语义一致的簇群.根据学习机制的不同, 现有方法可分为三类：生成方法[16, 17]、对抗方法[10]、对比方法[18].生成方法通常通过图自编码器重构节点属性或邻接矩阵, 并联合优化重构损失与聚类损失学习簇导向的节点表示.对抗方法通过生成对抗网络构建样本生成-判别机制, 提升节点表示的鲁棒性.然而, 这两类方法依赖聚类中心初始化质量, 容易导致性能不稳定[19].相比之下, 对比方法通过数据增强构建正负样本对, 利用对比损失最大化同类样本相似性, 在避免人工预训练过程的同时实现更一致的聚类性能.

在主流对比深度图聚类方法中, Hassani等[13]采用图扩散矩阵构建增强视图, IDCRN（Improved Dual Correlation Reduction Network）[20]和SCAGC（Self- Consistent Contrastive Attributed Graph Clustering）[21]通过随机边扰动或属性掩码生成对比视图.尽管这些人工增强策略被验证有效, 但其性能高度依赖先验设计的增强类型和参数, 特别是当增强操作（如随机边丢弃）破坏图语义结构时, 会导致节点表示的语义漂移.针对此问题, Liu等[22]提出SCGC（Sim- ple Contrastive Graph Clustering）, 采用参数非共享的孪生编码器生成差异化视图, 避免显式数据增强带来的干扰.然而, 方法依赖输入图的同配性假设, 仅利用原始图结构信息, 未能充分挖掘节点属性特征中隐含的拓扑关系, 难以规避异配图跨类边的类冲突干扰, 限制方法在异配图上的泛化性.

为了在对比学习过程中获取节点特征空间的相似性, 近期的图对比学习方法尝试通过构建KNN特征图（基于节点特征相似性）作为原始图的补充视图, 以增强对比学习的语义表达能力.Chen等[23]提出ASP, 将原始图、属性图和全局结构视图进行对比, 以增强节点表示的判别性.Zheng等[24]提出CLAGC, 通过生成保留簇结构的KNN特征图进行对比, 捕获特征空间的节点相似性.但是, 上述方法仍采用随机负采样策略, 可能将同簇的节点误判为负样本, 产生假阴性问题, 导致判别性不足.

Graph Debiased Contrastive Learning[25]和CCGC[14]利用不同类别的高置信度样本中心作为负样本, 提高负样本的可靠性, 保证样本对的语义一致性, 但其数据增强方法未考虑特征空间的节点相似性, 且以同类的高置信度节点作为正样本, 依然难以避免误选正样本问题.同时此类方法依旧依赖输入图同配性假设, 制约方法的可扩展性与鲁棒性, 难以避免负采样过程的高计算开销问题.

1.2 图表示学习中的特征冗余

在图表示学习中, 特征冗余是图表示学习领域的重大挑战之一.特征冗余指学到的节点或图表示中存在大量高度相关的特征维度, 导致信息重复且判别性降低.这种现象与视觉领域中的特征冗余问题类似, 如图像表示中不同通道特征可能因强相关性而无法有效区分语义信息.在图表示学习中, 特征冗余不仅会降低方法的泛化能力, 还可能引发表示崩溃, 即所有样本的表示在隐空间中被压缩到同一低维流形, 丧失区分性.

现有方法主要通过直接约束特征矩阵的统计特性以缓解冗余问题, 可分为如下两类.1）特征维度去相关.通过优化目标强制不同特征维度间的独立性.AGC-DRR[15]和Barlow Twins[26]通过最小化跨视图特征相关矩阵的非对角线元素, 使特征维度间近似正交.Zhang等[27]提出CCA-SSG（Canonical Co-rrelation Analysis Inspired Self-Supervised Learning on Graphs）, 结合规范相关分析与特征去相关损失, 在增强视图间语义一致性的同时减少特征维度冗余.2）信息瓶颈约束.通过互信息最大化或对比学习隐式减少冗余信息.Mo等[28]提出GCIL（Graph Contras- tive Invariant Learning）, 从因果视角出发, 利用光谱图增强和独立性目标分离因果特征与非因果特征.Fang等[29]提出SPGRL（Structure-Preserving Graph Re- presentation Learning）, 交换重构损失, 最大化原始图与特征嵌入的互信息, 间接约束特征空间的紧凑性.然而, 此类方法直接作用于特征矩阵, 可能忽略编码器本身的结构缺陷, 未考虑编码器权重相关性对特征冗余的影响[30].

2 基于无负采样和权重去相关对比网络的图无关聚类方法

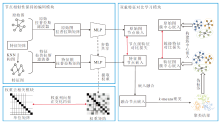
本文提出基于无负采样和权重去相关对比网络的图无关聚类方法（NFWD）, 整体架构如图1所示.NFWD主要包括3个模块.1）节点相似性保持的编码模块.在没有精心设计数据增强的情况下, 同时从拓扑与节点特征两个方面对比增强节点嵌入.2）双重特征对比学习模块.对两个视角的节点嵌入与聚类指导获得的簇中心嵌入分别构建节点级与簇级特征对比损失函数.3）权重去相关模块.增强编码器的表示能力, 减轻特征冗余问题.

图1 NFWD整体框架图Fig.1 Overall architecture of NFWD

2.1 符号定义

给定一个属性图g={V, ε}, 其中,

V={v1, v2, …, vN}

表示节点集, N表示节点数量.这些节点一般由特征矩阵X∈ RN× f描述, f表示节点的原始特征维度.同时, 这些节点属于C个类别, ε表示边集.g表示拓扑结构, 一般通过节点间的邻接矩阵A∈ RN× N表示, 如果第i个节点和第j个节点之间有连接边, 即（vi, vj）∈ ε, aij=1, 否则, aij=0.

属性图g的度矩阵为：

D=diag（d1, d2, …, dN）∈ RN× N,

其中

$d_{i}=\sum_{\left(v_{i}, v_{j}\right) \in \varepsilon} a_{i j} .$

拉普拉斯矩阵

L=D-A.

对图中每个节点加入自环, 得到带自环的邻接矩阵

A︿=A+I,

其中I∈ RN× N表示单位矩阵.然后, 对 A︿进行对称归一化, 得到正则拉普拉斯矩阵：

L˜=I- D︿-12A︿D︿-12.

2.2 节点相似性保持的编码模块

为了更好地表示特征空间中节点间相似关系结构, 并作为原始图结构的补充信息, 受文献[23]的启发, 通过KNN构造图gKNN={V, εKNN}.使用简单的欧氏距离计算节点相似度矩阵S, 元素sij即为第i个节点的特征向量xi与第j个节点的特征向量xj之间的相似性：

sij=||xi-xj||2.

对每个节点, 选择前k个最近邻, 得到特征图的边集εKNN和特征图的邻接矩阵AKNN∈ RN× N, 即该N× N矩阵中每行存在k个值为1的列元素, 表示N个节点中每个节点都与最近的k个节点存在边, 由此构建特征图的度矩阵：

DKNN=diag（d1KNN, d2KNN, …, dNKNN）∈ RN× N,

其中

$d_{i}^{\mathrm{KNN}}=\sum_{\left(v_{i}, v_{j}\right) \in \varepsilon \text { KNN }} a_{i j}^{\mathrm{KNN}} .$

该图的拉普拉斯矩阵

LKNN=DKNN-AKNN.

针对每个节点加入自环, 得到邻接矩阵：

A︿KNN=AKNN+I.

对 A︿KNN进行对称归一化, 得到该图的拉普拉斯矩阵：

L˜KNN=I-(D︿KNN) -12A︿KNN(D︿KNN) -12.

采用广泛使用的拉普拉斯滤波器分别在两个视角的图上进行邻居信息聚合, 得到平滑的节点特征矩阵：

$ \begin{array}{l} \widetilde{\boldsymbol{X}}^{v_{1}}=(\boldsymbol{I}-\widetilde{\boldsymbol{L}})^{t} \boldsymbol{X}, \\ \widetilde{\boldsymbol{X}}^{v_{2}}=\left(\boldsymbol{I}-\widetilde{\boldsymbol{L}}^{\mathrm{KNN}}\right)^{t} \boldsymbol{X}, \end{array}$ （1）

其中, L˜、 L˜KNN分别表示原始图和特征图的对称归一化图拉普拉斯矩阵, t表示拉普拉斯滤波器的层数.使用参数共享的MLP编码器对 X˜v1和 X˜v2分别进行编码, 第一视图和第二视图下的节点嵌入表示为：

H v1=MLP(X˜v1), H v2=MLP(X˜v2). （2）

使用l2范数得到归一化的嵌入表示：

H v1= Hv1Hv1||2, H v2= Hv2Hv2||2.

在本阶段中, 利用原始图与基于特征相似度构建的特征图, 形成两个相互补充的视图, 从而在对比学习过程中较好地保持节点相似度, 保证异配图场景中的有效性.

2.3 双重特征对比学习模块

本节设计双重特征对比学习模块, 挖掘聚类信息, 构建节点级特征对比损失和簇级特征对比损失, 充分学习两个级别的特征不变性信息.

首先, 融合两个视图下的节点嵌入表示：

H=λ H v1+（1-λ）H v2, （3）

其中λ表示两个视图的平衡超参数.对融合的节点嵌入表示H执行k-means聚类并得到节点的簇信息.根据相应的伪标签, 将H v1和H v2分组为C个不相交的簇, 即 Epv1（p=1, 2, …, C）和 Eqv2（q=1, 2, …, C）.基于此, 分别计算两个视图的簇中心：

$ \begin{array}{l} \boldsymbol{C}^{v_{1}}=\left\{\boldsymbol{C}_{1}^{v_{1}}, \boldsymbol{C}_{2}^{v_{1}}, \cdots, \boldsymbol{C}_{C}^{v_{1}}\right\}, \\ \boldsymbol{C}^{v_{2}}=\left\{\boldsymbol{C}_{1}^{v_{2}}, \boldsymbol{C}_{2}^{v_{2}}, \cdots, \boldsymbol{C}_{C}^{v_{2}}\right\}, \end{array}$ （4）

其中

C pv1=mean（Epv1）, p=1, 2, …, C,

C qv2=mean（Eqv2）, q=1, 2, …, C,

mean（· ）表示平均函数.

然后, 分析节点特征不变性, 构建节点级特征对比损失：

Lnode=||H v1-H v2|| F2. （5）

同样, 基于构建的簇中心嵌入, 分析簇级特征不变性, 构建簇级特征对比损失：

Lcluster=||C v1-C v2|| F2. （6）

同时学习节点级与簇级特征不变性, 不仅可提升样本的区分性, 还可确保显式的簇结构.

2.4 权重去相关模块

传统图编码器容易因权重耦合导致所学特征维度间相关性增强, 进而产生冗余特征, 降低聚类判别性.受特征解耦理论启发[31, 32], 通过约束编码器权重矩阵的列向量正交性, 强制不同权重特征通道间相互独立, 从而提升方法表示能力.

令W∈ RD× f表示编码器的权重矩阵, 权重去相关损失如下：

Lweight= 1D||WWT-I|| F2, （7）

其中, ||· || F2表示Frobenius范数, D表示编码器的输出维度.该正则项通过最小化权重矩阵协方差矩阵与单位矩阵的差异, 促使不同特征通道的权重向量趋于正交, 从而抑制特征维度间的冗余信息.

2.5 总体目标函数

NFWD的总体目标函数包括3个部分, 即节点级特征对比损失Lnode、簇级特征对比损失Lcluster、权重去相关损失Lweight, 具体公式如下：

L=Lnode+λ1Lcluster+λ2Lweight, （8）

其中λ1、λ2分别表示平衡Lcluster和Lweight的超参数.

2.6 算法步骤

NFWD的详细学习过程如算法1所示.

算法1 NFWD

输入g={V, ε}, 属性图, 迭代次数T,

超参数k, t, λ, λ1, λ2

输出 聚类结果R

通过KNN获取特征图gKNN={V, εKNN};

通过式（1）获得平滑特征 X˜v1和 X˜v2;

FOR i=1 to T

通过式（2）对 X˜v1和 X˜v2进行编码;

通过式（3）融合H v1和H v2, 得到H;

对H执行k-means, 获得聚类结果;

通过式（4）获得簇中心嵌入C v1和C v2;

通过式（5）计算节点级特征对比损失Lnode;

通过式（6）计算簇级特征对比损失Lcluster;

通过式（7）计算权重去相关损失Lweight;

通过最小化式（8）更新整个网络;

END FOR

在H上执行k-means, 获得聚类结果R;

返回R

3 实验及结果分析
3.1 实验数据集

为了验证本文方法的有效性, 在Cora[33]、Cite-seer[33]、Amap[20]、Cornell[34]、Wisconsin[34]、Actor[34]属性图数据集上进行实验.这些数据集基于同配率划分, 包括3个同配图类型数据集和3个异配图类型数据集, 详细信息如表1所示.

表1 实验数据集 Table 1 Experimental datasets

每个图的同配率[35]计算方式如下：

$\sum_{\left(v_{i}, v_{j}\right) \in \varepsilon}\left(\frac{\mathbb{I}\left(y_{v_{i}}=y_{v_{j}}\right)}{|\boldsymbol{\varepsilon}|}\right), $

其中 yvi表示节点vi的类别.

在Cora、Citeseer、Amap同配图数据集中：Cora、Citeseer数据集为引文网络数据集, 节点表示科研论文, 边表示引用连接.Amap数据集为商品关系数据集, 节点表示产品实体, 边表示购买或关联关系.在Cornell、Wisconsin、Actor异配图数据集中：Cornell、Wisconsin数据集均属于WebKB（Web Knowledge Base）网页数据集, 节点表示大学网页, 边表示超链接.Actor数据集为电影演员关系数据集, 节点表示演员, 边表示在电影中的合作出演关系.这些异配图在同配率上均显著低于同配图.数据集规模广泛且覆盖大部分应用场景, 可全面测试方法的鲁棒性.

3.2 实验设置

通过Adam（Adaptive Moment Estimation）优化器[36]优化网络参数, 对学到的节点嵌入表示执行k-means算法获得聚类结果.为了提升超参数调优效率, 采用Hyperopt工具[37]进行自动参数寻优, 调优次数设为200.

NFWD具体参数设置如下.1）遵循相关工作[14], 最大训练周期数设为400, MLP输出维度设为500.2）学习率设为1e-6, 1e-5, 1e-4, 1e-3, 1e-2.3）拉布拉斯过滤器的层数t=2, 4, 6, 8, 10.4）KNN构建特征图的参数k=1, 5, 10, 15, 20.5）两个视图特征融合参数λ=0.1, 0.3, 0, 5, 0.7, 0.9.6）两个损失函数的权衡参数λ1=0.01, 0.1, 1, 10, 100, λ2=0.01, 0.1, 1, 10, 100.

所有实验均独立运行10次, 获得结果的平均值及标准差.

实验硬件设备为NVIDIA A100服务器, 配备10核英特尔CPU和40 GB显存的GPU.

在对比实验中, 采用如下常用的两项指标评估聚类结果：准确度（Accuracy, ACC）和归一化互信息（Normalized Mutual Information, NMI）.

3.3 对比实验

本文选取如下10种基线方法进行对比实验.1）基于特征的聚类方法：AE（Auto-Encoder）、k-means.2）传统深度图聚类方法：DFCN（Deep Fusion Clustering Network）[17]、SDCN（Structural Deep Clus-tering Network）[38].3）对比深度图聚类方法：CCGC[14]、SCGC[22]、AGE（Adaptive Graph Encoder）[33]、HSAN（Hard Sample Aware Network）[39].4）专门用于异配图的深度图聚类方法：HGRL[35]、HoLe（Homophily-Enhanced Structure Learning for Graph Clustering）[40].

各对比方法在6个数据集上的聚类性能如表2和表3所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可见, NFWD在绝大多数情况下均取得较优的性能, 表明其有效性.具体分析如下.

表2 各方法在6个数据集上的ACC值 Table 2 ACC of different methods on 6 datasets %
表3 各方法在6个数据集上的NMI值 Table 3 NMI of different methods on 6 datasets %

1）在两个指标的平均值上, NFWD均超越所有对比方法.相比次优方法, 分别在ACC、NMI指标上提升4.96%和7.22%.仅在Cora、Cornell数据集上, NFWD的NMI指标值与最优方法存在微小差距, 由此表明NFWD的有效性.

2）在Cora、Citeseer、Amap同配图数据集上, 4种对比深度图聚类方法指标值优于两种传统深度图聚类方法, 因为对比深度图聚类方法在学习过程中考虑监督信息的使用, 可学到更具判别性的节点表示, 而两种仅使用特征信息的方法因为忽略拓扑信息的使用, 表现最差.在Cornell、Wisconsin、Actor异配图数据集上, 两种仅考虑特征信息的方法都优于6种同时考虑拓扑信息和特征信息的深度图聚类方法, 由此可见在异配图上特征信息的作用更重要, 而基于同配假设仅使用拓扑信息对最终性能甚至起反作用.

3）2种专门用于异配图的方法在3个同配图数据集上取得的聚类结果差于4种对比深度图聚类方法, 但在3个异配图数据集上的性能优于大多数基于同配性假设的深度图聚类方法.

4）在Actor数据集上, 所有对比方法在两个指标上的性能都不佳.这是因为该数据集包含多种节点和关系类型, 这种丰富的结构包含大量信息, 并且不同类型的关系极不平衡, 使得学习有效表示变得困难.从聚类结果可观察到, 2种仅使用特征信息的方法可取得较优值, 而NFWD取得最优值.这进一步验证充分利用特征信息构建特征图与双重特征对比损失的有效性.

综上所述, NFWD能同时适用于同配图数据集与异配图数据集, 有效学习属性图的节点表示, 取得优异的聚类性能.

3.4 消融实验

为了验证不同损失函数的有效性, 进行消融实验.为了简单起见, 定义w/o Lnode、w/o Lcluster、w/o Lweight分别表示在NFWD中移除节点级特征对比损失、簇级特征对比损失和权重去相关损失, 旨在探究不同损失函数对聚类性能的具体影响.

不同损失函数对聚类性能的影响如表4和表5所示, 表中黑体数字表示最优值.

表4 各损失函数的ACC值 Table 4 ACC of different loss functions %
表5 各损失函数的NMI值 Table 5 NMI of different loss functions %

由表4和表5可见, 节点级特征对比损失、簇级特征对比损失和权重去相关损失三者共同构成不可分割的有机整体.当移除任一损失项时, 聚类性能均出现系统性下降.去除权重去相关损失（w/o Lweight）导致表征空间解耦能力削弱, 特征冗余度上升, 除了Amap、Cornell数据集以外, 在其余数据集上性能都有所降低.簇级特征对比损失（w/o Lcluster）的缺失降低簇间分离度, 致使类边界模糊化, 除了在Cora、Wisconsin数据集上的ACC指标以外, 其余数据集上性能都有所降低.节点级特征对比损失（w/o Lnode）的缺失则导致在所有数据集上性能的降低, 主要原因是局部结构保持能力的退化, 节点嵌入的判别性显著降低.这种跨数据集的性能折损现象充分表明, 节点级监督保障微观结构建模, 簇级约束优化宏观簇分布, 权重去相关则通过抑制维度冗余提升表征紧致性, 三者通过多层次协同机制共同支撑NFWD的鲁棒性, 任何单一部分的缺失都将破坏方法的整体优化框架.

NFWD通过KNN构建特征图作为原始图结构的语义补充, 同时采用参数共享编码器进行表示学习, 保持特征空间节点相似性.为了验证其有效性, 设置双重对比实验.

1）与参数不共享的孪生编码器（Siamese Encoder）所学表示进行聚类性能对比.

2）与经典图数据增强方法, 包括边随机添加（Add-Edge）、边随机删除（DropEdge）、图扩散（Diffusion）、特征掩蔽（MaskFea）, 对比在相同参数共享编码器下的聚类性能.其中, AddEdge随机添加20%边、DropEdge随机丢弃20%边、Diffusion保持系数为0.2的图扩散, MaskFea随机掩码20%特征.

不同数据增强方法的指标值对比如表6和表7所示.表中黑体数字表示最优值.

表6 不同数据增强方法的ACC值 Table 6 ACC of different data augmentation methods %
表7 不同数据增强方法的NMI值 Table 7 NMI of different data augmentation methods %

由表6和表7可得如下结论.NFWD在6个数据集上均取得最优值, 相比次优方法, ACC、NMI指标的平均值分别提升9.80%和9.86%.这一优势源于其双重机制：在保留原始图拓扑语义结构的前提下, 通过特征图有效捕获节点相似性, 避免传统数据增强方法引发的语义偏移问题, 更好地适应异配图场景.Siamese Encoder和4种传统数据增强方法在3个同配图数据集上的性能与本文节点相似性保持的编码模块性能差距较少, 而在Cornell、Wisconsin、Actor异配图数据集上差距较大, 特别是在ACC指标上, 相比次优方法, NFWD分别提升23.44%, 19.76%和7.54%.由此可见, 仅依赖原始图的数据增强方法难以适应异配图场景.

综合上述结果可得：节点相似性保持的编码模块不仅可在同配图数据集上取得优异结果, 而且可较好地处理异配图场景, 并取得较优的聚类性能.

3.5 权重去相关模块有效性分析

为了深入探究本文提出的权重去相关模块在图聚类任务中的关键作用及其相比传统特征去相关方法的优势, 构建一个移除权重去相关模块的变体, 并在其对应位置引入标准的特征去相关约束, 损失函数定义如下：

Lfeature= 1D||（H v1）（H v2）T+I|| F2,

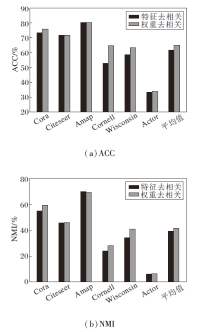
其中, D表示编码器的输出维度, 即节点嵌入矩阵H v1和H v2的特征维度.该变体在训练目标函数、网络架构、优化器配置及超参数调优策略等所有其它方面均与完整模型保持一致, 以此确保实验结果的公平性与可比性.

不同去相关机制的指标值对比如图2所示.由图可见, 采用权重去相关机制的完整模型在ACC指标上显著优于采用直接特征去相关的变体.这一结果有力说明, 相比直接在输出特征空间施加去相关约束, 在模型优化过程中约束权重向量的正交性能更有效引导模型学到对下游聚类任务更具判别性的表示.

图2 不同去相关机制的聚类性能对比Fig.2 Clustering performance comparison between 2 decorrelation mechanisms

在6个基准数据集上, 权重去相关机制在5个数据集上均优于或持平于特征去相关机制, 这充分说明权重去相关机制在大多数图数据场景下具有普适的有效性.在Amap数据集上, 特征去相关机制的NMI指标略优于权重去相关机制.这一现象可能反映Amap数据集独特的图结构或特征分布特性, 使得在该特定场景下直接约束输出特征的独立性产生更直接的效果, 但并不能从源头解决特征冗余问题.

3.6 运行时间和GPU运行内存

运行时间开销和GPU运行内存开销是评价算法效率的两个重要指标.本节通过与取得次优聚类性能的HSAN[39]和HoLe[40]进行对比, 证实NFWD的效率.

首先, 在Amap、Actor数据集上测试3种方法的运行时间.为了公平起见, 对所有方法进行400个轮次的训练, 结果如图3（a）所示.由图可知, NFWD在两个数据集上始终速度最快, 相比HSAN和HoLe, 分别平均提速2.5倍和7倍.关键原因在于NFWD的网络结构简单, 仅由两个MLP组成, 并采用低通去噪操作, 作为独立的预处理进行邻居信息聚合, 从而简化训练过程.

图3 各方法的效率对比Fig.3 Efficiency comparison of different methods

在2个数据集上对比3种方法的GPU运行内存, 结果如图3（b）所示.由图可见, NFWD与HoLe内存成本相当.相比HSAN, NFWD平均节省约84%的GPU内存资源.主要原因在于NFWD中使用MLP编码器是轻量级的.

3.7 参数敏感性分析

本节分析视图融合超参数λ、特征图邻居节点数k、簇级特征对比损失超参数λ1、权重去相关损失超参数λ2, 研究各超参数对NFWD性能的影响.

在固定其它参数条件下, 调整视图融合超参数λ, 定义λ=0.1, 0.3, …, 0.9, 其对NFWD聚类性能的影响如图4所示.由图可观察到, λ变化趋势与图的同配率密切相关.在Cora、Citeseer、Amap同配图数据集上, ACC、NMI指标在λ增加时均保持稳定或显著上升, 这是因为λ强化原始图信息的权重, 有效捕捉结构模式.

图4 λ对NFWD性能的影响Fig.4 Effect of λ on NFWD performance

相反, 在Wisconsin、Cornell、Actor异配图数据集上, ACC、NMI指标均随λ增加而显著下降, 这是由于异配图中属性信息更关键, 过度偏向原始图的拓扑结构容易破坏聚类的有效性.

这一结果表明, λ优化需依据具体图的同配特性进行自适应调整, 以此平衡信息融合视角, 提升方法的鲁棒性.

在固定其它参数条件下, 调整特征图邻居节点数k, 定义k=1, 5, 10, 15, 20, 其对NFWD聚类性能的影响如图5所示.

图5 k对NFWD性能的影响Fig.5 Effect of k on NFWD performance

由图5可观察到, 聚类性能变化趋势依旧与图的同配率相关.k对同配图影响较小, 而对异配图则相反.此外, 在5个数据集上k=1时性能最优, 并呈现随k值增大而性能衰减的趋势.从表1可发现, 这5个数据集的边数与节点数比值较低（从Citeseer的1.42倍至Actor的4.41倍）, 表明节点之间连通性较少, 节点属性间差异较大, 若构建特征图时k值过大, 容易引入不相似节点而增加学习干扰, 从而削弱节点表示的判别性.

相反, Amap数据集上边数与节点数比值高达15.57倍, 连接密集且同配率较高, 较大的k值能聚合更多的相似节点信息, 增强节点表示的判别性, 因此成为例外.综上所述, 在应用NFWD时, 依据图的同配率与连通密度设置特征图邻居节点数k, 是提升聚类性能的关键因素之一.

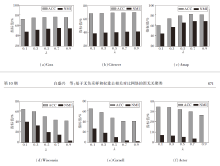
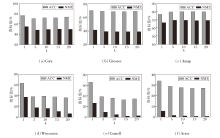
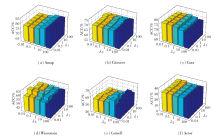
最后分析簇级特征对比损失超参数λ1和权重去相关损失超参数λ2的敏感性, 两者在6个数据集上的ACC、NMI值分别如图6和图7所示.

图6 λ1、λ2在ACC指标上对NFWD性能的影响Fig.6 Effect of λ1 and λ2 on NFWD performance in terms of ACC metric

图7 λ1、λ2在NMI指标上对NFWD性能的影响Fig.7 Effect of λ1 and λ2 on NFWD performance in terms of NMI metric

由图6和图7可知, 在Citeseer、Cora、Amap同配图数据集上, λ1表现出较强的鲁棒性, 从0.01到100的宽泛取值范围内, 对ACC、NMI指标的影响均较平缓, 表明簇级对比损失权重对同配结构聚类任务的稳定性较高.相比之下, λ2在同配图中较敏感, 取值变化容易导致性能波动, 尤其当λ2过小时权重去相关约束不足或λ2过大时形成过度抑制.

在Cornell、Wisconsin、Actor异配图数据集上, λ1与λ2均展现出显著的重要性, 二者取值需协同优化才能达到最佳, 单独调整任一参数均可能引起指标值大幅下降, 这说明异配图结构中同时平衡簇级特征对比损失与权重去相关损失对聚类质量至关重要.

3.8 可视化结果

为了更直观地对比方法性能, 在Amap、Actor数据集上, 将NFWD与CCGC[14]、SCGC[22]、AGE[33]、HGRL[35]、HSAN[39]、HoLe[40]所学的节点嵌入投影至二维空间中, 采用t-SNE（t-Distributed Stochastic Neighbor Embedding）[41]进行可视化分析, 结果如图8所示.由图可见, 在Amap数据集上, 4种对比深度图聚类方法AGE、CCGC、HSAN和SCGC学到的嵌入虽呈现一定的聚集趋势, 但簇间边界仍相对模糊, 存在部分重叠, 相同类别的节点较分散.在两种针对异配图的方法HGRL和HoLe所学嵌入的可视化结果中, 相同类别节点较集中, 但类间边界较模糊.相比之下, NFWD学到的嵌入在潜在空间中展现出更清晰的簇分离度和更紧凑的簇内结构, 为下游聚类任务提供更优基础.值得注意的是, 在Actor数据集上所有方法都无法很清楚地将不同类别的节点分开, 但NFWD可将多数相同类别节点学到较靠近的表示, 如图中黄色节点部分.

图8 各方法的可视化结果Fig.8 Visualization results of different methods

4 结束语

针对现有方法过度依赖图同配性假设的问题, 本文提出基于无负采样与权重去相关对比网络的图无关聚类方法（NFWD）.

首先, 设计节点相似性保持的编码模块, 构建属性驱动的特征图作为补充视图, 在保留节点相似性的同时增强方法对异配图场景的泛化能力.

然后, 设计节点级和簇级双重特征对比学习模块, 替代传统负采样机制, 解决异配图场景中的负采样假阴性问题与计算瓶颈.

最后, 设计权重去相关模块, 降低特征冗余, 提升表示的紧凑性与判别性.在涵盖同配图和异配图的基准数据集实验中, NFWD性能较优, 验证其作为图无关通用框架的高效性与鲁棒性.今后将进一步优化特征图构建的计算框架, 适应大规模动态图场景.

本文责任编委 王士同

Recommended by Associate Editor WANG Shitong

参考文献
[1] LIN Z P, KANG Z, ZHANG L Z, et al. Multi-view Attributed Graph Clustering. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(2): 1872-1880. [本文引用:1]
[2] XIE F, ZHANG Z, LI L, et al. EpiGNN: Exploring Spatial Transmission with Graph Neural Network for Regional Epidemic Forecasting // Proc of the European Conference on Machine Learning and Knowledge Discovery in Databases. Berlin, Germany: Springer, 2023: 469-485. [本文引用:1]
[3] GROVER A, LESKOVEC J. node2vec: Scalable Feature Learning for Networks // Proc of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2016: 855-864. [本文引用:1]
[4] COSCIA M, GIANNOTTI F, PEDRESCHI D. A Classification for Community Discovery Methods in Complex Networks. Statistical Analysis and Data Mining, 2011, 4(5): 512-546. [本文引用:1]
[5] WANG S P, YANG J B, YAO J, et al. An Overview of Advanced Deep Graph Node Clustering. IEEE Transactions on Computational Social Systems, 2024, 11(1): 1302-1314. [本文引用:1]
[6] 周丽娟, 吴梦琪, 李欣冉, 等. 基于不同学习范式的深度图聚类方法综述. 模式识别与人工智能, 2025, 38(3): 233-251.
(ZHOU L J, WU M Q, LI X R, et al. A Survey of Deep Graph Clustering Methods Based on Different Learning Paradigms. Pattern Recognition and Artificial Intelligence, 2025, 38(3): 233-251. ) [本文引用:1]
[7] YING R, HE R N, CHEN K F, et al. Graph Convolutional Neural Networks for Web-Scale Recommender Systems // Proc of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2018: 974-983. [本文引用:1]
[8] 方宝富, 张旭, 王浩. 联合深度图聚类与目标检测的像素级分割算法. 模式识别与人工智能. 2022, 35(2): 130-140.
(FANG B F, ZHANG X, WANG H. Pixel-Level Segmentation Algorithm Combining Depth Map Clustering and Object Detection. Pa-ttern Recognition and Artificial Intelligence, 2022, 35(2): 130-140. ) [本文引用:1]
[9] SHCHUR O, GÜNNEMANN S. Overlapping Community Detection with Graph Neural Networks[C/OL]. [2025-08-21]. https://arxiv.org/pdf/1909.12201. [本文引用:1]
[10] PAN S R, HU R Q, LONG G D, et al. Adversarially Regularized Graph Autoencoder for Graph Embedding // Proc of the 27th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2018: 2609-2615. [本文引用:2]
[11] KIPF T N, WELLING M. Variational Graph Auto-Encoders[C/OL]. [2025-08-21]. https://arxiv.org/pdf/1611.07308. [本文引用:1]
[12] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Gene-rative Adversarial Networks. Communications of the ACM, 2020, 63(11): 139-144. [本文引用:1]
[13] HASSANI K, AHMADI A H K. Contrastive Multi-view Representation Learning on Graphs // Proc of the 37th International Confe-rence on Machine Learning. San Diego, USA: JMLR, 2020: 4116-4126. [本文引用:2]
[14] YANG X H, LIU Y, ZHOU S H, et al. Cluster-Guided Contrastive Graph Clustering Network. Proc of the AAAI Conference on Artificial Intelligence, 2023, 37(9): 10834-10842. [本文引用:5]
[15] GONG L, ZHOU S H, TU W X, et al. Attributed Graph Clustering with Dual Redundancy Reduction // Proc of the 31st International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2022: 3015-3021. [本文引用:2]
[16] WANG C, PAN S R, HU R Q, et al. Attributed Graph Clustering: A Deep Attentional Embedding Approach // Proc of the 28th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2019: 3670-3676. [本文引用:1]
[17] TU W X, ZHOU S H, LIU X W, et al. Deep Fusion Clustering Network. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(11): 9978-9987. [本文引用:2]
[18] XIA J, WU L R, WANG G, et al. ProGCL: Rethinking Hard Negative Mining in Graph Contrastive Learning // Proc of the 39th International Conference on Machine Learning. San Diego, USA: JMLR, 2022: 24332-24346. [本文引用:1]
[19] LIU Y, XIA J, ZHOU S H, et al. A Survey of Deep Graph Clustering: Taxonomy, Challenge, and Application[C/OL]. [2025-08-21]. https://arxiv.org/pdf/2211.12875. [本文引用:1]
[20] LIU Y, ZHOU S H, YANG X H, et al. Improved Dual Correlation Reduction Network with Affinity Recovery. IEEE Transactions on Neural Networks and Learning Systems, 2025, 36(4): 6159-6173. [本文引用:2]
[21] XIA W, WANG Q Q, GAO Q X, et al. Self-Consistent Contrastive Attributed Graph Clustering with Pseudo-Label Prompt. IEEE Tran-sactions on Multimedia, 2023, 25: 6665-6677. [本文引用:1]
[22] LIU Y, YANG X H, ZHOU S H, et al. Simple Contrastive Graph Clustering. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(10): 13789-13800. [本文引用:3]
[23] CHEN J L, KOU G. Attribute and Structure Preserving Graph Contrastive Learning. Proceedings of the AAAI Conference on Artificial Intelligence, 2023, 37(6): 7024-7032. [本文引用:2]
[24] ZHENG Y M, JIA C Y, YU J. Attributed Graph Clustering under the Contrastive Mechanism with Cluster-Preserving Augmentation. Information Sciences, 2024, 681. DOI: DOI:10.1016/j.ins.2024.121225. [本文引用:1]
[25] ZHAO H, YANG X, WANG Z R, et al. Graph Debiased Contrastive Learning with Joint Representation Clustering // Proc of the 30th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2021: 3434-3440. [本文引用:1]
[26] ZBONTAR J, JING L, MISRA I, et al. Barlow Twins: Self-Supervised Learning via Redundancy Reduction // Proc of the 38th International Conference on Machine Learning. San Diego, USA: JMLR, 2021: 12310-12320. [本文引用:1]
[27] ZHANG H R, WU Q T, YAN J C, et al. From Canonical Correlation Analysis to Self-Supervised Graph Neural Networks // Proc of the 35th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2021: 76-89. [本文引用:1]
[28] MO Y H, WANG X, FAN S H, et al. Graph Contrastive Invariant Learning from the Causal Perspective. Proceedings of the AAAI Conference on Artificial Intelligence, 2024, 38(8): 8904-8912. [本文引用:1]
[29] FANG R Y, WEN L J, KANG Z, et al. Structure-Preserving Graph Representation Learning // Proc of the IEEE International Confe-rence on Data Mining. Washington, USA: IEEE, 2022: 927-932. [本文引用:1]
[30] HUA T Y, WANG W X, XUE Z H, et al. On Feature Decorrelation in Self-Supervised Learning // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2021: 9578-9588. [本文引用:1]
[31] LI S, JIA K, WEN Y X, et al. Orthogonal Deep Neural Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(4): 1352-1368. [本文引用:1]
[32] BANSAL N, CHEN X H, WANG Z Y. Can We Gain More from Orthogonality Regularizations in Training Deep CNNs?// Proc of the 32nd International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2018: 4266-4276. [本文引用:1]
[33] CUI G Q, ZHOU J, YANG C, et al. Adaptive Graph Encoder for Attributed Graph Embedding // Proc of the 26th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2020: 976-985. [本文引用:4]
[34] PEI H B, WEI B Z, CHANG K C C, et al. Geom-GCN: Geome-tric Graph Convolutional Networks[C/OL]. [2025-08-21]. https://arxiv.org/pdf/2002.05287. [本文引用:3]
[35] CHEN J F, ZHU G H, QI Y F, et al. Towards Self-Supervised Learning on Graphs with Heterophily // Proc of the 31st ACM International Conference on Information and Knowledge Management. New York, USA: ACM, 2022: 201-211. [本文引用:3]
[36] KINGMA D P, BA J. Adam: A Method for Stochastic Optimization[C/OL]. [2025-08-21]. https://arxiv.org/pdf/1412.6980. [本文引用:1]
[37] BERGSTRA J, YAMINS D, COX D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures // Proc of the 30th International Confe-rence on Machine Learning. San Diego, USA: JMLR, 2013: 115-123. [本文引用:1]
[38] BO D Y, WANG X, SHI C, et al. Structural Deep Clustering Network // Proc of the ACM Web Conference. New York, USA: ACM, 2020: 1400-1410. [本文引用:1]
[39] LIU Y, YANG X H, ZHOU S H, et al. Hard Sample Aware Network for Contrastive Deep Graph Clustering. Proceedings of the AAAI Conference on Artificial Intelligence, 2023, 37(7): 8914-8922. [本文引用:3]
[40] GU M, YANG G M, ZHOU S, et al. Homophily-Enhanced Struc-ture Learning for Graph Clustering // Proc of the 32nd ACM International Conference on Information and Knowledge Management. New York, USA: ACM, 2023: 577-586. [本文引用:3]
[41] VAN DER MAATEN L, HINTON G. Visualizing Data Using t-SNE. Journal of Machine Learning Research, 2008, 9(86): 2579-2605. [本文引用:1]