夏鸿斌,博士,教授,主要研究方向为个性化推荐、自然语言处理、计算机网络.E-mail:hbxia@163.com.
作者简介:
周 夕,硕士研究生,主要研究方向为推荐系统、深度学习.E-mail:Zhou730428@outlook.com. 
王晓锋,博士,教授,主要研究方向为计算机网络.E-mail:wangxf@pcl.ac.cn.
条件化扩散序列推荐模型大都直接从用户历史交互序列中提取指导信号,导致生成信号容易受到噪声干扰,无法提供足够的上下文信息,从而限制模型的生成能力.针对上述问题,文中提出基于小波变换增强引导的扩散序列推荐模型(Wavelet-Enhanced Guidance for Diffusion-Based Sequential Recommendation, WEG4Rec).首先,设计多兴趣学习模块,利用小波变换获得历史交互嵌入的多频段划分结果,在此基础上,采用自适应维度投影模块与线性注意力学习模块,生成多粒度兴趣嵌入.然后,使用多粒度兴趣嵌入指导扩散模型的反向还原过程.最后,利用多任务学习模块联合优化推荐模型.在四个真实数据集上的大量实验表明WEG4Rec性能较优.
XIA Hongbin, Ph.D., professor. His research interests include personalized recommendation, natural language processing, and computer networks.
About Author:
ZHOU Xi, Master student. His research interests include recommendation systems and deep learning.
WANG Xiaofeng, Ph.D., professor. His research interests include computer networks.
Since most conditional diffusion-based sequential recommendation models directly extract guiding signals from the historical interaction sequences of users, the generated signals are susceptible to noise and lack sufficient contextual information, thereby limiting the generation capability of the model. To address these issues, wavelet-enhanced guidance for diffusion-based sequential recommendation(WEG4Rec) is proposed in this paper. First, multi-frequency segmentation results of historical interaction embeddings are obtained via the wavelet transform. On this basis, adaptive dimensional projection and linear attention are introduced to generate multi-granularity interest embeddings. Second, the multi-granularity interest embeddings are employed to guide the reverse reconstruction process of the diffusion model. Finally, a multi-task strategy is adopted to jointly optimize the recommendation model during the training. Extensive experiments on four real-world datasets demonstrate the superior performance of WEG4Rec.
在现阶段电子商务、社交网络与流媒体服务平台中, 用户交互行为呈现出显著的事件序列特征, 这些特征既反映用户在不同情境下的不同行为模式, 也暗示其内在偏好随时间推移呈现动态演化的规律[1].这种动态变化不仅受用户个人兴趣、时代潮流以及社会环境等多重因素的影响, 而且在一些特定时期内还可能呈现出明显的波动性和阶段性特征.
序列推荐旨在根据用户的历史交互和兴趣偏好, 向用户推荐一系列按照特定顺序排列的推荐结果[2].早期序列推荐模型中, 研究者基于用户反馈、评论和意见, 利用协同过滤(Collaborative Filtering)筛选物品信息, 通过计算物品之间的相似度, 识别用户可能感兴趣的物品[3, 4].通常, 这类模型先对物品进行编码, 同时从领域中获取信息以补充物品信息, 再利用融合门控或注意力机制学习不同来源的物品特征.然而, 这类方法容易引入噪声, 影响推荐精度.
基于马尔可夫链(Markov Chain)的序列推荐模型对用户交互序列进行建模, 通过状态转移概率揭示用户的短期行为模式[5, 6, 7].尽管马尔可夫链能在一定程度上捕捉用户的动态偏好, 但随着链阶的提升, 模型稳定性逐步下降, 同时计算复杂度也相应增加.
随着深度学习技术的迅速发展, 循环神经网络(Recurrent Neural Network, RNN)在序列推荐模型中的应用日益广泛.基于循环门控单元(Gated Re-current Unit, GRU)[8]、长短期记忆网络(Long Short Term Memory, LSTM)及其变体构建的序列推荐模型[9]在此类任务中性能优异.这类模型具备多层次、跨时间步的信息传递能力, 能在更细粒度的时间域上有效捕捉并建模项目之间的时域转换关系, 为用户提供个性化精准推荐.
Transformer架构[10]的提出推动了基于自注意力机制的序列推荐模型的发展, 彻底改变用户交互序列的建模方式, 使序列推荐模型进入以全局上下文建模为核心的新阶段[11, 12].以SASRec(Self-Attentive Based Sequential Model)[11]为代表的自注意力模型, 通过动态权重分配机制, 突破传统序列建模的局限, 能在每个时间步上对用户历史行为序列中的所有项目进行全局相关性计算.这种设计在保留长期依赖关系的基础上, 实现对少量关键行为的预测, 标志序列推荐范式由局部模式识别向全局语义理解的转变.
此外, 研究人员采用胶囊网络(Capsule Net-work)[13]等技术提取用户意图, 将用户行为映射为具有语义一致性的兴趣向量胶囊, 通过动态调整兴趣向量权重, 平衡推荐系统的精准度和多样性[14].此外, 新近研究表明数据已成为重要瓶颈, 因此从无标签的数据中学习有效信息成为一个重要的研究方向.随着对比学习方法的广泛应用, 越来越多的模型通过构建正负样本对, 实现相似序列表示的聚合与不相关序列表示的分离, 有效缓解数据稀疏问题[15, 16, 17].
近年来, 扩散模型(Diffusion Model)在计算机视觉、序列建模和音频处理等领域取得显著进展[18].相比生成对抗网络(Generative Adversarial Networks, GANs)[19]和变分自编码器(Variational Autoencoder, VAE)[20], 扩散模型依托其特有的渐进式生成范式, 从根本上规避模式崩溃和训练震荡等问题.现阶段, 基于扩散模型的序列推荐方法[21, 22, 23]逐渐受到关注, 这一研究方向通过引入扩散概率模型, 并利用分阶段去噪过程, 精确刻画用户与项目交互的复杂数据分布, 为序列推荐领域开辟全新的研究范式.基于扩散模型的序列推荐方法直接生成目标项目, 同时建模用户潜在兴趣分布, 有效避免传统判别式推荐方法中因负样本采样偏差导致的分布偏移问题[22].
条件化扩散模型(Conditional Diffusion Model)作为扩散序列推荐方法的重要分支之一, 核心思想是从用户历史交互序列中提取有效的条件信号, 以此引导扩散模型的反向去噪过程, 生成更精准的推荐结果[24, 25].然而, 现有方法通常直接利用注意力机制或深度学习网络从原始用户交互序列中提取一个固定维度的兴趣嵌入作为条件信号.采用固定维度的向量表示无法根据具体需求自适应调整兴趣粒度, 导致长期兴趣的稳定性和短期兴趣的动态性之间产生相互干扰, 使指导信号中混入噪声, 削弱对去噪过程的指导能力.上述现象更根本的问题在于, 原始用户行为序列中往往包含大量与用户真实、稳定兴趣无关的噪声交互, 直接将用户行为简化为单一的时间序列模式进行兴趣建模, 不仅忽略用户行为的复杂性和用户兴趣的多元性, 还容易学到虚假的关联[26].Li等[27]指出, 传统的判别式方法容易受到“ 曝光偏差” 的影响, 即过度依赖互动频繁的项目, 而忽略低互动但可能高度相关的项目的重要性.当这些被污染的数据直接用于条件信号的生成时, 提供的上下文信息就不再纯净, 无法在去噪过程中稳定反映用户的核心偏好.例如:一位核心兴趣集中于科幻和悬疑题材的影迷, 绝大部分观影历史都集中于此.然而某次偶然原因他观看了一部爱情片, 但后续行为立刻回归到其主要兴趣域.在构建条件信号时, 如果方法简单地将此次偶然事件与代表其核心兴趣的交互等同视为条件信号, 那么在引导生成推荐列表时, 就可能不恰当地放大爱情片特征的权重, 导致生成结果偏离用户真实、长期的兴趣轨迹, 无法准确捕捉兴趣演化的真实模式.
针对上述问题, 本文提出基于小波变换增强引导的扩散序列推荐模型(Wavelet-Enhanced Guidance for Diffusion-Based Sequential Recommendation, WEG4- Rec), 融合小波变换的多尺度分析能力分解原始用户序列, 通过线性注意力机制从重构的兴趣分布中高效提取条件信号, 结合扩散模型的生成特性, 构建多粒度兴趣感知与动态偏好建模的协同建模框架.小波变换因其在多尺度信号分解中的独特优势, 能有效地从用户交互序列中提取不同频率层次的特征, 从而为条件化扩散模型提供丰富的上下文信息.首先, 设计多兴趣学习模块, 利用小波变换局部化分解特性, 不断从用户历史交互嵌入中提取短期突变信号, 将用户历史交互序列分解为不同频率的子带.在此基础上, 利用线性注意力学习模块捕获用户兴趣之间的依赖关系并生成指导信号.在生成阶段, 引入用户多粒度兴趣嵌入作为条件信息, 构建条件化扩散过程, 生成符合用户兴趣的个性化推荐项目.为了进一步提升模型的鲁棒性, 设计多任务学习模块, 联合优化推荐任务, 主任务通过交叉熵损失训练扩散模型的项目生成, 辅助任务通过改进噪声对比估计损失(Noise-Contrastive Estimation, NCE)[28]强化方法对用户偏好分布的建模能力, 约束生成后的项目序列.
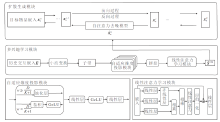
本文提出基于小波变换增强引导的扩散序列推荐模型(WEG4Rec), 整体框架如图1所示.
WEG4Rec主要包括3个模块.
1)多兴趣学习模块.由多频段划分模块、自适应维度投影模块和线性注意力学习模块构成.首先, 原始用户交互嵌入经过基于Haar小波的多频段划分模块处理后, 将用户交互的原始分布按不同频率分解为不同维度的子带表示, 在多个尺度上分离用户兴趣的高低频细节.然后, 自适应维度投影模块动态建立跨频段的非线性映射关系, 将不同维度的频率子带重新整合为统一维度的兴趣嵌入, 以适应模型后续处理的要求.最后, 引入线性注意力学习模块, 从重构后的兴趣分布中高效提取、聚合依赖关系, 形成用于引导扩散过程的用户多粒度兴趣表征.小波变换的多尺度分解特性使模型能分别关注短期动态偏好与长期稳定兴趣, 避免直接从原始稠密的用户交互序列中提取特征时引入噪声和虚假关联.
2)扩散生成模块.以多兴趣学习模块输出的条件嵌入作为引导信号, 构建条件化扩散模型, 学习生成符合用户偏好的推荐项目.多粒度兴趣嵌入作为上下文条件参与噪声预测, 使生成内容逐步对齐用户的核心兴趣.
3)多任务学习模块.首先改进噪声对比估计损失, 约束扩散模型的生成内容.然后, 引入均方误差损失, 监督多兴趣引导信号.同时, 结合正则化损失, 约束多兴趣学习模块, 避免过拟合.最后, 合并上述损失到主损失, 构建联合训练框架, 提升模型性能与鲁棒性.
对于项目集合V和用户集合U, 每个用户(u∈ U)和物品的交互记录按照时间顺序排列, 表示为seq=[
本文设计多兴趣学习模块, 结构分为3个部分.1)多频段划分模块, 旨在通过Harr小波基变换区分历史交互嵌入中的多频段兴趣信息.2)自适应维度投影模块, 自适应学习划分的数据, 实现不同维度子带的统一特征映射.3)线性注意力学习模块, 实现扩散指导信号的提取.
同时, 为了方便模型处理, 本文对用户交互序列seq进行特定转换, 将前n-1条交互记录作为历史交互嵌入E∈ RB× L× D, 最后一条交互记录作为目标嵌入Etarget∈ RB× D, 其中, B表示批次大小, L表示最大序列长度, D表示嵌入向量的维度.
1.2.1 多频段划分模块
在小波分析中, Haar小波基因其简单的矩形函数形式, 成为计算效率最高的离散小波变换基函数, 尤其适用于需快速提取序列多尺度特征的场景.其正交性保证信号能量在变换前后的守恒, 并能将序列分解为低频近似分量与高频细节分量.低频分量可近似反映用户的长期兴趣趋势, 高频分量用于捕捉短期动态变化.这种基于多分辨率分析的能力使Haar小波基在序列推荐任务中能有效区分用户历史交互中稳定的偏好模式与瞬时的兴趣波动.
多频段划分模块对历史交互嵌入E使用Haar小波基, 通过频域分析将历史交互拆分成不同频段的嵌入表示.本文对E在频域中进行逐层滤波与下采样, 将原始信号分解成不同频率成分的组合.分别使用低频分量滤波器
hlow=[
和高频分量滤波器
hhigh=[-
利用Harr小波基的正交性实现信号从粗粒度到细粒度的层次化特征提取.
对于用户原始交互嵌入E, 首先通过下采样操作Downsample(· )和卷积操作Conv(· , · )提取第一层低频分量L1和高频分量H1, 即
$\begin{array}{l} \boldsymbol{L}_{1}=\operatorname{Downsample}\left(\operatorname{Conv}\left(\boldsymbol{E}, \boldsymbol{h}_{\text {low }}\right)\right) \in \mathbf{R}^{B \times L \times \frac{D}{2}}, \\ \boldsymbol{H}_{1}=\operatorname{Downsample}\left(\operatorname{Conv}\left(\boldsymbol{E}, \boldsymbol{h}_{\text {high }}\right)\right) \in \mathbf{R}^{B \times L \times \frac{D}{2}}, \end{array}$
其中Conv(· , · )中两个参数分别表示输入张量和对应滤波器.
低频分量L1主要反映提取信号中缓慢变化的平稳趋势, 以近似反映用户的长期兴趣; 高频分量H1专注于捕捉信号中突变点, 提取信号的细节信息.通过上述操作, L1和H1的维度减少为原始信号E的一半.
为了进一步细化高频细节并拓展频率分辨率, 对第一层分解的低频分量L1进行递归分解, 从低频信号中进一步提取细节信息, 分解成多个不同的频段, 每个频段对应不同的频率范围, 从而实现多级兴趣的分解.设第i-1层低频分量Li-1∈
Li=Downsample(Conv(Li-1, hlow)),
Hi=Downsample(Conv(Li-1, hhigh)).
当分解层级达到预设的K层后停止分解, 最终获得K个不同频段的高频嵌入分量和1个低频近似分量, 构成完整的多频段兴趣表示
{H1, H2, …, HN, LK}.
随着层级i的增加, Li对应的频率范围逐渐降低, 逐步逼近信号的长期稳态趋势, 最终形成用户的长期兴趣偏好LK, 而{Hi}则对应K个不同频段的细节特征, 完整刻画用户兴趣的多尺度动态特征.
1.2.2 自适应维度投影模块
在基于小波变换的多频段划分模块中, 不同子带的维度呈现指数级衰减, 第j层分解后, 低频子带维度为原始信号的2-j, 而高频子带维度保持为2-j+1.分解K次后, 各子带的维度形成非对称结构
{
传统固定维度映射方法难以实现参数共享与特征对齐, 无法有效处理上述非对称结构.为此, 本文设计自适应维度投影模块, 动态建立跨频段的非线性映射关系.通过小波变换划分后, 子带嵌入的维度各不相同, 为了从所有的子带中获取信息, 通过全局平均池化器(Global Average Pooling, GAP)捕获子带嵌入维度大于
gi=
其中W表示小波变换后输出的维度.
为了从不同频率子带gi中提取用户的多元兴趣, 本文构造双层感知机, 在目标维度
其中, Wg、Wc表示权重向量, bg, bc表示偏置向量.最终将各子带投影特征沿通道维度拼接, 获得最终兴趣表示:
Xconcat=(
1. 2. 3 线性注意力学习模块
为了提升对多尺度特征的提取能力, 基于Trans-former架构设计线性注意力学习模块, 改进自注意力机制和深层特征学习, 有效捕捉序列中的全局上下文信息.通过多兴趣学习模块生成增强嵌入:
SL=Attention(XconcatWQ, XconcatWK, XconcatWV),
其中,
Attention(Q, K, V)=softmax(
WQ、WK、WV分别表示3个向量对应的可学习权重参数矩阵,
同时, 在传统Transformer架构中, 自注意力机制需要计算所有查询和键之间的点积.Softmax注意力的计算复杂度为O(N2), 导致在处理长序列时计算量和内存消耗急剧增加.为了缓解因Softmax运算导致矩阵规模过大的问题, 本文利用线性注意力机制, 近似计算点积以降低计算负担, 利用Elu(· )激活函数和Norm(· )归一化处理将查询与键映射到非负空间.首先计算键和值之间的乘积, 再与查询相乘, 从而避免直接进行高复杂度的计算, 可将增强嵌入改写为
SL=LinearAttention(Q, K, V)=
Norm(Elu(Q))(Norm(Elu(K))TV).
为了提高模型的泛化能力和防止过拟合, 还采用Dropout层和LayerNorm层归一化缓解过拟合问题.
最后, 通过扩散指导比率λ L将增强嵌入SL叠加到原始嵌入中, 生成最终的多兴趣嵌入:
Saug=E+λ LSL.
本文旨在利用扩散模型优异的生成能力生成预测项目, 受DiffuRec[21]启发, 本文同样将目标嵌入Elabel作为扩散模型原始特征x0, 并在扩散过程中逐步注入高斯噪声, 生成阶段使用多兴趣嵌入Saug, 指导生成历史项目
在正向扩散阶段中, 扩散模型通过马尔可夫链逐步向x0中注入高斯噪声xt, 经过T步迭代之后, 数据完全转化为噪声分布.具体来说, 每步注入的噪声都由预定义的噪声调度函数β t控制, 其中0< β t< 1, t=1, 2, …, T, 条件概率分布定义为
q(xt|xt-1)=N(xt;
递推后可获得任意时刻t的闭式采样概率:
$\begin{array}{c} q\left(\boldsymbol{x}_{t} \mid \boldsymbol{x}_{0}\right)=N\left(\boldsymbol{x}_{t} ; \sqrt{\overline{\alpha_{t}}} \boldsymbol{x}_{0}, \left(1-\overline{\alpha_{t}}\right) \boldsymbol{I}\right)= \\ \sqrt{\overline{\alpha_{t}}} \boldsymbol{x}_{0}+\sqrt{1-\overline{\alpha_{t}}} \boldsymbol{\epsilon}, \end{array}$
其中
$\begin{array}{l} \epsilon \sim N(0, \boldsymbol{I}) \\ \bar{\alpha}_{t}=\prod_{s=1}^{t} \alpha_{s}, \alpha_{s}=1-\beta_{t} \end{array}$
逆向重建的目标是逐步从完全噪声分布xT~N(0, I)中恢复原始数据x0.根据随机微分方程理论, 当扩散系数β t足够小时, 逆向过程中的每步可近似定义为条件高斯分布:
p(xs-1|}xs, x0)=N(xs-1;
其中
$\begin{array}{l} \widetilde{\mu}_{s}\left(\boldsymbol{x}_{s}, \boldsymbol{x}_{0}\right)=\left(\frac{\sqrt{\bar{\alpha}_{s-1}} \beta_{s}}{1-\bar{\alpha}_{s}}\right) \boldsymbol{x}_{0}+\left(\frac{\sqrt{\alpha_{s}}\left(1-\bar{\alpha}_{s-1}\right)}{1-\bar{\alpha}_{s}}\right) \boldsymbol{x}_{s} \\ \widetilde{\beta}_{s}=\left(\frac{1-\bar{\alpha}_{s-1}}{1-\bar{\alpha}_{s}}\right) \beta_{s} . \end{array}$
本文使用Transformer模型fθ (· ), 在多频段划分生成的多兴趣嵌入Saug指导下, 直接生成每个时间步t的目标项:
上述过程可通过最小化变分下界进行训练:
$\begin{array}{l} L_{\mathrm{vlb}}\left(\boldsymbol{x}_{0}\right)=E_{q\left(x_{1: t} \mid x_{0}\right)}\left[\ln \left(\frac{q\left(\boldsymbol{x}_{t} \mid \boldsymbol{x}_{0}\right)}{p\left(\boldsymbol{x}_{t}\right)}\right)+\right. \\ \left.\quad \sum_{s=2}^{t} \ln \left(\frac{q\left(\boldsymbol{x}_{s-1} \mid \boldsymbol{x}_{s}, \boldsymbol{x}_{0}\right)}{p\left(\boldsymbol{x}_{s-1} \mid \boldsymbol{x}_{s}\right)}\right)-\ln p\left(\boldsymbol{x}_{0} \mid \boldsymbol{x}_{1}\right)\right] . \end{array}$
DDPM(Denoising Diffusion Probabilistic Model)[18]中对时间步t进行均匀采样, 提升训练的稳定性和效率.Li等[21]指出忽略KL散度中的权重项可简化损失函数, 并在实际应用中获得更优效果.因此, 直接将p(xt-1|xt)和前向过程后验分布进行对比, 通过计算均方误差损失进行约束, 损失函数改写为
$\begin{array}{l} _{\text {diff }}= \\ \quad E_{t, x_{0}, \epsilon}\left[\left\|\boldsymbol{x}_{0}-f_{\theta}\left(\sqrt{\overline{\alpha_{t}}} \boldsymbol{x}_{0}+\sqrt{1-\overline{\alpha_{t}}} \epsilon, \boldsymbol{S}^{\text {aug }}, t\right)\right\|^{2}\right] .\end{array}$
为了提高模型的鲁棒性, 本文基于噪声对比估计设计对比损失函数.对于扩散生成的嵌入
$\begin{array}{l} L_{c}=-\frac{1}{B} \cdot \\ \sum_{i=1}^{B} \ln \left(\frac{\exp \left(\frac{\operatorname{sim}\left(\hat{x}_{0}^{i}, \hat{x}_{0}^{i+}\right)}{\tau}\right)}{\exp \left(\operatorname{sim}\left(\hat{x}_{0}^{i}, \hat{x}_{0}^{i+}\right)\right)+\sum_{j \neq i} \exp \left(\operatorname{sim}\left(\hat{x}_{0}^{i}, \hat{x}_{0}^{j}\right)\right)}\right), \end{array}$
其中τ 表示温度函数.
计算增强嵌入Saug和原始嵌入S之间的均方误差损失:
La=MSE(S, Saug),
确保多兴趣学习模块在不同层次上输出的一致性, 减少模型对输入数据微小变化的敏感性, 并实现对多兴趣学习模块的联合训练.
为了防止多兴趣学习模块出现过拟合, 在模块中引入L2正则化惩罚项:
Lr=
最后, 结合扩散生成损失, 通过超参数权值α 、 β 整合上述损失, 得到网络的最终损失:
L=Ldiff+α Lc+β La+Lr.
借助上述多任务学习模块, 模型既可同时学习去噪和特征增强任务, 又能在端到端网络框架下对去噪模型fθ (· )和多兴趣学习模块进行联合优化.
最后, 基于生成的预测项目表示
本文选择在Amazon Beauty、Amazon Toys、Steam、ML-1M这4个真实世界的基准数据集上进行实验.Amazon Beauty、Amazon Toys数据集收集亚马逊平台中美容产品和玩具分区近2年来用户的评分数据.Steam数据集整合Steam平台上各类游戏的详细信息.ML-1M数据集源于电影领域, 涵盖4 000部电影与6 000位用户贡献的1× 106条评分数据.本文采用与DiffuRec[21]相同的方式, 对用户-物品交互数据按时间顺序进行排序, 并过滤交互次数少于5次的记录, 其余交互记录少于预设长度的历史交互序列会用0填充, 超过预设长度的数据会截断最早的交互记录.具体数据集信息如表1所示.
| 表1 实验数据集 Table 1 Experimental datasets |
所有实验都在NVIDIA GeForce RTX 4090D GPU上进行.模型基于PyTorch实现, 并使用学习率为0.001的Adam(Adaptive Moment Estimation)对模型进行优化.设置最大训练轮次为500, 嵌入维度为128, 批次为512.扩散模型中的Dropout系数设为0.1, 多兴趣学习模块中的Dropout系数设为0.2, 项目嵌入的Dropout系数设为0.3.扩散模型的时间步T设为32.除了ML-1M数据集上最大序列长度设为200, 其余数据集上最大序列长度均设为50.在多频段划分模块中, 小波变换划分次数K=1, 3, 7, 扩散指导比率λ L=0.2, 0.4, 0.6, 0.8, 1.0.
在所有实验中, 保持上述参数设置在所有模型中均一致, 并且每五轮评估一次, 如果最高结果在10轮评估中保持不变, 提前停止训练.
为了评估模型性能, 采用序列推荐领域中常用的两个指标HR@N(Hits Ratio)和NDCG@N(Nor-malized Discounted Cumulative Gain)评估推荐性能.指标计算公式如下:
$ \begin{array}{l} H R @N=\frac{1}{M} \sum_{i=1}^{M} \sum_{j=1}^{N} r_{i, j} \\ N D C G @N=\sum_{i=1}^{M}\left(\frac{\sum_{j=1}^{N}\left(\frac{r_{i, j}}{\log _{2}(j+1)}\right)}{M \cdot I D C G_{i}}\right), \end{array} $
其中, M表示测试用户数量, 如果第i位用户的推荐物品排序列表中的第j个项目是正确样本, ri, j=1, 否则ri, j=0.NDCG的分子表示DCG@N(Discounted Cumulative Gain, DCG), IDCGi表示对第i位测试用户的最大可能DCG@N值, 其中N=5, 10, 20.
本文选择如下11种常用的序列推荐模型进行对比实验.
1)GRU4Rec[8].利用门控循环单元捕获用户行为序列中的时间依赖性.
2)SASRec[11].利用 Transformer 的自注意力机制处理用户历史交互序列中的偏好依赖关系.
3)ComiRec(Controllable Multi-interest Framework for the Sequential Recommendation)[14].通过动态路由和自注意力机制, 从用户行为序列中提取多重兴趣.
4)CL4SRec(Contrastive Learning for Sequential Recommendation)[15].通过序列级别的数据增强生成正样本对.
5)DuoRec[16].结合正样本采样策略和对比学习优化, 缓解推荐系统中的表示退化问题.
6)DiffuRec[21].利用去噪扩散概率模型对项目分布构建概率模型, 并通过由交互序列引导的去噪过程实现下一个预测项目的生成.
7)DreamRec[25].完全抛弃负采样, 利用条件扩散模型将序列推荐任务重塑为理想物品的生成任务.
8)DIN(Deep Interest Network)[29].利用注意力机制计算不同用户的交互行为权重.
9)BERT4Rec(Bidirectional Encoder Representa-tions from Transformers for Sequential Recommenda-tion)[30].采用双向自注意力对用户行为序列进行建模, 捕获用户交互中的双向依赖.
10)TiMiRec(Target-Interest Distillation Frame-work for Multi-interest Recommendation)[31].通过多兴趣提取器生成多个兴趣嵌入, 动态聚合兴趣嵌入以适应不同上下文.
11)STOSA(Stochastic Self-Attention)[32].通过随机嵌入策略和自注意力模块捕获交互间的协同传递性.
各模型在4个数据集上的指标值如表2~表5所示, 表中黑色数字表示最优值, 斜体数字表示次优值.由表可见, WEG4Rec在HR、NDCG指标上明显优于对比模型.
| 表2 各模型在Amazon Beauty数据集上的指标值对比 Table 2 Metric value comparison of different models on Amazon Beauty dataset |
| 表3 各模型在Amazon Toys数据集上的指标值对比 Table 3 Metric value comparison of different models on Amazon Toys dataset |
| 表4 各模型在Steam数据集上的指标值对比 Table 4 Metric value comparison of different models on Steam dataset |
| 表5 各模型在ML-1M数据集上的指标值对比 Table 5 Metric value comparison of different models on ML-1M dataset |
在传统判别模型中, GRU4Rec利用门控循环单元对用户交互序列进行建模, 在一定程度上缓解传统循环神经网络中梯度消失的问题.然而, 在处理长序列时, 仍然难以保留有效信息.DIN的静态注意力机制难以适配用户兴趣的动态转移, 在局部兴趣建模和解决数据稀疏性问题上都存在一定的局限性.WEG4Rec利用小波卷积对用户历史交互序列进行细粒度划分, 可增强模型对长序列信息的捕捉能力, 在不同的时间序列数据上表现良好.此外, 在训练过程中引入额外约束, 可避免模型在特定数据集上的过拟合, 减少对输入分布的敏感度, 使模型更专注于学习数据的通用特征, 从而提升鲁棒性, 降低对数据噪声的敏感性.
使用Transformer架构作为主体网络的模型(SASRec、BERT4Rec)极其关注序列中元素的位置顺序, 这意味着如果序列中元素位置发生改变, 输出结果可能会有所不同.用户历史行为中可能存在与当前预测无关的噪声项, 这种机制也会导致模型过度关注无关特征, 尤其在长序列情况下, 会出现注意力权重分散问题.此外, 这类模型通过Softmax计算注意力, 注意力计算复杂度为O(N2), 而BERT4Rec采用双向注意力, 实际计算中需要花费更多的成本.WEG4Rec在多兴趣学习中对历史交互进行细粒度切分和学习, 降低数据中的异常值和噪声点, 并且采用线性注意力进行合并, 避免常规Transformer架构中应该显式计算Softmax带来的开销, 最终将计算复杂度减少为O(N), 同时也减少模型因为数据噪声和异常值引起的不确定性.WEG4Rec使用扩散模型搭建主体网络, 直接预测交互项目中更符合序列推荐的任务目标, 通过扩散模型加噪去噪的训练过程, 使模型天然具备一定的抗噪声能力.
ComiRec、TiMiRec、STOSA通过动态路由和注意力机制从用户历史交互中提取多兴趣指导信息, 提升推荐的准确性和泛化性, 但是通过静态聚类或注意力权重直接筛选兴趣, 容易导致兴趣演化建模不足.WEG4Rec通过多频段划分, 允许模型在不同时间尺度上捕捉兴趣的局部突变和长期趋势, 避免传统方法中因固定粒度划分导致的兴趣重叠问题.
基于对比学习方法的模型(DuoRec、CL4SRec)引入自监督对比任务与数据增强策略, 提升稀疏场景下模型的学习能力.WEG4Rec同样采用对比学习策略, 通过设计噪声对比学习损失优化生成任务, 实现模型性能的增强.
基于扩散模型的推荐模型(DiffuRec、Dream-Rec)将用户行为序列建模为连续分布生成过程, 突破传统固定向量表征的局限性.扩散模型采取双向去噪过程和时间感知机制, 实现对动态兴趣演化的捕捉.相比传统判别模型, 基于扩散模型的序列推荐模型性能具有大幅提升, 因此WEG4Rec同样选择使用扩散模型作为主体网络, 并且在扩散过程中, 通过多兴趣学习模块生成的信号, 指导扩散过程的数据生成.
为了评估WEG4Rec中各模块对整体性能的影响, 设计如下变体, 并保持其它条件不变:1)Base, 移除多兴趣学习模块和多任务学习模块; 2)-MI, 移除多兴趣学习模块; 3)-MS, 移除多任务学习模块.在Amazon Beauty、Amazon Toys、Steam、ML-1M数据集上的消融实验结果如表6所示.
| 表6 各变体在4个数据集上的消融实验结果 Table 6 Ablation experiment results of various variants on 4 datasets |
在WEG4Rec上移除多兴趣学习模块后, 各指标值均出现一定程度的下降.这是因为扩散模型本质上属于非条件生成模型, 若缺乏条件指导, 只能完全依赖从随机噪声中还原数据.此时, 模型训练结果完全取决于其从噪声中学到的数据分布, 会导致模型的稳定性和准确性降低, 结果不理想.
在WEG4Rec上移除多任务学习模块后, 在多个数据集上性能略有下降.多任务学习模块为模型提供对比学习等额外的损失函数, 有助于约束模型学习过程, 防止过拟合.去除多任务学习模块后, 多兴趣学习模块容易陷入过拟合状态, 无法有效提取具有指导意义的信号, 进而影响扩散模型的生成效果, 同时也会降低模型的鲁棒性, 最终导致性能和可靠性下降.
最后, 在WEG4Rec移除多兴趣学习模块和多任务学习模块后, 各项指标都有大幅削弱, 特别是在Amazon Beauty数据集上, 这是由于Amazon Beauty数据集上数据量较少的同时交互较多, 存在很多噪声干扰, 因此最终导致模型学习效果受到大幅影响.
2.4.1 小波变换划分次数K
小波变换通过迭代分解原始数据, 逐层提取高频细节信息和低频全局特征.理论上, 增加小波变换划分次数K可获取更多的细节信息, 提升模型对用户多兴趣信号的学习能力, 但也会增加模型的复杂度和训练时间.合适的参数选择有助于提高模型的泛化能力.
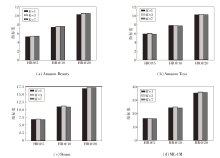
值得注意的是, 小波变换输出的高低频子带数量需与嵌入维度兼容, 因此实验设置小波变换划分次数K=1, 3, 7, 在4个数据集上对WEG4Rec性能的影响如图2所示.
由HR@20指标的对比结果可知, K=3时, WEG4Rec在4个数据集上均取得最优值.在Ama- zon Beauty、Steam、ML-1M数据集上, K=7时WEG4- Rec性能小幅回落, 而在Amazon Toys数据集上呈现差异化趋势, 这可能与该数据集上用户兴趣分布相对集中, 低层次划分已能捕捉核心偏好有关.K=1时, 小波变换仅进行一次粗粒度分解, 难以从历史交互序列中提取足够的高频细节信息, 导致指导信号受限.K=7时, 尽管进一步细分的高频子带可能蕴含更丰富的局部细节信息, 但过度分解并不一定会带来性能提升.
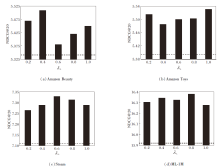
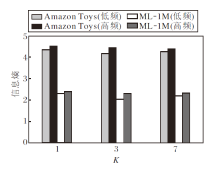
为了探究K对序列信息结构的作用, 在Amazon Toys、ML-1M这两种规模数据集上, 统计不同K值下高频子带与低频子带的平均信息熵对比, 结果如图3所示.
 | 图3 不同K值下高频子带与低频子带的平均信息熵Fig.3 Average information entropy of high and low frequency subbands with different K values |
分析图3可知, 在两种不同规模的数据集上, 低频子带的信息熵均显著低于高频子带的信息熵, 说明Haar小波基可有效提取序列中的稳定趋势信息, 而高频分量则保留用户兴趣波动引入的不确定性.同时, 在序列更长的ML-1M数据集上高低频信息熵均低于在Amazon Toys数据集上的信息熵, 反映大规模数据中用户行为模式更具一致性, 信息密度更高.
值得注意的是, K=3时, 各子带信息熵处于相对均衡且较低的水平, 说明该尺度在捕捉关键局部突变与控制冗余之间取得较好平衡, 与性能实验结论一致, 进一步支持K=3作为最优分解层数的合理性.结果显示, 在序列较短的Amazon Toys数据集上, 高频子带熵值在K=1、3、7时波动范围较小, 表明其局部细节信息有限, 过度细分未能提取更多的有效信息, 反而可能引入冗余.在序列较长的ML-1M数据集上, K=3时高频子带信息熵最低, K=7时信息熵上升, 说明中等粒度分解能有效捕捉关键局部突变, 而更细粒度可能导致噪声放大.该现象侧面说明分解粒度需与序列长度及信息密度匹配.短序列本身突变信息较少, 宜采用较粗粒度分解; 长序列则需中等粒度以兼顾整体趋势与局部细节, 避免过度分解带来的信息冗余.
综合来看, 设定小波变换划分次数K=3时能实现性能峰值, 验证中等划分次数在细节提取与复杂度控制间的平衡优势.
2.4.2 扩散指导比率λ L
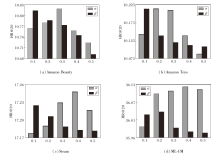
多兴趣学习模块通过扩散指导比率λ L实现学习嵌入与历史交互嵌入的融合, 改变λ L能有效调控模型的特征表达能力.为了探究λ L对WEG4Rec性能的影响, 在4个数据集上, 以NDCG@20为评估指标, 探究λ L=0.2, 0.4, 0.6, 0.8, 1.0时的WEG4Rec性能变化, 结果如图4所示, 图中虚线表示移除多兴趣学习模块和多任务学习模块后WEG4Rec的NDCG@20指标值.
由图4可知, λ L在不同数据集上对WEG4Rec性能的影响呈现显著差异.在Amazon Beauty数据集上, WEG4Rec对参数变化较敏感, λ L=0.2, 0.4时获得最优性能.在Amazon Toys数据集上, WEG4Rec整体波动较平稳, 鲁棒性较强.在Steam数据集上, λ L=0.6为最优参数点.在ML-1M数据集上, λ L=0.8时WEG4Rec获得最优性能.
2.4.3 多任务策略权重α 和β
为了探究多任务策略权重α 、 β 对推荐性能的影响, 设置α =0.1, 0.2, …, 0.5, β =0.1, 0.2, …, 0.5, 当α 或β 取任一值时, 另一个参数设为0, 其对WEG4Rec的性能影响如图5所示.
针对不同数据集上用户意图的直观程度差异, 优化模型权重系数可有效提升建模准确性.对于用户意图直观程度不同的数据集, 调整噪声对比损失权重α , 可有效提升模型对用户意图的捕捉精度.由图5可知, 随着α 增大, WEG4Rec性能呈现先增大后减小的趋势, 而随着β 增大, WEG4Rec性能出现下降趋势.这表明在模型训练中, 噪声对比损失对模型性能的影响更显著, 而均方误差损失在训练过程中容易出现数值过大的情况, 导致模型对多兴趣学习模块的过度拟合.因此, 适当降低均方误差损失权
重β , 有助于避免模型在训练过程中对多兴趣学习模块的过度拟合, 提高模型的泛化性和稳定性.同时α =0.2, 0.4时, WEG4Rec对不同规模数据集的泛化能力最优.
2.4.4 小波基
为了探究不同小波基对WEG4Rec的综合影响, 本文选取更高阶的Daubechies小波基(db4、db6)与Symlet小波基(sym2、sym4)作为对比组.这两类小波基均属于高阶小波基, 具有更长的支撑长度与更平滑的时频特性.Daubechies小波基因优异的信号去噪与特征保持能力被广泛应用, 同时Haar小波基是唯一不连续的Daubechies小波基.Symlet小波基通过对称化设计, 进一步降低信号重构中的失真.
首先, 为了评估不同小波基对WEG4Rec性能的影响, 在保持其它实验条件一致的前提下, 设置5组对比实验:
1)base, 原始WEG4Rec及Haar小波基.
2)db4, 将Haar小波基替换为4阶Daubechies小波基.
3)db6, 将Haar小波基替换为6阶Daubechies小波基.
4)sym2, 将Haar小波基替换为2阶Symlet小波基.
5)sym4, 将Haar小波基替换为4阶Symlet小波基.
为了确保实验可复现与结果一致性, 所有小波基均基于PyWavelets(pywt库)与PyTorch Wavelet Toolbox(ptwt库)实现, 并在4个数据集上进行测试, 结果如表7所示, 表中黑体数字表示最优值, 斜体数字表示次优值.
| 表7 不同小波基对WEG4Rec性能的影响 Table 7 Effect of different wavelet bases on WEG4Rec performance |
由表7可知, Haar小波基在绝大多数指标上表现最优, 尤其在中大型规模数据集(Steam、ML-1M)上, 各项指标值均实现大幅领先, 说明Haar小波基具备对大规模数据高效建模的能力.在部分数据集上, Haar小波基虽与其它小波基的性能差距较小, 但也展现出较强的普适性.
按数据集规模进一步分析可知, 在小规模数据集上, 相比高阶小波基(db6、sym4), 低阶小波基(db4、sym2)表现出一定优势, 并且与Haar小波基性能差距较小.由于小规模数据存在用户行为模式有限且噪声占比较高的特点, 低阶小波基通过较少的分解层数可有效捕捉信号的主要成分, 同时抑制噪声, 而高阶小波基可能因为过度捕捉高频噪声而引入一定干扰.Haar小波基结构简单, 虽牺牲部分局部拟合能力, 但泛化性更强, 同样适应噪声主导的小规模数据集.
在中大型数据集上, 高阶小波基(db6、sym4)性能全面超越低阶小波基, 但与Haar小波基性能差异较大.此时用户兴趣呈现长尾分布, 高频兴趣占比显著提升.
Haar小波基凭借强阈值效应, 能有效过滤低频噪声, 突出高频信号, 而高阶小波基的缓变特性可能导致噪声累积, 削弱对关键模式的捕捉.
综合来看, 用户行为序列中包含大量突发性兴趣变化, Haar小波基具有时域局部化能力, 能有效捕捉高频信号, 为后续扩散模型的生成式建模提供足够的指导.相比之下, db系列小波基和sym系列小波基虽在连续信号重构中平滑性更优, 但其基函数的缓变特性更适用于音频、图像这类慢变连续信号, 在以离散突变为主导的用户行为序列中, 要求模型对时域局部化敏感, 缓变特性会导致突变处的系数离散, 弱化对突发信号的捕捉能力.
为了进一步评估不同小波基的计算效率, 在4个数据集上, 对比5种小波基在单轮训练和推理过程中的平均训练时长和测试时长, 结果如表8所示.
| 表8 不同小波基单轮的训练时长和推理时长 Table 8 Training time and inference time per epoch for different wavelet bases s |
由表8可知, 在Amazon Beauty、Amazon Toys小型数据集上, 各小波基的计算开销差异不大.然而, 在Steam、ML-1M中大型数据集上, 不同小波基的时间开销差异显著.具体而言, 滤波器长度较短的Haar小波基始终计算速度最快.随着滤波器长度的增加, 训练时长与预测时长均呈现明显的增长趋势.这一现象与小波变换的原理直接相关, 小波变换的计算开销主要取决于滤波器的长度, 虽然上述所有小波的时间复杂度均为O(N), 但单次分解所需的计算量因滤波器长度而异.例如:Haar小波基的滤波器长度为2, 而db6小波基的滤波器长度为12, 单次分解的计算量理论上增加约6倍.在模型的训练和推理过程中, 单次操作计算的累加最终会导致计算开销的显著增长.当数据规模较小时, 这种计算差异可能被其它操作的开销所掩盖, 但随着数据集规模的扩大, 计算量的差异被放大, 从而在总耗时上体现出明显区别.
综合上述实验结果可发现, 对于用户行为序列这类富含突变信号的场景, 小波基的选择并非越复杂、越平滑越好.Haar小波基虽然在数学实现上最简单, 但其不连续性、时域局部化的特性和用户行为离散突变的特征高度匹配, 并且在保证性能优秀的同时, 拥有最低的计算复杂度.因此, 本文选择Haar小波基作为WEG4Rec的默认小波基.
2.4.5 注意力机制
为了进一步验证不同注意力机制在WEG4Rec中的建模能力与计算效率差异, 选取6种常用注意力机制进行对比实验.
1)base, 原始WEG4Rec, 默认使用线性注意力机制.
2)multi, 使用多头注意力机制.
3)adaptive, 使用自适应注意力机制[33].
4)local, 使用局部注意力机制[34].
5)sparse, 使用稀疏注意力机制[35].
6)performer, 使用Performer注意力机制[36].
7)mlp, 使用三层感知机.
为了确保实验可复现与结果一致性, 所有注意力机制均使用原始模型默认参数, 并在4个数据集上进行测试, 结果如表9~表12所示, 表中黑体数字表示最优值, 斜体数字表示次优值.
| 表9 Amazon Beauty数据集上不同注意力机制对WEG4Rec性能的影响 Table 9 Effect of different attention mechanisms on WEG4Rec performance on Amazon Beauty dataset |
| 表10 Amazon Toys数据集上不同注意力机制对WEG4Rec性能的影响 Table 10 Effect of different attention mechanisms on WEG4Rec performance on Amazon Toys dataset |
| 表11 Steam数据集上不同注意力机制对WEG4Rec性能的影响 Table 11 Effect of different attention mechanisms on WEG4Rec performance on Steam dataset |
| 表12 ML-1M数据集上不同注意力机制对WEG4Rec性能的影响 Table 12 Effect of different attention mechanisms on WEG4Rec performance on ML-1M dataset |
由表9~表12可知, 线性注意力(base)在整体性能上表现最优, 尤其在序列更长、用户行为更复杂的中大型数据集(Steam、ML-1M)上, 优势更明显.在Steam数据集上, 相比表现次优的performer, 线性注意力的HR@5、NDCG@5指标值提升约1.2%和0.9%.
在大规模数据集ML-1M上, 优势进一步扩大, HR@20、NDCG@20指标值提升约0.8%和4.0%, 展现出线性注意力在处理大规模序列数据时较强的建模能力.尽管在Amazon Beauty、Amazon Toys小规模数据集上, 各类注意力机制性能差距不大, 但线性注意力依然保持稳定且领先的表现, 表明其良好的适用性.
按数据集规模分析可发现, 在小规模数据集上, 由于用户行为模式相对简单且序列较短, 各类注意力机制均能有效捕捉主要特征, 性能差异不显著.在Steam、ML-1M中大型数据集上, 用户兴趣呈现长尾和突发性特点, 序列内部依赖关系复杂.值得注意的是, 在WEG4Rec中, 传递给线性注意力学习模块的数据已预先通过多频段划分模块处理.多频段划分模块将原始序列中的关键信号进行有效提取, 使序列的主要信息转换为更全局且平滑的特征表示.线性注意力机制能对这种经过提炼的全局特征进行高效聚合, 避免在原始稠密交互中直接捕捉高阶非线性特征.因此, 在WEG4Rec中, 序列建模的关键更侧重于高效捕获多频段划分模块提取的重要特征, 线性注意力学习模块因其计算高效且不易过拟合的特点, 在此特定任务中表现出良好的泛化能力.此外, performer作为另一种高效注意力机制, 性能紧随线性注意力之后, 也从侧面印证线性注意力对于WEG4Rec的适配性.
为了进一步验证线性注意力对多频段划分模块作用后的数据的增强和提取效果, 在Amazon Beauty数据集上绘制WEG4Rec各阶段特征空间的t-SNE(t-Distributed Stochastic Neighbor Embedding)可视化图像, 结果如图6所示.
观察t-SNE图像可发现, 原始数据本身具备一定的聚类结构, 通过多频段划分模块处理之后数据变得更分散, 这反映小波变换将序列信息分解到不同频率子带, 增强特征的多样性或区分度.最后在经过注意力机制处理后, 特征重新聚集, 形成新的、与经过小波变换处理后的特征分布相适应的聚类趋势.
这一可视化结果与前述性能分析表明, 线性注意力机制并不需要直接从原始稠密的用户交互序列中捕获高阶特征, 而是能有效地对经过多判断划分模块提炼后的特征进行聚合与增强, 优化最终表征.
最后, 为了验证线性注意力的计算开销, 统计4个数据集上不同注意力机制的单轮训练时长、推理时长及内存开销, 结果如表13所示.
综合计算开销可知, 线性注意力在4个数据集上均展现出优异且稳定的计算效率, 尤其在处理中大规模数据集时, 训练速度与推理速度优于或持平于多数参与对比的注意力机制.尽管MLP与多头注意力(multi)在部分开销指标上与线性注意力相当, 但结合模块性能考量, 线性注意力仍具优势.局部注意力(local)因滑动窗口操作破坏计算连续性, 导致时间开销显著增加.performer虽同属线性注意力范畴, 但其随机特征映射引入额外的计算步骤, 实际效率低于本文的线性注意力.因此, WEG4Rec最终采用线性注意力, 在模型性能与计算开销间取得最优平衡.
本文提出基于小波变换增强引导的扩散序列推荐模型(WEG4Rec).首先, 通过小波变换将用户历史交互序列进行多频段分解, 将嵌入映射到不同频率子带, 结合自适应维度投影与线性注意力机制, 实现对用户意图的多粒度提取, 为条件化扩散指导信号提供更多的上下文信息.然后, 引入扩散模型, 通过多粒度信号指导扩散模型反向生成符合用户兴趣的项目, 增强模型对复杂交互模式的捕捉能力, 缓解传统判别模型注意力捕获不足的缺陷.最后, 设计多任务学习模块, 对齐负样本分布, 缓解因采样偏差导致的兴趣信号偏移问题.对比实验表明WEG4Rec具有一定优势, 消融实验验证主要模块对推荐性能的贡献.今后将进一步探索对用户交互序列进行更细粒度的分解, 并尝试引入多源外部信息以提升模型性能.同时, 进一步研究不同扩散策略的影响, 验证模型在超大规模数据集上的扩展性与鲁棒性.
本文责任编委 林鸿飞
Recommended by Associate Editor LIN Hongfei
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|