引用本文
高程玲, 黄昌勤, 郑忠龙, 蒋云良. 基于局部感知图重构的点云异常检测网络. 模式识别与人工智能, 2025,38(11): 961-973
GAO Chengling, HUANG Changqin, ZHENG Zhonglong, JIANG Yunliang. Point Cloud Anomaly Detection Network Based on Local Perception Graph Reconstruction. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2025,38(11): 961-973.  
Doi: 10.16451/j.cnki.issn1003-6059.202511001
Permissions
Copyright©2025, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
基于局部感知图重构的点云异常检测网络
高程玲1,2, 黄昌勤1,3, 郑忠龙2, 蒋云良1,2,4,5
1.浙江师范大学 全省智能教育技术与应用重点实验室 金华 321004
2.浙江师范大学 计算机科学与技术学院 金华 321004
3.浙江大学 教育学院 杭州 310058
4.浙江师范大学 中国-莫桑比克“智慧农业”一带一路联合实验室 金华 321004;
5.湖州师范学院 信息工程学院 湖州 313000
通信作者:

黄昌勤,博士,教授,主要研究方向为机器学习、教育大数据、智能教育.E-mail:cqhuang@zju.edu.cn.

作者简介:

高程玲,博士研究生,主要研究方向为图表示学习、图异常检测.E-mail:chl_gao@zjnu.edu.cn.

郑忠龙,博士,教授,主要研究方向为机器学习、计算机视觉、智联网与区块链.E-mail:zhonglong@zjnu.edu.cn.

蒋云良,博士,教授,主要研究方向为智能信息处理、地理信息系统.E-mail:jyl2022@zjnu.cn.

收稿日期: 2025-10-20 接受日期: 2025-11-28
资助项目: 科技创新2030——“新一代人工智能”重大项目(No.2022Z D0117104)、国家自然科学基金项目(No.62337001)资助
摘要

点云异常检测旨在从整体数据分布中识别缺陷样本,并进一步定位其在空间中偏离预期模式的异常区域.针对现有全局匹配策略难以有效捕捉集中于局部细微几何结构异常的问题,文中提出基于局部感知图重构的点云异常检测网络.首先,将点云建模为图结构,通过局部敏感的边卷积操作挖掘点云的局部结构特征,提升对局部细微异常的识别能力.然后,基于子图结构对齐策略设计局部对齐重建损失,从结构层面放大正常样本与异常样本间的差异性.此外,引入局部异常生成策略,构建异常-正常样本对,约束网络学习异常样本向正常样本的模式映射.最后,采用局部匹配检测算法计算异常样本与期望正常样本之间的差异,实现对点云异常区域的检测.实验表明,文中网络显著增强对局部细节的感知能力,在多个类别的点云异常检测任务中均取得较优性能.

关键词: 图神经网络; 无监督学习; 异常检测; 点云
中图分类号:TP391
Point Cloud Anomaly Detection Network Based on Local Perception Graph Reconstruction
GAO Chengling1,2, HUANG Changqin1,3, ZHENG Zhonglong2, JIANG Yunliang1,2,4,5
1. Zhejiang Key Laboratory of Intelligent Education Technology and Application, Zhejiang Normal University, Jinhua 321004
2. School of Computer Science and Technology, Zhejiang Normal University, Jinhua 321004
3. College of Education, Zhejiang University, Hangzhou 310058
4. China-Mozambique Belt and Road Joint Laboratory on Smart Agriculture, Zhejiang Normal University, Jinhua 321004
5. School of Information Engineering, Huzhou University, Hu-zhou 313000
Corresponding author:
HUANG Changqin, Ph.D., professor. His research inte-rests include machine learning, big data in education, and intelligent education.

About Author:
GAO Chengling, Ph.D. candidate. Her research interests include graph representation learning and graph anomaly detection.
ZHENG Zhonglong, Ph.D., professor. His research interests include machine lear-ning, computer vision, artificial intelligence of things and blockchain.
JIANG Yunliang, Ph.D., professor. His research interests include intelligent information processing and geographic information systems.

Fund:Supported by Scientific and Technological Innovation 2030—"New Generation Artificial Intelligence" Major Project(No.2022ZD0117104), National Natural Science Foundation of China(No.62337001)
Abstract

Point cloud anomaly detection aims to identify defective samples from the overall data distribution and further locate the abnormal regions deviating from the expected pattern in space. Existing global matching strategies struggle to effectively capture anomalies concentrated in local subtle geometric structures. To address this issue, a point cloud anomaly detection network based on local perception graph reconstruction is proposed. First, the point cloud is modeled as a graph structure, and local sensitive edge convolution operations are utilized to mine local structural features to enhance the identification ability for local subtle anomalies. Second, a local alignment reconstruction loss is designed based on a subgraph structure alignment strategy to amplify the differences between normal and abnormal samples at the structural level. Furthermore, a local anomaly simulation strategy is introduced to construct an anomaly-normal sample pair. Through this strategy, the model is constrained to learn the pattern mapping from abnormal samples to normal samples. Finally, a local matching algorithm is applied to calculate the differences between abnormal samples and expected normal samples to achieve the detection of point cloud abnormal regions. Experimental results show that the proposed method significantly enhances the perception ability for local details and achieves excellent performance on multiple categories of point cloud anomaly detection tasks.

Key words: Graph Neural Network; Unsupervised Learning; Anomaly Detection; Point Cloud

点云作为一种典型的几何型数据, 由大量离散的三维采样点构成, 能天然映射为图结构数据.在图结构中, 节点不仅记录真实世界中物体表面的空间坐标信息, 还可反映其几何与物理属性的多维特征(如颜色和反射强度等), 从而实现对三维目标几何形态的完整刻画[1, 2].类似于图数据的异常检测任务, 点云异常检测旨在从整体数据分布中识别存在缺陷或异常的样本, 并进一步定位其在空间中偏离预期模式的区域[3, 4].这一过程在三维质量检验、结构健康监测、自动化建模等应用场景中具有重要意义.

由于收集并标注异常样本的成本高昂, 且异常种类繁多, 导致监督学习范式应用困难且泛化性较差.另一方面, 研究人类视觉原理及特点发现, 人类在认知过程中能根据少量正常样本, 区分数据中的预期偏差与异常值, 从而发现异常模式.因此, 在点云异常检测的研究中, 通常采用仅利用正常样本进行建模的无监督方法或单类学习方法[5].该类方法旨在学习正常点云数据的内在分布特征, 构建能刻画其几何结构与局部特征模式的表示空间, 并在推理阶段将偏离该分布的样本或区域判定为异常.

类似于传统的二维异常检测任务[6, 7], 目前点云异常检测方法主要分为基于记忆库的方法和基于重建的方法.

基于记忆库的方法通常利用传统特征提取算法或预训练的深度学习模型, 对训练集上的正常样本进行特征提取, 隐式构建正常样本的特征分布, 并据此构建记忆库.在测试推理阶段, 计算测试对象与记忆库中所有模板点云特征之间的欧氏距离, 将不符合记忆库分布的样本归类为异常, 实现无监督的点云异常检测.Horwitz等[8]提出BTF(Back to the Feature), 将手工制作的三维描述符与经典的二维异常检测方法PatchCore[6]结合, 构建三维异常检测的基本框架.Wang等[9]提出M3DM(Multi-3D-Memory), 合并点云与RGB图像特征, 改进异常检测推理能力.Cao等[10]提出CPMF(Complementary Pseudo Multi-modal Feature), 将点云转换为多视角二维图像, 采用预训练网络从这些图像中提取额外特征, 并通过信息融合增强检测能力.Rodulph等[11]提出AST(Asymmetric Student-Teacher Network), 通过深度信息抑制背景, 强化网络对异常区域(前景)的特征提取能力.Liu等[12]提出Reg3D-AD(Regis-tration-Based 3D-AD Method), 设计基于配准的方法, 在测试阶段使用RANSAC(Random Sample Consensus)[13]对齐每个样本, 再将其与记忆库模板进行对比.这类方法的训练过程相对简单, 但由于需要在记忆库中存储训练阶段的全部特征, 并在测试时将每个输入点云与库中所有样本进行对比, 显著增加内存占用和推理时间成本.这种效率瓶颈使得方法在实际工业生产线中难以大规模应用.

基于重建的方法[14, 15, 16]在训练阶段仅使用正常样本对重建网络进行学习, 使其能精确重构正常点云.在测试阶段, 利用该网络对输入点云进行重建, 并对比原始点云与重建结果之间的差异, 判定是否存在异常.Li等[17]提出IMRNet(Iterative Mask Reconstruction Network), 采用循环掩码重建策略训练网络, 并分别计算点云的显式空间坐标差异与隐式深层特征差异, 获得最终的异常得分.Zhao等[18]提出R3D-AD, 采用扩散模型构建点云重建网络, 生成更细致的点云, 用于后续的异常检测.然而, 这类方法在设计重建目标时, 由于点云具有不规则性与无序性, 往往倾向于采用全局匹配损失函数, 可能导致对局部细节的重构不足, 从而限制局部异常检测的性能.另一方面, 仅依赖有限的正常样本进行训练, 可能难以支撑重建网络的泛化能力, 甚至会引发模型坍缩现象[19], 使网络倾向于学习恒等映射, 而非捕捉正常模式的真实重构结果.

此外, 一些研究者[20, 21, 22, 23]尝试构建多模态输入, 增强三维物体的特征表示, 提升点云异常检测的性能.然而, 这类方法仍受限于点云建模能力的不足, 导致其在异常检测任务中的性能提升空间有限.

点云能天然映射为图结构数据, 这种表示方式不仅完整保留点云的几何拓扑信息, 还能为引入图神经网络(Graph Neural Networks, GNNs)提供天然的基础.已有研究者[24, 25, 26]在点云分类、分割和生成等多种监督学习任务中验证图神经网络的有效性并取得优异性能.一个直观的想法是将点云组织为图结构, 通过图卷积算子对局部邻域特征进行精细提取, 增强网络对局部异常的敏感度.另一方面, 由于异常往往表现为局部几何结构的偏差, 可考虑在点云中选取空间连续的局部子图, 并与正常参考子图进行匹配与对齐, 从结构层面放大局部差异, 提升异常检测的精确性.

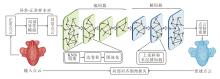
基于上述思想, 本文提出基于局部感知图重构的点云异常检测网络(Point Cloud Anomaly Detection Network Based on Local Perception Graph Reconstruc-tion, LPGR).首先, 针对局部细节重构不足, 构建局部感知点云图自编码器, 通过K近邻(k-Nearest Neighbor, KNN)及设计的局部敏感的边卷积算子, 增强对局部几何结构的捕捉能力.然后, 结合最大图池化算子, 构建层次化特征编码分支, 实现分层多尺度特征提取.在解码阶段, 通过上采样操作与反卷积, 逐步恢复点云分辨率并细化特征, 获取点云上每个节点的表示.最后, 将节点表示输入点云重建头中, 重建点云坐标, 并设计局部对齐的重建损失, 进一步强化网络对局部细节的感知能力.此外, 为了保证重建结果为正常模式, 引入局部异常生成策略, 模拟真实情况中多种异常模式, 构建异常-正常样本对, 使自监督模型在面对实际异常时能重构更真实的无异常形状.

1 问题描述

点云异常检测任务:给定一个特定类别(如飞机、汽车等)的点云异常检测训练集

Dtrainc={P(1), P(1), …, P(M)},

包含类别c的M个正常(无缺陷)的点云样本, 每个点云P(i)∈ RN× 3由N个三维点构成, 每个点记录其在三维空间中的坐标.给定同一类别的测试集

$\begin{array}{l} \boldsymbol{D}_{\text {test }}^{c}= \\ \quad\left\{\boldsymbol{P}^{(1)}, y_{s}^{(1)}, y_{n}^{(1)}, \boldsymbol{P}^{(2)}, y_{s}^{(2)}, y_{n}^{(2)}, \cdots, \boldsymbol{P}^{(T)}, y_{s}^{(T)}, y_{n}^{(T)}\right\}, \end{array}$

包含T个待检测的点云样本, ys(i)表示整个点云标签, yn(i)表示每个点对应的标签, 标签值为0表示正常, 1表示异常.

点云异常检测的目标是根据训练集 Dtrainc训练一个模型, 并构建整体点云异常评分函数φ ∶ RN× 3→ R与节点级异常评分函数ϕ ∶ RN× 3→ RN, 定量评估输入点云的异常程度, 并定位异常区域.

在训练阶段, 根据训练集 Dtrainc学习一个点云重构模型F(如点云自编码器).异常的稀有性与多样性使其难以被重建, 因此重构模型的输出通常被认为是期望的正常点云.在测试阶段, 输入测试集 Dtestc中任意一个点云样本P(u), 对应模型预测的正常结果为:

Precu=F(P(u)).

因此, 通过对比输入点云P(u)与该期望正常点云 Precu之间的差异, 即可构建点云异常评分函数, 实现无监督条件下点云异常检测.

2 基于局部感知图重构的点云异常检测网络

本文提出基于局部感知图重构的点云异常检测网络(LPGR), 整体架构如图1所示.

图1 LPGR架构图Fig.1 Architecture of LPGR

2.1 局部感知点云图自编码器

给定一个点云P={p1, p2, …, pn}作为输入, 对应的特征X={x1, x2, …, xn}, 其中每个点pi∈ R3表示在三维空间中的坐标.通过KNN将点云构建为图G(V, ε ), 其中V={1, 2, …, N}表示图的顶点集, ε ⊆V× V表示边集.

由于点云的异常区域通常集中于局部空间范围, 因此在特征提取过程中引入局部敏感的边卷积, 增强对局部几何特征的捕捉能力.首先对于邻域N(pi)中的任意一条边eij, 通过拼接相对坐标与节点特征构建边特征fε (eij), 即∀ pj∈ N(pi), 有

fε (eij)=[pj-pi‖ xj]∈ R3+d,

其中, xj∈ Rd表示邻域节点pj对应的特征, ‖ 表示通道拼接操作.然后, 采用多层感知器作为通道间的全连接映射层, 并在点云特征图的所有点之间共享参数.

该过程在具体实施时可等价为在点云特征图上施加1× 1卷积操作, 实现逐点的特征变换, 之后依次接入批量归一化层和非线性激活函数, 提升特征分布的稳定性并增强网络的表达能力.相应特征变换函数为:

M(fε (eij))=δ (BN(Conv1× 1(fε (eij)))),

其中, δ (· )表示非线性激活函数, BN(· )表示批量归一化, Conv1× 1(· )表示卷积操作.

获得边特征的逐点映射后, 应用局部嵌入函数

Local(· )=δ (BN(Conv1× k(· )))

聚合局部邻域N(pi)的特征, 得到中心节点pi的局部嵌入特征:

xi* =Local(M(fε (eij))|pj∈ N(pi)).

局部嵌入函数通过可学习的权重同时聚合局部上下文和映射几何特征.

在标准的二维卷积神经网络中, 池化操作在特征提取过程中发挥重要作用, 能在每个尺度范围内汇聚并保留主要的响应模式, 从而在压缩特征维度的同时保留关键信息, 为后续的高层语义建模和精细化特征提取奠定基础.在三维点云特征提取过程中, 池化操作同样是不可或缺的组成部分.本节引入图池化, 在保留重要结构信息的前提下降低图的规模, 生成更紧凑的粗化图结构.

借鉴PointNet++[27]与3D-GCN(3D Graph Con-volution Networks)[28]的设计, 首先采用最远点采样, 确定粗化图的代表性节点.然后利用KNN为每个采样节点构建局部邻域.最后, 采用池化函数将邻域内节点的特征聚合至对应的粗化节点.本文采用最大池化策略, 即对于每个特征维度, 选取邻域内所有节点的最大值作为该维度的聚合结果.给定一个粗化节点 p(pool)i, 则图池化后节点的特征为:

$\boldsymbol{x}_{i}^{(\mathrm{pool})}=\max \left\{\boldsymbol{x}_{j} \mid \forall \boldsymbol{p}_{j} \in N\left(\boldsymbol{p}_{i}^{(\mathrm{pool})}\right)\right\}, $

xi(pool)包含更大尺度的几何信息.

在编码分支中, 利用KNN将点云构建为图结构, 并结合边卷积和图池化操作实现单层编码.通过堆叠多层编码模块, 实现分层点云几何结构特征提取.在解码分支中, 通过上采样与多层感知器逐步恢复点云尺寸并细化节点特征, 再根据解码器最后一层的输出特征X(last)重建点云坐标.具体地, 以特征X(last)作为输入, 通过多层感知器预测点偏移矩阵

Δ P=tanh(MLP(X(last))),

则重建的点云可表示为

Prec=P+Δ P.

然后, 以输入点云P为真实目标, 通过重构损失对图自编码器进行端到端训练.

考虑到点云异常区域集中在局部区域, 这要求模型能更细致地重建点云局部细节, 因此, 本文通过设计局部对齐的倒角距离(Chamfer Distance, CD)构造重建损失函数.

首先, 通过最远点采样算法从输入点云P中采样M个点作为点云骨架结构, 记为

S= {s1, s2, …, sM}i=1M.

然后, 以骨架点为中心, 在输入点云与重建点云中分别利用KNN建立对应的邻域子图结构 NkP(si)和 NkPrec(si), 实现点云间的局部匹配.因此, 局部对齐的倒角距离损失:

$\begin{aligned} L_{\mathrm{rec}}= & \frac{1}{M} \sum_{i=1}^{M}\left(\frac{1}{K} \sum_{\boldsymbol{x} \in N_{k}^{P}\left(s_{i}\right)} \min _{\boldsymbol{y} \in N_{k}^{P} \text { rec }\left(s_{i}\right)}\|\boldsymbol{x}-\boldsymbol{y}\|_{2}^{2}+\right. \\ & \left.\frac{1}{K} \sum_{\boldsymbol{y} \in N_{k}^{P}\left(s_{i}\right)} \min _{\boldsymbol{x} \in N_{k}^{P r e c}\left(s_{i}\right)}\|\boldsymbol{x}-\boldsymbol{y}\|_{2}^{2}\right), \end{aligned}$

其中, M表示选择的骨架点数量, 即局部子图的数量,

$K=\left|N_{k}^{P}\left(\boldsymbol{s}_{i}\right)\right|=\left|N_{k}^{P_{\mathrm{rec}}}\left(\boldsymbol{s}_{i}\right)\right|, $

表示每个局部子图中的点数.该方法在子图结构上进行匹配对齐, 放大结构层面的局部差异, 并进一步细化局部结构的重构性能.

2.2 局部异常模拟

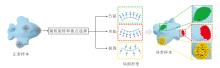
由于训练样本数量十分有限, 图自编码器在训练过程中难以充分学习正常模式的重构特征, 容易导致其倾向于实现恒等映射.换言之, 在测试阶段输入异常(缺陷)点云时, 模型的重建结果仍可能呈现为缺陷点云, 而非期望的正常点云.在2D图像异常检测中, 已有研究者[29, 30, 31]采用模拟异常生成的方法, 允许模型学习用于识别异常的判别性知识.借鉴这一思想, 本节提出局部异常模拟策略, 在正常点云中人为引入模拟的缺陷行为, 如凸起、凹陷和损毁, 以此扩充训练数据, 促使重建模型学习识别异常模式, 具体示意图如图2所示.将正常点云及其对应的多种模拟异常形态组合成训练样本对, 并利用这些样本对学习异常点云到正常点云的映射关系.该策略的核心思想在于, 通过引入多样化的模拟负样本, 使重构网络不再是简单记忆点云的完整形态, 而是能准确重建正常的点云形状.

图2 点云局部异常模拟策略示意图Fig.2 Illustration of point cloud local anomaly simulation strategy

首先, 对归一化后的点云P进行随机旋转变换:

PR=R(P),

其中R(· )表示随机旋转变换操作.通过在训练阶段对样本施加随机旋转增强操作, 可有效提升网络在测试阶段对不同空间姿态样本的泛化能力.

进一步地, 对于旋转变换后的点云PR, 在表面上随机选择一个视点pv.以该视点为中心, 检索距离其最近的K个点, 构建一个局部点云块Pv=NK(pv).对局部点云块施加随机缩放与平移变换, 以模拟各类缺陷情况, 变换后点的坐标为:

$\hat{\boldsymbol{p}}_{k}=\frac{1}{K} \sum_{\boldsymbol{p}_{k} \in \boldsymbol{P}_{v}} \boldsymbol{p}_{k}+\alpha\left(\boldsymbol{p}_{k}-\frac{1}{K} \sum_{\boldsymbol{p}_{k} \in \boldsymbol{P}_{v}} \boldsymbol{p}_{k}\right)+\boldsymbol{T}, $

其中, pk表示局部点云块中任意一点的坐标, α (· )表示随机缩放因子, T表示随机平移向量.以变换后的局部点云块作为局部异常模拟, 保持剩余点坐标不变, 生成具有局部异常的样本, 从而构建异常-正常样本对, 并作为网络输入.

2.3 局部匹配的点云异常检测

在训练阶段, 首先通过局部异常生成策略模拟真实场景中的异常数据, 并构建对应的异常-正常样本对.再将模拟的异常样本输入局部感知的点云图自编码器, 提取细粒度的局部几何特征, 并重建对应的正常点云样本.在重建过程中, 损失函数基于局部对齐策略, 匹配原始点云与重建点云在局部几何结构上的一致性, 提升网络对局部异常的敏感度与重构能力.整个训练流程如算法1所示.

算法1 局部感知点云图自编码器(训练阶段)

输入 点云样本P={p1, p2, …, pn}

输出 重建损失Lrec

step 1 归一化并下采样输入点云:

P'=Uniform(Normalize(P)),

采用局部异常生成操作, 生成异常点云 P︿, 构建异常-正常样本对$\left(\widehat{\boldsymbol{P}}, \boldsymbol{P}^{\prime}\right)$.

step 2 通过局部感知点云图自编码器提取细粒度局部特征X(last) , 预测点偏移矩阵:

Δ P=tanh(MLP(X(last))),

并重建点云Prec=P'+Δ P.

step 3 基于局部对齐策略计算点云P'与重建点云Prec的重建损失Lrec.

整个测试过程如算法2所示.首先对点云数据进行归一化处理, 并利用图自编码器对其进行重建, 以期获得正常点云.受PatchCore[6]的启发, 采用局部匹配的检测策略, 对比原始点云与其重建结果在局部块上的差异, 以此应对点云数据的无序性挑战.对于测试点云中的每个点, 提取其对应的局部块, 并计算原始局部块与重建局部块之间基于倒角距离的匹配分数.该分数被转换为该点的异常分数, 用于衡量该点对应的局部几何结构偏离正常的程度.最终每个节点的异常得分如下:

$A_{i}=L_{\mathrm{CD}}\left(\boldsymbol{P}_{i}, \widehat{\boldsymbol{P}}_{i}\right)$, (1)

其中,

$\boldsymbol{P}_{i}=N_{k}\left(\boldsymbol{p}_{i}^{\prime} \mid \boldsymbol{P}^{\prime}\right), $

表示输入点云上提取的对应局部点集,

$\widehat{\boldsymbol{P}}_{i}=N_{k}\left(\boldsymbol{p}_{i}^{\prime} \mid \boldsymbol{P}_{\text {rec }}\right), $

表示重建点云上提取的对应局部点集, P'表示归一化后的点云输入, Prec表示图自编码器重建的点云, p'i表示P'中第i个点, Nk(· )表示以该点为中心的K近邻搜索操作, LCD(· )表示倒角距离损失, 用于度量局部块之间的结构差异.

在异常检测过程中, 根据式(1)遍历所有节点, 可计算每个节点的异常得分.对于点云整体的异常检测, 选择最大异常得分作为样本整体的异常得分A, 实现对点云数据的异常检测, 并定位异常区域.

算法2 点云异常检测(测试阶段)

输入 点云样本P={p1, p2, …, pn}

输出 点云异常得分A

step 1 归一化并下采样输入点云:

P'=Uniform(Normalize(P)).

step 2 通过局部感知点云图自编码器提取细粒度局部特征X(last) , 预测点偏移矩阵:

Δ P=tanh(MLP(X(last))),

并重建点云

Prec=P'+Δ P.

step 3 提取输入点云P'与重建点云Prec对应的局部块.

step 4 遍历所有节点, 计算局部块之间的倒角距离, 并以此计算异常得分A.

3 实验及结果分析
3.1 实验环境

为了验证LPGR的有效性, 参照IMRNet[17]与R3D-AD[18]的实验设置, 在Real3D-AD( High-Reso-lution 3D Anomaly Detection Dataset)[12]、Anomaly-ShapeNet[17]这2个广泛使用的点云异常检测数据集上进行实验评估.

Real3D-AD数据集是一个基于真实三维模型采集的点云异常检测数据集, 每个样本具有较高的重建精度与密集的点集.数据集包含12类点云, 每个类别包含4个训练样本和100个测试样本.训练样本包含360° 完整的物体表面点云, 这些点云是通过手动标定和拼接物体多个侧面的扫描获得的.测试样本只扫描一侧, 与训练集有很大差异.

Anomaly-ShapeNet数据集是一个人工合成点云异常检测数据集, 通过对ShapeNet[32]中常用的三维模型进行修改而生成.数据集包含40个类, 超过1 600个表面点云样本.每个类别的训练集只包含4个样本, 而测试集旨在评估模型在正常样本和异常样本范围内的表现.测试集上广泛增加异常类型, 对网络的健壮性和通用性提出更高要求.

对于点云样本级异常检测, 根据每个样本的异常得分, 采用AUROC(Area Under the Receiver Opera-ting Characteristic Curve)[18]指标进行评估.对于点云节点级异常检测, 基于逐点异常得分计算该指标.AUROC分数为0.5表示网络没有辨别能力(相当于随机猜测), AUROC分数为1.0表示网络对正常样本和异常样本的区分完全正确.

在NVIDIA 48 GB RTX A6000 GPU, 2.30 GHz AMD EPYC 7642 48核CPU上以PyTorch[33]为深度学习框架进行网络搭建并训练LPGR.优化过程使用Adam(Adaptive Moment Estimation)[34]优化器, 初始学习率设为0.001.整个训练过程的批量大小设为128, 共进行100轮迭代.在 Anomaly-ShapeNet、Real3D-AD数据集上, 分别对所有输入的点云随机下采样至2 048个点和4 096个点的固定大小, 并将这些点云的重心设为坐标原点, 进行归一化处理.

3.2 对比实验

本文选择如下对比网络:PatchCore[6]、BTF[8]、M3DM[9]、CPMF[10]、Reg3D-AD[12]、IMRNet[17]、R3D-AD[18]、Group3AD[35]、FRM(Fusion-Restoration Mo-del)[36].PatchCore是一种二维异常检测网络, 通过替换特征提取器被应用于3D情境, FRM是一个多模态融合网络, FRM* 表示仅用三维点云这一个模态的数据作为输入.

3.2.1 样本级点云异常检测任务

在Anomaly-ShapeNet数据集上, 对比各网络在样本级异常检测任务中的性能, 结果如表1所示, 表中黑体数字表示最优值, 斜体数字表示次优值, Raw表示仅使用原始点云坐标作为特征输入, FPFH(Fast Point Feature Histogram)[37]表示利用快速点特征直方图提取特征并作为输入, PointMAE表示通过预训练的Point-MAE[38]提取特征并作为输入.

表1 各网络在Anomaly-ShapeNet数据集上样本级异常检测任务中AUROC指标对比 Table 1 AUROC comparison of different networks for sample-level anomaly detection task on Anomaly-ShapeNet dataset

由表1可见, LPGR在多数类别上均表现出优异的检测效果, 相比对比网络, 平均AUROC指标提升约2%~3%.由于不同类别的点云在形状、密度及空间分布方面存在显著差异, 对比网络在不同类别的异常检测任务中性能波动较大, 稳定性不足.相比之下, LPGR在多数类别的点云异常检测中均取得更优的性能.这在很大程度上归功于LPGR仅使用原始点云坐标作为输入, 以及通过局部感知的点云图自编码器提取几何结构特征并重建正常点云, 从而能适应不同形状与不同密度的点云特征提取与形状重建需求.

进一步在真实采样的Real3DAD数据集上进行对比实验, 相应样本级异常检测任务的性能对比如表2所示.表中黑体数字表示最优值, 斜体数字表示次优值.与AnomalyShapeNet数据集不同, Real3DAD数据集在测试阶段仅包含目标对象的部分扫描点云, 这种不完整的形状分布显著增加检测任务的难度.

表2 各网络在Real3-AD数据集上样本级异常检测任务中AUROC指标对比 Table 2 AUROC comparison of different networks for sample-level anomaly detection task on Real3-AD dataset

由表2可见, LPGR在多个类别的点云异常检测任务中均取得优异表现, 整体平均值达到最优水平, 充分验证其在处理真实、稀疏及局部缺失点云数据时的有效性与鲁棒性.

3.2.2 节点级点云异常检测任务

为了进一步验证LPGR对局部异常的感知能力, 在AnomalyShapeNet数据集上执行节点级别异常检测任务, 相应结果如表3所示, 表中黑体数字表示最优值, 斜体数字表示次优值.相比对比网络, LPGR在40个形状类别的节点异常检测中, 取得最优值或次优值的类别超过50%.从整体性能上看, LPGR平均AUROC指标相比其它网络提升约4%, 验证其在细粒度层面上对局部异常区域的有效感知与准确定位能力.

表3 各网络在Anomaly-ShapeNet数据集上节点级异常检测任务中AUROC指标对比 Table 3 AUROC comparison of different networks for node-level anomaly detection task on Anomaly-ShapeNet dataset

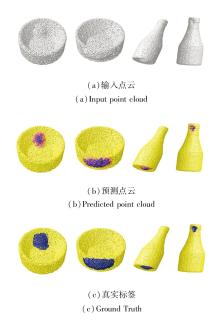
在Anomaly-ShapeNet数据集上进行节点级异常检测, 可视化结果如图3所示, 图中颜色深浅表示不同水平的异常得分.在节点级异常检测任务中, 计算输入点云与重建点云之间的差值, 直接生成异常图, 颜色越深表示对应节点的异常得分越高.图中示例涵盖不同类型的缺陷(如凸起、凹陷)以及不同类别的点云.

图3 LPGR在节点级异常检测任务中的可视化结果Fig.3 Visualization results of LPGR on node-level anomaly detection task

由图3可观察到, LPGR不仅能识别异常样本, 还能有效定位其局部异常区域, 充分体现其在细粒度异常检测任务中的有效性.

3.3 消融实验

本节旨在分析LPGR中不同组件对异常检测性能的影响.为此, 设计四组网络进行消融实验.

1)网络A:将图自编码器替换为以 PointNet++为骨干网络的编解码架构.

2)网络B:在图自编码器训练阶段引入全局匹配损失.

3)网络C:在训练阶段去除局部异常生成模块, 仅使用正常样本作为输入.

4)网络D:LPGR.

相应消融实验结果如表4所示, 表中S-AUROC表示样本级别异常检测精度, N-AUROC表示节点级异常检测精度.由表可得如下结论.

表4 各网络消融实验结果 Table 4 Ablation experiment results of different networks

1)图自编码器能有效刻画点云的局部结构特征, 显著提升网络对局部异常的敏感度.

2)全局匹配损失主要衡量两个整体点云之间的平均几何差异, 误差往往由大面积的正常区域主导.当异常仅发生在局部区域时, 全局损失容易被大量正常点“ 淹没” , 导致异常信号被弱化, 降低对局部异常的敏感性.相反地, 局部对齐损失通过对子图结构进行一致性约束, 使生成的正常点云更精细, 从结构层面放大局部差异, 进一步提升异常检测性能.

3)局部异常生成策略强制网络学习异常样本到正常样本的映射关系, 能获取用于识别异常的判别性知识, 显著增强异常检测能力.

3.4 超参数分析

本节分析如下5个关键超参数:骨架点数量M、子图结构大小K、局部异常区域大小$\left|N_{K}\left(\boldsymbol{p}_{v}\right)\right|$, 随机缩放因子α 、随机平移向量T.

定义骨架点数量

M=ρ N,

其中

ρ = 14, 18, 116, 132, 164

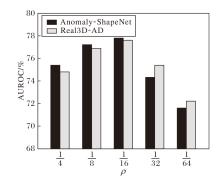
表示采样率.ρ 改变时LPGR在Anomaly-ShapeNet、Real3-AD数据集上的AUROC指标如图4所示.

图4 ρ 对LPGR性能的影响Fig.4 Effect of ρ on LPGR performance

由图4可知, 在ρ = 116时, LPGR性能达到最优.M过少时, 网络难以完整刻画局部几何结构, 导致检测性能下降; M过多则会引入较多冗余信息, 干扰特征提取过程, 性能同样有所降低.

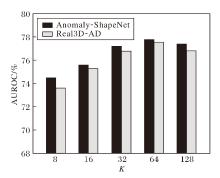
在局部对齐重建损失中, 定义子图结构大小K=8, 16, 32, 64, 128, K改变时, LPGR在2个数据集上的AUROC指标如图5所示.由图可知, 在K=64时, LPGR性能达到最优.这表明合适的子图大小有利于网络对局部几何结构的捕捉.较小的子图结构可能破坏点云局部几何结构, 而过大的子图结构可能使当前几何结构中混杂不相关节点, 导致网络性能下降.

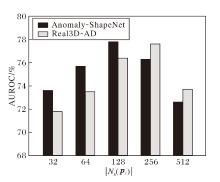
图5 K对LPGR性能的影响Fig.5 Effect of K on LPGR performance

定义生成的局部异常区域范围$\left|N_{K}\left(\boldsymbol{p}_{v}\right)\right|$=32, 64, 128, 256, 512, $\left|N_{K}\left(\boldsymbol{p}_{v}\right)\right|$改变时, LPGR在2个数据集上的AUROC指标如图6所示.

图6 局部异常区域大小对LPGR性能的影响Fig.6 Effect of different sizes of local abnormal area on LPGR performance

由图6可知, 在Anomaly-ShapeNet数据集上, 当$\left|N_{K}\left(\boldsymbol{p}_{v}\right)\right|=128$时, LPGR性能达到最优.在Real3D- AD数据集上, 当$\left|N_{K}\left(\boldsymbol{p}_{v}\right)\right|=256$时, LPGR性能达到最优.这表明在不同数据集上异常区域大小可能有所差异, 模拟的异常样本越接近真实异常样本分布, 性能提升越显著.

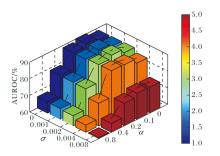
定义随机缩放因子α =0, 0.1, 0.2, 0.4, 0.8, 当α =0.1时表示对局部点云放大1.1倍或缩小至90%.当α =0时表示维持原始尺寸不变.同时分别从标准差σ =0, 0.001, 0.002, 0.004, 0.008的高斯分布中生成平移向量T.在Anomaly-ShapeNet数据集(Ashtray类别)上进行对比实验, 结果如图7所示.由图可见, 当α =0.1, 平移向量T中σ =0.002时, LPGR取得最优性能.相比平移变换, 缩放比例的大小对网络影响更显著.

图7 α , T对LPGR性能的影响Fig.7 Effect of α and T on LPGR performance

4 结束语

本文针对异常检测中点云局部细节重构不足导致的局部异常难以有效识别问题, 提出基于局部感知图重构的点云异常检测网络(LPGR), 充分发挥点云的图结构特性.引入局部敏感的边卷积算子, 实现对点云局部几何特征的高效建模, 提升网络对细粒度异常的感知能力.与此同时, 设计子图结构对齐机制, 在训练阶段对重建结果施加结构一致性约束, 能更精细还原正常样本的局部结构特征, 从结构层面放大正常样本与异常样本之间的差异.结合局部异常生成策略, 进一步学习异常样本到正常样本的映射关系, 提升网络综合检测性能.此外, 利用局部匹配检测算法, 为异常区域的空间定位提供更具针对性的计算方式, 有效实现从整体异常识别到局部异常定位的统一框架.大量实验验证LPGR在多个点云类别上的优异性能, 具备较强的普适性与泛化性.

尽管LPGR在性能上取得明显提升, 但仍存在值得进一步研究的方向.首先, 在复杂场景或密集点云数据中, 点与点之间的连接关系更复杂, 如何在保证局部结构准确刻画的同时, 降低图构建与信息聚合的计算开销, 是后续需要研究的重要问题.其次, 本文主要基于几何特征进行异常检测, 而在实际三维感知任务中, 往往伴随纹理、强度或语义等多模态信息.如何将点云的几何结构与其它模态信息进行高效融合, 实现多模态驱动的异常检测, 是未来值得探索的方向之一.

本文责任编委 高 隽

Recommended by Associate Editor GAO Jun

参考文献
[1] QI C R, SU H, MO K, et al. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 77-85. [本文引用:1]
[2] GUO Y L, WANG H Y, HU Q Y, et al. Deep Learning for 3D Point Clouds: A Survey. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(12): 4338-4364. [本文引用:1]
[3] MA X X, WU J, XUE S, et al. A Comprehensive Survey on Graph Anomaly Detection with Deep Learning. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(12): 12012-12038. [本文引用:1]
[4] BERGMANN P, JIN X, SATTLEGGER D, et al. The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and Localization[C/OL]. [2025-09-07]. https://arxiv.org/pdf/2112.09045v1. [本文引用:1]
[5] BERGMANN P, SATTLEGGER D. Anomaly Detection in 3D Point Clouds Using Deep Geometric Descriptors // Proc of the IEEE/CVF Winter Conference on Applications of Computer Vision. Washington, USA: IEEE, 2023: 2612-2622. [本文引用:1]
[6] ROTH K, PEMULA L, ZEPEDA J, et al. Towards Total Recall in Industrial Anomaly Detection // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 14298-14308. [本文引用:4]
[7] HE H Y, ZHANG J N, CHEN H X, et al. A Diffusion-Based Framework for Multi-class Anomaly Detection. Proc of the AAAI Conference on Artificial Intelligence, 2024, 38(8): 8472-8480. [本文引用:1]
[8] HORWITZ E, HOSHEN Y. Back to the Feature: Classical 3D Features Are(Almost) All You Need for 3D Anomaly Detection // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Re-cognition. Washington, USA: IEEE, 2023: 2968-2977. [本文引用:2]
[9] WANG Y, PENG J L, ZHANG J N, et al. Multimodal Industrial Anomaly Detection via Hybrid Fusion // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2023: 8032-8041. [本文引用:2]
[10] CAO Y K, XU X H, SHEN W M. Complementary Pseudo Multimodal Feature for Point Cloud Anomaly Detection. Pattern Recognition, 2024, 156. DOI: 10.1016/j.patcog.2024.110761. [本文引用:2]
[11] RUDOLPH M, WEHRBEIN T, ROSENHAHN B, et al. Asymme-tric Student-Teacher Networks for Industrial Anomaly Detection // Proc of the IEEE/CVF Winter Conference on Applications of Computer Vision. Washington, USA: IEEE, 2023: 2591-2601. [本文引用:1]
[12] LIU J Q, XIE G Y, CHEN R T, et al. Real3D-AD: A Dataset of Point Cloud Anomaly Detection // Proc of the 37th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2023: 30402-30415. [本文引用:3]
[13] HOLLES R C, FISCHLER M A. A RANSAC-Based Approach to Model Fitting and Its Application to Finding Cylinders in Range Data // Proc of the 7th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 1981: 637-643. [本文引用:1]
[14] HUANG C Q, XU Q W, WANG Y F, et al. Self-Supervised Mas-king for Unsupervised Anomaly Detection and Localization. IEEE Transactions on Multimedia, 2022, 25: 4426-4438. [本文引用:1]
[15] PIRNAY J, CHAI K. Inpainting Transformer for Anomaly Detection // Proc of the 21st International Conference on Image Analysis and Processing. Berlin, Germany: Springer, 2022: 394-406. [本文引用:1]
[16] YAN X D, ZHANG H D, XU X M, et al. Learning Semantic Context from Normal Samples for Unsupervised Anomaly Detection. Proc of the AAAI Conference on Artificial Intelligence, 2021, 35(4): 3110-3118. [本文引用:1]
[17] LI W X, XU X H, GU Y, et al. Towards Scalable 3D Anomaly Detection and Localization: A Benchmark via 3D Anomaly Synthesis and a Self-Supervised Learning Network // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2024: 22207-22216. [本文引用:4]
[18] ZHOU Z Y, WANG L, FANG N Y, et al. R3D-AD: Reconstruction via Diffusion for 3D Anomaly Detection // Proc of the 18th European Conference on Computer Vision. Berlin, Germany: Springer, 2024: 91-107. [本文引用:4]
[19] DOHMATOB E, FENG Y Z, KEMPE J. Model Collapse Demystified: The Case of Regression // Proc of the 38th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2024: 46979-47013. [本文引用:1]
[20] LI W Q, ZHENG B Z, XU X H, et al. Multi-sensor Object Ano-maly Detection: Unifying Appearance, Geometry, and Internal Properties // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2025: 9984-9993. [本文引用:1]
[21] ZHOU Q H, YAN J T, HE S B, et al. PointAD: Comprehending 3D Anomalies from Points and Pixels for Zero-Shot 3D Anomaly Detection // Proc of the 38th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2024: 84866-84896. [本文引用:1]
[22] SHI Y K, ZHAN X, LI Y Q, et al. Cycle-CFM: An Unsupervised Framework for Robust Multimodal Anomaly Detection in Industrial Settings. Expert Systems with Applications, 2026, 298(C). DOI: 10.1016/j.eswa.2025.129745. [本文引用:1]
[23] ZHU W B, WANG L D, ZHOU Z Q, et al. Real-IAD D3: A Real-World 2D/Pseudo-3D/3D Dataset for Industrial Anomaly Detection // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2025: 15214-15223. [本文引用:1]
[24] CHEN C F, QIAN S S, FANG Q, et al. HAPGN: Hierarchical Attentive Pooling Graph Network for Point Cloud Segmentation. IEEE Transactions on Multimedia, 2020, 23: 2335-2346. [本文引用:1]
[25] SIMONOVSKY M, KOMODAKIS N. Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs // Proc of the IEEE Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2017: 29-38. [本文引用:1]
[26] WANG Y, SUN Y B, LIU Z W, et al. Dynamic Graph CNN for Learning on Point Clouds. ACM Transactions on Graphics , 2019, 38(5). DOI: 10.1145/3326362. [本文引用:1]
[27] QI C R, YI L, SU H, et al. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space // Proc of the 31st International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2017: 5105-5114. [本文引用:1]
[28] LIN Z H, HUANG S Y, WANG Y F. Learning of 3D Graph Convolution Networks for Point Cloud Analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(8): 4212-4224. [本文引用:1]
[29] HU T, ZHANG J N, YI R, et al. AnomalyDiffusion: Few-Shot Anomaly Image Generation with Diffusion Model. Proc of the AAAI Conference on Artificial Intelligence, 2024, 38(8): 8526-8534. [本文引用:1]
[30] LI C L, SOHN K, YOON J, et al. CutPaste: Self-Supervised Lear-ning for Anomaly Detection and Localization // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 9659-9669. [本文引用:1]
[31] YE J N, ZHAO W G, YANG X, et al. PO3AD: Predicting Point Offsets Toward Better 3D Point Cloud Anomaly Detection // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2025: 1353-1362. [本文引用:1]
[32] CHANG A X, FUNKHOUSER T, GUIBAS L, et al. ShapeNet: An Information-Rich 3D Model Repository[C/OL]. [2025-09-07]. https://arxiv.org/pdf/1512.03012. [本文引用:1]
[33] PASZKE A, GROSS S, MASSA F, et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library // Proc of the 33th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2019: 8026-8037. [本文引用:1]
[34] KINGMA D P, BA J L. Adam: A Method for Stochastic Optimiza-tion[C/OL]. [2025-09-07]. https://arxiv.org/pdf/1412.6980. [本文引用:1]
[35] ZHU H Z, XIE G Y, HOU C B, et al. Towards High-Resolution 3D Anomaly Detection via Group-Level Feature Contrastive Lear-ning // Proc of the 32nd ACM International Conference on Multimedia. New York, USA: ACM, 2024: 4680-4689. [本文引用:1]
[36] WANG J X, NIU Y C, HUANG B Q. Fusion-Restoration Model for Industrial Multimodal Anomaly Detection. Neurocomputing, 2025, 637. DOI: 10.1016/j.neucom.2025.130073. [本文引用:1]
[37] RUSU R B, BLODOW N, BEETZ M. Fast Point Feature Histograms(FPFH) for 3D Registration // Proc of the IEEE Internatio-nal Conference on Robotics and Automation. Washington, USA: IEEE, 2009: 3212-3217. [本文引用:1]
[38] PANG Y J, WANG W X, TAY F E H, et al. Masked Autoenco-ders for Point Cloud Self-Supervised Learning // Proc of the 17th European Conference on Computer Vision. Berlin, Germany: Springer, 2022: 604-621. [本文引用:1]