引用本文
王依琳, 叶海良, 郭文慧, 曹飞龙. 不确定性原型学习的跨域情绪识别方法. 模式识别与人工智能, 2025,38(11): 974-985
WANG Yilin, YE Hailiang, GUO Wenhui, CAO Feilong. Uncertainty-Aware Prototypical Learning Method for Cross-Domain Emotion Recognition. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2025,38(11): 974-985.  
Doi: 10.16451/j.cnki.issn1003-6059.202511002
Permissions
Copyright©2025, 《模式识别与人工智能》编辑部
《模式识别与人工智能》编辑部
不确定性原型学习的跨域情绪识别方法
王依琳1, 叶海良1, 郭文慧1, 曹飞龙2
1.中国计量大学 理学院 杭州 310018
2.浙江师范大学 数学科学学院 金华 321004
通信作者:

曹飞龙,博士,教授,主要研究方向为深度学习、图像处理等.E-mail:icteam@163.com.

作者简介:

王依琳,硕士研究生,主要研究方向为深度学习、情感计算.E-mail:wangyl001101@163.com.

叶海良,博士,副教授,主要研究方向为深度学习、图像处理等.E-mail:yhl575@163.com.

郭文慧,博士,讲师,主要研究方向为深度学习、情感计算等.E-mail:whguo3823269@163.com.

收稿日期: 2025-10-04 接受日期: 2025-11-24
资助项目: 国家自然科学基金项目(No.62536006)、浙江省自然科学基金项目(No.LQN26F030010,LZ26F030003)资助
摘要

脑电情绪识别因其在心理健康监测、脑机交互等领域的广泛应用而备受关注.然而,现有方法仍面临电极空间信息利用不足、标注数据稀缺及跨域分布偏移等问题.为此,文中提出不确定性原型学习的跨域情绪识别方法.首先,设计位置编码引导的跨域图半监督学习模块,引入正余弦位置编码,将电极的空间拓扑结构嵌入邻接矩阵,突破传统方法仅依赖物理距离构建图结构的局限,有效融入符合脑电生理特性的空间先验知识.在此基础上,利用图结构的特征传播机制,协同挖掘标注样本与未标注样本中的深层拓扑表示,缓解标签稀缺带来的训练困难.然后,构建不确定性原型学习模块,量化样本特征的可靠性,动态优化各类别的情感原型,抑制噪声干扰与域间分布偏移,增强方法在不同域间的泛化能力.在多个公开脑电情绪数据集上的实验表明,文中方法在跨域识别任务中性能较优.

关键词: 图神经网络; 情绪识别; 深度学习; 半监督学习; 原型学习
中图分类号:TP181
Uncertainty-Aware Prototypical Learning Method for Cross-Domain Emotion Recognition
WANG Yilin1, YE Hailiang1, GUO Wenhui1, CAO Feilong2
1. College of Sciences, China Jiliang University, Hangzhou 310018
2. School of Mathematical Sciences, Zhejiang Normal University, Jinhua 321004
Corresponding author:
CAO Feilong, Ph.D., professor. His research interests include deep learning and image processing.

About Author:
WANG Yilin, Master student. Her re-search interests include deep learning and affec-tive computing.
YE Hailiang, Ph.D., associate professor. His research interests include deep learning and image processing.
GUO Wenhui, Ph.D., lecturer. Her re-search interests include deep learning and affec-tive computing.

Fund:Supported by National Natural Science Foundation of China(No.62536006), Natural Science Foundation of Zhejiang Province(No.LQN26F030010,LZ26F030003)
Abstract

Electroencephalogram(EEG)-based emotion recognition attracts increasing attention due to its broad applications in mental health monitoring and brain-computer interfaces. However, existing methods still suffer from inadequate utilization of electrode spatial information, limited labeled data, and cross-domain distribution shifts. To address these issues, an uncertainty-aware prototypical learning method for cross-domain emotion recognition is proposed. First, a position encoding-guided graph semi-supervised module is designed. The spatial topology is embedded into the adjacency matrix through incorporating sine-cosine positional encoding. Thus, the limitation of traditional graph constructions based solely on physical distance is broken through, and physiological priors of EEG signals are effectively integrated. Based on the above, the graph-based feature propagation mechanism is leveraged to collaboratively learn deep topological representations from both labeled and unlabeled samples, mitigating the challenge of label scarcity. Second, an uncertainty-aware prototype learning module is constructed to dynamically refine emotion prototypes by quantifying feature reliability. Thereby, noise and cross-domain shifts are suppressed while generalization ability of the model across different domains is enhanced. Experiments on multiple public EEG emotion datasets demonstrate that the proposed method outperforms state-of-the-art methods on cross-domain recognition tasks.

Key words: Graph Neural Networks; Emotion Recognition; Deep Learning; Semi-supervised Learning; Prototype Learning

情绪识别在人机交互[1]、精神障碍诊断与康复[2, 3]、交通管理[4]、安全防护[5]等多个领域发挥关键作用.相比面部表情、语音等容易被主观控制的外在信号, 脑电图(Electroencephalography, EEG)具有较高的时间分辨率, 受主观意志影响较小, 能更客观真实地反映个体的内在情绪状态[6].这一独特优势使得基于EEG的情感识别技术在提升情感感知系统的准确性与鲁棒性方面展现出巨大潜力, 成为近年来学术界的研究热点之一[7, 8].

当前, 大多数基于EEG的情感识别研究仍主要依赖于传统监督学习方法, 要求训练集上所有样本均具备精确的标注信息.然而, 获取高质量标注数据面临成本高昂、过程繁琐、耗费专业人力等诸多挑战.相比之下, 未标注数据的采集更容易, 数据规模更容易扩大.在此背景下, 半监督学习[9]作为一种能同时利用少量标注数据与大量未标注数据的学习范式, 表现出显著优势.它不仅有助于降低对人工标注的依赖, 还能有效缓解因标注样本稀缺而导致的模型表达能力受限的问题[10], 从而为构建更具泛化性能的情绪识别模型提供可行路径.Zhang等[11]采用MixMatch[12]进行脑电图表征, 证明MixMatch在标注数据稀缺场景中的有效性与优越性.Zhang等[13]提出PARSE(Pairwise Alignment of Representa-tions in Semi-supervised EEG Learning), 将整体式半监督学习与领域适应技术结合, 显著提升跨域情绪识别任务的性能.然而, 半监督学习的性能在很大程度上取决于模型能否从未标注数据中有效提取具有判别性的特征表示, 这要求模型能准确建模EEG信号中蕴含的内在数据结构.

在此背景下, 图神经网络(Graph Neural Networks, GNN)凭借其对非欧几里得数据结构的强大建模能力, 在生物医学数据处理领域取得巨大进展[14], 成为实现高效半监督情绪识别的理想技术框架之一.在情绪识别任务中, 基于GNN的方法不断涌现.Yang等[15]提出AEG(Adjacency-Explainable Graph Neural Network), 从互信息角度出发, 对重要脑电图通道进行全面识别, 增强情绪识别的可解释性.Zhong等[16]提出RGNN(Regularized Graph Neural Net-works), 引入局部特征与全局特征交互机制, 增强网络对复杂信号模式的捕捉能力.Zhang等[17]提出GCB-Net(Graph Convolutional Broad Network), 挖掘图结构数据中的深层次信息.Song等[18]提出V-IAG(Variational Instance-Adaptive Graph Method), 实现脑电通道关系的灵活建模.

随后的研究逐渐开始融合分层学习策略.Li等[19]提出GMSS(Graph-Based Multi-task Self-Super-vised Learning), 引入多个辅助任务, 有效缓解模型过拟合问题.Jin等[20]提出PGCN(Pyramidal Graph Convolutional Network), 从局部、中观到全局层级分层聚合脑电特征, 实现电极关系的精细刻画.Yan等[21]提出BGAGCN(Bridge Graph Attention-Based Graph Convolution Network), 结合图注意力机制与多尺度变换器, 增强特征提取的表达能力.综上可知, 基于GNN的情绪识别方法正朝着更精细的结构建模、多层次特征融合与自监督学习方向不断发展, 显著提升对EEG信号复杂时空依赖关系的建模能力.

近期, 学者进一步聚焦于增强模型的鲁棒性与优化其结构设计.An等[22]提出LGDAAN-Nets, 为EEG情绪识别提供新思路.Pan等[23]提出MSFR-GCN(Multi-scale Feature Reconstruction Graph Convo-lutional Network), 重点研究EEG特征本身的重要性.Gao等[24]提出CU-GCN(Connectivity Uncertainty GCN), 基于分布的不确定性方法表示EEG信号中的空间依赖性和时空相关性.Ye等[25]提出DS-AGC(Dual-Stream Self-Attentive Adversarial Graph Con-trastive Learning Framework), 结合多域适应与图对比学习, 有效解决跨域脑电情绪识别中的标注数据稀缺问题.上述方法均在不同程度上推动图神经网络在情绪识别中的广泛应用.

尽管这些方法在EEG情感识别任务中展现出一定成效, 但仍存在如下缺陷.

1)GNN中邻接矩阵未能有效融合电极空间位置的结构化信息.现有方法通常基于电极间的欧几里得距离构建邻接矩阵, 尽管在一定程度上反映电极的空间邻近关系, 但未将这种位置关系以结构化编码方式深度嵌入邻接矩阵.这种处理方式导致邻接矩阵仅体现距离远近的数值差异, 而无法显式编码电极在头皮上的空间布局特征, 使得GNN难以充分利用空间位置隐含的生理拓扑先验, 限制对脑电信号复杂空间模式的精准建模.

2)未标注数据利用不充分.现有方法大多局限于全监督学习范式, 即便部分研究提出半监督改进策略, 仍未能有效结合GNN的图结构传播机制以充分挖掘未标注样本中蕴含的潜在信息, 因此在标注数据稀缺场景中性能显著下降.

3)跨域[26]与原型学习[27]的适配性不足.当前方法缺乏对跨域特征空间与原型表示之间深层协同关系的建模, 难以充分挖掘跨域知识迁移的潜力.

为此, 本文提出不确定性原型学习的跨域情绪识别方法(Uncertainty-Aware Prototypical Learning Me-thod for Cross-Domain Emotion Recognition, UPLM).首先, 设计位置编码(Positional Encoding, PE)引导的跨域图半监督学习模块, 结合基于欧几里得距离构建的邻接矩阵与位置编码, 有效克服传统方法仅依赖物理距离、难以显式融入拓扑先验知识[28]的局限, 为后续图建模提供更符合EEG生理特性的结构基础.在此基础上, 提出跨域图半监督学习框架, 将图卷积网络(Graph Convolutional Network, GCN)引入EEG情绪识别任务, 利用GCN建模多通道EEG信号间复杂拓扑依赖关系, 同时, 借助图结构固有的信息传播机制, 挖掘未标注样本中潜在的特征分布模式, 有效弥补标注数据稀缺带来的信息缺失问题, 提升方法在低标签率条件下的表征能力, 缓解因标注稀缺带来的泛化性能约束.此外, 为了提升方法在跨域场景中的识别适应性与鲁棒性, 构建不确定性原型学习(Uncertainty Prototype Learning, UPL)模块, 引入不确定性量化机制[29], 优化各类别情感原型的估计过程, 有效抑制源域中噪声样本对原型表示的干扰.

1 不确定性原型学习的跨域情绪识别方法

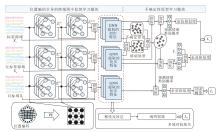
本文提出不确定性原型学习的跨域情绪识别方法(UPLM), 整体架构如图1所示.

图1 UPLM架构图Fig.1 Architecture of UPLM

对于训练集上的每位受试者, 本文选取前Ns位受试者作为带标签源域S(含EEG信号特征和标签), 其余Nu位受试者作为无标签源域U(仅提供EEG信号特征).对于测试集上的Nt位受试者(目标域T), 仅提供EEG信号特征用于性能评估, 不给予任何标签信息[10].标签源域S、无标签源域U和目标域T数据表示如下:

$\begin{array}{l} D_{s}=\left\{x_{i}^{s}, y_{i}^{s}\right\}_{i=1}^{N_{s}}, \\ D_{u}=\left\{x_{i}^{u}, y_{i}^{u}\right\}_{i=1}^{N_{u}}, \\ D_{t}=\left\{x_{i}^{t}, y_{i}^{t}\right\}_{i=1}^{N_{t}}, \end{array}$

其中 xis、 xiu、 xit表示样本, yis、 yiu、 yit表示对应的情绪标签, yiu在训练过程中是未知的.

如图1所示, UPLM包含两个核心模块:位置编码引导的跨域图半监督学习模块和不确定性原型学习模块.前者利用位置编码增强图结构, 即将位置编码融入基于欧几里得距离构建的邻接矩阵, 结构化嵌入电极空间位置信息, 弥补传统邻接矩阵仅依赖物理距离、无法显式编码拓扑先验知识的缺陷.之后, 考虑到训练过程中无法获取无标签源域的标签集合Yu和目标域的标签集合Yt, 将图半监督学习引入EEG情绪识别任务, 既能捕捉信号拓扑关联, 又能挖掘未标注样本特征以填补标注信息缺口.不确定性原型学习模块通过训练使3个域的区分度最小化, 同时维持域间分布偏移的一致性.最后, 采用源域半监督学习损失、目标域学习损失与多域对抗损失协同优化, 实现跨域情绪状态的识别.

1.1 位置编码引导的跨域图半监督学习模块

神经科学研究表明, 脑区间连接强度遵循距离平方反比定律, 即连接强度会随着距离增加而显著减弱[30].因此, 构建初始邻接矩阵A, 模拟电极之间的空间耦合特性.定义

âij= δdij2,

其中, dij表示节点之间的欧氏距离, δ =0.9表示稀疏因子.

为了确保稀疏性, 进一步对 âij进行阈值化处理.将数值小于ε =0.1的元素置0以过滤微弱关联, 将数值大于c=1的元素截断为1以削弱自环及极近距离电极的过度影响[20], 最终得到初始邻接矩阵A={aij}∈ Rn× n, n表示电极总数, A中元素

$a_{i j}=\left\{\begin{array}{ll} 1, & \hat{a}_{i j}> c \\ \frac{\delta}{d_{i j}^{2}}, & \varepsilon \leqslant \hat{a}_{i j} \leqslant c . \\ 0, & \hat{a}_{i j}< \varepsilon \end{array}\right.$

然而, 上述初始邻接矩阵仅依赖点对点的距离度量, 无法显式编码脑电信号的空间拓扑先验知识, 即无法区分同脑区电极的近距离关联与跨脑区电极的近距离关联, 也难以捕捉电极在全局脑区排布中的拓扑归属及多尺度相对位置关系, 导致后续图模型仅能依赖数据驱动学习拓扑特征, 建模精度易受物理距离的片面性影响.因此, 本文在现有邻接矩阵的基础上进一步引入位置编码以弥补这一缺陷.

给定n个电极, 为每个电极生成一个D维的位置编码向量.设电极位置索引p∈ [0, n-1], 编码维度索引q∈ [0, D-1], 则位置编码矩阵PE∈ Rn× D中元素定义如下:

$\begin{array}{l} e_{p, 2 q}=\sin \left(p \cdot 10000^{-\frac{2 q}{D}}\right) \\ e_{p, 2 q+1}=\cos \left(p \cdot 10000^{-\frac{2 q}{D}}\right) \end{array}$

其中, q表示编码向量的维度索引, 2q、2q+1分别表示编码向量的偶数维和奇数维.该编码机制引入不同周期的正弦-余弦函数, 使编码向量能精准捕捉电极间的相对位置关系.频率项10000-2q/D通过不同维度赋予独特波长, 实现对多尺度空间拓扑关系的有效刻画, 最终为邻接矩阵注入显式的拓扑先验信息, 提升其对脑电信号空间结构的建模能力.

采用这一方法的核心目的并非直接模拟复杂的大脑功能连接, 而是为缺乏先验连接信息的电极阵列提供一种连续、平滑且具备良好泛化能力的空间结构初始化表示.该编码机制在数学上保证空间邻近电极获得相似的位置嵌入, 在一定程度上与神经科学中空间邻近的脑区更可能具有功能耦合的普遍性原则契合[31].

将该编码矩阵PE={epq}与原始邻接矩阵A叠加, 最终得到增强邻接矩阵 A˜∈ Rn× n. A˜不仅保留原始矩阵中的物理距离关联信息, 更成功为邻接矩阵注入显式的空间拓扑先验知识, 提升矩阵对脑电信号复杂空间结构的建模能力.

位置编码引导的跨域图半监督学习模块以标签源域S、无标签源域U和目标域T为学习对象, 结合GCN的拓扑建模能力与半监督学习对无标签数据的优势, 提升方法在跨域场景中的情感识别性能.

首先计算增强邻接矩阵 A˜对应的拉普拉斯矩阵L, 然后通过GCN实现相邻节点间的信息传递[32], 第l层输出节点特征如下:

$\begin{array}{l} \boldsymbol{Z}_{u}^{(l+1)}=\sigma\left(L \boldsymbol{Z}_{u}^{(l)} \boldsymbol{W}_{u}^{(l)}\right), \\ \boldsymbol{Z}_{s}^{(l+1)}=\sigma\left(L \boldsymbol{Z}_{s}^{(l)} \boldsymbol{W}_{s}^{(l)}\right), \\ \boldsymbol{Z}_{t}^{(l+1)}=\sigma\left(L \boldsymbol{Z}_{t}^{(l)} \boldsymbol{W}_{t}^{(l)}\right), \end{array}$

其中, Z* l(* 表示u, s, t)表示第l层的输入节点特征, 初始输入特征 Z* 0为原始输入数据X* , W* l表示可学习权重矩阵, σ (· )表示激活函数.

为了避免GCN过平滑问题, 采用双层GCN架构并引入跳跃连接, 最终提取的特征为:

$\begin{array}{l} \widehat{\boldsymbol{X}}_{s}=F C\left(\operatorname{concat}\left(\boldsymbol{X}_{s}, \boldsymbol{Z}_{s}^{(1)}, \boldsymbol{Z}_{s}^{(2)}\right)\right) \in \mathbf{R}^{N_{s} \times h}, \\ \widehat{\boldsymbol{X}}_{u}=F C\left(\operatorname{concat}\left(\boldsymbol{X}_{u}, \boldsymbol{Z}_{u}^{(1)}, \boldsymbol{Z}_{u}^{(2)}\right)\right) \in \mathbf{R}^{N_{u} \times h}, \\ \widehat{\boldsymbol{X}}_{t}=F C\left(\operatorname{concat}\left(\boldsymbol{X}_{t}, \boldsymbol{Z}_{t}^{(1)}, \boldsymbol{Z}_{t}^{(2)}\right)\right) \in \mathbf{R}^{N_{t} \times h}, \end{array}$

其中, h表示特征维度, FC(· )表示全连接操作, concat(· )表示特征拼接操作.

1.2 不确定性原型学习模块

为了提升方法在跨域情绪识别场景中对数据分布偏移及噪声样本的鲁棒性, 设计不确定性原型学习模块.原型表征作为一种紧凑的嵌入向量, 能有效编码特定类别或关系的核心判别特征, 被视为该类别的质心表征, 在表示学习中具有重要作用[33].本文通过精确量化样本特征的不确定性, 并基于此动态优化类别原型表示, 实现更鲁棒的情绪类别中心建模.

不确定性原型学习模块的核心设计包含3个关键步骤.1)基于标签源域和无标签源域计算基础原型, 捕捉跨域场景中数据的整体统计特性.2)通过一个轻量级不确定性估计网络, 同时评估标签源域样本和无标签源域样本的特征可靠性, 并对其中置信度较低的样本进行自适应降权处理, 构建有效的加权原型.3)引入可学习的融合参数, 动态集成基础原型与不确定性加权原型.该设计使得最终生成的类别中心能充分融合源域中有标签样本的判别信息与无标签样本的分布结构, 在抑制噪声与域间偏移干扰的同时, 更准确刻画跨域场景中的真实数据分布.

1)基础原型计算.给定标签源域特征 X︿s∈ RNs×h与无标签源域特征 X︿u∈ RNu×h, 基础原型矩阵[10]表示如下:

$\boldsymbol{P}_{b}=\left(\boldsymbol{Y}^{\mathrm{T}} \boldsymbol{Y}\right)^{-1} \boldsymbol{Y}^{\mathrm{T}} \in \mathbf{R}^{C \times h}, $

其中

Y=concat(Ys, Yu)∈ R(Ns+Nu)×C

表示融合标签矩阵, Ys∈ RNs×C表示标签源域的标签, Yu∈ RNu×C表示无标签源域的标签, C表示类别数.Pb每行对应一个类别的中心特征.融合特征矩阵为:

$\boldsymbol{X}=\operatorname{concat}\left(\widehat{\boldsymbol{X}}_{s}, \widehat{\boldsymbol{X}}_{u}\right) \in \mathbf{R}^{\left(N_{s}+N_{u}\right) \times h} .$

由于训练过程中无标签源域的真实标签Yu∈ RNu×C未知, 初始化原型矩阵Pb为无标签样本生成伪标签:

$\widetilde{\boldsymbol{Y}}_{u}=S\left(\operatorname{Classifier}\left(\widehat{\boldsymbol{X}}_{u}\right)\right) \approx \boldsymbol{Y}_{u}, $

其中,

$\operatorname{Classifier}\left(\widehat{\boldsymbol{X}}_{u}\right)=\operatorname{softmax}\left(\widehat{\boldsymbol{X}}_{u}^{\mathrm{T}} \boldsymbol{B} \boldsymbol{P}_{b}\right) \text {, }$

Classifier(· )表示分类器, 通过特征与原型的相似度计算类别概率, S(· )表示锐化操作, 即高置信度者越强, 低置信度者越弱, B表示分类器的可学习权重矩阵.

2)特征不确定性估计与加权原型.为了量化样本特征的可靠性, 通过一个两层神经网络估计每个样本的不确定性分数:

U=Softplus(HW2+b2)∈ R(Ns+Nu)×1,

其中,

H=ReLU(XW1+b1)∈ R(Ns+Nu)×32,

表示隐藏层特征, W1、W2表示权重, b1、b2表示偏置, ReLU(· )和Softplus(x)=ln(1+ex)表示激活函数.之后, 对样本特征进行加权, 降低低可靠性样本对原型的影响, 得到不确定性加权原型:

$\boldsymbol{P}_{u}=\left(\boldsymbol{Y}^{\mathrm{T}} \boldsymbol{Y}\right)^{-1} \boldsymbol{Y}^{\mathrm{T}} \boldsymbol{X}_{w} \in \mathbf{R}^{C \times h}, $

其中,

Xw= XU+ϵ∈ R(Ns+Nu)×d,

d表示输入特征维度, $\epsilon$表示无穷小.

3)原型动态融合.为了平衡基础原型矩阵Pb与加权原型矩阵Pu的贡献权重, 引入可学习的置信度参数, 经Sigmoid函数归一化后实现动态融合, 最终融合原型为:

PC=WC☉Pb+(1-WC)☉Pu∈ RC× h,

其中, ☉表示逐元素乘积, WC∈ RC× h表示归一化后置信度权重矩阵, 用于动态调控基础原型在融合过程中的贡献.PC兼具基础原型的稳定性与加权原型的噪声鲁棒性, 可有效抵抗跨域场景中的噪声干扰与数据分布偏移.

1.3 协同损失优化

本文采用源域半监督学习损失、目标域学习损失与多域对抗损失协同优化的训练策略[10], 总体目标函数如下:

L= minθf, Bmaxθd[Lp(θ f, B)-λ Ld(θ f, θ d)],

其中, θ f、θ d表示网络中需要更新的参数, Lp(θ f, B)表示源域半监督学习损失与目标域学习损失之和, Ld(θ f, θ d)表示域判别损失.为了保障对抗训练过程的稳定性, 引入平衡超参数[34]:

λ = 1-e-μ1+e-μ,

其中, μ 表示与训练轮次相关的系数, 取值为当前训练轮次与总训练轮次之比.

1)源域半监督学习损失.计算源域样本特征间的预测余弦相似度矩阵

$\boldsymbol{R}_{p}^{s}=\operatorname{Sim}\left(\operatorname{Classifier}\left(\widehat{\boldsymbol{X}}_{s^{\prime}}\right), \operatorname{Classifier}\left(\widehat{\boldsymbol{X}}_{s^{\prime}}\right)^{\mathrm{T}}\right)$

与其真实标签的余弦相似度矩阵

Rs=Sim(Ys', YTs'),

其中,

Sim(K, V)= KV‖K‖‖V‖

表示余弦相似度,

$\widehat{\boldsymbol{X}}_{s^{\prime}}=\operatorname{concat}\left(\widehat{\boldsymbol{X}}_{s}, \widehat{\boldsymbol{X}}_{u}\right)$

表示源域中有标签样本与无标签样本的拼接特征,

$\widehat{\boldsymbol{Y}}_{s^{\prime}}=\operatorname{concat}\left(\widehat{\boldsymbol{Y}}_{s}, \widehat{\boldsymbol{Y}}_{u}\right)$

表示拼接标签.基于上述相似度矩阵, 源域半监督学习损失:

$L_{p}^{s}=\frac{1}{N_{s}+N_{u}} \sum_{i j} G_{i j}^{s}, $

其中 Gijs表示对 Rps, Rs求二元交叉熵损失后的输出矩阵Gs中元素.

2)目标域学习损失.计算目标域样本特征间的预测余弦相似度矩阵:

$\boldsymbol{R}_{p}^{t}=\operatorname{Sim}\left(\operatorname{Classifier}\left(\widehat{\boldsymbol{X}}_{t^{\prime}}\right), \text { Classifier }\left(\widehat{\boldsymbol{X}}_{t^{\prime}}\right)^{\mathrm{T}}\right) .$

由于目标域缺乏真实标签, 采用阈值方法构建伪标签相似度矩阵Rt, 元素

$R_{i j}^{t}=\left\{\begin{array}{ll} 1, & R_{p, i j}^{t} \geqslant \tau_{h} \\ 0, & R_{p, i j}^{t}< \tau_{l} \end{array}\right.$

其中,

$\begin{array}{l} \tau_{h}=\tau_{h}^{0}-\frac{\left(\tau_{h}^{0}-\tau_{l}^{0}\right)\left(1-\left(\frac{\text { epoch }-2}{\text { epoch }}\right)^{r}\right)}{2}, \\ \tau_{l}=\tau_{l}^{0}+\frac{\left(\tau_{h}^{0}-\tau_{l}^{0}\right)\left(1-\left(\frac{\text { epoch }-2}{\text { epoch }}\right)^{r}\right)}{2}, \end{array}$

表示动态阈值, epoch表示最大训练轮次, r表示当前训练轮次.进一步引入掩码矩阵M, 元素

mij= 0, Rijt∈[τl, τh)1, Rijt=0或Rijt=1

该矩阵用于筛选置信度较高的样本对参与损失计算.最终, 目标域学习损失为:

$L_{p}^{t}=\frac{\sum_{i, j} m_{i j} G_{i j}^{t}}{\sum_{i, j} m_{i j}}, $

其中 Gijt表示对 Rpt、Rt求二元交叉熵损失后的输出矩阵Gt中元素.

总之, 总原型学习损失为:

Lp(θ f, B)= Lps+γ Lpt+β ‖ PTCPC-I‖ F,

其中‖ PTCPC-I‖ F表示惩罚项, I表示单位矩阵, 用于防止原型学习[35]中特征提取的冗余.

3)多域对抗损失.为了提升方法在跨域场景中的泛化能力, 引入多域对抗损失, 旨在通过最小化源域S、无标签源域U与目标域T之间的H-散度, 有效控制方法的泛化误差上界.已有理论研究表明, 经验H-散度可被域判别器的分类误差近似[34, 36].因此, 通过对抗训练方式最大化域判别器的分类损失, 可实现域间H-散度的有效最小化.为了同时刻画3个域之间的分布差异, 构建三分类域判别器Dis(· ), 则域判别损失为:

$L_{d}\left(\boldsymbol{\theta}_{f}, \boldsymbol{\theta}_{d}\right)=L_{0}\left(\operatorname{Dis}\left(\operatorname{concat}\left(\widehat{\boldsymbol{X}}_{s}, \widehat{\boldsymbol{X}}_{u}, \widehat{\boldsymbol{X}}_{t}\right)\right)\right), $

其中, L0(· )表示交叉熵损失函数, 输入为标签源域特征、无标签源域特征与目标域样本特征的融合.

2 实验及结果分析
2.1 实验数据集

本文在上海交通大学吕宝粮团队提出的SEED[37]、SEED-IV[38]这2个脑电情感基准数据集上进行全面评估.

SEED数据集包含15名健康受试者(7名男性、8名女性)在标准化情绪诱导范式下采集的EEG数据, 涵盖积极、消极、中性这3种基本情绪状态.实验中选取15段经严格筛选的电影片段作为情绪诱发刺激(每种情绪对应5段, 单段时长约4 min), 所有片段采用随机无重复方式播放, 避免顺序效应干扰.为了保障数据可靠性, 每位受试者需在3个独立实验阶段完成相同测试流程, 通过重复采集降低个体随机误差.定量特征提取阶段, 本文以差分熵(Differential Entropy, DE)作为方法输入特征.

与SEED数据集类似, SEED-IV数据集包含15名受试者, 每位受试者需观看24段情绪诱导视频并同步记录脑电信号, 涵盖快乐、悲伤、恐惧、中性这4种情绪类别.单段视频时长约2 min.为了保障数据可靠性, 每位受试者需重复完成3次相同的数据采集流程, 共获得3组实验数据.同样采用差分熵特征分析.

2.2 实验设置

本文采用基于62个EEG通道与5个频段的差分熵特征作为输入.采用留一交叉验证法, 在受试者独立时评估性能.方法每次交叉验证时, 选取一名受试者的数据作为测试集, 其余受试者数据作为训练集.最终汇总所有受试者所有测试轮次的结果取平均值.

UPLM基于PyTorch深度学习框架实现, 训练过程在NVIDIA GeForce RTX 2080 Ti显卡上完成以提升运算效率.优化器采用RMSprop(Root Mean Square Propagation).训练超参数设置如下:批量大小为32, 初始学习率为0.1, 动态阈值的初始上限 τh0=0.9, 下限 τl0=0.5, 平衡参数γ 由常数因子η =2调控, 正则化系数为0.01.在数据划分方面, SEED数据集上设置标签源域样本数Ns=6, 无标签源域样本数Nt=9, SEED-IV数据集上设置标签源域样本数Ns=16, 无标签源域样本数Nt=8.

采用平均准确率及对应的标准差作为评估指标, 以此反映方法性能的稳定性与泛化性.

2.3 对比实验

本文选择如下主流方法作为对比方法:EEG-Match[10]、RGNN[16]、GMSS[19]、LGDAAN-Nets[22]、MSFR-GCN[23]、CU-GCN[24]、DS-AGC[25]、DGCNN(Dy- namical Graph Convolutional Neural Networks)[39]、 文献[40]方法、Flex-Match[41].这些方法在已有研究中均给出受试者无关的识别结果.

各方法在SEED、SEED-IV数据集上的平均准确率对比如表1所示.由表可见, 在SEED数据集上, UPLM的平均准确率最高, 达到93.37%(标准差为0.060 0).相比LGDAAN-Nets、DS-AGC等主流方法, UPLM的卓越表现充分表明其在学习受试者无关特征方面性能更优, 有效验证UPLM在跨受试者情绪识别任务中的有效性.

表1 各方法在2个数据集上的平均准确率对比 Table 1 Average accuracy comparison of different methods on 2 datasets

在SEED-IV数据集上, UPLM的平均准确率为74.58%, 指标最优.需注意的是, 相比SEED数据集, SEED-IV数据集包含更多情绪类别与样本, 数据更复杂, 而UPLM在这类复杂场景中仍能具有性能优势, 进一步验证其有效性.

UPLM在SEED、SEED-IV数据集上针对15名受试者的平均准确率如图2所示, 图中虚线表示全体受试者的平均准确率.由图可见, 大多数受试者的平均准确率集中于均值附近, 反映出UPLM具备良好的稳定性与预测可靠性.尽管存在个别受试者的性能与整体均值偏差较大, 这可能是由个体生理差异或数据采集波动所致, 但总体上, UPLM在不同受试者之间具备一致的泛化能力.

图2 UPLM在2个数据集上对每位受试者的平均准确率Fig.2 Average accuracy per subject of UPLM on 2 datasets

为了评估UPLM的分类效果, 在受试者无关设置下, UPLM在两个数据集上的混淆矩阵如图3所示, 图中结果直观反映UPLM在不同情感类别上的判别能力与混淆模式.

图3 UPLM在2个数据集上的混淆矩阵Fig.3 Confusion matrices of UPLM on 2 datasets

由图3可见, 在SEED数据集上, UPLM对积极情绪的识别性能显著优于中性情绪与消极情绪, 表明受试者对积极情绪可能具有更高的生理响应强度.然而, UPLM在消极情绪与中性情绪之间容易出现混淆, 反映出个体在这两类情绪状态下可能产生相似的神经生理模式.

在SEED-IV数据集上, UPLM对中性情绪与恐惧情绪的区分能力较优, 这得益于二者伴随的自主神经系统反应差异显著, 如皮肤电导增强与β 波功率提升等.相比之下, UPLM对快乐情绪与悲伤情绪的识别效果较差, 可能由于这两类情绪涉及更复杂的皮质-边缘系统动态耦合机制, 且其神经表征易受个体表达习惯的影响, 导致跨域识别难度增大.

2.4 消融实验

本节通过消融实验验证UPLM中位置编码引导的跨域图半监督学习模块、不确定性原型学习模块、位置编码的贡献, 结果如表2所示.由表可见, 移除位置编码后, 性能出现一定下降.移除不确定性原型学习模块后, 性能显著下降.由此表明2个模块对提升情感识别性能都具有不同贡献.

表2 在2个数据集上的消融实验结果 Table 2 Ablation experiment results on 2 datasets

同时移除位置编码与位置编码引导的跨域图半监督学习模块后, 性能出现显著下降, 降幅大于单独移除任一模块时的结果, 说明二者之间存在协同增强效应.而同时移除位置编码与不确定性原型学习模块后, 平均准确率虽低于UPLM, 但仍优于单独移除任一模块时的表现, 这一现象验证各模块在共同构成系统有效性基础的同时, 作用机制与耦合关系具有差异性.

2.5 超参数分析

首先讨论不同标签源域样本数Ns.在SEED数据集上定义Ns=3, 6, 7, 9, 12, 在SEED-IV数据集上定义Ns=4, 8, 12, 16, 其对UPLM性能的影响如表3所示.由表可知, Ns不同时, UPLM均能保持良好性能, 但随着Ns的减少, 性能呈现下降趋势.具体地, 在SEED数据集上, 当Ns=6时UPLM达到最优性能.在SEED-IV数据集上也观察到类似规律, 最优性能出现在Ns=16时.这一现象说明, 适度的Ns能为UPLM提供足够的监督信息, 过少的样本会导致监督信息不足, 过多的样本可能引入噪声或冗余信息, 影响UPLM对关键特征的提取能力.

表3 标签源域样本数Ns对UPLM性能的影响 Table 3 Effect of the number of samples in the labeled source domain Ns on UPLM performance

下面采用控制变量法开展超参数敏感性实验, 以此确定最优参数组合.第一步固定其它参数(含ε ), 测试超参数δ 对UPLM性能的影响.第二步基于δ 的最优候选值, 进一步探究ε 不同时的作用效果.通过多组候选参数组合的综合评估, 确定当δ =0.9, ε =0.1时, UPLM在评价指标上达到最优且稳定性最佳.

此外, 本文对比如下5种不确定性网络结构变体:原始结构(2层MLP, 隐藏层维度为32)、浅层宽网络(单隐藏层, 维度为128)、深层窄网络(3层MLP, 每层维度为16)、深层宽网络(4层MLP, 维度依次为64-64-32)、单层线性结构(无隐藏层, 直接映射).实验表明, 本文采用的2层32维MLP结构在不确定性建模能力、跨域泛化性能与计算效率三者之间实现良好平衡.进一步增加网络的深度或宽度, 不仅无法带来性能的实质性提升, 反而可能因过拟合问题降低方法在目标域上的鲁棒性.由此可见, 2层32维MLP结构的设计选择具备充分的合理性.

最后, 对比线性衰减、固定常数等多种不同的调度策略.实验表明, 本文采用的调度策略在跨域情绪识别任务中表现出更优且更稳定的性能.

2.6 可视化分析

为了系统揭示情绪识别过程中脑区的功能激活特性, 在SEED数据集上展开分析.选取一名典型受试者, 将其学习所得邻接矩阵的对角元素归一化至[0, 1]区间, 并以热力图形式可视化, 如图4所示.由图可见, 在三分类SEED任务中, 颞叶与枕叶区域呈现出高度显著的激活状态, 额叶区域也表现出明确的功能增强.这种多脑区协同激活的工作模式体现复杂情绪辨别任务对大脑神经网络功能整合的特异性需求.

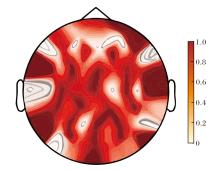图4 SEED数据集上邻接矩阵中自连接权重拓扑分布图Fig.4 Topological distribution of self-connected weights in adjacency matrix on SEED dataset

在此基础上, 进一步探究脑功能网络在情绪识别中的关键连接特性.通过关系环图(对角线元素已移除)对同一典型受试者邻接矩阵中排名前十的关键脑区连接进行可视化, 结果如图5所示.

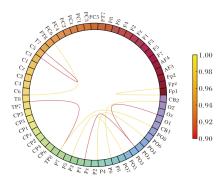图5 SEED数据集上邻接矩阵(移除自环)中Top-10连接Fig.5 Top-10 connections in adjacency matrix with self-loops removed on SEED dataset

由图5可见, 大多数显著连接集中分布于颞叶、额叶及枕叶区域, 这些脑区在情绪加工与视觉信息处理中均具有重要功能.该发现印证UPLM提取连接模式具有神经生理合理性, 与先前神经科学研究[42]的结论一致.

为了直观评估UPLM的分类性能, 对比分析方法训练前后的数据分布情况.采用t-SNE技术分别对原始输入数据与经过UPLM学习得到的协同表征嵌入进行可视化, 结果如图6所示.由图可见, 在SEED、SEED-IV数据集上的跨域实验中, 训练状态下的表征呈现出理想的聚类结构:类间差异显著、类内聚合度高、类别边界清晰.这一结果反映UPLM在层级信息提取方面的能力, 也体现UPLM在区分不同情绪类别及捕捉情绪特异性特征方面的有效性.

图6 UPLM在2个数据集上特征分布的t-SNE可视化结果Fig.6 t-SNE visualization results of feature distribution for UPLM on 2 datasets

3 结束语

本文提出不确定性原型学习的跨域情绪识别方法(UPLM).首先, 引入位置编码, 突破传统方法对物理距离的单一依赖, 为脑电信号建模建立更符合生理特性的图结构基础.在此基础上, 设计位置编码引导的跨域图半监督学习模块, 利用图结构传播机制, 充分挖掘标注样本与未标注样本中的深层拓扑特征, 缓解标注稀缺问题.此外, 构造不确定性原型学习模块, 量化样本特征的可靠性, 动态优化情感类别原型, 有效抑制噪声与域间偏移的干扰, 增强跨域情绪识别能力.在公开数据集上的实验表明, UPLM取得较优的分类性能.

然而, 当前研究仍存在如下两方面局限性, 有待进一步完善.

1)计算复杂度的现实约束.相比采用固定邻接矩阵的图神经网络, UPLM引入的基于学习的动态图构建机制与迭代式原型优化过程, 不可避免地增加额外的计算开销.这一特性在面向实时性要求较高的场景(如轻量化嵌入式脑机接口系统)时, 可能会对方法的实际部署可行性构成挑战, 今后可考虑聚焦于更高效的图卷积算子设计、原型向量的稀疏化更新策略等方向, 实现方法性能与推理效率的平衡.

2)复杂细粒度情绪状态的识别瓶颈.本文实验主要验证UPLM在基础情绪类别上的识别性能, 而针对复杂的混合情绪状态(如“ 悲喜交加” 这类复合情绪), 区分能力仍存在明显不足.未来需构建更精细化的情感计算框架, 可尝试将连续维度情感回归与动态时序建模结合, 更精准捕捉情绪状态的动态演变与微妙差异.

本文责任编委 何 清

Recommended by Associate Editor HE Qing

参考文献
[1] PILLALAMARRI R, SHANMUGAM U. A Review on EEG-Based Multi-modal Learning for Emotion Recognition. Artificial Intelli-gence Review, 2025, 58(5). DOI: 10.1007/s10462-025-11126-9. [本文引用:1]
[2] SAMAL P, HASHMI M F. Role of Machine Learning and Deep Learning Techniques in EEG-Based BCI-Emotion Recognition Sys-tem: A Review. Artificial Intelligence Review, 2024, 57(3). DOI: 10.1007/s10462-023-10690-2. [本文引用:1]
[3] ZOTEV V, MAYELI A, MISAKI M, et al. Emotion Self-Regulation Training in Major Depressive Disorder Using Simultaneous Real-Time fMRI and EEG Neurofeedback. NeuroImage: Clinical, 2020, 27. DOI: 10.1016/j.nicl.2020.102331. [本文引用:1]
[4] WU E Q, DENG P Y, QU X Y, et al. Detecting Fatigue Status of Pilots Based on Deep Learning Network Using EEG Signals. IEEE Transactions on Cognitive and Developmental Systems, 2021, 13(3): 575-585. [本文引用:1]
[5] LI J Y, YANG L, LÜ C, et al. GLF-STAF: A Global-Local-Facial Spatio-Temporal Attention Fusion Approach for Driver Emotion Re-cognition. IEEE Transactions on Consumer Electronics, 2025, 71(2): 3486-3497. [本文引用:1]
[6] ZHENG W L, ZHU J Y, LU B L, et al. Identifying Stable Patterns over Time for Emotion Recognition from EEG. IEEE Transactions on Affective Computing, 2019, 10(3): 417-429. [本文引用:1]
[7] ALARCÃO S M, FONSECA M J. Emotions Recognition Using EEG Signals: A Survey. IEEE Transactions on Affective Computing, 2019, 10(3): 374-393. [本文引用:1]
[8] SI X P, HE H, YU J Y, et al. Cross-Subject Emotion Recognition Brain-Computer Interface Based on fNIRS and DBJNet. Cyborg and Bionic Systems, 2023, 4. DOI: 10.34133/cbsystems.0045. [本文引用:1]
[9] 刘少鹏, 洪佳明, 梁杰鹏, 等. 面向医学图像分割的半监督条件生成对抗网络. 软件学报, 2020, 31(8): 2588-2602.
(LIU S P, HONG J M, LIANG J P, et al. Medical Image Segmentation Using Semi-supervised Conditional Generative Adversarial Nets. Journal of Software, 2020, 31(8): 2588-2602. ) [本文引用:1]
[10] ZHOU R S, YE W S, ZHANG Z G, et al. EEGMatch: Learning with Incomplete Labels for Semi-supervised EEG-Based Cross-Subject Emotion Recognition. IEEE Transactions on Neural Networks and Learning Systems, 2025, 36(7): 12991-13005. [本文引用:5]
[11] ZHANG G Y, ETEMAD A. Holistic Semi-supervised Approaches for EEG Representation Learning // Proc of the IEEE International Conference on Acoustics, Speech and Signal Processing. Washington, USA: IEEE, 2022: 1241-1245. [本文引用:1]
[12] BERTHELOT D, CARLINI N, GOODFELLOW I, et al. MixMa-tch: A Holistic Approach to Semi-supervised Learning // Proc of the 33rd International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2019: 5049-5059. [本文引用:1]
[13] ZHANG G Y, DAVOODNIA V, ETEMAD A. PARSE: Pairwise Alignment of Representations in Semi-supervised EEG Learning for Emotion Recognition. IEEE Transactions on Affective Computing, 2022, 13(4): 2185-2200. [本文引用:1]
[14] 李锦瑶, 杜肖兵, 朱志亮, 等. 脑电情绪识别的深度学习研究综述. 软件学报, 2023, 34(1): 255-276.
(LI J Y, DU X B, ZHU Z L, et al. Deep Learning for EEG-Based Emotion Recognition: A Survey. Journal of Software, 2023, 34(1): 255-276. ) [本文引用:1]
[15] YANG H, CHEN C L P, CHEN B N, et al. Improving the Interpretability Through Maximizing Mutual Information for EEG Emo-tion Recognition. IEEE Transactions on Affective Computing, 2025, 16(2): 744-757. [本文引用:1]
[16] ZHONG P X, WANG D, MIAO C Y. EEG-Based Emotion Recognition Using Regularized Graph Neural Networks. IEEE Transactions on Affective Computing, 2022, 13(3): 1290-1301. [本文引用:2]
[17] ZHANG T, WANG X H, XU X M, et al. GCB-Net: Graph Con-volutional Broad Network and Its Application in Emotion Recognition. IEEE Transactions on Affective Computing, 2022, 13(1): 379-388. [本文引用:1]
[18] SONG T F, LIU S Y, ZHENG W M, et al. Variational Instance-Adaptive Graph for EEG Emotion Recognition. IEEE Transactions on Affective Computing, 2023, 14(1): 343-356. [本文引用:1]
[19] LI Y, CHEN J, LI F, et al. GMSS: Graph-Based Multi-task Self-Supervised Learning for EEG Emotion Recognition. IEEE Transactions on Affective Computing, 2023, 14(3): 2512-2525. [本文引用:2]
[20] JIN M, DU C D, HE H G, et al. PGCN: Pyramidal Graph Convolutional Network for EEG Emotion Recognition. IEEE Transactions on Multimedia, 2024, 26: 9070-9082. [本文引用:2]
[21] YAN H C, GUO K L, XING X F, et al. Bridge Graph Attention Based Graph Convolution Network with Multi-scale Transformer for EEG Emotion Recognition. IEEE Transactions on Affective Computing, 2024, 15(4): 2042-2054. [本文引用:1]
[22] AN Y L, HU S H, LIU S Q, et al. LGDAAN-Nets: A Local and Global Domain Adversarial Attention Neural Networks for EEG Emo-tion Recognition. Knowledge-Based Systems, 2025, 318. DOI: 10.1016/j.knosys.2025.113613. [本文引用:2]
[23] PAN D, ZHENG H H, XU F F, et al. MSFR-GCN: A Multi-scale Feature Reconstruction Graph Convolutional Network for EEG Emotion and Cognition Recognition. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2023, 31: 3245-3254. [本文引用:2]
[24] GAO H X, WANG X Y, CHEN Z H, et al. Graph Convolutional Network with Connectivity Uncertainty for EEG-Based Emotion Recognition. IEEE Journal of Biomedical and Health Informatics, 2024, 28(10): 5917-5928. [本文引用:2]
[25] YE W S, ZHANG Z G, TENG F, et al. Semi-supervised Dual-Stream Self-Attentive Adversarial Graph Contrastive Learning for Cross-Subject EEG-Based Emotion Recognition. IEEE Transactions on Affective Computing, 2025, 16(1): 290-305. [本文引用:2]
[26] 班瑞阳, 周大鹏, 韩吉平, 等. 基于改进注意力机制的领域对抗网络的认知负荷识别模型. 小型微型计算机系统, 2024, 45(11): 2602-2608.
(BAN R Y, ZHOU D P, HAN J P, et al. Cognitive Load Recognition Model Based on Improved Attention Mechanism in Domain-Adversarial Networks. Journal of Chinese Computer Systems, 2024, 45(11): 2602-2608. ) [本文引用:1]
[27] 李平, 宋琦, 张锋. 引入局部特征对齐和原型修正的少样本图像分类模型. 小型微型计算机系统, 2025, 46(9): 2145-2152.
(LI P, SONG Q, ZHANG F. Few-Shot Image Classification Model by Introducing Local Feature Alignment and Prototype Rectification. Journal of Chinese Computer Systems, 2025, 46(9): 2145-2152. ) [本文引用:1]
[28] 徐祺津, 叶海良, 曹飞龙, 等. 基于全局-局部先验和纹理细节关注的图像修复. 模式识别与人工智能, 2025, 38(2): 101-115.
(XU Q J, YE H L, CAO F L, et al. Image Inpainting Based on Global-Local Prior and Details. Pattern Recognition and Artificial Intelligence, 2025, 38(2): 101-115. ) [本文引用:1]
[29] 侯冰震, 张桂梅, 彭昆. 基于不确定性引导和尺度一致性的肾肿瘤图像分割方法. 模式识别与人工智能, 2023, 36(2): 95-107.
(HOU B Z, ZHANG G M, PENG K. Kidney Tumor Image Segmentation Method Based on Uncertainty Guidance and Scale Consistency. Pattern Recognition and Artificial Intelligence, 2023, 36(2): 95-107. ) [本文引用:1]
[30] ANDRIC M, HASSON U. Global Features of Functional Brain Networks Change with Contextual Disorder. NeuroImage, 2015, 117: 103-113. [本文引用:1]
[31] LIU X H, LU B L, ZHENG W L. EEGMirror: Leveraging EEG Data in the Wild via Montage-Agnostic Self-Supervision for EEG to Video Decoding // Proc of the IEEE/CVF International Conference on Computer Vision. Washington, USA: IEEE, 2025: 18273-18283. [本文引用:1]
[32] DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering // Proc of the 30th International Conference on Neural In-formation Processing Systems. Cambridge, USA: MIT Press, 2016: 3844-3852. [本文引用:1]
[33] ZHOU R S, ZHANG Z G, FU H, et al. PR-PL: A Novel Proto-typical Representation Based Pairwise Learning Framework for Emo-tion Recognition Using EEG Signals. IEEE Transactions on Affec-tive Computing, 2024, 15(2): 657-670. [本文引用:1]
[34] GANIN Y, USTINOVA E, AJAKAN H, et al. Domain-Adversarial Training of Neural Networks. Journal of Machine Learning Research, 2016, 17(59): 1-35. [本文引用:2]
[35] PINHEIRO P O. Unsupervised Domain Adaptation with Similarity Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2018: 8004-8013. [本文引用:1]
[36] BEN-DAVID S, BLITZER J, CRAMMER K, et al. Analysis of Representations for Domain Adaptation[C/OL]. [2025-09-25]. https://proceedings.neurips.cc/paper_files/paper/2006/file/b1b0432ceafb0ce714426e9114852ac7-Paper.pdf. [本文引用:1]
[37] ZHENG W L, LU B L. Investigating Critical Frequency Band Sand Channels for EEG-Based Emotion Recognition with Deep Neural Networks. IEEE Transactions on Autonomous Mental Development, 2015, 7(3): 162-175. [本文引用:1]
[38] ZHENG W L, LIU W, LU Y F, et al. EmotionMeter: A Multimodal Framework for Recognizing Human Emotions. IEEE Transactions on Cybernetics, 2019, 49(3): 1110-1122. [本文引用:1]
[39] SONG T F, ZHENG W M, SONG P, et al. EEG Emotion Recognition Using Dynamical Graph Convolutional Neural Networks. IEEE Transactions on Affective Computing, 2020, 11(3): 532-541. [本文引用:1]
[40] CHEN Y Y, XU X D, QIN X W. Cross-Subject and Cross-Session EEG Emotion Recognition Based on Multi-source Structural Deep Clustering. IEEE Transactions on Cognitive and Developmental Systems, 2025, 17(5): 1245-1259. [本文引用:1]
[41] ZHANG B W, WANG Y D, HOU W H, et al. FlexMatch: Boosting Semi-supervised Learning with Curriculum Pseudo Labeling // Proc of the 35th International Conference on Neural Information Processing Systems. Cambridge, USA: MIT Press, 2021: 18408-18419. [本文引用:1]
[42] YIN Z, ZHAO M Y, WANG Y X, et al. Recognition of Emotions Using Multimodal Physiological Signals and an Ensemble Deep Learning Model. Computer Methods and Programs in Biomedicine, 2017, 140: 93-110. [本文引用:1]