基于Transformer融合的深度对比多视图聚类

引用本文

李顺勇, 原志英, 赵兴旺. 基于Transformer融合的深度对比多视图聚类. 模式识别与人工智能, 2025,38(12): 1057-1074
LI Shunyong, YUAN Zhiying, ZHAO Xingwang. Deep Contrastive Multi-view Clustering with Transformer Fusion. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2025,38(12): 1057-1074. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202512001
Permissions

《模式识别与人工智能》编辑部

基于Transformer融合的深度对比多视图聚类

李顺勇^1,², 原志英¹, 赵兴旺^3,⁴

1.山西大学数学与统计学院太原 030006

2.山西大学复杂系统与数据科学教育部重点实验室太原 030006

3.山西大学计算机与信息技术学院太原 030006

4.山西大学计算智能与中文信息处理教育部重点实验室太原 030006

通讯作者:

赵兴旺,博士,教授,主要研究方向为数据挖掘、机器学习.E-mail:zhaoxw@sxu.edu.cn.

作者简介:

李顺勇,博士,教授,主要研究方向为统计机器学习、大数据分析技术.E-mail:lisy75@sxu.edu.cn.

原志英,硕士研究生,主要研究方向为统计机器学习.E-mail:yuanzhiying@sxu.edu.cn.

收稿日期: 2025-11-17 接受日期: 2025-12-29

资助项目: 国家自然科学基金项目(No.82274360)、山西省留学回国人员科技活动择优项目(No.20250001)、山西省基础研究计划项目(No.202303021221054,202403021211086)、山西省回国留学人员科研项目(No.2024-002)、山西省研究生教育创新计划项目(No.2025JG0006,2025SJ032)资助

摘要

作为无监督学习的重要任务之一,多视图聚类旨在融合异构视图信息并挖掘一致的聚类结构.现有方法大都存在利用自编码器提取的低级特征缺乏跨视图语义一致性、简单融合策略缺乏对视图质量的动态评估、缺少多层面的对比约束和局部-全局标签对齐机制等问题.为此,文中提出基于Transformer融合的深度对比多视图聚类算法(Deep Contrastive Multi-view Clustering with Transformer Fusion, DCMCTF).首先,设计交替对抗学习模块,实现低级特征分布的跨视图对齐.然后,引入实例级和聚类级双重对比约束模块,增强跨视图一致性和特征判别能力.最后,构建基于Transformer的自适应融合模块,动态学习视图关联,结合质量感知评分生成鲁棒共识表示,并将由共识表示得到的全局标签与特定视图的局部标签进行对齐.在9个数据集上的实验表明,DCMCTF聚类性能较优.

关键词: 对抗学习; 对比学习; 深度多视图聚类; Transformer

中图分类号:TP181

Deep Contrastive Multi-view Clustering with Transformer Fusion

LI Shunyong^1,², YUAN Zhiying¹, ZHAO Xingwang^3,⁴

1. School of Mathematics and Statistics, Shanxi University, Tai-yuan 030006

2. Key Laboratory of Complex Systems and Data Science of Mi-nistry of Education, Shanxi University, Taiyuan 030006

3. School of Computer and Information Technology, Shanxi University, Taiyuan 030006

4. Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education, Shanxi University, Taiyuan 030006

Corresponding author:
ZHAO Xingwang, Ph.D., professor. His research interests include data mining and machine learning.

About Author:
LI Shunyong, Ph.D., professor. His research interests include statistical machine lear-ning and big data analytics techniques.
YUAN Zhinying, Master student. Her research interests include statistical machine learning.

Fund:National Natural Science Foundation of China(No.82274360), Program for the Scientific Activities of Selected Returned Overseas Professionals in Shanxi Province(No.20250001), Fundamental Research Program of Shanxi Province(No.202303021221054,202403021211086), Research Project of Shanxi Scholarship Council of China(No.2024-002), Graduate Education Innovation Program of Shanxi Province(No.2025JG0006,2025SJ032)

Abstract

As an important task of unsupervised learning, multi-view clustering is designed to fuse heterogeneous view information to mine a consistent clustering structure. In the existing methods, the low-level features extracted by autoencoders lack cross-view semantic consistency, and simple fusion strategies lack dynamic assessment of view quality. Additionally, there is an absence of multi-level contrast constraints and local-global label alignment mechanisms. To address these issues, a deep contrastive multi-view clustering algorithm with Transformer fusion(DCMCTF) is proposed. First, cross-view alignment of low-level feature distributions is achieved under an alternating adversarial learning mechanism, and then instance-level and cluster-level dual contrastive learning mechanisms are introduced to enhance cross-view consistency and feature discriminative ability. Second, a Transformer adaptive fusion module is leveraged to dynamically learn view relationships. Robust consensus representations are generated by combining quality-aware scoring, and the global labels obtained from consensus representations are aligned with local labels of specific views. Experiments on 9 datasets demonstrate that DCMCTF achieves excellent clustering performance.

Key words: Key Words Adversarial Learning; Contrastive Learning; Deep Multi-view Clustering; Transformer

文章图片

作为无监督学习领域的一项重要任务, 多视图聚类旨在充分利用多视图数据的互补优势, 融合来自不同视角的异构信息^[1], 挖掘隐藏在多个视图中的一致性聚类结构, 并将样本划分为若干语义相关的组^[2].得益于强大的无监督特征学习能力和对多源异构数据的有效整合能力, 多视图聚类现已成功应用于推荐系统中用户行为和社交关系的联合分析、医学图像分析中多模态医学影像的疾病诊断、社交网络分析中用户画像构建和社区发现等多个实际的应用场景.

传统多视图聚类方法利用矩阵分解^[3]、子空间学习^[4]、图学习^[5]等策略融合视图互补信息, 再执行如K均值、谱聚类等预定义的聚类策略以捕捉数据结构差异.但是, 这些方法依赖线性融合策略处理浅层特征, 难以有效建模数据中蕴含的非线性复杂关系^[6].

深度多视图聚类(Deep Multi-view Clustering, DMVC)则利用深度神经网络作为非线性嵌入函数, 结合预定义聚类策略进行端到端训练.典型方法包括基于深度嵌入聚类的方法^[7]、基于子空间聚类的方法^[8]、基于图卷积网络的方法^[9]及基于自编码器聚类的方法^[10].由于深度多视图聚类能在深层特征空间中捕获数据的非线性语义结构, 在聚类性能上实现对传统方法的显著超越.

虽然现有方法均取得良好的聚类性能, 但仍面临如下挑战.1)直接使用自编码器提取的低级特征包含视图特异性信息, 缺乏跨视图的语义一致性, 并且传统的特征对齐方法难以捕捉视图分布的动态变化.2)不同视图对聚类性能的贡献程度存在一定差异, 传统的简单平均或固定权重融合策略无法对视图质量进行动态评估和自适应调整.3)现有方法对于特定视图产生的局部聚类标签与共识表示产生的全局共识标签之间缺乏有效对齐, 对多视图数据集的互补性信息利用不足, 聚类一致性和判别性欠佳.

为了解决上述问题, 本文提出基于Transformer融合的深度对比多视图聚类算法(Deep Contrastive Multi-view Clustering with Transformer Fusion, DCM-CTF), 包含Auto-Encoder模块、交替对抗学习模块、双重对比约束模块、基于Transformer的自适应融合模块、局部与全局标签对齐模块.DCMCTF首先利用视图级交替对抗学习模块, 实现跨视图分布对齐.再分别通过实例级和聚类级多层感知机(Multi-layer Perceptron, MLP)将低级特征映射至高维空间和K维语义空间, 并在两个层面引入双重对比约束模块, 避免直接在含噪的低级特征上学习.然后设计基于Transformer的自适应融合模块, 动态整合多视图信息, 得到全局共识表示, 抑制低质量视图的负面影响, 增强高质量视图主导作用.最后将共识表示映射至聚类空间, 生成全局标签, 并利用Kullback-Leibler(KL)散度将视图特定局部标签与全局标签对齐, 联合优化所有模块.

1 相关工作

1.1 深度多视图聚类

近年来, DMVC凭借深度神经网络强大的表示学习能力, 突破传统方法难以在复杂数据上建模的局限性.现有方法按训练阶段可划分为两阶段方法^[11]和端到端方法^[12].两阶段方法将特征学习与聚类解耦, 先提取特征再执行聚类, 无法利用聚类反馈优化特征学习.端到端方法将两者嵌入统一框架下进行联合优化.根据信息聚合方式, 端到端方法又进一步分为基于聚合的方法和基于对比的方法.基于聚合的方法利用加权或注意力机制融合多视图特征, 常忽略视图间的复杂交互.基于对比的方法通过对比学习增强特征判别性, 难以充分挖掘视图间的信息交互.

从模型架构角度上看, DMVC主要包括如下四类.1)基于深度嵌入聚类的方法.将特征学习与聚类中心学习紧密耦合.Cui等^[13]提出DCMVC(Dual Contrastive Learning-Based Deep Multi-view Clustering Network), 利用动态簇扩散损失与可靠邻居引导的正对齐损失, 学习兼具类间分离性与类内紧凑性的聚类友好型共识表示.2)基于子空间聚类的方法.将多视图样本划分到不同的特征子空间中, 利用子空间建模捕获数据的低维流形结构.Zhu等^[14]提出MvDSCN(Multiview Deep Subspace Clustering Net-works), 构建深度卷积自编码器潜空间, 使用多样性网络学习视图特定自表示矩阵, 通用性网络学习通用自表示矩阵, 根据多样性正则项与普适性正则化约束划分多视图特征子空间.3)基于图卷积网络的方法.借助图卷积神经网络挖掘多视图数据的拓扑结构关系, 利用图结构增强特征的判别性.Liu等^[15]提出DMVGC(Deep Multi-view Graph Clustering Net-work with Weighting Mechanism and Collaborative Training), 构建含视图特定图编码器与统一图解码器的深度网络, 并在视图特定嵌入层与公共嵌入层协同自训练聚类目标.4)基于自编码器的方法.利用编码器-解码器重构约束学习判别性特征表示.Chen等^[16]提出3MC(Multi-layer Multi-level Compre-hensive Learning Framework for Deep Multi-view Clustering), 对各编码器层特征开展多视图间对比学习, 实现特征一致性, 借助层特定标签MLP转换为高层语义标签后进行层间对比学习, 获取多层一致的聚类分配.

多视图融合是DMVC的核心环节, 直接决定共识表示的质量.现有融合策略中基础的求和、串联或加权融合实现简单, 但忽略视图间的复杂关联.基于注意力的自适应融合为不同视图分配动态权重以捕获样本结构关系.

基于对比学习的融合借助中间变量对齐视图表示以减少私有信息干扰.但是, 当前方法仍存在明显局限:采用局部融合却忽略全局相关性, 关注特征对齐而忽视语义一致性, 依赖重构特征导致私有噪声干扰融合过程.

1.2 对比学习

对比学习作为一种强大的无监督表示学习范式, 因其通过在潜在空间中最大化正样本对的相似度的同时最小化负样本对的相似度以提取判别性特征, 已在多视图聚类领域受到广泛关注^[17].对比学习的正样本对通常由同一实例的不同视图或增强变体组成, 而负样本对由不同实例组成.Chen等^[18]提出SimCLR, 利用数据增强在批内构造样本对进行对比学习.He等^[19]提出MoCo(Momentum Contrast), 通过队列和动量编码器维护大规模字典, 提升对比效率.

近年来, 基于对比学习的深度多视图聚类方法不断涌现^[20].Bian等^[21]提出MCMC(Multilevel Con-trastive Multiview Clustering), 将潜在子空间中对象的最近邻作为正样本对, 针对聚类、实例和原型执行多层次对比学习, 捕捉数据多层次表示, 并通过对偶自监督学习关联不同层次结构表示.Fei等^[22]提出DMvCGSA(Deep Multi-view Contrastive Clustering via Graph Structure Awareness), 利用相似性引导的实例级对比学习, 使特定视图特征具备判别性, 同时采用簇级对比学习, 直接挖掘对聚类有益的一致性信息, 获取多视图样本的协同表示.

现有的基于对比学习的多视图聚类方法仍面临若干挑战, 如训练的早期阶段使用伪标签难以准确预测、大量错误伪标签限制学习特征的质量, 而且现有方法往往忽略视图私有信息和噪声影响, 可能导致聚类结果不准确.

2 基于Transformer融合的深度对比多视图聚类算法

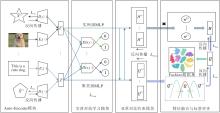
本文提出基于Transformer融合的深度对比多视图聚类算法(DCMCTF), 框架如图1所示.

	Figure Option View Download New Window
	图1 DCMCTF框架图Fig.1 Architecture of DCMCTF

首先, 利用视图特定的编码器提取低级特征表示, 利用解码器重构原始数据, 确保特征的有效性, 并引入交替对抗学习模块, 对齐跨视图特征分布, 削弱视图的异质性.然后, 引入双分支MLP, 将低级特征映射为高级表示和聚类标签, 并设计双重对比模块, 在实例级拉近样本在不同视图下的表征, 在聚类级增强类别的判别能力.最后, 利用基于Transformer的自适应融合模块, 动态学习视图关联, 结合质量感知评分生成鲁棒的共识表示, 并利用KL散度对齐各视图标签与全局共识标签, 统一多视图预测, 输出最终的聚类结果.

2.1 Auto-Encoder模块

原始的多视图数据在各视图上的特征维度不一定相同, 并且包含冗余和随机噪声.为了缓解不利信息对聚类结果的影响, 本文利用自编码器将原始的多视图数据投影至低级表示的特征空间, 并在对称的解码器中对数据进行重构还原, 确保学习的低级特征表示能全面反映原始数据的特征信息.

原始多视图数据进入特定视图的自编码器E_v(· )后, 学习得到低级特征:

$z_{i}^{(v)}$ =E_v( $x_{i}^{(v)}$ ; φ _v),

其中, $x_{i}^{(v)}$ 表示第v个视图的第i个样本, φ _v表示编码器E_v(· )的网络参数.再利用对称的特定视图的解码器D_v(· )对原始多视图数据进行重构, 得到相应的重构样本:

${\hat{x}}_{i}^{(v)}$ =D_v( $z_{i}^{(v)}$ ; ϕ _v),

其中, ϕ _v表示解码器D_v(· )的网络参数.

为了保证从输入数据中学习有效的特征表示, 利用L₂范数进行重构约束, 得到视图总重构损失:

L_Rec= $\overset{V}{\sum_{v = 1}} \overset{N}{\sum_{i = 1}}$ ‖ ${\hat{x}}_{i}^{(v)}$ -D_v(E_v( $x_{i}^{(v)}$ ))‖ $_{2}^{2}$ .

2.2 交替对抗学习模块

由于原始数据在不同视图下的分布存在差异, 直接通过自编码器提取的低级特征表示包含视图的特异性信息, 缺乏跨视图共享的语义一致性.对抗网络使用生成器与判别器的博弈机制, 突破传统的特征对齐方法无法捕捉视图分布动态变化的局限.为此, 本文提出视图级的交替对抗学习模块, 轮流将每个视图的低级特征表示作为锚点, 在交替博弈中实现跨视图特征分布一致性约束.将视图v的特征表示z⁽^v⁾作为锚点, 而将其它视图z⁽^u⁾(u≠ v)的潜在表示作为参考, 分别输出“ 1” 和“ 0” .单个判别器Dis_v(· )的损失为真实样本损失与伪造样本平均损失之和, 即

$L_{D_{v}}$ =MSE(Dis_v(z⁽^v⁾), 1)+
$\frac{1}{V - 1} \overset{V}{\sum_{u = 1, u \neq v}}$ SE(Disv₍z(^u⁾⁾, 0),

其中, V表示视图总数, 1表示全1的标签向量, 0表示全0的标签向量, MSE(· )表示平均损失.

对于每个生成器, 需要让其生成结果欺骗所有其它视图的判别器Dis_u(u≠ v), 使输出值趋近于真实标签1.单个生成器的损失为欺骗所有其它判别器的平均损失:

$L_{E_{v}}$ = $\frac{1}{V - 1} \overset{V}{\sum_{u = 1, u \neq v}}$ MSE(Dis_u(z⁽^v⁾), 1).

由此得到交替对抗学习模块总的损失函数:

L_Conf= $\frac{1}{V} \overset{V}{\sum_{v = 1}}$ ( $L_{D_{v}}$ + $L_{E_{v}}$ ).

2.3 双重对比约束模块

为了深度挖掘多视图数据中的互补性信息, 强化特征表示的一致性, 本文将提取的低级特征分别通过实例级和聚类级的MLP映射到高级特征表示空间和聚类标签语义空间, 并在两个空间中施加对比约束, 强化不同视图聚类结果的一致性.

2.3.1 实例级对比约束

为了避免低级特征表示中视图私有信息的干扰, 采用实例级的MLP( f_H(· )), 将 $z_{i}^{(v)}$ 映射至高级特征表示空间, 得到视图v中实例i的高级特征表示:

$h_{i}^{(v)}$ =f_H( $z_{i}^{(v)}$ ).

对于 $h_{i}^{(u)}$ , 有V-1个正样本{ $h_{i}^{(v)}$ }(v≠ u), V(N-1)个负样本{ $h_{j}^{(v)}$ }(j≠ i).类似于Sim- CLR^[18], 本文采用点积作为高级特征表示的相似性度量指标:

sim( $h_{i}^{(u)}$ , $h_{j}^{(v)}$ )= $\frac{(h_{i}^{(u)})^{T} \cdot h_{j}^{(v)}}{τ_{1}}$ ,

其中, τ₁表示温度参数, 可调节相似度分布的平滑程度.再利用InfoNCE(Information Noise-Contras-tive Estimation Loss)计算视图u、v的实例级对比损失:

$\begin{array}{l} L_{\text {ins }}^{u, v}= \\ -\frac{1}{2 N} \sum_{i=1}^{N}\left[\ln \left(\frac{\exp \left(\operatorname{sim}\left(\boldsymbol{h}_{i}^{(u)}, \boldsymbol{h}_{i}^{(v)}\right)\right)}{\sum_{j=1, j \neq i}^{N} \sum_{w \in\{u, v\}} \exp \left(\operatorname{sim}\left(\boldsymbol{h}_{i}^{(u)}, \boldsymbol{h}_{j}^{(w)}\right)\right)}\right)+\right. \\ \left.\ln \left(\frac{\exp \left(\operatorname{sim}\left(\boldsymbol{h}_{i}^{(v)}, \boldsymbol{h}_{i}^{(u)}\right)\right)}{\sum_{j=1, j \neq i}^{N} \sum_{w \in\{u, v\}} \exp \left(\operatorname{sim}\left(\boldsymbol{h}_{i}^{(v)}, \boldsymbol{h}_{j}^{(w)}\right)\right)}\right)\right] . \end{array}$

该约束最大化正样本对的相似度并同时最小化负样本对的相似度, 实现跨视图高级特征表示的对齐, 其中N表示样本量.

由此得到总的实例级对比损失:

L_ins= $\frac{1}{2} \underset{v = 1}{\underset{u = 1}{\overset{V}{\sum_{u \neq v}}}} L_{ins}^{u, v}$ .

L_ins强制要求每个样本在不同视图中的高级特征表示保持高度相似, 从而建立跨视图的一致性约束, 有效整合多视图的互补信息, 最终提升聚类性能.

2.3.2 聚类级对比约束

为了实现多视图场景中的语义一致性, 本文又引入聚类级MLP( f_Q(· )), 将低级特征表示映射至维数等于聚类数K的语义空间, 得到软聚类标签矩阵Q⁽^v⁾, Q⁽^v⁾的第i行

$q_{i ∶}^{(v)}$ =f_Q( $z_{i}^{(v)}$ ),

表示第i个样本在视图v下的聚类概率向量.相应地, 记 $q_{∶ k}^{(v)}$ 为第k列.此时每个维度的值反映样本归属于相应类簇的概率^[23].

对于视图u的第k个聚类簇 $q_{∶ k}^{(u)}$ , 有V-1个正样本{ $q_{∶ k}^{(v)}$ }(v≠ u), V(K-1)个负样本{ $q_{∶ l}^{(v)}$ }(l≠ k), v∈[1, V].聚类簇在不同视图下的相似度为:

sim( $q_{∶ k}^{(u)}$ , $q_{∶ k}^{(v)}$ )= $\frac{(q_{∶ k}^{(u)})^{T} \cdot q_{∶ k}^{(v)}}{τ_{2}}$ ,

其中τ₂表示温度参数.

基于上述相似性度量, 视图u、v的聚类级对比损失为:

$\begin{array}{l} L_{\mathrm{clus}}^{u, v}= \\ -\frac{1}{2 K} \sum_{k=1}^{K}\left[\ln \left(\frac{\exp \left(\operatorname{sim}\left(\boldsymbol{q}_{: k}^{(u)}, \boldsymbol{q}_{: k}^{(v)}\right)\right)}{\sum_{l=1, l \neq k}^{K} \sum_{w \in \backslash u, v} \exp \left(\operatorname{sim}\left(\boldsymbol{q}_{: k}^{(u)}, \boldsymbol{q}_{: l}^{(w)}\right)\right)}\right)+\right. \\ \left.\ln \left(\frac{\exp \left(\operatorname{sim}\left(\boldsymbol{q}_{: k}^{(v)}, \boldsymbol{q}_{: k}^{(u)}\right)\right)}{\sum_{l=1, l \neq k}^{K} \sum_{w \in\{u, v\}} \exp \left(\operatorname{sim}\left(\boldsymbol{q}_{: k}^{(v)}, \boldsymbol{q}_{: l}^{(w)}\right)\right)}\right)\right], \end{array}$

其中K表示聚类簇个数.为了避免方法退化将样本塌缩到单一簇的平凡解, 又引入基于KL散度的均衡正则项:

$L_{ent}^{u, v}$ = $\sum_{u \in {u, v}}$ [ln K+ $\overset{K}{\sum_{k = 1}} π_{k}^{(u)}$ (ln $π_{k}^{(u)}$ +ε)],

用于约束聚类分配趋于均衡, 其中,

$π_{k}^{(u)}$ = $\frac{\overset{N}{\sum_{i = 1}} q_{ik}^{(u)}}{\overset{K}{\sum_{k = 1}} \overset{N}{\sum_{i = 1}} q_{ik}^{(u)}}$ ,

$q_{ik}^{u}$ 表示视图u中实例i属于聚类簇k的概率, ε=10^-8表示数值稳定项.总的聚类级对比损失如下:

L_clus= $\frac{1}{2} \underset{v = 1}{\underset{u = 1}{\overset{V}{\sum_{u \neq v}}}} L_{clus}^{u, v}$ + $L_{ent}^{u, v}$ .

L_clus强制不同视图在同一语义类别的概率保持一致, 同时通过均衡正则项惩罚类别分布的不均衡性, 增强聚类稳定性和特征判别性, 最终提升聚类质量.

双重对比约束模块总的损失函数为:

L_Dcon=L_ins+L_clus.

2.4 基于Transformer的自适应融合模块

为了构建统一的特征表示需要整合来自各个观测角度的互补性信息, 而受噪声污染的视图信息可能会干扰聚类结果的准确性.传统的线性加权融合策略表达能力有限, 无法自适应学习视图间的关联性.受Transformer在序列建模中优异表现的启发, 设计基于Transformer的自适应融合模块, 用于捕捉视图间复杂的交互关系.

2.4.1 Transformer融合框架

对于高级特征表示{H⁽^v⁾ $}_{v = 1}^{V}$ , 将不同视图的特征沿序列维度进行堆叠, 构建多视图特征张量H_stack∈ $R^{B \times V \times d_{h}}$ , 其中, B表示批次大小, V表示视图总数, d_h表示高级特征维度.每个样本的多视图特征可被视为一个长度为V的序列.为了实现跨视图特征交互, 采用多头自注意力机制对多视图特征进行聚合.具体地, 通过可学习的线性变换矩阵将H_stack投影为查询矩阵Q⁽^m⁾、键矩阵K⁽^m⁾和值矩阵V⁽^m⁾:

$\begin{array}{l} \boldsymbol{Q}^{(m)}=\boldsymbol{H}_{\text {stack }} \boldsymbol{W}_{Q} \in \mathbf{R}^{B \times V \times d_{k}}, \\ \boldsymbol{K}^{(m)}=\boldsymbol{H}_{\text {stack }} \boldsymbol{W}_{K} \in \mathbf{R}^{B \times V \times d_{k}}, \\ \boldsymbol{V}^{(m)}=\boldsymbol{H}_{\text {stack }} \boldsymbol{W}_{V} \in \mathbf{R}^{B \times V \times d_{k}}, \end{array}$

其中, W_Q∈ $R^{B \times V \times d_{h}}$ , W_K∈ $R^{B \times V \times d_{h}}$ , W_V∈ $R^{B \times V \times d_{h}}$ 均表示第m个注意力头的权重矩阵, 通过反向传播在训练过程中学习得到, d_k=d_h/h表示每个注意力头的维度, h表示注意力头数, 本文设置为4.

对于第m个注意力头, 注意力机制表示为:

$\begin{aligned} \text { head }^{(m)}= & \operatorname{attention}\left(\boldsymbol{q}^{(m)}, \boldsymbol{k}^{(m)}, \boldsymbol{v}^{(m)}\right)= \\ & \operatorname{softmax}\left(\frac{\boldsymbol{q}^{(m)} \boldsymbol{k}^{(m) \mathrm{t}}}{\sqrt{d_{k}}}\right) \boldsymbol{v}^{(m)}, \end{aligned}$

其中, Attention(· )表示注意力函数, 缩放因子 $\sqrt[]{d_{k}}$ 用于防止点积值过大导致Softmax函数梯度消失.注意力权重

Softmax( $\frac{Q^{(m)} {K^{(m)}}^{T}}{\sqrt[]{d_{k}}}$ )∈R^B^×^V^×^V

表示第m个特征空间中每个视图对包括自身的所有视图的关注度.

多头注意力机制通过多头注意力函数MultiHead(· )并行计算h个注意力头, 从不同的表示子空间学习视图间的交互模式.所有注意力头的输出被Concat(· )函数拼接后经过线性变换, 得到最终融合多视图交互信息的增强特征表示:

$\begin{array}{l} \boldsymbol{A}_{\text {out }}=\operatorname{MultiHead}\left(\boldsymbol{H}_{\text {stack }}, \boldsymbol{H}_{\text {stack }}, \boldsymbol{H}_{\text {stack }}\right)= \\ \operatorname{Concat}\left(\boldsymbol{\operatorname { h e a d }}^{(1)}, \boldsymbol{\operatorname { h e a d }}^{(2)}, \cdots, \boldsymbol{\operatorname { h e a d }}^{(h)}\right) \boldsymbol{W}^{o} \in \mathbf{R}^{B \times V \times d_{h}}, \end{array}$

其中W^O∈ $R^{d_{h} \times d_{h}}$ 表示输出投影矩阵.由于查询、键、值矩阵均来自H_stack, 该机制实现多视图特征的自注意力聚合, 使每个视图能自适应融合其它视图的互补信息.

为了促进信息流动和缓解深度网络的训练难度, 在多头注意力层后引入残差连接和层归一化:

${\overset{︿}{H}}_{attn}$ =LayerNorm(H_stack+A_out),

其中LayerNorm(· )表示归一化层.然后, 应用位置式前馈神经网络(Feed-Forward Network, FFN), 对每个位置的特征进行非线性变换, 增强特征表达能力:

FFN(x)=ReLU(xW₁+b₁)W₂+b₂,

其中, FFN(· )表示FFN函数, ReLU=max(0, x)表示激活函数, x表示输入特征, W₁∈ $R^{d_{h} \times 2 d_{h}}$ 、W₂∈ $R^{2 d_{h} \times d_{h}}$ 表示权重, b₁、b₂表示偏差.FFN的隐藏层维度设置为2d_h, 以提供足够的非线性变换能力.针对FFN同样采用残差连接和层归一化, 得到融合后的多视图特征表示:

H_fusion=LayerNorm( ${\overset{︿}{H}}_{attn}$ +FFN( ${\overset{︿}{H}}_{attn}$ ))∈ $R^{B \times V \times d_{h}}$ .

将H_fusion沿视图维度分离, 得到视图v融合后的特征表示:

G⁽^v⁾=H_fusion[∶ , v, ∶ ]∈ $R^{B \times d_{h}}$ , v=1, 2, …, V,

2.4.2 自适应加权融合

为了实现对视图可靠性的动态量化, 将特征方差作为质量准则.方差较大的视图其特征分布具有良好的可分性, 蕴含丰富的类别区分信息, 而方差较小的视图往往分布过于集中, 可能携带大量冗余或噪声.

为了避免数值不稳定, 将沿特征维度的方差均值作为质量得分:

q⁽^v⁾= $\frac{1}{d_{h}} \overset{d_{h}}{\sum_{j = 1}}$ Var( $G_{∶, j}^{(v)}$ ),

其中, $G_{∶, j}^{(v)}$ 表示G⁽^v⁾的第j列, Var(· )表示特征维度方差.

再通过含温度参数τ的Softmax函数进行归一化, 将质量得分转化为融合权重:

w⁽^v⁾= $\frac{\exp (\frac{q^{(v)}}{τ})}{\overset{V}{\sum_{j = 1}} \exp (\frac{q^{(j)}}{τ})}$ .

本文设置温度参数τ=0.1, 用于强调高质量视图的重要作用.

然后通过加权求和, 得到最终的共识表示:

$\boldsymbol{H}=\sum_{v=1}^{V} \boldsymbol{w}^{(v)} \cdot \widehat{\boldsymbol{H}}^{(v)},$

其中$\widehat{\boldsymbol{H}}^{(v)}$表示第v个视图的高级特征表示.

为了强化各视图的高级特征表示与统一共识表示的一致性, 同时防止Transformer训练不稳定导致过拟合, 设计融合一致性约束损失函数:

L_Fus= $\overset{V}{\sum_{v = 1}}$ w⁽^v⁾|| ${\overset{︿}{H}}^{(v)}$ -H|| $_{2}^{2}$ .

L_Fus增强共识表示对各视图特定表示的引导能力, 强化高质量视图的主导作用.

2.5 局部与全局标签对齐模块

为了构建多视图数据的跨视图一致语义表征, 将统一共识表示H映射至聚类空间, 生成全局聚类语义标签, 并通过KL散度将特定视图的局部聚类语义标签与之对齐, 从而提升全局标签的质量以获得更优的聚类结果.

首先, 借助线性变换将共识表示映射为聚类响应向量:

L=HW+b,

其中, W∈ $R^{d_{H} \times K}$ 、b∈R^K分别表示可训练的权重矩阵和偏置向量.再通过Softmax归一化操作, 得到样本i属于簇k的概率:

q_ik= $\frac{\exp (l_{ik})}{\overset{K}{\sum_{s = 1}} \exp (l_{is})}$ ,

其中, l_ik表示样本i属于簇k的原始概率, l_is表示样本i属于簇s的原始概率.矩阵Q={q_ik}∈R^N^×^K表示所有实例的全局共识语义标签.

然后利用KL散度将聚类级对比约束的局部聚类语义标签Q⁽^v⁾与全局标签Q对齐, 得到标签对齐损失函数:

L_Ali= $\overset{V}{\sum_{v = 1}}$ KL(Q‖ Q⁽^v⁾)= $\overset{V}{\sum_{v = 1}} \overset{N}{\sum_{i = 1}} \overset{K}{\sum_{k = 1}}$ q_ikln( $\frac{q_{ik}}{q_{ik}^{v}}$ ).

L_Ali强制局部聚类语义标签与全局标签对齐, 可充分利用视图间的互补性信息.

2.6 损失函数

将DCMCTF中5个模块集成到一个统一框架内, 总目标损失函数如下所示:

L_total=L_Rec+λ₁L_Conf+λ₂L_Dcon+λ₃L_Fus+λ₄L_Ali,

其中, L_Rec表示重构损失, L_Conf表示交替对抗损失, L_Dcon表示双重对比损失, L_Fus表示融合一致性损失, L_Ali表示标签对齐损失, λ₁、λ₂、λ₃、λ₄表示权重参数.

联合优化整个目标函数, 并通过概率最大化方法, 从全局聚类语义标签Q中获得最后的聚类标签Y:

y_i=arg $\max_{k}$ q_ik.

2.7 算法步骤

DCMCTF具体步骤如下所示.

算法1 DCMCTF

输入多视图数据集X, 温度参数τ₁、τ₂,

权衡参数λ₁、λ₂、λ₃、λ₄, 聚类数K,

预训练轮数E_pre, 对比学习轮数E_con

输出聚类标签Y

随机初始化编码器、解码器及判别器的参数

对于每个epoch∈[1, E_pre]执行

通过编码器E_v(· )获取低级特征

通过解码器D_v(· )重构数据

计算重构损失

反向传播并更新参数

结束循环

对于每个epoch∈[E_pre+1, E_pre+E_con]执行

//特征提取

生成高级特征

生成聚类标签

计算各视图的增强特征

计算共识表示

生成全局聚类标签

//训练判别器(每5个批次一次)

满足训练频率更新判别器Dis_v(· )

//计算损失

计算重构损失

计算交替对抗损失

计算实例级对比损失

计算聚类级对比损失

计算融合一致性损失

计算标签对齐损失

组合所有损失项得到总损失

反向传播并训练整个模型(除判别器外)

结束循环

执行最大概率索引, 得到聚类标签Y

2.8 时间复杂度分析

Auto-Encoder模块主要通过编码解码操作提取和重构数据特征, 时间复杂度为O(VNd_vd), 其中, d_v表示第v个视图的原始特征维度, d表示低级特征维度.交替对抗学习模块需要训练V个判别器和生成器, 时间复杂度为O(V²Nd), 但由于每5个批次才更新一次判别器, 实际计算量显著降低.双重对比约束模块中实例级对比需要计算所有样本对的相似度, 时间复杂度为O(V²N²d_h), 其中d_h表示高级特征维度, 聚类级对比的时间复杂度为O(V²K²N).基于Transformer的自适应融合模块采用多头注意力机制学习视图间关联信息, 时间复杂度为O(NV²d_h).局部与全局标签对齐模块计算KL散度, 实现局部与全局标签的一致性约束, 时间复杂度为O(VNK).考虑到在实际问题中K≪N, 总体时间复杂度为O(V²· N²d_h).实例级对比为DCMCTF主要的计算瓶颈.

3 实验及结果分析

3.1 实验设置

本文采用ACC(Accuracy)、NMI(Normalized Mutual Information)和PUR(Purity)作为评价指标.

所有实验均采用PyTorch1.12.1实现, 硬件配置为NVIDIA GeForce RTX 4060.批次大小设为256, 算法学习率设为0.000 3, 判别器学习率设为0.000 1.为了确保不同数据集上方法性能的可比性, 对所有数据集采用统一的超参数配置:τ₁=0.5, τ₂=1.0, λ₁=1.0, λ₂=0.01, λ₃=0.05, λ₄=0.05.

选择在如下数据集上进行实验.

1)BDGP数据集^[24].涵盖2 500幅果蝇胚胎图像, 每幅图像包含1 750维视觉特征向量和79维文本特征向量.

2)Hdigit数据集^[25].涵盖10 000个手写数字样本, 每个样本由784维和256维不同特征视图构成.

3)MNIST_USPS数据集^[26].融合MNIST、USPS数据集, 共计5 000个手写数字样本, 特征维度均为784.

4)NGs数据集.涵盖500篇新闻文本, 每篇文本通过3种预处理方式生成3个2 000维特征视图.

5)UCI-digit数据集.涵盖2 000个0~9范围的手写数字样本, 每个样本有3个维度.

6)synthetic3d数据集^[27].由高斯混合模型生成, 包含600个样本, 每个样本具有3个特征维度均为3的视图.

7)Fashion数据集^[28].涵盖10 000幅28×28的图像, 类别包括运动鞋、裤子、包等10种商品类型.

8)Cifar10数据集^[29].包含10类50 000个日常物体样本, 每个样本的3个特征维度分别为512、2 048和1 024.

9)Caltech数据集^[30].由1 400幅RGB图像构成, 涵盖7类, 每幅图像提取5个特征视图.

数据集具体信息如表1所示.

表1 实验数据集 Table 1 Experimental datasets

3.2 对比实验

为了检验DCMCTF聚类性能, 本文选取3种传统的多视图聚类算法和10种深度多视图聚类算法作为对比算法.

1)传统多视图聚类算法.

(1)FastMICE(Fast Multi-view Clustering via Ensembles)^[3].设计早-晚期融合混合策略, 实现高效多阶段融合.

(2)PLCMF(Pseudo-Label Guided Collective Ma-trix Factorization)^[31].在所有视图上单独聚类生成伪标签, 并在集体矩阵分解中引入伪标签作为约束.

(3)LMVSC(Large-Scale Multi-view Subspace Clus-tering)^[32].借鉴锚图机制, 为每个视图构建紧凑图结构.

2)深度多视图聚类算法.

(1)SSLNMVC^[7].通过U-Projection Module提纯共识高级特征表示, 结合语义标签双向校准机制挖掘多视图互补信息, 有效提升标签质量.

(2)SiMVC(Simple Multi-view Clustering)^[33].完全放弃表征对齐机制, 验证无对齐策略也可达到先进性能.

(3)CoMVC(Contrastive Multi-view Clustering)^[33].引入选择性对比对齐机制, 同时保留对齐带来的局部结构保持与视图不变性优势.

(4)CONAN(Contrastive Fusion Network)^[34].从信息瓶颈理论出发, 通过中间变量对齐与对比学习进行多视图融合, 在保留视图特异性特征的同时, 提取多视图一致的公共表示.

(5)DEMVC(Deep Embedded Multi-view Cluste-ring with Collaborative Training)^[35].将轮流参考各视图与共享视图辅助分布的协同训练引入深度多视图聚类, 既保持深度学习的强表示能力, 又实现多视图信息的高效融合.

(6)GCFAggMVC(Global and Cross-View Feature Aggregation for Multi-view Clustering)^[36].学习全局样本结构关系, 生成鲁棒共识表示, 并且通过结构引导的对比学习模块, 促使具有高结构相关性的不同样本的视图特定表示趋于一致.

(7)MFLVC(Multi-level Feature Learning for Con-trastive Multi-view Clustering)^[37].设计多级特征学习框架与双对比学习一致性约束, 并利用高维特征聚类信息微调语义标签.

(8)MSCIB(Multi-view Semantic Consistency Based Information Bottleneck for Clustering)^[38].通过变分自编码器保障视图内信息的完整性, 利用信息瓶颈过滤无关冗余信息, 最终学习具有强判别性的全局一致表示.

(9)MAGA(Multi-view Contrastive Clustering with Integrated Graph Aggregation and Confidence Enhancement)^[39].利用跨视图谱图聚合模块, 将各视图的图嵌入特征聚合至统一特征空间, 并通过最大化聚类分配置信度, 让同簇样本的分配更一致.

(10)MS2FA-CMVC(Multi-branch Space Sharing Feature Aggregation for Contrastive Multi-view Clustering)^[40].学习跨批次共享表示空间, 聚合全局样本关联与跨视图互补信息, 强化多视图表示的一致性.

各算法在8个数据集上的指标值对比如表2和表3所示, 表中黑体数字表示最优值, 斜体数字表示次优值.

表2 各算法在Fashion、MNIST_USPS、Cifar10、synthetic3d数据集上的指标值对比 Table 2 Metric value comparison of different algorithms on Fashion, MNIST_USPS, Cifar10 and synthetic3d datasets

表3 各算法在BDGP、UCI-digit、NGs、Hdigit数据集上的指标值对比 Table 3 Metric value comparison of different algorithms on BDGP, UCI-digit, NGs and Hdigit datasets

由表2和表3可见, 相比3种传统多视图聚类算法(LMVSC、PLCMF和FastMICE), 深度多视图聚类算法的聚类性能在大部分情况下都明显更优.这是因为传统的算法局限于提取的线性特征, 无法建模复杂的非线性关系, 而深度算法得益于神经网络强大的数据处理能力, 可捕捉更深层次的结构信息.

相比10种深度多视图聚类算法, DCMCTF仅在BDGP、Cifar10、MNIST_USPS数据集上的NMI值次优, 在其余数据集上的结果均为最优.SiMVC、CoMVC和CONAN融合机制简单, 未考虑视图质量差异.DEMVC依赖解码器重构的低维特征进行协同融合, 含部分视图私有信息.GCFAggMVC缺乏实例级特征判别性约束.MFLVC依赖标签对比损失拉近距离, 缺乏显式的分布对齐机制, 而MSCIB和SSLNMVC仅针对高级特征或标签分布进行显式匹配, 学习的低级特征仍可能残留视图特异性噪声.MAGA和MS2FA-CMVC在进行视图融合时未融入质量感知加权, 无法动态弱化低质量视图的干扰, 标签质量受低质量视图影响较大.

相比其它算法, DCMCTF采用交替对抗学习模块, 通过生成器-判别器博弈实现跨视图低级特征分布的对齐, 又引入双重对比约束模块, 在实例级和聚类级层面同步施加对比约束, 强化跨视图表征一致性.然后设计基于Transformer的自适应融合模块, 利用多头注意力机制动态学习视图间的关联性, 并结合质量感知的加权策略生成鲁棒的共识表示, 最终通过局部与全局标签对齐模块提升聚类质量.

为了探究交替对抗学习模块以及融合机制与视图数量的关系, 继续在Caltech数据集上进行对比实验, 结果如表4所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可见, 随着视图数量的增加, 对抗任务中判别器的伪造源由1个增至4个, 丰富的对抗信号改善跨视图低级特征分布的对齐效果, 并且在高级特征融合过程中, 当V=2时, 每个视图只能与1个其它视图交互, 信息流动路径有限, 而V=5时, 每个视图可以与4个其它视图交互, 能更有效地利用视图间的互补性信息.ACC值由Cal- tech-2V上的0.628 6增至Caltech-5V上的0.887 1, 验证视图数量的增加对于多视图聚类任务的重要意义.

表4 各算法在Caltech数据集上的指标值对比 Table 4 Metric value comparison of different algorithms on Caltech dataset

表4显示, DCMCTF在Caltech-4V数据集上聚类性能提升明显, 而在其它数据集上提升幅度有限.这与数据集的基线性能和视图特性密切相关.Fashion、MNIST-USPS、NGs数据集的基线性能已较高, 进一步提升的空间有限.Caltech-4V数据集具有4个不同维度的视图, 视图间异质性较强, 本文的交替对抗学习模块能有效对齐跨视图特征分布, 基于Transformer的自适应融合模块能动态学习不同质量视图的贡献权重, 因此DCMCTF在高异质性场景中展现出更明显的优势.

3.3 统计检验

为了评估DCMCTF与对比的10种深度多视图聚类算法的性能差异, 进行非参数统计分析.

首先进行Friedman检验.ACC、NMI和PUR的p值分别为5.63×10^-14, 2.03×10^-13, 1.31×10^-14, 均小于显著性水平0.1, 这表明各算法的聚类性能存在显著差异.再进行Nemenyi检验和Wilcoxon符号秩检验, 检验结果如表5所示, 表中黑体数字表示p值小于0.1的结果, 即表示DCMCTF显著优于相应的对比算法.

表5 各算法的Nemenyi检验和Wilcoxon符号秩检验结果 Table 5 Results of Nemenyi and Wilcoxon signed-rank tests for different algorithms

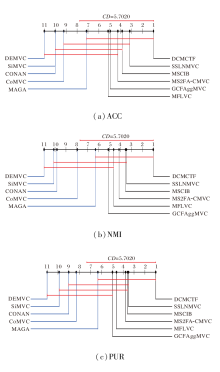
将Nemenyi检验结果进行可视化, 临界差分图如图2所示, 横轴上的排名表示算法的聚类性能排名, DCMCTF在3个评价指标上均位列第一.当两种算法的排名差距超过临界距离值时, 则认为二者性能存在显著差异.

	Figure Option View Download New Window
	图2 各算法Nemenyi检验的临界差分图Fig.2 Critical difference diagram of different algorithms for Nemenyi test

3.4 参数敏感性分析

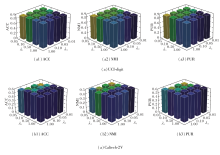
为了探究DCMCTF中双重对比损失的2个温度参数τ₁、τ₂、总目标损失函数中的4个权重参数λ₁、λ₂、λ₃、λ₄对聚类性能的影响, 将上述6个参数分为3组, 在UCI-digit、Caltech-2V数据集上分别进行网格搜索.参考文献[7], 设置温度参数τ₁=0.5, τ₂=1.0, 再按照经验设置λ₃=λ₄=0.05, λ₁=0.05, 0.10, 0.50, 1.0, λ₂=0.01, 0.05, 0.10, 1.0, 相应的性能对比如图3所示.

	Figure Option View Download New Window
	图3 λ₁、λ₂对DCMCTF性能的影响Fig.3 Effect of λ₁ and λ₂ on DCMCTF performance

由图3可知, 设置较大的λ₁和较小的λ₂时性能更优.这是因为对抗学习通过生成器-判别器博弈在低级特征空间快速消除视图间的分布差异, 有助于后续学习, 因此需要较大权重以加速分布对齐, 而对比学习在高级特征空间和语义空间中持续优化样本级表征的判别性, 较小权重有助于避免训练初期因假阴性样本导致的过度惩罚, 使特征空间能平滑演化.

保持温度参数τ₁、τ₂不变, 设置λ₁=1, λ₂=0.01.λ₃=0.01, 0.05, 0.10, 0.50, 1.0, λ₄=0.01, 0.05, 0.10, 0.50, 1.0.

相应的性能对比如图4所示.

	Figure Option View Download New Window
	图4 λ₃、λ₄对DCMCTF性能的影响Fig.4 Effect of λ₃ and λ₄ on DCMCTF performance

由图4可知, 在UCI-digit数据集上, 当λ₃=0.01, 0.05, 0.10, λ₄取任意值时, DCMCTF性能都保持稳定, 而在Caltech-2V数据集上呈现出较高的敏感性.当λ₃=λ₄=0.05时, DCMCTF在3个指标上均达到最优值.这说明融合对齐和标签对齐作为辅助性约束, 二者都需要在强化一致性和保留视图特异性之间取得平衡, 因此应采用相对较小且相近的权重.

将4个权重参数设置为统一值后, 定义τ₁=0.3, 0.4, 0.5, 0.6、τ₂=0.7, 0.8, 0.9, 1.0.相应的性能对比如图5所示, 由图可知, 当τ₁=0.5, τ₂=1.0时, DCMCTF在3个指标上均达到最优值.这是因为实例级对比学习旨在对齐同一样本的跨视图表示, 正负样本对界限明确, 因此需要较小的温度参数以维持较高的区分度, 而聚类级对比学习旨在对齐不同视图的聚类结构, 簇内样本存在一定多样性, 因此需要较大的温度参数.

	Figure Option View Download New Window
	图5 τ₁、τ₂对DCMCTF性能的影响Fig.5 Effect of τ₁ and τ₂ on DCMCTF performance

3.5 消融实验

为了验证DCMCTF中各核心组件的有效性, 构建如下算法.

1)消除交替对抗学习模块(w/o L_Conf);

2)消除双重对比约束模块(w/o L_Dcon);

3)消除基于Transformer的自适应融合模块(w/o L_Fus);

4)消除局部与全局标签对齐模块(w/o L_Ali);

5)使用简单加权平均代替基于Transformer融合的算法(w/o T_rans).

在synthetic3d、NGs、Fashion、Caltech-5V基准数据集上进行实验, 结果如表6所示, 表中黑体数字表示最优值, 斜体数字表示次优值.由表可见, 双重对比约束模块是DCMCTF的核心基础, 移除后的算法在所有数据集上的性能都出现明显下降, ACC值在NGs数据集上从0.940 0降至0.390 0, 在Fashion数据集上从0.993 8降至0.259 1.这是因为实例级对比学习通过最大化同一样本在不同视图间的一致性以学习视图不变特征, 而聚类级对比学习则通过增强类别可分离性以提升聚类判别能力.

表6 各模块在4个数据集上的消融实验结果 Table 6 Ablation experiment results of different modules on 4 datasets

共识标签对齐机制在统一多视图预测方面至关重要.移除局部与全局标签对齐模块后, ACC值在NGs数据集上降至0.594 0, 在Fashion数据集上降至0.200 1, 在Caltech-5V数据集上降至0.407 1.这是因为共识标签对齐机制通过全局标签一致性约束有效协调各视图的预测结果, 避免视图间的冲突和模型陷入局部最优.

基于Transformer的自适应融合模块在复杂场景中具有优势.当使用简单平均替代Transformer时, ACC值在Caltech-5V数据集上从0.887 1降至0.847 1, 降幅高达到4.5%.这是因为基于Trans-former的多头自注意力机制能有效捕捉视图间的复杂交互模式, 动态建模能力在处理多视图数据时显著优于简单加权融合方法.

融合对齐模块和对抗学习模块提供稳定的性能增益.移除基于Transformer的自适应融合模块后, ACC值在Caltech-5V数据集上下降最明显, 为2.38%, 这是因为质量感知的特征融合模块能有效优化多视图信息整合.移除交替对抗学习模块后, 在4个数据集上性能下降均较小, 说明对抗学习主要起辅助作用, 通过对抗训练可增强特征的鲁棒性和视图聚类结果的一致性.

3.6 t-SNE可视化

为了展示DCMCTF在不同训练阶段下的聚类结果, 利用t-SNE^[41]在Fashion、Hdigit、Caltech-5V数据集上进行可视化实验, 训练轮次(Epoch)改变时, 相应聚类结果如图6所示, 图中不同颜色表示不同的聚类簇.

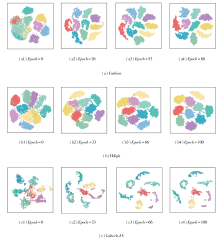	Figure Option View Download New Window
	图6 Fashion、Hdigit和Caltech-5V数据集上在不同训练阶段的可视化结果Fig.6 Visualization results of different training stages on Fashion, Hdigit and Caltech-5V datasets

图6第1列表明训练初期不同类别的样本呈现高度混杂的分布状态, 第2列显示样本点开始向各自的簇中心进行迁移, 而在第3列中部分聚类簇已形成相对稳定的聚集区域, 只有少量边界样本处于模糊地带.当达到最大训练轮次时(第4列), 呈现出高度有序的聚类模式, 这说明随着训练轮次的增加, DCMCTF的特征判别能力和聚类质量也在不断提高.

3.7 收敛性分析

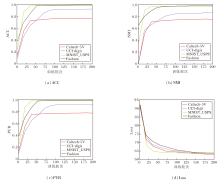
为了研究DCMCTF的收敛性, 在Caltech-5V、UCI-digit、MNIST_USPS、Fashion数据集上进行实验, 具体收敛曲线如图7所示.针对Loss指标, Caltech-5V、UCI-digit数据集上在100个训练轮次内达到收敛, MNIST_USPS数据集上在20个训练轮次内快速收敛, Fashion数据集上在80个训练轮次趋于平稳.针对ACC、NMI、PUR指标, 在Caltech-5V、MNIST_USPS、Fashion数据集上, 均在20个训练轮次内快速上升并收敛, 而UCI-digit数据集上在50个训练轮次达到收敛.上述结果表明DCMCTF在不同规模的数据集上均表现出良好的收敛情况.

	Figure Option View Download New Window
	图7 各指标收敛性分析结果Fig.7 Convergence analysis results of metrics

3.8 运行时间对比

考虑到DCMCTF的时间复杂度主要与双重对比模块有关, 本节将其与SSLNMVC^[7]、GCFAgg-MVC^[36]、MFLVC^[37]、MSCIB^[38]、MAGA^[39]、MS2FA-CMVC^[40]这6个深度多视图聚类算法进行对比.实验在synthetic3d、BDGP、NGs、Fashion数据集上开展.具体运行时间对比如表7所示, 表中黑体数字表示最优值.由表可见, 在小规模数据集synthetic3d、BDGP、NGs上, DCMCTF与聚类性能最优的基线算法(MS2FA-CMVC和SSLNMVC)运行速度相当.在较大规模Fashion数据集上, 相比MSCIB和MAGA, DCMCTF的运行时间分别缩短2/5和3/4.这说明DCMCTF在保持高聚类精度的同时, 实现效率与性能的良好平衡.

表7 各算法在4个数据集上的运行时间对比 Table 7 Running time comparison of different algorithms on 4 datasets

4 结束语

本文提出基于Transformer融合的深度对比多视图聚类(DCMCTF), 解决传统方法难以有效整合多视图互补信息和处理视图质量差异的问题.设计交替对抗学习模块, 有效削弱视图间的异质性, 实现跨视图低级特征分布的对齐.引入实例级和聚类级双重对比约束模块, 增强跨视图表征的判别性和一致性.构建基于Transformer的自适应融合模块, 动态捕捉视图间的复杂关联, 有效融合高级特征表示, 再结合质量感知的加权策略, 进一步抑制低质量视图的负面影响.设计局部与全局标签对齐模块, 统一各视图的聚类预测结果, 在9个公开数据集上与13种算法进行对比实验, 充分验证DCMCTF的优越性和有效性.

今后将继续探索如何更充分地挖掘跨视图信息的互补性, 并尝试将DCMCTF扩展至不完整多视图聚类和大规模数据场景中.

本文责任编委欧阳丹彤

Recommended by Associate Editor OUYANG Dantong

参考文献

文献选项

[1]	REDDY M G, REDDY P V N, REDDY P R. Multi-modal Medical Image Fusion Using 3-Stage Multiscale Decomposition and PCNN with Adaptive Arguments. International Journal of Image and Gra-phics, 2023, 23(3). DOI: 10.1142/S0219467822400101. [本文引用:1]
[2]	WANG Y. Survey on Deep Multi-modal Data Analytics: Collaboration, Rivalry, and Fusion. ACM Transactions on Multimedia Computing, Communications, and Applications, 2021, 17(1s). DOI: 10.1145/3408317. [本文引用:1]
[3]	HUANG D, WANG C D, LAI J H. Fast Multi-view Clustering via Ensembles: Towards Scalability, Superiority, and Simplicity. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(11): 11388-11402. [本文引用:2]
[4]	QIN Y L, FENG G R, REN Y L, et al. Consistency-Induced Multiview Subspace Clustering. IEEE Transactions on Cybernetics, 2022, 53(2): 832-844. [本文引用:1]
[5]	赵兴旺, 王淑君, 刘晓琳, 等. 基于二部图的联合谱嵌入多视图聚类算法. 软件学报, 2023, 35(9): 4408-4424. (ZHAO X W, WANG S J, LIU X L, et al. Joint Spectral Embe-dding Multi-view Clustering Algorithm Based on Bipartite Graphs. Journal of Software, 2023, 35(9): 4408-4424.) [本文引用:1]
[6]	LI Z Y, WANG Q Q, TAO Z Q, et al. Deep Adversarial Multi-view Clustering Network // Proc of the 28th International Joint Confe-rence on Artificial Intelligence. San Francisco, USA: IJCAI, 2019: 2952-2958. [本文引用:1]
[7]	YAN W Q, YANG T Y, TANG C. Self-Supervised Semantic Soft Label Learning Network for Deep Multi-view Clustering. IEEE Transactions on Multimedia, 2025, 27: 4971-4983. [本文引用:4]
[8]	WANG J, WU B, REN Z W, et al. Decomposed Deep Multi-view Subspace Clustering with Self-Labeling Supervision. Information Sciences, 2024, 653. DOI: 10.1016/j.ins.2023.119798. [本文引用:1]
[9]	王静红, 陈潇, 王熙照, 等. 基于自适应结构增强的对比协同多视图属性图聚类. 模式识别与人工智能, 2025, 38(9): 809-819. (WANG J H, CHEN X, WANG X Z, et al. Contrastive Collaborative Multi-view Attribute Graph Clustering Based on Adaptive Structure Enhancement. Pattern Recognition and Artificial Intelligence, 2025, 38(9): 809-819.) [本文引用:1]
[10]	LI D, WANG H B, WANG Y F, et al. Instance-Wise Multi-view Representation Learning. Information Fusion, 2023, 91: 612-622. [本文引用:1]
[11]	WANG J, FENG S H, LÜ G Y, et al. Triple-Granularity Contrastive Learning for Deep Multi-view Subspace Clustering // Proc of the 31st ACM International Conference on Multimedia. New York, USA: ACM, 2023: 2994-3002. [本文引用:1]
[12]	YAN W Q, ZHANG Y Y, TANG C, et al. Anchor-Sharing and Cluster-Wise Contrastive Network for Multiview Representation Learning. IEEE Transactions on Neural Networks and Learning Systems, 2024, 36(2): 3797-3807. [本文引用:1]
[13]	CUI J R, LI Y T, HUANG H, et al. Dual Contrast-Driven Deep Multi-view Clustering. IEEE Transactions on Image Processing, 2024, 33: 4753-4764. [本文引用:1]
[14]	ZHU P F, YAO X J, WANG Y, et al. Multiview Deep Subspace Clustering Networks. IEEE Transactions on Cybernetics, 2024, 54(7): 4280-4293. [本文引用:1]
[15]	LIU J, CAO F Y, JING X C, et al. Deep Multi-view Graph Clustering Network with Weighting Mechanism and Collaborative Training. Expert Systems with Applications, 2024, 236. DOI: 10.1016/j.eswa.2023.121298. [本文引用:1]
[16]	CHEN Z, WU X J, XU T Y, et al. Multi-layer Multi-level Comprehensive Learning for Deep Multi-view Clustering. Information Fusion, 2025, 116. DOI: 10.1016/j.inffus.2024.102785. [本文引用:1]
[17]	CHEN X L, HE K M. Exploring Simple Siamese Representation Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 15745-15753. [本文引用:1]
[18]	CHEN T, KORNBLITH S, NOROUZI M, et al. A Simple Framework for Contrastive Learning of Visual Representations // Proc of the 37th International Conference on Machine Learning. San Diego, USA: JMLR, 2020: 1597-1607. [本文引用:2]
[19]	HE K M, FAN H Q, WU Y X, et al. Momentum Contrast for Unsupervised Visual Representation Learning // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2020: 9726-9735. [本文引用:1]
[20]	张凯涵, 冯晨娇, 姚凯旋, 等. 基于对比学习和语义增强的多模态推荐算法. 模式识别与人工智能, 2024, 37(6): 479-490. (ZHANG K H, FENG C J, YAO K X, et al. Multimodal Reco-mmendation Algorithm Based on Contrastive Learning and Semantic Enhancement. Pattern Recognition and Artificial Intelligence, 2024, 37(6): 479-490.) [本文引用:1]
[21]	BIAN J T, LIN Y X, XIE X H, et al. Multilevel Contrastive Multiview Clustering with Dual Self-Supervised Learning. IEEE Transactions on Neural Networks and Learning Systems, 2025, 36(6): 10422-10436. [本文引用:1]
[22]	FEI L K, HE J L, ZHU Q, et al. Deep Multi-view Contrastive Clustering via Graph Structure Awareness. IEEE Transactions on Image Processing, 2025, 34: 3805-3816. [本文引用:1]
[23]	CHENG J F, WANG Q Q, TAO Z Q, et al. Multi-view Attribute Graph Convolution Networks for Clustering // Proc of the 29th International Joint Conference on Artificial Intelligence. San Francisco, USA: IJCAI, 2020: 2973-2979. [本文引用:1]
[24]	CAI X, WANG H, HUANG H, et al. Joint Stage Recognition and Anatomical Annotation of Drosophila Gene Expression Patterns. Bioinformatics, 2012, 28(12): i16-i24. [本文引用:1]
[25]	CHEN M S, LIN J Q, LI X L, et al. Representation Learning in Multi-view Clustering: A Literature Review. Data Science and Engineering, 2022, 7(3): 225-241. [本文引用:1]
[26]	PENG X, HUANG Z Y, LÜ J C, et al. COMIC: Multi-view Clustering without Parameter Selection // Proc of the 36th International Conference on Machine Learning. San Diego, USA: JMLR, 2019: 5092-5101. [本文引用:1]
[27]	KUMAR A, RAI P, DAUMÉ H. Co-regularized Multi-view Spectral Clustering[C/OL]. [2025-10-25]. https://proceedings.neurips.cc/paper/2011/file/31839b036f63806cba3f47b93af8ccb5-Paper.pdf. [本文引用:1]
[28]	XIAO H, RASUL K, VOLLGRAF R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms[C/OL]. [2025-10-25]. https://arxiv.org/abs/1708.07747. [本文引用:1]
[29]	KRIZHEVSKY A. Learning Multiple Layers of Features from Tiny Images. Technical Report. Toronto, Canada: University of Toronto, 2009. [本文引用:1]
[30]	LI F F, FERGUS R, PERONA P. Learning Generative Visual Mo-dels from Few Training Examples: An Incremental Bayesian Approach Tested on 10Object Categories // Proc of the Conference on Computer Vision and Pattern Recognition Workshop. Washington, USA: IEEE, 2004. DOI: 10.1109/CVPR.2004.383. [本文引用:1]
[31]	WANG D, HAN S W, WANG Q, et al. Pseudo-Label Guided Co-llective Matrix Factorization for Multiview Clustering. IEEE Transactions on Cybernetics, 2022, 52(9): 8681-8691. [本文引用:1]
[32]	KANG Z, ZHOU W T, ZHAO Z T, et al. Large-Scale Multi-view Subspace Clustering in Linear Time. Proc of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 4412-4419. [本文引用:1]
[33]	TROSTEN D J, LØKSE S, JENSSEN R, et al. Reconsidering Re-presentation Alignment for Multi-view Clustering // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2021: 1255-1265. [本文引用:2]
[34]	KE G Z, HONG Z Y, ZENG Z Q, et al. CONAN: Contrastive Fusion Networks for Multi-view Clustering // Proc of the IEEE International Conference on Big Data. Washington, USA: IEEE, 2021: 653-660. [本文引用:1]
[35]	XU J, REN Y Z, LI G F, et al. Deep Embedded Multi-view Clustering with Collaborative Training. Information Sciences, 2021, 573: 279-290. [本文引用:1]
[36]	YAN W Q, ZHANG Y Y, LÜ C L, et al. GCFAgg: Global and Cross-View Feature Aggregation for Multi-view Clustering // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Re-cognition. Washington, USA: IEEE, 2023: 19863-19872. [本文引用:2]
[37]	XU J, TANG H Y, REN Y Z, et al. Multi-level Feature Learning for Contrastive Multi-view Clustering // Proc of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington, USA: IEEE, 2022: 16030-16039. [本文引用:2]
[38]	YAN W B, ZHOU Y Y, WANG Y F, et al. Multi-view Semantic Consistency Based Information Bottleneck for Clustering. Know-ledge-Based Systems, 2024, 288. DOI: 10.1016/j.knosys.2024.111448. [本文引用:2]
[39]	BIAN J T, XIE X H, LAI J H, et al. Multi-view Contrastive Clustering via Integrating Graph Aggregation and Confidence Enhancement. Information Fusion, 2024, 108. DOI: 10.1016/j.inffus.2024.102393. [本文引用:2]
[40]	ZHANG Y Y, YAN W Q, TANG C, et al. Multi-branch Space Sharing Feature Aggregation for Contrastive Multi-view Clustering. Pattern Recognition, 2025. DOI: 10.1016/j.patcog.2025.111704. [本文引用:2]
[41]	VAN DER MAATEN L, HINTON G. Visualizing Data Using t-SNE. Journal of Machine Learning Research, 2008, 9(86): 2579-2605. [本文引用:1]

2023

0.0

... 作为无监督学习领域的一项重要任务,多视图聚类旨在充分利用多视图数据的互补优势,融合来自不同视角的异构信息^[1],挖掘隐藏在多个视图中的一致性聚类结构,并将样本划分为若干语义相关的组^[2] ...

2021

0.0

2023

0.0

... 传统多视图聚类方法利用矩阵分解^[3]、子空间学习^[4]、图学习^[5]等策略融合视图互补信息,再执行如K均值、谱聚类等预定义的聚类策略以捕捉数据结构差异 ...

... (1)FastMICE(Fast Multi-view Clustering via Ensembles)^[3] ...

2022

0.0

2023

0.0

2019

0.0

... 但是,这些方法依赖线性融合策略处理浅层特征,难以有效建模数据中蕴含的非线性复杂关系^[6] ...

2025

0.0

... 典型方法包括基于深度嵌入聚类的方法^[7]、基于子空间聚类的方法^[8]、基于图卷积网络的方法^[9]及基于自编码器聚类的方法^[10] ...

... (1)SSLNMVC^[7] ...

... 参考文献[7],设置温度参数#cod#x003c4 ...

... 8 运行时间对比考虑到DCMCTF的时间复杂度主要与双重对比模块有关,本节将其与SSLNMVC^[7]、GCFAgg-MVC^[36]、MFLVC^[37]、MSCIB^[38]、MAGA^[39]、MS2FA-CMVC^[40]这6个深度多视图聚类算法进行对比 ...

2024

0.0

... 典型方法包括基于深度嵌入聚类的方法^[7]、基于子空间聚类的方法^[8]、基于图卷积网络的方法^[9]及基于自编码器聚类的方法^[10] ...

2025

0.0

... 典型方法包括基于深度嵌入聚类的方法^[7]、基于子空间聚类的方法^[8]、基于图卷积网络的方法^[9]及基于自编码器聚类的方法^[10] ...

2023

0.0

... 典型方法包括基于深度嵌入聚类的方法^[7]、基于子空间聚类的方法^[8]、基于图卷积网络的方法^[9]及基于自编码器聚类的方法^[10] ...

2023

0.0

... 现有方法按训练阶段可划分为两阶段方法^[11]和端到端方法^[12] ...

2024

0.0

... 现有方法按训练阶段可划分为两阶段方法^[11]和端到端方法^[12] ...

2024

0.0

... Cui等^[13]提出DCMVC(Dual Contrastive Learning-Based Deep Multi-view Clustering Network),利用动态簇扩散损失与可靠邻居引导的正对齐损失,学习兼具类间分离性与类内紧凑性的聚类友好型共识表示 ...

2024

0.0

... Zhu等^[14]提出MvDSCN(Multiview Deep Subspace Clustering Net-works),构建深度卷积自编码器潜空间,使用多样性网络学习视图特定自表示矩阵,通用性网络学习通用自表示矩阵,根据多样性正则项与普适性正则化约束划分多视图特征子空间 ...

2024

0.0

... Liu等^[15]提出DMVGC(Deep Multi-view Graph Clustering Net-work with Weighting Mechanism and Collaborative Training),构建含视图特定图编码器与统一图解码器的深度网络,并在视图特定嵌入层与公共嵌入层协同自训练聚类目标 ...

2025

0.0

... Chen等^[16]提出3MC(Multi-layer Multi-level Compre-hensive Learning Framework for Deep Multi-view Clustering),对各编码器层特征开展多视图间对比学习,实现特征一致性,借助层特定标签MLP转换为高层语义标签后进行层间对比学习,获取多层一致的聚类分配 ...

2021

0.0

... 2 对比学习对比学习作为一种强大的无监督表示学习范式,因其通过在潜在空间中最大化正样本对的相似度的同时最小化负样本对的相似度以提取判别性特征,已在多视图聚类领域受到广泛关注^[17] ...

2020

0.0

... Chen等^[18]提出SimCLR,利用数据增强在批内构造样本对进行对比学习 ...

... 类似于Sim- CLR^[18],本文采用点积作为高级特征表示的相似性度量指标: ...

2020

0.0

... He等^[19]提出MoCo(Momentum Contrast),通过队列和动量编码器维护大规模字典,提升对比效率 ...

2024

0.0

... 近年来,基于对比学习的深度多视图聚类方法不断涌现^[20] ...

2025

0.0

... Bian等^[21]提出MCMC(Multilevel Con-trastive Multiview Clustering),将潜在子空间中对象的最近邻作为正样本对,针对聚类、实例和原型执行多层次对比学习,捕捉数据多层次表示,并通过对偶自监督学习关联不同层次结构表示 ...

2025

0.0

... Fei等^[22]提出DMvCGSA(Deep Multi-view Contrastive Clustering via Graph Structure Awareness),利用相似性引导的实例级对比学习,使特定视图特征具备判别性,同时采用簇级对比学习,直接挖掘对聚类有益的一致性信息,获取多视图样本的协同表示 ...

2020

0.0

... 此时每个维度的值反映样本归属于相应类簇的概率^[23] ...

2012

0.0

... 1)BDGP数据集^[24] ...

2022

0.0

... 2)Hdigit数据集^[25] ...

2019

0.0

... 3)MNIST_USPS数据集^[26] ...

0.0

... 6)synthetic3d数据集^[27] ...

0.0

... 7)Fashion数据集^[28] ...

2009

0.0

... 8)Cifar10数据集^[29] ...

2004

0.0

... 9)Caltech数据集^[30] ...

2022

0.0

... (2)PLCMF(Pseudo-Label Guided Collective Ma-trix Factorization)^[31] ...

2020

0.0

... (3)LMVSC(Large-Scale Multi-view Subspace Clus-tering)^[32] ...

2021

0.0

... (2)SiMVC(Simple Multi-view Clustering)^[33] ...

... (3)CoMVC(Contrastive Multi-view Clustering)^[33] ...

2021

0.0

... (4)CONAN(Contrastive Fusion Network)^[34] ...

2021

0.0

... (5)DEMVC(Deep Embedded Multi-view Cluste-ring with Collaborative Training)^[35] ...

2023

0.0

... (6)GCFAggMVC(Global and Cross-View Feature Aggregation for Multi-view Clustering)^[36] ...

2022

0.0

... (7)MFLVC(Multi-level Feature Learning for Con-trastive Multi-view Clustering)^[37] ...

2024

0.0

... (8)MSCIB(Multi-view Semantic Consistency Based Information Bottleneck for Clustering)^[38] ...

2024

0.0

... (9)MAGA(Multi-view Contrastive Clustering with Integrated Graph Aggregation and Confidence Enhancement)^[39] ...

2025

0.0

... (10)MS2FA-CMVC(Multi-branch Space Sharing Feature Aggregation for Contrastive Multi-view Clustering)^[40] ...

2008

0.0

... 6 t-SNE可视化为了展示DCMCTF在不同训练阶段下的聚类结果,利用t-SNE^[41]在Fashion、Hdigit、Caltech-5V数据集上进行可视化实验,训练轮次(Epoch)改变时,相应聚类结果如图6所示,图中不同颜色表示不同的聚类簇 ...