面向集值决策系统的集值模糊粒球粗糙集模型与属性约简算法

引用本文

罗忠团, 谭安辉, 顾沈明, 吴伟志. 面向集值决策系统的集值模糊粒球粗糙集模型与属性约简算法. 模式识别与人工智能, 2025,38(12): 1075-1090
LUO Zhongtuan, TAN Anhui, GU Shenming, WU Weizhi. Set-Valued Fuzzy Granular Ball Rough Set Model and Attribute Reduction Algorithm for Set-Valued Decision Systems. PATTERN RECOGNITION AND ARTIFICIAL INTELLIGENCE, 2025,38(12): 1075-1090. 复制到剪切板

Doi: 10.16451/j.cnki.issn1003-6059.202512002
Permissions

《模式识别与人工智能》编辑部

面向集值决策系统的集值模糊粒球粗糙集模型与属性约简算法

罗忠团¹, 谭安辉², 顾沈明¹, 吴伟志¹

1.浙江海洋大学信息工程学院舟山 316022

2.华侨大学数学科学学院泉州 362021

通讯作者:

顾沈明,硕士,教授,主要研究方向为粗糙集、粒计算、深度学习.E-mail:gsm@zjou.edu.cn.

作者简介:

罗忠团,硕士研究生,主要研究方向为粗糙集、粒计算.E-mail:3118790376@qq.com.

谭安辉,博士,教授,主要研究方向为粒计算、不确定性数据处理、智能计算.E-mail:20100@hqu.edu.cn.

吴伟志,博士,教授,主要研究方向为粗糙集、粒计算、数据挖掘、人工智能.E-mail:wuwz@zjou.edu.cn.

收稿日期: 2025-11-19 接受日期: 2025-12-30

资助项目: 国家自然科学基金项目(No.12571497,12371466)、浙江海洋大学浙江省学科建设项目(No.1106406022102)资助

摘要

粒球计算作为一种有效的多粒度数据处理范式,在复杂数据分析与知识约简领域展现出巨大潜力.然而,现有粒球计算模型未能充分刻画集值属性蕴含的模糊性与不确定性,限制其在集值决策系统中的应用.为此,文中提出集值模糊粒球粗糙集模型,并设计相应的属性约简算法.首先,提出基于集值数据的粒球生成算法,实现依据集值特征的数据空间动态粒化.然后,引入模糊粒球容差关系与近似算子,系统分析其数学性质并给出证明.进一步地,基于依赖度构建前向贪心属性约简算法,实现属性约简.实验表明,文中属性约简算法不仅能获得更精简的属性约简集,还在CART、SVM分类器上取得较高的平均分类精度,验证算法在集值决策系统中的有效性与优越性.

关键词: 集值数据; 粒球计算; 模糊粗糙集; 依赖度; 属性约简

中图分类号:TP18

Set-Valued Fuzzy Granular Ball Rough Set Model and Attribute Reduction Algorithm for Set-Valued Decision Systems

LUO Zhongtuan¹, TAN Anhui², GU Shenming¹, WU Weizhi¹

1. School of Information Engineering, Zhejiang Ocean University, Zhoushan 316022

2. School of Mathematical Sciences, Huaqiao University, Quan-zhou 362021

Corresponding author:
GU Shenming, Master, professor. His research interests include rough sets, granular computing, and deep learning.

About Author:
LUO Zhongtuan, Master student. Her research interests include rough sets and granular computing.
TAN Anhui, Ph.D., professor. His research interests include granular computing, uncertain data processing, and intelligent com-puting.
WU Weizhi, Ph.D., professor. His research interests include rough sets, granular computing, data mining, and artificial intelligence.

Fund:National Natural Science Foundation of China(No.12571497,12371466), Discipline Construction Program of Zhejiang Province under Grant(No.1106406022102)

Abstract

As an effective multi-granularity data processing paradigm, granular ball computing(GBC) exhibits significant potential in the fields of complex data analysis and knowledge reduction. However, existing GBC models fail to fully characterize the fuzziness and uncertainty inherent in set-valued attributes, restricting their application in set-valued decision systems. To address this limitation, a set-valued fuzzy granular ball rough set model is proposed and a corresponding attribute reduction algorithm is designed. Firstly, an adaptive granular ball generation algorithm is proposed to enable the dynamic granulation of the data space based on the characteristics of set-valued data. Secondly, fuzzy granular ball tolerance relations and approximation operators are introduced, and their mathematical properties are systematically analyzed and proven. Furthermore, a forward greedy attribute reduction algorithm is constructed based on dependency degree to achieve efficient attribute reduction. Finally, experimental results demonstrate that the proposed algorithm not only obtains more compact attribute reducts but also achieves higher average classification accuracy with CART and SVM classifiers. These results validate its effectiveness and superiority in set-valued decision systems.

Key words: Key Words Set-Valued Data; Granular Ball Computing; Fuzzy Rough Set; Dependency Degree; Attribute Reduction

文章图片

信息技术与人工智能飞速发展的今天, 人们正处在一个被海量数据包围的时代.这些数据往往呈现出高维度、不完整及不精确等复杂特性, 给传统的机器学习和数据挖掘技术带来前所未有的挑战.为了从这些复杂数据中高效提取有价值的知识并做出智能决策, 研究者开发多种理论与方法.粒计算(Granular Computing, GrC)^[1]作为一种模拟人类思维多粒度、多层次认知问题的计算范式, 近年来受到学术界的广泛关注.它以“ 粒(Granule)” 为基本计算单元, 通过不同粒度层次的数据组织与推理实现从粗到细的认知与计算过程, 为处理模糊、不确定及动态数据提供有效支持.

近年来, 粒计算理论被广泛应用于模式识别^[2]、特征选择^[3]和机器学习^[4]等任务中, 并展现出显著的可解释性与鲁棒性.

在粒计算框架下, 由Pawlak^[5]提出的粗糙集理论作为一种无需先验知识即可处理不确定数据的重要工具, 构成粒计算思想的核心基础, 已被成功应用于数据挖掘^[6]、机器学习^[7]和知识发现^[8]等领域.在实际应用中, 受限于客观采集条件, 数据往往是不完整的, 将此类不完备信息转化为集值信息系统是一种有效的处理策略^[9].

目前, 学者们针对集值系统的信息结构与不确定性度量, 做出相关性的研究.Chen等^[10]从粒计算的视角出发, 定义对象间距离并利用高斯核方法, 构建信息粒结构, 为集值信息系统提出一种信息结构分析与不确定性度量方法.Peng等^[11]利用模糊对称关系, 提出4种针对集值信息系统的不确定性度量.Wu等^[12]提出基于半单层覆盖的可靠近似算子, 可高效计算高质量近似集.Qian等^[13]将集值信息系统扩展至集值有序信息系统, 提出处理集值有序信息系统的粗糙集模型.Zhang等^[14]研究近似集的动态更新方法, 丰富集值数据的处理理论.Chen等^[15]研究不完备集值信息系统的不确定性度量, 利用高斯核进行子系统的最优选择.

属性约简是粗糙集的重要内容之一, 目的是去除数据中冗余和不相关的信息, 简化数据结构.基于等价关系的属性约简不再适用于集值信息系统, 并且现实世界中的数据还常伴随模糊性.为了应对这类数据中存在的问题, Couso等^[16]提出模糊粗糙集模型, 并引入集值信息系统.Dai等^[17]定义模糊相似关系, 保留数据模糊性, 为处理集值数据提供有效工具.Wei等^[18]提出2种模糊粗糙模型, 并定义相容性矩阵与相容性函数, 用于改进属性约简.Singh 等^[19]基于模糊容差关系, 提出FSRS, 引入相似度阈值, 构建模糊容差类, 并利用依赖度度量属性重要性以实现属性约简.Zhang等^[20]利用D-S证据理论, 研究集值决策系统的属性约简.尽管上述研究在处理不确定与模糊知识方面取得重要成果, 但现有方法大多依赖静态粒度结构, 缺乏动态粒化与多层粒度建模能力, 并且未能充分刻画集值属性蕴含的模糊性与不确定性, 在集值模糊数据环境下仍存在局限性.

与此同时, 作为粒计算领域的一项前沿技术, 粒球计算(Granular Ball Computing, GBC)^[21]为自适应的粒度划分提供新的解决思路.它将数据表示为粒球, 模拟人类的思维过程.Xia等^[22]将粒球计算引入邻域粗糙集, 提出GBNRS(Granular-Ball Neighbor-hood Rough Sets), 构建覆盖样本空间的自适应粒球以近似邻域结构, 有效解决传统邻域粗糙集在大规模数据集上计算效率低下的问题.Xia等^[23]提出GBRS(Granular-Ball Rough Set), 实现Pawlak粗糙集与邻域粗糙集的统一表达, 为粗糙集理论的动态粒度刻画提供新方向.Xia等^[24]将GBC引入模糊集, 提出粒球模糊集框架.GBC凭借数据驱动的自适应粒度划分、高效的计算性能及对噪声的鲁棒性, 能精准灵活地捕捉数据的内在结构, 成功应用于特征选择中.Peng等^[25]提出VPGB(Variable Parameter Granular-Ball Model), 在标签噪声环境中同时实现属性约简和分类.

为了知识表示能在更精细粒度上运行, 以及更准确地处理来自多源的复杂不确定数据, Huang等^[26]融合基于覆盖的模糊粗糙集与多粒度粗糙集, 提出多粒度粗糙模糊集模型.Zhang等^[27]引入粒球质量指标, 判断决策类的可分离度, 并在此指标的基础上, 提出快速可变粒球生成模型, 提升属性约简性能.由于GBC能在保持结构完整性的同时抑制噪声影响, 研究者已将其成功应用于分类^[28]、聚类^[29]等任务.

然而, 现有的粒球计算理论和算法完全构建于欧几里得空间或度量空间中的“ 点” 对象之上, 核心的“ 中心” 和“ 半径” 概念无法直接推广至属性值为集合的非度量空间中.因此, 如何将粒球计算这种强大的自适应粒化思想引入集值决策系统的分析中, 克服传统模糊粗糙集模型在动态粒度刻画上的局限性, 成为一个亟待解决的问题.

针对上述问题, 本文提出集值模糊粒球粗糙集模型.首先, 在集值数据下重新定义粒球的生成机制, 实现对集值数据的自适应粒化.然后, 定义基于集值数据的模糊粒球容差关系和上、下近似, 并在此基础上设计基于集值模糊粒球粗糙集的属性约简算法(Set-Valued Fuzzy Granular Ball Rough Set, SV-FGBRS).最后, 通过实验验证SV-FGBRS在处理集值数据上的有效性.

1 基础知识

1.1 集值信息系统

定义1^[30] 在四元组(U, A, V, f )中, U为非空对象集, 称为论域; A为非空属性集, V_a为属性a的值域; f为U×A到V的一个映射, 对于∀a∈A, x∈U, 有f(x, a)∈V_a.如果每个属性有唯一的属性值, 当

V= $\cup_{a}^{\in}$ V_a

时, 则(U, A, V, f )为一个单值信息系统.

如果一个系统不是一个单值信息系统, 那么称为集值信息系统, 定义如下,

定义2^[30] 设S=(U, A, V, f )为一个集值信息系统, U为论域, A为属性集, V为值域, f为U×A到V的映射, 满足f∶ U×A→2^V时, f则为一个集值映射.在此条件下,

∀a∈A, x∈U, |f(x, a)|≥ 1.

定义3^[30] 设S=(U, A, V, f )为一个集值信息系统, ∀a∈A, 相容关系:

T_a={(x, y)|a(x)∩ a(y)≠ Ø},

对∀B∈A, 相容关系

T_B={(x, y)|∀a∈B, a(x)∩ a(y)≠ Ø},

即

T_B= $\cap_{a}^{\in}$ T_a,

当(x, y)∈T_B时, 称x与y是不可分辨的或x与y是相容的.

定义4^[9] 称一个四元组S=(U, A, V, f )为一个集值决策系统, 若属性集 A=A∪ D为条件属性的非空有限集, D为决策属性的非空集合, 且C∩ D=Ø, 则称该信息系统为集值决策系统.这里V=V_C∪ V_D, 其中, V_C表示条件属性值集合, V_D表示决策属性值集合.h为从U×C∪ D到D的映射, h∶ U×C→ $2^{V_{C}}$ 为一个集值映射, 而h∶ U×C→V_D为一个单值映射.

定义5^[19] 设S=(U, A, V, f )为一个集值信息系统, 对∀a∈A, 模糊关系:

${\tilde{R}}_{a}$ (x, y)= $\frac{2 | a (x) ⋂ a (y) |}{| a (x) | + | a (y) |}$ .

对于一组属性B⊆A, 模糊关系:

${\tilde{R}}_{B}$ (x, y)= $\inf_{a \in B}$ ${\tilde{R}}_{a}$ (x, y).

对∀x∈U, ∀B⊆A, 模糊关系 ${\tilde{R}}_{B}$ 满足

1)自反性: 对于∀x∈U, ${\tilde{R}}_{B}$ (x, x)=1,

2)对称性: ∀x∈U, y∈U,

${\tilde{R}}_{B}$ (x, y)= ${\tilde{R}}_{B}$ (y, x),

因此, ${\tilde{R}}_{B}$ 为一个模糊容差关系.

1.2 粒球计算

粒球计算(GBC)^[21]是一种高效的粒计算实现方法, 核心思想是将样本空间使用一系列超球体(即“ 粒球” )进行完全覆盖或部分覆盖, 并以粒球作为数据处理的基本单元.每个粒球可通过中心与半径两个参数进行描述.用粒球替代海量原始样本点, GBC能在保持关键信息的同时, 显著减少计算输入, 提升运算效率, 并增强对噪声数据的鲁棒性.

定义6^[21] 设S=(U, A∪ D, V, f )为一个集值决策系统,

GB={GB₁, GB₂, …, GB_k}

为在A上生成的粒球列表,

GB_j={x₁, x₂, …, x_t}

为一个粒球, x_i为GB_j中的对象, t为GB_j中对象数量.粒球GB_j的中心

c_j= $\frac{1}{t} \overset{t}{\sum_{i = 1}}$ x_i,

半径

r_j= $\frac{1}{t} \overset{t}{\sum_{i = 1}}$ |x_i-c_j|,

其中|x_i-c_j|为x_i到c_j的欧几里得距离.这里, 半径为GB_j中所有对象到其中心的平均距离, 半径也可设置为最大距离.

定义7^[22] 设S=(U, A∪ D, V, f )为集值决策系统,

GB={GB₁, GB₂, …, GB_k}

为在A上生成的粒球列表, GB_j被划分为m个互斥的决策类(p₁, p₂, …, p_m), 根据其类别, GB_j的纯度:

purity(GB_j)= $\frac{\overset{m}{\max_{i = 1}} (| p_{i} |)}{\overset{m}{\sum_{i = 1}} | p_{i} |}$ ,

其中|p_i|为GB_j中第i类的样本数,

0< p(GB_j)≤ 1.

粒球的生成是一个递归分裂的迭代过程.首先将整个数据集视为一个初始粒球, 再检查纯度.若纯度不满足预设阈值, 利用k-mean将其分裂为两个子球.此过程反复进行, 直至所有粒球的纯度达标.

2 集值决策系统中的集值模糊粒球粗糙集模型

为了有效处理集值属性数据, 本文构建集值模糊粒球粗糙集模型.首先, 引入适用于集值数据的距离度量, 在此基础上, 提出基于集值数据的粒球生成算法.然后, 结合粒计算与模糊容差关系, 构造粗糙近似算子, 建立完整的集值模糊粒球粗糙集模型.

2.1 集值数据的粒球生成

经典的粒球生成算法使用k-means或k-divi-sion, 核心运算(如计算簇的算术平均值作为中心)要求数据必须为数值型.然而, 这一前提在集值信息系统中不成立, 导致经典算法无法直接应用.因此, 本文提出适用于集值数据的粒球生成算法.

在该算法中, 粒球的几何中心是重新定义的关键.传统的k-means通过计算均值定义中心, 并不总是适用于集值数据.为此, 借鉴k-medoids的思想, 将中心点定义为粒球内部的一个实际数据点, 它能最有效地代表该粒球内的数据分布.在粒球生成的过程中, 重新定义几何中心和半径, 使粒球的生成更贴合集值数据的特性.粒球的半径被定义为每个数据点到粒球中心的平均距离, 从而反映粒球的分布范围和数据点的离散程度.这样能在保证计算效率的同时, 准确捕捉数据中的内在结构和不确定性, 而粒球的质量评估标准— — 纯度则与经典模型保持一致.因此, 重新定义粒球的中心与半径如下.

定义8 设S=(U, A∪ D, V, f )为集值决策系统,

GB={GB₁, GB₂, …, GB_k}

为在A上生成的粒球列表,

GB_j={x₁, x₂, …, x_t}

为一个粒球, 其中, x_i为GB_j中的对象, t为GB_j中对象的数量.GB_j的中心

x_medoid=arg $\min_{x_{i} \in G B_{j}} \underset{k \neq i}{\overset{t}{\sum_{k = 1}}}$ SD_B(x_i, x_k),

半径

$r_{j}=\frac{1}{t} \sum_{\substack{i=1 \\ x_{i} \neq x_{\text {medoid }}}}^{t} S D_{B}\left(x_{i}, x_{\text {medoid }}\right),$

其中

$S D_{B}\left(x_{i}, x_{k}\right)=1-\left|\frac{a\left(x_{i}\right) \cap a\left(x_{k}\right)}{a\left(x_{i}\right) \cup a\left(x_{k}\right)}\right|$

为Jaccard距离, 距离度量的值越小, 表示两个对象在该属性上的相似度越高, 否则表示相似度越低.该度量为粒球生成和模糊粗糙集的构建奠定基础, 能有效量化数据点间的相似性和距离, 为后续的粒球划分和属性约简提供支持.

本文提出基于集值数据的粒球生成算法, 主要包括三个阶段.

1)初始化粒球.使用k-medoids对整个数据集进行初步划分.

2)迭代提纯.该迭代过程主要由粒球纯度和最小样本数驱动, 对不满足阈值的粒球进行递归分裂.为了确保算法在任何数据分布下的收敛性和计算效率, 引入最大分裂深度作为辅助终止条件, 防止在复杂边界区域出现过度分裂, 使列表中所有的粒球都满足要求.

3)后处理.对生成的稳定粒球进行筛选, 移除不满足预设样本数的粒球, 并分别计算粒球的中心和半径.算法详细步骤如算法1所示.

算法1 基于集值数据的粒球生成算法

输入集值决策系统S=(U, A∪ D, V, f ),

纯度阈值P, 粒球最小样本数S

输出粒球列表GB'

对数据集U应用k-medoids生成k个初始粒球, 形成粒球列表GB={GB₁, GB₂, …, GB_k},

GB'← Ø;

for each GB_i∈GB do

计算粒球GB_i的纯度purity(GB_i);

if purity(GB_i)< P and |GB_i|> S then

对GB_i应用k-medoids(k=2), 将GB_i分裂成

2个子粒球{GB'₁, GB'₂}

GB=GB-{GB_i}, GB=GB+{GB'₁, GB'₂};

else

GB'=GB'+{GB_i}, GB=GB-{GB_i};

break for

end if

end for

for each GB_i∈GB' do

计算GB_i的中心x_medoid;

计算GB_i的半径r_i;

end for

移除异质粒球之间的重叠;

return GB'

通过算法1的迭代分裂与后处理, 得到一个覆盖整个论域 U的最终粒球列表GB'.值得强调的是, 该粒球列表是对论域的一次完整信息颗粒化.由于最小样本数和最大分裂深度的终止限制, GB'中可能会包含一部分纯度未达到预设阈值的粒球.这些低纯度粒球不应被视为“ 噪声” 或“ 无效结果” 而被丢弃, 恰恰相反, 它们表征在当前属性子集下, 决策类别之间难以清晰划分的模糊边界区域.因此, 考虑到模糊边界区域, 将包括这些边界区域粒球在内的完整粒球列表GB'用于后续的模糊粒球容差关系和依赖度计算, 这是对属性集分类能力进行全局性评估的关键.若忽略这些区域, 会丢失数据中固有的不确定性信息, 导致对属性集区分能力的误判.这一处理方式确保集值模糊粒球粗糙集模型能真实刻画数据内在的复杂性和不确定性.

对算法1的时间复杂度分析如下: 设n为样本数量, 算法的核心是k-medoids, 时间复杂度由O(n²)主导.算法首先对所有n个样本执行1次k-medoids, 成本为O(n²), 然后最多进行D层(常数)分裂, 每层分裂最多也是在n个样本上执行O(n²)的聚类操作.由于聚类和分裂的次数都是常数, 总的计算成本由n²主导, 因此算法1的时间复杂度为O(n²).

2.2 基于集值数据的模糊粒球容差关系辅助的粗糙逼近

为了在粒度化后的空间中衡量对象间的关系, 首先定义单个属性上的模糊粒球相似度, 然后将其推广至属性集, 形成模糊粒球关系.

定义9 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性子集B⊆A,

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 对于∀a∈B, 在属性a上x、y之间的模糊粒球相似度定义如下:

${\tilde{R}}_{a}^{G B_{j}}$ (x, y)= $\{\begin{array}{l} {\tilde{R}}_{a} (x, y), & x \in G B_{j}, y \in G B_{j} \\ 0, & 其它 \end{array}$

其中

${\tilde{R}}_{a}$ (x, y)= $\frac{2 | a (x) ⋂ a (y) |}{| a (x) | + | a (y) |}$ .

对于B⊆A, x、y在属性集B上的模糊粒球关系为:

${\tilde{R}}_{B}^{G B_{j}}$ (x, y)= $\inf_{a \in B}$ ${\tilde{R}}_{a}^{G B_{j}}$ (x, y).

性质1 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性子集B⊆A,

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 则模糊粒球容差关系 ${\tilde{R}}_{B}^{G B_{j}}$ 满足

1)自反性:对∀x∈U, 有(x, x)∈ ${\tilde{R}}_{B}^{G B_{j}}$ , 即

${\tilde{R}}_{B}^{G B_{j}}$ (x, x)=1,

2)对称性:对∀x∈U, y∈U, ∀x∈GB_j, y∈GB_j, 有(x, y)∈ ${\tilde{R}}_{B}^{G B_{j}}$ , 即

${\tilde{R}}_{B}^{G B_{j}}$ (x, y)= ${\tilde{R}}_{B}^{G B_{j}}$ (y, x).

上述定义的模糊粒球关系 ${\tilde{R}}_{B}^{G B_{j}}$ 提供任意两个对象间相似程度的连续性度量.然而, 为了构建粗糙集理论中的上、下近似空间, 需要一个明确、非模糊的划分基础, 即为每个对象确定一个清晰的粒球容差类.为此, 本文引入相似度阈值δ , 刻画两个对象之间的模糊粒球关系.通过这种方式, 模糊关系被转化为一个经典的二元关系, 为后续明确定义每个对象的容差类构造近似算子奠定基础.基于此考虑给出新的二元关系, 定义如下.

定义10 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性子集B⊆A,

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表,

GB_j={x₁, x₂, …, x_t}

为一个粒球, 给定一个阈值λ, 对于每个属性子集B⊆A上的二元容差关系:

${\tilde{R}}_{B}^{G B_{j}, λ}$ ={(x, y)| ${\tilde{R}}_{B}^{G B_{j}}$ (x, y)≥ λ, ∀a∈B},

其中, λ∈[0, 1]为相似度阈值, 给出在容差类内插入对象的相似度级别.

引理1 ${\tilde{R}}_{B}^{G B_{j}, λ}$ 为一个模糊粒球容差关系.

证明 1)因为

${\tilde{R}}_{a}^{G B_{j}}$ (x, y)= $\{\begin{array}{l} {\tilde{R}}_{a} (x, y), & x \in G B_{j}, y \in G B_{j} \\ 0, & 其它 \end{array}$

所以

${\tilde{R}}_{a}$ (x, x)= $\frac{2 | a (x) ⋂ a (x) |}{| a (x) | + | a (x) |}$ = $\frac{2 | a (x) |}{| a (x) |}$ =1,

即

(x, x)∈ ${\tilde{R}}_{B}^{G B_{j}, λ}$ .

2)当(x, y)∈GB_j时, 设(x, y)∈ ${\tilde{R}}_{B}^{G B_{j}, λ}$ , 有

${\tilde{R}}_{a}$ (x, y)= $\frac{2 | a (x) ⋂ a (y) |}{| a (x) | + | a (y) |}$ ≥ λ,

又因为

${\tilde{R}}_{a}$ (y, x)= $\frac{2 | a (y) ⋂ a (x) |}{| a (y) | + | a (x) |}$ = ${\tilde{R}}_{a}$ (x, y)≥ λ,

故

(y, x)∈ ${\tilde{R}}_{B}^{G B_{j}, λ}$ .

定义11 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性集B⊆A, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_t}

为在B上生成的粒度球列表, ${\tilde{R}}_{B}^{G B_{j}, λ}$ 为由属性集B⊆A和阈值λ导出的模糊粒球容差关系, 对∀x_i∈U, 相对于B的模糊粒球容差类定义如下:

[x_i $]_{B}^{G B_{j}, λ}$ ={x∈U|(x, y)∈ ${\tilde{R}}_{B}^{G B_{j}, λ}$ }.

基于模糊粒球容差关系, 导出模糊粒球容差类, 即当x∈GB_j, y∈GB_j时, 将相似度大于或等于给定的阈值分组到容差类中.

定义12 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性子集B⊆A和∀X⊆U, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_t}

为在B上生成的粒度球列表, 在粒度球GB_j上, 对象集X相对于属性集B的模糊粒球下、上近似分别定义如下:

$\underline{\tilde{R}_{B}^{G{{B}_{j}}, \lambda }}\left( X \right)=\left\{ x\in U\left| \left[ x \right]_{B}^{G{{B}_{j}}, \lambda }\subseteq X \right. \right\}$

$\overline{\tilde{R}_{B}^{G{{B}_{j}}, \lambda }}\left( X \right)=\left\{ x\in U\left| \left[ x \right]_{B}^{G{{B}_{j}}, \lambda }\cap X\ne \varnothing \right. \right\}$

称( $\bar{{\tilde{R}}_{B}^{G B_{j}, λ}}$ (X), $\bar{{\tilde{R}}_{B}^{G B_{j}, λ}}$ (X))为集值决策系统下的集值模糊粒球粗糙集, 并称

PO $B_{B}^{G B_{j}, λ}$ (X)= $\bar{{\tilde{R}}_{B}^{G B_{j}, λ}}$ (X)

为X关于B的正域,

BN $D_{B}^{G B_{j}, λ}$ (X)= $\bar{{\tilde{R}}_{B}^{G B_{j}, λ}}$ (X)- $\bar{{\tilde{R}}_{B}^{G B_{j}, λ}}$ (X)

为X关于B的边界域.

定义13 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性集B⊆A和∀X⊆U,

U/D={D₁, D₂, …, D_r}

为由决策属性D导出的论域划分, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 在粒度球GB_j上, 决策属性D相对于条件属性B的模糊粒球下、上近似分别定义如下:

$\begin{array}{l} \widetilde{R}_{B}^{G B_{j}, \lambda}(D)=\bigcup_{i=1}^{r} \widetilde{R}_{B}^{G B_{j}, \lambda}\left(D_{i}\right), \\ \overline{\widetilde{R}_{B}^{G B_{j}, \lambda}}(D)=\bigcup_{i=1}^{r} \overline{\widetilde{R}_{B}^{G B_{j}, \lambda}}\left(D_{i}\right), \end{array}$

其中

$\begin{array}{l} \widetilde{R}_{B}^{G B_{j}, \lambda}\left(D_{i}\right)=\left\{x \in U \mid[x]_{B}^{G B_{j}, \lambda} \subseteq D_{i}\right\}, \\ \overline{\widetilde{R}_{B}^{G B_{j}, \lambda}}\left(D_{i}\right)=\left\{x \in U \mid[x]_{B}^{G B_{j}, \lambda} \cap D_{i} \neq \emptyset\right\} . \end{array}$

性质2 设S=(U, A∪ D, V, f )为集值决策系统, 对于∀X⊆U, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 在粒度球GB_j上, 若B₁⊆B₂⊆A, 则有

1) $\bar{{\tilde{R}}_{B_{1}}^{G B_{j}, λ}}$ (X)⊆ $\bar{{\tilde{R}}_{B_{2}}^{G B_{j}, λ}}$ (X),

2) $\bar{{\tilde{R}}_{B_{2}}^{G B_{j}, λ}}$ (X)⊆ $\bar{{\tilde{R}}_{B_{1}}^{G B_{j}, λ}}$ (X).

证明先证1).设∀x∈ $\bar{{\tilde{R}}_{B_{1}}^{G B_{j}, λ}}$ (X), 由下近似的定义知

[x $]_{B_{1}}^{G B_{j}, λ}$ ⊆X,

因为B₁⊆B₂, 则

[x $]_{B_{2}}^{G B_{j}, λ}$ ⊆[x $]_{B_{1}}^{G B_{j}, λ}$ ,

所以

[x $]_{B_{2}}^{G B_{j}, λ}$ ⊆X,

故

$\bar{{\tilde{R}}_{B_{1}}^{G B_{j}, λ}}$ (X)⊆ $\bar{{\tilde{R}}_{B_{2}}^{G B_{j}, λ}}$ (X).

再证2).设∀x∈ $\bar{{\tilde{R}}_{B_{2}}^{G B_{j}, λ}}$ (X), 由上近似的定义知

[x $]_{B_{2}}^{G B_{j}, λ}$ ∩ X≠ Ø,

因为B₁⊆B₂, 则

[x $]_{B_{2}}^{G B_{j}, λ}$ ⊆[x $]_{B_{1}}^{G B_{j}, λ}$ ,

所以

[x $]_{B_{1}}^{G B_{j}, λ}$ ∩ X≠ Ø,

即

x∈ $\bar{{\tilde{R}}_{B_{1}}^{GB, λ}}$ (X),

故

$\bar{{\tilde{R}}_{B_{2}}^{G B_{j}, λ}}$ (X)⊆ $\bar{{\tilde{R}}_{B_{1}}^{G B_{j}, λ}}$ (X). 证毕.

性质3 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性子集B⊆A和∀X⊆U, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 在粒度球GB_j上, 若λ₁≤ λ₂, 有

1) $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{1}}}$ (X)⊆ $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{2}}}$ (X),

2) $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{2}}}$ (X)⊆ $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{1}}}$ (X).

证明先证1).设∀x∈ $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{1}}}$ (X), 且有

[x $]_{B}^{G B_{j}, λ_{1}}$ ⊆X,

因为

[x $]_{B}^{G B_{j}, λ_{1}}$ ={y∈U| ${\tilde{R}}_{B}^{G B_{j}}$ (x, y)> λ₁, ∀a∈B},

且

[x $]_{B}^{G B_{j}, λ_{2}}$ ={y∈U| ${\tilde{R}}_{B}^{G B_{j}}$ (x, y)> λ₂, ∀a∈B},

又因为λ₁≤ λ₂, 故

[x $]_{B}^{G B_{j}, λ_{2}}$ ⊆[x $]_{B}^{G B_{j}, λ_{1}}$ ,

由于

[x $]_{B}^{G B_{j}, λ_{1}}$ ⊆X,

从而

[x $]_{B}^{G B_{j}, λ_{2}}$ ⊆X,

于是

x∈ $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{2}}}$ (X),

因此

$\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{1}}}$ (X)⊆ $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{2}}}$ (X).

再证2).设∀x∈ $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{2}}}$ (X),

[x $]_{B}^{G B_{j}, λ_{2}}$ ∩ X≠ Ø,

根据1)有

[x $]_{B}^{G B_{j}, λ_{2}}$ ⊆[x $]_{B}^{G B_{j}, λ_{1}}$ ,

所以

[x $]_{B}^{G B_{j}, λ_{1}}$ ∩ X≠ Ø,

即

x∈ $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{1}}}$ (X),

故

$\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{2}}}$ (X)⊆ $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{1}}}$ (X). 证毕.

3 基于集值模糊粒球粗糙集的属性约简算法

定义14 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性子集B⊆A和∀X⊆U,

U/D={D₁, D₂, …, D_r}

为由决策属性D导出的论域划分, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 在粒度球GB_j上, 决策属性D相对于条件属性B的模糊粒球正域定义如下:

PO $S_{B}^{G B_{j}, λ}$ (D)= $\bar{{\tilde{R}}_{B}^{G B_{j}, λ}}$ (D).

性质4 设S=(U, A∪ D, V, f )为集值决策系统, λ∈[0, 1], GB={GB₁, GB₂, …, GB_k}为在B上生成的粒度球列表, 在粒度球GB_j上, 若B₁⊆B₂⊆A, 则有

PO $S_{B_{1}}^{G B_{j}, λ}$ (D)⊆PO $S_{B_{2}}^{G B_{j}, λ}$ (D).

证明因为B₁⊆B₂, 由性质2的1)可得

$\underset{D_{i} \in U / D}{\cup} \underline{\widetilde{R}_{B_{1}}^{G B_{j}, \lambda}}\left(D_{i}\right) \subseteq \underset{D_{i} \in U / D}{\cup} \underline{\widetilde{R}_{B_{2}}^{G B_{j}, \lambda}}\left(D_{i}\right),$

故

$\operatorname{POS}_{B_{1}}^{G B_{j}, \lambda}(D) \subseteq \operatorname{POS}_{B_{2}}^{G B_{j}, \lambda}(D) .$证毕.

性质5 设S=(U, A∪ D, V, f )为集值决策系统, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 对∀X⊆U, 在粒度球GB_j上, 若λ₁≤ λ₂, 则有

PO $S_{B}^{G B_{j}, λ_{1}}$ (D)⊆PO $S_{B}^{G B_{j}, λ_{2}}$ (D).

证明根据性质3的1)有

$\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{1}}}$ (X)⊆ $\bar{{\tilde{R}}_{B}^{G B_{j}, λ_{2}}}$ (X),

所以

$\underset{D_{i} \in U / D}{\cup} \xrightarrow{\widetilde{R}_{B}^{G B_{j}, \lambda_{1}}}\left(D_{i}\right) \subseteq \cup_{D_{i} \in U / D}^{\cup} \xrightarrow{\widetilde{R}_{B}^{G B_{j}, \lambda_{2}}}\left(D_{i}\right),$

故

$\operatorname{POS}_{B}^{G B_{j}, \lambda_{1}}(D) \subseteq \operatorname{POS}_{B}^{G B_{j}, \lambda_{2}}(D)$ 证毕.

定义15 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性子集B⊆A和∀X⊆U, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 在粒度球GB_j上, D相对于B的依赖度定义如下:

$γ_{B}^{G B_{j}, λ}$ (D)= $\frac{| PO S_{B}^{G B_{j}, λ} (D) |}{| U |}$ ∈[0, 1],

其中|· |表示集合的基数.

性质6 (单调性) 假设B为条件属性集A的一个子集(B⊆A), a为A中任意一个不属于B的属性.设D为决策属性集, λ∈[0, 1]为给定阈值, 则有

$γ_{B ⋃ {a}}^{G B_{j}, λ}$ (D)≥ $γ_{B}^{G B_{j}, λ}$ (D).

证明因为

${\tilde{R}}_{B}^{G B_{j}, λ}$ ={(x, y)| ${\tilde{R}}_{B}^{G B_{j}}$ (x, y)≥ λ},

${\tilde{R}}_{B ⋃ {a}}^{G B_{j}, λ}$ {(x, y) | ${\tilde{R}}_{B ⋃ {a}}^{G B_{j}}$ x, y)≥ λ},

则有

${\tilde{R}}_{B ⋃ {a}}^{G B_{j}, λ}$ ⊆ ${\tilde{R}}_{B}^{G B_{j}, λ}$ ,

因此

[x_i $]_{B ⋃ {a}}^{G B_{j}, λ}$ ⊆[x_i $]_{B}^{G B_{j}, λ}$ ,

故有

$\bar{R_{B}^{G B_{j}, λ}}$ (D)⊆ $\bar{R_{B ⋃ {a}}^{G B_{j}, λ}}$ (D),

又因为

PO $S_{B}^{G B_{j}, λ}$ (D)= $\bar{{\tilde{R}}_{B}^{G B_{j}, λ}}$ (D),

所以

PO $S_{B}^{G B_{j}, λ}$ (D)⊆PO $S_{B ⋃ {a}}^{G B_{j}, λ}$ (D),

由于

$γ_{B}^{G B_{j}, λ}$ (D)= $\frac{| PO S_{B}^{G B_{j}, λ} (D) |}{| U |}$ ,

因此

$γ_{B}^{G B_{j}, λ}$ (D)≤ $γ_{B ⋃ {a}}^{G B_{j}, λ}$ (D).

性质7 设S=(U, A∪ D, V, f )为集值决策系统, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 在粒度球GB_j上, 若B₁⊆B₂⊆A, 则有

$γ_{B_{1}}^{G B_{j}, λ}$ (D)≤ $γ_{B_{2}}^{G B_{j}, λ}$ (D).

性质8 设S=(U, A∪ D, V, f )为集值决策系统, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 对∀X⊆U, 在粒度球GB_j上, 若λ₁≤ λ₂, 则有

$γ_{B}^{G B_{j}, λ_{1}}$ (D)≤ $γ_{B}^{G B_{j}, λ_{2}}$ (D).

定义16 设S=(U, A∪ D, V, f )为集值决策系统, 对于给定的属性子集B⊆A, λ∈[0, 1],

GB={GB₁, GB₂, …, GB_k}

为在B上生成的粒度球列表, 在粒度球GB_j上, 如果B满足

1) $γ_{B}^{G B_{j}, λ}$ (D)= $γ_{A}^{G B_{j}, λ}$ (D),

2) $γ_{B - {a}}^{G B_{j}, λ}$ (D)< $γ_{B}^{G B_{j}, λ}$ (D), ∀a∈B,

则称B是A的一个约简.

依赖度反映属性子集的分类能力, 可用于衡量候选属性的重要性.本文采用一种前向贪心策略寻找属性约简, 即通过迭代计算依赖度增益确定是否将一个候选属性加入最优属性子集中.对于给定的参数λ, 将属性约简B初始化为一个空集, 计算模糊容差关系 ${\tilde{R}}_{a_{i}}$ (x, y), a_i∈A.对于A中的每个属性a_i, 计算模糊容差关系 ${\tilde{R}}_{B ⋃ {a_{i}}}$ (x, y).应用基于B∪ a_i的k-medoids生成一组与之对应的全新粒球列表

GB={GB₁, GB₂, …, GB_k}.

对于给定的参数λ, 基于粒球列表计算模糊粒球容差类[x $]_{{B ⋃ a_{i}}}^{G B_{j}, λ}$ .由此可计算每个属性a_i对应的依赖度 $γ_{{B ⋃ a_{i}}}^{G B_{j}, λ}$ (D).如果

$γ_{{B ⋃ a_{k}}}^{G B_{j}, λ}$ (D)≥ $γ_{B}^{G B_{j}, λ}$ (D),

a_k将被添加到B中并从A中去除.算法详细步骤如算法2所示.

算法2 基于集值模糊粒球粗糙集的属性约简算

法(SV-FGBRS)

输入集值决策系统S=(U, A∪ D, V, f ),

参数λ

输出约简B

初始化B← Ø;

计算属性集A中的每个属性a_i的模糊容差关系

${\tilde{R}}_{a_{i}}$ =(x, y);

While |A|≠ Ø

For each a_i in A

计算模糊容差关系 ${\tilde{R}}_{B ⋃ {a_{i}}}$ =(x, y);

利用算法1在B∪ {a_i}上生成粒球列表

GB={GB₁, GB₂, …, GB_k};

基于粒球列表计算模糊粒球容差关系

${\tilde{R}}_{B ⋃ {a_{i}}}^{G B_{j}}$ =(x, y);

计算模糊粒球容差类[x $]_{{B ⋃ a_{i}}}^{G B_{j}, λ}$ ;

计算决策类的上、下近似;

计算依赖度 $γ_{B ⋃ {a_{i}}}^{G B_{j}, λ}$ (D);

End for

找出最大依赖度 $γ_{B ⋃ {a_{k}}}^{G B_{j}, λ}$ (D)的属性c_k;

If $γ_{B ⋃ {a_{k}}}^{G B_{j}, λ}$ (D)≥ $γ_{B}^{G B_{j}, λ}$ (D) then

B← B+a_k;

A← A-a_k;

Else

Return B;

End if

End while

算法2的时间复杂度分析如下:样本数平均大小为n, 属性数平均大小为m, 集合的平均大小为l.首先计算所有属性的相似度矩阵, 时间复杂度为O(mn²l).在主循环中, 算法采用前向选择策略, 在每轮迭代中选择能最大化依赖度的属性.此过程在最坏情况下需要O(n²)次迭代评估.在每次评估中, 最耗时的操作是构建关系矩阵, 成本在最坏情况下与当前属性数和样本数的平方成正比, 即O(mn²).因此, 整个搜索过程的时间复杂度为O(m³n²), 故算法2的总时间复杂度为 O(n²(ml+m³)).算法2主要计算瓶颈在于前向选择循环, 导致复杂度与样本数n的平方和属性数m的立方成正比, 这使得该算法对n和m的增长都非常敏感, 计算成本较高.

例1 表1为一个集值决策系统, 其中

U={x₁, x₂, …, x₉}, A={a₁, a₂, a₃, a₄},

D为决策属性, U/D={D₁, D₂}, 其中

D₁={x₁, x₂, x₄, x₇, x₉},

D2₌{x3_,x5_,x6_,x8_},

纯度阈值p=0.6.

表1 集值决策系统 Table 1 Set-valued decision system

首先设置纯度阈值为0.6, 最小样本数为2, 然后利用算法1和算法2, 得到在属性a₁上生成的粒球列表GB={GB₁, GB₂}, 其中,

GB₁={x₁, x₂, x₄, x₆, x₇, x₈, x₉},

GB₂={x₃, x₅}.

根据定义9的模糊粒球关系, 对于∀x_i∈U, x_j∈U, 可计算属性a₁上由关系矩阵表示的模糊粒球容差关系:

${\tilde{R}}_{a_{1}}^{GB}$ = $(\begin{array}{l} 1 & 0.5 & 0 & 0.67 & 0 & 0 & 1 & 0 & 0.67 \\ 0.5 & 1 & 0 & 0.8 & 0 & 0.5 & 0.5 & 0.5 & 0.8 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0.67 & 0.8 & 0 & 1 & 0 & 0.67 & 0.67 & 0.67 & 1 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0.5 & 1 & 0.67 & 0 & 1 & 0 & 1 & 0.67 \\ 1 & 0.5 & 0 & 0.67 & 0 & 0 & 1 & 0 & 0.67 \\ 0 & 0.5 & 0 & 0.67 & 0 & 1 & 0 & 1 & 0.67 \\ 0.67 & 0.8 & 0 & 1 & 0 & 0.67 & 0.67 & 0.67 & 1 \end{array})$ .

设参数λ=0.6, 根据定义11计算粒球容差如下:

[x₁ $]_{a_{1}}^{GB, λ}$ ={x₁, x₄, x₇, x₉},

[x₂ $]_{a_{1}}^{GB, λ}$ ={x₂, x₄, x₉},

[x₃ $]_{a_{1}}^{GB, λ}$ ={x₃, x₅},

[x₄ $]_{a_{1}}^{GB, λ}$ ={x₁, x₂, x₄, x₆, x₇, x₈, x₉},

[x₅ $]_{a_{1}}^{GB, λ}$ ={x₃, x₅},

[x₆ $]_{a_{1}}^{GB, λ}$ ={x₄, x₆, x₈, x₉},

[x₇ $]_{a_{1}}^{GB, λ}$ ={x₁, x₄, x₇, x₉},

[x₈ $]_{a_{1}}^{GB, λ}$ ={x₄, x₆, x₈, x₉},

[x₉ $]_{a_{1}}^{GB, λ}$ ={x₁, x₂, x₄, x₆, x₇, x₈, x₉}.

因为U/D={D₁, D₂}, 其中

D₁={x₁, x₂, x₄, x₇, x₉},

D2₌{x3_,x5_,x6_,x8_},

从而根据定义13可计算决策类相对于属性a₁的下近似:

$\bar{R_{B}^{GB, λ}}$ (D₁)={x₁, x₂, x₇},

$\bar{R_{B}^{GB, λ}}$ D2₎={x3_,x5},

因此属性a₁的正域为:

PO $S_{a_{1}}^{GB, λ}$ (D)= $\cup_{i}^{=} \bar{{\tilde{R}}_{a_{1}}^{GB, λ}}$ (D_i)=

$\bar{{\tilde{R}}_{a_{1}}^{GB, λ}}$ (D₁)∪ $\bar{{\tilde{R}}_{a_{1}}^{GB, λ}}$ D2₎=

{x₁, x₂, x₇}_∪{ x₃, x₅}₌

{x₁, x₂, x₃, x₅, x₇}.

故决策属性D相对于属性a₁的依赖度为:

$γ_{a_{1}}^{GB, λ}$ (D)= $\frac{| PO S_{a_{1}}^{GB, λ} |}{| U |}$ =0.56.

类似地, 可计算决策属性相对于其它条件属性的依赖度:

$γ_{a_{2}}^{GB, λ}$ (D)= $\frac{| PO S_{a_{2}}^{GB, λ} |}{| U |}$ =0.11,

$γ_{a_{3}}^{GB, λ}$ (D)= $\frac{| PO S_{a_{3}}^{GB, λ} |}{| U |}$ =0.11,

$γ_{a_{4}}^{GB, λ}$ (D)= $\frac{| PO S_{a_{4}}^{GB, λ} |}{| U |}$ =0.44.

因为

$γ_{a_{1}}^{GB, λ}$ (D)> $γ_{a_{4}}^{GB, λ}$ (D)> $γ_{a_{2}}^{GB, λ}$ (D)= $γ_{a_{3}}^{GB, λ}$ (D),

因此选择属性a₁添加到约简集上, 将其它属性逐一添加到a₁中.

与上述步骤相同, 并通过定义15计算相应的的依赖度:

$γ_{{a_{1}, a_{2}}}^{GB, λ}$ (D)= $\frac{| PO S_{{a_{1}, a_{2}}}^{GB, λ} |}{| U |}$ =0.44,
$γ_{{a_{1}, a_{3}}}^{GB, λ}$ (D)= $\frac{| PO S_{{a_{1}, a_{3}}}^{GB, λ} |}{| U |}$ 0.56,
$γ_{{a_{1}, a_{4}}}^{GB, λ}$ (D)= $\frac{| PO S_{{a_{1}, a_{4}}}^{GB, λ} |}{| U |}$ =1.

由于依赖度最大值为1, 因此B={a₁, a₄}为表1中集值决策系统的约简.

4 实验及结果分析

为了验证SV-FGBRS的有效性与可行性, 从UCI数据库上选取10个数据集进行实验, 数据集的详细信息如表2所示.

表2 实验数据集 Table 2 Experimental datasets

在实际应用中, 由于存在多个特征, 数据集通常以集值的形式表示, 但是没有可直接使用的设定值数据, 因此需要对数据集进行预处理, 本文借鉴文献[31]的转化思想, 将不完备信息系统转化为集值信息系统.

实验中选择如下属性约简算法作为对比算法:基于模糊关系的粗糙集算法(文献[17]算法)、基于模糊相似度的粗糙集算法(FSRS^[19])、基于相关性和决策错误率的SVDIS(Set-Valued Decision Infor-mation System)属性约简算法(DECE^[31])、基于相似关系的粗糙集算法(文献[32]算法)、基于条件熵的属性约简算法(CEIS^[33])、基于相对邻域粒度的单调前向属性约简算法(MRNG(Monotonic Forward Attribute Reduction Algorithm Based on Relative Neighborhood Granularity)^[34]).

各算法最优属性子集个数如表3所示.根据选择的最优属性子集, 对比CART、SVM分类器上的分类准确率, 结果如表4和表5所示, 表中黑体数字表示最优值.

表3 各算法的最优属性子集个数 Table 3 Number of optimal attribute subsets for different algorithms

表4 各算法在CART分类器上约简数据的分类准确率对比 Table 4 Classification accuracy comparison of different algorithms with CART classifier %

表5 各算法在SVM分类器上约简数据的分类准确率对比 Table 5 Classification accuracy comparison of different algorithms with SVM classifier %

由表4可观察到, 在CART分类器上, SV-FGBRS在7个数据集上实现最优分类准确率, 在大多数数据集上的分类效果都很好, 平均分类准确率最优, 达到81.36%.DECE的平均分类准确率为76.20%, 仅次于SV-FGBRS.DECE通常表现得很有竞争力, 尤其是在Indian、German、Car数据集上.

由表5可观察到, 在SVM分类器上, SV-FGBRS在7个数据集上实现最优分类准确率, 在大多数数据集上性能优于对比算法, 平均分类准确率最高, 达到79.87%, 尤其是在Zoo、Soybean数据集上表现更优.DECE的平均分类准确率为76.00%, 仅次于SV-FGBRS.只有相对较少的算法才能达到最优分类准确率.

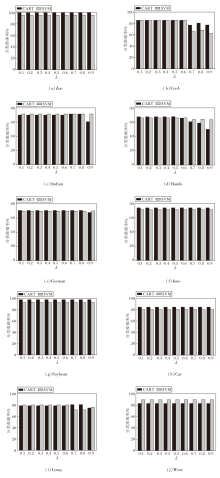
在SV-FGBRS中, 参数λ的取值在某些范围会影响属性约简.为了探究λ对分类性能的影响, 验证算法的稳定性, 在每个数据集上进行参数敏感性实验.设置λ=0.1, 0.2, …, 0.9, 分别记录CART、SVM分类器的分类准确率, 具体如图1所示.

	Figure Option View Download New Window
	图1 各数据集上λ对SV-FGBRS的影响Fig.1 Effect of λ on SV-FGBRS on different datasets

由图1可看出, 随着λ的增加, CART、SVM分类器的分类准确率在大多数数据集上均呈现出高度的平稳性.即使λ在较宽的范围内波动, 分类准确率始终维持在较高水平.

这一现象归因于 SV-FGBRS独特的自适应粒球生成机制.与传统固定半径的邻域粗糙集不同, SV-FGBRS能根据数据的局部密度自适应调整粒球大小, 即使λ设置较小(容差较宽), SV-FGBRS依然能通过生成较大的高纯度粒球覆盖同质区域; 反之亦然.这种多粒度自适应能力确保算法在不同参数设置下均能捕捉核心的决策特征.实验结果有力验证SV-FGBRS具有极强的参数鲁棒性.这意味着在实际应用中, SV-FGBRS对参数初值的选择不敏感, 无需进行繁琐的参数微调即可获得优异性能, 具有良好的实用价值.

为了评价算法的统计意义, 利用Friedman检验和Nemenyi检验, 进一步验证SV-FGBRS的稳定性.在使用Friedman检验之前, 根据表4和表5中7种算法的分类精度, 对每种算法在所有数据集上的分类准确率进行排序.

Friedman检验作为统计学中的一种非参数检验方法, 检验不同算法之间是否存在显著差异.如果存在分歧, 将进行下一步检验, 即Nemenyi检验.Nemenyi检验用于确定哪些算法在性能上存在统计性差异.

假设k表示算法, N表示数据集数量, r_i表示所有数据集上分配给算法i的平均排名.Friedman检验的计算公式如下:

F_F= $\frac{(N - 1) χ_{F}^{2}}{N (k - 1) - χ_{F}^{2}}$ ,

其中

$χ_{F}^{2}$ = $\frac{12 N}{k (k + 1)} \overset{k}{\sum_{i = 1}} r_{i}^{2}$ -3N(k+1).

检验统计量F_F是一个具有(k-1)和(k-1)(N-1)自由度的F分布.如果F_F值超过临界值((k-1), (k-1)(N-1)), 则拒绝零假设, 也就是说算法之间存在显著差异, 因此需要Nemenyi检验以区分这些算法.

CD_α临界差的定义如下.设定q_α=2.949, k=7, N=10.如果任意两种算法之间的平均排名差值大于CD_α, 检验结果表明两种算法在分类器上的性能存在显著差异, 否则, 两者在统计上没有差别.

根据分类准确率的排名, 进行2次Friedman检验, 在7种算法和10个数据集的条件下, 检验统计量F_F服从6个和54个自由度的F分布.在显著性水平α=0.05的条件下, Fisher分布的临界值F₀_.₀₅(6, 54)为2.34, 不同分类器上的Friedman检验结果如表6所示.

表6 不同分类器上的检验统计量F_F的值 Table 6 Values of test statistic F_F with different classifiers

从表6中可看出, 在CART、SVM分类器上, 计算出检验统计量F_F的值均远大于临界值 2.34, 这意味着在显著性水平α=0.05的条件下拒绝零假设.结果表明, 这些算法之间的分类精度在统计上存在显著差异.

因此, 进一步使用Nemenyi检验对比不同算法之间的显著差异, 在显著性水平α=0.05时, 计算相应的临界差CD_α=2.849 0.

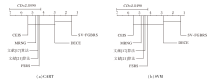
在CART、SVM分类器上的临界差(Critical Distance, CD)图如图2所示.根据每种算法在每个数据集上的分类准确率计算每种算法的排名, 以此确保对算法的综合评估的有效性.

	Figure Option View Download New Window
	图2 各算法在2个分类器上的CD图Fig.2 CD diagrams of different algorithms with 2 classifiers

从图2可看出, SV-FGBRS在统计上显著不同于其它算法, 在CART分类器上, SV-FGBRS的分类准确率大于大部分算法, 而与DECE无统计学差异.在SVM分类器上, SV-FGBRS与DECE无统计学差异, 与其它算法在统计上存在显著性差异.这些结果表明SV-FGBRS的有效性和可行性.

5 结束语

本文针对集值信息系统中的复杂知识发现难题, 提出集值模糊粒球粗糙集模型及其属性约简算法(SV-FGBRS).首先, 引入粒球计算机制, 设计不依赖均值的基于集值数据的粒球生成算法, 突破传统粒球计算依赖欧几里得空间与数值均值的局限性.重新定义集值环境下的粒球生成机制与距离度量, 实现对非度量空间数据的自适应粒化.然后, 定义集值决策系统中的模糊粒球容差关系, 利用模糊粒球容差关系刻画样本间的相似性与近似算子, 成功捕捉集值属性中蕴含的模糊性与不确定性, 为复杂数据的多粒度认知与结构化描述提供理论框架.最后, 结合前向贪心策略与依赖度, 进行属性约简.为了验证SV-FGBRS的有效性, 在10个数据集上进行综合对比实验, 结果表明, 相比现有算法, SV-FGBRS不仅能获得极小的属性约简集, 还在CART、SVM分类器上取得最高的平均分类准确率.进一步的Friedman和Nemenyi统计检验也证实SV-FGBRS在性能上显著优于大多数对比算法.这些结果充分说明, SV-FGBRS能有效去除冗余特征, 并在保留关键分类信息方面表现出极高的鲁棒性, 是一种处理集值数据的强大而有效的新工具.此外, 本研究在医疗诊断、金融风控及文本分类等包含集值属性的实际场景中具有广阔的应用前景, SV-FGBRS具有在解决不确定性问题上的实用价值.

尽管本文在完备集值系统的粒计算建模上取得进展, 但在更复杂的现实场景中仍有进一步探索的空间.未来工作将重点关注如下两个方向:1)将粒球计算框架扩展至不完备集值信息系统, 应对数据缺失带来的挑战; 2)探索相似度参数的自适应优化机制, 并致力于优化算法在大规模数据集上的计算效率, 进一步增强算法的适应性与应用广度.

本文责任编委梁吉业

Recommended by Associate Editor LIANG Jiye

参考文献

文献选项

[1]	ZADEH L A. Fuzzy Sets and Information Granularity // KLIR G J, YUAN B, eds. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A Zadeh. London, UK: World Scientific, 1996: 433-448. [本文引用:1]
[2]	LI C, HUANG Q, MAO Y C, et al. Multi-granular Spatial-Temporal Synchronous Graph Convolutional Network for Robust Action Recognition. Expert Systems with Applications, 2024, 257. DOI: 10.1016/j.eswa.2024.124980. [本文引用:1]
[3]	GUO S X, ZHAO H, YANG W Y. Hierarchical Feature Selection with Multi-granularity Clustering Structure. Information Sciences, 2021, 568: 448-462. [本文引用:1]
[4]	PEDRYCZ W. Granular Computing for Machine Learning: Pursuing New Development Horizons. IEEE Transactions on Cybernetics, 2025, 55(1): 460-471. [本文引用:1]
[5]	PAWLAK Z. Rough Sets. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356. [本文引用:1]
[6]	刘清, 黄兆华, 刘少辉, 等. 带 Rough 算子的决策规则及数据挖掘中的软计算. 计算机研究与发展, 1999, 36(7): 800-804. (LIU Q, HUANG Z H, LIU S H, et al. Decision Rules with Rough Operators and Soft Computing in Data Mining. Journal of Computer Research and Development, 1999, 36(7): 800-804.) [本文引用:1]
[7]	BAZAN J, PETERS J F, SKOWRON A, et al. Rough Set Approach to Pattern Extraction from Classifiers. Electronic Notes in Theoretical Computer Science, 2003, 82(4): 20-29. [本文引用:1]
[8]	PAL N R, PAL S K. Entropy: A New Definition and Its Applications. IEEE Transactions on Systems, Man, and Cybernetics, 1991, 21(5): 1260-1270. [本文引用:1]
[9]	GUAN Y Y, WANG H K. Set-Valued Information Systems. Information Sciences, 2006, 176(17): 2507-2525. [本文引用:2]
[10]	CHEN N P, HE J L. Information Structures in a Set-Valued Informa-tion System Based on Granular Computing. Journal of Intelligent and Fuzzy Systems, 2019, 36(6): 5319-5331. [本文引用:1]
[11]	PENG Y C, ZHANG Q L. Uncertainty Measurement for Set-Valued Data and Its Application in Feature Selection. International Journal of Fuzzy Systems, 2022, 24(3): 1735-1756. [本文引用:1]
[12]	WU Z J, WANG H, CHEN N, et al. Semi-monolayer Covering Rough Set on Set-Valued Information Systems and Its Efficient Computation. International Journal of Approximate Reasoning, 2021, 130: 83-106. [本文引用:1]
[13]	QIAN Y H, DANG C Y, LIANG J Y, et al. Set-Valued Ordered Information Systems. Information Sciences, 2009, 179(16): 2809-2832. [本文引用:1]
[14]	ZHANG J B, LI T R, RUAN D, et al. Rough Sets Based Matrix Approaches with Dynamic Attribute Variation in Set-Valued Information Systems. International Journal of Approximate Reasoning, 2012, 53(4): 620-635. [本文引用:1]
[15]	CHEN L J, LIAO S M, XIE N X, et al. Measures of Uncertainty for an Incomplete Set-Valued Information System with the Optimal Selection of Subsystems: Gaussian Kernel Method. IEEE Access, 2020, 8: 212022-212035. [本文引用:1]
[16]	COUSO I, DUBOIS D . RoughSets, Coverings and Incomplete Information. Fundamenta Informaticae, 2011, 108(3/4): 223-247. [本文引用:1]
[17]	DAI J H, TIAN H W. Fuzzy Rough Set Model for Set-Valued Data. Fuzzy Sets and Systems, 2013, 229: 54-68. [本文引用:2]
[18]	WEI W, CUI J B, LIANG J Y, et al. Fuzzy Rough Approximations for Set-Valued Data. Information Sciences, 2016, 360: 181-201. [本文引用:1]
[19]	SINGH S, SHREEVASTAVA S, SOM T, et al. A Fuzzy Similarity-Based Rough Set Approach for Attribute Selection in Set-Valued Information Systems. Soft Computing, 2020, 24(6): 4675-4691. [本文引用:3]
[20]	ZHANG Q L, LI L L. Attribute Reduction for Set-Valued Data Based on D-S Evidence Theory. International Journal of General Systems, 2022, 51(8): 822-861. [本文引用:1]
[21]	XIA S Y, LIU Y S, DING X, et al. Granular Ball Computing Classifiers for Efficient, Scalable and Robust Learning. Information Sciences, 2019, 483: 136-152. [本文引用:3]
[22]	XIA S Y, ZHANG H, LI W H, et al. GBNRS: A Novel Rough Set Algorithm for Fast Adaptive Attribute Reduction in Classification. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(3): 1231-1242. [本文引用:2]
[23]	XIA S Y, WANG C, WANG G Y, et al. GBRS: A Unified Granular-Ball Learning Model of Pawlak Rough Set and Neighborhood Rough Set. IEEE Transactions on Neural Networks and Learning Systems, 2025, 36(1): 1719-1733. [本文引用:1]
[24]	XIA S Y, LIAN X Y, WANG G Y, et al. Granular-Ball Fuzzy Set and Its Implement in SVM. IEEE Transactions on Knowledge and Data Engineering, 2024, 36(11): 6293-6304. [本文引用:1]
[25]	PENG X L, WANG P, XIA S Y, et al. VPGB: A Granular-Ball Based Model for Attribute Reduction and Classification with Label Noise. Information Sciences, 2022, 611: 504-521. [本文引用:1]
[26]	HUANG Z H, LI J J. Covering Based Multi-granulation Rough Fu-zzy Sets with Applications to Feature Selection. Expert Systems with Applications, 2024, 238(C). DOI: 10.1016/j.eswa.2023.121908. [本文引用:1]
[27]	ZHANG J J, SUN K, HUANG B, et al. Attribute Reduction Based on a Rapid Variable Granular Ball Generation Model. Expert Systems with Applications, 2025, 265. DOI: 10.1016/j.eswa.2024.126030. [本文引用:1]
[28]	YANG J, KUANG J C, WANG G Y, et al. Adaptive Three-Way KNN Classifier Using Density-Based Granular Balls. Information Sciences, 2024, 678. DOI: 10.1016/j.ins.2024.120858. [本文引用:1]
[29]	CHENG D D, LIU S S, XIA S Y, et al. Granular-Ball Computing-Based Manifold Clustering Algorithms for Ultra-Scalable Data. Expert Systems with Applications, 2024, 247. DOI: 10.1016/j.eswa.2024.123313. [本文引用:1]
[30]	周悦丽. 基于集值信息系统的局部粗糙集方法研究. 硕士学位论文. 漳州: 闽南师范大学, 2022. (ZHOU Y L. The Approach to Local Rough Sets Based on Set-Va-lued Information Systems. Master Dissertation. Zhangzhou, China: Minnan Normal University, 2022.) [本文引用:3]
[31]	YANG T L, LI Z W, LI J J. Attribute Reduction for Set-Valued Data Based on Prediction Label. International Journal of General Systems, 2023, 52(6): 745-775. [本文引用:2]
[32]	HU J, HUANG S Y, SHAO R. Attribute Reduction of Set-Valued Decision Information System // Proc of the 17th International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems. Berlin, Germany: Springer, 2018: 455-466. [本文引用:1]
[33]	ZHANG Y X, CHEN Z Z. Information Entropy-Based Attribute Reduction for Incomplete Set-Valued Data. IEEE Access, 2022, 10: 8864-8882. [本文引用:1]
[34]	DAI J H, ZHU Z L, LI M, et al. Attribute Reduction for Heterogeneous Data Based on Monotonic Relative Neighborhood Granula-rity. International Journal of Approximate Reasoning, 2024, 170. DOI: 10.1016/j.ijar.2024.109210. [本文引用:1]

1996

0.0

... 粒计算(Granular Computing, GrC)^[1]作为一种模拟人类思维多粒度、多层次认知问题的计算范式,近年来受到学术界的广泛关注 ...

2024

0.0

... 近年来,粒计算理论被广泛应用于模式识别^[2]、特征选择^[3]和机器学习^[4]等任务中,并展现出显著的可解释性与鲁棒性 ...

2021

0.0

... 近年来,粒计算理论被广泛应用于模式识别^[2]、特征选择^[3]和机器学习^[4]等任务中,并展现出显著的可解释性与鲁棒性 ...

2025

0.0

... 近年来,粒计算理论被广泛应用于模式识别^[2]、特征选择^[3]和机器学习^[4]等任务中,并展现出显著的可解释性与鲁棒性 ...

1982

0.0

... 在粒计算框架下,由Pawlak^[5]提出的粗糙集理论作为一种无需先验知识即可处理不确定数据的重要工具,构成粒计算思想的核心基础,已被成功应用于数据挖掘^[6]、机器学习^[7]和知识发现^[8]等领域 ...

1999

0.0

2003

0.0

1991

0.0

2006

0.0

... 在实际应用中,受限于客观采集条件,数据往往是不完整的,将此类不完备信息转化为集值信息系统是一种有效的处理策略^[9] ...

... 定义4^[9] 称一个四元组S=(U,A,V, f )为一个集值决策系统,若属性集 A=A#cod#x0222a ...

2019

0.0

... Chen等^[10]从粒计算的视角出发,定义对象间距离并利用高斯核方法,构建信息粒结构,为集值信息系统提出一种信息结构分析与不确定性度量方法 ...

2022

0.0

... Peng等^[11]利用模糊对称关系,提出4种针对集值信息系统的不确定性度量 ...

2021

0.0

... Wu等^[12]提出基于半单层覆盖的可靠近似算子,可高效计算高质量近似集 ...

2009

0.0

... Qian等^[13]将集值信息系统扩展至集值有序信息系统,提出处理集值有序信息系统的粗糙集模型 ...

2012

0.0

... Zhang等^[14]研究近似集的动态更新方法,丰富集值数据的处理理论 ...

2020

0.0

... Chen等^[15]研究不完备集值信息系统的不确定性度量,利用高斯核进行子系统的最优选择 ...

2011

0.0

... 为了应对这类数据中存在的问题,Couso等^[16]提出模糊粗糙集模型,并引入集值信息系统 ...

2013

0.0

... Dai等^[17]定义模糊相似关系,保留数据模糊性,为处理集值数据提供有效工具 ...

... 实验中选择如下属性约简算法作为对比算法:基于模糊关系的粗糙集算法(文献[17]算法)、基于模糊相似度的粗糙集算法(FSRS^[19])、基于相关性和决策错误率的SVDIS(Set-Valued Decision Infor-mation System)属性约简算法(DECE^[31])、基于相似关系的粗糙集算法(文献[32]算法)、基于条件熵的属性约简算法(CEIS^[33])、基于相对邻域粒度的单调前向属性约简算法(MRNG(Monotonic Forward Attribute Reduction Algorithm Based on Relative Neighborhood Granularity)^[34]) ...

2016

0.0

... Wei等^[18]提出2种模糊粗糙模型,并定义相容性矩阵与相容性函数,用于改进属性约简 ...

2020

0.0

... Singh 等^[19]基于模糊容差关系,提出FSRS,引入相似度阈值,构建模糊容差类,并利用依赖度度量属性重要性以实现属性约简 ...

... 定义5^[19] 设S=(U,A,V, f )为一个集值信息系统,对#cod#x02200 ...

2022

0.0

... Zhang等^[20]利用D-S证据理论,研究集值决策系统的属性约简 ...

2019

0.0

... 与此同时,作为粒计算领域的一项前沿技术,粒球计算(Granular Ball Computing, GBC)^[21]为自适应的粒度划分提供新的解决思路 ...

... 2 粒球计算粒球计算(GBC)^[21]是一种高效的粒计算实现方法,核心思想是将样本空间使用一系列超球体(即#cod#x0201c ...

... 定义6^[21] 设S=(U,A#cod#x0222a ...

2022

0.0

... Xia等^[22]将粒球计算引入邻域粗糙集,提出GBNRS(Granular-Ball Neighbor-hood Rough Sets),构建覆盖样本空间的自适应粒球以近似邻域结构,有效解决传统邻域粗糙集在大规模数据集上计算效率低下的问题 ...

... 定义7^[22] 设S=(U,A#cod#x0222a ...

2025

0.0

... Xia等^[23]提出GBRS(Granular-Ball Rough Set),实现Pawlak粗糙集与邻域粗糙集的统一表达,为粗糙集理论的动态粒度刻画提供新方向 ...

2024

0.0

... Xia等^[24]将GBC引入模糊集,提出粒球模糊集框架 ...

2022

0.0

... Peng等^[25]提出VPGB(Variable Parameter Granular-Ball Model),在标签噪声环境中同时实现属性约简和分类 ...

2024

0.0

... 为了知识表示能在更精细粒度上运行,以及更准确地处理来自多源的复杂不确定数据,Huang等^[26]融合基于覆盖的模糊粗糙集与多粒度粗糙集,提出多粒度粗糙模糊集模型 ...

2025

0.0

... Zhang等^[27]引入粒球质量指标,判断决策类的可分离度,并在此指标的基础上,提出快速可变粒球生成模型,提升属性约简性能 ...

2024

0.0

... 由于GBC能在保持结构完整性的同时抑制噪声影响,研究者已将其成功应用于分类^[28]、聚类^[29]等任务 ...

2024

0.0

... 由于GBC能在保持结构完整性的同时抑制噪声影响,研究者已将其成功应用于分类^[28]、聚类^[29]等任务 ...

2022

0.0

... 1 集值信息系统定义1^[30] 在四元组(U,A,V, f )中,U为非空对象集,称为论域 ...

... 定义2^[30] 设S=(U,A,V, f )为一个集值信息系统,U为论域,A为属性集,V为值域, f为U#cod#x000D7 ...

... 定义3^[30] 设S=(U,A,V, f )为一个集值信息系统,#cod#x02200 ...

2023

0.0

... 在实际应用中,由于存在多个特征,数据集通常以集值的形式表示,但是没有可直接使用的设定值数据,因此需要对数据集进行预处理,本文借鉴文献[31]的转化思想,将不完备信息系统转化为集值信息系统 ...

2018

0.0

2022

0.0

2024

0.0