张晓明,博士,副教授,主要研究方向为群体智能、智能决策.E-mail:xmzhang@ustc.edu.
作者简介:

牛长宇,硕士研究生,主要研究方向为复杂网络及其应用.E-mail:q23201171@stu.ahu.edu.cn.

张海峰,博士,教授,主要研究方向为复杂网络结构挖掘与动力学分析、人工智能算法.E-mail:haifengzhang1978@gmail.com.
网络对齐致力于挖掘不同网络间节点的对应关系,是跨不同领域集成信息的关键任务之一,但现有方法大多关注普通图,忽略现实世界系统中普遍存在的高阶群体交互,而为数不多的现有超图对齐方法往往只依赖浅层的局部拓扑信息,无法捕捉深层的结构语义.为了解决此问题,文中提出超图-团展开对比学习(HCCL)的多视图对比学习方法,从高阶与低阶两个互补的层面协同捕捉节点的结构特征,旨在有效利用超图丰富的结构信息完成对齐任务.具体而言,同时利用原始超图及其团展开图作为两个视图:原始超图通过超图卷积网络学习高阶群组关系,团展开图通过图卷积网络捕捉低阶成对关系.在此基础上引入跨视图对比学习机制,最大化同一节点在不同视图下嵌入表示的一致性,提取跨越不同结构尺度且更鲁棒和全面的节点特征.在真实数据集上的大量实验充分表明HCCL的有效性.
ZHANG Xiaoming, Ph.D., associate professor. His research interests include swarm intelligence and intelligent decision making.
About Author:
NIU Changyu, Master student. His research interests include complex networks and their applications.
ZHANG Haifeng, Ph.D., professor. His research interests include structure mining and dynamics analysis of complex networks and artificial intelligence algorithms.
Network alignment is intended to mine node correspondences between different networks, and it is crucial for integrating information across diverse domains. However, most existing methods focus on ordinary graphs and overlook the prevalent high-order group interactions in real-world systems. There are only a few hypergraph alignment methods relying solely on shallow local topological information and failing to capture the deep structural semantics of nodes. To address this issue, a multi-view contrastive learning method for hypergraph alignment is proposed, named hypergraph-clique expansion contrastive learning (HCCL). A multi-view contrastive learning framework is constructed. Node structural features are collaboratively captured from both higher-order and lower-order complementary perspectives to more effectively leverage the rich structural information of hypergraphs for alignment tasks. The original hypergraph and its clique expansion graph are utilized as dual views simultaneously. The original hypergraph learns higher-order group relationships through hypergraph neural networks, while its clique expansion graph captures lower-order pairwise relationships via graph convolutional networks. On this basis, a cross-view contrastive learning mechanism is introduced to extract more robust and intrinsic node features spanning different structural scales by maximizing the consistency of node embeddings across both views. Extensive experiments on real-world datasets fully validate the effectiveness and robustness of HCCL.
网络对齐旨在识别并匹配不同网络中代表的同一现实世界实体的节点[1].这些在不同网络中对应同一实体的节点称为锚节点, 它们之间的跨网络链接称为锚链接[2].然而, 由于隐私保护限制、数据异构性及网络结构的固有差异, 这些跨网络的节点对应关系通常是隐性、未知的, 使得节点精准对齐成为一项富有挑战性的研究[3, 4].
网络对齐对于促进多源信息融合与知识发现具有至关重要的作用, 应用价值体现在多个领域中, 例如:对齐不同物种的蛋白质相互作用以评估这些蛋白质形成的功能组件是否保守[5]、对齐不同网络平台的用户账户以辅助跨域推荐系统解决冷启动与数据稀疏问题[6]、利用多个相互关联的网络捕捉疾病在不同渠道中传播的复杂性和多面性[7]等.
传统的普通图结构由节点和二元成对关系组成, 在刻画现实世界中普遍存在的多实体间复杂协作时, 表现出固有的局限性[8].例如:在科研合作网络中, 一篇由多位作者共同完成的论文形成的关系; 在电子商务中, 一个购物车内多种商品被同时购买的组合关系.这些都无法使用简单的成对连接来无损表达.
超图通过允许一条超边连接任意数量的节点, 为精确建模这类高阶群组性关系提供强大的工具, 能更真实地反映现实世界系统的复杂性[9, 10].但在网络对齐领域, 针对超图对齐的研究却相对较少, 绝大多数研究集中在普通图对齐[11, 12].目前存在的少数超图对齐方法, 还停留在基于拓扑指标的层面, 如计算共同匹配邻居、一阶邻居和二阶邻居的数量[13].这些传统方法虽然具有一定的可解释性, 但其本质上依赖于浅层、局部的统计信息, 难以捕捉节点在网络全局结构中扮演的深层、潜在角色, 仅能根据预定义的、通常是局部的结构属性进行对齐, 因此无法全面概括一个节点在复杂网络拓扑中嵌入的多尺度、高阶的结构语义, 忽略更全局的、潜在的复杂结构模式[14].
针对现有超图对齐方法往往忽略高阶群体交互且仅依赖浅层拓扑信息的局限性, 本文提出超图-团展开对比学习(Hypergraph-Clique Expansion Con-trastive Learning, HCCL)的多视图对比学习方法, 创新性地构建多视图协同机制, 旨在从互补的结构尺度全面刻画节点特征:一方面保留原始超图结构, 通过超图卷积网络(Hypergraph Convolutional Network, HGCN)[15]直接学习其中蕴含的深层高阶群组关系; 另一方面利用团展开策略将高阶交互转化为低阶成对关联, 并通过图卷积网络(Graph Convolu-tional Networks, GCN)[16]显式捕捉节点间的局部邻域信息.在此基础上, 设计跨视图对比学习机制, 最大化同一节点在不同视图下嵌入表示的一致性, 克服单一视图潜在的结构噪声与局限性, 挖掘跨越不同结构尺度的鲁棒特征.在多个真实世界数据集上的实验表明, HCCL能有效融合高阶结构语义与低阶结构语义, 对齐精度较高, 消融实验也证实高阶视图与低阶视图对于提升对齐精度的关键作用.
超图嵌入, 又称超图表示学习, 旨在将超图中的节点、超边等元素映射至低维向量空间, 同时保留超图固有的高阶结构信息和属性信息[9].这些生成的向量表示可有效应用于各类下游任务, 如节点分类[17]、链接预测[18]、聚类[19]等, 尤其是在生物信息学和医学等复杂领域中, 超图嵌入已经展示其独特的应用价值.Kim等[20]提出HIT(Hypergraph Interac-tion Transformer), 引入注意力机制, 有效捕捉基因、本体与疾病间的错综关联.Peng等[21]提出HRLC-DR, 利用HGCN构建细胞与药物的高阶交互图, 用于提取关键特征, 显著提升癌症药物反应预测的准确性.
最基础的超图嵌入方法使用超图展开策略, 将超图转换为普通图以复用现有的普通图嵌入技术[22].尽管团展开和星形展开等经典方法应用广泛, 但往往因简化拓扑结构而导致高阶结构信息的丢失, 因此研究者们探索更复杂的扩展策略以保留高阶拓扑特性[23].Yang等[24]提出LE(Line Expan-sion), 将顶点-超边对视为新节点以构建连接, 实现超图到简单图的同构映射.Yan等[25]提出HJRL(Hypergraph Joint Representation Learning), 将超顶点与超边统一转化为图节点, 旨在通过显式的连接构建引入更丰富的关系语义.
除了上述基于图展开的方法以外, 随机游走策略提供另一种捕获节点间邻近性的视角.这类方法的核心机制通常遵循“ 节点-超边-节点” 的交互路径生成序列, 并结合Skip-Gram模型学习表示[26].Zhang等[27]提出HRW, 降低构建混合状态的成本.Luo等[28]利用面向大规模超图的无偏随机游走采样, 通过延迟接受技术消除简单游走的高度偏差.Liang等[29]提出WCRW-MLP, 使用带有加权和聚类偏差的游走策略, 引入共现权重与三元闭包信息, 引导游走倾向于超图结构上更重要的区域.
随着图神经网络在普通图数据上展现出的强大特征提取和表示能力, 研究者们开始致力于将其应用到超图数据上, 旨在将超图结构中的节点映射至低维向量空间, 从而有效捕捉和学习超图中存在的高阶关系[30].在此背景下, 学者们相继提出各类超图神经网络模型.Bai等[15]提出GCN, 定义超图上的卷积操作并引入注意力机制, 实现对非成对关系的灵活建模.为了处理更复杂的潜在关联, Gao等[31]提出HGNN+, 构建超边组, 并利用自适应融合策略与空间域卷积学习通用表示.此外, 傅晨波等[32]提出基于超图嵌入和有限注意力的社会化推荐模型(Social Recommendation Based on Hypergraph Embedding and Limited Attention, SRBHL), 提取并融合用户行为与社交信息, 有效缓解数据稀疏问题并过滤噪声.
网络对齐旨在识别和匹配不同网络中属于同一实体的节点, 其核心目标是基于节点的拓扑结构或属性特征, 在两个或多个网络之间建立节点间的一致性对应关系[1, 2].现有的网络对齐研究绝大多数集中在普通图上, 即只考虑节点之间成对关系的网络.
基于相似度指标的方法是早期网络对齐的主流策略.这类方法首先为不同网络中的节点对定义一个相似性指标, 该指标通常结合节点的局部拓扑信息或全局拓扑信息, 如节点度、公共邻居和节点中心性等.再通过各种优化算法求解最优的节点匹配矩阵.Ding等[33]提出SOIDP(Second-Order Iterative De- gree Penalty), 综合一阶与二阶共同邻居信息并引入度惩罚机制, 有效提升多层网络间链接预测的准确性.Tang等[34]提出CPNA(Community Partition-Based Network Alignment Method), 将全局对齐任务分解为社区内更小规模的矩阵运算, 显著降低处理大规模网络时的空间复杂度.Lá zaro等[35]证明概率推理模型能输出对齐的完整后验分布而非单一结果, 证明即使在最大似然估计失效时利用分布信息仍能实现高可解释性且准确的节点匹配.
随着图表示学习的兴起, 基于表示学习的方法逐渐成为主流的网络对齐方法, 其核心思想是首先将图中的节点嵌入低维向量空间中, 使节点的拓扑邻近性在向量空间中得以保持, 进而计算这些嵌入向量之间的相似性, 进而衡量节点之间的对应关系.Park等[36]提出Grad-Align, 引入逐层重构损失与双感知相似性度量, 有效捕获一阶邻域及高阶邻域结构.针对节点异质性挑战, Peng等[37]提出CHNA(Co-mmunity View to Alleviate the Impact of Heterogeneity in Network Alignment), 利用跨网络社区对齐关系辅助节点级对齐.Jiao等[38]提出IMNA(Interactive Graph Learning for Multilevel Network Alignment), 建模幂律分布等复杂拓扑特性, 综合利用多层次结构与属性信息.
超图对齐领域的研究尚处于起步阶段, 现有工作多局限于依赖拓扑与属性指标的浅层方法.这类方法侧重于利用显式的拓扑统计特征直接构建相似性度量.Peng等[13]设计融合度惩罚机制的超边相似度指标, 量化节点间高阶关联的强度与数量.Wu等[14]刻画相邻超边的局部同构特征, 构建更精细的节点结构表示.尽管上述方法都引入高阶统计指标, 在一定程度上提升对齐效果, 但本质上仍依赖于手工设计的结构特征.因此, 如何利用图神经网络等深度学习技术自动挖掘超图中的潜在高阶依赖特征用于网络对齐, 仍是当前值得进一步探索的方向.
一个超图可以定义为H=(V, Ε), 其中,
V={v1, v2, …, vN}
表示节点集合,
Ε={ε1, ε2, …, εM}
表示超边集合.与普通图不同的是, 每条超边εi∈Ε都可包含任意数量的节点.这种结构使超图能精确捕捉超越成对交互的高阶关系.通过超图的邻接矩阵B∈RN×M表示超图, 当节点vi属于超边εj时, bij=1, 否则bij=0.
基于B, 可定义节点的超度d(vi) 为包含该节点的超边数量, 即
d(vi)=
类似地, 超边的度|εj|定义为该超边包含的节点数量, 即
|εj|=
在此基础上, 定义节点超度矩阵Dv∈RN×N, 为一个对角矩阵, 对角元素
dii=d(vi).
定义超边度矩阵De∈RM×M, 为一个对角矩阵, 对角元素
djj=|εj|.
超图的一个重要特例是K一致超图:如果一个超图中所有的超边都具有相同的度K, 即 ∀εj∈Ε, |εj|=K, 则称该超图为K一致超图.特别地, 当K=2时, 2一致超图退化为普通图.
团展开是一种将超图转换为普通图的常用方法.其核心思想是:对于超图中的每条超边ε∈Ε, 在其包含的所有节点之间两两建立一条边.通过这种方式, 团展开显式表达超边内部隐含的成对关系.团展开图C=(V, E)的邻接矩阵为:
A=BBT,
其中, aij∈A表示节点vi、vj共同属于的超边数量.因此C通常被视为一个加权图.如果忽略边的权重, 即只考虑节点间是否存在共同所属的超边而不关心其具体数量, 那么C也可视为一个无权图.
对比学习中有许多常用的损失函数, 本文采用的是经典的InfoNCE(Information Noise Contrastive Estimation)损失函数[39].如果节点对 (vi, vj)为一个正样本, 对比损失为:
Lcl(vi, vj)=
其中,
l(vi, vj)=-ln
xi、xj分别表示节点vi、vj的嵌入表示, τ表示温度参数, s(· , · )表示余弦相似度函数, neg表示选取的负样本数量.
在负样本的选择上, 本文采用随机采样策略, 对于每个正节点对, 从除了其对应的正样本之外的所有其它节点构成的候选集合中, 随机抽取neg个节点构成负样本.该损失函数的直观目标是:在嵌入空间中将正样本对(vi, vj)的表示 xi、xj拉得更近, 同时将vi与其所有neg个负样本vk的表示xi、xk推得更远.
给定超图Hs=(Vs, Εs), Ht=(Vt, Εt), 已知2个超图中的部分节点之间存在锚链接, 即已知部分节点之间的对应关系, 记已知的锚链接集合 Φ ⊂Vs×Vt.超图对齐任务的目标是发现2个网络中剩余未知的锚链接集合Ψ , 这等价于学习一个对齐函数f, 即对于任意节点对(
f(
其中
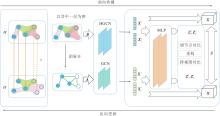
为了解决现有方法难以捕捉超图深层结构语义的问题, 本文提出超图-团展开对比学习(HCCL)的多视图对比学习方法, 具体框架如图1所示.
HCCL首先构建原始超图及其对应的团展开图, 分别作为捕捉高阶群组关系和低阶成对关系的互补视图.然后, 分别利用超图卷积网络(HGCN)[15]和图卷积网络(GCN)[16]并行提取节点在不同视图上的嵌入表示.为了获得更具鲁棒性的节点特征, 设计包含跨视图对比损失、网络重构损失及锚节点对比损失的混合目标函数, 通过协同优化, 最大化不同结构尺度下的一致性.最后, 基于学习的节点嵌入计算跨网络相似度矩阵, 实现精确的网络对齐.
3.1.1 超图编码器
对于原超图Hs和Ht, HCCL采用HGCN作为编码器, 提取高阶结构特征, 不同于普通图卷积, HGCN将超边视为一个完整的集合实体, 直接汇聚同一超边内所有节点的特征, 能保留超边内部的高阶群组语义, 避免因结构分解而导致的信息损失.第l+1层超图编码器的节点特征矩阵为:
l=0, 1, …, k-1,
其中, ReLu(x)=max(0, x)表示激活函数, Dv表示节点超度矩阵, B表示超图的邻接矩阵, De表示超边度矩阵,
3.1.2 团展开编码器
为了捕捉与高阶信息互补的低阶成对关系, HCCL基于团展开策略, 构建超图Hs和Ht的团展开图Cs和Ct, 同时采用GCN作为编码器, 提取低阶结构特征.虽然超图结构能有效建模高阶群组关系, 但团展开图作为一种显式的低阶结构表示, 能将群组交互转化为节点间的成对连接, 利用GCN的邻域聚合能力, 在此成对连接结构上执行特征的传播与更新, 专注于捕捉节点间的成对交互语义.这种基于低阶视角的特征提取与基于高阶视角的超图编码形成有效互补, 从而为高阶视图提供必要的语义补充.编码过程中第l+1层团展开图编码器的节点特征矩阵为:
l=0, 1, …, k-1,
其中,
值得注意的是, 当超边规模较大时, 团展开策略会引入大量的冗余边.然而, 在缺乏先验知识的情况下, 超图中节点间确切的真实低阶成对关系往往是隐式且未知的.在此背景下, 团展开可被视为一种低阶结构的近似表示, 尽管它引入冗余, 但这种对潜在交互的全连接建模能作为高阶超图结构的有效低阶补充, 显式捕捉并强化群组内部潜在的成对交互语义.
3.1.3 非线性映射
HCCL在编码器后引入一个非线性映射, 用于解耦表示学习与优化对比损失.该映射将编码器输出的特征X投影至一个新空间, 第l+1层映射得到的特征为:
Z(l+1)=ReLu(Θ (l)Z(l)+b(l)), l=0, 1, …, k-1,
其中, Z(l)表示第l层映射得到的特征, b(l)表示第l层映射的偏置.
在此空间内优化对比损失, 旨在高效学习针对数据增强的不变性.在进行对齐任务时, 舍弃该映射, 使用其原始输入Z0=Xk, 即编码器输出的特征Xk, 从而保留更通用和丰富的特征信息, 提升模型的泛化能力.
为了保证一致性, 对于Hs和Ht的不同视图使用共享参数的映射.
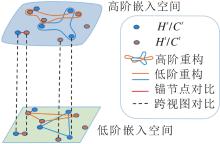
为了生成既保留丰富结构语义又具备跨网络一致性的节点表示, HCCL构建包含多重约束的总损失函数, 旨在协同优化高阶特征空间与低阶特征空间, 具体示意图如图2所示.该损失函数主要由3个互补的损失项构成.首先, 为了确保嵌入表示能有效保留原始数据的拓扑信息, 分别在高阶嵌入空间与低阶嵌入空间中引入重构损失.然后, 为了充分融合不同视角的互补信息, 在网络内部引入跨视图对比损失, 最大化同一节点在高阶超图视图与低阶团展开视图下嵌入表示的一致性.最后, 为了实现源网络与目标网络的精准对齐, 利用已知的锚节点对作为监督信号, 构建锚节点对比损失.在上述损失的协同约束下, HCCL能在统一的潜在空间中拉近对应节点的距离, 同时有效保持其内在的多尺度结构特征.
3.2.1 重构损失
本文引入重构损失, 确保节点在被编码到潜在空间后, 依然能保持原始图的内在拓扑结构信息.具体来说, 对于团展开图Cs和Ct, 约束具有连边的两个节点的嵌入更相似, 从而保留节点的低阶结构信息, 则团展开图的低阶重构损失如下:
$\begin{aligned} l_{\text {rec } c}=- & \frac{1}{|E|}\left[\sum_{\left(v_{i}, v_{j}\right) \in E} \ln \left(\boldsymbol{\sigma}\left(\boldsymbol{z}_{c, i}^{\mathrm{T}} \cdot \boldsymbol{z}_{c, j}\right)\right)-\right. \\ & \left.\sum_{\left(v_{i}, v_{k}\right) \notin E} \ln \left(1-\boldsymbol{\sigma}\left(\boldsymbol{z}_{c, i}^{\mathrm{T}} \cdot \boldsymbol{z}_{c, k}\right)\right)\right], \end{aligned}$
其中, σ=
为了构建负样本, 本文采用随机负采样策略, 即对于每条正边 (vi, vj)∈E, 在非邻接节点集合中随机采样一条负边(vi, vk)∉E进行优化.
总的低阶重构损失为:
其中
对于超图Hs和Ht, 约束在同一条超边内部的节点的嵌入更相似, 从而保留节点的高阶结构信息, 则超图的高阶重构损失如下:
$\begin{aligned} l_{\text {rech }}= & -\frac{1}{|E|}\left[\sum_{\varepsilon \in E} \sum_{\substack{v_{i} \in \varepsilon \\ v_{j} \in \varepsilon}} \ln \left(\sigma\left(\boldsymbol{z}_{h, i}^{\mathrm{T}} \cdot \boldsymbol{z}_{h, j}\right)\right)-\right. \\ & \left.\sum_{\varepsilon \in E} \sum_{\substack{v_{i} \in \varepsilon \\ v_{k} \notin \varepsilon}} \ln \left(1-\sigma\left(\boldsymbol{z}_{h, i}^{\mathrm{T}} \cdot \boldsymbol{z}_{h, k}\right)\right)\right] . \end{aligned}$
其中zh, i、zh, j、zh, k分别表示超图中节点vi、vj、vk的嵌入表示.
与低阶重构类似, 在计算该损失时同样采用随机负采样策略.具体而言, 对于超边ε中的每个节点 vi∈ε, 在节点集合中随机采样一个不属于该超边的节点 vk∉ε 作为负样本进行优化.
总的高阶重构损失为:
其中
总的重构损失为高阶重构损失和低阶重构损失之和:
Lrec=
3.2.2 超图-团展开对比损失
为了融合不同视图之间的信息, 在超图-团展开之间引入跨视图对比学习机制, 旨在通过最大化同一节点在不同视图下表示的一致性, 提取兼具高阶特性与低阶特性的特征.具体而言, 将同个节点vi在不同视图中的表示zh, i和zc, i视为一对正样本, 则超图-团展开对比损失为:
lhc=
总的层内跨视图对比损失为Hs和Ht超图-团展开对比损失之和:
Lintra=
其中,
3.2.3 锚节点对比损失
锚节点对比学习用于保证跨网络锚节点嵌入的一致性, 将已知的锚节点对集合 Φ 中的元素视为正样本, 拉近其在嵌入空间中的距离, 则超图Hs和Ht的锚节点对比损失为:
$l_{\mathrm{hg}}=\sum_{\left(v_{i}^{s}, v_{j}^{t}\right) \in \Phi} L_{\mathrm{cl}}\left(\boldsymbol{z}_{h, i}^{s}, \boldsymbol{z}_{h, j}^{t}\right),$
其中,
$l_{\mathrm{cu}}=\sum_{\left(v_{i}^{s}, v_{j}^{t}\right) \in \Phi} L_{\mathrm{cl}}\left(\boldsymbol{z}_{c, i}^{s}, \boldsymbol{z}_{c, j}^{l}\right),$
其中,
跨层的总锚节点对比损失为不同视图锚节点对比损失之和:
Linter=lhg+lcu.
3.2.4 总损失
总的损失函数是由层内跨视图损失、层间跨网络损失及重构损失通过加权求和得到, 即
Ltotal=(1-α)(Linter+Lrec)+αLintra,
其中α表示平衡不同损失项的权重参数.
在训练之后, HCCL分别得到超图中节点嵌入X
S(
其中,
实验数据集源于DBLP学术合作网络[13].每个数据集均由不同的学术期刊构成源网络与目标网络.在这些网络中, 节点表示作者, 而一篇由多位作者共同完成的学术论文构成一条连接所有合著者的超边, 在源网络与目标网络期刊中均发表论文的同一位作者被定义为锚节点.数据集具体信息如表1所示.
| 表1 实验数据集统计信息 Table 1 Statistics of experimental datasets |
为了充分利用超图的拓扑结构特征, 将初始节点特征矩阵设定为超图的关联矩阵, 即X(0)=B.对于HCCL, 设定GCN和HGCN编码器的输出维度d=128, 层数k=2, 权重参数α=0.9, 学习率lr=0.001, 温度系数τ=0.2, 负样本数量 neg=5.
本文采用Precision@K和MRR作为评价指标.
本文选择如下方法作为对比方法.
1)HGCN[15].在每层超图上使用超图卷积网络提取结构特征, 然后使用多层感知机(Multi-layer Perceptron, MLP)根据已知的锚节点学习两个网络间的映射关系.
2)GCN[16].在每层超图的团展开图上使用图卷积网络提取结构特征, 再使用MLP根据已知的锚节点学习两个网络间的映射关系.
3)CAMU(Cycle-Consistent Adversarial Mapping Model for the User Alignment Problem)[40].建立两个不同嵌入空间之间的映射关系, 通过生成器与判别器之间的对抗训练, 结合循环一致性训练, 使用训练好的生成器建立不同网络间的对应关系.
4)HOT(Hierarchical Multi-marginal Optimal Trans-port)[41].通过FGW(Fused Gromov-Wasserstein)重心将多个网络分解为更小的对齐簇, 并将 FGW 距离推广至多边际设置以描绘高阶关联.
5)CCNE(Collaborative Cross-Network Embe-dding)[42].利用图神经网络保留网络内部和网络间的特征, 将两个网络统一至同一个潜在空间中, 采用硬负样本采样策略区分锚节点及其采样的邻居.
6)JOENA(Joint Optimal Transport and Embe-dding Framework for Network Alignment)[43].将降噪的最优传输映射作为自适应采样策略, 直接建模所有跨网络节点对, 实现鲁棒的网络嵌入, 同时最优传输成本可逐步以端到端的方式在已学习的嵌入基础上进行训练, 进一步提升对齐质量.
为了更好地评价HCCL对不同视图信息的提取能力, 引入两种变体作为对比方法.
1)HCCL-H.仅利用高阶超图视图的嵌入计算对齐相似度矩阵, 验证高阶信息的有效性.
2)HCCL-C.仅利用低阶团展开视图的嵌入计算对齐相似度矩阵, 验证低阶信息的有效性.
为了全面评估HCCL的有效性, 在5个数据集上对训练集比例为20%、50%、80%的场景进行实验, 结果如表2、表3和图3所示.
| 表2 各方法在5个数据集上及不同训练集比例下的Precision@5指标 Table 2 Precision@5 of methods under different training set ratios on 5 datasets % |
| 表3 各方法在5个数据集上及不同训练集比例下的MRR指标对比 Table 3 MRR of methods under different training set ratios on 5 datasets % |
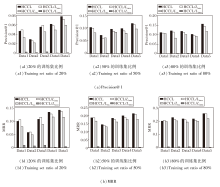
 | 图3 各方法在5个数据集上不同训练集比例下的Precision@K总和对比Fig.3 Comparison of precision@K sums for different algorithms under different training set ratios on 5 datasets |
表2和表3详细列出各方法在不同数据集上以及训练集比例下的Precision@5和MRR指标.图3通过累加条形图的形式, 展示各方法在更广泛K值范围(K=1, 5, 10, 15, 20, 25, 30)下的Precision@K累加求和结果.条形的总体长度直观反映方法在不同排名阈值下的综合对齐能力, 是对表2和表3中单一指标的补充.
由表2、表3和图3可见, HCCL网络对齐性能最优.图3的累加条形图直观显示, HCCL的Preci-sion@K累计值在11个场景中最优, 表明其综合排名能力的优越性.表2和表3的定量数据证实这一点, HCCL在Precision@5和MRR指标上总体保持领先.在绝大多数训练集比例下, HCCL均取得领先的对齐精度, 即便在个别场景中未取得最优值, 也能取得次优值.这说明引入的跨视图对比学习机制的有效性, 即使在训练集比例只有20%、缺乏充足监督信号的情况下, HCCL通过不同视图挖掘数据的多尺度结构信息作为自监督信号, 也能取得最优值.此外, HCCL性能优于仅使用单一视图的HCCL-H和HCCL-C, 这表明超图代表的高阶群组关系与团展开图代表的低阶成对关系这两种信息是互补的, 二者的有效融合能生成更全面、鲁棒的节点表示, 从而在对齐任务中取得更优性能.
观察不同方法在不同训练集比例下的性能变化, 发现随着训练集比例从20%升至80%, 所有方法的性能均得到普遍提升, 这表明更丰富的监督信息能帮助方法学习更具泛化能力的表示.在对比方法中, GCN和HGCN表现稳定, 但二者性能互有优劣, 这可能与网络的拓扑特征相关, 即某些网络更侧重于低阶成对关系, 而另一些网络则更依赖超图蕴含的高阶群组交互.这表明无论是低阶结构信息还是高阶结构信息, 对于提升网络对齐性能均具有积极作用, 关键在于网络本身更倾向于显现何种特征.JOENA和CCNE表现出较强的竞争力, 在部分实验设置下的性能接近甚至超过HCCL, 其中JOENA有时能在Precision@5和MRR指标上取得最优值, CCNE在图3(e1)、(e2)中Precision@K指标取得最优累计值.值得注意的是, HCCL的两个变体甚至在特定场景中能取得次优值乃至最优值.例如:对于Data 4的Precision@5, HCCL-H就取得次优值, 在图3(d1)、(d2)中甚至优于HCCL.这一现象可能是因为Data 4 中蕴含的高阶结构特征具有主导性, 且低阶视图可能引入额外的结构噪声.在这种特定情况下, 专注于单一视图的变体能不受另一视图噪声的干扰, 从而在特定的数据分布下实现更优的对齐效果.
为了探究超参数对HCCL性能的影响, 在Data 1、Data 4数据集上进行参数敏感性实验.主要关注3个核心参数:嵌入维度d、对比损失中的温度系数τ, 平衡不同损失项的权重参数α.定义d=32, 64, 128, 256, 384, 512, τ=0.1, 0.2, 0.5, 0.7, 1.0, 2.0, 5.0, α=0, 0.1, …, 1.0.具体结果如图4所示.
对于3.1节所述超图、团展开图编码器和映射模块, 本文设置网络层数为2, 因此编码器输出特征X
从图4(a1)、(b1)可看出, 当嵌入维度d从一个较小的值开始增加时, Precision@1和MRR指标均随之快速提升.这表明过低的维度无法充分捕捉节点丰富的结构和语义信息.在d=128之后, 若继续增加维度, 性能趋于平稳甚至略有下降, 这可能是因为过高的维度会增加HCCL复杂度和过拟合的风险, 同时并未带来额外的信息增益.
τ是对比学习损失函数中用于调节正负样本对区分难易程度的参数, 如图4(a2)、(b2)所示, 随着τ从0.1开始增加, HCCL性能先小幅上升后急剧下降, 约在τ=0.2时取得最大值.
权重参数α表示视图间对比学习损失在总损失中占的比例, 如图4(a3)、(b3)所示, α=0时, HCCL完全未利用超图与团展开图之间的一致性, 性能相对受限, 这验证跨视图对比机制的必要性.值得注意的是, HCCL在α=0.9附近取得最优值, 这主要归因于不同损失函数在数值量级上的天然差异:重构损失的原始值通常显著高于对比损失, 因此采用较大的α值实质上是将重构损失缩至与跨视图损失匹配的贡献量级, 从而避免优化过程被数值较大的辅助任务主导.当α=1时, 即HCCL仅关注视图间的一致性而完全忽略网络本身的结构信息和跨网络的监督信息时, 性能出现急剧下降, 这表明拓扑重构和锚链接监督为模型提供必要的结构约束与导向, 是HCCL能有效捕捉底层拓扑结构与关键语义信息的重要保障.
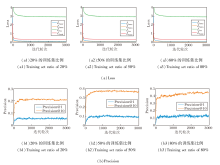
为了验证HCCL的训练稳定性, 在Data 3数据集上分析其收敛性.HCCL在训练集比例为20%、50%、80%时的收敛情况如图5所示.
图5(a)分别展示3种训练集比例下总损失函数Ltotal及其主要组成部分(Linter, Lintra, Lrec)在训练过程中的变化情况.由图可看出, 在所有情况下, 总损失及其各分量损失在训练初期均呈现快速下降的趋势.大约在1 000个迭代轮次之后, 所有损失曲线都逐渐趋于平缓, 并最终收敛到稳定的低值.
同时, 图5(b)记录相应训练比例下Precision@1和Precision@10随训练轮数的变化情况.与损失函数的下降趋势对应, 两个指标在训练初期都得到迅速提升, 并在损失函数收敛后, 也相应稳定在一个较高的水平.这一致的现象表明, 无论监督信号的强弱, HCCL的优化过程均具有良好的稳定性与收敛速度, 能有效最小化预设的损失函数.这也证实本文设计的损失函数的优化目标与网络对齐任务的性能提升是高度一致的.
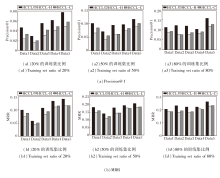
为了验证HCCL中各个核心组件的有效性, 在5个数据集上设计消融实验, 对比HCCL、HCCL-H、HCCL-C, 具体结果如图6所示.
由图6可观察到, 在所有训练集比例下, HCCL在Precision@1和MRR指标上均显著优于两个仅使用单一视图的变体, 这一结果证实HCCL设计的有效性, 即超图捕捉的高阶群组关系和团展开图捕捉的低阶成对关系是互补且缺一不可的, HCCL通过跨视图的协同学习与信息融合, 能捕捉底层网络结构更丰富的拓扑特性, 生成更全面、鲁棒的节点表示, 最终显著提升网络对齐精度.对比变体可发现, HCCL-C优于HCCL-H, 这表明尽管高阶信息能提供有益的补充, 但由团展开图提供的丰富、显式的低阶成对局部邻域信息仍是网络对齐任务的关键基础.
下面对不同损失项进行消融实验, 设计如下3个变体.
1)HCCL\Linter:移除跨网络的锚节点对比损失.
2)HCCL\Lrec:移除网络重构损失.
3)HCCL\Lintra:移除跨视图的超图-团展开对比损失.
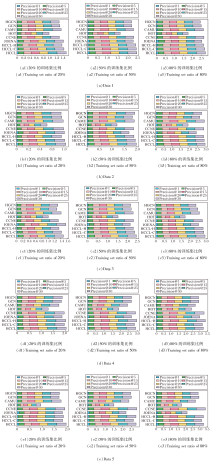
各损失函数消融实验结果如图7所示.由图可发现, HCCL\Linter在所有数据集上均表现出大幅的性能下降, 表明锚节点对比作为监督信号是方法学习跨网络映射的决定性因素.同时, HCCL\Lrec的性能显著低于HCCL, 证实拓扑重构能提供关键的结构约束, 防止HCCL在对齐过程中丢失原始拓扑信息.此外, HCCL\Lintra在大多数情况下性能不及HCCL, 这验证联合高阶超图与低阶团展开进行协同学习的有效性.但值得注意的是, HCCL\Lintra在少数情况下性能优于或接近HCCL, 这说明虽然低阶视图提供丰富信息, 但在强制对齐高阶特征和低阶特征的过程中也可能引入结构干扰或噪声, 影响对齐效果.
综上所述, 锚节点对比损失提供显式的跨网络监督, 重构损失保留网络的拓扑结构, 而超图-团展开对比损失负责跨视图的高低阶语义协同与互补, 这3种损失在优化过程中都发挥关键且互补的作用, 共同确保HCCL的最优性能.
为了直观展示HCCL在学习节点表示上的有效性, 在Data 4、Data 5数据集上对锚节点的嵌入进行可视化.将HCCL及其两个变体HCCL-H、HCCL-C学习的锚节点嵌入通过t-SNE(t-Distributed Stochas-tic Neighbor Embedding)降维至二维空间, 具体可视化结果如图8所示, 星形表示来自源网络的节点, 三角形表示来自目标网络的节点, 相同颜色表示它们是锚节点对, 而它们之间的连线距离表示其嵌入表示的差异.
对比图8(a)、(b)可看到不同视图融合的互补优势.以Data 4数据集为例, 节点27的对齐更依赖于HCCL-C捕捉的低阶信息, 而HCCL-H则表现不佳.对于节点4和节点20, HCCL-H和HCCL-C均无法有效对齐它们, 而HCCL通过融合两种视图的信息, 成功将其距离缩短.
类似地, 在Data 5数据集上, 节点23在HCCL-H中对齐良好, 但在HCCL-C中相距甚远, 而节点1和节点16在HCCL-C中对齐较好, 在HCCL-H中表现不佳.HCCL则综合两者优势, 对大部分节点都实现较好的对齐.这些案例直观证实高阶信息与低阶信息的互补性, 凸显HCCL融合多尺度信息实现对齐的必要性和优越性.
本文聚焦于现实世界中普遍存在但现有研究较少关注的超图对齐问题, 提出超图-团展开对比学习(HCCL)的多视图对比学习方法.HCCL构建多视图对比学习机制, 在互补的高阶超图与低阶团展开图视图间进行对比, 从而学习跨越不同结构尺度、更鲁棒的节点表示.在多个真实世界数据集上进行的全面实验充分验证HCCL的有效性.实验表明, HCCL的性能在不同条件下均较优, 其成功的关键在于高阶结构信息与低阶结构信息的有效融合与互补, 这使方法能捕捉更全面的深层结构语义, 实现精准对齐.
今后可考虑进行如下扩展.首先, HCCL主要关注网络的拓扑结构, 未来可考虑将节点的属性信息融入对比学习框架中, 处理更复杂的属性超图或异构网络.其次, 针对团展开在大规模超边下可能引入的结构冗余问题, 一个值得深入探究的是自适应的稀疏化展开策略, 旨在保留关键低阶语义的同时降低结构噪声.最后, 尝试引入更多样化的超图结构变换策略或数据增强方法, 构建语义信息更丰富的对比视图, 进一步提升超图对齐的性能.
本文责任编委 陈松灿
Recommended by Associate Editor CHEN Songcan
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|