杨 军,博士,教授,主要研究方向为计算机图形学、遥感影像分析与处理、深度学习.E-mail:yangj@mail.lzjtu.cn.
作者简介:

薛又中,硕士研究生,主要研究方向为三维模型对应关系计算、深度学习.E-mail:1614429903@qq.com.
针对现有非等距模型簇对应关系计算方法准确率较低且泛化能力较差的问题,文中提出耦合映射的非等距三维模型簇对应关系计算方法.首先,使用DiffusionNet直接从三维模型中提取初始特征,获取具有鉴别能力的特征描述符.然后,使用描述符分别计算函数映射矩阵与逐点映射矩阵,并对两种矩阵分别施加结构正则化约束与执行Softmax归一化,得到最优耦合映射矩阵.最后,基于虚拟模板的模型簇匹配模块以模型初始特征作为输入,结合耦合映射构建的点分类器,直接预测模型与虚拟模型之间的匹配关系,通过Gumbel-Sinkhorn归一化,得到最终的非等距模型簇对应关系.实验表明,文中方法能有效处理非等距模型簇中的伪影噪声,对应关系计算的测地误差较小,结果较准确,泛化性较优.
YANG Jun, Ph.D., professor. His research interests include computer graphics, remote sensing image analysis and processing, and deep learning.
About Author:
XUE Youzhong, Master student. His research interests include 3D shape correspondence and deep learning.
To address the issues of low accuracy and poor generalization ability in existing non-isometric 3D shape collection correspondence calculation methods, a correspondence calculation method for non-isometric 3D shape collection via coupled maps is proposed. First, DiffusionNet is employed to directly extract initial features from the 3D shape, and thus discriminative feature descriptors are obtained. Then, functional maps matrix and point-to-point maps matrix are computed using these descriptors. Structural regularization constraints and softmax normalization are applied to both matrices, respectively, to obtain an optimal coupled maps matrix. Finally, a shape collection matching module based on a virtual template takes the initial model features as input and employs a point classifier constructed with the coupled maps to directly predict the correspondence between the shapes and the virtual templates. The final correspondence for the non-isometric shape collection is obtained through Gumbel-Sinkhorn normalization. Experimental results demonstrate that the proposed method effectively handles topological noise within non-isometric shapes, achieves low geodesic error in correspondence calculation, provides accurate results, and exhibits strong generalization ability.
三维模型之间的对应关系计算是计算机图形学与计算机视觉领域中一项重要的基础性研究工作, 旨在建立两个或多个三维模型之间的相似性或一致性映射关系, 广泛应用于自动驾驶、元宇宙、文物修复和电影动画等领域[1, 2, 3, 4].
研究者们最初聚焦于解决两个三维模型之间的稀疏对应问题, 逐步发展出一套适用于等距模型及近似等距模型的对应关系计算方法, 但针对非等距模型的对应关系计算仍面临诸多挑战.由于非等距模型间几何特征差异较大, 且对应关系计算不能遵循等距模型上对应两点的测地距离固定不变的计算准则[5], 因此, 当前多数基于深度学习的非等距模型的对应关系算法仍依赖人工制作的标志点进行辅助计算.这些标志点虽然提供真实值, 但质量参差不齐, 难以确保算法的准确性和泛化性.同时, 随着模型分析领域的快速发展和多样化三维模型数据集的不断涌现, 研究焦点也从计算两个模型的对应关系逐渐转向协同计算多个模型的对应关系, 这一转变带来更复杂的计算挑战, 包括需要确保多个模型之间的语义一致性和对应准确性.
理论上, 计算模型簇中所有模型对之间的对应关系就能解决模型簇的匹配问题, 然而由于这种方法基于两两对应, 多个模型间的映射难以满足“ 循环一致性” 准则[6].因此, 为了满足模型簇中的循环一致性, 一部分传统的模型簇算法通常使用参考的模板模型, 解决其它模型与模板模型的匹配问题, 但这种方法严重受制于模板模型的构造, 计算误差较大.
针对上述问题, 本文提出耦合映射的非等距三维模型簇对应关系计算方法.由模型初始特征直接计算函数映射与逐点映射, 利用函数映射与逐点映射之间的关系构建耦合映射损失, 将非等距模型的匹配流程构建为无监督的深度神经网络, 并以端到端的方式进行训练.使用虚拟模板直接预测多个模型间的对应关系, 通过Gumbel-Sinkhorn归一化, 保持模型簇循环一致性的同时避免模型顶点数的限制, 提高非等距模型簇对应的准确性, 消除拓扑噪声对对应关系结果的影响.
目前, 不论是非等距三维模型间的对应关系计算问题, 还是模型簇对应关系计算问题, 相应的解决方法主要分为基于函数映射的方法和基于深度学习的方法.
函数映射(Functional Maps, FM)[7]作为非刚性三维模型对应关系计算的里程碑算法之一, 创新性地将模型对应关系表示为低维矩阵, 在模型的函数空间中建立映射, 实现模型间的对应, 简化传统方法中逐点对应的计算过程.FM一经提出就得到研究者们的广泛关注.Ren等[8]在函数映射框架中引入方向保持约束, 并结合双射性和连续的ICP(Iterative Closest Point), 计算非等距模型间的对应关系, 但优化步骤复杂, 计算效率较低.Panine等[9]结合函数映射与标志点, 辅助计算非等距三维模型对应关系, 利用固有斯捷克洛夫(Steklov)算子的特征分解, 引入自适应标志点基, 实现共形映射的函数分解.然而, 由于对标志点的依赖, 算法无法在非等距三维模型之间实现全自动对应关系计算.Kim等[10]提出全自动计算非等距三维模型间对应关系算法, 基于面积保持和映射平滑性的混合权重, 将多个映射组合为加权混合映射, 确保非等距模型间对应关系的一致性, 然而无法保证大尺度形变的三维模型对应关系计算的准确性.
大量实际应用场景对计算多个三维模型之间对应关系的需求日益增长, 越来越多的学者提出针对三维模型簇的对应关系算法.由于函数映射在处理两个非刚性模型之间对应问题时的高效性, 一些研究人员将FM引入模型簇对应关系计算中.Huang等[11]提出异构模型簇一致性对应关系的计算框架.将每个模型与一个双线性函数空间关联, 并将模型之间的对应关系编码为函数空间之间的线性算子, 实现异构模型簇对应关系的协同一致计算.杨军等[12]使用DFPS(Dijkstra Farthest Point Sampling), 从三维模型簇中获取初始采样点, 结合函数映射理论与循环一致性约束, 将模型对的映射关系转化为模型簇的对应关系, 但在计算函数映射矩阵时依赖人工调参, 限制算法的泛化性.Huang等[13]提出Consistent ZoomOut, 将ZoomOut[14]扩展到多模型对应中, 通过多模型之间的相互映射以保证模型的循环一致性, 但对应关系的准确性依赖初始模型对之间映射矩阵的质量, 导致对应关系结果在很大程度上受初始化参数的影响, 难以实现自动计算.Gao等[15]提出IsoMuSh(Isometric Multi-shape Matching), 结合模板模型与多个模型之间的置换矩阵和函数映射矩阵, 实现模型簇对应关系计算, 但计算结果取决于初始化参数的优劣.
随着深度学习技术的飞速发展, 计算机视觉领域涌现出许多超越传统算法的新技术, 众多研究者开始尝试将深度学习应用于非等距三维模型对应关系的计算并取得显著效果.Litany等[16]将函数映射理论与深度学习结合, 提出FMNet, 优化特征描述符并计算函数映射矩阵, 建立对应关系, 但该方法依赖大量标注数据, 而获取准确的标注数据需要耗费大量时间和人力成本.为了解决此问题, Donati等[17]提出无监督非刚性三维模型对应关系算法, 无需标签数据, 直接使用函数映射对齐模型表面上的切线束, 使算法具有方向感知能力的同时促进映射的一致性.然而, 在处理几何结构差异较大的非等距模型时, 算法的对应关系准确率不高.Li等[18]结合FM与谱注意力机制, 提出无监督设置下的非等距模型对应关系计算网络, 但该网络需要为不同模型选择适合的频谱分辨率, 大幅增加计算时间, 并且非等距模型上的分辨率通常难以选择, 导致对应关系准确率下降.
深度学习由于在计算两个模型间对应关系时表现出的良好性能, 因此也被研究人员应用于三维模型簇对应关系的计算.杨军等[19]利用三维点云模型的特征信息优化FM矩阵, 提高非刚性变换的三维模型簇对应关系计算的准确率, 并通过无监督方式实现模型簇对应关系的协同计算.然而, 该方法在处理非等距三维模型簇时存在一定局限性.Groueix等[20]提出Deep Deformation Networks, 学习输入模型与模板模型之间的变换参数, 将对应问题转换为寻找多个模型与共同模板模型之间的匹配问题, 然而这种基于显式模板的方法受制于模板质量的好坏, 泛化性较差.Cao等[21]提出基于FM的无监督三维模型簇对应关系算法, 无需显式的模板模型, 使用全局分类器预测多模型之间的一致性对应关系, 然而分类器能预测模型的最大顶点数是固定的, 无法处理顶点数超过这个固定值的三维模型.Sun等[22]以深度函数映射[11]框架为基准, 结合谱域和空间域两种循环一致性约束, 提高非等距模型对应关系计算准确率, 但该方法在谱域和空间域上交替优化, 导致计算量过大.Groueix等[23]构建预测模型间的变形参数, 无需依赖模板模型, 并以循环一致性约束作为自监督信号训练网络.然而, 该方法的对应关系准确性依赖初始标注数据, 且构建的循环一致性损失可能会计算次优的模型簇对应关系.
综上所述, 现有方法解决非等距三维模型对应关系计算问题的效果仍有待提升, 大部分需要人工提前制作标志点, 效率较低.三维模型簇的对应关系算法大多局限在等距或近似等距模型中, 容易受到公共模板和初始化映射的影响, 计算准确率较低.
给定一对使用三角网格表示的源模型X和目标模型Y, 分别包含nX、nY个顶点, 计算两模型间函数映射的基本过程如下.
1)计算源模型X和目标模型Y的离散拉普拉斯-贝尔特拉米算子(Laplace Beltrami Operator, LBO)的前k个特征向量, 记为ΦX∈
2)分别计算源模型X和目标模型Y的特征描述符, 将描述符函数在基函数上的系数作为矩阵的列, 分别存储在基矩阵A、B中.
3)求解如下优化问题:
$\begin{aligned} \boldsymbol{C}_{\text {opt }}= & \arg \min _{\boldsymbol{C}} E_{\text {desc }}(\boldsymbol{C})+\alpha E_{\text {reg }}(\boldsymbol{C})= \\ & \arg \min _{\boldsymbol{C}}\|\boldsymbol{C} \boldsymbol{A}-\boldsymbol{B}\|^{2}+\alpha\left\|\boldsymbol{\Lambda}_{Y} \boldsymbol{C}-\boldsymbol{C} \boldsymbol{\Lambda}_{X}\right\|^{2}, \end{aligned}$
获得最优函数映射矩阵.其中:Edesc(C)表示描述符项, 旨在计算最优的函数映射矩阵C; 为了确保Copt的准确性, 添加正则化项Ereg(C)对描述符进行正则化约束; ΛX、ΛY分别表示X和Y的Laplace算子特征值的对角矩阵; α表示权重值.
4)将函数映射矩阵C恢复到点对点映射T.
两个非等距模型之间构建的函数映射具有双射性约束[24]、正交性约束[25]等性质, 这些良好的性质可约束得到质量更优的函数映射矩阵.
双射性是指对于给定一对模型, 从源模型到目标模型的函数映射矩阵和从目标模型到源模型的函数映射矩阵为互逆矩阵.利用这一性质, 通过两个矩阵的乘积趋于单位矩阵实现约束, 定义如下:
Ebij=‖ CXYCYX-I‖ 2+‖ CYXCXY-I‖ 2,
其中, CXY表示模型X到模型Y的函数映射矩阵, CYX表示模型Y到模型X的函数映射矩阵, I表示单位矩阵.
正交性约束是指对于给定一对模型, 当且仅当它们之间的函数映射矩阵正交时, 点到点的映射结果才能保持局部最优.该约束定义如下:
Eorth=‖
其中,
给定一个由三角网格构成的三维模型簇S, 对于任意模型对X和Y, 它们之间的点到点映射矩阵为:
Π XY∈{Π ∈{0, 1}
Π XY的大小为两模型顶点数的乘积nX×nY.该矩阵有两个约束条件:
1)Π
2)
这两个约束条件共同保证Π XY表示的点到点对应关系是双射的.
循环一致性是三维模型簇对应关系计算的理想属性, 即在理想情况下三维模型簇中任意两个模型间的映射结果等于两个模型之间匹配组合映射结果的乘积.以任意给定的三个模型X∈S, Y∈S, Z∈S为例, 它们构成一个三元组, 此时如果一个模型簇中所有三元组的循环一致性成立, 那么任何更高阶的匹配组合也都具有循环一致性.这是因为可结合多个三元组构造更高阶的匹配组合.因此, 模型间的循环一致性可显式表示为
Π XZ=Π XYΠ YZ.
以上约束在数学上通常表现为一个复杂的非凸优化问题, 因为涉及到多个模型之间的匹配关系, 这些关系通常不是线性的, 并且可能包含多个局部最优解.为了避免直接建模这种非凸的循环一致性约束, 文献[21]使用模型到虚拟模板模型的匹配表示, 避免显式建模三元组中的循环一致性约束, 不需要一个具体的网格模型, 而是假设存在一个模型, 使得模型簇S中的所有模型的每个点都有一个虚拟的对应点.具体来说, 将虚拟模型的顶点数表示为m, 则Γ X∈
Γ XY=Γ X
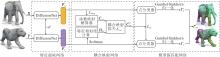
针对现有非等距三维模型簇对应关系计算方法准确率较低、泛化能力较差的问题, 本文结合耦合映射关联、深度函数映射理论与循环一致性约束, 构建耦合映射的非等距三维模型簇对应关系计算方法, 具体框架如图1所示.本文方法主要由三维模型特征提取网络、耦合映射网络、模型簇匹配网络组成.
本文方法具体实现步骤如下.
1)三维模型特征提取网络采用DiffusionNet[26], 通过孪生网络形式实现参数共享, 从原始的三维模型中学习特征描述符FX和FY.
2)将特征描述符输入耦合映射网络, 自动计算模型对耦合映射结果.首先, 由函数映射解算器计算CYX, 并使用Lfmap不断优化函数映射矩阵.然后, 计算特征FX和FY的相似度, 得到模型对逐点映射结果Π XY.最后, 使用耦合的无监督损失项Lcou将函数映射矩阵CYX与逐点映射矩阵Π XY关联, 得到耦合映射结果
3)结合耦合映射结果, 以无监督方式构建基于虚拟模板的模型簇匹配网络.基于虚拟模板的点分类器直接将两个模型的特征描述符作为输入, 通过Gumbel-Sinkhorn归一化[27]分别预测源模型X和目标模型Y到虚拟模型的匹配矩阵Γ X、Γ Y, 组合得到每个模型到虚拟模板模型的匹配矩阵Γ XY, 结合
三维模型对应关系计算的前提是能从原始几何模型中提取有意义的特征, 特别对于大尺度变形的三维模型, 更需要准确稳定的特征提取算法.本文采用DiffusionNet构建特征提取网络, 不仅可较好地处理非刚性变换的三维模型, 而且对于离散化表示的三维模型具有较强的鲁棒性.特征提取以共享参数的方式进行, 输出为每个模型的顶点特征描述符FX和FY.该特征描述符既适用于计算函数映射矩阵, 也适用于预测每个模型到虚拟模板之间的匹配矩阵.
DiffusionNet主要利用简单的可学习扩散层(DiffusionLayer, DL)替代模型表面上复杂且昂贵的卷积和池化操作, 基本原理如下.
首先, 在三维模型表面是连续且平滑的前提下, 将三维模型上的标量场信息的特征传播建模为热扩散模型, 使用热扩散方程表示为
Δ d(t)=
其中, d(t)表示在t时间内的热量分布, Δ 表示三维模型的LBO, 即热量在连续表面上的扩散过程.该扩散过程可通过热算子ht表示为
ht(d(0))=
其中d(0)为初始的热量分布.
然后, 对于由点云或网格等表示的离散状态下的三维模型, 为了对热扩散进行离散化, 将三维模型的LBO表示为一个稀疏矩阵:
L=W-1O=ΦΛΦTW , (3)
其中, W表示面积权重矩阵, O表示余切拉普拉斯矩阵, Φ表示保存特征函数的矩阵, Λ表示保存余切拉普拉斯矩阵特征值
Ht(D)=Φ
其中, ☉表示矩阵点乘, ΦTWD表示谱系数矩阵, 即不同频谱分量的权重,
最后, 计算模型曲面上的每个点的切平面特征信息的空间梯度内积, 与式(4)的结果馈送至每点的多层感知机(Multilayer Perceptron, MLP), 获得模型特征FX和FY.
耦合映射建立在函数映射和点对点映射的基础之上, 通过函数映射解算模块对其施加无监督加权正则化约束项, 从而增强全局映射属性, 优化得到的函数映射矩阵.加权正则化约束项为:
Lfmap=λbijEbij+λorthEorth.
通过大量实验, 得出各约束相应的权重值为:
λbij=1, λorth=1.
函数映射将模型间的对应关系表示为一个低阶矩阵, 要获得模型间的密集对应还需将函数映射转化为点对点映射, 然而, 函数映射无法保证与点对点映射的对应关系.虽然已有许多后处理技术用于恢复点对点映射, 但现有大多数方法都是解耦两种映射之间的关系, 影响对应关系计算的准确率.为了解决该问题, Ren等[28]提出EFMR(Effective Functional Map Refinement).受此启发, 本文构建能耦合两种映射关系的模块.
由于虚拟模板模型的顶点数量事先未知, 本文在文献[21]的基础上, 在计算点对点映射的过程中构建特征相似度计算模块.该模块利用模型上定义的特征FX、FY之间的相似性, 通过Softmax算子直接计算特征之间的相似度, 生成点对点映射的软对应矩阵:
$\boldsymbol{\Pi}_{X Y}=\operatorname{Softmax}\left(\frac{\boldsymbol{F}_{X} \boldsymbol{F}_{Y}^{\mathrm{T}}}{\boldsymbol{\tau}}\right) .$
其中:τ表示确定对应矩阵柔软度的比例因子, 设为0.06; Softmax算子应用于矩阵的每行, 确保对应矩阵的非负性和对应概率的总和为1.
由函数映射解算器通过特征描述符直接计算得到函数映射矩阵CYX, 通过函数映射与点对点映射之间的关系, 得到耦合函数映射:
其中,
Lcou=
Lcou用于衡量模型X和模型Y之间的函数映射与点对点映射之间的差异, 可获得精确的初始化成对模型之间的对应关系, 同时其优化后的结果也可用于模型簇对应关系的计算过程.
模型簇对应关系以两个模型之间的对应关系作为基础, 通过特征描述符为每个源模型X和目标模型Y分别预测其到虚拟模板模型的匹配矩阵Γ X、Γ Y, 则两模型上的每个点都需要准确分类为一个虚拟模板上的点, 并且一个虚拟类只能对应一个模型, 因此模型到虚拟模板模型的匹配矩阵Γ X和Γ Y必须都为双随机矩阵, 使得Γ X的行总和与Γ Y的列总和均为1, 即
$\begin{array}{l} \boldsymbol{\Gamma}_{X} \in\left\{\boldsymbol{\Gamma} \in\{0, 1\}^{n_{X} \times m}: \boldsymbol{\Gamma} \mathbf{1}_{m}=\mathbf{1}_{n_{X}}, \mathbf{1}_{n_{X}}^{\mathrm{T}} \boldsymbol{\Gamma} \leqslant \mathbf{1}_{m}^{\mathrm{T}}\right\}, \\ \boldsymbol{\Gamma}_{Y} \in\left\{\boldsymbol{\Gamma} \in\{0, 1\}^{m \times n_{Y}}: \boldsymbol{\Gamma} \mathbf{1}_{n_{Y}}=\mathbf{1}_{m}, \mathbf{1}_{m}^{\mathrm{T}} \boldsymbol{\Gamma} \leqslant \mathbf{1}_{n_{Y}}^{\mathrm{T}}\right\} . \end{array}$
Γ X和Γ Y的求解过程可理解为计算两个模型到虚拟模板模型之间特征向量的相似性度量函数矩阵, 可转化为一个线性规划问题, 本文引入Gumbel-
Sinkhorn归一化求解该问题.首先对初始的代价矩阵添加随机噪声, 然后使用Sinkhorn算法进行归一化, 最后得到两个双随机矩阵Γ X和Γ Y.
首先, 将特征描述符FX、FY作为初始代价矩阵.以特征描述符FX为例, 对其添加Gumbel噪声, 即
GX=-ln(-ln FX),
其中FX矩阵中的元素均是(0, 1)区间上均匀分布的随机数.通过这种方式生成的GX将作为一个噪声项添加到初始代价矩阵中, 形成一个新的随机代价矩阵:
F'X=FX+GX.
然后, 使用Sinkhorn算法对F'X的每行和每列进行归一化:
$\begin{array}{l} \boldsymbol{\Gamma}_{X}^{i}=\frac{\left(\boldsymbol{F}_{X}^{\prime}\right)_{i j}^{k}}{\sum_{j}\left(\boldsymbol{F}_{X}^{\prime}\right)_{i j}^{k}}, \\ \boldsymbol{\Gamma}_{X}^{j}=\frac{\left(\boldsymbol{F}_{X}^{\prime}\right)_{i j}^{k+1}}{\sum_{i}\left(\boldsymbol{F}_{X}^{\prime}\right)_{i j}^{k+1}}, \end{array}$
其中,
行和列归一化交替进行, 直至矩阵收敛, 得到一个逼近双随机矩阵的匹配矩阵Γ X.同理, 通过式(1)得到每个模型到虚拟模板的匹配矩阵Γ XY.
该过程确保每个模型上的点都被分类到虚拟模板上唯一的特征类, 并且不能多次选择特征类.
为了以无监督的方式训练基于虚拟模板的点分类器, 利用耦合映射矩阵与模型簇匹配矩阵构建一个分类损失函数:
Lcls=
用于衡量虚拟模板的点分类误差.Lcls衡量模型顶点特征与虚拟模板特征之间的匹配误差, 而无需任何真实对应关系的标注.
在Lcls损失函数中, 充分考虑初始映射对模型簇循环一致性的影响, 并且耦合映射和预测的点对点映射在训练期间得到进一步的改进.Lcls对于
综上所述, 总的损失函数为:
Ltotal=Lfmap+λcouLcou+λclsLcls,
其中, λcou、λcls表示加权超参数, 用于平衡正则化项的权重.
通过反向传播更新网络模型参数, 不断优化损失函数Ltotal, 迭代此过程直至网络收敛.
算法的编程语言为Python3.8, 运算平台为CUDA-Toolkit11, 深度学习框架为PyTorch-GPU, 版本号为1.12, 硬件为Core i9处理器和NVIDIA GeForce RTX3090 GPU(24 GB显存).
实验中设置批处理尺寸大小为1, 使用Adam(Adaptive Moment Estimation)优化器, 学习率为0.001, 采用端到端的方式训练, 训练过程最大迭代次数为10 000.经过大量实验优化, 得出总损失函数中各项损失的权重值, 分别设置为
λcou=1, λcls=0.01.
本文选择SMAL[29]、DEFORM THINGS4D-MAT-CHING[30](简记为DT4D)、SHREC'16 Topology[31]、SHREC'19[32]、FAUST[33]、SCAPE[34]、SHREC'16 Partial这7个三维模型数据集进行定性和定量实验.
SMAL数据集通过扫描动物雕像获取8类动物, 共49个三维模型.DT4D数据集是一个合成数据集, 包含56个动物类别和8个人体类别, 每个类别包含15~50个不同姿态的三维模型.SHREC'16 Topology数据集包含25个进行非刚性变换的模型, 存在大量的拓扑伪影和噪声.SHREC'19数据集来源于11个不同数据库上的44个原始人体模型, 共包括430个男性和女性人体模型.FAUST数据集由10个不同的高分辨率人体模型组成, 每个模型以30种不同的姿态进行扫描, 形成300个近等距三角网格模型.SCAPE数据集包含72个近等距的不同姿态的人体模型, 具有不同的网格分辨率和连通性.SHREC'16 Partial数据集包含8类共200个三维模型, 每类都有一个完整的模型, 用于匹配其它残缺模型.按照缺失形态的不同, 该数据集分为部件缺失的CUTS和表面存在孔洞的HOLES两个子集.
本文选择IsoMuSh[15]、文献[18]方法、文献[21]方法和文献[35]方法进行非等距模型簇对应关系计算的定性对比实验.由于文献[18]方法采用的谱注意力机制只能计算得到完整模型表面上的频谱信息, 不适用于残缺模型对应关系计算, 因此本文只与IsoMuSh、文献[21]方法和文献[35]方法进行残缺模型簇对应关系计算的定性对比实验.文献[35]方法是一种具有代表性的无监督对应关系计算方法, 能处理近等距、非等距和残缺模型等多种问题, 具有良好的泛化性能.为了确保公平对比, 上述方法的实验环境及参数设置均与本文方法相同.
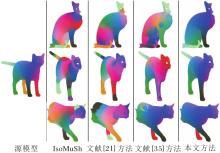
各方法在SMAL数据集上构建的非等距模型簇对应关系结果对比如图2所示, 图中使用颜色迁移方式(对应点使用相同的颜色)定性评估方法对应关系结果的准确性, 源模型为牛, 目标模型分别为狐狸、狗、狼和马.
 | 图2 各方法在SMAL数据集上构建的非等距模型簇对应关系结果对比Fig.2 Comparison of correspondence results in non-isometric shape collection constructed by different methods on SMAL dataset |
由图2可见, 文献[18]方法在非等距模型上只能计算出分辨率较低的函数映射矩阵, 出现小斑块状的映射错误.IsoMuSh利用模型簇构造公共模型作为模板模型, 但是构造非等距模型簇的公共模板模型是有难度的, 且方法受模型自身对称性影响, 在狐狸、狗、狼模型上除了头部能够正确对应以外, 其余身体部分呈现斑块状的大面积对应失真, 如在马模型中, 由于四条腿均出现不同程度的非刚性形变, 增加对应关系计算的难度, 导致算法失效.文献[21]方法是基于FM的深度学习方法, 整体对应结果大致正确, 但在狐狸、狗和马的腹部出现对应不连续的问题, 在狼模型上出现对称性匹配错误.文献[35]方法学习鲁棒的频谱特征以提高非等距模型对应关系计算准确率, 总体对应关系计算准确率较高, 在颈部及尾巴还是出现颜色渲染(对应)不平滑的现象.本文方法不仅能有效区分模型的对称特性, 解决模型自身对称性影响对应关系计算的问题, 而且对应的语义颜色信息相对最平滑自然, 能计算高质量的非等距模型簇对应关系.然而, 本文方法也存在一些问题, 在狐狸和狼模型的腹部及脖颈处的对应有些不平滑.
各方法在DT4D数据集上构建的非等距模型簇对应关系对比结果如图3所示, 图中源模型和目标模型都是类人的合成模型, 源模型为Crypto, 目标模型分别为Drake、Prisoner、Skeletonzombie和Ninja.
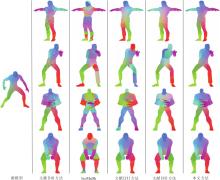 | 图3 各方法在DT4D数据集上构建的非等距模型簇对应关系结果对比Fig.3 Comparison of correspondence results in non-isometric shape collection constructed by different methods on DT4D dataset |
由图3可看出, 文献[18]方法在DT4D数据集上受模型自身对称性的影响较大, 在第1个模型和第3个模型的胳膊处出现错误对应.IsoMuSh对4个目标模型的对应结果有严重的误差, 算法很难处理非等距模型.文献[21]方法也受模型自身对称性的影响, 对应关系计算结果质量较低, 在第1个模型~第3个模型中均出现错误对应.文献[35]方法在第1个模型、第3个模型和第4个模型中都有不错的表现, 但还是存在对应部件映射不平滑的现象, 在第2个残缺模型中无法计算正确的对应关系结果, 这表明模型的对应关系算法无法像模型簇算法那样生成高质量的对应关系结果, 从而支持其它模型之间的协同一致对应计算.
由于本文方法在模型簇匹配中利用高质量的初始模型对及虚拟模板, 最大限度保证循环一致性, 以优异的初始化信息结合虚拟模板实现模型簇对应关系计算, 即使在一些特殊模型(如第2个目标模型)上, 其右边的断手和左边的完整手都可正确映射到源模型上, 由此说明本文方法在保持良好局部细节的同时对应关系误差最小.
各方法在SHREC'16 Topology数据集上构建的非等距三维模型簇对应关系结果对比如图4所示.SHREC'16 Topology数据集上的模型含有大量的拓扑伪影噪声, 是由模型的部分重叠造成拓扑合并与变形产生的, 如第1行中目标模型的小腿弯曲处以及手和脚踝的接触处, 第2行中手和小腿的接触处和跳跃状态下模型的双脚都是典型的区域重叠.
 | 图4 各方法在SHREC′16 Topology数据集上构建的非等距模型簇对应关系结果对比Fig.4 Comparison of correspondence results in non-isometric shape collection constructed by different methods on SHREC'16 Topology dataset |
由图4可看出, 文献[18]方法在4个目标模型的各部件上都无法产生正确的对应结果且方法易受模型自身对称性影响.IsoMuSh虽然可处理第1行左侧的模型中接触面积较小的拓扑噪声, 但当接触面积较大时对应关系计算误差较大, 第1行右侧模型的手与脚的接触处产生对应错误.文献[21]方法中大部分模型的对应关系可视化效果较平滑, 映射较连续, 但第1行右侧模型的拓扑伪影噪声处理失败, 手掌与脚映射到同一个地方.文献[35]方法中模型整体的对应关系准确率较高, 但是在模型某些局部映射不连续, 如第1列模型的手臂和大腿处.本文方法对所有模型的拓扑伪影噪声部件的对应关系计算大致正确, 对应误差最小, 由此说明其可更好地解决拓扑伪影噪声问题.但是, 本文方法也存在一些问题, 如第1行的两个模型的手臂处对应效果不平滑.
各方法在FAUST、SCAPE数据集上构建的模型簇对应关系结果对比如图5所示:FAUST数据集上源模型为tr_reg_085, 目标模型为te_reg_097; SCAPE数据集上源模型为mesh053, 目标模型为mesh071.如图所示, 文献[18]方法还是出现斑块状的映射错误.IsoMuSh受到模型自身对称性的影响, 在两个数据集上均出现左右对应错误.文献[21]方法在FAUST数据集上的映射效果是5种方法中最平滑的, 但在SCAPE数据集上模型胳膊上出现映射不连续的现象.文献[35]方法能计算质量较高的对应关系, 但也存在映射不平滑的现象, 两个模型胳膊与肩膀的连接处稍有映射不平滑.
 | 图5 各方法在2个数据集上构建模型簇对应关系结果对比Fig.5 Comparison of correspondence results in shape collection constructed by different methods on 2 datasets |
本文方法在两个数据集上可计算精确的对应关系, 有效避免模型自身的对称性带来的影响, 说明本文方法在近似等距模型上也具有良好效果.
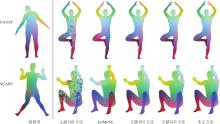
各方法在SHREC'16 Partial CUTS数据集上构建的残差模型簇对应关系结果对比如图6所示.
 | 图6 各方法在SHREC′16 Partial CUTS数据集上构建残缺模型簇对应关系结果对比Fig.6 Comparison of correspondence results in partial shape collection constructed by different methods on SHREC'16 Partial CUTS dataset |
CUTS数据集上模型主要表现为因切割导致的部件缺失.由于IsoMuSh基于模板模型进行模型簇对应关系计算, 需要为每个模型计算一个模板模型, 因此设定4个模型为一组以保证对应关系准确率和计算效率.为了公平起见, 对比方法也采用4个模型为一组进行模型簇对应关系计算.由图可以看出IsoMuSh在除了头部之外的其它部件上计算的对应关系结果都出现严重误差.文献[21]方法受模型自身对称性的影响, 对应关系计算结果质量较低, 在第2个模型和第3个模型腿部均出现错误对应.文献[35]方法也受模型自身对称性的影响, 无法准确计算各部件之间的对应关系, 在第2个模型和第3个模型头部及背部出现错误对应.本文方法能有效避免模型部件缺失和自身的对称性带来的影响, 对应关系准确率较高, 说明其在部件缺失的残缺模型上也有良好的性能.但是, 本文方法也存在一些问题, 在第1个模型和第2个模型中尾部及背部的映射不平滑.
各方法在SHREC'16 Partial HOLES数据集上构建的残差模型簇对应关系结果对比如图7所示.HOLES数据集主要包含表面存在各种孔洞的残缺模型.IsoMuSh和文献[21]方法均受模型自身对称性影响, 在第1行模型中左右胳膊处出现对应错误.文献[35]方法能计算质量较高的对应关系, 但也存在映射错误以及不平滑的现象, 在第1行模型的脚面处映射不平滑, 第2行第2个模型面部存在对应错误.本文方法的对应关系准确率较高, 但映射的连续性还有待提高, 在3个目标模型上左边胳膊处的映射不连续.
 | 图7 各方法在SHREC′16 Partial HOLES数据集上构建残缺模型簇对应关系结果对比Fig.7 Comparison of correspondence results in partial shape collection constructed by different methods on SHREC'16 Partial HOLES dataset |
各方法在SHREC'19、DT4D数据集上通过纹理迁移得到的对应关系结果如图8所示.在SHREC'19数据集上, 源模型为男人模型, 编号为33, 目标模型为女人模型, 编号为41; 在DT4D数据集上, 源模型为Shuffling096, 目标模型为Shuffling188.从图中局部细节的放大框上可看出, 文献[18]方法、IsoMuSh和文献[21]方法出现大面积的对应失真, 文献[35]方法虽然能计算高质量的映射结果, 但局部仍出现对应失真, 如模型的左侧大臂与肩膀连接处出现纹理扭曲, 而本文方法能生成高质量的映射结果, 纹理迁移效果平滑自然.
 | 图8 各方法在2个数据集上通过纹理迁移得到的对应关系结果对比Fig.8 Comparison of correspondence results obtained through texture transfer by different methods on 2 datasets |
而在DT4D数据集上, 卡通老鼠模型的头部与腹部相比其它模型更大, 且腹部区域的几何分布不规则, 在处理这些区域时, 需要在映射过程中保持模型间的一致性, 从而能更好地验证方法的映射质量与泛化性能.文献[18]方法和IsoMuSh总体映射误差很大, 纹理扭曲程度较大.文献[21]方法出现左右颠倒的现象, 说明受模型自身对称性影响, 在不同数据集上的泛化性较差.文献[35]方法整体对应质量较高, 但在模型的头部出现较轻微的纹理扭曲.本文方法映射的平滑性最好, 总体映射误差最小, 纹理迁移的结果最接近真实值, 映射质量最优.
本节在SMAL、DT4D、SHREC'16 Topology、SHR-EC'19、FAUST、SCAPE这6个数据集上定量评估各方法计算非等距三维模型簇对应关系的能力.
采用PBP(Princeton Benchmark Protocol)评估不同算法的对应关系准确率.假设y为目标模型Y上一点, x*和x分别为源模型X上与y的真实对应点和实际对应点, x与y的测地误差e(y)是点x与x*的测地距离在源模型X的面积平方根
e(y)=
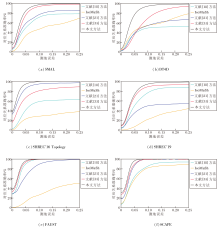
本文方法与文献[18]方法、IsoMuSh、文献[21]方法、文献[35]方法在各数据集上的测地误差曲线如图9所示.测地误差曲线是一种累积分布曲线, 用于反映算法对应关系的性能.由图9可见, 在SMAL数据集上, 本文方法最先到达100%的对应关系准确率, 且总体对应关系准确率始终最高.在DT4D数据集上, 5种方法在测地误差为0.25之前都未达到100%的准确率, 这是因为该数据是合成的类人数据集, 模型变形程度很大, 即使测地误差很大时也难以达到完全正确的对应.在SHREC'16 Topology数据集上, 本文方法与文献[21]方法的曲线很接近, 然而在测地误差小于0.1时本文方法具有一定优势, 且对应关系准确率也最高.在SHREC'19数据集上, 本文方法与文献[35]方法的曲线很接近, 但本文方法总体对应关系准确率最高.在FAUST、SCAPE两个近等距模型数据集上, 本文方法虽然与文献[35]方法的曲线较接近, 但是总体准确率最高, 在误差为0.1时在SCAPE数据集上达到100%的对应关系准确率, 这说明本文方法能有效处理模型采集过程中由真实扫描造成的伪影噪声.
为了进一步验证本文方法的泛化性, 与Iso-MuSh、文献[21]方法和文献[35]方法在SHREC'16 Partial CUTS、SHREC'16 Partial HOLES数据集上进行测地误差曲线的对比, 结果如图10所示.
在SHREC'16 Partial CUTS数据集上, 4种方法在测地误差为0.25之前都未达到100%的对应关系准确率, 这是因为在残缺模型簇对应关系计算过程中对应误差会被不断放大, 导致最终的对应关系准确率不高.
在SHREC'16 Partial HOELS数据集上, 虽然本文方法的对应关系准确率最高, 但是由于该数据集上存在许多残缺率较高的模型, 导致方法很难达到100%的对应关系准确率.
综上所述, 不论是在非等距数据集、近似等距数据集或残缺数据集上, 本文方法都更精确, 在不同数据集上的计算结果差异更小, 泛化性更强.
下面进一步评价这5种方法的对应关系计算结果, 对比各方法在6个数据集上的平均测地误差, 结果如表1所示, 表中黑体数字表示最优值.由表可见, 本文方法在6个数据集上平均测地误差均为最低, 与本文方法效果最相近的是文献[35]方法, 然而文献[35]方法仅限于计算两个模型之间的对应关系, 无法联合多个模型进行学习和协同一致计算, 导致泛化性能受限.本文方法能充分利用循环一致性准确计算三维模型簇对应关系, 具有较强的泛化性.
| 表1 各方法在6个数据集上的平均测地误差 Table 1 Average geodesic errors of different methods on 6 datasets |
为了验证本文方法的有效性, 在SMAL、DT4D、SHREC'16 Topology、SHREC'19数据集上进行消融实验, 结果如表2所示, 表中数据为平均测地误差, 黑体数字表示最优值.
| 表2 各模块消融实验结果 Table 2 Ablation experiment results of different modules |
由表2可看出, 在不包含Lcou和Gumbel-Sink-horn归一化设置下, 本文方法只有函数映射的结构正则化约束损失, 在计算每个模型到虚拟模板的匹配矩阵中采用Softmax归一化, 此时平均测地误差最高.这是因为单纯函数映射的结构正则化只适用于近似等距的数据集, 无法处理非等距模型的对应关系计算.Softmax归一化在含有拓扑伪影噪声的非等距数据集上的预测效果不佳, 无法正确将特征类别分类到虚拟模板上, 导致最终的对应关系准确率不高.在包含Lcou、不包含Gumbel-Sinkhorn归一化时, 平均测地误差有所下降, 这是因为耦合映射结合函数映射的结构正则化约束与基于特征相似度的点对点映射, 能有效应对非等距模型之间的特征差异, 计算较高精度的对应关系.在不包含Lcou、包含Gumbel-Sinkhorn归一化设置下, 平均测地误差也有一定程度的下降, 但是下降率少于包含耦合映射损失的, 这是因为Gumbel-Sinkhorn归一化在数据归一化时以添加噪声的方式, 提高模型簇匹配网络在噪声干扰下准确预测模型簇对应关系的能力, 并将点对点映射结果优化为双随机矩阵的形式, 主要解决非等距模型中包含的拓扑伪影噪声问题, 增强模型的泛化性.例如:在SHREC'16 Topology数据集上, 在只包含Gumbel-Sinkhorn归一化时, 相比初始设置, 平均测地误差下降0.028, 这表明其在处理拓扑伪影噪声时的有效性.同时包含两种设置时, 在4个数据集上平均测地误差达到最优值, 由此可看出, Lcou与Gumbel-Sinkhorn归一化之间能够相互促进, 因此本文方法能有效解决非等距模型上存在的对应准确率较低、泛化性能较差的问题.
本节对比本文方法与文献[18]方法、IsoMuSh、文献[21]方法、文献[35]方法在SMAL、DT4D、SHREC'16 Topology、SHREC'19、FAUST、SCAPE数据集上计算一组非等距模型簇(共5个模型)对应关系, 以及在SHREC'16 Partial数据集上计算一组残缺模型簇(共4个模型)对应关系所需的平均运行时间, 以此衡量各方法的计算效率.IsoMuSh需要其它算法提供初始化模型对的映射矩阵, 在实验中采用最简单快速的FM生成初始化参数, 因此该方法实际运行时间要加上FM计算的时间.
各方法运行时间对比如表3所示.由表可见, 文献[18]方法计算多分辨率的函数映射矩阵且结合细化算法, 运行时间随着模型顶点数的增加而延长.IsoMuSh基于显式模板进行计算, 交替优化置换矩阵和函数映射矩阵, 运行过程十分耗时.文献[21]方法、文献[35]方法和本文方法均为无监督方法.文献[21]方法通过全局分类器直接预测模型到模板的匹配结果, 运行时间最短.文献[35]方法同时优化函数映射和点对点映射, 也相对减少运行时间.本文方法的运行时间与模型顶点数相关, 使用点分类器直接生成点对点矩阵, 实际运行时间仅大于文献[21]方法.由此可看出, 本文方法不仅能获得高质量的非等距三维模型簇对应关系, 而且在计算效率上也具有优势.
| 表3 各方法在7个数据集上的运行时间对比 Table 3 Running time comparison of different methods on 7 datasets |
非刚性三维模型对应关系计算是计算机视觉与图形学中的一个核心问题, 而非等距模型簇对应关系计算更是该问题中的难点之一.本文提出耦合映射的非等距三维模型簇对应关系计算方法, 主要由三维模型特征提取网络、耦合映射网络和基于虚拟模板的模型簇匹配网络组成.三维模型特征提取网络主要采用DiffusionNet, 以孪生网络的形式实现参数共享, 从原始的三维模型中提取顶点特征描述符.耦合映射网络使用由DiffusionNet获取的模型的初始特征, 首先由函数映射解算出函数映射矩阵, 再利用Softmax生成点对点的软对应矩阵, 最后利用函数映射与点对点映射之间的关系, 计算耦合映射, 用于后续的模型簇匹配.基于虚拟模板的模型簇匹配网络以模型初始特征作为输入, 使用点分类器直接预测模型与虚拟模板之间的匹配矩阵, 分类损失由耦合映射与匹配矩阵之间的差异构建, 并使用Gumbel-Sinkhorn归一化得到最终的非等距模型簇对应关系结果.实验表明, 相比现有的三维模型簇对应关系方法和针对非等距模型对的对应关系方法, 本文方法在非等距模型簇上的对应关系准确率更高, 在不同数据集上的泛化性更强.如何解决更普遍的模型间对应关系问题以及模型在大尺度形变下的对应关系计算, 如残缺三维模型簇对应关系计算问题, 是今后需要继续研究的方向.
本文责任编委 徐 勇
Recommended by Associate Editor XU Yong
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|