李金海,博士,教授,主要研究方向为认知计算、粒计算、大数据分析、概念格、粗糙集.E-mail:jhlixjtu@163.com.
作者简介:

范 敏,博士,副教授,主要研究方向为数据挖掘、粗糙集、粒计算、社会网络分析.E-mail:fmkmust@163.com.

陈 瑞,硕士研究生,主要研究方向为网络形式背景、双层网络传染病模型.E-mail:chenrui1@stu.kust.edu.cn.
双层网络传染病模型已成为复杂网络动力学中的热点问题之一. 然而,现有研究忽略防疫意识和行为对传染病传播的影响,在遇到个体防疫行为差异较大时,难以反映实际的传染病传播情况.因此,文中从行为模式识别的角度出发,结合形式概念分析与微观马尔可夫链方法(Microscopic Markov Chain Approach, MMCA),提出基于网络形式背景的双层网络传染病模型.首先,定义双层网络形式背景、网络概念及其特征参数,建立形式概念分析与传染病模型的联系,不仅可描述双层网络中的概念及行为模式对应的特征参数,还可定义衰减因子,进一步借助MMCA实现上下层信息融合.然后,考虑大众媒体和政策干预对信息传播的影响,改进大众媒体函数和MMCA,并推导疫情爆发阈值.最后,通过仿真实验分析重要参数对疫情传播规模和疫情传播阈值的影响.
LI Jinhai, Ph.D., professor. His research interests include cognitive computing, granular computing, big data analysis, concept lattice and rough set.
About Author:
FAN Min, Ph.D., associate professor. Her research interests include data mining, rough set, granular computing and social network analysis.
CHEN RUI, Master student. His research interests include network formal context and two-layer network based epidemic model.
Two-layer network based epidemic models are one of the hot topics in complex network dynamics. However, existing studies overlook the impact of epidemic awareness and behavior on epidemic transmission. As a result, when there are significant differences in individual prevention behaviors, these models fail to accurately reflect real-world disease spread. To address this issue, a two-layer network based epidemic model is proposed by integrating formal concept analysis with the microscopic Markov chain approach(MMCA) from the perspective of behavioral pattern recognition. First, the two-layer network formal context, network concepts and their characteristic parameters are defined, and a bridge between formal concept analysis and epidemic models is established. This method not only describes the concepts and characteristic parameters corresponding to behavioral patterns in the two-layer network, but also defines a decay factor to further facilitate the integration of information across layers using MMCA. Second, the influence of mass media and policy interventions on information diffusion is taken into account, the mass media function and the MMCA model are improved, and the epidemic outbreak threshold is derived. Finally, simulation experiments are conducted to analyze the impact of several key parameters on epidemic spread scale and threshold.
1982年, 数学家Wille首次提出形式概念分析(Formal Concept Analysis, FCA)的理论[1, 2].FCA的主要目标是将数据构造成概念格, 以便更好地理解复杂数据的概念和层次.随着研究的深入, FCA被证明是一种强大的数据分析工具, 广泛应用于机器学习[3, 4]、数据挖掘[5, 6]、概念认知[7, 8]、复杂网络分析[9, 10]等领域.FCA还与模糊集[11, 12]、粒计算[13, 14]、三支决策[15, 16]等理论结合, 为各种场景提供复杂全面的解决方案.此外, FCA在信息融合[17, 18]、冲突分析[19]和样例分类[20]方面也取得一些成果.
近年来, FCA与复杂网络分析的结合逐渐成为一个新的研究方向[21, 22, 23, 24, 25].该研究主要将图论中的邻接矩阵与形式背景进行信息融合, 构建一种称为网络形式背景的新型数据框架, 并在此基础上研究具体应用系统的数据分析和建模方法.Fan等[21]提出NFC3WD(Network Formal Context of Three-Way De- cision), 并应用于COVID-19诊断实例中, 验证该方法的有效性.范敏等[22]将网络形式背景应用于推荐系统, 提出变精度弱概念集, 诱导出包含较多信息量的邻域, 并在此基础上提出基于因果力的邻域推荐算法.进一步地, Fan等[23]结合FCA与图卷积神经网络, 提出FECCM(Fuzzy Entropy Causality Classifi-cation Method), 引入模糊熵与因果力, 显著提升图数据的分类性能.Yan等[24]在全局网络和局部网络连通时分别定义粒概念, 研究这些概念在网络形式背景下的动态更新机制.上述研究表明, 网络形式背景理论及其方法在与复杂网络拓扑结构和个体属性特征进行信息融合、数据分析和建模方面具有显著优势.
传染病的传播对人类健康和社会发展构成重大威胁, 历史上曾经多次爆发大规模疫情, 如SARS、埃博拉以及近年的COVID-19.如何理解传染病的传播机制, 探索控制与阻止其扩散的方法, 已成为亟需解决的重要问题之一[26, 27].随着网络和信息技术的发展, 信息的传播速度显著加快, 而信息的传播对传染病的控制也起到重要的作用.双层网络的引入为传染病模型的研究带来新的思路[28, 29, 30, 31, 32, 33, 34, 35, 36, 37].从信息融合的观点来看, 新的挑战在于如何研究传染病扩散模型中信息传播模型与传染病传播模型的融合问题.
Granell等[29]构建一个双层复杂网络, 上层表示信息传播层, 下层表示传染病传播层, 用于模拟信息扩散和疾病传播, 并借助微观马尔科夫动力学方法(Microscopic Markov Chain Approach, MMCA)建立动力学方程.实验表明, 疾病传播阈值与信息传播层中获得信息个体的密度密切相关.在此基础上, 为了进一步模拟疫情中大众媒体对信息扩散的促进作用, Granell等[30]又引入大众媒体, 深入探讨大众媒体对传染病的影响.为了更好地模拟疫情期间不同类型的信息传播, Wang等[31]讨论积极预防信息和消极预防信息下的疫情传播行为, 证实积极预防信息和消极预防信息的共存可大幅降低疫情爆发规模, 并影响导致疫情大规模扩散的临界阈值.此外, 随着COVID-19的爆发, 双层网络传染病模型为疫情的防控提供更好的解释.He等[32]模拟新冠肺炎的传播方式, 构建双层传染病模型, 强调信息扩散对疾病传播的影响.随后Ma等[35]提出UAU-SEIR(Un-aware Aware Unaware Susceptible Exposed Infected Re-covered), 进一步引入大众媒体对信息传播的影响, 指出通过大众媒体传播信息可有效抑制疫情蔓延并提高疫情传播阈值.
随着此领域研究的不断深入, 学者们开始多方面关注不同个体属性、信息传播拓扑结构及信息类型对疫情扩散的影响, 提出多种改进模型[38, 39, 40, 41].Wang等[38]在多层网络中引入无症状感染者与自发意识传播机制, 发现无症状感染会削弱防疫意识的传播, 影响疫情发展.Zhou等[39]研究带有社区结构的虚拟接触网络, 发现提升信息传播速率或降低信息遗忘率有助于遏制疫情扩散.Feng等[40]进一步探讨信息传播层节点的拓扑结构对疫情扩散的作用, 表明高中心度个体的防疫行为可有效抑制疾病传播.Hu等[41]研究不同个体对疫情信息的接受度如何影响疾病传播, 并揭示防疫信息传播对疫情控制的关键作用.上述研究主要从信息扩散影响疫情传播的角度出发, 通过MMCA建模, 探究信息与疫情传播之间的关系, 并未考虑疫情期间个体防疫行为的差异性, 即忽略防疫行为的异质性.
行为模式识别通过分析个体或群体的行为数据, 识别潜在的规律和模式, 被广泛应用于心理学、社会学及计算机科学领域[42, 43, 44], 核心技术包括聚类分析、支持向量机(Support Vector Machine, SVM)和深度学习, 在智能监控、个性化推荐和情感分析等领域取得显著成果[45, 46].因此, 结合行为模式的属性特征与网络结构下的信息传播, 构造一个随机衰减因子, 融入信息传播对疾病传播影响的分析中, 为多层网络上的疫情传播建模提供新的视角.
在双层网络传染病模型中, 研究大众媒体对传染病传播的影响也是热点问题之一.针对大众媒体影响的研究主要分为两种.第一种方法是在信息传播层中加入大众媒体对信息传播的影响, 通常是引入一个固定的概率值, 概率越大表示大众媒体的影响越大[30, 35], 即在模拟疫情传播的过程中, 大众媒体对信息传播的影响保持不变.然而, 这种方法显然不符合实际情况.第二种方法认为大众媒体对信息传播层的影响是一个动态过程, 会随着事件热度的变化而变化, 并非一个固定值.因此, Wang等[47]在双层网络传染病模型中引入大众媒体对信息层的影响随传染个体比例变化的模型, 模拟大众媒体的动态影响.此外, Ma等[35]提出UAU-SEIR, 认为潜伏状态的节点具有感染性, 状态转移过程以一定的概率逐一转化, 但是实际上, 受COVID-19传播过程的启发, 即使个体转化到潜伏状态, 也不一定会被感染, 同样可能以一定的概率转回易感状态.
基于上述讨论, 本文提出基于网络形式背景的双层网络传染病模型.首先, 定义多层网络形式背景, 给出其特殊形式— — 双层网络形式背景, 刻画多层网络下个体行为与疫情传播的相互作用.然后, 给出双层网络概念及其特征参数, 描述行为模式特征, 在不同的子网络中, 可得到各项防疫行为的参数.进一步得到防疫衰减因子, 并嵌入下层的MMCA状态转移方程中, 使上下层的信息融合, 从而精细刻画信息传播如何动态影响个体防疫策略, 并进一步作用于疫情扩散过程.最后, 提出改进的MMCA并验证其有效性.针对SEIR(Susceptible Exposed Infected Recovered)中的潜伏期因素, 引入潜伏期人群比例, 改进大众媒体函数和MMCA中潜伏期转移概率, 更精确描述疫情中随机衰减因子及大众媒体对疫情传播规模和疫情传播阈值的影响.优化后的模型更具普适性, 适用于不同疫情场景下的信息-传染病传播研究.
双层网络中信息表征和信息融合是一个重要的研究课题.本文结合形式概念分析与复杂网络分析, 通过双层对象和属性概念, 讨论信息表征和信息融合.首先提出沟通二者的一个数据框架, 然后通过网络概念、网络概念的特征值进行模式识别, 得到不同参数, 进一步融合上下两层信息.
定义1[1] 三元组(U, A, I)称为形式背景.其中:
U={x1, x2, …, xn}
表示非空有限对象集,
A={a1, a2, …, am}
表示非空有限属性集, I表示笛卡儿积U×A上的二元关系.约定(x, a)∈I表示对象x拥有属性a.(x, a)∉I表示对象x不拥有属性a.为了从形式背景(U, A, I)中诱导概念, 需进一步给出如下算子:
$\begin{array}{l} \forall X \subseteq U, B \subseteq A, \\ X^{*}=\{a \in A \mid \forall x \in X, (x, a) \in I\}, \\ B^{*}=\{x \in U \mid \forall a \in B, (x, a) \in I\}, \end{array}$
其中, X*表示X中所有对象共同拥有的属性组成的集合, B*表示拥有B中所有属性的对象组成的集合.
定义2[21] 四元组(U, M, A, I)为网络形式背景.其中:
U={x1, x2, …, xn}
表示非空有限个体集;
M={M1, M2, …, Mk}
表示网络的结构矩阵, M1表示网络的一阶邻接矩阵, Mk表示网络的k阶邻接矩阵;
A={a1, a2, …, am}
表示非空有限属性集;
I={I1, I2, …, Ik, Ik+1},
I1, I2, …, Ik表示笛卡儿积U×U上的二元关系, Ik+1表示笛卡儿积U×A上的二元关系.约定(xi, xj)∈Il表示个体xi、xj是l阶邻接的, (xi, aj)∈Ik+1表示个体xi拥有属性aj.
表1为一个网络形式背景示例.
| 表1 网络形式背景示例 Table 1 Example for formal context network |
下面定义多层网络形式背景, 再给出其一般形式— — 双层网络形式背景, 并得到对应的网络概念和特征参数.
定义3 四元组(U, LM, LA, I)称为多层复合网络形式背景.其中:
U={x1, x2, …, xn},
xi表示不同网络层上的节点, 并且不同网络层上的节点表示同一个对象;
LM={
表示网络的邻接矩阵,
LA={
表示不同网络层上节点的非空属性集合,
表示第s层网络上节点的属性, 1≤s≤m,
I={I1, I2, …, In, I
I1, I2, …, In表示笛卡尔积U×U上的二元关系, I
约定(xi, xj)∈Is表示个体xi、xj在第s层网络上是一阶邻接的.
表2为一个多层复合网络形式背景示例.
| 表2 多层复合网络形式背景示例 Table 2 Example for multi-layer multiplex network formal context |
进一步给出双层复合网络形式背景的定义.
定义4 四元组(U, M, B, A, I)称为双层复合网络形式背景.其中:
U={x1, x2, …, xn},
xi表示不同网络层上的节点; M={MB, MA}表示网络的邻接矩阵, MB表示第一层网络的一阶邻接矩阵, MA表示第二层网络的一阶邻接矩阵;
B={B1, B2, …, Bm}
表示第一层网络个体的非空属性集合, bij表示个体xi在第一层中的第j个属性Bj下的取值, 0≤bij≤1, 0<j<m1;
A={A1, A2, …, Am}
表示第二层网络个体的非空属性集合, aij表示个体xi在第二层中的第j个属性Aj下的取值, 0≤aij≤1, 0<j<m2;
I={I1, I2, I3, I4},
I1、I2表示笛卡尔积U×U上的二元关系, I3表示笛卡尔积U×B上的二元关系, I4表示笛卡尔积U×A上的二元关系.约定(xi, xj)∈I1表示个体xi、xj在第一层网络上是邻接的, (xi, xj)∈I2表示个体xi、xj在第二层网络上是邻接的.
表3为一个双层复合网络形式背景示例.
| 表3 双层复合网络形式背景示例 Table 3 Example for two-layer multiplex network formal context |
定义5 设有双层复合网络形式背景(U, M, B, A, I), X⊆U, ∀ xi∈X, |X|表示X中的个体数量, 记” |X|=n.X中个体拥有共同属性个数记为m, 则X在第一层网络个体的属性均值
Bμ(X)=
X在第一层网络个体的属性方差
$B_{\sigma^{2}}(X)=\frac{1}{m} \sum_{j=1}^{m} \sum_{i=1}^{n}\left|b_{i j}-\sum_{i=1}^{n} \frac{b_{i j}}{n}\right| .$
同理, X在第二层网络个体的属性均值
$A_{\mu}(X)=\frac{1}{m n} \sum_{j=1}^{m} \sum_{i=1}^{n} a_{i j}$
X在第二层网络个体的属性方差
$A_{\sigma^{2}}(X)=\frac{1}{m} \sum_{j=1}^{m} \sum_{i=1}^{n}\left|a_{i j}-\sum_{i=1}^{n} \frac{a_{i j}}{n}\right| .$
定义6 在双层复合网络形式背景中, 网络概念
$\begin{array}{l} \left(X, X^{*A}, X^{*B}, \left(A_{\mu}(X), A_{\sigma^{2}}(X), B_{\mu}(X), B_{\sigma^{2}}(X)\right), \right. \left.\quad m^{A}, m^{B}\right) \end{array}$
称为双层对象网络概念.其中:X*A表示子网络X中共同具有第二层中的属性, X*B表示子网络X中共同具有第一层中的属性; Bμ(X)、
表示网络概念内部的差异程度, N表示网络中个体个数, L表示网络中属性个数, cD(i)表示个体xi的个体度, cDmax表示邻接节点中最大的个体度, 概念平均度
表示网络概念在网络中的相对重要性, 同理可得到mA的表达方式, mB、mA统称为第二类特征参数.
$m_{2}^{B}=\frac{1}{(N-1)(L+1)} \sum_{i=1}^{N} c_{D}(i), $
称为双层复合网络属性概念.其中:(B, A)*表示在第一层中拥有A中属性且在第二层中拥有B中属性的个体; Bμ(B, A)*、
基于上述的网络概念及其特征值, 可对其进行特征提取和分类, 识别传染病网络中不同的行为模式和特征群体.这一过程有助于防疫中将网络划分为若干子网络(或社区), 并采取相应措施, 确定最优的防疫策略和参数.该过程还能更精准刻画个体及群体间的差异性, 进一步合理分配防疫的人力物力.下面以例1进行说明.
例1 设有双层复合传染病网络, 下层表示疾病传播层, 上层表示信息传播层.从这个双层复合传染病网络中可得到一个双层复合网络形式背景.上下层网络邻接矩阵如表4所示, 个体对应属性取值如表5所示.在表中:
U={x1, x2…, x10}
表示传染病网络中的10个节点, 也就是实际的个体; MB、MA分别表示上下层的一阶邻接矩阵; A表示个体在下层中表现的传染病症状, 记为a1, a2, a3, a4, 分别表示无症状、咳嗽、发烧、咽痛; B表示信息传播层中个体采取的防疫行为, 也就是在疫情期间不同信念驱使下采取的措施, 记为b1, b2, b3, b4, b5, b6, 分别表示避免与他人接触、穿防护服、戴口罩、居家隔离、勤洗手、保持社交距离.考虑在疫情期间, 下层属性都是确定性事件, 可用0、1表示.然而在讨论个体采取的防疫行为时, 采取的防疫行为是一个概率值, 并不仅仅是采取或不采取.例如:对于戴口罩这项防疫行为, 个体虽然认识到疫情的危害且认为戴口罩是有用的, 但可能因为一些原因忘记戴口罩, 所以本文使用概率描述这一现象会更符合实际情况.值得注意的是, 在信息传播过程中, 受到影响的是个体的防疫意识.不同的个体在获取和理解这些信息后, 基于自身的认知水平和态度, 采取不同的防疫行为, 最终表现出各自独特的行为模式.因此, 信息的传播与个体行为的变化之间存在密切关联.
| 表4 例1对应的双层复合网络形式背景的邻接矩阵 Table 4 Adjacency matrix of two-layer multiplex network formal context corresponding to example 1 |
| 表5 例1对应的双层复合网络形式背景的属性取值 Table 5 Attribute values of two-layer multiplex network formal context corresponding to example 1 |
在该双层复合网络形式背景中, X*B表示对象集X在上层共同采取的防疫行为, X*A表示对象集X表现出来的相同症状.B*表示都采取B中防疫行为的个体, A*表示都具有A中症状的个体.
$\begin{array}{l} \left(X, X^{*A}, X^{*B}, \left(A_{\mu}(X), A_{\sigma^{2}}(X), B_{\mu}(X), B_{\sigma^{2}}(X)\right), \right. \left.\quad m^{A}, m^{B}\right) \end{array}$
描述对象集X中的对象共同采取的防疫行为X*B, 并且都表现出相同症状.给出这个网络概念在不同网络层中的第一类特征参数
(Aμ(X),
和第二类特征参数mB、mA.第一类特征参数中Bμ(X)、
令
X1={x1, x2, x5, x6},
得到网络对象概念:
({x1, x2, x5, x6}, ({a1}, {b1, b2, b4}), (1, 0),
(0.608, 1.492), (0.07, 0.333), (0.03, 0.316)).
令
X2={3, 7, 9, 10},
得到网络对象概念:
({x3, x7, x9, x10}, ({a3, a4, a5}, {b3, b4, b5}), (1, 0),
(0.567, 1.7), (0.125, 0.541), (0.104, 0.313)).
令
B0=b2, b3, A0=a1,
得到如下的属性概念:
(({b2, b3}, {a1}), {1, 2, 6, 8}, (0.675, 0.45),
(1, 0), (0.013, 0.238), (0.04, 0.24)).
由对象集X1、X2中的网络对象概念, 可获得不同对象集的上下层网络结构参数以及各对象的防疫行为参数, 如共同防疫行为的均值和方差等, 同时还可获得病症相关参数.借助这些参数, 能有效描述不同群体间防疫行为的差异, 并揭示群体内个体在防疫措施上的差异.在属性概念中, 同样可得到相应的网络结构参数和属性参数.通过对这些特征参数进行模式识别, 能更精准地描述群体和个体间的防疫行为差异.
由于COVID-19已过去两年, 若通过问卷调查获取个体在疫情期间的防疫行为数据, 可能会受到回忆偏差和主观性误差的影响.因此, 本文在理论建模时, 假设个体的防疫行为是一个服从正态分布的随机变量.具体而言, 个体防疫严格程度(即衰减因子)被建模为均值为μ、方差为σ2的正态分布.由于正态分布具有可加性, 所有个体的防疫行为严格度之和仍然服从正态分布, 可由定义5和定义6计算其期望和方差, 并进一步传递到下层传染病传播模型中, 进行仿真实验.
在双层网络传染病模型的构建中, 个体的防疫行为(如佩戴口罩、社交距离、居家隔离等)具有随机性, 而且个体间防疫行为既有中心趋势又有差异性, 所以假设个体的防疫行为服从正态分布, 如下理由支持该假设.
1)行为科学与社会心理学支持.在公共卫生危机中, 人群的防疫行为通常受到从众效应(Con-formity Effect)[48]和个体风险感知[49]的双重影响, 使得大多数人的防疫行为接近某个均值, 少数人执行极端严格或极端松懈的防疫措施, 这种趋势在许多社会行为研究中表现为正态分布.
2)流行病学中的典型观察.在实际疫情期间, 个体防疫措施的执行程度往往呈现中心化趋势, 即大部分人会选择“ 适度防疫” , 而少数人采取极端严格的措施(如完全隔离)或完全忽视防疫(如拒绝戴口罩).这一模式在COVID-19数据分析中已有观察.例如:IHME COVID-19 Health Service Utilization Fore-casting团队[50]对美国不同地区的口罩佩戴率分析表明, 大多数人采取的防疫措施在某个均值附近波动, 符合正态分布的特征.
3)经验数据的支持.在以往的传染病研究中, 个体的防疫行为往往服从钟形分布, 例如:Rogers等[51]提出Diffusion of Innovations, 指出在应对新兴健康威胁时, 人群可被分为极端谨慎者(Innova-tors)、大多数适应者(Early/Late Majority)和极端忽视者(Laggards), 这一模式也符合正态分布的假设.
综上所述, 本文假设个体防疫行为服从正态分布, 具有行为科学、流行病学和经验数据的支持.这一假设有助于描述个体防疫行为的变异性, 更好地反映群体层面的防疫策略影响.
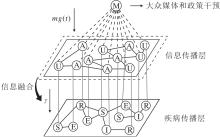
本文提出的基于网络形式背景的双层网络传染病模型由疾病传播层和信息传播层组成, 结构如图1所示.在图中, 下层表示通过身体接触或面对面交流传播的物理接触网络, 上层表示通过大众媒体、微信、QQ等信息平台传播的传染病信息网络, 通过个体的防疫行为特征反映上层的防疫信息或意识的传播.值得注意的是, 双层网络中的每个节点都对应实际生活中的一个个体, 表示该个体既参与疾病的物理传播, 也参与信息的传播.此外, 物理接触层和信息传播层均为无向无权网络, 下文分别称为下层网络和上层网络.
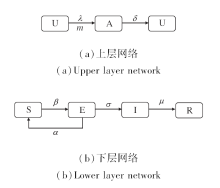
在上层网络中, 本文采用UAU(Unaware-Aware-Unaware), 如图2(a)所示.上层网络的个体分为两类:有意识个体(Aware, A)和无意识个体(Unaware, U).有意识个体掌握有关传染病的信息, 会采取防疫行为避免感染, 并主动向其邻居传播信息, 使无意识个体转变为有意识个体.相反, 无意识个体缺乏相关信息, 不会采取防疫行为.为了更贴近防疫期间的实际情况, 大众媒体和不同时段的政策干预都会在某种程度上转化为对人们防疫行为的影响.因此, 本文引入大众媒体和政策干预对信息传播层的影响.进一步地, 大众媒体的报道力度以及政策干预力度会随着传染病的传播情况而变化.例如:当感染人数增加时, 媒体的报道频率和强度会增加, 政策干预力度也是如此, 进而促使更多人意识到疾病的存在; 反之, 感染人数减少时, 相关报道也会减少.为此, 本文引入一个时变函数mg(t), 描述大众媒体和政策干预力度对信息传播层的影响, 定义如下:
mg(t)=
其中:m0表示没有传染病时, 大众媒体传递相关信息的基本概率; ρ(t)表示t时刻传播性个体在群体中的比例, 在本文模型中, 考虑到潜伏状态的个体也具有感染性, 故将文献[47]中大众媒体函数中的
ρ(t)=ρI(t)
修改为
ρ(t)=ρE(t)+ρI(t);
K≥ 0表示大众媒体和政策干预力度对信息层的影响大小, K越大, 表明个体在疫情期间受大众媒体和政策干预力度影响的程度越大.
在下层网络中, 考虑到新冠疫情中存在潜伏者, 它的比例影响疫情传播规模和疫情传播阈值, 所以, 本文采用SEIR, 将所有个体分为4类:易感者(Susceptible, S)、潜伏者(Exposed, E)、感染者(In-fected, I)、康复者(Recovered, R), 如图2(b)所示.在SEIR中, 假设E状态(潜伏期)和I状态(感染期)的个体均具有感染性, 可以以一定概率使其邻居中的S状态个体感染并转变为E状态.传统模型通常假设所有处于潜伏期的个体最终都会进入感染状态, 但在现实中, 并非所有的潜伏者都会发展为感染者.例如:在COVID-19期间的无症状感染者, 当发现个体具有与传染病匹配的症状时, 并不一定确诊为COVID-19, 也有可能是普通感冒.因此, 本文对E状态的转化过程进行调整, 更准确地反映这一实际情况, 具体为潜伏期状态的个体会以一定的概率转变为I状态, 也可能转化为S状态, 这样可更全面描述不同状态之间的转化.I状态的个体经过治疗以后, 以一定的概率康复为R状态, 同时假设康复后的个体不会再次被感染.
由于上下层的个体表示同一个个体, 且上层网络与下层网络相互影响, 本文结合上下层的状态, 共有8种状态:US(无意识易感者)、AS(有意识易感者)、UE(无意识潜伏者)、AE(有意识潜伏者)、UI(无意识感染者)、AI(有意识感染者)、UR(无意识康复者)、AR(有意识康复者).以往的研究大多假设感染状态的个体会立即意识到自己感染, 在信息层中变为有意识状态, 因此忽略UI状态.然而, 在现实中, 仍存在UI状态.因此, 在本文模型中, 保留UI状态, 并设定其会以概率κ转化为AI状态.
在本文模型中, 上层网络中处于A状态的个体会以概率λ使其邻居中U状态个体转化为A状态, 同时以概率δ遗忘传染病信息并转变为U状态.考虑到大众传媒对信息传播及政策干预的影响, U状态的个体在接收到传染病相关报道以后, 会以概率m转化为A状态.
在上层网络中, U状态个体转变为A状态的途径有3种:1)受到邻居中有意识个体的影响; 2)受到大众媒体及政策干预的影响; 3)在下层网络中感染疾病.
在下层网络中, 处于S状态的个体在接触E状态和I状态的个体以后, 以概率β转化为E状态.E状态表示潜伏期, 经过一段时间的观察, 部分个体以概率σ转化为I状态, 而另一部分未感染的个体以概率α回到S状态.I状态的个体经过治疗以后, 以概率 μ康复并转变为R状态.
为了区分有意识个体和无意识个体在下层网络中感染疾病时的不同感染概率, 本文引入衰减因子γ0, 0<γ0<1, 有意识个体的感染概率为βA, 无意识个体的感染概率为βU, 则
βA=γ0βU.
因此, γ0越小, βA也越小, 说明这些个体能更好地防范感染.设
所以
然而, 由第1节可知, 个体之间采取的防疫行为是有差异的.在下层传染病传播网络中, 这些措施的差异会直接影响个体的感染概率.因此, 尽管双层网络形式背景能描述这种异质性特征, 但由于缺乏大量的真实数据支撑个体防护行为的异质性, 无法直接在模型中使用基于双层网络形式背景的属性数据.
为了在实验中模拟双层网络形式背景中描述的个体行为的异质性, 本文假设γ为服从正态分布的随机变量, 即
$\gamma \sim N\left(\mu_{\gamma}, \sigma_{\gamma}^{2}\right), $
其中, μγ为γ的均值,
γi~N(μγ,
所以
βA=γiβU.
这种设置可近似表达双层网络形式背景描述的个体防疫行为的异质性, 该异质性是由于实际个体对信息理解和响应不同而产生的.
在传染病传播动力学的研究中, 疫情传播阈值是一个重要指标.近年来, 许多学者一直在研究计算疫情传播阈值的方法.Gó mez等[52, 53]提出MMCA, 已被广泛应用于求解双层网络中信息与传染病传播交互模型.MMCA具有求解传播动态精度高、可显示个体感染信息等优点.因此, 本文使用MMCA对本文模型进行理论分析, 并计算疫情传播阈值.
上层网络和下层网络的邻接矩阵如下所示:
MB=(bij)n×n, MA=(aij)n×n,
网络中每个节点表示实际生活中的一个个体.如果bij=1, 表示在上层网络中个体xi、xj有连边, 即它们之间可以进行消息传播; 如果bij=0, 表示这两个个体之间无信息往来.同理, 如果aij=1, 表示在下层网络中个体xi、xj有连边, 即它们之间有接触; 如果aij=0, 表示这两个个体之间无接触.在t时刻, 任意个体xi都以一个确定的概率处于第2节提到的8个状态之一, 记作
在上层网络中, 在t时刻, 无意识个体xi不被有意识的邻居告知相关消息的概率, 即个体xi未转变成有意识个体的概率为:
ri(t)=
其中,
表示对节点i的邻居进行计算.
在下层网络中, 在t时刻, 个体xi在上层中处于无意识状态、在下层中处于S状态, 且不被其邻居感染成潜伏态个体的概率为:
在t时刻, 个体xi在上层中处于有意识状态、在下层中处于S状态, 且不被其邻居感染成潜伏态个体的概率为:
$\begin{aligned} q_{i}^{\mathrm{A}}(t)= & \prod_{j}\left\{1-b_{j i}\left[p_{j}^{\mathrm{UE}}(t)+p_{j}^{\mathrm{AE}}(t)+\right.\right. \\ & \left.\left.p_{j}^{\mathrm{UI}}(t)+p_{j}^{\mathrm{AI}}(t)\right] \beta^{\mathrm{A}}\right\} . \end{aligned}$(4)
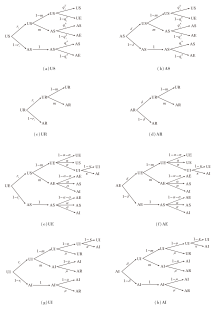
把每个时间步分为4个连续的过程:个体间的信息传播(UAU过程), 大众媒体和政策干预导致的信息传播(在动力学方程中记为m), 传染病传播过程(SEIR过程), UI状态转化为AI状态的过程.在这8个状态之间构建起马尔可夫状态转移概率树, 表示状态之间的转化, 具体如图3所示.
根据式(2)~式(4)和马尔可夫状态转移概率树, 得到各个状态的MMCA方程如下:
其中, t和t+1表示节点从当前时间步到下一个时间步的状态演化.在任意时间步MMCA方程都要满足下面的归一化条件, 即
基于3.1节改进的MMCA方程, 下面使用稳态时的MMCA方程推导得到疫情传播阈值.
定理1 给定基于双层网络UAU-SEIR的信息-传染病传播模型的动力学方程(如式(5)~式(12)所示), 本文模型中疫情传播阈值为:
βC=
其中, Λmax(H)表示矩阵
H=(
的最大特征值.
证明 当系统达到稳态时, 即t足够大的时候, 满足
其中,
对于SEIR, 在疫情传播阈值附近, 潜伏个体和感染个体比例约等于0, 故假设
$P_{i}^{\mathrm{E}}=P_{i}^{\mathrm{AE}}+P_{i}^{\mathrm{UE}}=\epsilon_{i} \ll 1 .$
由于系统中考虑UI状态, 所以
ρI=
即
所以式(9)和式(10)相加后得
由于$P_{i}^{\mathrm{E}}=\epsilon_{i}$, 故
$P_{i}^{\mathrm{I}}=\frac{\sigma}{\mu} P_{i}^{\mathrm{E}}=\frac{\sigma}{\mu} \epsilon_{i}, $
所以式(3)和式(4)可表示为
$q_{i}^{\mathrm{U}} \approx 1-\left(1+\frac{\sigma}{\mu}\right) \beta^{\mathrm{U}} \sum_{j} b_{j i} \epsilon_{j}=1-\left(1+\frac{\sigma}{\mu}\right) \eta_{i}, $
$\begin{aligned} q_{i}^{A}(t) \approx & 1-\left(1+\frac{\sigma}{\mu}\right) \beta^{\mathrm{A}} \sum_{j} b_{j i} \epsilon_{j}= \\ & 1-\left(1+\frac{\sigma}{\mu}\right) \gamma_{0} \eta_{i}, \end{aligned}$
其中
$\eta_{i}=\beta^{\mathrm{U}} \sum_{j} b_{j i} \epsilon_{j} .$
进一步地, 式(7)和式(8)相加后得
$\begin{aligned} P_{i}^{\mathrm{E}}= & (1-\sigma-\alpha) P_{i}^{\mathrm{E}}+ \\ & P_{i}^{\mathrm{US}}\left\{r_{i}(1-m)\left(1-q_{i}^{\mathrm{U}}\right)+\right. \\ & {\left.\left[1-(1-m) r_{i}\right]\left(1-q_{i}^{\mathrm{A}}\right)\right\}+ } \\ & P_{i}^{\mathrm{AS}}\left\{\delta(1-m)\left(1-q_{i}^{\mathrm{U}}\right)+\right. \\ & {\left.[1-(1-m) \delta]\left(1-q_{i}^{\mathrm{A}}\right)\right\} . } \end{aligned}$(13)
把
$\begin{aligned} \epsilon_{i}= & (1-\sigma-\alpha) \epsilon_{i}+ \\ & p_{i}^{\mathrm{US}}\left\{r_{i}(1-m)\left(1+\frac{\sigma}{\mu}\right) \eta_{i}+\right. \\ & {\left.\left[1-(1-m) r_{i}\right]\left(1+\frac{\sigma}{\mu}\right) \gamma_{0} \eta_{i}\right\}+ } \\ & p_{i}^{\mathrm{AS}}\left\{\delta(1-m)\left(1+\frac{\sigma}{\mu}\right) \eta_{i}+\right. \\ & {\left.[1-(1-m) \delta]\left(1+\frac{\sigma}{\mu}\right) \gamma_{0} \eta_{i}\right\} . } \end{aligned}$(14)
在疫情传播阈值附近,
$\begin{array}{l} P_{i}^{\mathrm{UE}} \rightarrow 0, P_{i}^{\mathrm{AE}} \rightarrow 0, P_{i}^{\mathrm{AI}} \rightarrow 0, \\ P_{i}^{\mathrm{UI}} \rightarrow 0, P_{i}^{\mathrm{UR}} \rightarrow 0, P_{i}^{\mathrm{AR}} \rightarrow 0, \end{array}$
可得
故
因此, 式(14)可写为
$\begin{aligned} \epsilon_{i}= & (1-\sigma-\alpha) \epsilon_{i}+ \\ & {\left[P_{i}^{\mathrm{U}} r_{i}(1-m)+P_{i}^{\mathrm{A}}(1-m)\right]\left(1+\frac{\sigma}{\mu}\right) \eta_{i}+} \\ & \left\{P_{i}^{\mathrm{U}}\left[1-(1-m) r_{i}\right]+P_{i}^{\mathrm{A}}[1-(1-m) \delta]\right\} \cdot \\ & \left(1+\frac{\sigma}{\mu}\right) \gamma_{0} \eta_{i} . \end{aligned}$(15)
在稳定状态时, 忽略高阶项O($\epsilon_{i}$), 根据式(5)和式(6)可得
$\begin{array}{l} P_{i}^{\mathrm{U}}=P_{i}^{\mathrm{U}} r_{i}(1-m)+P_{i}^{\mathrm{A}} \delta(1-m), \\ P_{i}^{\mathrm{A}}=P_{i}^{\mathrm{U}}\left[1-(1-m) r_{i}\right]+P_{i}^{\mathrm{A}}[1-(1-m) \delta] . \end{array}$
由于
把上式代入式(15), 可得
$\begin{aligned} \epsilon_{i}= & (1-\sigma-\alpha) \epsilon_{i}+P_{i}^{\mathrm{U}}\left(1+\frac{\sigma}{\mu}\right) \eta_{i}+ P_{i}^{\mathrm{A}}\left(1+\frac{\sigma}{\mu}\right) \gamma_{0} \eta_{i} . \end{aligned}$
在上述公式中, γ0为一个固定值, 表示所有个体防疫行为的严格程度相同.为了更真实反映实际情况, 设γ为一个服从正态分布的随机变量, 即γ~N(μγ,
$\begin{aligned} \epsilon_{i}= & (1-\sigma-\alpha) \epsilon_{i}+ \\ & P_{i}^{\mathrm{U}}\left(1+\frac{\sigma}{\mu}\right) \eta_{i}+P_{i}^{\mathrm{A}}\left(1+\frac{\sigma}{\mu}\right) \gamma_{i} \eta_{i}, \end{aligned}$(16)
所以, 由式(16), 得
$\frac{\mu(\sigma+\alpha)}{\beta(\mu+\sigma)} \epsilon_{i}=\sum_{j}\left(P_{i}^{\mathrm{U}}+\gamma_{i} P_{i}^{\mathrm{A}}\right) \epsilon_{j} b_{j i} .$(17)
进一步地, 式(17)可转化为线性方程组的形式:
$\sum_{j}\left[\left(P_{i}^{\mathrm{U}}+\gamma_{i} P_{i}^{\mathrm{A}}\right) b_{j i}-\frac{\mu(\sigma+\alpha)}{\beta(\mu+\sigma)} \alpha_{j i}\right] \epsilon_{j}=0, $(18)
其中, γi表示个体xi的个体异质化参数.αij表示单位矩阵中的元素, 定义矩阵H中元素
hij=(
故式(18)可用矩阵的形式表示, 即
$\boldsymbol{H} \boldsymbol{\epsilon}=\frac{(\sigma+\alpha) \mu}{\beta(\sigma+\mu)} \boldsymbol{\epsilon}, $
其中
$\boldsymbol{\epsilon}=\left(\epsilon_{1}, \epsilon_{2}, \cdots\right)^{\mathrm{T}}$
在这种情况下, 由于γi是从正态分布中随机抽取的, hij也表现出随机性.
显然, H的特征值等于
疫情传播阈值βC为上式最小值, 因此
βC=
其中Λmax(H)表示H中最大特征值.
在H中元素
hij=(
由定理1可知, βC与下层的传播参数α、σ、 μ, 以及下层网络的拓扑结构有关.
本文模型通过整合个体防疫意识、信息传播和疾病传播, 能有效描述防疫措施对疫情传播的影响.然而, 为了更准确地理解模型的适用范围与局限性, 进行如下讨论.
3.3.1 适用性
本文模型的适用性主要体现在如下方面.
1)适用于个体防疫行为具有异质性的场景.本文采用正态分布假设建模个体防疫行为的严格程度(衰减因子), 从而能刻画不同个体在防疫意识上的差异.对于缺乏强制性防疫政策(如疫情后期政府主要依赖个人防护决策)的情境, 本文模型可更准确模拟个体差异对疫情传播的影响.
2)适用于信息传播在疫情防控中起关键作用的场景.通过构建双层网络, 本文模型可描述大众媒体、社交媒体和政策干预对个体防疫意识的影响.对于受信息传播影响较大的传染病(如COVID-19), 模型能反映信息扩散在防疫策略中的作用.
3)适用于不同防疫政策的评估.通过引入媒体政策函数, 本文模型可量化政策对疫情传播规模的影响, 从而为政策制定者提供理论支持.
3.3.2 局限性
尽管本文模型在描述疫情传播机制方面具有一定优势, 但仍存在如下局限性.
1)正态分布假设的局限性.本文假设个体防疫行为的严格程度服从正态分布, 但在如下情况下, 该假设可能不成立:当强制性防疫政策(如封锁、强制佩戴口罩)在疫情初期或信息传播不足时, 个体行为可能呈现偏态分布, 即部分人高度警惕, 而大多数人缺乏防疫意识, 或相反的情况.
2)未考虑不同类型的信息传播效应.本文主要考虑大众媒体和政策干预对疫情传播的影响, 但现实中信息传播的复杂性可能导致不同的影响:(1)谣言和虚假信息可能会降低个体防疫意识, 使部分人放松防疫措施的执行; (2)科学宣传和医疗建议可能会增强个体防疫意识, 提高防疫措施执行率.今后可考虑引入多层信息传播模型, 更全面描述信息传播对疫情防控的作用.
3)未考虑疫苗接种等长期防控因素.本文主要关注短期疫情传播过程, 但在长期防控中, 疫苗接种、免疫力衰减和病毒变异等因素可能会影响疫情传播:(1)疫苗接种率上升可能会降低疫情传播阈值, 使疫情消退; (2)病毒变异可能会降低疫苗的有效性, 改变疾病传播的动力学机制.
疫情传播规模是衡量传染病扩散范围和严重程度的一个关键指标, 通过传播规模的分析, 能直观了解疫情对群体的影响程度, 进而评估不同防控措施的有效性.疫情传播阈值是传染病控制的一个关键点, 当传染病的基本再生数低于该阈值时, 疫情逐渐消失, 一旦超过该阈值, 疫情迅速扩散.因此, 研究疫情传播规模和疫情传播阈值对于制定科学的防控策略具有重要意义, 可帮助判断疫情的临界条件, 进而指导防控策略的设计和实施.所以接下来本文将围绕疫情传播规模和疫情传播阈值进行实验.
本文采用与文献[31]、文献[34]~文献[37]相同的方法, 即用蒙特卡洛(Monte Carlo, MC)方法与本文改进的MMCA进行对比实验, 得到它们之间的相对误差.
信息传播层网络和疾病传播层网络设置如下:1)在物理接触层中, 采用包含1 000个节点的Bara-bási-Albert(BA)无标度网络.它从M0=10个随机连接的节点开始, 每增加一个新节点, 就向现有节点增加M=5条边.2)在信息传播层中, 使用与物理接触层相同的网络, 但增加400个额外的随机链路(与之前的不重叠).
为了更好地描述传染病的传播过程, 在UAU-SEIR中, 稳态时康复者(R状态)个体比例是衡量传染病传播的重要参数, 可描述传染病的传播趋势.所以, 定义稳态时康复者个体比例为ρR.在MC中,
ρR=
其中, NR表示稳态时处于R状态节点的总数, 即
NR=NAR+NUR,
N表示总的节点个数.
在改进的MMCA中,
ρR=
其中
此外, 可用同样的方法表示ρA、 ρU、 ρS、 ρE、 ρI.需要注意的是, 本文的每组实验结果都是经过50次独立实验取平均值之后得到的.
本节中疫情传播规模依据式(5)~式(12)描述的MMCA演化过程计算得到.这些方程通过刻画不同个体状态的转化概率, 动态模拟疫情传播过程中个体间的相互作用, 最终反映疫情在全局层面上的传播规模.
4.1.1 衰减因子γ0
为了验证改进的MMCA的有效性, 与MC进行对比实验, 对比二者在不同衰减因子γ0下疫情传播规模.实验参数设置如下:
λ=0.6, δ=0.2, σ=0.5, μ=0.5, α=0.3,
κ=0.8, m0=0.3, K=5, γ0=0, 0.2, 0.8.
该部分实验结果依据式(5)~式(12)计算得到.
不同γ0下感染概率β对康复个体比例ρR的影响如图4所示.
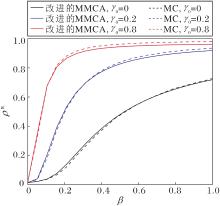 | 图4 γ0不同时感染概率对康复个体比例的影响Fig.4 Effect of infection rates with different γ0 on proportion of recovered individuals |
由图4可得如下结论.
1)疫情传播规模随感染概率的变化而变化.随着感染概率β的增加, 康复者个体比例ρR呈现上升趋势, 这表明更高的感染概率会导致更大的疫情传播规模.
2)改进的MMCA与MC的一致性.对于每个γ0, MMCA的结果与MC模拟结果高度一致, 说明本文改进的MMCA在预测疫情传播规模方面具有良好的准确性.同时, 计算3种不同γ0下改进的MMCA和MC的相对误差, 分别为0.21%, 0.65%, 0.89%, 即两者之间的相对误差极小, 由此验证改进的MMCA的有效性.
3)衰减因子对传播规模的影响.较小的γ0值意味着更严格的防疫行为, 当γ0=0时, 对应的
达到最大值, 表示个体采取最严格的防疫行为.此时, ρR值最低, 说明疫情传播受到有效抑制.较大的γ0值意味着防疫行为减弱, 随着γ0增大(如γ0=0.8),
因此, 衰减因子γ0的变化直接反映防疫行为的有效性:较小的γ0值(更严格的防疫行为)有助于抑制疫情的传播.
基于上述讨论, 在后续实验中主要采用改进后的MMCA进行分析和研究, 充分显示其在预测疫情传播规模方面的高效性和准确性.
4.1.2 γ~N(μγ,
由图4可看出, 不同的衰减因子γ0对疫情传播影响显著不同.基于双层网络形式背景的分析, 个体在采取防疫行为上存在明显差异, 即每个个体的衰减因子γi并不相同.为了模拟这种个体间的异质性, 将γ设定为服从正态分布的随机变量, 即
γ~N(μγ,
实验相关参数设置如下:
λ=0.6, δ=0.2, σ=0.5, μ=0.5,
α=0.3, κ=0.8, m0=0.3, K=10.
对于服从正态分布的γ值, 均值μγ=0.3.该部分实验结果依据式(5)~式(12)计算得到.
首先, 对比γ为固定值和γ服从正态分布时疫情传播规模的差异, 结果如图5(a)所示, 图中方差
 | 图5 γ不同时感染概率对康复个体比例的影响Fig.5 Effect of infection rates with different γ on proportion of recovered individuals |
其次, 为了深入理解这一现象, 进一步研究不同正态分布方差下的疫情传播情况, 结果如图5(b)所示, 图中方差
因此, 在制定防控策略时, 需要考虑个体防疫行为的差异性, 采取措施减少这种异质性, 提高疫情防控的整体效果.
4.1.3 时变函数mg(t)
本节探究时变函数mg(t)中不同关键参数对疫情传播规模的影响.mg(t)的主要参数包括初始传播概率m0和大众媒体对疫情的响应能力与政策干预力度K, 分别表示媒体传播的初始强度和政策干预力度.通过调整参数, 分析大众媒体在疫情不同阶段对传播规模的动态影响.相关参数设置如下:
λ=0.6, δ=0.2, σ=0.6, μ=0.5,
α=0.2, κ=0.8, γ0=0.
该部分实验结果依据式(1)、式(5)~式(12)计算得到.
定义m0=0, 0.3, 0.5, 0.8, K=0, 3, 5, m0、K不同时感染概率对康复个体比例的影响如图6所示.由图6(a)可看出, m0=0时, 图中三条线重合, 因为此时mg(t)恒为0, 即在没有大众媒体影响的情况下, K不会对信息传播产生影响.相比(b)~(d), 该情况下疫情传播规模明显大于有大众媒体影响的情况, 表明大众媒体在抑制疫情传播方面起到显著作用.由图6(b)~(d)可知, 随着K值的增大, 疫情传播规模逐渐减小, 这说明当大众媒体对疫情的响应能力和政策干预力度增强时, 信息传播的抑制效果变强, 有效减少疫情的扩散规模.值得注意的是, 在感染概率β较低时, K值对疫情传播规模的影响相对较小, 各曲线之间的差异不明显.然而, 随着β的增大, K值对疫情传播规模的影响变得显著.尤其是在β较大时, 不同K值对应的疫情传播规模差异更明显, K越大, 传播规模越小.这表明, 在高传播率情况下, 增强大众媒体对疫情的响应能力和政策干预力度(即增大K值)对于控制疫情扩散具有重要作用.
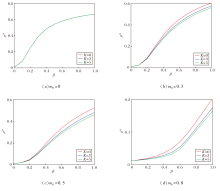 | 图6 m0、K不同时感染概率对康复个体比例的影响Fig.6 Effect of infection rates with different m0 and K on proportion of recovered individuals |
为了进一步探讨函数mg(t)中ρ(t)的动态变化对疫情传播规模的影响, 对比在mg(t)中考虑潜伏期状态(即同时考虑E状态和I状态, ρ(t)=ρE(t)+ρI(t))与不考虑潜伏期状态(仅考虑I状态, ρ(t)=ρI(t))对疫情传播规模的影响.实验相关参数设置如下:
λ=0.6, δ=0.2, σ=0.3, μ=0.5,
α=0.2, γ0=0, κ=0.8, K=5.
该部分实验结果依据式(5)~式(12)计算得到.
定义m0=0.3, 0.8, m0、 ρ(t)变化时感染概率对康复个体比例的影响如图7所示.由图可观察到, 当感染概率β较小时, 在考虑与不考虑潜伏期状态的模型之间, 疫情传播规模差异并不明显.这表明在低感染概率下, 潜伏期个体对疫情传播规模的影响相对较小.当β增至0.2以上时, 考虑E状态的模型显示出更低的疫情传播规模.这说明在高感染概率条件下, 潜伏期个体对疫情传播规模起到显著作用.这一结果反映如下现实情况:潜伏期个体虽然尚未表现出明显症状, 但如果忽略他们的存在, 可能会导致更多的个体被传染, 加剧疫情扩散.
 | 图7 m0、 ρ(t)不同时感染概率对康复个体比例的影响Fig.7 Effect of infection rates with different m0 and ρ(t) on proportion of recovered individuals |
因此, 在实际疫情防控中, 不仅要关注显性感染者, 还应加强对潜伏期个体的检测和隔离措施.通过及时识别和隔离潜伏期个体, 可有效降低疫情扩散速度, 提升整体防控效果, 即全面监测和快速反应在疫情防控中具有重要作用.
4.1.4 潜伏期转化速度(α、σ)
本节实验旨在探讨潜伏期节点转化参数α和σ对疫情传播规模的影响, 进一步揭示潜伏期节点对疫情控制的关键作用.实验参数设置如下:
λ=0.6, δ=0.2, μ=0.5, κ=0.8,
m0=0.3, K=5, γ0=0.3.
该部分实验结果依据式(5)~式(12)计算得到.
固定σ=0.3, α=0.2, 0.4, 0.6, 此时感染概率对康复个体比例的影响如图8(a)所示.由图可知, 随着α值的增加, 疫情传播规模显著减小.这表明, 当潜伏期转化为S状态的速率增大(即α值增大)时, 潜伏期节点以一定概率返回S状态, 从而有效减缓疫情的传播规模.
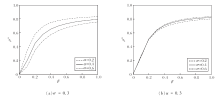 | 图8 α、σ不同时感染概率对康复个体比例的影响Fig.8 Effect of infection rates with different α and σ on proportion of recovered individuals |
固定α=0.3, σ=0.2, 0.4, 0.6, 此时感染概率对康复个体比例的影响如图8(b)所示.由图可知, 随着σ值的增大, 疫情传播规模逐渐增大, 尽管不同σ值之间的差异并不显著.这表明节点从E状态转化为I状态的概率增大, 导致疫情传播规模在一定程度上上升.
由上述实验可得, 尽管增加E状态向S状态转移的概率以及降低E状态向I状态转化的概率均能减小疫情传播规模, 但增加E状态向S状态转移的概率在控制疫情传播方面效果更显著.
进一步地, 探讨潜伏期节点转化参数α+σ与疫情传播规模之间的关系.α+σ值不同时感染概率对康复个体比例的影响如图9所示.
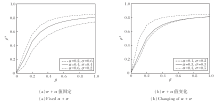 | 图9 α+σ不同时感染概率对康复个体比例的影响Fig.9 Effect of infection probability with varying α+σ on proportion of recovered individuals |
由图9(a)可知, 当α+σ值相同时, 不同的α和σ组合会对疫情传播规模产生不同的影响, 当α较大(即潜伏期节点更可能从E状态转化为S状态)时, 疫情传播规模较小.这说明在α+σ相同时α的增加起到抑制疫情传播的作用.
由图9(b)可知, 随着α的增加, 对应的疫情传播规模逐渐减小.这与之前的实验结论一致, 进一步验证在潜伏期动态控制中, 增大潜伏期节点向健康状态转化的概率(即提高α), 并降低其向感染状态转化的概率(即减少σ), 是有效控制疫情传播的重要手段之一.
综上所述, 通过对潜伏期转化参数α和σ的分析可得出如下结论.潜伏期节点从E状态转化为健康状态(S)的概率越高(α越大), 疫情传播规模越小; 在潜伏期转化参数的组合影响下, 提高α并降低σ, 可显著降低疫情传播规模.因此, 实际疫情防控中应注重对潜伏期节点的检测与隔离, 优化转化路径, 尤其是加强对潜伏期个体的管理, 减少其感染他人的可能性, 从而有效遏制疫情扩散.
本文模型通过式(19)计算得出疫情传播阈值βC, 其大小受信息传播速率、个体防疫行为、媒体作用等因素的影响, 下面将探究这些参数与疫情传播阈值之间的关系.
4.2.1 潜伏期转化速度(α+σ)
本节探讨α+σ对疫情传播阈值βC的影响.实验固定如下关键参数以确保结果的可比性:
γ0=0, m0=0, κ=0.8, K=5.
通过这些参数的设置, 实验能更聚焦于探讨α+σ对疫情传播阈值βC的影响.该部分实验结果依据式(19)计算得到.
定义α+σ=0.3, 0.6, 0.9, 其对βC的影响如图10所示.固定δ=0.1, μ=0.6, 信息传播率λ对βC的影响如图10(a)所示.由图可知, 随着λ的增加, βC迅速增长并趋于稳定, 较大的α+σ值对应更高的βC, 这表明增强信息传播能有效降低疫情控制的难度.固定λ=0.6, δ=0.1, 康复率 μ对βC的影响如图10(b)所示, 由图可知, 较高的μ值显著提高βC, 说明加快康复速度对疫情控制至关重要.固定μ=0.6, λ=0.6, 遗忘概率δ对βC的影响如图10(c)所示.
由图10可知, 随着δ的增加, βC逐渐降低, 说明信息遗忘降低疫情防控的效果.
总之, 较大的α+σ值在这3种情况下均对应更高的疫情传播阈值, 这说明潜伏期转化速度在疫情防控中具有重要作用.
4.2.2 大众媒体m0与防疫行为的异质性(μγ、σγ)
首先, 探讨m0=0.1, 0.3, 0.6时, 衰减因子γ0和疫情传播阈值βC之间的关系.实验中相关参数设置如下:
λ=0.6, δ=0.1, σ=0.3,
μ=0.6, κ=0.8, K=5.
该部分实验结果依据式(19)计算得到.
m0不同时, γ0对βC的影响如图11所示.
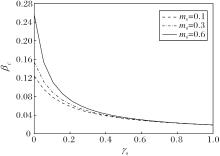 | 图11 m0不同时衰减因子对疫情传播阈值的影响Fig.11 Effect of decay factors with different m0 on epidemic spread threshold |
由图11可知, 当m0值较大时, 对应的βC也较大, 表明大众媒体在信息传播中的作用能显著提高疫情传播阈值、延缓疫情扩散.然而, 随着γ0的增大(
下面进一步分析γ的异质性对疫情传播阈值βC的影响, 实验中相关参数设置如下:
λ=0.5, δ=0.1, α=0.1, σ=0.3,
μ=0.6, κ=1, m0=0.3, K=5,
μγ∈[0, 0.3], σγ∈[0, 0.3].
该部分实验结果依据式(19)计算得到.
不同μγ、
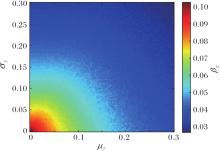 | 图12 个体防护措施异质性对疫情传播阈值的影响Fig.12 Effect of heterogeneity in individual protective measures on epidemic spread threshold |
由图12可知, 当μγ越小(γ*越大), 即个体采取的防疫行为越严格, 并且防疫行为的差异性(
因此, 本文提出如下建议:在疫情防控中, 应加强大众媒体信息传播和政策干预的力度, 提高疫情传播阈值, 同时, 需要鼓励个体采取严格且统一的防疫行为, 特别是在防疫行为差异性较小时, 能显著提高疫情传播阈值, 减少疫情传播风险.这些措施对于有效控制疫情扩散具有重要意义.
本文结合形式概念分析理论与传染病模型, 提出基于网络形式背景的双层网络传染病模型.研究重点是如何将个体防疫行为信息融入传染病传播模型中.为此, 定义双层网络形式背景、网络概念及其特征参数, 并构造防疫行为衰减因子, 通过MMCA实现上下层信息的耦合.此外, 改进大众媒体函数及MMCA, 更精确描述信息传播对疫情扩散的动态影响, 并推导疫情传播阈值.实验表明, 大众媒体的传播力度和政策干预程度、个体防疫行为的差异性以及潜伏期个体的识别速度等因素, 均显著影响疫情传播规模和疫情传播阈值, 由此验证信息传播与疫情控制的复杂相互作用.
本文模型在一定程度上模拟双层网络中传染病传播的实际情况, 仍存在改进空间.首先, 模型中的下层网络结构是静态的, 而现实中个体之间的物理接触网络往往是动态变化的, 因此, 今后可考虑将下层静态网络扩展为动态网络, 更准确模拟疫情传播的动态过程.其次, 由于缺乏上层信息传播层的实际数据, 本文的参数设置主要依赖假设和仿真实验, 如果能在疫情期间利用真实的社交网络数据进行拟合和验证, 将有助于进一步提升模型的预测精度, 从而更有效指导实际疫情防控策略的制定.
本文责任编委 王士同
Recommended by Associate Editor WANG Shitong
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
|
| [47] |
|
| [48] |
|
| [49] |
|
| [50] |
|
| [51] |
|
| [52] |
|
| [53] |
|