李永强,博士,副教授,主要研究方向为强化学习、控制理论.E-mail:yqli@zjut.edu.cn.
作者简介:

胡 磊,硕士研究生,主要研究方向为深度强化学习、智能博弈.E-mail:211122030031@zjut.edu.cn.

冯 宇,博士,教授,主要研究方向为多智能体博弈、深度强化学习、最优与鲁棒控制.E-mail:yfeng@zjut.cedu.cn.

冯远静,博士,教授,主要研究方向为医学影像处理、机器视觉、脑机智能.E-mail:fyjing@zjut.edu.cn.
强化学习中的策略梯度方法因其通用性而广泛应用于连续决策问题,但高梯度方差导致的低样本利用率始终制约其实际应用性能.文中提出海森辅助的概率策略梯度方法(Hessian Aided Probabilistic Policy Gradient Method, HAPPG),在PAGE(Probabilistic Gradient Estimator)的基础上设计双模态梯度估计机制:在大批量估计中增加历史动量,限制梯度下降的波动性;在小批量估计中引入策略参数空间的二阶曲率信息,构建基于海森矩阵辅助技术的方差缩减估计形式.理论分析表明,HAPPG在非凸优化条件下达到 O($\epsilon$-3)的样本复杂度,在多项基准控制任务上性能较优.更进一步,通过嵌入Adam优化器的自适应学习率机制,将海森辅助概率策略梯度估计器与PPO(Proximal Policy Optimization)结合,提出HAP-PPO,性能优于PPO,且文中设计的梯度估计器能进一步提升主流强化学习方法性能.
LI Yongqiang, Ph.D., associate professor. His research interests include reinforcement learning and control theory.
About Author:
HU Lei, Master student. His research interests include reinforcement learning and intelligent games.
FENG Yu, Ph.D., professor. His research interests include multi-agent games, deep reinforcement learning, optimal and robust control.
FENG Yuanjing, Ph.D., professor. His research interests include medical image processing, machine vision and brain intelligence.
Policy gradient methods in reinforcement learning are widely applied to continuous decision-making problems due to their generality. However, their practical performance is consistently constrained by low sample utilization caused by high gradient variance. In this paper, a Hessian-aided probabilistic policy gradient method(HAPPG) is proposed, and a bimodal gradient estimation mechanism is designed based on the probabilistic gradient estimator. Historical momentum is added to large-batch-size estimation to restrict optimization fluctuation of gradient descent, and variance-reduced estimation based on the Hessian-aided technique is constructed by introducing the second-order curvature information of the policy parameters into the small-batch-size estimation. Theoretical analysis demonstrates that HAPPG achieves an O($\epsilon$-3) sample complexity under non-convex optimization conditions, attaining the best convergence rate among the existing methods. Experimental results validate its superior performance across multiple benchmark control tasks. Furthermore, the Hessian-aided probabilistic policy gradient estimator is combined with the proximal policy optimization(PPO) by embedding the adaptive learning rate mechanism of Adam optimizer, resulting in HAP-PPO. HAP-PPO outperforms PPO, and the designed gradient estimator can be applied to further enhance mainstream reinforcement learning algorithms.
策略梯度方法是一种经典的强化学习方法, 核心思想是将与累计奖励有关的连续函数表示成策略的目标, 通过优化算法, 最大化连续函数以获得最优策略[1].REINFORCE[2]是最早提出的一种基于蒙特卡洛方法的策略梯度方法, 通过随机采样轨迹估计策略梯度, 并使用梯度下降方法更新策略参数.在无模型强化学习的设定中, 无法获取准确的梯度, 通常的解决办法是利用样本数据近似估计梯度值, 因此策略梯度方法总会受到梯度估计器高方差的影响, 导致收敛速度下降.
为了解决策略梯度方法的高方差问题, 学者们提出一系列的解决方法.这些方法一般分为两类.一类方法通过开发替代的目标函数降低方差带来的影响, 如在目标函数中增加基线、直接减小目标函数求梯度时产生的计算方差等.Actor-Critic Algorithms[3]通过估计值函数替代目标函数中的累计期望奖励, 减轻大方差的影响.GAE(Generalized Advantage Estimation)[4]控制优势函数估计量多步加权平均的步长, 平衡偏差与方差.TRPO(Trust Region Policy Optimization)[5]使用Kullback-Leibler散度惩罚项约束更新后的策略接近当前策略.相似地, PPO(Proximal Policy Optimization)[6]采用剪裁的替代目标函数实现与TRPO相同的目的.
另一类方法是在策略梯度下降的优化过程中加入方差缩减的思想, 直接降低梯度估计值的方差.一般机器学习常被设定为期望形式的风险最小化问题, 强化学习问题被考虑为期望形式的累计奖励最大化问题.由于无法直接拟合完整数据, 学者们会通过采样数据子集, 利用随机优化解决这一问题.随机梯度下降(Stochastic Gradient Descent, SGD)是常使用的优化方法之一.然而, 由于SGD的采样随机性, 相同数据的二次采样有可能会使梯度估计产生额外的方差, 进而影响收敛速度.
考虑到历史梯度在趋近收敛时也是对局部点的近似估计, SVRG(Stochastic Variance Reduced Gra-dient)[7]、SAG(Stochastic Average Gradient)[8]、SA-RAH(Stochastic Recursive Gradient Algorithm)[9]、SPIDER(Stochastic Path-Integrated Differential Estimator)[10]、STORM(Stochastic Recursive Momen-tum)[11]、PAGE(Probabilistic Gradient Estimator)[12]等梯度估计器设计一类将历史梯度信息代入梯度更新的方差缩减技术, 成功降低梯度估计的方差, 提高优化算法的收敛速度.
强化学习中的数据必须通过与初始未知环境交互而主动采样获得.昂贵的样本数据导致强化学习需要限制估计值的方差, 提高样本利用率, 引入方差缩减的梯度估计器能有效缓解策略梯度中出现的高方差问题, 提高样本的利用率.近年来, 学者们基于现有的方差缩减技术, 进一步开发一些直接用于无模型强化学习问题的方差缩减策略梯度估计器.这类基于方差缩减技术的策略梯度方法虽在一定程度上完成方差缩减的目的, 但是受限于多层循环的复杂结构, 导致采样规模较大或处理策略分布偏移产生额外偏差, 在实际任务上的适用性不足, 在仿真实验上的表现也仍缺乏竞争力[13].
为了将方差缩减的思想引入策略梯度中, 本文提出海森辅助的概率策略梯度方法(Hessian Aided Probabilistic Policy Gradient Method, HAPPG), 采用近年来在监督学习中被成功验证的PAGE, 这种梯度估计器可避免多层循环的大规模采样, 仅使用两个不同大小的批量交替采集数据.针对非有限和形式的强化学习优化目标, 本文利用蒙特卡洛近似方法获得的梯度估计值近似有效梯度.同时利用历史梯度动量约束梯度下降方向的波动性.其次, 为了解决强化学习的采样分布偏移问题, 引进海森辅助技术[14], 利用二阶曲率信息替代方差修正估计中的一阶梯度偏差量.一般通过重要性采样处理此偏差量, 过程中产生的额外偏差必然会导致梯度估计方差的增大.此外, 为了有效地从理论上证明方差缩减的有效性, 还提供HAPPG的收敛性证明, 证明方法能够在采样O($\epsilon$-3)个轨迹内, 达到一个$\epsilon$-平稳策略.在复杂控制任务上的仿真实验验证HAPPG性能较优.
为了验证估计器的泛化性, 还结合HAPPG与PPO, 提出HAP-PPO.该算法在PPO的基础上, 通过改变数据的收集和采样方式, 融入对策略目标函数方差缩减的梯度估计过程, 并且将产出后的梯度估计值进一步代入Adam(Adaptive Moment Estimation)优化器进行梯度方向的优化, 最终更新参数.该过程在实际应用中更具普适性.通过一组连续动作空间上的任务, 验证其在收敛速度和稳定性上的提升.
强化学习通常被描述成一个离散时间马尔可夫决策过程(Markov Decision Process, MDP)问题:
M={S, A, P, R, γ, ρ}.
其中:S表示状态空间; A表示动作空间; P(s'|s, a)表示在状态s下采取动作a转移到s'的状态转移概率; R表示奖励函数, 在状态s下采取动作a会获得r(s, a)的奖励; γ∈(0, 1]表示折扣因子; ρ表示初始状态的分布.
智能体根据策略π 选择动作a, π (·|s)表示在状态s下动作空间A上的策略分布.在这里, 假设策略π 由向量θ ∈Rd参数化, 简记策略π θ (a|s)为π θ .
若到达终止状态的时刻为T, 在策略π θ 下获得轨迹
τ={s0, a0, …, sT-1, aT-1},
沿着轨迹τ的累计折扣奖励为:
R(τ)=
在状态初始分布ρ的条件下, 轨迹τ的概率为:
p(τ|θ )=ρ(s0)
强化学习的目标在于找到一个最优策略π θ , 使轨迹的期望累计折扣奖励最大化, 即
其中J(θ )表示性能函数.为了解决这个问题, Su-tton等[1]提出策略梯度方法, 首先计算J(θ )的梯度:
$\begin{aligned} \nabla J(\boldsymbol{\theta})= & \int R(\boldsymbol{\tau}) \nabla p(\boldsymbol{\tau} \mid \boldsymbol{\theta}) \mathrm{d} \boldsymbol{\tau}= \\ & \int R(\boldsymbol{\tau}) \frac{\nabla p(\boldsymbol{\tau} \mid \boldsymbol{\theta})}{p(\boldsymbol{\tau} \mid \boldsymbol{\theta})} p(\boldsymbol{\tau} \mid \boldsymbol{\theta}) \mathrm{d} \tau= \\ & E_{\tau \sim p(\tau \mid \boldsymbol{\theta})}[\nabla \log p(\boldsymbol{\tau} \mid \boldsymbol{\theta}) \cdot R(\boldsymbol{\tau})]= \\ & E_{\tau \sim p(\tau \mid \boldsymbol{\theta})}\left[\sum_{t=0}^{T-1}\left(\nabla \log \pi_{\boldsymbol{\theta}}\left(a_{t}^{i} \mid s_{t}^{i}\right) \cdot R(\boldsymbol{\tau})\right)\right] \end{aligned}$
由于p(τ|θ )未知, 所以无法获取上式中的完整梯度.考虑蒙特卡洛近似方法, 策略梯度方法从分布p(τ|θ )中采样一个批量的轨迹数据
N={τi
以获取随机梯度:
$\widehat{\nabla} J(\boldsymbol{\theta})=\frac{1}{|N|} \sum_{i \in N} g\left(\tau_{i}, \boldsymbol{\theta}\right)=$
$\frac{1}{|N|} \sum_{i \in N} \sum_{t=0}^{T-1}\left(\nabla \log \pi_{\boldsymbol{\theta}}\left(a_{t}^{i} \mid s_{t}^{i}\right) \cdot R\left(\boldsymbol{\tau}_{i}\right)\right), $
其中g(τi, θ )表示在轨迹τi上的无偏随机梯度估计, 该估计器正是REINFORCE[2].
t时刻下参数θ 的更新如下:
θ t+1=θ t+η t
其中η t> 0表示学习率.
为了进一步减小梯度估计的方差, 实际使用中会添加基线b(s), 并且由于当前动作与先前奖励的无关性, Baxter等[15]提出改进后的梯度估计器GPOMDP:
$\begin{array}{l} g\left(\boldsymbol{\tau}_{i}, \boldsymbol{\theta}\right)= \\ \sum_{t=0}^{T-1} \sum_{j=0}^{t}\left(\nabla_{\boldsymbol{\theta}} \log \pi_{\boldsymbol{\theta}}\left(a_{j}^{i} \mid s_{j}^{i}\right) \cdot\left(\gamma^{h} r\left(s_{\imath}^{j}, a_{\iota}^{j}\right)-b\left(s_{\imath}^{j}\right)\right)\right) . \end{array}$
监督学习问题一般可转换为有限和经验风险最小化问题, 形式如下:
其中:n表示训练数据集
D={(xi, yi)}
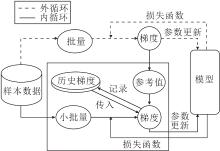
的样本数量; L表示衡量真实值yi与预测值f(xi, θ )之间偏差的损失函数.如果f(·, ·)是光滑的, 并且满足Polyak-Schojasiewicz条件, 当选定恒定的步长时, 梯度下降具有全局线性收敛速率[16].由于计算成本代价过高, 并且需要每次计算全部样本数据的梯度, 所以仅使用随机采样子集数据的小批量SGD成为目前梯度估计的主流方法, 但该方法受方差影响较大, 仅满足次线性收敛条件.较低的迭代计算成本是以较慢的次线性收敛速率为代价的.SVRG、SARAH、SPIDER等一系列方差缩减技术在计算成本和收敛速度之间实现更好的平衡.具体方差缩减技术框架如图1所示.
这类技术一方面通过大批量的采样近似获取一个较准确的梯度估计值作为梯度更新的参考方向.记录当前时刻的参数作为参考值
$\widetilde{\boldsymbol{h}}^{s}=\frac{1}{n} \sum_{i=1}^{n} \nabla f_{i}\left(\widetilde{\boldsymbol{\theta}}^{s}\right) .$
另一方面加入历史梯度信息, 使用小批量采样更新对每个时刻下的梯度估计值进行修正.梯度修正公式为:
$\boldsymbol{h}_{t}^{s}=\widetilde{\boldsymbol{h}}^{s}+\frac{1}{|B|} \sum_{i \in B}\left(\nabla f_{i}\left(\boldsymbol{\theta}_{t}\right)-\nabla f_{i}\left(\widetilde{\boldsymbol{\theta}}^{s}\right)\right), $
其中, B表示从{0, 1, …, n}中随机选取的小批量子集, 满足条件B≪n.一般来说, 小批量和大批量均从相同的样本数据集上采样, 小批量的修正是对样本数据的重复利用, 可提高利用率.历史梯度的引入则是减小梯度估计时的方差, 一定程度上提高方法的收敛速度.
采用方差缩减技术解决强化学习中的策略梯度问题时需要进行如下调整.1)策略梯度的优化目标是期望形式, 非有限和问题.2)MDP中的动态未知, 因此利用全梯度下降更新参数不可行, 全梯度通常由蒙特卡洛采样的大批量梯度估计代替.3)由于性能函数的非凸性, 寻找全局最优解的收敛性验证方法不可行, 只能从梯度有界的角度验证方法收敛到一个$\epsilon$-稳定解.于是为了获取梯度的Lipschitz性质的有界定义, 需要假设性能函数J(θ )满足Lipschitz平滑性, 这对于经常使用高斯策略和Softmax策略的强化学习是一个合理的假设[17, 18].4)在强化学习的设定中, 样本数据(xi, yi)对应轨迹τ.不同于监督学习中稳定的采样分布, 这些服从轨迹的分布随策略参数的更新进行动态变化.例如:在t-1时刻下的梯度估计采样的轨迹实际服从于t-1时刻的策略
其中权重
ω (τ|θ t, θ t-1)=
几乎所有在强化学习中应用的方差缩减方法都会使用重要性采样技术[19].该技术显著影响算法性能, 因为梯度估计在很大程度上取决于这些权重.
SVRPG(Stochastic Variance-Reduced Policy Gra-dient)[13]是最早将方差缩减技术与强化学习设定结合的方法, 使用一个双层循环结构.在第s个外部循环处, 计算当前迭代参数
在每个外部循环内, 存在一个t=1, 2, …, m的内部循环, 每步先更新参数
再根据当前策略参数
在内部循环迭代m次以后, 通过
ht=ht-1+
其中
近年来, 为了克服SVRG等双环结构利用大批量数据与小批量数据双重更新的复杂交替过程, 学者们引入递归动量的思想.Yuan等[20]提出STORM-PG(Stochastic Recursive Momentum for Policy Gra-dient).在STORM被有效证实其有效性以后, Huang等[21]结合动量自适应方法的估计形式, 提出ISMBPG(Important-Sampling Momentum-Based Policy Gradient)和HA-MBPG(Hessian-Aided Momentum-Based Policy Gradient).Salehkaleybar等[22]提出SHARP(Stochastic Hessian Aided Recursive Policy Gradient), 将二阶信息代入递归动量中, 改良STORM.
与此同时, 也有学者设定概率选择估计方法的形式, 取缔大批量数据和小批量数据的叠加估计, 这在一定程度上避免叠加后的过度计算.Li等[12]提出用于非凸优化的PAGE.后续在强化学习领域, Gargiani等[23]基于PAGE, 提出PAGE-PG(Probabi-listic Gradient Estimation for Policy Gradient), 收敛速度较快.
上述讨论的方差缩减的策略梯度方法大多依赖重要性采样的有界假设, 由于权重系数会随轨迹时间步长呈现指数增长[24], 无法验证这个假设.在实际应用中, 需要采取非常小的步长以保证这一假设, 这会导致收敛速度的急剧减慢.
方差缩减技术与强化学习的结合能有效降低梯度估计时产生的方差, 进一步高效利用强化学习与环境交互过程产生的昂贵数据.
本文提出海森辅助的概率策略梯度方法(HA- PPG), 基于PAGE的思想, 以一个概率在双模态估计之间切换估计形式, 在梯度估计时降低方差, 提高方法的收敛速率.
PAGE梯度更新的特点在于以概率的形式自由切换更新方法, 要么使用概率为p的大批量SGD更新, 要么以概率1-p重用先前的梯度进行小批量修正更新.梯度估计更新如下:
ht=
在PAGE框架上, HAPPG针对大批量的估计增加动量项, 在每次估计时有效结合之前的梯度方向信息; 针对小批量的修正估计增加海森近似项, 取代一阶梯度的偏差量.二阶方法包含局部曲率的信息, 因此能提高优化速度, 在学习率的设定上更鲁棒.此外该海森近似项仅使用小批量的样本子集计算对应的梯度信息以近似全局的海森矩阵, 避免过大的计算量.
文献[14]中首次提出海森近似的辅助技术.性能函数J(θ )的梯度差为:
$\begin{aligned} \nabla J\left(\boldsymbol{\theta}_{t}\right)- & \nabla J\left(\boldsymbol{\theta}_{t-1}\right)= \\ & \int_{0}^{1} \nabla^{2} J\left(\boldsymbol{\theta}_{b}\right)\left(\boldsymbol{\theta}_{t}-\boldsymbol{\theta}_{t-1}\right) \mathrm{d} b= \\ & {\left[\int_{0}^{1} \nabla^{2} J\left(\boldsymbol{\theta}_{b}\right) \mathrm{d} b\right] \cdot\left(\boldsymbol{\theta}_{t}-\boldsymbol{\theta}_{t-1}\right) } \end{aligned}$(1)
对J(θ )求二阶导数, 有
$\begin{array}{l} \nabla^{2} J(\boldsymbol{\theta})= \\ \quad E_{\tau}\left[\nabla \Phi(\boldsymbol{\theta}, \boldsymbol{\tau}) \nabla \log p\left(\boldsymbol{\tau} \mid \boldsymbol{\pi}_{\boldsymbol{\theta}}\right)^{\mathrm{T}}+\nabla^{2} \Phi(\boldsymbol{\theta}, \boldsymbol{\tau})\right], \end{array}$
其中
$\Phi(\boldsymbol{\theta}, \boldsymbol{\tau})=\sum_{t=0}^{T-1} \sum_{i=t}^{T-1} \gamma^{t} r\left(s_{i}, a_{i}\right) \nabla \log \pi_{\boldsymbol{\theta}}\left(a_{t} \mid s_{t}\right) .$
于是定义
$\begin{array}{l} M(\tau, \boldsymbol{\theta}):= \\ \quad \nabla \Phi(\boldsymbol{\theta}, \boldsymbol{\tau}) \nabla \log p\left(\boldsymbol{\tau} \mid \boldsymbol{\pi}_{\boldsymbol{\theta}}\right)^{\mathrm{T}}+\nabla^{2} \Phi(\boldsymbol{\theta}, \boldsymbol{\tau}) \end{array}$
对于任意一条给定的轨迹τ, M(τ, θ )都是对
式(1)中的积分项可表示成期望
Eb~U[0, 1][
这可由无偏估计器M(
HAPPG基于海森近似和PAGE梯度估计这两个主要技术.具体地, 方法首先以初始化参数θ 0采样N个轨迹, 获取一个初始的梯度估计值h0, 在t> 0时, 梯度估计的更新如下:
ht=
其中:动量系数β∈[0, 1); 二阶近似估计项
Δ t=
bt表示当前t时刻下[0, 1]中采样的随机数.
最后将更新后的梯度估计值ht代入θ 的更新:
θ t+1=θ t+η tht.
式(2)中p表示切换概率.当概率为p时, 此时梯度估计值的更新选择式(2)中的第1行, 即大批量的带有动量项的蒙特卡洛采样估计.当概率为1-p时, 梯度估计值更新式(2)选择第2行, 即小批量带有二阶近似估计项的修正估计.
HAPPG具体步骤如算法1所示:
算法1 HAPPG
输入 迭代次数T, 大批量N, 小批量B,
动量系数β∈[0, 1), 步长η > 0,
切换概率p∈(0, 1]
输出 策略网络参数θ
从
h0=
For t to T do
根据概率p构建伯努利分布, 获取随机数pt
If pt=1
构建均匀分布U(0, 1), 采样随机数mt
从
ht=ht-1+Δ t
Else
从
ht=βht-1+(1-β)
End if
参数更新θ t+1=θ t+η ht
End for
当参数选择p=1, β=0时, HAPPG可恢复成SGD更新的REINFORCE或GPOMDP.当切换概率p趋于1时, HAPPG倾向于大样本数据的探索.反之当切换概率p趋于0时, HAPPG往往会选择更多的小批量修正估计.这是对已有轨迹历史进行的一次重复利用, 从而提高收敛速度.文献[23]提出在实际训练中动态调整p以调节探索水平.例如, 可以在训练早期, 选择一个较大的p值, 然后随着训练的进行逐步减小.这可在训练的早期阶段促进探索, 同时在训练结束时产生更稳定的梯度估计, 潜在防止陷入某些较差的局部最大值.
考虑到计算海森矩阵的复杂度过大, 本文参考一种常见的解决办法, 利用有限差分法计算海森向量积[21], 使用向量vt表示θ t-θ t-1, 单个轨迹的无偏估计为:
$\begin{aligned} M\left(\tau_{j}^{b}, \boldsymbol{\theta}_{t}^{b}\right) & \left(\boldsymbol{\theta}_{t}-\boldsymbol{\theta}_{t-1}\right)= \\ & \nabla \Phi\left(\tau_{j}^{b}, \boldsymbol{\theta}_{t}^{b}\right) \nabla \log p\left(\boldsymbol{\tau}_{j}^{b} \mid \pi_{\boldsymbol{\theta}_{t}^{b}}\right)^{\mathrm{T}} \cdot \boldsymbol{v}_{t}+ \\ & \nabla^{2} \Phi\left(\tau_{j}^{b}, \boldsymbol{\theta}_{t}^{b}\right) \cdot \boldsymbol{v}_{t} \end{aligned}$
上式中右边第1项可直接计算, 第2项的海森向量积可由有限差分法处理.设定扰动量δ> 0为一个极小的标量, 通过中值定理可得
$\begin{array}{l} \nabla^{2} \Phi\left(\tau_{j}^{b}, \boldsymbol{\theta}_{t}^{b}\right) \cdot \boldsymbol{v}_{t} \approx \\ \quad \frac{\nabla \Phi\left(\boldsymbol{\tau}_{j}^{b}, \boldsymbol{\theta}_{t}^{b}+\delta \boldsymbol{v}_{t}\right)-\nabla \Phi\left(\tau_{j}^{b}, \boldsymbol{\theta}_{t}^{b}-\delta \boldsymbol{v}_{t}\right)}{2 \delta} \boldsymbol{v}_{t}, \end{array}$
在δ足够小时, 近似估计量的数值近似足够精准.
方差缩减策略梯度方法的理论分析通常集中在某些假设中, 这些假设一般是人为设定合理条件, 推导出实现$\epsilon$-稳定解所需的采样轨迹的样本复杂度.本节首先给出有关奖励函数和策略π θ 的一些有界性假设.其次, 在满足收敛条件下, 探究合理选择参数以实现最优样本复杂度.
假设1 有界的奖励函数 对于任意的s∈S, a∈A, 且R0为一个大于0的任意常数, 奖励函数满足:
$|r(s, a)| \leqslant R_{0} .$
假设2 有界的策略参数 存在常数G、L, 使对任意θ ∈Rd和任意s∈S, a∈A, 有
$\begin{array}{l} \left\|\nabla \log \pi_{\boldsymbol{\theta}}(a \mid s)\right\| \leqslant G, \\ \left\|\nabla^{2} \log \pi_{\boldsymbol{\theta}}(a \mid s)\right\| \leqslant L . \end{array}$
引理1 一般梯度估计偏差的有界性和海森估计的有界性 在假设1和假设2的条件下, 文献[14]证明一般梯度估计的均方误差和海森估计满足上界:
$\begin{array}{l} E\left[\|g(\boldsymbol{\tau}, \boldsymbol{\theta})-\nabla J(\boldsymbol{\theta})\|^{2}\right] \leqslant \sigma_{g}^{2}, \\ E\left[\|M(\tau, \boldsymbol{\theta})\|^{2}\right] \leqslant \sigma_{B}^{2}, \end{array}$
其中
$\begin{aligned} \sigma_{g}^{2} & =\frac{G^{2} R^{2}}{(1-\gamma)^{4}} \\ \sigma_{B}^{2} & =\frac{T^{2} G^{4} R^{2}+L^{2} R^{2}}{(1-\gamma)^{4}} \end{aligned}$
定理1 HAPPG中累计梯度估计偏差的有界性在引理 1 的条件下, HAPPG中T步内累计梯度估计的误差满足
$\begin{array}{l} \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}\right] \leqslant \\ \quad \frac{\sigma_{B}^{2} \eta^{2}}{p(1-\beta)}\left(\frac{\beta^{2} p}{1-\beta}+\frac{1-p}{B}\right) \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]+ \\ \quad \frac{T(1-\beta) \sigma_{g}^{2}}{N}+\frac{\sigma_{g}^{2}}{N p(1-\beta)} . \end{array}$
证明 记Ft表示迭代t时刻的状态信息, 有
$\begin{array}{l} E\left[\left\|\boldsymbol{h}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2}\right]= \\ E\left[E\left[\left\|\boldsymbol{h}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]\right] . \end{array}$
首先简记
$\begin{array}{l} \boldsymbol{G}_{t+1}=\frac{1}{N} \sum_{i=1}^{N} g\left(\boldsymbol{\tau}_{i}, \boldsymbol{\theta}_{t+1}\right), \\ \boldsymbol{M}_{t+1}=\frac{1}{B} \sum_{j=1}^{B} M\left(\tau_{j}^{m}, \boldsymbol{\theta}_{t+1}^{m}\right)\left(\boldsymbol{\theta}_{t+1}-\boldsymbol{\theta}_{t}\right), \end{array}$
于是由全期望公式, 得
$\begin{array}{l} E\left[\left\|\boldsymbol{h}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]= \\ \quad(1-p) E\left[\left\|\boldsymbol{h}_{t}+\boldsymbol{M}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]+ \\ \quad p E\left[\left\|\beta \boldsymbol{h}_{t}+(1-\beta) \boldsymbol{G}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right] . \end{array}$
单独化简上式中的两项.第1项化简如下:
$\begin{array}{l} E\left[\left\|\boldsymbol{h}_{t}+\boldsymbol{M}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]= \\ \\ E\left[\left\|\boldsymbol{h}_{t}+\boldsymbol{M}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t}\right)+\nabla J\left(\boldsymbol{\theta}_{t}\right)-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]= \\ \\ E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+2 E\left[\left\langle\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right), E\left[\boldsymbol{M}_{t+1} \mid F_{t}\right]-\left(\nabla J\left(\boldsymbol{\theta}_{t+1}\right)-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right)\right\rangle \mid F_{t}\right]+ \\ \quad E\left[\left\|\boldsymbol{M}_{t+1}-\left(\nabla J\left(\boldsymbol{\theta}_{t+1}\right)-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right)\right\|^{2} \mid F_{t}\right] \stackrel{(\mathrm{a})}{=} \\ \\ \quad E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+E\left[\left\|\boldsymbol{M}_{t+1}-\left(\nabla J\left(\boldsymbol{\theta}_{t+1}\right)-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right)\right\|^{2} \mid F_{t}\right] \stackrel{(\mathrm{b})}{\lessgtr} \\ \\ E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+E\left[\left\|\boldsymbol{M}_{t+1}\right\|^{2} \mid F_{t}\right] \stackrel{(\mathrm{c})}{\lessgtr} \\ \\ E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+\frac{(1-p) \sigma_{B}^{2}}{B} E\left[\left\|\boldsymbol{\theta}_{t+1}-\boldsymbol{\theta}_{t}\right\|^{2}\right]= \\ \\ \\ E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+\frac{(1-p) \sigma_{B}^{2} \eta^{2}}{B} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right] . \end{array}$
由于
$E_{\tau}\left[\boldsymbol{M}_{t+1}\right]=\nabla J\left(\boldsymbol{\theta}_{t+1}\right)-\nabla J\left(\boldsymbol{\theta}_{t}\right), $
等式(a)成立.
由于
E[‖ X-E(X)‖ 2]≤E[‖ X‖ 2],
不等式(b)成立.
代入引理1的条件和学习率, 不等式(c)成立.
第2项化简如下:
$\begin{aligned} E\left[\| \beta \boldsymbol{h}_{t}+\right. & \left.(1-\beta) \boldsymbol{G}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right) \|^{2} \mid F_{t}\right]= \\ & E\left[\left\|\beta \boldsymbol{h}_{t}+(1-\beta) \boldsymbol{G}_{t+1}-(1-\beta) \nabla J\left(\boldsymbol{\theta}_{t+1}\right)-\beta \nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]= \\ & \beta^{2} E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]+(1-\beta)^{2} E\left[\left\|\boldsymbol{G}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right] \stackrel{(\mathrm{a})}{\leqslant} \\ & \beta^{2} E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]+\frac{(1-\beta)^{2} \sigma_{g}^{2}}{N} \stackrel{(\mathrm{~b})}{\leqslant} \\ & \beta^{2}\left(\frac{1}{\beta} E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+\frac{1}{1-\beta} E\left[\left\|\nabla J\left(\boldsymbol{\theta}_{t+1}\right)-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]\right)+\frac{(1-\beta)^{2} \sigma_{g}^{2}}{N} \leqslant \\ & \beta E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+\frac{\beta^{2} \sigma_{B}^{2} \eta^{2}}{1-\beta} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]+\frac{(1-\beta)^{2} \sigma_{g}^{2}}{N} . \end{aligned}$
由引理1中的条件, 等式(a)成立.由不等式
$\|\boldsymbol{a}+\boldsymbol{b}\|^{2} \leqslant(1+\boldsymbol{\epsilon})\|\boldsymbol{a}\|^{2}+\left(1+\frac{1}{\boldsymbol{\epsilon}}\right)\|\boldsymbol{b}\|^{2}, $
可设置系数
$\epsilon=\frac{1-\beta}{\beta}> 0$
则等式(b)成立.
结合上述两项, 式(3)可化简为
$\begin{array}{l} E\left[\left\|\boldsymbol{h}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]= \\ \quad(1-p) E\left[\left\|\boldsymbol{h}_{t}+\boldsymbol{M}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right]+p E\left[\left\|\beta \boldsymbol{h}_{t}+(1-\beta) \boldsymbol{G}_{t+1}-\nabla J\left(\boldsymbol{\theta}_{t+1}\right)\right\|^{2} \mid F_{t}\right] \leqslant \\ \quad(1-p)\left(E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+\frac{\sigma_{B}^{2} \eta^{2}}{B} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]\right)+ \\ \quad p\left(\beta E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+\frac{\beta^{2} \sigma_{B}^{2} \eta^{2}}{1-\beta} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]+\frac{(1-\beta)^{2} \sigma_{g}^{2}}{N}\right)= \\ \quad(1-p(1-\beta)) E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right]+\sigma_{B}^{2} \eta^{2}\left(\frac{\beta^{2} p}{1-\beta}+\frac{1-p}{B}\right) E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]+\frac{(1-\beta)^{2} \sigma_{g}^{2} P}{N} . \end{array}$
对上式两边同时求和, 并作差, 得
$\begin{array}{l} p(1-\beta) \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2} \mid F_{t}\right] \leqslant \\ \sigma_{B}^{2} \eta^{2}\left(\frac{\beta^{2} p}{1-\beta}+\frac{1-p}{B}\right) \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]+\frac{T P(1-\beta)^{2} \sigma_{g}^{2}}{N}+E\left[\left\|\boldsymbol{h}_{0}-\nabla J\left(\boldsymbol{\theta}_{0}\right)\right\|^{2}\right]- \\ \quad E\left[\left\|\boldsymbol{h}_{T}-\nabla J\left(\boldsymbol{\theta}_{T}\right)\right\|^{2}\right] \leqslant \\ \sigma_{B}^{2} \eta^{2}\left(\frac{\beta^{2} p}{1-\beta}+\frac{1-p}{B}\right) \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]+\frac{T P(1-\beta)^{2} \sigma_{g}^{2}}{N}+\frac{1}{N^{2}} E\left[\sum_{i=0}^{N}\left\|g\left(\tau_{i}, \boldsymbol{\theta}_{0}\right)-\nabla J\left(\boldsymbol{\theta}_{0}\right)\right\|^{2}\right] \leqslant \\ \sigma_{B}^{2} \eta^{2}\left(\frac{\beta^{2} p}{1-\beta}+\frac{1-p}{B}\right) \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]+\frac{T P(1-\beta)^{2} \sigma_{g}^{2}}{N}+\frac{\sigma_{g}^{2}}{N} . \end{array}$
最终可得到定理1的结论.
定理2 平均期望梯度的有界性 在假设1和假设2的条件下, 参数满足
$\begin{array}{l} p \in(0,1), \beta \in(0,1), B \ll N, \\ \eta \leqslant \frac{\sqrt{1+2 w}-1}{2 \sigma_{B} w}, \\ w=\frac{\beta^{2}}{(1-\beta)^{2}}+\frac{1-p}{B p(1-\beta)}>0, \end{array}$
T步时间内平均期望梯度满足
$\begin{array}{l} \frac{1}{T} \sum_{t=0}^{T-1} E\left[\left\|\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}\right] \leqslant \\ \quad \frac{2\left(J^{*}-J\left(\boldsymbol{\theta}_{0}\right)\right)}{\eta T}+\frac{(1-\beta) \sigma_{g}^{2}}{N}+\frac{\sigma_{g}^{2}}{N p(1-\beta) T} \end{array}$
证明 由引理1可知, 性能函数满足Lipschitz 平滑性, Lipschitz系数为σB, 则
$\begin{aligned} \left\|\nabla^{2} J(\boldsymbol{\theta})\right\|= & \left\|E_{\tau}[M(\tau, \boldsymbol{\theta})]\right\| \leqslant \\ & E_{\tau}[\|M(\tau, \boldsymbol{\theta})\|] \leqslant \sigma_{B}, \end{aligned}$
于是有如下不等式成立:
$\begin{array}{l} J\left(\boldsymbol{\theta}_{t+1}\right) \geqslant \\ \quad J\left(\boldsymbol{\theta}_{t}\right)+\left\langle\nabla J\left(\boldsymbol{\theta}_{t}\right), \boldsymbol{\theta}_{t+1}-\boldsymbol{\theta}_{t}\right\rangle-\frac{\sigma_{B}}{2}\left\|\boldsymbol{\theta}_{t+1}-\boldsymbol{\theta}_{t}\right\|^{2} \stackrel{(\mathrm{a})}{=} \\ \quad J\left(\boldsymbol{\theta}_{t}\right)+\eta\left\langle\nabla J\left(\boldsymbol{\theta}_{t}\right), \boldsymbol{h}_{t}\right\rangle-\frac{\sigma_{B}}{2}\left\|\boldsymbol{\theta}_{t+1}-\boldsymbol{\theta}_{t}\right\|^{2} \stackrel{(\mathrm{~b})}{=} \\ \quad J\left(\boldsymbol{\theta}_{t}\right)-\frac{\eta}{2}\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}+\frac{\eta}{2}\left\|\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}+\frac{\eta}{2}\left(1-\sigma_{B} \eta\right)\left\|\boldsymbol{h}_{t}\right\|^{2} \end{array}$
由策略参数θ 更新式, 上式中等式(a)成立.由
<x, y> =
等式(b)成立.
对上式左边T次求和作差, 并求期望, 且对于任意的θ ∈Rd都有J*≥ J(θ ), 因此有
$\begin{aligned} J\left(\boldsymbol{\theta}_{0}\right)-J^{*} \leqslant & J\left(\boldsymbol{\theta}_{0}\right)-E\left[J\left(\boldsymbol{\theta}_{T}\right)\right] \leqslant \sum_{t=0}^{T-1} E\left[J\left(\boldsymbol{\theta}_{t}\right)-J\left(\boldsymbol{\theta}_{t+1}\right)\right] \leqslant \\ & \frac{\eta}{2} \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}-\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}\right]-\frac{\eta}{2} \sum_{t=0}^{T-1} E\left[\left\|\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}\right]-\frac{\eta}{2}\left(1-\sigma_{B} \eta\right) \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right] . \end{aligned}$
然后, 将定理1中的结论代入上式, 可进一步推导出如下结果:
$\begin{array}{l} J\left(\boldsymbol{\theta}_{0}\right)-J^{*} \leqslant \\ \begin{array}{l} \frac{\eta}{2}\left(\frac{\sigma_{B}^{2} \eta^{2}}{p(1-\beta)}\left(\frac{\beta^{2} p}{1-\beta}+\frac{1-p}{B}\right) \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]+\frac{T(1-\beta) \sigma_{g}^{2}}{N}+\frac{\sigma_{g}^{2}}{N_{p}(1-\beta)}\right)- \\ \frac{\eta}{2} \sum_{t=0}^{T-1} E\left[\left\|\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}\right]-\frac{\eta}{2}\left(1-\sigma_{B} \eta\right) \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]= \\ - \frac{\eta}{2}\left(1-\sigma_{B} \eta\left(1+\sigma_{B} \eta\left(\frac{\beta^{2}}{(1-\beta)^{2}}+\frac{1-p}{B p(1-\beta)}\right)\right)\right) \sum_{t=0}^{T-1} E\left[\left\|\boldsymbol{h}_{t}\right\|^{2}\right]- \end{array} \end{array}$
$\frac{\eta}{2} \sum_{t=0}^{T-1} E\left[\left\|\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}\right]+\frac{\eta}{2}\left(\frac{T(1-\beta) \sigma_{g}^{2}}{N}+\frac{\sigma_{g}^{2}}{N_{p}(1-\beta)}\right)$
设置
$\begin{array}{l} w=\frac{\beta^{2}}{(1-\beta)^{2}}+\frac{1-p}{B p(1-\beta)}> 0, \\ \eta \leqslant \frac{\sqrt{1+4 w}-1}{2 \sigma_{B} w}, \end{array}$
于是
$\begin{aligned} J\left(\boldsymbol{\theta}_{0}\right)-J^{*} \leqslant & -\frac{\eta}{2} \sum_{t=0}^{T-1} E\left[\left\|\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}\right]+ \\ & \frac{\eta}{2}\left(\frac{T(1-\beta) \sigma_{g}^{2}}{N}+\frac{\sigma_{g}^{2}}{N_{p}(1-\beta)}\right) . \end{aligned}$
最终, 调整上式, 得出定理2.
定理2表明, 选择合适的步长、批量大小和转换概率p, T次迭代后性能函数的平均期望梯度以
$O\left(\frac{1}{T}+\frac{1}{N T}+\frac{1}{N}\right)$
收敛.该定理在学习率的设定上受Lipschitz性质条件的约束, 收敛速度达到同类先进算法讨论的最快速度.由于不完全依赖小批量B的更新, 而是以概率选择的形式适当选择使用小批量B的更新, HAPPG避免O(B-1)带来的影响.这在理论上超越无法避免小批量影响的SVRPG和STORM-PG.
总之, HAPPG 利用PAGE, 实现较优的收敛速度, 同时也避免双环结构复杂性.不同于PAGE-PG, HAPPG还利用海森辅助, 避免重要性采样技术, 在理论上进一步降低由重要性权重带来的偏差, 实际训练中学习率的选择也会更广泛.由于动量项的增加, 概率交替过程中的更新也能保留之前梯度的主要方向, 提高收敛稳定性.
推论1 梯度收敛的样本复杂度 在定理2成立的条件下, 设定
$\begin{array}{l} p=\frac{1}{N}, \beta=\frac{1}{N}, \eta=\frac{\sqrt{1+4 w}-1}{2 \sigma_{B} w}, \\ N=O\left(\epsilon^{-2}\right), B=O(1) . \end{array}$
于是在O($\epsilon$-3)的样本复杂度的轨迹下, 且$\epsilon$→ 0, 性能函数J(θ t)在T步时间内梯度范数的平均期望满足
$\frac{1}{T} \sum_{t=0}^{T-1} E\left[\left\|\nabla J\left(\boldsymbol{\theta}_{t}\right)\right\|^{2}\right] \leqslant \epsilon^{2}$
推论1表明HAPPG在获得$\epsilon$-稳定解时, 最少需要O($\epsilon$-3)的样本复杂度和O(1)的小批量样本复杂度.表1给出5种基于方差缩减技术的策略梯度方法的样本复杂度与相关技术的对比.
| 表1 各方法获得稳定解的采样复杂度与相关技术 Table 1 Sampling complexity and related techniques for different methods to obtain a stable point |
HAPPG的本质是对目标函数进行梯度估计时创新方法, 引入方差缩减的梯度估计器, 使估计的梯度包含历史梯度的信息.在梯度下降时, 一个较优秀的方向作为参考值可帮助梯度更快地收敛, 从而提高样本的利用率.鉴于其形式的可移植性和容易实现, 本文在使用蒙特卡洛估计形式的PPO中引入海森辅助的概率策略梯度估计器, 并与Adam优化器进一步结合, 提出HAP-PPO, 在梯度下降中, 融合梯度估计器和梯度优化器.HAP-PPO先估计一个含有历史信息的梯度, 再应用自适应学习率框架, 获取梯度的指数移动平均, 最终再对策略更新参数.
HAP-PPO遵循PPO中On-Policy的性质, 只根据当前策略收集数据并学习.为了增加数据的利用率, PPO通过对目标函数增加重要性权重, 保证在多次更新的周期中数据的有效性.因此在利用同样目标函数的HAP-PPO中, 在相同经验池中的小批量数据和大批量数据的切换形式采样也支持On-Policy学习.本文虽未给出HAP-PPO的收敛性分析, 但基于策略梯度类方法的性质可以看出, 这是一个可行的应用方案.HAP-PPO具体步骤如算法2所示.
算法2 HAP-PPO
输入 迭代次数T, 经验池大小D, 大批量N, 小批量B, 更新周期E, 切换概率P
输出 策略网络参数θ , 价值网络参数ϕ
For t to T do
轨迹收集部分:
For i to D do
智能体根据策略π θ 与环境进行交互, 产生轨迹
数据τi, 将数据存储在经验池中
End for
数据学习部分:
For j to E do
根据概率P构建伯努利分布, 获取随机数p
If p=1
从经验池中随机采样批量B轨迹
由轨迹计算蒙特卡洛回报和优势函数:
At=
由PPO-clip原理, 计算策略的目标函数:
$\begin{aligned} J\left(\boldsymbol{\theta}_{t}\right)= & \frac{1}{\left|D_{B}\right| T_{\tau \in D_{B}}} \sum_{t=0}^{T} \min \left(\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\boldsymbol{\theta}_{k}}\left(a_{t} \mid s_{t}\right)} A_{t}, \right. \\ & \left.\operatorname{clip}\left(\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\boldsymbol{\theta}_{k}}\left(a_{t} \mid s_{t}\right)}, 1-\varepsilon, 1+\varepsilon\right) A_{t}\right) \end{aligned}$
由梯度修正形式估计目标函数的梯度:
ht=ht-1+
Else
从经验池中随机采样批量N轨迹
优势函数和目标函数计算同p=1时
由动量形式估计目标函数的梯度:
ht=βht-1+(1-β)Ñ
End if
将梯度估计值代入Adam优化器, 定义一阶动量mt, 二阶动量vt, 分别表示当前梯度值的均值和方差, 计算梯度的指数移动平均:
$\begin{array}{l} \boldsymbol{m}_{t}=\beta_{1} \boldsymbol{m}_{t-1}+\left(1-\beta_{1}\right) \boldsymbol{h}_{t} \\ \boldsymbol{v}_{t}=\beta_{2} \boldsymbol{v}_{t-1}+\left(1-\beta_{2}\right) \boldsymbol{h}_{t}^{2} \\ \hat{\boldsymbol{v}}_{t}=\max \left(\hat{\boldsymbol{v}}_{t-1}, \boldsymbol{v}_{t}\right) \end{array}$
更新策略网络参数
θ t=θ t-1-
其中, η 表示学习率, ε 表示一个极小值, 防止除
数为0
同理, 价值网络的损失函数为蒙特卡洛回报和值函数的均方误差:
$L(\boldsymbol{\theta})=\frac{1}{\left|D_{k}\right| T_{\tau \in D_{k}}} \sum_{t=0}^{T}\left(V_{\phi}\left(s_{t}\right)-\widehat{R_{t}}\right)^{2}$
利用Adam优化器更新价值网络参数ϕ
End for
End for
实验选择Open-AI Gym中经典控制类任务和Mujoco多关节机器人类任务作为基准测试的多个任务.为了全面有效评估HAPPG在不同难度的任务中动作控制决策的表现能力, 选用Open-AI Gym中两种离散动作控制任务和Mujoco中两种连续动作控制任务.具体任务场景信息如表2所示.
| 表2 实验任务场景 Table 2 Experimental task environment |
Cartpole环境是一个经典的控制问题, 一根杆子通过一个不活动的关节连接到一辆小车上, 小车沿着一条无摩擦的轨道移动.摆锤直立放置在小车上, 目标是通过对小车施加左右方向的力以平衡杆子并防止钟摆翻倒.在杆子保持直立的时间步之内, 每步都会获得+1的奖励.当杆子与竖直方向间的夹角不在12° 的范围内或推车从其初始位置移动超过2.4个单位时, 一个回合终止.状态空间是4维连续的, 动作空间是离散的, 有2个可用的动作:对推车施加+1或-1的力.当角度超过限定范围时或经过500个时间步, 任务结束.
Acrobot环境是一个简单机器人系统, 包括两个关节和两个连杆, 其中两个连杆之间的关节是灵活的.最初, 链接是向下悬挂的, 目标是通过施加扭矩将底部连杆的末端摆动到给定高度.每次目标未实现时, 奖励为-1.一旦达到目标高度或经过500个时间步, 环境结束.状态空间是6维连续的, 动作空间是离散的, 可选择3种可用的动作: 施加正扭矩、施加负扭矩、没有动作.
Hopper环境是一个二维的单腿模型, 由4个主要身体部分组成: 顶部的躯干、中部的大腿、底部的腿、支撑整个身体的一只脚.目标是通过对连接身体4个部分的3个关节施加扭矩, 使机器人能向前跳跃.动作是一个3维的连续控制量, 对应3个扭矩, 且限定范围是-1至1.每次动作之后给定一个奖励.奖励一共有3个部分:跳跃后是否处于健康状态的健康奖励、跳跃方向是否为正的方向奖励、限制行动过大的惩罚.整个仿真的结束信号为机器人是否处于不健康状态的位姿判定和经过1 000个时间步.
Walker环境是在Hopper环境的基础上通过添加另一组腿的模型, 使机器人可向前行走而不是跳跃, 因此在动作的控制量上增至6维.环境的目标在于对每个连杆的关节施加扭矩, 使机器人尽可能快地向前走而不摔倒.奖励信号的组成和结束判定均与Hopper环境一致.
实验平台为Intel I9 13900K CPU和Nvidia RTX 3090 GPU.使用深度学习计算框架PyTorch作为主要的开发环境.
为了验证HAPPG在实际任务中降低梯度估计方差的效果, 可验证算法的收敛速度.收敛速度可表示为在不同轨迹样本数量下算法的平均轨迹回报.
为了建模基于离散动作空间控制任务的策略, 本文部署一个具有两个隐藏全连接层的神经网络, 两层的宽度都是32, Tanh作为激活函数, Softmax回归处理离散动作.针对连续动作空间任务的策略建模, 网络的层数依然选择两个全连接层作为隐藏层, 但宽度增至128维, ReLU作为激活函数, 高斯策略分布处理连续动作.此外, 所有实验中的每种方法都在固定的5个随机种子数下进行5次实验, 计算平均回报和95%的置信误差带, 最终在此基础上绘制曲线.
为了评估HAPPG 在方差缩减类策略梯度方法中的优势, 在不同任务场景下验证HAPPG性能.同时选择如下对比方法:SVRPG[13], HAPG[14], GPO-MDP[15], SHARP[22], PAGE-PG[23].
离散动作空间控制任务参照PAGE-PG中的实验设定, 具体任务场景为Acrobot、Carpole.
各方法在两种任务场景上的平均回报曲线如图2所示.由图可见, 在Acrobot任务上, GPOMDP作为经典的策略梯度类方法, 是其它方法横向对比的基准, 其前期震荡明显, 收敛速度最慢.SVRPG在GPOMDP的基础上, 利用方差缩减技术, 在收敛速度上略有提升.PAGE-PG在前期训练速度上优于GPOMPP和SVRPG, 但在300~1 800回合的中期训练中震荡较明显, 存在大幅值误差带.HAPPG收敛速度最快, 能在前200回合的数据内达到-200左右的平均回报, 在800回合的数据下逼近收敛.总之, Acrobot任务场景较简单, 5种方法在该任务下都能快速收敛, 方差缩减的实际效果差距较小, HAPPG和SHARP拥有波动较小的误差带和较快的收敛速度.
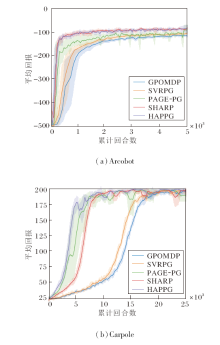 | 图2 各方法在2种离散动作空间控制任务上的平均回报曲线Fig.2 Average return curves of different methods on 2 discrete action space control tasks |
在Carpole任务上, HAPPG达到最快的收敛速度及最优的收敛效果.在早期的5 000回合内, HAPPG以最快的速度几乎逼近收敛.后期的训练中PAGEPG震荡平缓, 稳定性较好.PAGE-PG在前期的收敛效果次优, 但明显出现大幅度的误差带, 平均回报的不确定性会限制策略模型学习的准确度, 在训练中后期仍存在幅值较大的震荡, 方法的不稳定性较明显.SHARP在前期的稳定性较好, 但收敛速度慢于两个使用PAGE形式估计的方法, 在后期存在波动.SVRPG和GPOMDP稳定性较好, 但是收敛速度较慢, 在20 000回合左右才能逼近收敛.
连续动作空间控制任务参照HAPG中的实验设定, 具体任务场景为Hopper、Walker.各方法在2种任务上的平均回报曲线如图3所示.由于当前任务的复杂度较高, 回合间的时间长度并不一致, 大幅影响收集数据点的分布情况, 因此此处将x轴变成与环境的交互次数.
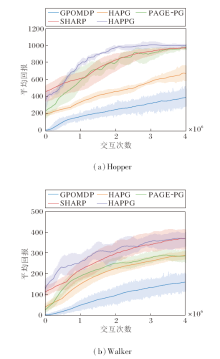 | 图3 各方法在2种连续动作空间控制任务上的平均回报曲线Fig.3 Average return curves of different methods for 2 continuous action space control tasks |
在Hopper任务上, HAPPG收敛速度很快, 在早期就获得较高的回报, 平均回报曲线在整个训练过程中一直保持领先, 并且在前期的训练过程中, 曲线无震荡, 保证良好的收敛稳定性.PAGE-PG依然维持在早期波动较大的特性, 分析原因可能是由于PAGE框架估计形式的概率切换导致的, 不同批量大小的估计形式必然导致学习效果的浮动.HAPPG则通过动量框架的约束限制第一估计形式SGD存在的震荡情况, 因此在震荡情况上有所缓解.GPO-MDP和HAPG仍在训练速度上与使用PAGE的两种方法有一定的差距, 在训练后期存在较大的误差带, 两者之间HAPG通过二阶海森信息的引入改善误差带的幅值.SHARP通过二阶信息的STORM的无环先进结构, 在收敛速度上领先SVRG的类双环结构, 但在前期还存在大范围的误差带, 表现略差于HAPPG.
在Walker任务上, 由于任务难度的增加, 所有方法的整体表现差于Hopper任务.HAPPG仍保持最高的平均回报曲线, 训练前期的收敛速度依然是一大优势, 但在训练后期存在较大的震荡误差带.在复杂任务下, 估计形式的改变对整个训练的稳定性是一个严峻的考验.GPOMDP在前50%训练周期中存在明显的误差带, 但平均回报仍保持稳定的上升, HAPG带有SPIDER这一方差缩减技术, 训练速度快于GPOMDP, 并且二阶信息的利用使HAPG的震荡更小, 在4种方法中最稳定.PAGE-PG在该任务中与HAPG的收敛速度相当, 在实际训练中, 学习率的选择较敏感, 为了保证方法的收敛, 参数选择较保守, 因此该任务上此方法的收敛速度并没有体现.SHARP在收敛速度上仅次于HAPPG, 但两者都存在较大范围的误差带.
由于PAGE本身存在双批量大小的交替使用, 在实际实验中, 批量大小的选择对方法性能存在一定影响.参考文献[12]中PAGE不同批量的对照实验, 对比HAPPG在不同批量大小组合下的性能差异, 找到最优参数.
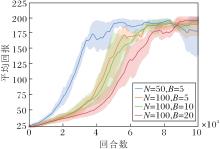
N、B不同时, HAPPG的平均回报曲线如图4所示.
由图4可见, 当N=50, B=5时, HAPPG收敛速度最快, 收敛速度随着N的增大而降低.在深度学习中, 小批量的SGD更新会使目标函数在优化过程中收敛到一个平坦的极小值点, 而大批量的SGD倾向于收敛到一个尖锐的极小值点, 因此使用批量较小的数据进行更新会更高效.所以在固定小批量B时, 拥有更小的批量N的蓝线要比橙线在收敛效果上更优.此外, 在固定批量N时, 小批量B的增加也会降低方法的收敛速度.
梯度修正估计是对历史梯度的重复利用, 估计准确度取决于样本池的深度.在前期训练样本数量匮乏时, 历史信息与最优值的偏差是存在的, 使用较大的批量B更新反倒会限制梯度估计的准确性.因此仅需要一个极小的批量即可.
总结4种任务上的实验结果不难发现, PAGE的使用有效降低梯度估计的方差, 提升方法性能.具体地, 在相同的交互回合下, PAGE-PG和HAPPG都表现出良好的收敛速度, 而海森辅助技术的使用, 能提高梯度下降方向的平缓性.HAPG和HAPPG这类使用该技术的方法都显示出更优的收敛稳定性, 训练误差带的幅值也更小.此外, 拥有无环单步更新结构的STORM在收敛速度上也具有一定优势, 在参数选择上更宽容.
在实际训练过程中发现, 基于PAGE的策略梯度方法在训练后期会产生明显波动, 在某些局部点出现陡降的情况.原因可能在于单一学习率和静态切换频率会对双形式估计的训练过程产生一定限制.
具体地, 由于批量大小的不同:SGD估计在大批量的情况下是一个偏差较小、方差较大的估计形式; 小批量方差缩减估计受限于样本数量, 是一个偏差较大、方差较小的估计形式.在训练前期, 由于总体样本池轨迹数量的匮乏, 如何高效利用样本快速实现收敛是主要目的, 因此在训练的前期重新使用历史梯度进行修正是必要的.在训练后期, 由于策略模型逐渐收敛, 稳定性取代收敛速度成为主要目的.大偏差的小批量估计对后期稳定性影响较大, 可适当降低选择频率.因此在实际训练中, 可考虑使用策略学习率退火技术和切换频率退火技术.在训练前期保证一个较大的学习率和切换频率, 随着训练周期的增加, 学习率以指数衰减, 切换频率以周期性降低.
为了验证HAPPG中提出的基于海森辅助的策略梯度估计器是否具有更高的适用性, 本文参考同为on-policy的策略梯度方法PPO.
PPO作为目前强化学习领域主流方法之一, 在各领域适用性较强、性能较优.与此同时, 各类改良技术也逐步被提出.本文也将 HAPPG中的估计器作为一个改良技术使用在PPO中, 提出HAP-PPO.
本节旨在对比PPO和HAP-PPO的性能.2种方法均采用GAE形式的目标函数作为PPO近似优化的目标.区别于在理论部分提出的简单利用MC(Monte Carlo)估计获取的目标函数, 这是一种利用AC(Actor-Critic)框架和TD(Temporal Difference)进一步降低目标函数的方差缩减技巧, 在PPO的各类任务中广泛使用.
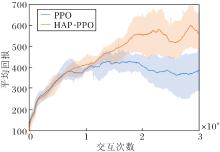
实验场景选择Walker任务, 这是一个较难的机器人控制任务, 状态维度达到17维, 动作空间是连续的6维.PPO和HAP-PPO的平均回报曲线如图5所示.
由图5可见, 在前期训练中, 两者保持良好的收敛速度, 几乎一致.在训练中后期, HAP-PPO收获更高的平均回报, 比PPO提升约25%.不难发现, 无论是HAP-PPO还是PPO在训练中后期都存在较大的误差带.适当的增加训练周期和利用GAE估计优势函数替代目前使用的蒙特卡洛回报估计可缓解这一问题.当然由于PPO性能的优异, 两种方法都在3×106最大交互次数内达到不错的平均回报.
为了解决策略梯度方法中存在的方差过大问题, 本文参考在一般监督学习中成功验证的方差缩减的梯度估计器, 针对强化学习的具体设定, 引入蒙特卡洛近似估计和海森辅助技术, 克服强化学习的非有限和形式和策略分布随时间偏移等问题, 设计海森辅助的概率策略梯度估计方法(HAPPG).该方法基于PAGE, 引入海森估计替代在梯度修正估计中存在的一阶梯度差异量.以一个概率切换估计器的形式, 利用大批量带有动量的SGD 更新维持梯度更新的方向或利用小批量历史梯度修正估计, 重复利用历史梯度信息, 最终实现一个能以线性收敛的方差缩减的策略梯度估计方法.在理论证明方面, 本文利用随机优化的思路, 在性能函数非凸时, 推导梯度的收敛性.最终验证HAPPG在实现$\epsilon$-稳定解所需的样本复杂度.在应用拓展方面, 提出结合海森辅助策略梯度估计器的HAP-PPO.通过两组不同控制环境下的实验, 对比目前的基于方差缩减技术的策略梯度方法, 表明HAPPG具有较快的收敛速度, 一定程度上证实其能显著降低梯度估计时的方差.此外, HAP-PPO的对比实验也验证海森辅助策略梯度估计器的广泛适用性, 在主流的AC框架算法中仍可应用此类技术以提高方法性能.
今后可考虑从如下方面开展研究.
1)HAPPG这种方差缩减的技术与AC框架下降低方差的技术并不同源, TD、GAE等技术都是通过改变目标函数的形式减小方差.而HAPPG在梯度估计时利用随机优化理论, 通过适当的对估计值缩减操作, 减少梯度估计中的噪声, 加速收敛.这意味着两者没有对比性, 可叠加使用.在轨迹数据on-policy的前提下, 既可利用GAE等技术改变目标函数本身以降低方差, 同时也可在对目标函数进行梯度估计时使用方差缩减技术以进一步降低方差.今后可探索将方差缩减技术与AC框架下的先进算法结合.
2)现有实验表明, HAPPG存在较多需要调节的超参数.首先, 切换概率的选择仍是一个关键问题.如何合理选择切换概率, 平衡两种估计方式之间的转换, 从而权衡方法的收敛稳定性与收敛速度, 仍需要进一步探讨.其次, 在学习率方面, 尽管引入二阶曲率信息理论上能减少HAPPG对学习率参数的敏感性, 但实际应用中依然需要仔细调整该参数.目前, 主流的自适应优化方法在降低学习率调整的复杂度上取得有效进展, 如何将其应用于方差缩减框架, 仍是值得后续研究的方向.
本文责任编委 兰旭光
Recommended by Associate Editor LAN Xuguang
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|