文中$\left| X \right|$表示集合X的基数, ¬ X表示集合X关于U的补集, 即

$\neg X=U-X=\left\{ x\in U\left| x \right.\notin X \right\}$.

设U={x₁, x₂, ···, x_n}为一个非空有限对象集, 即论域.记P(U)为U的幂集.本节主要回顾区间集、区间集信息系统和区间集决策熵的概念及相关性质.

定义1^[11] 称S=(U, A)为一个信息系统, 其中, U={x₁, x₂, ···, x_n}为论域, A={a₁, a₂, ···, a_m}为一个非空有限属性集, 对于∀ a_j∈ A, 有a_j:U→ V_j, 其中V_j为a_j的值域.

称S=(U, A∪ {d})为一个决策系统, 其中, (U, A)为一个信息系统, d∉A为决策, d:U→ V_d, V_d为d的值域.

定义2^[39] 设U为一个非空有限集, 若集合A_l∈ P(U), A_u∈ P(U)且A_l⊆A_u, 则称A=[A_l, A_u]为P(U)上的一个区间集, 其中, A_l为A的下边界集, A_u为A的上边界集.记

$I(U)=\left\{ \left[ {{A}_{l}}, {{A}_{u}} \right]\left| {{A}_{l}} \right., {{A}_{u}}\in \mathcal{P}\left( U \right), \text{ }{{A}_{l}}\subseteq {{A}_{u}} \right\}$

为P(U)上所有区间集构成的集合.

定义3^[39] 设U为一个非空有限集,

A=[A_l, A_u]∈ I(U), B=[B_l, B_u]∈ I(U),

定义

$\begin{align} & \mathcal{A}\sqcap \mathcal{B}=\left[ {{A}_{l}}\cap {{B}_{l}}, {{A}_{u}}\cap {{B}_{u}} \right], \\ & \mathcal{A}\sqcup \mathcal{B}=\left[ {{A}_{l}}\cup {{B}_{l}}, {{A}_{u}}\cup {{B}_{u}} \right], \\ & \mathcal{A}\backslash \mathcal{B}=\left[ {{A}_{l}}-{{B}_{u}}, {{A}_{u}}-{{B}_{l}} \right], \\ \end{align}$

$\neg \mathcal{A}=\neg \left[ {{A}_{l}}, {{A}_{u}} \right]=\left[ U, U \right]\backslash \left[ {{A}_{l}}, {{A}_{u}} \right]=\left[ U-{{A}_{u}}, U-{{A}_{l}} \right]$

定义4^[39] 设U为一个非空有限集,

A=[A_l, A_u]∈ I(U), B=[B_l, B_u]∈ I(U),

若A_l⊆B_l且A_u⊆B_u, 则称A包含于B, 记作$\mathcal{A}\sqsubseteq \mathcal{B}$.

性质1^[39] 设U为一个非空有限集,

A=[A_l, A_u]∈ I(U), B=[B_l, B_u]∈ I(U),

则

$\begin{align} & \text{1) }\mathcal{A}\sqsubseteq \mathcal{B}\Leftrightarrow \mathcal{A}\sqcap \mathcal{B}=\mathcal{A}\mathcal{A}\sqcup \mathcal{B}=\mathcal{B}\text{, } \\ & \text{2) }\mathcal{A}\sqsubseteq \mathcal{B}\Leftrightarrow {{A}_{l}}\cap {{B}_{l}}={{A}_{l}}{{A}_{u}}\cap {{B}_{u}}={{A}_{u}}, \\ \end{align}$

$3)\text{ }\mathcal{A}\sqsubseteq \mathcal{B}\Leftrightarrow {{A}_{l}}\cup {{B}_{l}}={{B}_{l}}{{A}_{u}}\cup {{B}_{u}}={{B}_{u}}.$

定义5^[43] 设U为一个非空有限集,

A=[A_l, A_u]∈ I(U), B=[B_l, B_u]∈ I(U),

则A、B的相似度定义如下:

S(A, B)= |Al⋂Bl|+|Au⋂Bu||Al⋃Bl|+|Au⋃Bu|.

性质2^[43]S(A, B)具有如下性质:

1)0≤ S(A, B)≤ 1,

2)S(A, B)=1⇔ A=B,

3)S(A, B)=S(B, A).

定义6^[41] 称S=(U, A)为一个区间集信息系统, 其中, U={x₁, x₂, ···, x_n}为论域, A={a₁, a₂, ···, a_m}为一个非空有限属性集, 且对于∀ a_j∈ A, 有a_j:U→ I(V_j), 其中, V_j为a_j的值域.

与普通的信息系统不同, 区间集信息系统中对象的属性值都是区间集, 即对于∀ x∈ U, 若设 Cjlower(x)与 Cjupper(x)分别为区间集a_j(x)的下边界集与上边界集, 则

$C_{j}^{lower}\left( x \right)\subseteq C_{j}^{upper}\left( x \right)\subseteq {{V}_{j}}$,

因此a_j(x)可表示为

${{a}_{j}}(x)=\left[ C_{j}^{lower}\left( x \right), C_{j}^{upper}\left( x \right) \right]\in I\left( {{V}_{j}} \right)$.

定义7^[43] 设S=(U, A)为一个区间集信息系统, 对于∀ B⊆A, a∈ B, 给定一个阈值δ ∈ [0, 1], 则由a和δ 确定的相似关系

$R_{a}^{\delta }=\left\{ \left. \left( x, y \right)\in U\times U \right|S\left( a(x), a(y) \right)\ge \delta \right\}$,

由B和δ 确定的相似关系

$R_{B}^{\delta }=\left\{ \left( x, y \right)\in U\times U\left| S \right.\left( a(x), a(y) \right)\ge \delta , \forall a\in B \right\}=\underset{a\in B}{\mathop{\bigcap }}\, R_{a}^{\delta }$,

记x关于 RBδ的相似类

$\left[ x \right]_{B}^{\delta }=\left\{ \left. y\in U \right|\left( x, y \right)\in R_{B}^{\delta } \right\}$,

记由 RBδ生成的所有相似类构成的集合

${U}/{R_{B}^{\delta }}\; =\left\{ \left. \left[ x \right]_{B}^{\delta } \right|x\in U \right\}$.

定义8^[43] 称S=(U, A∪ {d})为一个区间集决策系统, 其中, (U, A)为一个区间集信息系统, d∉A为决策, 且d:U→ V_d, V_d为d的值域.

由d导出的等价关系定义为

${{R}_{d}}=\left\{ \left( x, y \right)\in U\times \left. U \right|d\left( x \right)=d\left( \text{y} \right) \right\}$,

不妨设V_d={1, 2, ···, t}, 则R_d将U中对象粒化为互不相交的等价类, 它们构成U的一个划分:

${U}/{{{R}_{d}}}\; =\left\{ \left. {{\left[ x \right]}_{d}} \right|x\in U \right\}=\left\{ {{D}_{1}}, {{D}_{2}}, \cdots , {{D}_{t}} \right\}$,

其中

${{D}_{k}}=\left\{ y\in U\left| d\left( y \right)=k \right. \right\}, $, k∈ {1, 2, ···, t}.

进一步地, 若 RAδ⊆R_d, 则称区间集决策系统S是协调的, 否则称S是不协调的.

定义9^[43] 设S=(U, A∪ {d})为一个区间集决策系统, U/R_d={D₁, D₂···, D_t}, B⊆A, δ ∈ [0, 1], 则d关于B和δ 的区间下近似与区间上近似分别定义如下:

$\underline{R_{B}^{\delta }}({U}/{{{R}_{d}}}\; )=\underset{1\le k\le t}{\mathop \bigcup }\, \underline{R_{B}^{\delta }}({{D}_{k}})$,

$\overline{R_{B}^{\delta }}({U}/{{{R}_{d}}}\; )=\underset{1\le k\le t}{\mathop \bigcup }\, \overline{R_{B}^{\delta }}({{D}_{k}})$,

其中

$\begin{align} & \underline{R_{B}^{\delta }}({{D}_{k}})=\left\{ x\in \left. U \right|\left[ x \right]_{B}^{\delta }\subseteq {{D}_{k}} \right\}, \\ & \overline{R_{B}^{\delta }}({{D}_{k}})=\left\{ x\in \left. U \right|\left[ x \right]_{B}^{\delta }\bigcap {{D}_{k}}\ne \varnothing \right\}, \\ & k\in \left\{ 1, 2, \cdots , t \right\}.\end{align}$

d关于B和δ 的区间近似精度与区间粗糙度分别定义如下:

$\alpha _{B}^{\delta }\left( {U}/{{{R}_{d}}}\; \right)=\frac{\sum{_{{{D}_{k}}\in {U}/{{{R}_{d}}}\; }\left| \underline{R_{B}^{\delta }}\left( {{D}_{k}} \right) \right|}}{\sum{_{{{D}_{k}}\in {U}/{{{R}_{d}}}\; }}\left| \overline{R_{B}^{\delta }}\left( {{D}_{k}} \right) \right|}$,

$\rho _{B}^{\delta }\left( {U}/{{{R}_{d}}}\; \right)=1-\alpha _{B}^{\delta }\left( {U}/{{{R}_{d}}}\; \right)=1-\frac{\sum{_{{{D}_{k}}\in {U}/{{{R}_{d}}}\; }}\left| \underline{R_{B}^{\delta }}\left( {{D}_{k}} \right) \right|}{\sum{_{{{D}_{k}}\in {U}/{{{R}_{d}}}\; }}\left| \overline{R_{B}^{\delta }}\left( {{D}_{k}} \right) \right|}$.

定义10^[43] 设S=(U, A∪ {d})为一个区间集决策系统, U/R_d={D₁, D₂, ···, D_t}, B⊆A, δ ∈ [0, 1], 则d关于B和δ 的条件熵定义如下:

${{H}^{\delta }}\left( \left. d \right|B \right)=-\sum\limits_{i=1}^{n}{\sum\limits_{k=1}^{t}{\frac{\left| \left[ {{x}_{i}} \right]_{B}^{\delta }\bigcap {{D}_{k}} \right|}{U{{}^{2}}}{{\log }_{2}}\frac{\left| \left[ {{x}_{i}} \right]_{B}^{\delta }\bigcap {{D}_{k}} \right|}{\left| \left[ {{x}_{i}} \right]_{B}^{\delta } \right|}}}$

其中, n为U的基数, t为U/R_d的基数, 约定log₂0=0.

定义11^[43] 设S=(U, A∪ {d})为一个区间集决策系统, B⊆A, δ ∈ [0, 1], 则d关于B和δ 的区间集决策熵定义如下:

$ID{{H}^{\delta }}\left( \left. d \right|B \right)=\rho _{B}^{\delta }\left( {U}/{{{R}_{d}}}\; \right){{H}^{\delta }}\left( \left. d \right|B \right)$.

定义12^{[23, 30]} 称S=(U, A)为一个广义多尺度信息系统, 其中, U={x₁, x₂, ···, x_n}为论域, A={a₁, a₂, ···, a_m}为一个非空有限属性集, 且每个a_j∈ A都是多尺度属性.若对于a_j∈ A, a_j具有I_j个尺度, 则一个广义多尺度信息系统可表示为

$\left( U, A \right)=\left( U, \left\{ \left. a_{j}^{l} \right|l=1, 2, \cdots , {{I}_{j}}, j=1, 2, \cdots , m \right\} \right)$,

其中 ajl:U→ V jl, V jl为a_j在第l个尺度下的值域, 且对于j∈ {1, 2, ···, m}, l∈ {2, 3, ···, I_j}, 存在一个满射 gjl, l-1:V jl→ V jl-1, 使得

$a_{j}^{l-1}=g_{j}^{l, l-1}\circ a_{j}^{l}$,

即对于∀ x∈ U, 有

$a_{j}^{l-1}\left( x \right)=g_{j}^{l, l-1}\left( a_{j}^{l}\left( x \right) \right)$,

称 gjl, l-1为信息粒度变换.

进一步地, 称

$S=\left( U, A\bigcup \left\{ d \right\} \right)=\left( U, \left\{ \left. a_{j}^{l} \right|l=1, 2, \cdots , {{I}_{j}}, j=1, 2, \cdots , m \right\}\bigcup \left\{ d \right\} \right)$

为一个广义多尺度决策系统, 其中, (U, A)为一个广义多尺度信息系统, d∉A为决策, 且d:U→ V_d, V_d为d的值域.

定义13^[30] 设S=(U, A∪ {d})为一个广义多尺度决策系统, 对于a_j∈ A(j∈ {1, 2, ···, m}), l_j∈ {0, 1, ···, I_j}, 若l_j=0, 表示删除a_j, 进一步地, 若l_j≠ 0, 表示a_j选择第l_j个尺度, 记L=(l₁, l₂, ···, l_m), 则称L为S的一个尺度组合.

记S的尺度组合全体为L, 则每个尺度组合

$L=({{l}_{1}}, {{l}_{2}}, \cdots , {{l}_{m}})\in \mathcal{L}$

对应一个单尺度决策系统S^L=(U, A^L∪ {d}), 其中

${{A}^{L}}=\left\{ a_{1}^{{{l}_{1}}}, a_{2}^{{{l}_{2}}}, \cdots , a_{m}^{{{l}_{m}}} \right\}$.

本节给出广义多尺度区间集决策系统和该系统下区间集决策熵的相关概念.

定义14 称S=(U, A)为一个广义多尺度区间集信息系统, 其中U={x₁, x₂, ···, x_n}为论域, A={a₁, a₂, ···, a_m}为一个非空有限属性集, 每个a_j∈ A有I_j个尺度(j∈ {1, 2, ···, m}), 且每个对象在每个尺度下的属性取值均为区间集.这样的一个广义多尺度区间集信息系统可表示为

$S=\left( U, A \right)=\left( U, \left\{ \left. a_{j}^{l} \right|l=1, 2, \cdots , {{I}_{j}}, j=1, 2, \cdots , m \right\} \right)$,

其中 ajl:U→ I(V jl), V jl为a_j在第l个尺度下的值域, 即对于∀ x∈ U有

$a_{j}^{l}(x)=\left[ C_{j, l}^{lower}\left( x \right), C_{j, l}^{upper}\left( x \right) \right]\in I(V_{j}^{l})$,

$C_{j, l}^{lower}\left( x \right)\subseteq C_{j, l}^{upper}\left( x \right)\subseteq V_{j}^{l}$.

并且对于j∈ {1, 2, ···, m}, l∈ {2, 3, ···, I_j}, 存在两个满射, 其中一个是信息粒度变换

gjl, l-1:V jl→ V jl-1,

即

vjl-1= gjl, l-1( vjl), vjl∈ V jl;

另一个是信息值的变换

γjl, l-1:I(V jl)→ I(V jl-1),

使得对于∀ x∈ U有

$\begin{align} & a_{j}^{l-1}\left( x \right)=\gamma _{j}^{l, l-1}\left( a_{j}^{l}\left( x \right) \right) \\ & =\gamma _{j}^{l, l-1}\left( \left[ C_{j, l}^{lower}\left( x \right), C_{j, l}^{upper}\left( x \right) \right] \right) \\ & =\left[ g_{j}^{l, l-1}\left( C_{j, l}^{lower}\left( x \right) \right), g_{j}^{l, l-1}\left( C_{j, l}^{upper}\left( x \right) \right) \right] \\ & =\left[ \left\{ g_{j}^{l, l-1}(v)|v\in C_{j, l}^{lower}\left( x \right) \right\}, \left\{ g_{j}^{l, l-1}\left( w \right)|w\in C_{j, l}^{upper}\left( x \right) \right\} \right] \\ & =\left[ C_{j, l-1}^{lower}\left( x \right), C_{j, l-1}^{upper}\left( x \right) \right]. \end{align}$

定义15 称

$S=\left( U, A\bigcup \left\{ d \right\} \right)=\left( U, \right.\left\{ a_{j}^{l}\text{ }\!\!|\!\!\text{ }l=1, \right.2, \cdots , $${{I}_{j}}, j=\left. \left. 1, 2, \cdots , m \right\}\bigcup \left\{ d \right\} \right)$

为一个广义多尺度区间集决策系统, 其中, (U, A)为一个广义多尺度区间集信息系统, d∉A为决策, 且d:U→ V_d, V_d为d的值域.

定义16 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, 对于a_j∈ A, l_j∈ {0, 1, ···, I_j}, j∈ {1, 2, ···, m}, 若l_j=0, 表示删除a_j, 进一步地, 若l_j≠ 0, 表示a_j选择第l_j个尺度, 记L=(l₁, l₂, ···, l_m), 称L为S的一个尺度组合.

记S的尺度组合全体为L, 则每个尺度组合

$L=({{l}_{1}}, {{l}_{2}}, \cdots , {{l}_{m}})\in \mathcal{L}$

对应一个单尺度区间集决策系统

${{S}^{L}}=\left( U, {{A}^{L}}\bigcup \left\{ d \right\} \right)$,

其中

${{A}^{L}}=\left\{ \left. a_{j}^{{{l}_{j}}} \right|\text{ }j=1, 2, \cdots , m \right\}$

为A在尺度组合L上的限制.

例如, 若A={a₁, a₂, a₃}, 且L=(2, 0, 1)∈ L, 则A^L={ a12, a31}.

定义17 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统,

L₁=( l11, l21, ···, lm1)∈ L, L₂=( l12, l22, ···, lm2)∈ L,

若对于∀ j∈ {1, 2, ···, m}, 有 lj1≤ lj2, 则称尺度组合L₁弱于L₂或称L₂强于L₁, 记为L₂⪰L₁.进一步, 若存在j∈ {1, 2, ···, m}, 使得 lj1< lj2, 则称尺度组合L₁严格弱于L₂或称L₂严格强于L₁, 记为L₂≻L₁.

定义18 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, 对于

L₁=( l11, l21, ···, lm1)∈ L, L₂=( l12, l22, ···, lm2)∈ L,

记

L₁∧ L₂=( l11∧ l12, l21∧ l22, ···, lm1∧ lm2),

L₁∨ L₂=( l11∨ l12, l21∨ l22, ···, lm1∨ lm2),

其中

$l_{j}^{1}\wedge l_{j}^{2}=\min \left\{ l_{j}^{1}, l_{j}^{2} \right\}, \text{ }l_{j}^{1}\vee l_{j}^{2}=\text{max}\left\{ l_{j}^{1}, l_{j}^{2} \right\}, $

$j\in \left\{ 1, 2, \cdots , m \right\}.$

易知, (L, ⪰, ∧ , ∨ )为一个完备格, 最小元为L_l=(0, 0, ···, 0), 最大元为L₀=(I₁, I₂, ···, I_m).

以下恒记L₀=(I₁, I₂, ···, I_m).

例1 表1 为一个广义多尺度区间集决策系统S=(U, A∪ {d}), 其中, U={x₁, x₂, ···, x₈}表示上海某艺术学校的8名学生, A={a₁, a₂, a₃}, a₁表示乐器的演奏能力, a₂表示乐器品质的鉴别能力, a₃表示乐器相关文化知识的掌握能力.第三个尺度下的属性值D、H、G、F、S分别表示架子鼓、二胡、古筝、笛子、唢呐; 第二个尺度下的属性值Pe、St、Bl分别表示打击乐器、弦乐器、吹奏乐器; 第一个尺度下的属性值W、C分别表示西洋乐器、民族乐器.V_d={0, 1}, d为1表示该学生是音乐特长生, d为0表示该学生不是音乐特长生.

表1

Table 1

表1(Table 1)

表1 一个广义多尺度区间集决策系统 Table 1 A generalized multi-scale interval-set decision system U a1 a2 a3 d $\text{ }a_{1}^{3}\xrightarrow{\text{ }\gamma _{1}^{3, 2}\text{ }}a_{1}^{2}\xrightarrow{\text{ }\gamma _{1}^{2, 1}\text{ }}a_{1}^{1}$ $\text{ }a_{2}^{2}\xrightarrow{\text{ }\gamma _{2}^{2, 1}\text{ }}a_{2}^{1}$ $\text{ }a_{3}^{2}\xrightarrow{\text{ }\gamma _{3}^{2, 1}\text{ }}a_{3}^{1}$ x1 [{D}, {D}] [{Pe}, {Pe}] [{W}, {W}] [{St}, {St}] [{C}, {C}] [{Pe}, {Pe}] [{W}, {W}] 1 x2 [{Ø }, {D}] [{Ø }, {Pe}] [{Ø }, {W}] [{Bl}, {Bl}] [{C}, {C}] [{Pe}, {Pe, Bl}] [{W}, {W, C}] 0 x3 [{H, G}, {H, G, F}] [{St}, {St, Bl}] [{C}, {C}] [{Pe}, {Pe, Bl}] [{W}, {W, C}] [{Pe}, {Pe}] [{W}, {W}] 1 x4 [{D}, {D}] [{Pe}, {Pe}] [{W}, {W}] [{Bl}, {St, Bl}] [{C}, {C}] [{St}, {St}] [{C}, {C}] 1 x5 [{Ø }, {G}] [{Ø }, {St}] [{Ø }, {C}] [{St}, {St}] [{C}, {C}] [{Bl}, {Bl}] [{C}, {C}] 1 x6 [{H, G}, {H, G, D}] [{St}, {St, Pe}] [{C}, {C, W}] [{St}, {St}] [{C}, {C}] [{Bl}, {Bl, St}] [{C}, {C}] 0 x7 [{S}, {F, S}] [{Bl}, {Bl}] [{C}, {C}] [{Pe}, {Pe}] [{W}, {W}] [{Bl}, {Bl}] [{C}, {C}] 1 x8 [{F}, {F}] [{Bl}, {Bl}] [{C}, {C}] [{Bl}, {Bl}] [{C}, {C}] [{Ø }, {St}] [{Ø }, {C}] 0

表1 一个广义多尺度区间集决策系统 Table 1 A generalized multi-scale interval-set decision system

例如:表1中

a13(x₃)=[{H, G}, {H, G, F}]

表明学生x₃会演奏二胡和古筝, 可能会演奏笛子,

a12(x₃)=[{St}, {St, Bl}]

表明学生x₃会鉴别弦乐器品质的优劣, 可能会鉴别吹奏乐器品质的优劣,

a11(x₃)=[{C}, {C}]

表明学生x₃了解民族乐器的历史发展和文化背景.

属性值域的信息粒度变换如下:

g13, 2(u)= Pe, u∈{D}St, u∈{H, G}Bl, u∈{F, S}

gj2, 1(v)= W, v∈{Pe}C, v∈{St, Bl}

j=1, 2, 3.

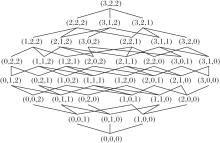
系统尺度组合的格结构图1所示.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 尺度组合的格结构Fig.1 Lattice structure of scale combinations

文中对于∀ a_j∈ A, l_j∈ {2, 3, ···, I_j}, 假设存在一系列阈值 δjlj∈ [0, 1], 且满足

0≤ δjlj-1≤ δjlj.

同时, 对于∀ L∈ L, 记

${{\delta }^{L}}=\left\{ \left. \delta _{j}^{{{l}_{j}}} \right|a_{j}^{{{l}_{j}}}\in {{A}^{L}} \right\}$

为L对应的阈值集合.

定义19 设

$S=\left( U, A\bigcup \left\{ d \right\} \right)=\left( U, \right.\left\{ \left. a_{j}^{l} \right|l=1, \right.2, \cdots , $${{I}_{j}}, j=\left. \left. 1, 2, \cdots , m \right\}\bigcup \left\{ d \right\} \right)$

为一个广义多尺度区间集决策系统, 对于∀ a_j∈ A, l_j∈ {1, 2, ···, I_j}, δjlj∈ [0, 1], 定义由 ajlj和 δjlj导出的相似关系如下:

$R_{a_{j}^{{{l}_{j}}}}^{\delta _{j}^{{{l}_{j}}}}=\left\{ \left( x, y \right)\in U\times \left. U \right|S\left( a_{j}^{{{l}_{j}}}(x), a_{j}^{{{l}_{j}}}(y) \right)\ge \delta _{j}^{{{l}_{j}}} \right\}, $,

其中S( ajlj(x), ajlj(y))表示在定义5意义下对象x、y关于 ajlj的相似度.

命题1 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, a_j∈ A, l_j∈ {2, 3, ···, I_j}, δjlj∈ [0, 1], 若

δjlj-1≤ γlj, lj-1≤ δjlj,

其中

${{\gamma }^{{{l}_{j}}, {{l}_{j}}-1}}=\min \left\{ \underset{\left( x, y \right)\in R_{a_{j}^{{{l}_{j}}}}^{\delta _{j}^{{{l}_{j}}}}}{\mathop{\min }}\, S\left( a_{j}^{{{l}_{j}}-1}(x), a_{j}^{{{l}_{j}}-1}(y) \right), \text{ }\delta _{j}^{{{l}_{j}}} \right\}$

则

Rajljδjlj⊆ Rajlj-1δjlj-1.

证明 对于∀ (x, y)∈ Rajljδjlj, 由定义19可得

S( ajlj-1(x), ajlj-1(y))≥ γlj, lj-1≥ δjlj-1,

所以

(x, y)∈ Rajlj-1δjlj-1,

即

Rajljδjlj⊆ Rajlj-1δjlj-1. 证毕.

注1 命题1表明, 同一属性在相邻尺度下导出的对象集上的相似关系关于尺度满足反单调性, 即尺度越大, 对应的二元关系越小.

注2 本文以下讨论中恒假设

δjlj-1≤ γlj, lj-1≤ δjlj,

其中, l_j∈ {2, 3, ···, I_j}, j∈ {1, 2, ···, m}.

例2 (续例1) 设

δ13=0.6, δ22=0.5, δ32=0.5,

对于a₁, 计算得

$U / R_{a_{1}^{3}}^{\delta_{1}^{3}}=\left\{\left\{x_{1}, x_{4}\right\}, \left\{x_{2}\right\}, \left\{x_{3}, x_{6}\right\}, \left\{x_{5}\right\}, \left\{x_{7}\right\}, \left\{x_{8}\right\}\right\}, $

$\begin{aligned} \delta_{1}^{2}= & \gamma_{1}^{3, 2}= \\ & \min \left\{\min _{\substack{\delta_{1}^{3} \\ (x, y) \in R_{a_{1}^{3}}^{3}}}\left(S\left(a_{1}^{2}(x), a_{1}^{2}(y)\right)\right), \delta_{1}^{3}\right\}=0.5, \end{aligned}$

$U / R_{a_{1}^{2}}^{\delta_{1}^{2}}=\left\{\left\{x_{1}, x_{2}, x_{4}\right\}, \left\{x_{5}\right\}, \left\{x_{3}, x_{6}\right\}\left\{x_{7}, x_{8}\right\}\right\}, $

$\begin{aligned} \delta_{1}^{1}= & \gamma_{1}^{2, 1}= \\ & \min \left\{\min _{(x, y) \in R_{a_{1}^{2}}^{2}}\left(S\left(a_{1}^{1}(x), a_{1}^{1}(y)\right)\right), \delta_{1}^{2}\right\}=0.5, \end{aligned}$

$\begin{array}{r} U / R_{a_{1}^{1}}^{\delta_{1}^{1}}=\left\{\left\{x_{1}, x_{2}, x_{4}\right\}, \left\{x_{3}, x_{5}, x_{6}, x_{7}, x_{8}\right\}, \right. \\ \\ \left.\left\{x_{3}, x_{5}, x_{7}, x_{8}\right\}, \left\{x_{3}, x_{6}, x_{7}, x_{8}\right\}\right\} . \end{array}$

对于a₂, 计算得

$U / R_{a_{2}^{2}}^{\delta_{2}^{2}}=\left\{\left\{x_{1}, x_{5}, x_{6}\right\}, \left\{x_{2}, x_{4}, x_{8}\right\}, \left\{x_{3}, x_{7}\right\}\right\}, $

$\begin{aligned} \delta_{2}^{1}= & \gamma_{2}^{2, 1}= \\ & \min \left\{\min _{(x, y) \in R_{a_{2}^{2}}^{\delta_{2}^{2}}}\left(S\left(a_{2}^{1}(x), a_{2}^{1}(y)\right)\right), \delta_{2}^{2}\right\}=0.5, \end{aligned}$

$U / R_{a_{2}^{1}}^{\delta_{2}^{1}}=\left\{\left\{x_{1}, x_{2}, x_{4}, x_{5}, x_{6}, x_{8}\right\}, \left\{x_{3}, x_{7}\right\}\right\} .$

对于a₃, 计算得

${U}/{R_{a_{3}^{2}}^{\delta _{3}^{2}}}\; =\left\{ \left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{3}} \right\}, \left\{ {{x}_{4}}, {{x}_{8}} \right\}, \left\{ {{x}_{5}}, {{x}_{6}}, {{x}_{7}} \right\} \right\}, $

$\delta _{3}^{1}=\gamma _{3}^{2, 1}=\min \left\{ \underset{\left( x, y \right)\in R_{a_{3}^{2}}^{\delta _{3}^{2}}}{\mathop{\min }}\, \left( S\left( a_{3}^{1}(x), a_{3}^{1}(y) \right) \right), \delta _{3}^{2} \right\}=0.5, $

${U}/{R_{a_{3}^{1}}^{\delta _{3}^{1}}}\; =\left\{ \left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{3}} \right\}, \left\{ {{x}_{4}}, {{x}_{5}}, {{x}_{6}}, {{x}_{7}}, {{x}_{8}} \right\} \right\}.$

定义20 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, L=(l₁, l₂, ···, l_m)∈ L, 若存在j∈ {1, 2, ···, m}, 使得l_j≠ 0, 则定义由A^L和δ ^L导出的相似关系如下:

$R_{{{A}^{L}}}^{{{\delta }^{L}}}=\left\{ \left( x, y \right)\in U\times \left. U \right|\left( x, y \right)\in R_{a_{j}^{{{l}_{j}}}}^{\delta _{j}^{{{l}_{j}}}}, \forall a_{j}^{{{l}_{j}}}\in {{A}^{L}} \right\}$.

记x关于 RALδL的相似类

$\left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}=\left\{ y\in \left. U \right|\left( x, y \right)\in R_{{{A}^{L}}}^{{{\delta }^{L}}} \right\}$, $x\in U$.

.

记由 RALδL生成的所有相似类构成的集合

${U}/{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\; =\left\{ \left. \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}} \right|x\in U \right\}$.

例3 (续例2) 给定4个尺度组合:

L₀=(3, 2, 2) ∈ L, L₃=(3, 0, 1)∈ L,

L4₌(2, 0, 1)∈ L, L5₌(3, 0, 0) ∈ L,

经计算可得

${U}/{R_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}}\; =\left\{ \left\{ {{x}_{1}} \right\}, \left\{ {{x}_{2}} \right\}, \left\{ {{x}_{3}} \right\}, \left\{ {{x}_{4}} \right\}, \left\{ {{x}_{5}} \right\}, \left\{ {{x}_{6}} \right\}, \left\{ {{x}_{7}} \right\}, \left\{ {{x}_{8}} \right\} \right\}, $

${U}/{R_{{{A}^{{{L}_{3}}}}}^{{{\delta }^{{{L}_{3}}}}}}\; =\left\{ \left\{ {{x}_{1}} \right\}, \left\{ {{x}_{2}} \right\}, \left\{ {{x}_{3}} \right\}, \left\{ {{x}_{4}} \right\}, \left\{ {{x}_{5}} \right\}, \left\{ {{x}_{6}} \right\}, \left\{ {{x}_{7}} \right\}, \left\{ {{x}_{8}} \right\} \right\}, $

$\begin{align} & {U}/{R_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}}\; =\left\{ \left\{ {{x}_{1}}, {{x}_{2}} \right\}, \left\{ {{x}_{3}} \right\}, \left\{ {{x}_{4}} \right\}, \left\{ {{x}_{5}} \right\}, \left\{ {{x}_{6}} \right\}, \left\{ {{x}_{7}}, {{x}_{8}} \right\} \right\}, \\ & {U}/{R_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}}\; =\left\{ \left\{ {{x}_{1}}, {{x}_{4}} \right\}, \left\{ {{x}_{2}} \right\}, \left\{ {{x}_{3}}, {{x}_{6}} \right\}, \left\{ {{x}_{5}} \right\}, \left\{ {{x}_{7}} \right\}, \left\{ {{x}_{8}} \right\} \right\}, \\ \end{align}$

${U}/{{{R}_{d}}}\; =\left\{ \left\{ {{x}_{1}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{7}} \right\}, \left\{ {{x}_{2}}, {{x}_{6}}, {{x}_{8}} \right\} \right\}=\left\{ {{D}_{1}}, \text{ }{{D}_{2}} \right\}.$

命题2 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, 对于L₁∈ L, L₂∈ L, 若L₂⪰L₁, 则 RAL2δL2⊆ RAL1δL1.

证明 对于∀ (x, y)∈ RAL2δL2, 设

L₁=( l11, l21, ···, lm1), L₂=( l12, l22, ···, lm2),

由L₂⪰L₁以及定义17可得, 对于∀ j∈ {1, 2, ···, m}, 有 lj1≤ lj2.记

$J=\left\{ \left. j \right|\text{ }l_{j}^{1}\ne 0, j\in \left\{ 1, 2, \cdots , m \right\} \right\}$.

由

$R_{{{A}^{{{L}_{2}}}}}^{{{\delta }^{{{L}_{2}}}}}=\bigcap\limits_{a_{j}^{l_{j}^{2}}\in {{A}^{{{L}_{2}}}}}{R_{a_{j}^{l_{j}^{2}}}^{\delta _{j}^{l_{j}^{2}}}}$

知,

$\left( x, y \right)\in \bigcap\limits_{a_{j}^{l_{j}^{2}}\in {{A}^{{{L}_{2}}}}}{R_{a_{j}^{l_{j}^{2}}}^{\delta _{j}^{l_{j}^{2}}}}$

由于对于任意j∈ J, 由命题1可得

$R_{a_{j}^{2}}^{\delta_{j}^{2}} \subseteq R_{a_{j}^{1}}^{\delta_{j}^{1}}$,

于是

$\bigcap\limits_{a_{j}^{l_{j}^{2}}\in {{A}^{{{L}_{2}}}}}{R_{a_{j}^{l_{j}^{2}}}^{\delta _{j}^{l_{j}^{2}}}}=\bigcap\limits_{j\in J}{R_{a_{j}^{l_{j}^{2}}}^{\delta _{j}^{l_{j}^{2}}}}\subseteq \bigcap\limits_{j\in J}{R_{a_{j}^{l_{j}^{1}}}^{\delta _{j}^{l_{j}^{1}}}}$,

从而

$\left( x, y \right)\in \bigcap\limits_{j\in J}{R_{a_{j}^{l_{j}^{1}}}^{\delta _{j}^{l_{j}^{1}}}}=R_{{{A}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}$,

因此, $R_{A L_{2}}^{\delta L_{2}} \subseteq R_{A L_{1}}^{\delta L_{1}}$. 证毕.

性质3 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, B⊆A, C⊆A, L₁∈ L, L₂∈ L, 若B⊆C, 且L₂⪰L₁, 则

1)$R_{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\subseteq R_{{{B}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}$,

2)$R_{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\subseteq R_{{{B}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}$,

3)$R_{{{A}^{L}}}^{{{\delta }^{{{L}_{2}}}}}\subseteq R_{{{A}^{L}}}^{{{\delta }^{{{L}_{1}}}}}$,

4)$\left[ x \right]_{{{A}^{L}}}^{{{\delta }^{{{L}_{2}}}}}\subseteq \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{{{L}_{1}}}}}$, $x\in U$.

证明 先证1).因为B⊆C⊆A, 所以

$\begin{align} & R_{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}=\left\{ \left( x, y \right)\in U\times U\left| S\left( a(x), a(y) \right)\ge {{\delta }^{{{L}_{1}}}}, \forall a\in C \right. \right\} \\ & \subseteq \left\{ \left( x, y \right)\in U\times U\left| S\left( a(x), a(y) \right)\ge {{\delta }^{{{L}_{1}}}}, \forall a\in B \right. \right\} \\ & =R_{{{B}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}, \end{align}$

即 RCL1δL1⊆ RBL1δL1.

再证2).由1)即得.

再证3).由命题2可得.

最后证4).由3)即得. 证毕.

定义21 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, U/R_d={D₁, D₂, ···, D_t}, L∈ L, 则d关于A^L和δ ^L的区间下近似与区间上近似分别定义如下:

$\underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}({U}/{{{R}_{d}}}\; )=\underset{1\le k\le t}{\mathop \bigcup }\, \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}({{D}_{k}})$,

$\overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}({U}/{{{R}_{d}}}\; )=\underset{1\le k\le t}{\mathop \bigcup }\, \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}({{D}_{k}})$,

其中,

$\begin{array}{l} \underline{R_{A^{L}}^{\delta^{L}}}\left(D_{k}\right)=\left\{x \in U \mid[x]_{A^{L}}^{\delta^{L}} \subseteq D_{k}\right\}, \\ \overline{R_{A^{L}}^{\delta^{L}}}\left(D_{k}\right)=\left\{x \in U \mid[x]_{A^{L}}^{\delta^{L}} \cap D_{k} \neq \emptyset\right\}, \\ k \in\{1, 2, \cdots, t\} . \end{array}$

进一步地, d关于A^L和δ ^L的区间近似精度与区间粗糙度分别定义如下:

$\alpha _{{{A}^{L}}}^{{{\delta }^{L}}}\left( {U}/{{{R}_{d}}}\; \right)=\frac{\sum{_{{{D}_{k}}\in {U}/{{{R}_{d}}}\; }}\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{k}} \right) \right|}{\sum{_{{{D}_{k}}\in {U}/{{{R}_{d}}}\; }}\left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{k}} \right) \right|}$,

$\rho _{{{A}^{L}}}^{{{\delta }^{L}}}\left( {U}/{{{R}_{d}}}\; \right)=1-\alpha _{{{A}^{L}}}^{{{\delta }^{L}}}\left( {U}/{{{R}_{d}}}\; \right)=1-\frac{\sum{_{{{D}_{k}}\in {U}/{{{R}_{d}}}\; }\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{k}} \right) \right|}}{\sum{_{{{D}_{k}}\in {U}/{{{R}_{d}}}\; }\left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{k}} \right) \right|}}$.

性质4 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, U/R_d={D₁, D₂, ···, D_t}, 对于B⊆A, C⊆A, L₁∈ L, L₂∈ L, 若B⊆C, 且L₂⪰L₁, 则

1) αBL1δL1(U/R_d)≤ αCL1δL1(U/R_d),

2) ρCL1δL1(U/R_d)≤ ρBL1δL1(U/R_d),

3) αAL1δL1(U/R_d)≤ αAL2δL2(U/R_d),

4) ρAL2δL2(U/R_d)≤ ρAL1δL1(U/R_d).

证明 先证1).对于∀ D∈ U/R_d和∀ x∈ $\underline{R_{B L_{1}}^{\delta L_{1}}}(D) $, 由下近似的定义知[x ]BL1δL1⊆D.由于B⊆C, 由性质3得

[x ]CL1δL1⊆[x ]BL1δL1,

于是[x ]CL1δL1⊆D.再由下近似的定义得

$x\in \underline{R_{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right)$,

从而

$\underline{R_{{{B}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right)\subseteq \underline{R_{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right)$,

即得

$\left| \underline{R_{{{B}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right) \right|\le \left| \underline{R_{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right) \right|$,

因此

$\sum{_{D\in {U}/{{{R}_{d}}}\; }\left| \underline{R_{{{B}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right) \right|}\le \sum{_{D\in {U}/{{{R}_{d}}}\; }\left| \underline{R_{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right) \right|}$.

另一方面, 对于∀ D∈ U/R_d和$\forall x \in \overline{R_{C L_{1}}^{\delta L_{1}}}(D) $, 由上近似的定义知

[x ]CL1δL1∩ D≠ Ø .

又因为[x ]CL1δL1⊆[x ]BL1δL1, 从而

[x ]BL1δL1∩ D≠ Ø ,

再由上近似的定义知

$x \in \overline{R_{B L_{1}}^{\delta L_{1}}}(D) $,

因此

$\overline{R_{C L_{1}}^{\delta L_{1}}}(D) \subseteq \overline{R_{B L_{1}}^{\delta L_{1}}}(D) $,

即得

$\left| \overline{R_{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right) \right|\le \left| \overline{R_{{{B}^{L}}}^{{{\delta }^{L}}}}\left( D \right) \right|$,

因此

$\sum{_{D\in {U}/{{{R}_{d}}}\; }\left| \overline{R_{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right) \right|}\le \sum{_{D\in {U}/{{{R}_{d}}}\; }\left| \overline{R_{{{B}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}}\left( D \right) \right|}$,

故

$\frac{\sum_{D \in U / R_{d}}\left|\underline{R_{B L_{1}}^{\delta L_{1}}}(D)\right|}{\sum_{D \in U / R_{d}}\left|\overline{R_{B L_{1}}^{\delta L_{1}}}(D)\right|} \leqslant \frac{\sum_{D \in U / R_{d}}\left|\underline{R_{C L_{1}}^{\delta L_{1}}}(D)\right|}{\sum_{D \in U / R_{d}}\left|\overline{R_{C L_{1}}^{\delta L_{1}}}(D)\right|}, $

即

$\alpha _{{{B}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\left( {U}/{{{R}_{d}}}\; \right)\le \alpha _{{{C}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\left( {U}/{{{R}_{d}}}\; \right)$.

再证2).由1)可得.

再证3).由性质3和类似于1)的证明可得.

最后证4).由3)可得. 证毕.

例4 (续例3) 给定尺度组合L₀、L₃、L₄、L₅下的区间近似精度和区间粗糙度的计算如下.

由于

$\begin{align} & \left[ {{x}_{1}} \right]_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}=\left\{ {{x}_{1}} \right\}, \text{ }\left[ {{x}_{2}} \right]_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}=\left\{ {{x}_{2}} \right\}, \text{ }\left[ {{x}_{3}} \right]_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}=\left\{ {{x}_{3}} \right\}, \text{ } \\ & \left[ {{x}_{4}} \right]_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}=\left\{ {{x}_{4}} \right\}, \text{ }\left[ {{x}_{5}} \right]_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}=\left\{ {{x}_{5}} \right\}, \text{ }\left[ {{x}_{6}} \right]_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}=\left\{ {{x}_{6}} \right\}, \\ & \left[ {{x}_{7}} \right]_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}=\left\{ {{x}_{7}} \right\}, \text{ }\left[ {{x}_{8}} \right]_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}=\left\{ {{x}_{8}} \right\}, \\ \end{align}$

经计算有

$\begin{align} & \underline{R_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}}\left( {{D}_{1}} \right)=\left\{ {{x}_{1}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{7}} \right\}, \\ & \overline{R_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}}\left( {{D}_{1}} \right)=\left\{ {{x}_{1}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{7}} \right\}, \\ & \underline{R_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}}\left( {{D}_{2}} \right)=\left\{ {{x}_{2}}, {{x}_{6}}, {{x}_{8}} \right\}, \\ & \overline{R_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}}\left( {{D}_{2}} \right)=\left\{ {{x}_{2}}, {{x}_{6}}, {{x}_{8}} \right\}, \\ \end{align}$

因此, d关于 AL0和 δL0的区间近似精度和区间粗糙度如下所示:

$\begin{align} & \alpha _{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}\left( {U}/{{{R}_{d}}}\; \right)=\frac{\left| \underline{R_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}}\left( {{D}_{1}} \right) \right|+\left| \underline{R_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}}\left( {{D}_{2}} \right) \right|}{\left| \overline{R_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}}\left( {{D}_{1}} \right) \right|+\left| \overline{R_{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}}\left( {{D}_{2}} \right) \right|}=1, \\ & \rho _{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}\left( {U}/{{{R}_{d}}}\; \right)=1-\alpha _{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}\left( {U}/{{{R}_{d}}}\; \right)=0. \\ \end{align}$

因为

U/ RAL3δL3=U/ RAL0δL0,

所以易得d关于 AL3和 δL3的区间近似精度和区间粗糙度:

$\begin{align} & \alpha _{{{A}^{{{L}_{3}}}}}^{{{\delta }^{{{L}_{3}}}}}\left( {U}/{{{R}_{d}}}\; \right)=\alpha _{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}\left( {U}/{{{R}_{d}}}\; \right)=1, \\ & \rho _{{{A}^{{{L}_{3}}}}}^{{{\delta }^{{{L}_{3}}}}}\left( {U}/{{{R}_{d}}}\; \right)=\rho _{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}\left( {U}/{{{R}_{d}}}\; \right)=0. \\ \end{align}$

由于

$\begin{align} & \left[ {{x}_{1}} \right]_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}=\left[ {{x}_{2}} \right]_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}=\left\{ {{x}_{1}}, {{x}_{2}} \right\}, \text{ }\left[ {{x}_{3}} \right]_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}=\left\{ {{x}_{3}} \right\}, \\ & \left[ {{x}_{4}} \right]_{{{A}^{{{L}_{2}}}}}^{{{\delta }^{{{L}_{4}}}}}=\left\{ {{x}_{4}} \right\}, \text{ }\left[ {{x}_{5}} \right]_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}=\left\{ {{x}_{5}} \right\}, \text{ }\left[ {{x}_{6}} \right]_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}=\left\{ {{x}_{6}} \right\}, \\ & \left[ {{x}_{7}} \right]_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}=\left[ {{x}_{8}} \right]_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}=\left\{ {{x}_{7}}, {{x}_{8}} \right\}, \\ \end{align}$

经计算有

$\begin{align} & \underline{R_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}}\left( {{D}_{1}} \right)=\left\{ {{x}_{3}}, {{x}_{4}}, {{x}_{5}} \right\}, \\ & \overline{R_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}}\left( {{D}_{1}} \right)=\left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{3}}, {{x}_{4}}, {{x}_{5}}, {{x}_{7}}, {{x}_{8}} \right\}, \\ & \underline{R_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}}\left( {{D}_{2}} \right)=\left\{ {{x}_{6}} \right\}, \\ & \overline{R_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}}\left( {{D}_{2}} \right)=\left\{ {{x}_{1}}, {{x}_{2}}, {{x}_{6}}, {{x}_{7}}, {{x}_{8}} \right\}, \\ \end{align}$

因此, d关于 AL4和 δL4的区间近似精度和区间粗糙度如下所示:

$\alpha _{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}\left( {U}/{{{R}_{d}}}\; \right)=\frac{\left| \underline{R_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}}\left( {{D}_{1}} \right) \right|+\left| \underline{R_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}}\left( {{D}_{2}} \right) \right|}{\left| \overline{R_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}}\left( {{D}_{1}} \right) \right|+\left| \overline{R_{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}}\left( {{D}_{2}} \right) \right|}=\frac{1}{3}, $

$\rho _{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}\left( {U}/{{{R}_{d}}}\; \right)=1-\alpha _{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}\left( {U}/{{{R}_{d}}}\; \right)=\frac{2}{3}.$

由于

$\begin{align} & \left[ {{x}_{1}} \right]_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}=\left[ {{x}_{4}} \right]_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}=\left\{ {{x}_{1}}, {{x}_{4}} \right\}, \text{ }\left[ {{x}_{2}} \right]_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}=\left\{ {{x}_{2}} \right\}, \\ & \left[ {{x}_{3}} \right]_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}=\left[ {{x}_{6}} \right]_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}=\left\{ {{x}_{3}}, {{x}_{6}} \right\}, \text{ }\left[ {{x}_{5}} \right]_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}=\left\{ {{x}_{5}} \right\}, \\ & \left[ {{x}_{7}} \right]_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}=\left\{ {{x}_{7}} \right\}, \text{ }\left[ {{x}_{8}} \right]_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}=\left\{ {{x}_{8}} \right\}, \\ \end{align}$

经计算有

$\begin{array}{l} \underline{R_{A L_{5}}^{\delta L_{5}}}\left(D_{1}\right)=\left\{x_{1}, x_{4}, x_{5}, x_{7}\right\}, \\ \overline{R_{A L_{5}}^{\delta L_{5}}}\left(D_{1}\right)=\left\{x_{1}, x_{3}, x_{4}, x_{5}, x_{6}, x_{7}\right\}, \\ R_{A L_{5}}^{\delta L_{5}}\left(D_{2}\right)=\left\{x_{2}, x_{8}\right\}, \\ \overline{R_{A L_{5}}^{\delta L_{5}}}\left(D_{2}\right)=\left\{x_{2}, x_{3}, x_{6}, x_{8}\right\}, \end{array}$

因此, d关于 AL5和 δL5的区间近似精度和区间粗糙度如下所示:

$\begin{align} & \alpha _{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}\left( {U}/{{{R}_{d}}}\; \right)=\frac{\left| \underline{R_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}}\left( {{D}_{1}} \right) \right|+\left| \underline{R_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}}\left( {{D}_{2}} \right) \right|}{\left| \overline{R_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}}\left( {{D}_{1}} \right) \right|+\left| \overline{R_{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}}\left( {{D}_{2}} \right) \right|}=\frac{3}{5}, \\ & \rho _{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}\left( {U}/{{{R}_{d}}}\; \right)=1-\alpha _{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}\left( {U}/{{{R}_{d}}}\; \right)=\frac{2}{5}. \\ \end{align}$

定义22 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, U/R_d={D₁, D₂, ···, D_t}, 对于L∈ L, d关于A^L和δ ^L的条件熵定义如下:

${{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=-\sum\limits_{i=1}^{n}{\sum\limits_{k=1}^{t}{\frac{\left| \left[ {{x}_{i}} \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{k}} \right|}{U{{}^{2}}}{{\log }_{2}}\frac{\left| \left[ {{x}_{i}} \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{k}} \right|}{\left| \left[ {{x}_{i}} \right]_{{{A}^{L}}}^{{{\delta }^{L}}} \right|}}}$.

性质5 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, U/R_d={D₁, D₂, ···, D_t}, B⊆A, C⊆A, L₁∈ L, L₂∈ L, 则

1)若L₂⪰L₁, 则${{H}^{{{\delta }^{{{L}_{2}}}}}}\left( \left. d \right|{{A}^{{{L}_{2}}}} \right)\le {{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{A}^{{{L}_{1}}}} \right)$,

2)若B⊆C, 则${{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{C}^{{{L}_{1}}}} \right)\le {{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{B}^{{{L}_{1}}}} \right)$.

证明 先证1).若L₂⪰L₁, 对于∀ x∈ U和∀ D_k∈ U/R_d, 由性质3得

[x ]AL2δL2⊆[x ]AL1δL1,

所以

$\begin{align} & \left| \left[ x \right]_{{{A}^{{{L}_{2}}}}}^{{{\delta }^{{{L}_{2}}}}}\bigcap {{D}_{k}} \right|\le \left| \left[ x \right]_{{{A}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\bigcap {{D}_{k}} \right|, \\ & \left| \left[ x \right]_{{{A}^{{{L}_{2}}}}}^{{{\delta }^{{{L}_{2}}}}}\bigcap \neg {{D}_{k}} \right|\le \left| \left[ x \right]_{{{A}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\bigcap \neg {{D}_{k}} \right|\text{. } \end{align}$

记

$f(x, y)=-x \log _{2}\left(\frac{x}{x+y}\right) $,

则d关于 AL1和 δL1的条件熵如下所示:

${{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{A}^{{{L}_{1}}}} \right)=\frac{1}{{{\left| U \right|}^{2}}}\sum\limits_{i=1}^{n}{\sum\limits_{k=1}^{t}{f\left( \left| \left[ {{x}_{i}} \right]_{{{A}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\bigcap {{D}_{k}} \right| , \left| \left[ {{x}_{i}} \right]_{{{A}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\bigcap \neg {{D}_{k}} \right| \right)}}.$

同样地, d关于 AL2和 δL2的条件熵如下所示:

${{H}^{{{\delta }^{{{L}_{2}}}}}}\left( \left. d \right|{{A}^{{{L}_{2}}}} \right)=\frac{1}{{{\left| U \right|}^{2}}}\sum\limits_{i=1}^{n}{\sum\limits_{k=1}^{t}{f\left( \left| \left[ {{x}_{i}} \right]_{{{A}^{{{L}_{2}}}}}^{{{\delta }^{{{L}_{2}}}}}\bigcap {{D}_{k}} \right|, \left| \left[ {{x}_{i}} \right]_{{{A}^{{{L}_{2}}}}}^{{{\delta }^{{{L}_{2}}}}}\bigcap \neg {{D}_{k}} \right| \right)}}.$

因为当x> 0, y≥ 0时, f(x, y)为单调递增函数^[43], 因此

$\begin{align} & 0\le f\left( \left| \left[ {{x}_{i}} \right]_{{{A}^{{{L}_{2}}}}}^{{{\delta }^{{{L}_{2}}}}}\bigcap {{D}_{k}} \right|, \left| \left[ {{x}_{i}} \right]_{{{A}^{{{L}_{2}}}}}^{{{\delta }^{{{L}_{2}}}}}\bigcap \neg {{D}_{k}} \right| \right) \\ & \text{ }\le \text{ }f\left( \left| \left[ {{x}_{i}} \right]_{{{A}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\bigcap {{D}_{k}} \right|, \left| \left[ {{x}_{i}} \right]_{{{A}^{{{L}_{1}}}}}^{{{\delta }^{{{L}_{1}}}}}\bigcap \neg {{D}_{k}} \right| \right), \\ \end{align}$

从而

${{H}^{{{\delta }^{{{L}_{2}}}}}}\left( \left. d \right|{{A}^{{{L}_{2}}}} \right)\le {{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{A}^{{{L}_{1}}}} \right)$

再证2).由性质3和类似于1)的证明可得.

证毕.

定义23 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, U/R_d={D₁, D₂, ···, D_t}, L∈ L, 定义d关于A^L和δ ^L的区间集决策熵如下:

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=\rho _{{{A}^{L}}}^{{{\delta }^{L}}}\left( {U}/{{{R}_{d}}}\; \right){{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)$.

性质6 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统, B⊆A, C⊆A, L₁∈ L, L₂∈ L, 则

1)若L₂⪰L₁, 则

$ID{{H}^{{{\delta }^{{{L}_{2}}}}}}\left( \left. d \right|{{A}^{{{L}_{2}}}} \right)\le ID{{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{A}^{{{L}_{1}}}} \right)$,

2)若B⊆C, 则

$ID{{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{C}^{{{L}_{1}}}} \right)\le ID{{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{B}^{{{L}_{1}}}} \right)$.

证明 先证1).若L₂⪰L₁, 则由性质4可知

ρAL2δL2(U/R_d)≤ ρAL1δL1(U/R_d),

又由性质5知

${{H}^{{{\delta }^{{{L}_{2}}}}}}\left( \left. d \right|{{A}^{{{L}_{2}}}} \right)\le {{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{A}^{{{L}_{1}}}} \right)$,

因此

$ID{{H}^{{{\delta }^{{{L}_{2}}}}}}\left( \left. d \right|{{A}^{{{L}_{2}}}} \right)\le ID{{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{A}^{{{L}_{1}}}} \right)$.

再证2).若B⊆C, 由性质4可知

ρCL1δL1(U/R_d)≤ ρBL1δL1(U/R_d),

又由性质5知

${{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{C}^{{{L}_{1}}}} \right)\le {{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{B}^{{{L}_{1}}}} \right)$,

所以

$ID{{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{C}^{{{L}_{1}}}} \right)\le ID{{H}^{{{\delta }^{{{L}_{1}}}}}}\left( \left. d \right|{{B}^{{{L}_{1}}}} \right)$. 证毕.

本节基于区间集决策熵讨论协调广义多尺度区间集决策系统中的最优尺度组合、熵最优尺度组合和对应的最优尺度约简问题.

定义24 设S=(U, A∪ {d})为一个广义多尺度区间集决策系统,

L₀=(I₁, I₂, ···, I_m)∈ L,

若 RAL0δL0⊆R_d, 则称S是协调的, 否则称S是不协调的.

定义25 设S=(U, A∪ {d})为一个协调广义多尺度区间集决策系统, L∈ L, 则

1)若 RALδL⊆R_d, 则称S^L关于S是协调的, 否则称S^L关于S是不协调的,

2)若

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=ID{{H}^{{{\delta }^{_{{{L}_{0}}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)$,

则称S^L关于S是熵协调的, 否则称S^L关于S不是熵协调的.

定义26 设S=(U, A∪ {d})为一个协调广义多尺度区间集决策系统, L∈ L, 若S^L关于S是协调的, 且对于满足L≻K的任意K∈ L, S^K关于S是不协调的, 则称L为S的一个最优尺度组合, 同时称A^L为S的一个最优尺度约简.

注3 定义26说明, L∈ L是协调广义多尺度区间集决策系统S=(U, A∪ {d})的一个最优尺度组合当且仅当L是格(L, ⪰, ∧ , ∨ )中使区间集决策系统S^L是协调的一个极小元.A^L为S的一个最优尺度约简当且仅当L是格(L, ⪰, ∧ , ∨ )中使得S^L是协调的一个极小元.

定义27 设S=(U, A∪ {d})为一个协调广义多尺度区间集决策系统, L∈ L, 若S^L关于S是熵协调的, 且对于满足L≻K的任意K∈ L, S^K关于S不是熵协调的, 则称L为S的一个熵最优尺度组合, 同时称A^L为S的一个熵最优尺度约简.

注4 定义27说明, L∈ L是协调广义多尺度区间集决策系统S=(U, A∪ {d})的一个熵最优尺度组合当且仅当L是格(L, ⪰, ∧ , ∨ )中使区间集决策熵$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)$与格(L, ⪰, ∧ , ∨ )最大元对应的区间集决策熵$ID{{H}^{{{\delta }^{_{{{L}_{0}}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)$相同的一个极小元.A^L为S的一个熵最优尺度约简当且仅当L是格(L, ⪰, ∧ , ∨ )中使区间集决策熵$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)$与格(L, ⪰, ∧ , ∨ )最大元对应的区间集决策熵$ID{{H}^{{{\delta }^{_{{{L}_{0}}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)$相同的一个极小元.

定理1 设S=(U, A∪ {d})为一个协调广义多尺度区间集决策系统, L∈ L, 则$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0$当且仅当S^L关于S是协调的.

证明 必要性.若$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0$, 则

$\rho _{{{A}^{L}}}^{{{\delta }^{L}}}\left( {U}/{{{R}_{d}}}\; \right){{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0$,

于是或者 ρALδL(U/R_d)=0, 或者${{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0$.

若 ρALδL(U/R_d)=0, 可得 αALδL(U/R_d)=1, 即对于∀ D∈ U/R_d, 有

$\sum{_{D\in {U}/{{{R}_{d}}}\; }}\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right) \right|=\sum{_{D\in {U}/{{{R}_{d}}}\; }}\left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right) \right|, \text{ }$,

又因为

$\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right) \right|\le \left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right) \right|$,

所以

$\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right) \right| =\left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right) \right|$,

从而由

$\underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right)\subseteq D\subseteq \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right)$,

可得

$\underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right) =\overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right)=D$.

对于∀ x∈ U, 取D'∈ U/R_d, 使得

[x]_d=D',

又因为

$\underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D' \right) =D'$,

从而

$x\in \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D' \right)$.

于是由下近似的定义知

$\left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\subseteq {{\left[ x \right]}_{d}}=D'$,

由x∈ U的任意性得 RALδL⊆R_d, 故S^L关于S是协调的.

若${{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0$, 则对于∀ x∈ U和∀ D∈ U/R_d, 由性质5证明过程可得

$\frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap D \right|}{{{\left| U \right|}^{2}}}{{\log }_{2}}\frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap D \right|}{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}} \right|}=0$,

即

$\frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap D \right|}{{{\left| U \right|}^{2}}}{{\log }_{2}}\frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap D \right|}{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap D \right|+\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap \neg D \right|}=0$,

于是可得

$\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap D \right|\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap \neg D \right|=0$.

在上式中取D=[x]_d, 显然

$\left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{\left[ x \right]}_{d}}\ne \varnothing $,

因此

$\left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap \left( \neg {{\left[ x \right]}_{d}} \right)=\varnothing $,

于是[x ]ALδL⊆[x]_d, 由x∈ U的任意性即得 RALδL⊆R_d, 即S^L关于S是协调的.

充分性.若S^L关于S是协调的, 即 RALδL⊆R_d, 即对于∀ x∈ U, 有[x ]ALδL⊆[x]_d.不妨设

U/R_d={D₁, D₂, ···, D_t},

选取k'∈ {1, 2, ···, t}, 使得D_k'=[x]_d, 则对于∀ k∈ {1, 2, ···, t}, 有

[x ]ALδL∩ D_k= [x]ALδL, k=k'Ø, k≠k'

于是当k=k'时, 有

${{\log }_{2}}\frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{k}} \right|}{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}} \right|}={{\log }_{2}}\frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}} \right|}{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}} \right|}={{\log }_{2}}1=0$

当k≠ k'时, 有

$\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{k}} \right|=0$.

综上, 由x∈ U的任意性和D_k∈ U/R_d的任意性且根据${{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)$的定义即得

${{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0$,

从而进一步可得

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0.$. 证毕.

定理2 设S=(U, A∪ {d})为一个协调广义多尺度区间集决策系统, L∈ L, 则下列结论等价:

1)S^L关于S是协调的,

2)S^L关于S是熵协调的.

证明 1)⇒ 2).若S^L关于S是协调的, 由定义25知 RALδL⊆R_d, 从而由定理1可得

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0$,

又因为S是协调的, 即 RALoδLo⊆R_d, 因此

$ID{{H}^{{{\delta }^{{{L}_{0}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)=0$.

于是

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=ID{{H}^{{{\delta }^{{{L}_{0}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)=0$,

即S^L关于S是熵协调的.

2)⇒ 1).假设S^L关于S是不协调的, 即

RALδL⊈R_d,

则存在x∈ U和j∈ {1, 2, ···, t}, 使得d(x)=j, 并且

$\left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{j}}\ne \varnothing $,

但

$\left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\nsubseteq {{D}_{j}}$,

即

$\left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{j}}\ne \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}$,

于是

$\frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{j}} \right|}{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}} \right|}< 1$,

从而

${{\log }_{2}}\left( \frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{j}} \right|}{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}} \right|} \right)< 0$,

因此

$H\left( \left. d \right|{{C}^{L}} \right)\ge -\frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{j}} \right|}{{{n}^{2}}}{{\log }_{2}}\left( \frac{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}}\bigcap {{D}_{j}} \right|}{\left| \left[ x \right]_{{{A}^{L}}}^{{{\delta }^{L}}} \right|} \right)> 0$.

另一方面, 由于

[x ]ALδL⊂D_j

且

[x ]ALδL∩ D_j≠ Ø ,

即

x∉ RALδL¯(D_j)

且

$x\in \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{j}} \right), $

所以

$ \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{j}} \right)\subsetneq \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{j}} \right), $

故

$\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{j}} \right) \right|< \left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{j}} \right) \right|$

而对于∀ D_k∈ U/R_d(k≠ j), 显然

$\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{k}} \right) \right|\le \left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{k}} \right) \right|$

因此

$\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{j}} \right) \right|+\sum\limits_{k\ne j}{\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{k}} \right) \right|}< \left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{j}} \right) \right|+\sum\limits_{k\ne j}{\left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( {{D}_{k}} \right) \right|}$

即

$\sum{_{D\in {U}/{{{R}_{d}}}\; }}\left| \underline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right) \right|< \sum{_{D\in {U}/{{{R}_{d}}}\; }}\left| \overline{R_{{{A}^{L}}}^{{{\delta }^{L}}}}\left( D \right) \right|$

从而

αALδL(U/R_d)< 1, ρALδL(U/R_d)> 0,

故

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)\text{}0$.

又因为S^L关于S是熵协调的, 所以

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=ID{{H}^{{{\delta }^{{{L}_{0}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)$,

而S是协调的, 即 RALoδLo⊆R_d, 于是由定理1得

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=ID{{H}^{{{\delta }^{{{L}_{0}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)=0$.

这与$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)\text{}0$矛盾, 故假设不成立. 证毕.

定理3 设S=(U, A∪ {d})为一个协调广义多尺度区间集决策系统, L∈ L, 则下列结论等价:

1)L是S的一个最优尺度组合,

2)L是S的一个熵最优尺度组合.

证明 由定理2、定义25、定义26和定义27

可得. 证毕.

定理4 设S=(U, A∪ {d})为一个协调广义多尺度区间集决策系统, L∈ L, 则下列结论等价:

1)A^L是S的一个最优尺度约简,

2)A^L是S的一个熵最优尺度约简.

证明 由定理2、定义25、定义26和定义27

可得. 证毕.

注5 定理1~定理4表明, 对于一个协调广义多尺度区间集决策系统S=(U, A∪ {d}), 最优尺度组合的概念与熵最优尺度的概念是等价的, 同时, 最优尺度约简的概念与熵最优尺度约简的概念也是等价的.并且L与A^L分别是S=(U, A∪ {d})的一个最优尺度组合与一个最优尺度约简当且仅当L是格(L, ⪰, ∧ , ∨ )中使区间集决策熵

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0$

的一个极小元, 即

$ID{{H}^{{{\delta }^{L}}}}\left( \left. d \right|{{A}^{L}} \right)=0$,

并且对于(L, ⪰, ∧ , ∨ )中严格弱(小)于L的任何元素K都有

$ID{{H}^{{{\delta }^{K}}}}\left( \left. d \right|{{A}^{K}} \right)> 0$,

而在具体计算中, 只须验证格(L, ⪰, ∧ , ∨ )中L的所有子节点对应的区间集决策熵大于0即可.

例5 (续例4) 根据例3中尺度组合下的相似类计算可得

RAL3δL3⊆R_d, RAL4δL4⊈R_d, RAL5δL5⊈R_d,

因为L₃≻L₄, L₃≻L₅, 且(U, RAL3δL3∪ {d})是协调的, (U, RAL4δL4∪ {d})和(U, RAL5δL5∪ {d})是不协调的, 又由于完备格L中严格弱于L₃的子节点中只有L₄与L₅, 所以由定义26得L₃=(3, 0, 1)是S的一个最优尺度组合, 同时 AL3={ a13, a31}是S的一个最优尺度约简.

另一方面, 经计算有

$\begin{array}{c} H^{\delta L_{0}}\left(d \mid A^{L_{0}}\right)=-\frac{1}{8^{2}}\left(\log _{2}\left(\frac{1}{1}\right)+\log _{2}\left(\frac{1}{1}\right)+\right. \\ \log _{2}\left(\frac{1}{1}\right)+\log _{2}\left(\frac{1}{1}\right)+\log _{2}\left(\frac{1}{1}\right)+ \\ \left.\log _{2}\left(\frac{1}{1}\right)+\log _{2}\left(\frac{1}{1}\right)+\log _{2}\left(\frac{1}{1}\right)\right)=0 \end{array}$

$H^{\delta L_{3}}\left(d \mid A^{L_{3}}\right)=H^{\delta L_{0}}\left(d \mid A^{L_{0}}\right)=0$

$\begin{array}{c} H^{\delta L_{4}}\left(d \mid A^{L_{4}}\right)=-\frac{1}{8^{2}}\left(\log _{2}\left(\frac{1}{2}\right)+\log _{2}\left(\frac{1}{2}\right)+\right. \\ \log _{2}\left(\frac{1}{2}\right)+\log _{2}\left(\frac{1}{2}\right)+\log _{2}\left(\frac{1}{2}\right)+ \\ \left.\log _{2}\left(\frac{1}{2}\right)+\log _{2}\left(\frac{1}{2}\right)+\log _{2}\left(\frac{1}{2}\right)\right)=\frac{1}{8} \end{array}$

$\begin{array}{c} H^{\delta L_{5}}\left(d \mid A^{L_{5}}\right)=-\frac{1}{8^{2}}\left(2 \log _{2}\left(\frac{2}{2}\right)+2 \log _{2}\left(\frac{2}{2}\right)+\right. \\ \log _{2}\left(\frac{1}{2}\right)+\log _{2}\left(\frac{1}{2}\right)+\log _{2}\left(\frac{1}{2}\right)+ \\ \left.\log _{2}\left(\frac{1}{2}\right)\right)=\frac{1}{16} . \end{array}$

$\begin{align} & ID{{H}^{{{\delta }^{{{L}_{0}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)=\rho _{{{A}^{{{L}_{0}}}}}^{{{\delta }^{{{L}_{0}}}}}\left( {U}/{{{R}_{d}}}\; \right){{H}^{{{\delta }^{{{L}_{0}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)=0, \\ & ID{{H}^{{{\delta }^{{{L}_{3}}}}}}\left( \left. d \right|{{A}^{{{L}_{3}}}} \right)=\rho _{{{A}^{{{L}_{3}}}}}^{{{\delta }^{{{L}_{3}}}}}\left( {U}/{{{R}_{d}}}\; \right){{H}^{{{\delta }^{{{L}_{3}}}}}}\left( \left. d \right|{{A}^{{{L}_{1}}}} \right)=0, \\ & ID{{H}^{{{\delta }^{{{L}_{4}}}}}}\left( \left. d \right|{{A}^{{{L}_{4}}}} \right)=\rho _{{{A}^{{{L}_{4}}}}}^{{{\delta }^{{{L}_{4}}}}}\left( {U}/{{{R}_{d}}}\; \right){{H}^{{{\delta }^{{{L}_{4}}}}}}\left( \left. d \right|{{A}^{{{L}_{4}}}} \right)=\frac{1}{12}, \\ \end{align}$

$ID{{H}^{{{\delta }^{{{L}_{5}}}}}}\left( \left. d \right|{{A}^{{{L}_{5}}}} \right)=\rho _{{{A}^{{{L}_{5}}}}}^{{{\delta }^{{{L}_{5}}}}}\left( {U}/{{{R}_{d}}}\; \right){{H}^{{{\delta }^{{{L}_{5}}}}}}\left( \left. d \right|{{A}^{{{L}_{5}}}} \right)=\frac{1}{40}.$

由此可见$ID{{H}^{{{\delta }^{{{L}_{3}}}}}}\left( \left. d \right|{{A}^{{{L}_{3}}}} \right)$等于0, 且与$ID{{H}^{{{\delta }^{{{L}_{0}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)$相等, 而$ID{{H}^{{{\delta }^{{{L}_{4}}}}}}\left( \left. d \right|{{A}^{{{L}_{4}}}} \right)$和$ID{{H}^{{{\delta }^{{{L}_{5}}}}}}\left( \left. d \right|{{A}^{{{L}_{5}}}} \right)$均不等于0, 与$ID{{H}^{{{\delta }^{{{L}_{0}}}}}}\left( \left. d \right|{{A}^{{{L}_{0}}}} \right)$不相等.根据定义25可得 SL3关于S是熵协调的, SL4和 SL5关于S不是熵协调的.又因为L₃≻L₄, L₃≻L₅, 且完备格L中严格弱于L₃的子节点中只有L₄与L₅, 因此由定义27得L₃=(3, 0, 1)是S的一个熵最优尺度组合, 同时 AL3={ a13, a31}是S的一个熵最优尺度约简.

在广义多尺度粗糙集数据分析模型中, 最优尺度组合选择与属性约简是知识获取的两个关键问题.本文提出广义多尺度区间集决策系统的概念, 构造广义多尺度区间集信息系统在不同尺度组合下对象集的相似关系, 获得相应的信息粒集合.结合区间粗糙度和条件熵给出区间集决策熵的概念与性质.在协调广义多尺度区间集决策系统中证明最优尺度组合概念与熵最优尺度组合概念的等价性, 也证实最优尺度约简概念与熵最优尺度约简概念的等价性, 有助于进一步研究广义多尺度区间集决策系统的知识获取问题.今后将考虑进一步讨论不协调广义多尺度区间集决策系统、不完备广义多尺度区间集决策系统以及决策也是多尺度的广义多尺度区间集信息系统等复杂数据类型的最优尺度组合选择与最优尺度约简问题, 并进一步研究动态混合多尺度数据的最优尺度选择与知识获取问题.

本文责任编委 梁吉业

Recommended by Associate Editor LIANG Jiye