定义1^[1] 称(G, M, I)为一个形式背景, 其中, G为对象集, M为属性集, I⊆G× M为G和M之间的二元关系.若对象x∈ G与属性a∈ M满足(x, a)∈ I, 则称对象x具有属性a, 记为xIa.

在形式背景(G, M, I)中, 对于任意对象子集X⊆G和属性子集B⊆M, Ganter等^[2]定义一对导出算子如下:

${{X}^{* }}=\{a\in M|\forall x\in X, xIa\}, $

${{B}^{* }}=\{x\in G|\forall a\in B, xIa\}.$

其中, X^* 表示X中所有对象共同具有的属性集合, B^* 表示共同具有B中所有属性的对象集合.若二元组(X, B)满足X^* =B且X=B^* , 则称(X, B)为形式概念, 简称概念, X称为概念的外延, B称为概念的内涵.

为了简化表述, 使用x^* 表示{x}^* (x∈ G), a^* 表示{a}^* (a∈ M).若形式背景(G, M, I)满足∀ x∈ G, y∈ G, 当x^* =y^* 时必有x=y; ∀ a∈ M, b∈ M, 当a^* =b^* 时必有a=b, 则称其是净化的^[2].若∀ x∈ G, x^* ≠ Ø 且x^* ≠ M; ∀ a∈ M, a^* ≠ Ø 且a^* ≠ G, 则称形式背景(G, M, I)是正则的^[24].

本文所有形式背景均为净化且正则的形式背景.

性质1^[2] 设(G, M, I)为形式背景, ∀ X∈ G, X₁∈ G, X₂⊆G且∀ B⊆M, B₁⊆M, B₂⊆M, 如下性质成立:

1) ${{X}_{1}}\subseteq {{X}_{2}}\Rightarrow X_{2}^{* }\subseteq X_{1}^{* }, {{B}_{1}}\subseteq {{B}_{2}}\Rightarrow B_{2}^{* }\subseteq B_{1}^{* }; $

2) $X\subseteq {{X}^{* * }}, B\subseteq {{B}^{* * }}; $

3) ${{X}^{* }}={{X}^{* * * }}, {{B}^{* }}={{B}^{* * * }}; $

4) $X\subseteq {{B}^{* }}\Leftrightarrow B\subseteq {{X}^{* }}; $

5) ${{({{X}_{1}}\bigcup {{X}_{2}})}^{* }}=X_{1}^{* }\bigcap X_{2}^{* }, {{({{B}_{1}}\bigcup {{B}_{2}})}^{* }}=B_{1}^{* }\bigcap B_{2}^{* }; $

6) ${{({{X}_{1}}\bigcap {{X}_{2}})}^{* }}\supseteq X_{1}^{* }\bigcup X_{2}^{* }, {{({{B}_{1}}\bigcap {{B}_{2}})}^{* }}\supseteq B_{1}^{* }\bigcup B_{2}^{* }.$

∀ x∈ G, (x^{* *} , x^* )称为对象概念; 类似地, ∀ a∈ M, (a^* , a^{* *} )称为属性概念^[2].

使用L(G, M, I)表示形式背景(G, M, I)的全体概念, 记

(X₁, B₁)≤ (X₂, B₂)⇔ X₁⊆X₂(⇔ B₁⊇B₂),

则“ ≤ ” 表示L(G, M, I)上的偏序关系, (L(G, M, I), ≤ )表示偏序集, 且是完备格, 其中任意两个概念之间的下确界和上确界的定义如下:

$({{X}_{1}}, {{B}_{1}})\wedge ({{X}_{2}}, {{B}_{2}})=({{X}_{1}}\bigcap {{X}_{2}}, {{({{B}_{1}}\bigcup {{B}_{2}})}^{* * }}), $

$({{X}_{1}}, {{B}_{1}})\vee ({{X}_{2}}, {{B}_{2}})=({{({{X}_{1}}\bigcup {{X}_{2}})}^{* * }}, {{B}_{1}}\bigcap {{B}_{2}}).$

称(L(G, M, I), ≤ )为概念格, 简记为L(G, M, I)^[2].

定义2^[2] 在概念格L(G, M, I)中, 若

(X₁, B₁)≤ (X₂, B₂),

则称(X₁, B₁)为(X₂, B₂)的亚概念, (X₂, B₂)为(X₁, B₁)的超概念.进一步地, 若不存在(Y, C),

(Y, C)≠ (X₁, B₁), (Y, C)≠ (X₂, B₂),

使

(X₁, B₁)≤ (Y, C)≤ (X₂, B₂),

则称(X₁, B₁)为(X₂, B₂)的子概念, (X₂, B₂)为(X₁, B₁)的父概念, 记为

(X₁, B₁)≺(X₂, B₂).

在概念格上可定义同余关系.

定义3^[2] 设L为一个概念格, θ 为L上的一个等价关系, 且满足

∀ (X_t, B_t)∈ L, (C_t, D_t)∈ L,

若

(X_t, B_t)θ (C_t, D_t),

则

$(\underset{t\in T}{\mathop{\vee }}\, ({{X}_{t}}, {{B}_{t}}))\theta (\underset{t\in T}{\mathop{\vee }}\, ({{C}_{t}}, {{D}_{t}}))$,

$(\underset{t\in T}{\mathop{\wedge }}\, ({{X}_{t}}, {{B}_{t}}))\theta (\underset{t\in T}{\mathop{\wedge }}\, ({{C}_{t}}, {{D}_{t}}))$,

T为索引集, 称θ 为L上的一个同余关系.

定义4^[2] 设θ 为格L的同余关系,

$L/\theta :=\{{{[a]}_{\theta }}|$$a\in L\}$

上两个运算∨ , ∧ 的定义如下:∀ a∈ L, b∈ L,

$\begin{array}{l} {[a]_{\theta} \vee[b]_{\theta}:=[a \vee b]_{\theta}, } \\ {[a]_{\theta} \wedge[b]_{\theta}:=[a \wedge b]_{\theta}, } \end{array}$

则(L/θ ; ∧ , ∨ )为一个格, 称为L关于模θ 的商格, 简记为L/θ .

本节首先介绍↗和↙关系的定义, 然后给出通过属性概念和对象概念获取↗和↙关系的方法.

定义5^[2] 设(G, M, I)为形式背景, g∈ G, h∈ G, m∈ M, n∈ M, 则

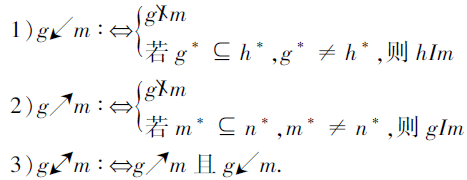
定理1描述如何从属性概念出发获取形式背景中满足↗关系的对象-属性对.

定理1 设K=(G, M, I)为形式背景, L(K)为其概念格,

$AC=\{(m_{i}^{* }, m_{i}^{* * })|{{m}_{i}}\in M\}$.

在AC∪ {(G, G^* )}中,

$(m_{i}^{* }, m_{i}^{* * })(Z, D)$

若不存在(Y, C),

$(Y, C) \neq\left(m_{i}^{* }, m_{i}^{* * }\right), (Y, C) \neq(Z, D) $,

使

$\left(m_{i}^{* }, m_{i}^{* * }\right) \leqslant(Y, C) \leqslant(Z, D) $,

则称(Z, D)为$(m_{i}^{* }, m_{i}^{* * })$在AC∪ {(G, G^* )}上的父概念, 记作

$(m_{i}^{* }, m_{i}^{* * }){{\prec }_{AC}}(Z, D)$,

${{P}_{i}}=\{({{X}_{j}}, {{B}_{j}})|(m_{i}^{* }, m_{i}^{* * }){{\prec }_{AC}}$$({{X}_{j}}, {{B}_{j}})\}$,

$i=1, 2, \ldots , |M|$,

于是有

1)若$|{{P}_{i}}|=1$, 则

$\forall (g, m)\in ({{X}_{j}}-m_{i}^{* })\times (m_{i}^{* * }-{{B}_{j}})$,

满足g↗m;

2)若$|{{P}_{i}}|> 1$, 则

$\forall (g, m)\in (\underset{s\in \tau }{\mathop{\bigcap }}\, {{X}_{js}}-m_{i}^{* })\times (m_{i}^{* * }-\underset{s\in \tau }{\mathop{\bigcup }}\, {{B}_{js}})$

τ 为索引集, 满足g↗m.

证明 先证1).当$|{{P}_{i}}|=1$时, 分如下两种情况讨论.

(1)若

$(m_{i}^{* }, m_{i}^{* * }){{\prec }_{AC}}(G, {{G}^{* }})$

已知

$G-m_{i}^{* }=\{g$$\in G|g\notin m_{i}^{* }\}$,

$m_{i}^{* * }-{{G}^{* }}=\{m\in m_{i}^{* * }|m\notin {{G}^{* }}\}$,

则

$G-m_{i}^{* }\nsubseteq m_{i}^{* }$, $m\subseteq m_{i}^{* * }-{{G}^{* }}\subset m_{i}^{* * }$,

于是$\forall g\in (G-m_{i}^{* })$, 有

$(g, m)\notin $$(m_{i}^{* }, m_{i}^{* * })$,

即 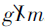.而

$(m_{i}^{* }, m_{i}^{* * }){{\prec }_{AC}}(G, {{G}^{* }})$

说明不存在n∈ M, 使 mi*⊂n^* 成立.于是有g↗m, 其中

m∈ ( mi* *-G^* ), g∈ (G- mi*).

(2)若

( mi*, mi* *)≺_AC( mj*, mj* *),

易知

mi* *- mj* *=m_i,

又 mi*⊂ mj*, 且m_j是唯一的, 则

∀ g∈ ( mj*- mi*),

有g \in m_{j}^{*}, g \notin m_{i}^{*}, 即gIm_j, 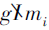, 由定义5可知

∀ (g, m)∈ ( mj*- mi*)× ( mi* *- mj* *),

满足g↗m.

再证2).当$|{{P}_{i}}|> 1$时, 不妨设$|{{P}_{i}}|=2$.设在AC∪ {(G, G^* )}中( mi*, mi* *)的父概念为(a^* , a^{* *} ), (b^* , b^{* *} ), a∈ M, b∈ M.易知

mi* *-(a^{* *} ∪ b^{* *} )=m_i,

又

mi*⊂a^* , mi*⊂b^* ,

于是

$\forall g\in ({{a}^{* }}\bigcap {{b}^{* }})-m_{i}^{* }$,

有

$g\in {{a}^{* }}, g\in {{b}^{* }}, g\notin m_{i}^{* }$,

即 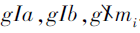.由定义5知,

$\forall (g, m)\in (({{a}^{* }}\bigcap {{b}^{* }})-m_{i}^{* })\times (m_{i}^{* * }-({{a}^{* * }}\bigcup {{b}^{* * }}))$

满足g↗m.

类似地, 可得以对象概念获取形式背景中满足↙关系的对象-属性对的方法.

定理2 设K=(G, M, I)为形式背景, L(K)为其概念格,

$OC=\{(g_{i}^{* * }, g_{i}^{* })|{{g}_{i}}\in G\}$.

在OC∪ {(M^* , M)}中,

(Z, D)≤ (g^{* *} , g^* ),

若不存在(Y, C),

(Y, C)≠ ( gi* *, gi*), (Y, C)≠ (Z, D),

使

(Z, D)≤ (Y, C)≤ ( gi* *, gi*),

则称(Z, D)为( gi* *, gi*)在OC∪ {(M^* , M)}上的子概念, 记作

$(Z, D){{\prec }_{OC}}(g_{i}^{* * }, g_{i}^{* })$,

${{Q}_{i}}=\{({{C}_{j}}, {{D}_{j}})|({{C}_{j}}, {{D}_{j}}){{\prec }_{OC}}(g_{i}^{* * }, g_{i}^{* })\}$,

$i=1, 2, \ldots , |G|$,

于是有

1)若$|{{Q}_{i}}|=1$, 则

$\forall (g, m)\in (g_{i}^{* * }-{{C}_{j}})\times ({{D}_{j}}-g_{i}^{* })$,

满足g↙m;

2)若$|{{Q}_{i}}|> 1$, 则

$\forall (g, m)\in (g_{i}^{* * }-\underset{s\in \tau }{\mathop{\bigcup }}\, {{C}_{js}})\times (\underset{s\in \tau }{\mathop{\bigcap }}\, {{D}_{js}}$$-g_{i}^{* })$,

τ 为索引集, 满足g↙m.

证明 与定理1证明类似, 省略.

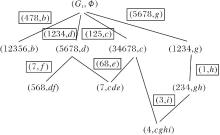
例1 对教育电影《生物与水》的形式背景进行预处理, 得到形式背景K₁=(G₁, M₁, I₁), 如表1所示.对象集G₁包含如下8个对象:x₁表示水蛭, x₂表示鲤科鱼, x₃表示青蛙, x₄表示狗, x₅表示棘草, x₆表示芦苇, x₇表示豆类, x₈表示玉米.为了方便表述, 下文简记为1, 2, 3, 4, 5, 6, 7, 8.属性集M₁包含如下8个属性:b 表示生活在水中, c表示生活在陆地, d表示需要叶绿素生产食物, e表示双子叶, f表示单子叶, g表示可以移动, h表示有四肢骨骼, i表示哺乳类.

表1

Table 1

表1(Table 1)

表1 形式背景K1=(G1, M1, I1) Table 1 Formal context K1=(G1, M1, I1) b c d e f g h i x1 1 0 0 0 0 1 0 0 x2 1 0 0 0 0 1 1 0 x3 1 1 0 0 0 1 1 0 x4 0 1 0 0 0 1 1 1 x5 1 0 1 0 1 0 0 0 x6 1 1 1 0 1 0 0 0 x7 0 1 1 1 0 0 0 0 x8 0 1 1 0 1 0 0 0

表1 形式背景K1=(G1, M1, I1) Table 1 Formal context K1=(G1, M1, I1)

根据定义5, 可得表1中的↗和↙关系, 如表2所示.

表2

Table 2

表2(Table 2)

表2 形式背景K1=(G1, M1, I1)的↗和↙关系 Table 2 The ↗ and ↙ relations of formal context K1=(G1, M1, I1) b c d e f g h i x1 1 ↗ ↗ 0 0 1 ↗ 0 x2 1 ↗↙ ↗ 0 0 1 1 0 x3 1 1 ↗↙ ↙ ↙ 1 1 ↗↙ x4 ↗↙ 1 ↗↙ ↙ ↙ 1 1 1 x5 1 ↗↙ 1 0 1 ↗ 0 0 x6 1 1 1 ↗↙ 1 ↗↙ ↙ ↙ x7 ↗↙ 1 1 1 ↗↙ ↗↙ ↙ ↙ x8 ↗↙ 1 1 ↗ 1 ↗ 0 0

表2 形式背景K1=(G1, M1, I1)的↗和↙关系 Table 2 The ↗ and ↙ relations of formal context K1=(G1, M1, I1)

该形式背景的属性b、c、d、e、 f、g、h、i对应的属性概念分别为:

(12356, b), (34678, c), (5678, d), (7, cde),

(568, df), (1234, g), (234, gh), (4, cghi).

对象x₁、x₂、x₃、x₄、x₅、x₆、x₇、x₈对应的对象概念分别为:

(123, bg), (23, bgh), (3, bcgh), (4, cghi),

(56, bdf), (6, bcdf), (7, cde), (68, cdf).

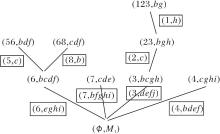
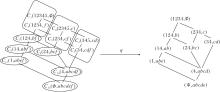
依据定理1和定理2, 从属性概念和对象概念出发分别获取形式背景中所有的↗和↙关系.首先获取属性概念在AC∪ {(G, G^* )}上的父概念和对象概念在OC∪ {(M^* , M)}上的子概念.然后根据定理1和定理2获取所有↗和↙关系, 结果如图1和图2所示.在图中, (7, cde)既是由e生成的属性概念, 也是由7生成的对象概念.

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 基于属性概念获取的↗关系Fig.1 The ↗ relations obtained based on attribute concepts

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于对象概念获取的↙关系Fig.2 The ↙ relations obtained based on object concepts

在图1中, (7, cde)的父概念有两个:

(5678, d), (34678, c),

$\begin{array}{l} \cap_{s \in \tau} X_{j s}-m_{i}^{*}= \\ \quad\{\{5, 6, 7, 8\} \cap\{3, 4, 6, 7, 8\}-\{7\}\}=\{6, 8\}, \end{array}$

$m_{i}^{* *}-\cup_{s \in \tau} B_{j s}=\{\{c, d, e\}-(\{c\} \cup\{d\})\}=\{e\} .$

由定理1可知与属性e具有↗关系的对象为6和8, 即6↗e, 8↗e.

在图2中, (7, cde)的子概念只有(Ø , M₁),

gi* *-C_j={7}-Ø ={7},

${{D}_{j}}-g_{i}^{* }={{M}_{1}}-\{c, d, e\}=\{b, $$f, g, h, i\}$

由定理2可知与对象7具有↙关系的属性有b、 f、g、h、i, 即7↙b, 7↙f, 7↙g, 7↙h, 7↙i.

其它具有箭头关系的对象-属性对可以类似计算.

本节将以箭头封闭关系为基础, 给出获取兼容子背景的方法, 再依据兼容子背景与概念格上同余关系之间的联系, 确定概念格上的同余关系.

定义6^[2] 设K=(G, M, I)为形式背景, L(K)为其概念格, 若∀ (X, B)∈ L(K), (X∩ H, B∩ N)为K的子背景(H, N, I∩ H× N)的概念, 则该子背景称为兼容子背景.

定义7^[2] 形式背景(G, M, I)的子背景(H, N, I∩ H× N)满足箭头封闭关系, 当且仅当如下条件成立:

1)若h↗m且h∈ H, 则m∈ N;

2)若g↙n且n∈ N, 则g∈ H.

定义8^[2] 设K=(G, M, I)为一个形式背景, ∀ x∈ G, a∈ M, 若xI\a, 则∃y∈ G, b∈ M, 使x↗b且a^* ⊆b^* , y↙a且x^* ⊆y^* , 那么称形式背景K为双建立背景.

有限形式背景都是双建立的, 由于本文研究的背景均为有限形式背景, 故本文中的形式背景都是双建立的.

命题1^[2] 每个兼容子背景都满足箭头封闭关系.双建立背景的每个满足箭头封闭关系的子背景都是兼容子背景.

命题1表明双建立背景的箭头封闭子背景与其兼容子背景是等价的, 所以获取兼容子背景即获取箭头封闭子背景.

定理3 设K=(G, M, I)为形式背景, g∈ G, h∈ G, m∈ M, n∈ M, (H, N, I∩ H× N)为K的箭头封闭子背景, 当且仅当如下条件成立:

1)若h↗m, 当m∉N, 则h∉H;

2)若g↙n, 当g∉H, 则n∉N.

证明 定理3是定义7的逆否命题, 故自然成立.

定理3借助剪枝思想, 在定义7的基础上, 给出获取所有兼容子背景的方法.

例2 形式背景K₂=(G₂, M₂, I₂)如表3所示, 其中, 对象集

G₂={1, 2, 3, 4, 5},

属性集

M₂={a, b, c, d, e, f}.

表3

Table 3

表3(Table 3)

表3 形式背景K2=(G2, M2, I2) Table 3 Formal context K2=(G2, M2, I2) a b c d e f 1 1 1 ↗↙ ↙ 1 1 2 ↗↙ 1 1 ↗↙ 0 1 3 ↙ ↗↙ 1 1 0 1 4 1 1 1 1 ↗↙ 1 5 0 0 1 1 0 ↗↙

表3 形式背景K2=(G2, M2, I2) Table 3 Formal context K2=(G2, M2, I2)

由定理1和定理2得到具有↗关系的对象-属性对集合:

DA={(1, c), (2, a), (2, d), (3, b), (4, e), (5, f)}.

具有↙关系的对象-属性对集合如下:

DO={(1, c), (1, d), (2, a), (2, d), (3, a), (3, b), (4, e), (5, f)}.

由定理3可知, 若删除对象5, 已知5↙f, 为得到箭头封闭子背景, 则此时应该删除属性f, 而与属性f有↗关系的对象只有对象5, 那么从形式背景K₂中, 删除对象5和属性f之后, 得到的子背景

$K{{C}_{\{5\}}}=({{G}_{2}}-\{5\}, {{M}_{2}}-\{f\}, {{I}_{2}}\bigcap ({{G}_{2}}-\{5\})\times ({{M}_{2}}-\{f\}))$

满足箭头封闭关系, 即KC_{5}为K₂的兼容子背景.

若删除属性a, 由于2↗a, 为了得到箭头封闭子背景, 应删除对象2, 又因为2↙a, 2↙d, 于是在删除对象2之后, 还应再删除属性d, 又因为与属性d具有↗关系的只有对象2, 此时说明, 子背景

$K{{C}_{\{a\}}}=({{G}_{2}}-\{2\}, {{M}_{2}}-\{a, f\}, {{I}_{2}}\bigcap ({{G}_{2}}-\{2\})\times ({{M}_{2}}-\{a, $$f\}))$

满足箭头封闭关系, 即KC_{a}为K₂的一个兼容子背景.

由于任意形式背景(G, M, I)都有兼容子背景(G, M, I)和(Ø , Ø , I∩ Ø × Ø ), 但这两个兼容子背景在概念格压缩方面并无实际意义, 所以需判断原形式背景是否具有兼容子背景(H, N, I∩ H× N), 其中H⊂G, N⊂M, H≠ Ø , N≠ Ø .为了表述方便, 下文所指的兼容子背景均不包含(G, M, I)和(Ø , Ø , I∩ Ø × Ø ).

由定理3可知, 若要判断形式背景(G, M, I)是否具有兼容子背景, 最多应先删除M的幂集的所有子集或G的幂集的所有子集, 再以箭头封闭关系判断删除属性集或对象集后, 是否可以产生兼容子背景, 即按照定理3, 要判断形式背景(G, M, I)是否具有兼容子背景, 最多要尝试2^{min(|G|, |M|)}种情况.

为了简化判断过程, 本文将兼容子背景与概念格上的同余关系结合起来进行分析.下面先介绍兼容子背景的概念格与原形式背景的概念格之间的关系以及格上的同余判定定理.

引理1^[2] 设θ 为格L的同余关系, 则L/θ 为格且

q(a):=[a]_θ

的自然商映射q:L→ L/θ 为同态映射.

定理4^[2] 设K=(G, M, I)为形式背景, L(K)为其概念格,

(X₁, B₁)∈ L(K), (X₂, B₂)∈ L(K),

(H, N, I∩ H× N)为K的兼容子背景, θ 为L(K)上的同余关系, 若满足θ =θ _{H, N}, 则称该兼容子背景可诱导同余关系θ , 其中θ _{H, N}定义如下:

$\begin{align} & ({{X}_{1}}, {{B}_{1}}){{\theta }_{H, N}}({{X}_{2}}, {{B}_{2}})\Leftrightarrow {{X}_{1}}\bigcap H={{X}_{2}}\bigcap H \\ & \Leftrightarrow {{B}_{1}}\bigcap N={{B}_{2}}\bigcap N. \end{align}$

定理5^[23] 设L为格, θ 为L上的等价关系, 则θ 为格上的同余关系, 当且仅当

1)每个θ 的块为L的子集;

2)每个θ 的块为凸集;

3)θ 的块是四边形封闭的.

定义9^[23] 设L为格, {a, b, c, d}为L上的4-元素子集.若

a< b, c< d

且

a∨ d=b, a∧ d=c

或

b∨ c=d, b∧ c=a,

则称a, b和c, d为四边形(a, b, c, d)的对边.

定义10^[23] 当四边形的对边a, b和c, d满足a∈ A, b∈ A(其中A为某一分块)时, 必然有c∈ B, d∈ B(其中B为某一分块), 则称L的这个分区的块是四边形封闭的.

由定理4可知, 概念格上满足同余关系的概念在保留共同核心的前提下, 可初步理解为“ 删除不同的部分” .进一步由定理5可知, 在概念格上满足同余关系的概念, 也需满足四边形封闭的条件.由定义10可知, 四边形封闭是指只要任意四个概念之间满足四边形对边的条件, 那么对边上的元素将属于不同的同余块.本文规定以A_i表示形式背景K=(G, M, I)的概念格L(K)上不同的同余块.其中

$1< i< |L(K)|, i\in {{N}^{+}}$.

此时, 满足同余关系的概念一定位于相同的同余块中, 因此需初步删除四边形一条边上概念的不同部分, 由此引入初始删除属性集定义如下.

定义11 设K=(G, M, I)为形式背景, L(K)为K的概念格, 称

$\begin{aligned} \text { Sta }= & \left\{B_{i}-B_{j} \mid\left(X_{i}, B_{i}\right) \in L(K), \left(X_{j}, B_{j}\right) \in L(K), \right. \\ & i=1, 2, \cdots, |L(K)|, j=1, 2, \cdots, |L(K)|, \\ & i \neq j\} \end{aligned}$

为初始删除属性集族,

$M_{(i, j)}^{0}={{B}_{i}}-{{B}_{j}}$

为初始删除属性集, 本文规定$M_{(i, j)}^{0}$为属于Sta的初始删除属性集.

初始删除对象集可类似定义.

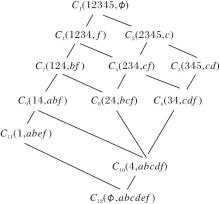
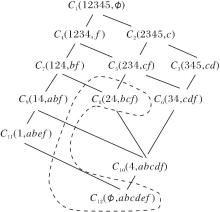
例3 (续例2) 例2中形式背景K₂=(G₂, M₂, I₂)的概念格如图3所示, 以概念C₈、C₁₂为四边形一条边, 如图4所示, 此时

$M_{(12, 8)}^{0}=\{a, b, c, d, e, f\}-\{b, c, f\}$$=\{a, d, e\}$

为初始删除属性集.

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 K2的概念格Fig.3 Concept lattice of K2

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 M 12, 80在概念格上的表示Fig.4 Representation of M 12, 80 on concept lattice

由定理5可知, 若删除M 12, 80形成的格上的等价块是一个同余块, 则该块需满足子格、凸集, 于是

C₈∈ A₁, C₁₀∈ A₁, C₁₂∈ A₁.

然后获取格上形成四边形封闭的块, 具体过程如下.

1)由定义9可知,

C₁₂< C₈, C₁₁< C₇

且

C₁₁∨ C₈=C₇, C₁₁∧ C₈=C₁₂,

则C₈, C₁₂与C₇, C₁₁为四边形(C₈, C₇, C₁₁, C₁₂)的对边, 由定义10可知, 因为

C₈∈ A₁, C₁₂∈ A₁,

所以

C₇∈ A₂, C₁₁∈ A₂,

又A₂若是格上的一个同余块, 则需满足子格、凸集, 于是

C₇∈ A₂, C₉∈ A₂, C₁₁∈ A₂.

2)由定义9可知,

C₁₀< C₈, C₆< C₅

且

C₆∨ C₈=C₅, C₆∧ C₈=C₁₀,

则C₁₀, C₈与C₆, C₅为四边形(C₅, C₆, C₈, C₁₀)的对边, 由定义10知, 因为

C₈∈ A₁, C₁₀∈ A₁,

所以

C₅∈ A₃, C₆∈ A₃.

3)由定义9可知,

C₁₀< C₈, C₃< C₂

且

C₃∨ C₈=C₂, C₃∧ C₈=C₁₀,

则C₁₀, C₈与C₂, C₃为四边形(C₂, C₃, C₈, C₁₀)的对边, 由定义10知, 因为

C₈∈ A₁, C₁₀∈ A₁,

所以

C₂∈ A₄, C₃∈ A₄.

4)由定义9知, 剩余的C₁, C₄无法与A₁中的元素形成四边形对边, 于是, 由定义10知,

C₁∈ A₅, C₄∈ A₆.

此时, 已完整找到通过初步删除C₈, C₁₂的不同部分生成的, 满足子格、凸集与四边形封闭的格上所有的块.由定理5可知, 这些块构成格上的同余关系θ 的一个划分, 如图5所示.

图5

Fig.5

	Figure Option ViewDownloadNew Window
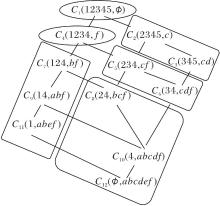	图5 由M 12, 80获取的概念格上的同余关系划分的块Fig.5 Blocks partitioned by congruence relations on concept lattice derived from M 12, 80

在初步删除M (i, j)0后, 以四边形封闭可获取概念格上的同余关系, 同时概念格上的同余关系也可由兼容子背景诱导, 则初步删除M (i, j)0.由定理3可得形式背景K=(G, M, I)的兼容子背景

KC_i=(H_i, N_i, I∩ H_i× N_i),

简称为由M (i, j)0生成兼容子背景KC_i, 下文均使用KC_i表示由M (i, j)0生成的兼容子背景.

由定义11可得如下命题2~命题4.

命题2 由$M_{(i, j)}^{0}\left(1< i< |L(K)|, 1< j< |L(K)|, i \in \mathbf{N}^{+}, j \in \mathbf{N}^{+}, i \neq j\right) $可生成K=(G, M, I)的所有兼容子背景.

证明 1)∀ M (i, j)0=B_i-B_j, 设

(X_i, B_i)< (X_j, B_j),

若

∃(C_i, D_i)∈ L(K), (C_j, D_j)∈ L(K),

其中

(C_i, D_i)< (C_j, D_j),

且

$({{X}_{i}}, {{B}_{i}})\vee ({{C}_{j}}, {{D}_{j}})=({{X}_{j}}, {{B}_{j}})$,

$({{X}_{i}}, {{B}_{i}})\wedge ({{C}_{j}}, {{D}_{j}})=({{C}_{i}}, {{D}_{i}})$

或

$({{X}_{j}}, {{B}_{j}})\vee ({{C}_{i}}, {{D}_{i}})=({{C}_{j}}, {{D}_{j}})$,

$({{X}_{j}}, {{B}_{j}})\wedge ({{C}_{i}}, {{D}_{i}})=({{X}_{i}}, {{B}_{i}})$,

则由定理5可获取概念格上全部同余关系, 又因为格上的同余关系与兼容子背景一一对应, 故由M (i, j)0可生成K=(G, M, I)的所有兼容子背景.

(2)∀ M (i, j)0=B_i-B_j, 设

(X_i, B_i)< (X_j, B_j),

若不存在

(C_i, D_i)< (C_j, D_j),

使

$({{X}_{i}}, {{B}_{i}})\vee ({{C}_{j}}, {{D}_{j}})=({{X}_{j}}, {{B}_{j}})$,

$({{X}_{i}}, {{B}_{i}})\wedge ({{C}_{j}}, {{D}_{j}})=({{C}_{i}}, {{D}_{i}})$

或

$({{X}_{j}}, {{B}_{j}})\vee ({{C}_{i}}, {{D}_{i}})=({{C}_{j}}, {{D}_{j}})$,

$({{X}_{j}}, {{B}_{j}})\wedge ({{C}_{i}}, {{D}_{i}})=({{X}_{i}}, {{B}_{i}})$,

则四边形封闭自然成立.由定理5可获取概念格上所有同余关系.此时, 通过首先删除M (i, j)0获得的同余关系划分为(X_i, B_i), (X_j, B_j)属于一个同余块, 其余概念各自属于一个同余块.

命题3 设K=(G, M, I)为形式背景, L(K)为K的概念格,

$\begin{array}{l} \left(X_{i}, B_{i}\right) \in L(K), \left(X_{j}, B_{j}\right) \in L(K) \\ i=1, 2, \cdots, |L(K)|, j=1, 2, \cdots, |L(K)|, i \neq j \end{array}$

则

M (i, j)0=B_i-(B_i∩ B_j).

证明 1)设

(X_i, B_i)< (X_j, B_j),

此时B_j⊆B_i, 于是

B_i∩ B_j=B_j,

可得

$M_{(i, j)}^{0}=B_{i}-B_{j}=B_{i}-\left(B_{i} \cap B_{j}\right) $.

2)设(X_i, B_i), (X_j, B_j)不可比, 由集合差运算可知

(1)若B_i∩ B_j=Ø , 则

$M_{(i, j)}^{0}={{B}_{i}}-{{B}_{j}}={{B}_{i}}-({{B}_{i}}\bigcap {{B}_{j}})={{B}_{i}}-\varnothing $;

(2)若B_i∩ B_j≠ Ø , 则

$M_{(i, j)}^{0}={{B}_{i}}-{{B}_{j}}={{B}_{i}}-({{B}_{i}}\bigcap {{B}_{j}})$.

综上所述, 命题3成立.

命题3说明, 对于

$\begin{array}{l} \left(X_{i}, B_{i}\right) \in L(K), \left(X_{j}, B_{j}\right) \in L(K), \\ i=1, 2, \cdots, |L(K)|, j=1, 2, \cdots, |L(K)|, i \neq j, \end{array}$

删除

M (i, j)0=B_i-B_j,

即初步删除以(X_i, B_i)和(X_j, B_j)形成的凸集中所有概念的不同部分.

命题4 设K=(G, M, I)为形式背景, L(K)为K的概念格,

$\begin{array}{l} \left(X_{i}, B_{i}\right) \in L(K), \left(X_{j}, B_{j}\right) \in L(K), (X, B) \in L(K), \\ i=1, 2, \cdots, |L(K)|, j=1, 2, \cdots, |L(K)|, i \neq j, \\ K C_{i}=\left(H_{i}, N_{i}, I \cap H_{i} \times N_{i}\right) \end{array}$

是由M (i, j)0∈ Sta生成的兼容子背景, θ 为由KC_i诱导的概念格上的同余关系.记

$C{{h}_{i}}=\{(X, B)|({{X}_{i}}, {{B}_{i}})(X, B)(({{X}_{i}}, {{B}_{i}})\vee ({{X}_{j}}, {{B}_{j}}))\}$,

若在K中首先删除M (i, j)0, 则∀ (X, B)∈ Ch_i,

$B_{i}-M_{(i, j)}^{0}=B-M_{(i, j)}^{0}=\left(B_{i} \cap B_{j}\right)-M_{(i, j)}^{0}$,

此时Ch_i为子格、凸集且

$\left(X_{j}, B_{j}\right) \in\left[\left(X_{i}, B_{i}\right)\right]_{\theta} \subseteq C h_{i}$,

其中[(X_i, B_i)]_θ 表示与(X_i, B_i)满足同余关系θ 的概念组成的同余类.

证明 由命题3易知, Ch_i为子格, 凸集.删除

M (i, j)0=B_i-B_j,

1)若

(X_i, B_i)< (X_j, B_j),

则

$\begin{aligned} \left(X_{j}, B_{j}\right)= & \left(X_{i}, B_{i}\right) \vee\left(X_{j}, B_{j}\right)= \\ & \left(\left(X_{i} \cup X_{j}\right)^{* * }, B_{i} \cap B_{j}\right), \end{aligned}$

即

B_j=B_i∩ B_j.

又

$\begin{array}{l} (X, B) \in L(K) \\ \left(X_{i}, B_{i}\right)< (X, B)< \left(X_{j}, B_{j}\right) \end{array}$

即

B_j⊂B⊂B_i,

则

$\begin{aligned} B_{i}-M_{(i, j)}^{0}= & B_{i}-\left(B_{i}-B_{j}\right)= \\ & \left\{m \in B_{i} \mid m \notin\left(B_{i}-B_{j}\right)\right\}=B_{j}, \\ B-M_{(i, j)}^{0}= & B-\left(B_{i}-B_{j}\right)= \\ & \left\{m \in B \mid m \notin\left(B_{i}-B_{j}\right)\right\}=B_{j}, \\ B_{j}-M_{(i, j)}^{0}= & B_{j}-\left(B_{i}-B_{j}\right)= \\ & \left\{m \in B_{j} \mid m \notin\left(B_{i}-B_{j}\right)\right\}=B_{j}, \end{aligned}$

于是

$\begin{array}{c} B_{i}-M_{(i, j)}^{0}=B-M_{(i, j)}^{0}=B_{j}-M_{(i, j)}^{0}= \\ \left(B_{i} \cap B_{j}\right)-M_{(i, j)}^{0} \end{array}$

成立, 且

$\left(B_{i}-M_{i, j}^{0}\right) \cap N_{i}=B_{j} \cap N_{i} . $

又从属性集M中初步删除M (i, j)0, 显然

N_i⊆M-M (i, j)0,

此时

B_i∩ N_i=B_j∩ N_i,

即

(X_i, B_i)θ (X_j, B_j).

同时

$\begin{array}{l} \left(B_{i}-M_{(i, j)}^{0}\right) \cap N_{i} \subseteq \\ \quad\left(B_{i}-M_{(i, j)}^{0}\right) \cap\left(M-M_{(i, j)}^{0}\right)= \\ \quad\left(B-M_{(i, j)}^{0}\right) \cap\left(M-M_{(i, j)}^{0}\right)= \\ \quad\left(\left(B_{i}-B_{j}\right)-M_{(i, j)}^{0}\right) \cap\left(M-M_{(i, j)}^{0}\right), \end{array}$

于是可得

$\left[\left(X_{i}, B_{i}\right)\right]_{\theta} \subseteq C h_{i} . $

2)若(X_i, B_i), (X_j, B_j)不可比,

(X_i, B_i)< ((X_i, B_i)∨ (X_j, B_j))

一定成立, 于是同1)可得

$B_{i}-M_{(i, j)}^{0}=B-M_{(i, j)}^{0}=\left(B_{i} \cap B_{j}\right)-M_{(i, j)}^{0}$,

且

$\left(X_{j}, B_{j}\right) \in\left[\left(X_{i}, B_{i}\right)\right]_{\theta} \subseteq C h_{i} $.

命题4说明, 初步删除M (i, j)0可以首先保证映射到兼容子背景同一个概念上的原形式背景的概念集, 满足子格、凸集, 而要保证四边形封闭还需进一步删除对象集或属性集.

由命题3可知, 根据定义11中形式概念内涵差的方式构造初始删除属性集的过程主要分为两种情况:

1)若

(X_i, B_i)< (X_j, B_j),

则

$\begin{array}{l} M_{(i, j)}^{0}=B_{i}-B_{j}=B_{i}-\left(B_{i} \cap B_{j}\right), \\ M_{(j, i)}^{0}=B_{j}-B_{i}=\emptyset, \end{array}$

此时M (j, i)0作为初始删除属性集为空集, 故在后续判断原形式背景是否具有兼容子背景时无需考虑.

2)若(X_i, B_i), (X_j, B_j)不可比, 则

$\begin{array}{l} M_{(i, j)}^{0}=B_{i}-B_{j}=B_{i}-\left(B_{i} \cap B_{j}\right), \\ M_{(j, i)}^{0}=B_{j}-B_{i}=B_{j}-\left(B_{i} \cap B_{j}\right) . \end{array}$

由概念格的定义可知

$\left(X_{i}, B_{i}\right) \vee\left(X_{j}, B_{j}\right)=\left(\left(X_{i} \cup X_{j}\right)^{* * }, B_{i} \cap B_{j}\right), $

且

$\begin{array}{l} \left(X_{i}, B_{i}\right)< \left(\left(X_{i} \cup X_{j}\right)^{* * }, B_{i} \cap B_{j}\right), \\ \left(X_{j}, B_{j}\right)< \left(\left(X_{i} \cup X_{j}\right)^{* * }, B_{i} \cap B_{j}\right), \end{array}$

由此可得, 一定存在某对具有严格偏序关系的概念, 其概念内涵差与任意一对不可比的概念(X_i, B_i), (X_j, B_j)的内涵差M (i, j)0, M (j, i)0一致.

若形式背景K=(G, M, I)的概念格L(K)中的概念之间均存在严格的偏序关系(如全序链), 此时初始删除属性集M (i, j)0∈ Sta的个数为

$\frac{1}{2}|L(K)|(|L(K)|-1) $,

若概念格L(K)存在不可比的概念, 则初始删除属性集的个数将小于

$\frac{1}{2}|L(K)|(|L(K)|-1) $ .

综上所述, 以M (i, j)0∈ Sta为初始删除属性集, 通过定理3判断形式背景K=(G, M, I)是否具有兼容子背景, 需要尝试的情况将由$2^{\min (|G|, |M|)}$种变为

$\frac{1}{2}|L(K)|(|L(K)|-1) \text { 种. }$.

这对于稀疏的形式背景, 可显著简化判断过程, 但是当密集的形式背景的概念数

$|L(K)| \approx 2^{\min (|G|, |M|)}$

时, 以M (i, j)0∈ Sta为初始删除属性集仍未使判断过程得到有效简化.

接下来, 定理6将继续优化初始删除属性集.

定理6 设K=(G, M, I)为形式背景, L(K)为K的概念格,

$St{{a}^{1}}=\{M_{(p, q)1}^{0}={{B}_{p}}-{{B}_{q}}\mid ({{X}_{p}}, {{B}_{p}})\prec ({{X}_{q}}, {{B}_{q}}), $

$({{X}_{p}}, {{B}_{p}}), ({{X}_{q}}, {{B}_{q}})\in L(K)\}$

记由M (p, q)10∈ Sta¹生成的兼容子背景为

$K{{C}_{p1}}=({{H}_{p1}}, {{N}_{p1}}, I\bigcap {{H}_{p1}}\times {{N}_{p1}})$

一定∃M (p, q)10∈ Sta¹, 使KC_i为KC_p1的兼容子背景.

证明 要证定理6, 只需证

∀ M (i, j)0∈ Sta,

一定存在与其在生成兼容子背景时等价的

M (p, q)10∈ Sta¹,

即或证

M (i, j)0=M (p, q)10,

或证当

M (p, q)10⊆M (i, j)0,

在箭头封闭关系下删除M (p, q)10, 一定还会删除

M (i, j)0-M (p, q)10.

此时, 可将Sta分成Sta¹、Sta²、Sta³这3个非空集合进行讨论, 其中

$St{{a}^{1}}\bigcap St{{a}^{2}}\bigcap St{{a}^{3}}=\varnothing , St{{a}^{1}}\bigcup St{{a}^{2}}\bigcup St{{a}^{3}}=Sta$

1)∀ M (p, q)10∈ Sta¹, ∃M (i, j)0∈ Sta,

使

M (p, q)10=M (i, j)0,

则KC_i与KC_p1显然一致.又因为一个形式背景是其自身的一个兼容子背景, 因此结论成立.

2)因为

$\begin{aligned} S t a^{2}= & \left\{M_{(s, t) 2}^{0} \mid\left(X_{s}, B_{s}\right)< (X, B)< \left(X_{t}, B_{t}\right), \right. \\ & \left(X_{s}, B_{s}\right) \in L(K), (X, B) \in L(K), \\ & \left.\left(X_{t}, B_{t}\right) \in L(K)\right\}, \end{aligned}$

设与(X_s, B_s), (X_t, B_t)构成四边形对边的概念(X_p, B_p), (X_q, B_q)满足

(X_p, B_p)≺(X_q, B_q),

即

M (p, q)0=M (p, q)10∈ Sta¹,

且

M (p, q)0⊆M (s, t)20∈ Sta².

若在M中首先删除M (p, q)0, 易知由M (p, q)0生成的兼容子背景KC_p中的属性集

N_p⊆M-M (p, q)0,

由命题4可知,

B_p-M (p, q)0=B_q-M (p, q)0,

则

(B_p-M (p, q)0)∩ N_p=(B_q-M (p, q)0)∩ N_p,

于是

B_p∩ N_p=B_q∩ N_p

成立, 即

(X_p, B_p)∈ A₁, (X_q, B_q)∈ A₁.

而若要四边形封闭, 则需

(X_s, B_s)∈ A₂, (X_t, B_t)∈ A₂

也成立, 即

B_s∩ N_p=B_t∩ N_p,

于是必然会删除

M (s, t)20=B_s-B_t.

上述分析说明在箭头封闭关系下, 首先删除M (p, q)0与首先删除M (s, t)20等价, 即由M (p, q)0生成的兼容子背景与由M (s, t)20生成的兼容子背景一致, 又已知

M (p, q)10=M (p, q)0,

则KC_p1与由

M (s, t)20∈ Sta²⊂Sta

生成的兼容子背景KC_s2一致, 已知一个形式背景是其自身的一个兼容子背景, 因此结论成立.

3)因为

$\begin{aligned} S t a^{3}= & \left\{M_{(m, n) 3}^{0} \mid M_{(s, t) 2}^{0} \subseteq M_{(m, n) 3}^{0}=B_{m}-B_{n}, \right. \\ & \left.\left(X_{m}, B_{m}\right) \in L(K), \left(X_{n}, B_{n}\right) \in L(K)\right\}, \end{aligned}$

设由M (m, n)30生成的兼容子背景为

$K{{C}_{m3}}=({{H}_{m3}}, {{N}_{m3}}, I\bigcap {{H}_{m3}}\times {{N}_{m3}}), M_{(m, n)3}^{0}\bigcap {{N}_{p}}\ne \varnothing , M_{(s, t)2}^{0}$$\subseteq M_{(m, n)3}^{0}$,

则在箭头封闭关系下, 在KC_s2的属性集N_s2中再删除M (m, n)30-M (s, t)20, 可生成KC_s2的兼容子背景

$KC_{s2}^{\prime }=(H_{s2}^{\prime }, N_{s2}^{\prime }, I\bigcap H_{s2}^{\prime }\times N_{s2}^{\prime })$,

显然

$K{{C}_{m3}}=KC_{s2}^{\prime }$.

下文以M (p, q)i0表示属于初始删除集族Staⁱ的初始属性集, 且KC_pi是由M (p, q)i0生成的兼容子背景

定理6说明, 由M (i, j)0∈ Sta生成的兼容子背景, 一定是由某一M (p, q)10∈ Sta¹生成的兼容子背景的兼容子背景.这说明, 由M (p, q)10∈ Sta¹生成的兼容子背景相对于由M (i, j)0∈ Sta生成的兼容子背景信息损失较小.若要得到原形式背景所有兼容子背景, 按照定理3, 继续删除较小信息损失的兼容子背景的对象集和属性集即可.此时, 要判断形式背景K=(G, M, I)是否具有兼容子背景, 最多需删除Sta¹中所有元素, 即最多需尝试的情况由

$\frac{1}{2}|L(K)|(|L(K)|-1) \text { 种 }$

减少为$\left|S_{t a}{ }^{1}\right|$种.

定理7 设K=(G, M, I)为形式背景, L(K)为K的概念格,

$St{{a}^{4}}=\{M_{(u, v)4}^{0}|M_{(u, v)4}^{0}=m_{u}^{* * }-{{B}_{v}}, {{m}_{u}}\in M, $

$(m_{u}^{* }, m_{u}^{* * }){{\prec }_{AC}}({{X}_{v}}, {{B}_{v}})\}$,

由M (u, v)40∈ Sta⁴生成的兼容子背景为

$K{{C}_{u4}}=({{H}_{u4}}, {{N}_{u4}}, I\bigcap {{H}_{u4}}\times {{N}_{u4}})$

一定∃M (u, v)40∈ Sta⁴, 使

KC_p1=KC_u4.

证明 按照定理1的表述易知, ( mu*, mu* *)的$|{{P}_{u}}|1$, 于是分如下两种情况证明.

(1)当$|{{P}_{u}}|=1$.时,

$\begin{array}{l} \forall\left(X_{s}, B_{s}\right) \in L(K), \left(X_{t}, B_{t}\right) \in L(K), \\ \left(X_{s}, B_{s}\right) \prec_{A C}\left(X_{t}, B_{t}\right), \end{array}$

一定∃m_u∈ M, 使

$m_{u}^{* * }\bigcap {{B}_{t}}={{B}_{v}}, $$m_{u}^{* }\bigcap {{X}_{t}}={{X}_{s}}$,

又

$(m_{u}^{* }, m_{u}^{* * })\vee ({{X}_{t}}, {{B}_{t}})=({{(m_{u}^{* }\bigcup {{X}_{t}})}^{* * }}, m_{u}^{* * }\bigcap {{B}_{t}}), $

$(m_{u}^{* }, m_{u}^{* * })\wedge ({{X}_{t}}, {{B}_{t}})=(m_{u}^{* }\bigcap {{X}_{t}}, {{(m_{u}^{* * }\bigcup {{B}_{t}})}^{* * }})$,

于是可得

$\begin{array}{l} \left(m_{u}^{* }, m_{u}^{* * }\right) \vee\left(X_{t}, B_{t}\right)=\left(X_{v}, B_{v}\right), \\ \left(m_{u}^{* }, m_{u}^{* * }\right) \wedge\left(X_{t}, B_{t}\right)=\left(X_{s}, B_{s}\right), \end{array}$

即一定∃m_u∈ M, 使( mu*, mu* *), (X_v, B_v)一定是(X_s, B_s), (X_t, B_t)的四边形对边.

删除 mu* *-B_v, 首先

( mu*, mu* *)∈ A₁, (X_v, B_v)∈ A₁,

且其四边形对边

(X_s, B_s)∈ A₂, (X_t, B_t)∈ A₂,

此时则需删除B_s-B_t, 这说明首先删除 mu* *-B_v与首先删除 mu* *-B_v等价, 即KC_u4与由B_s-B_t生成的兼容子背景一致.

(2)当$|{{P}_{u}}|> 1$时,

$\forall (m_{u}^{* }, m_{u}^{* * }), ({{X}_{us}}, {{B}_{us}}), s=1, 2, \cdots , |{{P}_{u}}|$,

$(m_{u}^{* }, m_{u}^{* * }){{\prec }_{AC}}({{X}_{us}}, {{B}_{us}})$,

则一定∃m_i∈ M,

$\left(m_{i}^{* }, m_{i}^{* * }\right) \prec_{A C}\left(X_{j}, B_{j}\right), \left|P_{i}\right|=1, $

使

$m_{i}^{* * } \cap B_{u s}=B_{j}, m_{i}^{* } \cap X_{u s}=m_{u}^{* }, $

同上, 说明一定∃m_i∈ M, 使( mi*, mi* *), (X_j, B_j)一定是( mu*, mu* *), (X_us, B_us)的四边形对边.

此时, 首先删除 mu* *-B_us与首先删除 mi* *-B_j等价, 由(1)知, 其也与首先删除B_s-B_t等价, 即由 mu* *-B_us生成的兼容子背景与由B_s-B_t生成的兼容子背景一致.

定理7说明, 由M (u, v)40∈ Sta⁴生成的兼容子背景与由M (p, q)10∈ Sta¹生成的兼容子背景一致.

推论1 设K=(G, M, I)为形式背景, 若KC_u4均为(Ø , Ø , I∩ Ø × Ø ), 则形式背景K的兼容子背景只有(G, M, I)和(Ø , Ø , I∩ Ø × Ø ).

证明 若KC_u4均为(Ø , Ø , I∩ Ø × Ø ), 则在箭头封闭关系下

$KC_{u4}^{\prime }=(\varnothing , \varnothing , I\bigcap \varnothing \times \varnothing )$

必然是KC_u4的兼容子背景, 于是可得K的兼容子背景只有(G, M, I)和(Ø , Ø , I∩ Ø × Ø ).

推论1说明, 判断一个形式背景K=(G, M, I)是否有兼容子背景, 只需判断以∀ M (u, v)40, u=1, 2, …, $|St{{a}^{4}}|$为初始删除属性集, 在箭头封闭关系下是否会生成(H, N, I∩ H× N), 其中H≠ Ø , N≠ Ø .此时, 判断形式背景K=(G, M, I)是否具有兼容子背景, 最多需尝试的情况将会由$|St{{a}^{1}}|$种减少为$|St{{a}^{4}}|$种.

若要得到K的所有兼容子背景, 只需获取每个KC_u4的所有兼容子背景, 可以简称KC_u4的所有兼容子背景为形式背景K在M (u, v)40维度下的兼容子背景.于是可首先获取M (u, v)40维度下所有兼容子背景中极小信息损失的兼容子背景, 而形式背景的二元关系细于其子背景的二元关系.为了度量其信息损失情况, 本文将Jaccard信息损失系数推广至形式背景上, 定义兼容子背景信息损失度.

定义12 设K=(G, M, I)为形式背景,

KC=(H, N, I∩ H× N)

为K的兼容子背景, KC的信息损失度定义如下:

Loss_KC=1- |I⋂H×N||I|.

定义13 设K=(G, M, I)为形式背景, 在M (u, v)40维度下的兼容子背景K Cu4t(t为索引集)中, 信息损失度极小的兼容子背景称为形式背景K在M (u, v)40维度下的极小信息损失的兼容子背景, 并将所有M (u, v)40∈ Sta⁴维度下的极小信息损失兼容子背景简称为极小信息损失兼容子背景.

定理8 设K=(G, M, I)为形式背景, 由M (u, v)40生成的兼容子背景KC_u4为M (u, v)40维度下的极小信息损失兼容子背景.

证明 已知在M (u, v)40维度下的兼容子背景个数$|KC_{u4}^{t}|1$, 不妨设t=2, 即M (u, v)40维度下有兼容子背景K Cu41, K Cu42, 假设

$K C_{u 4}=K C_{u 4}^{1}$,

那么K Cu42为KC_u4的兼容子背景, 即

$|I\bigcap {{H}_{u4}}\times {{N}_{u4}}|> |I\bigcap H_{u4}^{2}\times N_{u4}^{2}|$,

所以

$Los{{s}_{KC_{u4}^{2}}}> Los{{s}_{K{{C}_{u4}}}}$,

说明由M (u, v)40生成的KC_u4为极小信息损失兼容子背景.

定理9 设K=(G, M, I)为形式背景, 由$\{{{m}_{u}}\}$(${{m}_{u}}\in M, u=1, 2, \cdots , |M|$)生成的兼容子背景为M (u, v)40维度下的极小信息损失兼容子背景.

证明 已知K为正则且净化的兼容子背景, 所以M (u, v)40与{m_u}对应相等, 即由{m_u}生成的兼容子背景为M (u, v)40维度下极小信息损失兼容子背景.

定理9说明要得到极小信息损失兼容子背景, 只需得到K的所有属性单点集生成的兼容子背景即可.

从对象单点集出发, 以类似的方法也可获取极小信息损失兼容子背景.

在获取极小信息损失的兼容子背景之后, 由定理10得到兼容子背景诱导同余关系的方法.

定理10^[2] 设K=(G, M, I)为形式背景, L(K)为其概念格, 其任一兼容子背景(H, N, I∩ H× N)的概念格L(H, N, I∩ H× N)总是同构于K的某个商格, 即兼容子背景(H, N, I∩ H× N)会在L(K)上诱导一个完全同余关系θ _{H, N}, 该同余关系是完全同态Π _{H, N}的核, 且满足

$L(H, N, I \cap H \times N) \cong L(G, M, I) / \theta_{H, N}$ .

例4 (续例2) 由例2知,

$\begin{aligned} K C_{\{5\}}= & \left(G_{2}-\{5\}, M_{2}-\{f\}, \right. \\ & \left.I_{2} \cap\left(G_{2}-\{5\}\right) \times\left(M_{2}-\{f\}\right)\right) \end{aligned}$

为形式背景K₂=(G₂, M₂, I₂)由{5}生成的兼容子背景, 即KC_{5}为形式背景K₂的一个极小信息损失的兼容子背景.KC_{5}如表4所示.

表4

Table 4

表4(Table 4)

表4 兼容子背景KC{5} Table 4 Compatible subcontext KC{5} a b c d e 1 1 1 0 0 1 2 0 1 1 0 0 3 0 0 1 1 0 4 1 1 1 1 0

表4 兼容子背景KC{5} Table 4 Compatible subcontext KC{5}

根据定理10可得形式背景K₂=(G₂, M₂, I₂)的概念格L(K₂)上的同余关系θ , 如图6左图所示.兼容子背景KC₂的概念格L(K₂)/θ 如图6右图所示.由引理1知, 兼容子背景KC₂的概念格是形式背景K₂概念格的商格, 且q:L(K₂)→ L(K₂)/θ 为同态映射.

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 概念格上的同余关系与商格Fig.6 Congruence relations on concept lattice and quotient lattice

本节给出获取形式背景↗和↙关系的算法.

算法1 获取箭头关系的算法

输入 形式背景K=(G, M, I)

输出 满足↗关系的对象-属性对集合DA,

满足↙关系的对象-属性对集合DO

1. DA← Ø , DO← Ø

2. for each m∈ M, g∈ G do:

3. DA_i← Ø , DO_i← Ø , Sup_i← Ø , Sub_i← Ø

4. 计算( mi*, mi* *), ( gi* *, gi*)

5. for each m_j∈ mi* *-{m_i}, g_j∈ gi* *-{g_i} do:

6. 计算( mj*, mj* *), ( gj* *, gj*)

7. Sup_i=Sup_i∪ ( mj*, mj* *)

8. Sub_i=Sub_i∪ ( gj* *, gj*)

9. end

10. for each (X_j, B_j)∈ Sup_i, (C_j, D_j)∈ Sub_i do:

11. $D A_{i}=D A_{i} \cup\left(\cap_{s \in \tau} X_{j s}-m_{i}^{*}, m_{i}^{* *}-\cup_{s \in \tau} B_{j s}\right)$

12. $D O_{i}=D O_{i} \cup\left(g_{i}^{* *}-\cup_{s \in \tau} C_{j s}, \bigcap_{s \in \tau} D_{j s}-g_{i}^{*}\right)$

13. end

14. end

15. DA=DA∪ DA_i, DO=DO∪ DO_i

16. return DA, DO

算法1中的Sup_i为属性概念( mi*, mi* *)的所有属于AC的超概念.由性质1可知, 对( mi*, mi* *)所有超概念的外延作交的结果, 与定理1中( mi*, mi* *)的所有父概念的外延作交结果一致, 而对( mi*, mi* *)所有超概念的内涵作并的结果与 mi* *只差m, 这与定理1中, 从 mi* *中去掉( mi*, mi* *)所有父概念内涵交集的结果一致.对应地, 对象概念也按照类似的方法进行处理.于是, 步骤2~9按照上述方法分别获取( mi*, mi* *)的所有父概念和( gi* *, gi*)的所有子概念, 可减少计算成本.步骤10~13是以定理1和定理2为基础, 获取形式背景中具有↗和↙关系的对象-属性对.

算法1的外层循环遍历所有属性和对象, 时间复杂度为$O(|G||M|)$, 内层循环遍历每个闭包的元素, 假设闭包的平均大小为k, 则内层循环复杂度为O(k²), 因此算法1的时间复杂度为

$O\left(|G||M| k^{2}\right) $.

下面给出极小信息损失兼容子背景获取算法.

算法2 极小信息损失兼容子背景的获取算法

输入 形式背景K=(G, M, I)

输出 KC=(H, N, I∩ H× N), Loss_KC

1. 调用算法1计算DA, DO

2. for each m∈ M do:

3. G_ del← Ø , M_del← {m}, i← 1

4. KC← (Ø , Ø , I∩ Ø × Ø )

5. while True do:

6. G_ prev← G_del

7. for each (A, B)∈ DA do:

8. if B∩ M_del≠ Ø then:

9. G_del← G_del∪ A

10. end

11. if G_del==G_ prev then:

12. break

13. end

14. end

15. M_ prev← M_del

16. for each (C, D)∈ DO do:

17. if C∩ G_del≠ Ø then:

18. M_del← M_del∪ D

19. end

20. end

21. if M_del==M_prev then:

22. break

23. end

24. i← i+1

25. end

26. if G_del==G 或 M_del==M then:

27. continue

28. else if G_del 停止变化:

29. KC← (G-G_del, M-M_ prev,

I∩ (G-G_del)× (M-M_ prev))

30. else if M_del 停止变化:

31. KC← (G-G_ prev, M-M_del,

I∩ (G-G_ prev)× (M-M_del))

32. 计算Loss_KC

33. end

34.end

35.return KC, LOSS_KC

算法2的步骤2的外部循环是遍历所有属性, 共计$|M|$次, 步骤5~25是将形式背景所有属性单点集作为初始删除属性集, 在定理3的箭头封闭基础上, 以while循环交替更新获取极小信息损失兼容子背景需删除的对象集G_del和属性集M_del, 在此过程中, 每次需添加至少一个元素到G_del或M_del中, 所以时间复杂度最多为

$O(|G|+|M|)$,

而在每次的while循环中, 还需遍历DA和DO中的所有元素, 时间复杂度为

$O(|DA|$$+|DO|)$, ,

因此, 算法2在最坏的情况下, 总时间复杂度为

$\begin{array}{l} O\left(\left(|G||M| k^{2}\right)+\right. \\ \quad O(|M|(|G|+|M|)(|D A|+|D O|)) \end{array}$

算法2的步骤26~33, 是外层循环的两种终止条件.

1)第1种情况.当G_del=G或M_del=M时, 说明由{m}生成兼容子背景的过程中, 将删掉原形式背景中所有的二元关系, 认为这种兼容子背景是无意义的, 此时进入下一次循环.

2)第2种情况.当G_del或M_del停止变化时, 说明达到收敛, 由此可输出由{m}生成的极小信息损失的兼容子背景.

算法2适合形式背景K=(G, M, I)的$|G|$和$|M|$相差不大或者$|M|$≪$|G|$的情况.当$|G|$≪$|M|$时, 为了减少计算成本, 只需以相同的方法遍历所有对象单点集, 即可获得K=(G, M, I)形式背景极小信息损失的兼容子背景.

最后给出概念格上同余关系的获取算法.

算法3 概念格上同余关系的获取算法

输入 K=(G, M, I)的所有概念C

输出 同余关系θ

1. 调用算法2获取KC=(H, N, I∩ H× N)

2. Cla← Ø , θ ← Ø

3. for each (X, B)∈ C do:

4. S=B∩ N

5. k← Sort(List(S))

6. if k∉Cla then:

7. Cla[k]← Ø

8. end

9. Cla[k]← Cla[k]∪ {(X, B)}

10. θ ← θ ∪ Cla[k]

11. end

12. return θ

算法3是根据定理10实现由兼容子背景获取格上的同余关系.步骤4进行集合交集, 已知B⊆N, 实际上只需遍历B中的元素即可确认交集, 于是时间复杂度为$O(|B|)$.步骤5是对集合进行排序, 时间复杂度为

$O\left(|B| \log _{2}|B|\right), $

步骤6~10是进行哈希表查找和插入以及集合合并操作.因此, 在最坏的情况下, 算法3总时间复杂度为

$O\left(|C||N| \log _{2}|N|\right) $ .

下面以例5说明本文给出的通过获取形式背景极小信息损失的兼容子背景确定概念格上同余关系的方法的可行性.

例5 (续例2) 以表3所示的形式背景K₂=(G₂, M₂, I₂)为例, 通过获取形式背景极小信息损失的兼容子背景确定概念格上同余关系.详细步骤如下.

1)形式背景预处理.由于K₂是正则且净化的, 无需进行预处理.

2)由定理9知, 由K₂的所有属性单点集生成的兼容子背景是极小信息损失的兼容子背景, 于是, 删除{a}, 则

$\begin{array}{l} M_{-} d e l_{0}=\{a\}, G \_d e l_{1}=\{2\}, \\ M_{-} d e l_{1}=\{a, d\}, G \_d e l_{2}=\{2\} . \end{array}$

此时

$G \_d e l_{1}=G \_d e l_{2}$,

于是, 由{a}生成兼容子背景:

$\begin{aligned} K C_{\{a\}}= & (\{1, 3, 4, 5\}, \{b, c, e, f\}, \\ & I \cap\{1, 3, 4, 5\} \times\{b, c, e, f\}) . \end{aligned}$

其它极小信息损失的兼容子背景可类似计算.

3)形式背景K₂的概念格L(K₂)如图3所示, 可得KC_{a}诱导的概念格上的同余关系如下:

$\begin{aligned} \theta_{\{a\}}= & \left\{\left(C_{1}, C_{1}\right), \left(C_{2}, C_{2}\right), \left(C_{3}, C_{3}\right), \left(C_{2}, C_{3}\right), \right. \\ & \left(C_{3}, C_{2}\right), \left(C_{4}, C_{4}\right), \left(C_{5}, C_{5}\right), \left(C_{6}, C_{6}\right), \\ & \left(C_{5}, C_{6}\right), \left(C_{6}, C_{5}\right), \left(C_{7}, C_{7}\right), \left(C_{9}, C_{9}\right), \\ & \left(C_{7}, C_{9}\right), \left(C_{9}, C_{7}\right), \left(C_{8}, C_{8}\right), \left(C_{10}, C_{10}\right), \\ & \left.\left(C_{8}, C_{10}\right), \left(C_{10}, C_{8}\right), \left(C_{11}, C_{11}\right), \left(C_{12}, C_{12}\right)\right\} . \end{aligned}$

由其它极小信息损失的兼容子背景诱导的概念格上的同余关系可由类似计算获得.

由{a}生成的兼容子背景与由{d}生成的兼容子背景一致, 所以利用算法3得到的极小信息损失的兼容子背景共计有5个, 同时也可验证由K₂的所有对象单点集生成的兼容子背景与上述5个兼容子背景一致.

本文实验是在Intel(R) Core(TM) i5-8250U CPU, 12 GB内存的硬件环境下进行的, 使用Python实现通过获取极小信息损失兼容子背景确定概念格上同余关系的算法, 进而对概念格进行压缩.

为了验证算法的有效性, 从加州大学欧文分校Learning Repository数据库选取Ballons、Lenses、Zoo、Hayes-Roth 、Glass Identification(简称Glass)、Forest Fires(简称Forest)这6个公开数据集以及本文例1中形式背景K₁.

由于形式背景为二元数据集, 且本文要求的形式背景为正则且净化的, 因此需对这7个数据集进行预处理.首先对数据进行二值化, 对于无序多值分类属性, 将其至少分为3个互不相交的区间, 然后将原始属性值替换为其所在的区间值, 再以区间值作为新的属性, 从而形成新的二元形式背景.对于有序多值属性, 将每个属性值作为新的属性, 若原始属性值小于等于新属性, 替换为1, 否则替换为0.对于连续型属性, 首先获取5等分点, 然后将每个等分点作为新的属性, 若原始属性值小于等于新属性, 替换为1, 否则替换为0.然后获取新形式背景正则且净化的背景, 预处理之后的数据集详细信息如表5所示.

表5

Table 5

表5(Table 5)

表5 实验数据集统计信息 Table 5 Statistical information of experimental data 名称 样本数 属性数 预处理后 对象个数 预处理后 属性个数 形式 概念数 K1 8 9 8 8 19 Ballons 20 4 14 4 16 Lenses 24 4 24 6 33 Zoo 101 16 59 21 261 Hayes-Roth 160 5 79 13 226 Glass 214 9 106 35 29983 Forest 517 12 499 66 42502

表5 实验数据集统计信息 Table 5 Statistical information of experimental data

本文给出通过获取兼容子背景确定概念格上同余关系的方法, 其核心是以算法2获取形式背景的极小信息损失的兼容子背景.在文献[25]中, 使用箭头关系的传递闭包获取新形式背景, 并由其概念(G-H, N)得到原形式背景的所有兼容子背景(H, N, I∩ H× N).可以发现, 本文定义的极小信息损失的兼容子背景可由文献[25]中新形式背景的所有对象概念(g^{* *} , g^* )对应的(G-g^{* *} , g^* )得到, 即在文献[25]中, 极小信息损失的兼容子背景为

$\left(G-g^{* * }, g^{* }, I \cap\left(\left(G-g^{* * }\right) \times g^{* }\right)\right) \text {. }$

为了进一步验证算法2的性能, 将文献[25]中获取极小信息损失兼容子背景的算法与本文算法2在运行时间上进行对比, 结果如表6所示.在这7个数据集上, 算法2运行时间都短于文献[25]算法, 这是因为文献[25]算法需计算数据集箭头关系的传递闭包, 而算法2只需检查与当前元素相关的箭头关系, 无需预计算全局路径, 可减少冗余操作.这说明本文算法在获取原形式背景的极小信息损失的兼容子背景上具有有效性.

表6

Table 6

表6(Table 6)

表6 算法2与文献[25]算法的运行时间对比 Table 6 Runtime comparison between Algorithm 2 and algorithm in reference[25] ms 数据集 算法2 文献[25]算法 K1 1 1 Ballons 2 4 Lenses 3 8 Zoo 4 21.9 Hayes-Roth 2 36.6 Glass 11 58.5 Forest 222.5 957.2

表6 算法2与文献[25]算法的运行时间对比 Table 6 Runtime comparison between Algorithm 2 and algorithm in reference[25] ms

根据形式概念分析理论, 形式背景生成的形式概念个数通常呈超线性增长趋势, 其规模在多数实际场景下显著超越原始对象个数与属性个数, 所以由算法3获取格上同余关系时, 时间复杂度主要取决于形式概念个数, 本文选取上述7个形式背景的形式概念数量呈现跨越4个数量级的分布特征.同时, 随着实验数据的增大, 采用算法3产生的极小信息损失兼容子背景个数将增多, 为了量化评估概念格压缩效果, 引入计算同余类数量的3个指标:极大同余类数、平均同余类数和极小同余类数.由定理10知, 原概念格中某一同余关系对应的同余类数量等于该同余关系对应的兼容子背景的概念数.因此, 极大同余类数、极小同余类数分别表征所有极小信息损失兼容子背景诱导的概念格同余关系中同余类数量的极大值或极小值.平均同余类数是通过计算所有极小信息损失兼容子背景对应同余类数量的算术平均值获得.对上述7个形式背景的极小信息损失兼容子背景及其诱导的概念格上的同余关系计算结果取整, 具体结果如表7所示.

表7

Table 7

表7(Table 7)

表7 算法3实验结果 Table 7 Experimental results of Algorithm 3 数据集 概念数 极小信息损失 兼容子背景 个数 极小信息损失 兼容子背景平均 信息损失度 平均保留 对象数 平均保留 属性数 极大 同余类数 平均 同余类数 极小 同余类数 K1 19 2 0.3846 6 6 17 13 10 Ballons 16 4 0.6786 7 3 8 8 8 Lenses 33 3 0.6000 12 5 17 17 17 Zoo 261 1 0.0298 59 20 261 261 261 Hayes-Roth 226 13 0.6798 31 8 226 87 9 Glass 29983 35 0.9978 2 2 8 7 4 Forest 42502 66 0.9541 25 5 42502 1939 4

表7 算法3实验结果 Table 7 Experimental results of Algorithm 3

在形式背景K₁中, 基于属性c、h构建两个极小信息损失的兼容子背景, 其诱导的概念格上的同余关系分别包含10个同余类和17个同余类.这表明在保持原形式背景概念格代数结构特征, 且信息损失极小化的前提下, 可使原19个概念被分别压缩映射至10个概念和17个概念.这种通过同余关系实现的粒度约简, 可有效提升概念格的表示效率.除了Zoo数据集以外, 在其余数据集上的实验结果也同样表明以同余关系对概念格进行压缩的有效性.

值得注意的是, 在Zoo、Hayes-Roth、Forest数据集上, 会出现原概念格与极小信息损失的兼容子背景概念格之间是同构的情况.通过分析可发现, 当数据存在如下两种特征时, 原概念格与极小信息损失的兼容子背景概念格之间是同构的.

1)在形式背景(G, M, I)中, 若∃a∈ M, 使∀ x∈ G, 都不满足x↗a, 说明以a为初始删除属性, 不会引发形式背景中的任意一个对象被删减.

2)根据箭头关系的定义可知, 若至少存在两个属性b∈ M, c∈ M, 使

$b^{* } \cap c^{* }=a^{* }$

且

$b^{* } \nsubseteq c^{* }, c^{* } \nsubseteq b^{* }, $

则∀ x∈ G, 都不满足x↗a, 于是删除a也不会引发形式背景中的任意一个对象被删减.

在上述两种数据特征下, 删除属性a将不会导致概念合并, 即子背景(G, M-{a}, I)为(G, M, I)的兼容子背景, 且其概念格与原形式背景概念格同构.

概念格在知识发现、推荐系统、认知计算及大数据分析的应用中, 常面临规模爆炸的问题, 亟需在保持结构完整性和核心信息的前提下进行压缩.不同于传统的通过相似性或启发式规则等可能破坏格结构或损失核心信息的约简方法, 本文聚焦于基于同余关系的构建商格的压缩本质, 在严格保证运算封闭性与层次关系的基础上, 创新性地结合四边形封闭, 借助箭头封闭关系快速获取极小信息损失的兼容子背景, 进而诱导同余关系实现概念格压缩.该方法的核心优势在于:在对概念格进行压缩的过程中, 严格遵循原概念格中的序关系与运算封闭性, 确保压缩结果仍保持原概念格核心结构信息.该方法可结合应用场景细化信息度量, 今后在社区发现、面向动态数据的更新等处理大规模复杂数据方面具有一定潜力.

在实验中发现, 部分形式背景的概念格与其极小信息损失兼容子背景的概念格同构, 后续将研究如何基于原格结构特征压缩此类概念格.同时, 随着数据量的爆炸式增长, 数据压缩的重要性日益凸显, 如何使用概念格上的同余关系解决实际问题, 也将成为今后进一步展开的工作.

本文责任编委 张燕平

Recommended by Associate Editor ZHANG Yanping